Решение варианта СтатГрад 29.11 ОГЭ 2023 Математика
Решение и ответы заданий варианта МА2290201 СтатГрад 29 ноября ОГЭ 2023 по математике. ГДЗ профиль для 9 класса. Решебник для 9 класса. Ответы с решением. Полный разбор всех заданий.
Все материалы получены из открытых источников и публикуются после окончания тренировочного экзамена в ознакомительных целях.
ЧАСТЬ 1
Задание 1-5.
На плане изображён дачный участок по адресу: п. Сосновка, ул. Зелёная, д. 19 (сторона каждой клетки на плане равна 2 м). Участок имеет прямоугольную форму. Выезд и въезд осуществляются через единственные ворота.
При входе на участок слева от ворот находится гараж. Справа от ворот находится сарай площадью 24 кв. м, а чуть подальше – жилой дом.
Напротив жилого дома расположены яблоневые посадки. Также на участке есть баня, к которой ведёт дорожка, выложенная плиткой, и огород с теплицей внутри (огород отмечен на плане цифрой 6). {6}}.
Задание 9.
Найдите корень уравнения \frac{11}{x–9}=-10.
Задание 10.
Вероятность того, что новая шариковая ручка пишет плохо (или не пишет), равна 0,26. Покупатель в магазине берёт одну шариковую ручку. Найдите вероятность того, что эта ручка пишет хорошо.
Задание 11.
На рисунках изображены графики функций вида y = ax2+ bx + c. Установите соответствие между графиками функций и знаками коэффициентов a и c.
ГРАФИКИ
КОЭФФИЦИЕНТЫ
1) а > 0, c > 0
2) а > 0, c < 0
3) а < 0, c > 0
В таблице под каждой буквой укажите соответствующий номер.
Задание 12.
Площадь четырёхугольника можно вычислить по формуле S=\frac{d_{1}d_{2}sin\alpha}{2}, где d1 и d2 – длины диагоналей четырёхугольника, α – угол между диагоналями. Пользуясь этой формулой, найдите длину диагонали d2, если d1 = 17, sinα = \frac{1}{3}, S = 51.
Задание 13.
Укажите неравенство, решение которого изображено на рисунке.
1) x2 − 25 > 0
2) x2 − 25 < 0
3) x2 + 25 < 0
4) x2 + 25 > 0
Задание 14.
В амфитеатре 15 рядов, причём в каждом следующем ряду на одно и то же число мест больше, чем в предыдущем. В третьем ряду 26 мест, а в седьмом ряду 38 мест. Сколько мест в последнем ряду амфитеатра?
Задание 15.
В прямоугольном треугольнике катет и гипотенуза равны 40 и 41 соответственно. Найдите периметр этого треугольника.
Задание 16.
Треугольник ABC вписан в окружность с центром в точке O. Точки O и C лежат в одной полуплоскости относительно прямой AB. Найдите угол ACB, если угол AOB равен 153°. Ответ дайте в градусах.
Задание 17.
Найдите острый угол параллелограмма ABCD, если биссектриса угла A образует со стороной BC угол, равный 15°. Ответ дайте в градусах.
Задание 18.
На клетчатой бумаге с размером клетки 1×1 отмечены три точки: A, B и C. Найдите расстояние между точкой A и серединой отрезка BC.
Задание 19.
Какое из следующих утверждений верно?
1) Смежные углы всегда равны.
2) Каждая из биссектрис равнобедренного треугольника является его высотой.
3) Существует прямоугольник, диагонали которого взаимно перпендикулярны.
В ответе запишите номер выбранного утверждения.
ЧАСТЬ 2
Задание 20.
Решите уравнение x3 + 5x2 = 4x + 20.
Задание 21.
Баржа прошла по течению реки 80 км и, развернувшись, прошла ещё 60 км, затратив на весь путь 10 часов.
Найдите собственную скорость (скорость в неподвижной воде) баржи, если скорость течения реки равна 5 км/ч.
Задание 22.
Постройте график функции
Определите, при каких значениях m прямая y = m имеет с графиком ровно две общие точки.
Задание 23.
Найдите боковую сторону AB трапеции ABCD, если углы ABC и BCD равны соответственно 45° и 120°, а CD = 34.
Задание 24.
В трапеции ABCD с основаниями AD и BC диагонали пересекаются в точке O. Докажите, что площади треугольников AOB и COD равны.
Задание 25.
В треугольнике ABC биссектриса BE и медиана AD перпендикулярны и имеют одинаковую длину, равную 20. Найдите стороны треугольника ABC.
Источник варианта: СтатГрад/statgrad.org.
Есть три секунды времени? Для меня важно твоё мнение!
Насколько понятно решение?
Средняя оценка: 5 / 5.
Количество оценок: 1
Оценок пока нет. Поставь оценку первым.
Расскажи, что не так? Я исправлю в ближайшее время!
В отзыве оставь любой контакт для связи, если хочешь, что бы я тебе ответил.
- Запись опубликована:30.11.2022
- Рубрика записи+ Типовые экзаменационные варианты ОГЭ
- Автор записи:Andrei Maniakin
Докажите что для любых а справедливо равенство sin п а sin a
Обоснуйте ,что для всех а правосудно равенство sin(п-а)=sin a
Докажем, что для всех а справедливо равенство sin (п — а) = sin a.
Применим формулу сложения либо формулы приведения тригонометрии. Получаем:
sin (pi) * cos a — cos (pi) * sin a = sin a;
Используем тригонометрические углы, где sin pi = 0 и cos (pi) = -1. Тогда получаем:
0 * cos a — (-1) * sin a;
Так как, перед скобками стоит символ минус, то он меняет знаки чисел снутри скобок при раскрытии на обратный символ.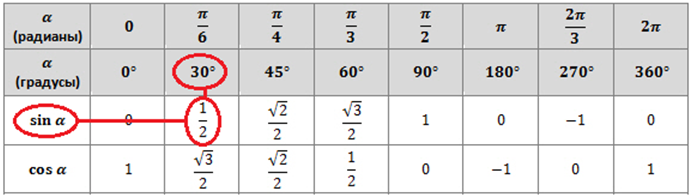
Докажите , что для любых а справедливо равенство sin(п — а) = sin a?
Докажите , что для любых а справедливо равенство sin(п — а) = sin a.
ПО ФОРМУЛАМ ПРИВЕДЕНИЯ
найдем угол П — а : П находится у нас на точке х = — 1 в единичной окружности, вычитаем угол а, который у нас по определению всегда острый, то есть наш угол (п — а) находится во второй четверти, а мы знаем, что синус в этой четверти положительный (если хочешь, могу объяснить, почему синус положительный именно здесь) значит синус П — а равен синусу П.
Докажите, что для любых a справедливо равенство sin(pi — a) = sina?
Докажите, что для любых a справедливо равенство sin(pi — a) = sina.
Докажите справедливость равенства : а) (sin a + sin3a) / (cos a + cos 3a) = tg2a ?
Докажите справедливость равенства : а) (sin a + sin3a) / (cos a + cos 3a) = tg2a ;
Докажите что для любых альфа справедливо равенство?
Докажите что для любых альфа справедливо равенство.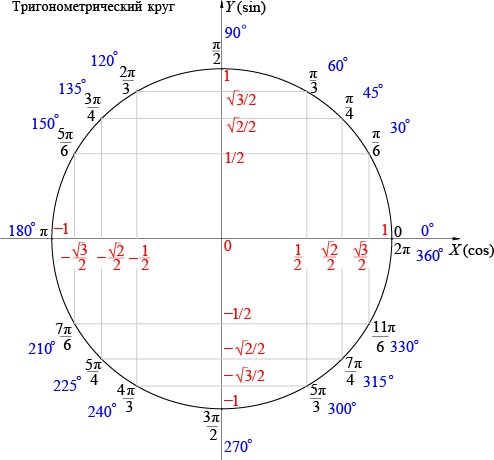
Докажите справедливость равенства : cos(п / 2 + альфа) = — sin альфа помогите пжл?
Докажите справедливость равенства : cos(п / 2 + альфа) = — sin альфа помогите пжл.
Д — ть что для любых альфа справедливо равенство sin (п — альфа) = sin альфа?
Д — ть что для любых альфа справедливо равенство sin (п — альфа) = sin альфа.
Докажите, что для любого альфа справедливы равенства sin(p — a) = sin a p — число Пи a — альфа?
Докажите, что для любого альфа справедливы равенства sin(p — a) = sin a p — число Пи a — альфа.
Докажите справедливость равенства?
Докажите справедливость равенства.
Докажите справедливость равенства : sin 3п / 5 — sin 2п / 5 = 0?
Докажите справедливость равенства : sin 3п / 5 — sin 2п / 5 = 0.
Верно ли, что для любого х справедливо равенство sin( — x) = — sinx ?
Верно ли, что для любого х справедливо равенство sin( — x) = — sinx ?
Докажите справедливость равенства?
Докажите справедливость равенства.
Вы открыли страницу вопроса Докажите , что для любых а справедливо равенство sin(п — а) = sin a?. Он относится к категории Алгебра. Уровень сложности вопроса – для учащихся 10 — 11 классов. Удобный и простой интерфейс сайта поможет найти максимально исчерпывающие ответы по интересующей теме. Чтобы получить наиболее развернутый ответ, можно просмотреть другие, похожие вопросы в категории Алгебра, воспользовавшись поисковой системой, или ознакомиться с ответами других пользователей. Для расширения границ поиска создайте новый вопрос, используя ключевые слова. Введите его в строку, нажав кнопку вверху.
Докажите что для любых а справедливо равенство sin п а sin a
Нажимая на кнопку «Задать вопрос», я даю согласие на обработку персональных данных
- 05 March 2013 Українська мова
- Автор: Ваня380
Докажите, что для любого угла А справедливо равенство sin (П-А) = sinA.
Заранее большое спасибо!
- 05 March 2013
- Ответ оставил: Milli205
Докажите, что для любого угла А справедливо равенство sin (П-А) = sinA.
Заранее большое спасибо!
- НЕ НАШЛИ ОТВЕТ?
Нажимая на кнопку «Ответить на вопрос», я даю согласие на обработку персональных данных
Последние опубликованные вопросы
- Алгебра
- Английский язык
- Беларуская мова
- Беларуская мова
- Биология
- География
- Геометрия
- Другие предметы
- Другое
- Информатика
- История
- Қазақ тiлi
- Литература
- Математика
- Обществознание
- Право
- Русский язык
- Українська література
- Українська мова
- Физика
- Химия
- Экономика
спросил
Изменено 1 месяц назад
Просмотрено 4к раз
$\begingroup$
Можно доказать, что $\sin n$ расходится, используя плотность натуральных чисел по модулю $2\pi$.
2)$ выглядит гораздо более деликатным, так как это подпоследовательность первого. Я твердо верю, что эта последовательность расходится, но не могу этого доказать. 9a)$ расходится при $a>0$?
- пределы
- тригонометрия
- схождение-расхождение
- равнораспределение
$\endgroup$
$\begingroup$
Обобщить Ответ Михаила :
Теорема. Для любого непостоянного многочлена $f(X)\in\Bbb Q[X]$ последовательность $\sin f(n)$ имеет бесконечно много предельных точек.
Доказательство. (По индукции).
Пусть $f(X)\in\Bbb Q[X]$ степени $d$.
Если $d=1$, то хорошо известно, что $\{\,f(n)\bmod 2\pi\mid n\in\Bbb N\,\}$ плотно в $[0,2 \pi]$, потому что $\pi$ иррационально. Тогда $\{\,\sin f(n)\mid n\in\Bbb N\,\}$ плотно в $[-1,1]$.
4$ предельных точек, что противоречит предположению индукции. $\квадрат$ 9\альфа$.
$\endgroup$
Зарегистрируйтесь или войдите в систему
Зарегистрируйтесь с помощью GoogleЗарегистрироваться через Facebook
Зарегистрируйтесь, используя электронную почту и пароль
Опубликовать как гость
Электронная почта
Требуется, но никогда не отображается
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie
.