вывод формул, примеры. Формулы суммы и разности синусов и косинусов
Данный электронный ресурс является отличным материалом для проведения интерактивного обучения в современных школах. Он составлен грамотно, обладает четкой структурой и соответствует школьному плану. Благодаря подробным объяснениям, тема, которая представлена в видеоуроке станет понятна как можно большему количеству учеников в классе. Учителя должны помнить, что не все ученики имеют одинаковую степень восприятия, быстроты понимания, базу. Справиться с трудностями и догнать своих сверстников, исправить успеваемость, помогут подобные материалы. С помощью них в домашней спокойной обстановке, самостоятельно либо вместе с репетитором, ученик может разобраться в той или иной теме, изучить теорию и просмотреть примеры практического применения той или иной формулы и т.д.
Данный видеоурок посвящен теме «Синус и косинус разности аргументов». Подразумевается, что ученики уже изучили основы тригонометрии, ознакомлены с основными функциями и их свойствами, формулами привидения и таблицами тригонометрических значений.
Также, до того, как перейти к изучению данной темы, необходимо иметь понятие о синусе и косинусе суммы аргументов, знать две основные формулы и уметь ими пользоваться.
Вначале видеоурока диктор напоминает школьникам эти две формулы. Далее демонстрируется первая формула — синус разности аргументов. Помимо того, как выводится сама формула, показывается каким образом она получается от другой. Таким образом, школьнику не придется зазубривать новую формулу без понимания, что является частой ошибкой. Это очень важно для учеников в этом классе. Нужно всегда помнить, что перед знаком минуса всего можно добавить знак +, а минуса на знак плюс в итоге превратится в минус. С помощью такого нехитрого шага, можно воспользоваться формулой синуса суммы и получить формулу синуса разности аргументов.
Аналогичным образом выводится формула косинуса разности из формулы косинуса суммы аргументов.
Диктор пошагово все объясняет, а в результате выводится общая формула косинуса суммы и разности аргументов и синуса, аналогично.
Первый пример из практической части данного видеоурока предлагает найти косинус Пи/12. Предлагается представить данное значение в виде некоторой разности, при котором уменьшаемое и вычитаемое будут являться табличными значениями. Далее применятся формула косинуса разности аргументов. Заменив выражение, можно подставить полученные значения и получить ответ. Диктор зачитывает ответ, который выводится в конце примера.
Второй пример представляет собой уравнение. И в правой, и в левой сторонах мы видим косинусы разностей аргументов. Диктор напоминает формулы приведений, которые используются для замены и упрощения этих выражения. Эти формулы записываются с правой стороны, чтобы школьники могли понять, откуда появляются те или иные изменения.
Еще один пример, третий, представляет собой некоторую дробь, где и в числителе и в знаменателе имеем тригонометрические выражения, а именно, разности произведений.
Здесь также при решении используются формулы приведений. Таким образом, школьники могут убедиться, что пропустив одну тему в тригонометрии, понять остальные будет все сложнее.
И, наконец, четвертый пример. Это также уравнение, при решении которых необходимо использовать новые изученные и старые формулы.
Примеры, которые приводятся в видеоуроке, можно рассмотреть более подробно и попробовать решить самостоятельно. Их можно задать в качестве домашнего задания школьникам.
ТЕКСТОВАЯ РАСШИФРОВКА:
Тема занятия «Синус и косинус разности аргументов».
На предыдущем курсе мы познакомились с двумя тригонометрическими формулами синус и косинус суммы аргументов.
sin(x + y) = sin x cos y + cos x sin y,
cos (x + y) = cos x cos y — sin x sin y.
синус суммы двух углов равен сумме между произведением синуса первого угла и косинусом второго угла и произведением косинуса первого угла и синуса второго угла;
косинус суммы двух углов равен разности между произведением косинусов этих углов и произведением суммы этих углов.
При помощи этих формул выведем формулы Синус и косинус разности аргументов.
Синус разности аргументов sin(x- y)
Две формулы (синус суммы и синус разности) можно записать в виде:
sin(x y) = sin x cos y cos x sin y.
Аналогично выведем формулу косинуса разности:
Косинус разности аргументов перепишем в виде суммы и применим уже известную формулу косинуса суммы: cos (x + y) = cosxcosy — sinxsiny.
только для аргументов х и -y. Подставив данные аргументы в формулу, получим cosxcos(- y) — sinxsin(- y).
sin(- y)= — siny). и получим окончательное выражение cosxcosy + sinxsiny.
cos (x — y) = cos (x +(- y)) =cos xcos(- y) — sin x sin(- y)= cosx cos y + sin xsin y.
Значит, cos (x — y) = cosxcos y + sin xsin y.
косинус разности двух углов равен сумме между произведением косинусов этих углов и произведением синусов этих углов.
Объединяя две формулы (косинус суммы и косинус разности) в одну, запишем
cos (x y) = cosxcos y sin xsin y.
Запомним, что формулы на практике можно применять как слева направо, так и наоборот.
Рассмотрим примеры.
ПРИМЕР 1. Вычислить cos (косинус пи, деленное на двенадцать).
Решение. Запишем пи, деленное на двенадцать, как разность пи на три и пи, деленное на четыре: = — .
Подставим значения в формулу косинуса разности: cos (x — y) = cosxcosy + sinxsiny, таким образом cos = cos (-) = cos cos + sin sin
Нам известно, что cos = , cos = sin= , sin = . Показать таблицу значений.
Заменим значение синуса и косинуса числовыми значениями и получим ∙ + ∙ при умножении дробь на дробь числители и знаменатели перемножаем, получаем
cos = cos (-) = cos cos + sin sin = ∙ + ∙ = = =.
Ответ: cos =.
ПРИМЕР 2. Решить уравнение cos(2π — 5х) = cos(- 5х) (косинус два пи минус пять икс равно косинусу от пи на два минус пять икс).
Решение. К левой и правой частям уравнения применим формулы приведения cos(2π — cos (косинус два пи минус альфа равен косинусу альфа) и cos(- = sin (косинус пи на два минус альфа равно синусу альфа), получим cos 5х = sin 5х, приведем его к виду однородного уравнения первой степени и получим cos 5х — sin 5х = 0. Это однородное уравнение первой степени. Разделим почленно обе части уравнения на cos 5х. Имеем:
cos 5х: cos 5х — sin 5х: cos 5х = 0, т.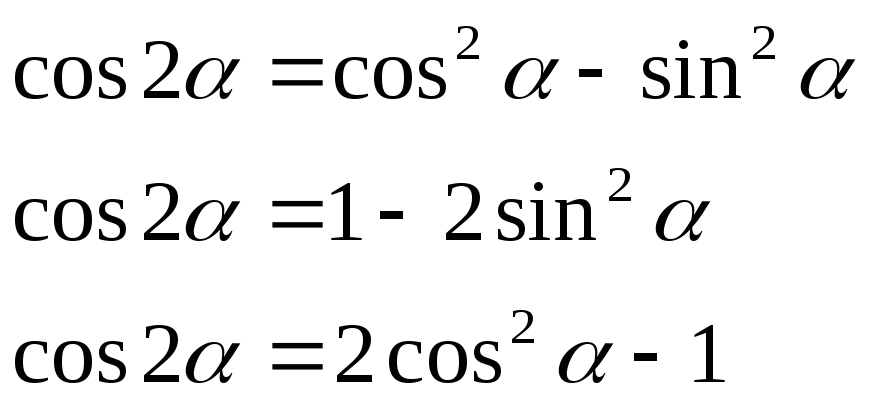
Так как мы уже знаем, что уравнение tgt = а имеет решение t = arctgа + πn, а так как у нас t=5х, а =1, то получим
5x = arctg 1 + πn,
а значение arctg 1, тогда tg 1= Показать таблицу
подставим значение в уравнение и решим его:
Ответ: х = + .
ПРИМЕР 3. Найти значение дроби. (в числителе разность произведения косинусов семидесяти пяти градусов и шестидесяти пяти градусов и произведения синусов семидесяти пяти градусов и шестидесяти пяти градусов, а в знаменателе разность произведения синуса восьмидесяти пяти градусов и косинуса тридцати пяти градусов и произведения косинуса восьмидесяти пяти градусов и синуса тридцати пяти градусов).
Решение. В числителе данной дроби разность можно «свернуть» в косинус суммы аргументов 75° и 65°, а в знаменателе — разность «свернем» в синус разности аргументов 85° и 35°. Получим
Ответ: — 1.
ПРИМЕР 4. Решить уравнение: cos(-х) + sin(-х) = 1(косинус разности пи на четыре и икс плюс синус разности пи на четыре и икс равно одному).
Решение. Применим формулы косинус разности и синус разности.
Показать общую формулу косинуса разности
Тогда cos (-х) = cos cos х + sinsinх
Показать общую формулу синуса разности
а sin (-х)= sin cosх — cos sinх
Подставим данные выражения в уравнение cos(-х) + sin(-х) = 1 и получим:
cos cos х + sinsin х + sin cos х — cos sin х = 1,
Так как cos= и sin= Показать таблицу значение синуса и косинуса
Получим ∙ cos х + ∙ sinх + ∙ cos х — ∙ sinх = 1,
второе и четвертое слагаемые противоположны, поэтому взаимно уничтожаются, остается:
∙ cos + ∙ cos = 1,
Решим данное уравнение и получим, что
2∙ ∙ cos x= 1,
Так ка мы уже знаем, что уравнение cos = а имеет решение t = arcos a + 2π k , а так как у нас t=x, а =, то получим
х = arccos + 2πn,
а так как значение arccos, тогда cos =
Формулы суммы и разности синусов и косинусов для двух углов α и β позволяют перейти от суммы указанных углов к произведению углов α + β 2 и α — β 2 . Сразу отметим, что не стоит путать формулы суммы и разности синусов и косинусов с формулами синусов и косинусов суммы и разности. Ниже мы перечислим эти формулы, приведем их вывод и покажем примеры применения для конкретных задач.
Сразу отметим, что не стоит путать формулы суммы и разности синусов и косинусов с формулами синусов и косинусов суммы и разности. Ниже мы перечислим эти формулы, приведем их вывод и покажем примеры применения для конкретных задач.
Yandex.RTB R-A-339285-1
Формулы суммы и разности синусов и косинусов
Запишем, как выглядят формулы суммы и разности для синусов и для косинусов
Формулы суммы и разности для синусов
sin α + sin β = 2 sin α + β 2 cos α — β 2 sin α — sin β = 2 sin α — β 2 cos α + β 2
Формулы суммы и разности для косинусов
cos α + cos β = 2 cos α + β 2 cos α — β 2 cos α — cos β = — 2 sin α + β 2 cos α — β 2 , cos α — cos β = 2 sin α + β 2 · β — α 2
Данные формулы справедливы для любых углов α и β . Углы α + β 2 и α — β 2 называются соответственно полусуммой и полуразностью углов альфа и бета. Дадим формулировку для каждой формулы.
Определения формул сумм и разности синусов и косинусов
Сумма синусов двух углов равна удвоенному произведению синуса полусуммы этих углов на косинус полуразности.
Разность синусов двух углов равна удвоенному произведению синуса полуразности этих углов на косинус полусуммы.
Сумма косинусов двух углов равна удвоенному произведению косинуса полусуммы и косинуса полуразности этих углов.
Разность косинусов двух углов
Вывод формул суммы и разности синусов и косинусов
Для вывода формул суммы и разности синуса и косинуса двух углов используются формулы сложения. Приведем их ниже
sin (α + β) = sin α · cos β + cos α · sin β sin (α — β) = sin α · cos β — cos α · sin β cos (α + β) = cos α · cos β — sin α · sin β cos (α — β) = cos α · cos β + sin α · sin β
Также представим сами углы в виде суммы полусумм и полуразностей.
α = α + β 2 + α — β 2 = α 2 + β 2 + α 2 — β 2 β = α + β 2 — α — β 2 = α 2 + β 2 — α 2 + β 2
Переходим непосредственно к выводу формул суммы и разности для sin и cos.
Вывод формулы суммы синусов
В сумме sin α + sin β заменим α и β на выражения для этих углов, приведенные выше. Получим
sin α + sin β = sin α + β 2 + α — β 2 + sin α + β 2 — α — β 2
Теперь к первому выражению применяем формулу сложения, а ко второму — формулу синуса разностей углов (см. формулы выше)
sin α + β 2 + α — β 2 = sin α + β 2 cos α — β 2 + cos α + β 2 sin α — β 2 sin α + β 2 — α — β 2 = sin α + β 2 cos α — β 2 — cos α + β 2 sin α — β 2 sin α + β 2 + α — β 2 + sin α + β 2 — α — β 2 = sin α + β 2 cos α — β 2 + cos α + β 2 sin α — β 2 + sin α + β 2 cos α — β 2 — cos α + β 2 sin α — β 2 Раскроем скобки, приведем подобные слагаемые и получим искомую формулу
sin α + β 2 cos α — β 2 + cos α + β 2 sin α — β 2 + sin α + β 2 cos α — β 2 — cos α + β 2 sin α — β 2 = = 2 sin α + β 2 cos α — β 2
Действия по выводу остальных формул аналогичны.
Вывод формулы разности синусов
sin α — sin β = sin α + β 2 + α — β 2 — sin α + β 2 — α — β 2 sin α + β 2 + α — β 2 — sin α + β 2 — α — β 2 = sin α + β 2 cos α — β 2 + cos α + β 2 sin α — β 2 — sin α + β 2 cos α — β 2 — cos α + β 2 sin α — β 2 = = 2 sin α — β 2 cos α + β 2
Вывод формулы суммы косинусов
cos α + cos β = cos α + β 2 + α — β 2 + cos α + β 2 — α — β 2 cos α + β 2 + α — β 2 + cos α + β 2 — α — β 2 = cos α + β 2 cos α — β 2 — sin α + β 2 sin α — β 2 + cos α + β 2 cos α — β 2 + sin α + β 2 sin α — β 2 = = 2 cos α + β 2 cos α — β 2
Вывод формулы разности косинусов
cos α — cos β = cos α + β 2 + α — β 2 — cos α + β 2 — α — β 2 cos α + β 2 + α — β 2 — cos α + β 2 — α — β 2 = cos α + β 2 cos α — β 2 — sin α + β 2 sin α — β 2 — cos α + β 2 cos α — β 2 + sin α + β 2 sin α — β 2 = = — 2 sin α + β 2 sin α — β 2
Примеры решения практических задач
Для начала, сделаем проверку одной из формул, подставив в нее конкретные значения углов.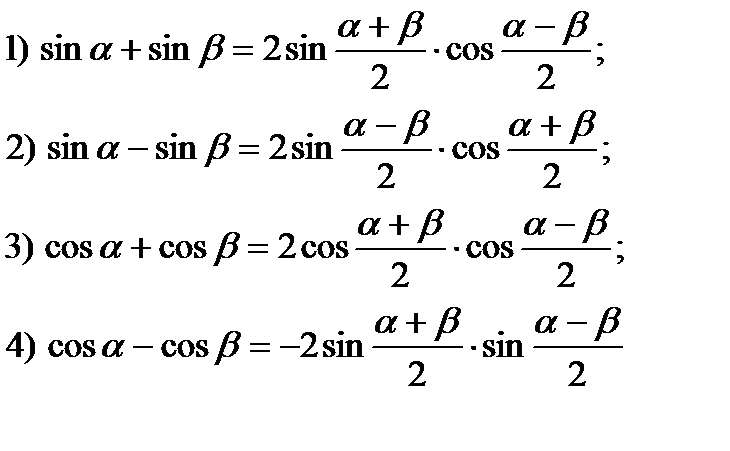 Пусть α = π 2 , β = π 6 . Вычислим значение суммы синусов этих углов. Сначала воспользуемся таблицей основных значений тригонометрических функций, а затем применим формулу для суммы синусов.
Пусть α = π 2 , β = π 6 . Вычислим значение суммы синусов этих углов. Сначала воспользуемся таблицей основных значений тригонометрических функций, а затем применим формулу для суммы синусов.
Пример 1. Проверка формулы суммы синусов двух углов
α = π 2 , β = π 6 sin π 2 + sin π 6 = 1 + 1 2 = 3 2 sin π 2 + sin π 6 = 2 sin π 2 + π 6 2 cos π 2 — π 6 2 = 2 sin π 3 cos π 6 = 2 · 3 2 · 3 2 = 3 2
Рассмотрим теперь случай, когда значения углов отличаются от основных значений, представленных в таблице. Пусть α = 165 ° , β = 75 ° . Вычислим значение разности синусов этих углов.
Пример 2. Применение формулы разности синусов
α = 165 ° , β = 75 ° sin α — sin β = sin 165 ° — sin 75 ° sin 165 — sin 75 = 2 · sin 165 ° — sin 75 ° 2 cos 165 ° + sin 75 ° 2 = = 2 · sin 45 ° · cos 120 ° = 2 · 2 2 · — 1 2 = 2 2
С помощью формул суммы и разности синусов и косинусов можно перейти от суммы или разности к произведению тригонометрических функций. Часто эти формулы называют формулами перехода от суммы к произведению. Формулы суммы и разности синусов и косинусов широко используются при решении тригонометрических уравнений и при преобразовании тригонометрических выражений.
Формулы суммы и разности синусов и косинусов широко используются при решении тригонометрических уравнений и при преобразовании тригонометрических выражений.
Если вы заметили ошибку в тексте, пожалуйста, выделите её и нажмите Ctrl+Enter
Этапы урока | Деятельность учителя | Деятельность обучающихся |
1. Организация начала урока, 1 мин | Здравствуйте, присаживайтесь. Какой раздел мы изучаем? | Занимают свои места. Отвечают: тригонометрические формулы и функции. |
2. Актуализация субъективного опыта. Постановка проблемы. 8 мин | Прежде чем приступить к изучению новой темы, давайте повторим ранее изученный материал. Организует актуализация опорных знаний.
Замените тригонометрической функцией угла α:
Вычислите: Вычислите: 1. 2. 3. 4. 5. 6. 7. | Отвечают на вопросы.
|
| Почему мы не можем вычислить задания 6,7? Какие формулы нужно знать, чтобы выполнить эти задания? Давайте сформулируем тему и цель нашего урока. Запишите тему в тетрадь. | Это не табличные углы 105=60+45 15=60-45 Чтобы вычислить sin 1050, надо применить формулу синус суммы, а sin 150 формулу синус разности. Формулируют тему «Синус суммы и синус разности двух углов» и цель: вывести формулы и научиться применять их к преобразованию выражений. Записывают тему в тетрадь. |
| Вспомним правила парной работы. Поработаем в парах. Вывести формулы вам поможет карточка. Нужно заполнить пропуски, используя формулы для доп.углов и косинуса суммы и разности двух углов. Контролирует работу, помогает, если возникают затруднения. Проверьте вывод формул на стр. 264 в учебнике Можем ли мы теперь вычислить sin 1050 ,sin 150? Сделайте это в своих тетрадях. | Проговаривают правила: работать тихо, работать вместе, помогать друг другу, уважать мнение друг друга. Работают в парах с карточкой 4 минуты, записывают формулы в тетрадь. Одна пара выходит и записывает полученные формулы на доске. Остальной класс проверяет. Да Записывают: |
| Сложите руки перед лицом, двигайте их влево/вправо, вверх/вниз, по кругу. Следите глазами за своими руками | Выполняют упражнения для глаз |
| Научимся применять формулы синуса суммы и разности двух углов, выполняя упражнения № 9.28 (в,г), 9.27 (а,б) из учебника –самостоятельно, №9.29 а – 1 учащийся решает на доске, остальные – в тетради. Составим алгоритм для решения № 9.31 а. Контролирует работу пар, помогает, если возникают вопросы. | Выполняют № 9.28 (в,г), 9.27 (а,б) из учебника –самостоятельно, №9. Устно составляют алгоритм: 1. Вычислить недостающие значения синуса и косинуса, используя основное тригонометрическое тождество; 2. Применить формулу синуса суммы или синуса разности двух углов. Решают пример 9.31 а по алгоритму в парах. Проверяют решение слайд 5 |
| Организует разноуровневую самостоятельную работу. | Выбирают уровень. Выполняют с/р, сдают тетради. |
| Выучить формулы, выполнить № 9.26 г-е,9.27 в,г, 9.29 б, 9.31б | Записывают домашнее задание |
| Организует рефлексию. | Отвечают на вопросы анкеты, сдают анкету. |
| Подведем итог урока. Выставляет оценки за урок. | Отвечают на вопрос. |
тригонометрия — Доказательство идентичности синуса суммы для всех углов
спросил
Изменено 4 года, 1 месяц назад
Просмотрено 2к раз
$\begingroup$Кто-нибудь может представить доказательство идентичности синуса суммы для любой пары углов $a$, $b$?
$$\sin(a+b) = \sin(a) \cos(b) + \cos(a) \sin(b)$$
Большинство доказательств основано на геометрическом подходе (углы $<90 $ в этом случае). Но обратите внимание, что формула должна работать для любой пары углов.
Другой известный мне вывод использует формулу Эйлера, а именно этот.
Есть одна вещь, с которой я не чувствую себя комфортно: мы знаем, что при умножении двух комплексных чисел углы складываются. Это доказывается тождеством синусов суммы. Итак, сначала мы докажем, как работает умножение двух комплексных экспонент, используя тождество синуса суммы, а затем используем умножение комплексных экспонент, чтобы доказать тождество синуса суммы. Можете ли вы сказать мне, как это не циклический аргумент?
- тригонометрия
вот геометрическое доказательство, которое я видел в старом американском ежемесячнике по математике, в котором используется единичный круг. сначала покажите, что квадрат хорды, соединяющей $(1,0)$ и $(\cos t, \sin t)$, равен $2(1-\cos t)$, используя формулу расстояния. теперь переинтерпретируйте $$\text{ длина хорды, образующей угол $t$ в центре, равна } 2 — 2\cos t $$
теперь вычислите квадрат длины между $\cos t, \sin t), (\cos s, \sin s)$ двумя разными способами:
(i) формула расстояния дает вам $2 — \cos t \cos s — \sin t \sin s$
(ii) хорда, образующая угол $t — s$ равна $2 — \cos(t-s)$
приравнивание двух дает $$\cos (t-s) = \cos t \ cos s + \sin t \sin s \tag 1$$
теперь используйте факт $\cos \pi/2$, чтобы вывести $\cos (\pi/2 — s) = \sin s$, положив $t = \pi/2$ в $(1)$
положить $t=0,$, чтобы получить $\cos$ — четная функция.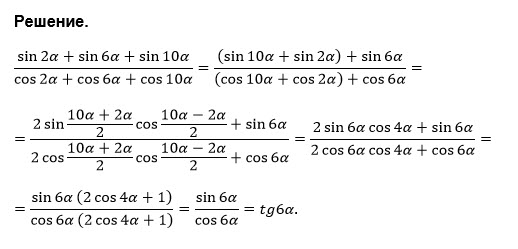 поставьте $t = -\pi/2,$, чтобы показать, что $\sin$ — нечетная функция. после всего этого вы получаете
$$\sin(t-s) = \sin t \cos t — \cos t \sin s $$ и два для сумм. 9{ix}$.
поставьте $t = -\pi/2,$, чтобы показать, что $\sin$ — нечетная функция. после всего этого вы получаете
$$\sin(t-s) = \sin t \cos t — \cos t \sin s $$ и два для сумм. 9{ix}$.
Мы никогда не признавали существование идентичности суммы углов в этом доказательстве, следовательно, нет кругового рассуждения.
$\endgroup$ 0Тригонометрические функции суммы и разности двух углов
Тригонометрия — раздел математики, изучающий углы, длины и высоты треугольников и их соотношения. Это сыграло важную роль для вычисления сложных функций или больших расстояний, которые невозможно было вычислить без тригонометрии. При решении задач по тригонометрии мы сталкивались со многими ситуациями, когда приходится вычислять тригонометрические решения для суммы углов или разности углов. Например.
Здесь,
Это касательное тригонометрическое отношение с углом, противоположным BC.
tan(θ+Φ) =
Если θ = 30° и Φ = 45°. Мы знаем тригонометрические углы 45° и 30°, но не знаем тригонометрический угол (45° + 30° = 75°). Таким образом, чтобы упростить эти типы проблем. Мы изучим тригонометрические формулы или тождества суммы и разности двух углов, что облегчит задачу.
Мы знаем тригонометрические углы 45° и 30°, но не знаем тригонометрический угол (45° + 30° = 75°). Таким образом, чтобы упростить эти типы проблем. Мы изучим тригонометрические формулы или тождества суммы и разности двух углов, что облегчит задачу.
Прежде чем двигаться дальше, сначала мы увидим знаки тригонометрических функций в четырех квадрантах. Эти знаки играют важную роль в тригонометрии.
Тригонометрические тождестваТеперь найдем тригонометрические тождества. Поскольку мы знаем, что
sin(-x) = – sin x
cos(-x) = cos x
Потому что только cos и sec положительны в четвертом квадранте. Итак, теперь мы докажем некоторые результаты относительно суммы и разности углов:
Рассмотрим единичный круг (радиус которого равен 1) с центром в начале координат. Пусть x будет ∠DOA, а y будет ∠AOB. Тогда (x + y) — это ∠DOB. Также пусть (– y) будет ∠DOC.
Следовательно, координаты A, B, C и D равны
A = (cos x, sin x)
B = [cos (x + y), sin (x + y)]
C = [ cos (– y), sin (– y)]
D = (1, 0).
As, ∠AOB = ∠COD
Складывая, ∠BOC обе стороны, получаем
∠AOB + ∠BOC = ∠COD + ∠BOC
∠AOC = ∠БПК
В △ AOC и △ БПК
OA = OB (радиус окружности)
∠AOC = ∠BOD (доказано ранее)
OC = OD (радиус окружности)
△ AOC ≅ △ БПК по конгруэнтности SAS.
Используя формулу расстояния, для
AC 2 = [cos x – cos (– y)] 2 + [sin x – sin(–y] 2
AC 2 90 155 = 2 – 2 (cos x cos y – sin x sin y) …………….(i)
И, теперь
Аналогично, используя формулу расстояния, получаем
BD 2 = [1 – cos (x + у)] 2 + [0 – sin (x + y)] 2
BD 2 = 2 – 2 cos (x + y) …………….(ii)
As, △ AOC ≅ △ БПК
AC = BD, поэтому AC 2 = BD 2
Из уравнения (i) и уравнения (ii) получаем
2 – 2 (cos x cos y – sin x sin y) = 2 – 2 cos (x + y)
Итак,
cos (x + y) = cos x cos y – sin x sin y
Возьмем y = -y, получим
cos (x + (-y)) = cos x cos (-y) – sin x sin (-y)
cos (x – y) = cos x cos y + sin x sin y
Сейчас , взяв
потому что (-(x + y)) = cos ((-x) – y) (cos (-θ) = sin θ)
sin(x – y) = sin x cos y – cos x sin y cos x sin (-y)
sin (x + y) = sin x cos y + cos x sin y
Полученные формулы для тригонометрических отношений составных углов следующие:
sin (A + B) = sin A cos B + cos A sin B ……………….
.(1)
sin (A – B) = sin A cos B – cos A sin B ………………..(2)
cos (A + B) = cos A cos B – sin A sin B .. ………………(3)
cos (A – B) = cos A cos B + sin A sin B ………………..(4)
Используя эти формулы, мы можем получить важную и наиболее часто используемую форму:
(1) Возьмем A =
В уравнении (1) и (3) мы получим
sin (+B) = cos B
cos (+B) = – sin A
(2 ) Возьмем, A = π
В уравнениях (1), (2), (3) и (4) мы получаем
sin (π + B) = – sin B
sin (π – B) = sin B
cos ( π ± B) = – cos B
(3) Возьмем A = 2π
В уравнении (2) и (4) получаем
sin (2π – B) = – sin B
cos (2π – B) = cos B
Аналогично для cot A, tan A, sec A и cosec A
(4)
Здесь A, B и (A + B) не являются нечетное число, кратное π/2, поэтому cosA, cosB и cos(A + B) отличны от нуля
tan(A + B) = sin(A + B)/cos(A + B)
Из уравнения (1) и (3) мы получаем
tan(A + B) = sin A cos B + cos A sin B/cos A cos B – sin A sin B
Теперь разделим числитель и знаменатель на cos A cos B, получим
tan(A + B) =
(5)
Так как мы знаем, что
Таким образом, полагая B = -B, мы получаем
(6)
Здесь A, B и (A + B) не кратно π, поэтому sinA, sinB и sin(A + B) отличны от нуля
cot(A + B) = cos(A + B)/sin(A + B)
Из уравнения (1) и (3) мы получаем
cot(A + B) = cos A cos B – sin A sin B/sin A cos B + cos A sin B
Теперь разделим числитель и знаменатель на sin A sin B, получим
cot(A + B) =
(7)
9 0118Поскольку мы знаем, что
Итак, поставив B = -B, мы получим
Здесь мы установим два набора формул преобразования: формулы факторизации и дефакторизации.
Формулы дефакторизации
В тригонометрии дефакторизация означает преобразование произведения в сумму или разность. Формулы с детокаторизацией:
(1) 2 sin a cos b = sin (a + b) + sin (a — b)
Доказательство:
Как мы знаем,
SIN (A + B) = sin A cos B + cos A sin B …………………………(1)
sin (A – B) = sin A cos B – cos A sin B ……………………… …(2)
Складывая уравнение (1) и (2), мы получаем
2 sin A cos B = sin (A + B) + sin (A – B)
(2) 2 cos A sin B = sin (A + B) – sin (A – B)
Доказательство:
Поскольку мы знаем, что
sin (A + B) = sin A cos B + cos A sin B …………………………(1)
sin (A – B) = sin A cos B – cos A sin B …………………………(2)
Вычитая уравнение (2) из (1), получаем
2 cos A sin B = sin (A + B) – sin (A – B)
(3) 2 cos A cos B = cos (A + B) + cos (A – B)
Доказательство:
Поскольку мы знаем, что
cos (A + B) = cos A cos B – sin A sin B …………………………(1)
cos (A – B) = cos A cos B + sin A sin B …………………………(2)
Складывая уравнения (1) и (2), мы получаем
2 cos A cos B = cos (A + B) + cos (A – B)
(4) 2 sin A sin B = cos (A – B) – cos (A + B)
Доказательство:
cos (A + B) = cos A cos B – sin A sin B ………………………(1)
cos (A – B) = cos A cos B + sin A sin B …………………………(2)
Вычитая уравнение (3) из (4), мы получаем
2 sin A sin B = cos (A – B) – cos (A + B)
Пример 1. Преобразуйте каждое из следующих произведений в сумму или разность.
Преобразуйте каждое из следующих произведений в сумму или разность.
(i) 2 sin 40° cos 30°
(ii) 2 sin 75° sin 15°
(iii) cos 75° cos 15° 901 02
Решение:
(и) Дано: A = 40° и B = 30°
Теперь подставим все эти значения в формулу
2 sin A cos B = sin (A + B) + sin (A – B)
Получим
2 sin 40° cos 30° = sin (40 + 30) + sin (40 – 30)
= sin (70°) + sin (10°)
(ii) Дано: A = 75° и B = 15°
Теперь подставим все эти значения в формулу
2 sin A sin B = cos (A – B) – cos (A + B)
Получим
2 sin 75° sin 15° = cos (75-15) – cos (75+15)
= cos (60°) – cos (90°)
(iii) Дано: A = 75° и B = 15°
Теперь подставьте все эти значения в формулу
2 cos A cos B = cos (A + B) + cos (A – B)
Получаем
cos 75° cos 15° = 1/2(cos (75+15) + cos (75-15))
= 1/ 2 (cos (90°) + cos (60°))
Пример 2. Найдите
Найдите
Решение:
Используя формулу
2 cos A cos В = потому что (А + В) + cos (А – В)
=
=
=
Следовательно,
= 0
Формулы факторизации
В тригонометрии факторизация означает преобразование суммы или разности в произведение. Формулы факторизации:
(1) sin (C) + sin (D) = 2 sin cos
Доказательство:
Имеем
90 002 2 sin A cos B = sin (A + B) + sin (A – B) ………………………(1)Итак, теперь мы берем
A + B = C и A – B = D
Тогда A = и B =
Теперь поместите все эти значения в уравнение (1), мы получим
2 sin () cos () = sin (C ) + sin (D)
Или
sin (C) + sin (D) = 2 sin () cos ()
(2) sin (C) – sin (D) = 2 cos sin
Доказательство:
Имеем
2 cos A sin B = sin (A + B) – sin (A – B) ………………………(1)
Итак, теперь, мы берем
A + B = C и A – B = D
Тогда A = и B =
Теперь поместите все эти значения в уравнение (1), мы получим
2 cos () sin () = sin (C) – sin (D)
Или
sin ( C) – sin (D) = 2 cos () sin ()
(3) cos (C) + cos (D) = 2 cos cos
Доказательство:
901 18У нас есть
2 cos A cos B = cos (A + B) + cos (A – B) …………………………(1)
Итак, теперь мы берем
A + B = C и A – B = D
Тогда A = и B =
Теперь поместите все эти значения в уравнение (1), мы получим
2 cos () cos () = cos (C) + cos (D)
Или
cos (C) + cos (D) = 2 cos () cos ()
(4) cos (C) – cos (D) = 2 sin sin
Доказательство:
Имеем
2 sin A sin B = cos ( A – B) – cos (A + B) …………………………(1)
Итак, теперь мы берем
A + B = C и A – B = D
Тогда, А = и В =
Теперь поместите все эти значения в уравнение (1), мы получим
2 sin () sin () = cos (C) – cos (D)
Или
cos (C) – cos (D) = 2 sin () sin ()
Объясните 1. Выразите каждое из следующих чисел в виде произведения
Выразите каждое из следующих чисел в виде произведения
(i) sin 40° + sin 20°
(ii) sin 60° – sin 20° 901 02
(iii) cos 40° + cos 80°
Решение:
(i) Дано: C = 40° и D = 20°
Теперь подставим все эти значения в формулу,
sin (C) + sin (D) = 2 sin cos
Получим
sin 40° + sin 20° = 2 sin cos
= 2 sin cos 9000 5
= 2 sin 30° cos 10°
(ii) Дано: C = 60° и D = 20°
Теперь подставьте все эти значения в формулу
sin (C) – sin (D) = 2 cos sin
Получаем
sin 60° – sin 20° = 2 cos sin
= 2 cos sin
= 2 cos 40° sin 20°
(iii) Дано: C = 80° и D = 40°
Теперь подставим все эти значения в формулу
cos (C) + cos (D) = 2 cos cos
Получим
900 02 cos 40° + cos 80° = 2 cos cos= 2 cos cos
= 2 cos 60° cos 20°
Пример 2. Докажите, что: 1 + cos 2x + cos 4x + cos 6x = 4 потому что x cos 2x cos 3x
Докажите, что: 1 + cos 2x + cos 4x + cos 6x = 4 потому что x cos 2x cos 3x
Решение:
Возьмем LHS
1 + cos 2x + cos 4x + cos 6x
Здесь, cos 0x = 1
Итак,
(cos 0x + cos 2x) + (cos 4x + cos 6x)
Используя формулу
cos (C) + cos (D) = 2 cos cos
Получаем
(2 cos cos) + (2 cos cos)
(2 cos x cos x) + (2 cos 5x cos x)
Взяв 2 cos x общие, имеем
2 cos x (cos x + cos 5x)
Снова используя формулу
cos (C) + cos (D) = 2 cos cos
Получаем
2 cos x (2 cos cos)
2 cos x (2 cos 3x cos 2x)
4 cos x cos 2x cos 3x
LHS = RHS
Отсюда доказано
Тригонометрические отношения кратных углов (2A) через угол A 9010 3
Тригонометрические отношения угла в прямоугольном треугольнике определяют отношение между углом и длиной его сторон. sin 2x или cos 2x и т. д. также являются одной из таких тригонометрических формул, также известных как формула двойного угла, поскольку в ней есть двойной угол.
(1) sin 2A = 2 sin A cos A
Доказательство:
Поскольку мы знаем, что
sin (A + B) = sin A cos B + cos A sin B ………………..(1)
Теперь примем B = A , в уравнении (1) мы получаем
sin (A + A) = sin A cos A + cos A sin A
sin 2A = 2 sin A cos A
(2) cos 2A = cos 2 (1) )
Теперь принимая B = A, в уравнении (1) мы получаем
cos (A + A) = cos A cos A + sin A sin A
cos 2A = cos 2 A – sin 2 A
(3) cos 2A = 2cos 2 A – 1
Доказательство:
Как мы знаем,
90 002 cos 2A = cos 2 A – sin 2 A ……… ………..(1)Мы также знаем, что
sin 2 A + cos 2 A = 1
Итак, sin 2 A = 1 – cos 2 A
Теперь подставим значение sin 2 A в уравнение (1), получим
cos 2A = cos 2 A – (1 – cos 9015 4 2 A)
cos 2A = cos 2 A – 1 + cos 2 A
cos 2A = 2cos 2 A – 1
(4) cos 2A = 1 – 2sin 2 A
Доказательство:
Поскольку мы знаем, что
cos 2A = 2cos 2 A – 1 ……………….
.(1)
Мы также знаем, что
sin 2 A + cos 2 A = 1
Итак, cos 2 A = 1 – sin 2 A
Теперь введите значение sin 2 A в уравнении (1) мы получаем
cos 2A = 2(1 – sin 2 A) – 1
cos 2A = 2 – 2sin 2 A) – 1
cos 2A = 1 – 2sin 9 0154 2 A
(5) cos 2A =
Доказательство:
Как мы знаем,
cos 2A = cos 2 A – sin 2 A
Итак, делим теперь на sin 2 A + cos 2 A = 1, получаем
900 02 cos 2A =Снова разделив числитель и знаменатель на cos 2 A, получаем
cos 2A =
cos 2A =
(6) sin 2A =
90 101 Доказательство:
Поскольку мы знаем, что
sin ( A + B) = sin A cos B + cos A sin B ……………….
.(1)
Теперь принимая B = A, в уравнении (1) мы получаем
sin (A + A) = sin A cos A + cos A sin A
sin 2A = 2 sin A cos A
Поскольку мы также знаем, что sin 2 A + cos 2 A = 1
Итак, делим теперь на sin 2 A + cos 2 A = 1, получаем
sin 2A =
Теперь о делении числителя и знаменатель на cos 2 А, получаем
sin 2A =
(7) tan 2A =
Доказательство:
Поскольку мы знаем, что
………………..(1)
Теперь, взяв B = A, в уравнении (1) мы получим
tan(A + A) =
tan 2A =
Пример: Докажите, что
(i) = tan θ
(ii) 9010 2 = кроватка θ
(iii) cos 4x = 1 – 8 sin 2 x cos 2 x
Решение:
(i) sin 2θ = 2 sin θ cos θ ……….
.(из тождества 1)
и, 1 + cos 2θ = 2cos 2 θ ………..(из тождества 3)
=
= tan θ
Отсюда доказано 9000 5
(ii) sin 2θ = 2 sin θ cos θ ………..(из тождества 1)
и, 1 – cos 2θ = 2sin 2 θ ………..(из тождества 4)
=
= cot θ
Отсюда Доказано
(iii) cos 4x = cos 2(2x)
= 1 – 2sin 2 (2x) (с использованием 16)
= 1 – 2(sin(2x)) 2
= 1 – 2(2 sin x cos x) 2 (с использованием тождества 1)
= 1 – 2(4 sin 2 x cos 2 x)
cos 4x = 1 – 8 sin 2 x cos 2 x
Отсюда доказано
Тригонометрические отношения кратных углов (3A) через угол A
Тригонометрические отношения угла в прямоугольном треугольнике определяют соотношение между углом и длина его сторон. sin 3x или cos 3x и т. д. также являются одной из таких тригонометрических формул, также известных как формула тройного угла, поскольку в ней есть тройной угол.
(1) sin 3A = 3sin A – 4 sin 3 A
Доказательство:
Возьмем LHS
sin 3A = sin(2A + A)
Использование идентификатора
sin ( A + B) = sin A cos B + cos A sin B
Получаем
sin 3A = sin 2A cos A + cos 2A sin A
= 2sin A cos A cos A + (1 – 2 sin 2 А)sin А
= 2sin А(1 – sin 2 А) + sin А – 2 sin 3 А
= 2sin A – 2sin 3 A + sin A – 2 sin 3 A
sin 3A = 3sin A – 4 sin 3 A
902 23(2) cos 3A = 4 cos 3 A – 3cos A
Доказательство:
Возьмем LHS
sin 3A = sin(2A + A)
Используя тождество
900 02 cos (A + B) = cos A cos B – sin A sin BПолучаем
cos 3A = cos 2A cos A – sin 2A sin A
= (2cos 2 A – 1)cos A – 2sin A cos A sin A
= (2cos 2 A – 1)cos A – 2cos A(1 – cos 2 A)
= 2cos 3 A — потому что A – 2cos A + 2cos 3 A)
cos 3A = 4 cos 3 A – 3cos A
(3) tan 3A =
900 02 Доказательство:Возьмем LHS
tan 3A = tan(2A + A)
Используя идентификатор
Получаем
tan 3A =
=
=
=
Пример 1.




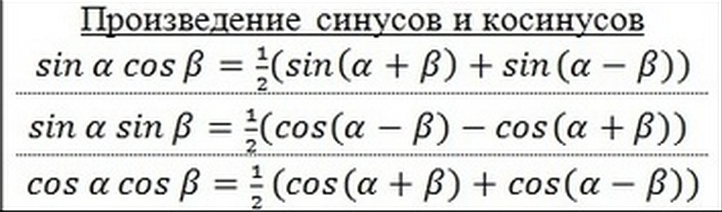 29 а – 1 учащийся решает на доске, остальные – в тетради.
29 а – 1 учащийся решает на доске, остальные – в тетради. Ответим на вопрос: достигли мы цели нашего урока?
Ответим на вопрос: достигли мы цели нашего урока?
 .(1)
.(1) 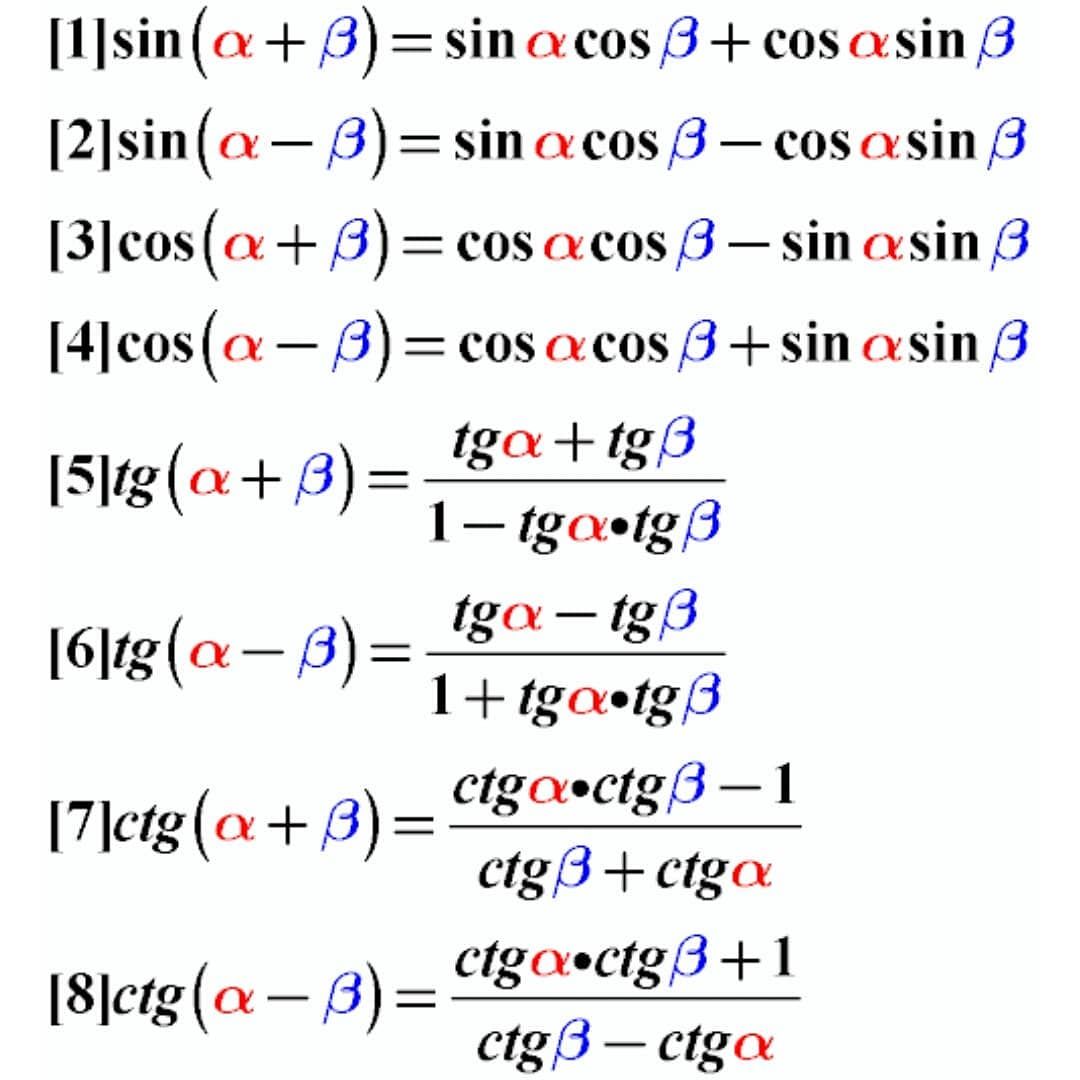 .(1)
.(1) .(1)
.(1) .(из тождества 1)
.(из тождества 1)