Sin x 4 1: Решите уравнение sin(x/4)=-1 (синус от (х делить на 4) равно минус 1)

alexxlab / / Разное

Mathway | Популярные задачи

1Найти точное значениеsin(30)
2Найти точное значениеsin(45)
3Найти точное значениеsin(30 град. )
4Найти точное значениеsin(60 град. )
5Найти точное значениеtan(30 град. )
6Найти точное значениеarcsin(-1)
7Найти точное значениеsin(pi/6)
8
Найти точное значение		cos(pi/4)
9Найти точное значениеsin(45 град. )
10Найти точное значениеsin(pi/3)
11Найти точное значениеarctan(-1)
12Найти точное значениеcos(45 град. )
13Найти точное значениеcos(30 град. )
14Найти точное значениеtan(60)
15
Найти точное значение		csc(45 град. )
16Найти точное значениеtan(60 град. )
17Найти точное значениеsec(30 град. )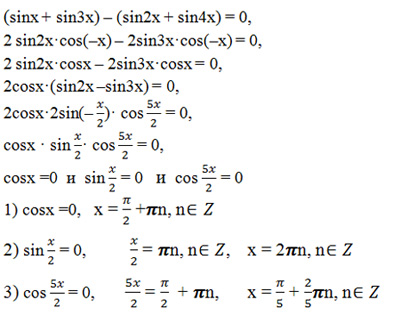
18Найти точное значениеcos(60 град. )
19Найти точное значениеcos(150)
20Найти точное значениеsin(60)
21Найти точное значениеcos(pi/2)
22Найти точное значениеtan(45 град. )
23Найти точное значениеarctan(- квадратный корень из 3)
24Найти точное значениеcsc(60 град. )
25Найти точное значениеsec(45 град. )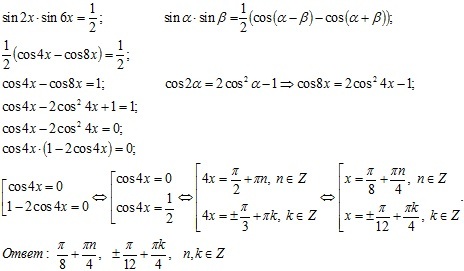
26Найти точное значениеcsc(30 град. )
27Найти точное значениеsin(0)
28Найти точное значениеsin(120)
29Найти точное значениеcos(90)
30Преобразовать из радианов в градусыpi/3
31Найти точное значениеtan(30)
32Преобразовать из градусов в радианы45
33Найти точное значениеcos(45)
34Упроститьsin(theta)^2+cos(theta)^2
35Преобразовать из радианов в градусыpi/6
36Найти точное значениеcot(30 град. )
37Найти точное значениеarccos(-1)
38Найти точное значениеarctan(0)
39Найти точное значениеcot(60 град. )
40Преобразовать из градусов в радианы30
41Преобразовать из радианов в градусы(2pi)/3
42Найти точное значениеsin((5pi)/3)
43Найти точное значениеsin((3pi)/4)
44Найти точное значениеtan(pi/2)
45Найти точное значениеsin(300)
46Найти точное значениеcos(30)
47Найти точное значениеcos(60)
48Найти точное значениеcos(0)
49Найти точное значениеcos(135)
50Найти точное значениеcos((5pi)/3)
51Найти точное значениеcos(210)
52Найти точное значениеsec(60 град. )
53Найти точное значениеsin(300 град. )
54Преобразовать из градусов в радианы135
55Преобразовать из градусов в радианы150
56Преобразовать из радианов в градусы(5pi)/6
57Преобразовать из радианов в градусы(5pi)/3
58Преобразовать из градусов в радианы89 град.
59Преобразовать из градусов в радианы60
60Найти точное значениеsin(135 град. )
61Найти точное значениеsin(150)
62Найти точное значениеsin(240 град. )
63Найти точное значениеcot(45 град. )
64Преобразовать из радианов в градусы(5pi)/4
65Найти точное значениеsin(225)
66Найти точное значениеsin(240)
67Найти точное значениеcos(150 град. )
68Найти точное значениеtan(45)
69Вычислитьsin(30 град. )
70Найти точное значениеsec(0)
71Найти точное значениеcos((5pi)/6)
72Найти точное значениеcsc(30)
73Найти точное значениеarcsin(( квадратный корень из 2)/2)
74Найти точное значениеtan((5pi)/3)
75Найти точное значениеtan(0)
76Вычислитьsin(60 град. )
77Найти точное значениеarctan(-( квадратный корень из 3)/3)
78Преобразовать из радианов в градусы(3pi)/4
79Найти точное значениеsin((7pi)/4)
80Найти точное значениеarcsin(-1/2)
81Найти точное значениеsin((4pi)/3)
82Найти точное значениеcsc(45)
83Упроститьarctan( квадратный корень из 3)
84Найти точное значениеsin(135)
85Найти точное значениеsin(105)
86Найти точное значениеsin(150 град. )
87Найти точное значение sin((2pi)/3)
88Найти точное значениеtan((2pi)/3)
89Преобразовать из радианов в градусыpi/4
90Найти точное значениеsin(pi/2)
91Найти точное значениеsec(45)
92Найти точное значениеcos((5pi)/4)
93Найти точное значениеcos((7pi)/6)
94Найти точное значение
arcsin(0)
95Найти точное значениеsin(120 град. )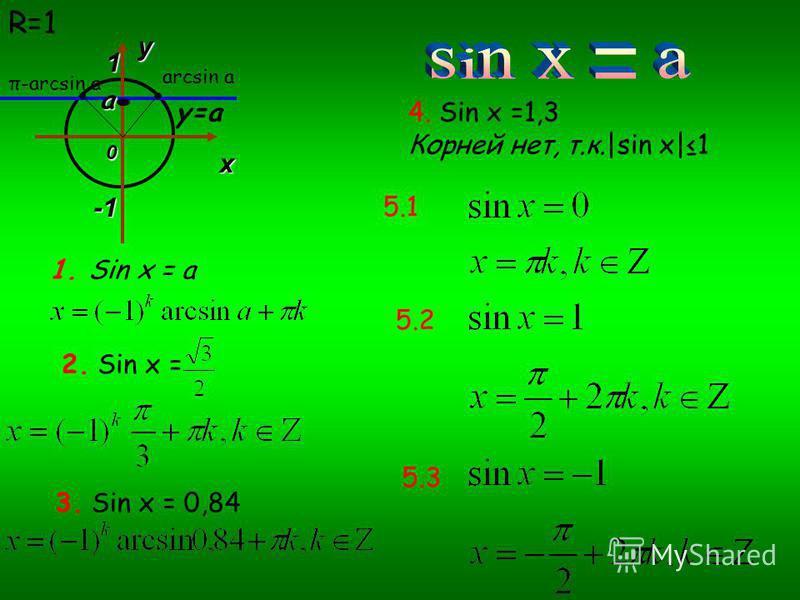
96Найти точное значениеtan((7pi)/6)
97Найти точное значениеcos(270)
98Найти точное значениеsin((7pi)/6)
99Найти точное значениеarcsin(-( квадратный корень из 2)/2)
100Преобразовать из градусов в радианы88 град.

Решите уравнение sin (x + π/4 ) = √2/2 на промежутке (0; 2𝜋) — Учеба и наука

Лучший ответ по мнению автора
15. 10.19
Лучший ответ по мнению автора

Михаил Александров
Читать ответы

Андрей Андреевич
Читать ответы

Eleonora Gabrielyan
Читать ответы

Посмотреть всех экспертов из раздела Учеба и наука > Математика

Похожие вопросы

Решено

найдите -20cos(3п/2+a), если cosa=7/25 и a принадлежит (1,5п;2п)

Решено

В треугольнике АВС В1-середина АС, точка А1 лежит на стороне ВС так, что ВА1 : А1С = 1 : 2.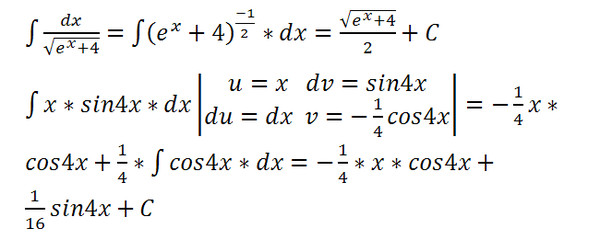 2-4x+4 и решение

Пользуйтесь нашим приложением

3-8 9 Оценить квадратный корень из 12 10 Оценить квадратный корень из 20 11 Оценить квадратный корень из 50 94 18 Оценить квадратный корень из 45 19 Оценить квадратный корень из 32 20 Оценить квадратный корень из 18 92

Решите это уравнение: sin(x + (π/4)) – sin(x – (π/4) = 1

значок-вопрос Спросите репетитора

Начать бесплатную пробную версию

Скачать PDF PDF Цитата страницы Цитировать Поделиться ссылкой Делиться

Укажите эту страницу следующим образом:

«Решите это уравнение: грех( х + ( π / 4)) – грех( x – ( π / 4) = 1 дюйм Редакция eNotes , 20 апреля 2013 г. , https://www.enotes.com/homework-help/solve-this-equation-sin-x-4- грех-х-4-1-429252. По состоянию на 12 декабря 2022 г.

Ответы экспертов

`sin(x+pi/4) — sin(x-pi/4)=1`

Для решения можно использовать тождество суммы и произведения синуса, которое равно `sinA-sinB=2cos( (A+B)/2)sin((A-B)/2)` .

Итак,

`2cos(((x+pi/4)+(x-pi/4))/2)sin(((X+pi/4)-(x-pi/4))/2 )=1`

Затем упростите выражение в скобках.

`2cos((2x)/2)sin((pi/2)/2)=1`

`2cosxsin(pi/4)=1`

Так как `sin(pi/4)=sqrt2/2 ` , уравнение упрощается до:

`2cosx*sqrt2/2=1`

`sqrt2cosx=1`

`cosx=1/sqrt2`

Рационализируйте знаменатель для дальнейшего упрощения.

`cosx=1/sqrt2*sqrt2/sqrt2`

`cos x=sqrt2/2`

Ссылаясь на модуль…

См.


Этот ответ сейчас

Запустите 48-часовую бесплатную пробную версию , чтобы разблокировать этот и тысячи других ответов. Наслаждайтесь eNotes без рекламы и отмените подписку в любое время.

Получите 48 часов бесплатного доступа

Уже зарегистрированы? Войдите здесь.

`sin(x+pi/4) — sin(x-pi/4)=1`

Для решения можно использовать тождество суммы и произведения синуса, которое равно `sinA-sinB=2cos((A+B )/2)sin((AB)/2)` .

Итак,

`2cos(((x+pi/4)+(x-pi/4))/2)sin(((X+pi/4)-(x-pi/4))/2 )=1`

Затем упростите выражение в скобках.

`2cos((2x)/2)sin((pi/2)/2)=1`

`2cosxsin(pi/4)=1`

Поскольку `sin(pi/4)=sqrt2/2`, уравнение упрощается до:

`2cosx*sqrt2/2=1`

`sqrt2cosx=1`

`cosx=1/sqrt2`

Рационализируйте знаменатель для дальнейшего упрощения.

`cosx=1/sqrt2*sqrt2/sqrt2`

`cos x=sqrt2/2`

Ссылаясь на диаграмму Unit Circle, значения угла x:

`x=pi/4 , (7pi) /4`

Поскольку косинус повторяется через каждые 2pi, общее решение данного уравнения:

`x_1= pi/4+2pik `     и     `x_2=(7pi)/4+2pik`

, где k — любое целое число.

Утверждено редакцией eNotes

Используйте тождество для суммы двух углов для синуса и разности двух углов для синуса.

sin(a + b) = sinacosb + cosasinb и sin(a — b) = sinacosb — cosasinb

Итак, мы будем иметь:

`sinxcos(pi/4) +cosxsin(pi/4) — (sinxcos(pi/4) — cosxsin(pi/4)) = 1`

`sinxcos(pi/4) + cosxsin(pi/4) ) — sinxcos(pi/4) + cosxsin(pi/4)) = 1`

Комбинируйте одинаковые термины.

`2cosxsin(pi/4) = 1`  

Подставить значение sin(pi/4).

`2cosx(sqrt(2)/2)) = 1`

`sqrt2cosx = 1`

Изолировать cosx с левой стороны.

`cosx = 1/sqrt(2)`

Вычисление обратного косинуса обеих сторон.

x = пи/4, 7пи/4 дюйма [0. 2пи) .

 

Утверждено редакцией eNotes

Математика

Последний ответ опубликован 07 сентября 2010 г.

No related posts.

Добавить комментарий

Ваш адрес email не будет опубликован. Обязательные поля помечены *