Sint cost: Представить в виде произведения cost+sint

Mathway | Популярные задачи

1	Найти точное значение	sin(30)
2	Найти точное значение	sin(45)
3	Найти точное значение	sin(30 град. )
4	Найти точное значение	sin(60 град. )
5	Найти точное значение	tan(30 град. )
6	Найти точное значение	arcsin(-1)
7	Найти точное значение	sin(pi/6)
8	Найти точное значение	cos(pi/4)
9	Найти точное значение	sin(45 град. )
10	Найти точное значение	sin(pi/3)
11	Найти точное значение	arctan(-1)
12	Найти точное значение	cos(45 град. )
13	Найти точное значение	cos(30 град. )
14	Найти точное значение	tan(60)
15	Найти точное значение	csc(45 град. )
16	Найти точное значение	tan(60 град. )
17	Найти точное значение	sec(30 град. )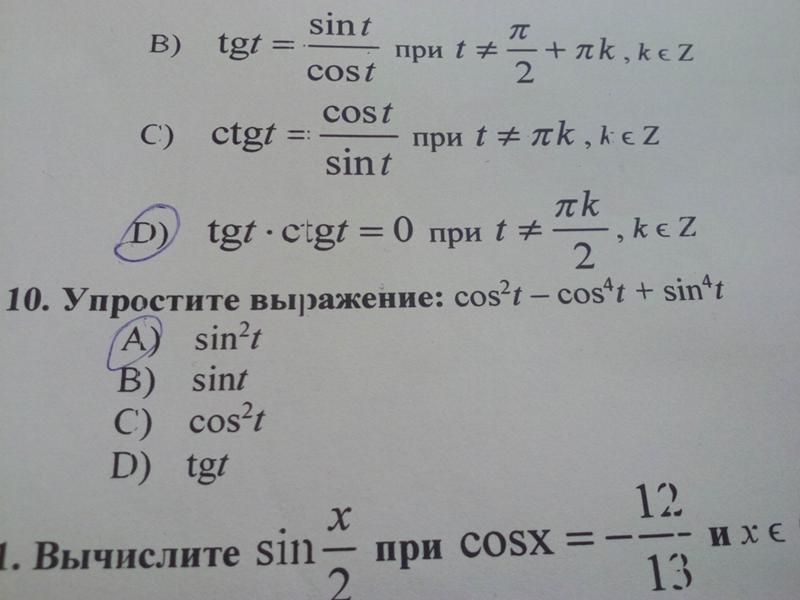
18	Найти точное значение	cos(60 град. )
19	Найти точное значение	cos(150)
20	Найти точное значение	sin(60)
21	Найти точное значение	cos(pi/2)
22	Найти точное значение	tan(45 град. )
23	Найти точное значение	arctan(- квадратный корень из 3)
24	Найти точное значение	csc(60 град. )
25	Найти точное значение	sec(45 град. )
26	Найти точное значение	csc(30 град. )
27	Найти точное значение	sin(0)
28	Найти точное значение	sin(120)
29	Найти точное значение	cos(90)
30	Преобразовать из радианов в градусы	pi/3
31	Найти точное значение	tan(30)
32	Преобразовать из градусов в радианы	45
33	Найти точное значение	cos(45)
34	Упростить	sin(theta)^2+cos(theta)^2
35	Преобразовать из радианов в градусы	pi/6
36	Найти точное значение	cot(30 град. )
37	Найти точное значение	arccos(-1)
38	Найти точное значение	arctan(0)
39	Найти точное значение	cot(60 град. )
40	Преобразовать из градусов в радианы	30
41	Преобразовать из радианов в градусы	(2pi)/3
42	Найти точное значение	sin((5pi)/3)
43	Найти точное значение	sin((3pi)/4)
44	Найти точное значение	tan(pi/2)
45	Найти точное значение	sin(300)
46	Найти точное значение	cos(30)
47	Найти точное значение	cos(60)
48	Найти точное значение	cos(0)
49	Найти точное значение	cos(135)
50	Найти точное значение	cos((5pi)/3)
51	Найти точное значение	cos(210)
52	Найти точное значение	sec(60 град. )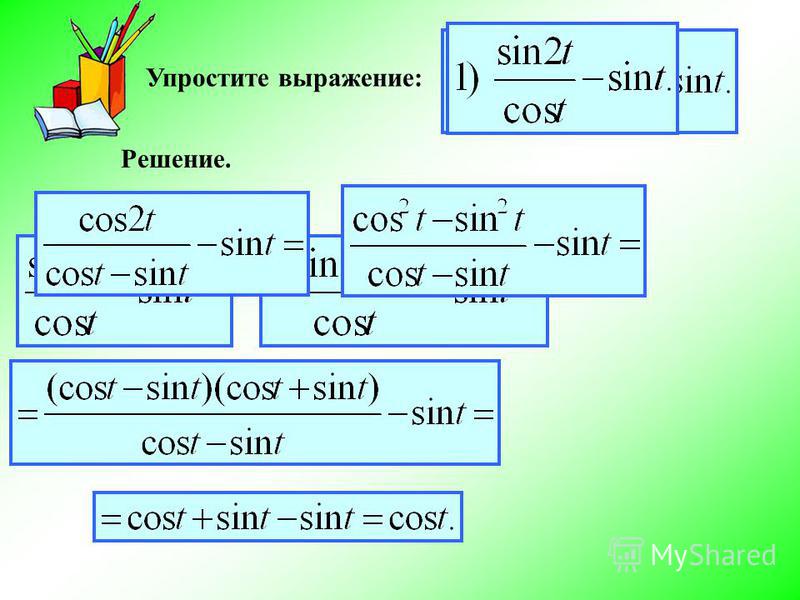
53	Найти точное значение	sin(300 град. )
54	Преобразовать из градусов в радианы	135
55	Преобразовать из градусов в радианы	150
56	Преобразовать из радианов в градусы	(5pi)/6
57	Преобразовать из радианов в градусы	(5pi)/3
58	Преобразовать из градусов в радианы	89 град.
59	Преобразовать из градусов в радианы	60
60	Найти точное значение	sin(135 град. )
61	Найти точное значение	sin(150)
62	Найти точное значение	sin(240 град. )
63	Найти точное значение	cot(45 град. )
64	Преобразовать из радианов в градусы	(5pi)/4
65	Найти точное значение	sin(225)
66	Найти точное значение	sin(240)
67	Найти точное значение	cos(150 град. )
68	Найти точное значение	tan(45)
69	Вычислить	sin(30 град. )
70	Найти точное значение	sec(0)
71	Найти точное значение	cos((5pi)/6)
72	Найти точное значение	csc(30)
73	Найти точное значение	arcsin(( квадратный корень из 2)/2)
74	Найти точное значение	tan((5pi)/3)
75	Найти точное значение	tan(0)
76	Вычислить	sin(60 град. )
77	Найти точное значение	arctan(-( квадратный корень из 3)/3)
78	Преобразовать из радианов в градусы	(3pi)/4
79	Найти точное значение	sin((7pi)/4)
80	Найти точное значение	arcsin(-1/2)
81	Найти точное значение	sin((4pi)/3)
82	Найти точное значение	csc(45)
83	Упростить	arctan( квадратный корень из 3)
84	Найти точное значение	sin(135)
85	Найти точное значение	sin(105)
86	Найти точное значение	sin(150 град. )
87	Найти точное значение	sin((2pi)/3)
88	Найти точное значение	tan((2pi)/3)
89	Преобразовать из радианов в градусы	pi/4
90	Найти точное значение	sin(pi/2)
91	Найти точное значение	sec(45)
92	Найти точное значение	cos((5pi)/4)
93	Найти точное значение	cos((7pi)/6)
94	Найти точное значение	arcsin(0)
95	Найти точное значение	sin(120 град. )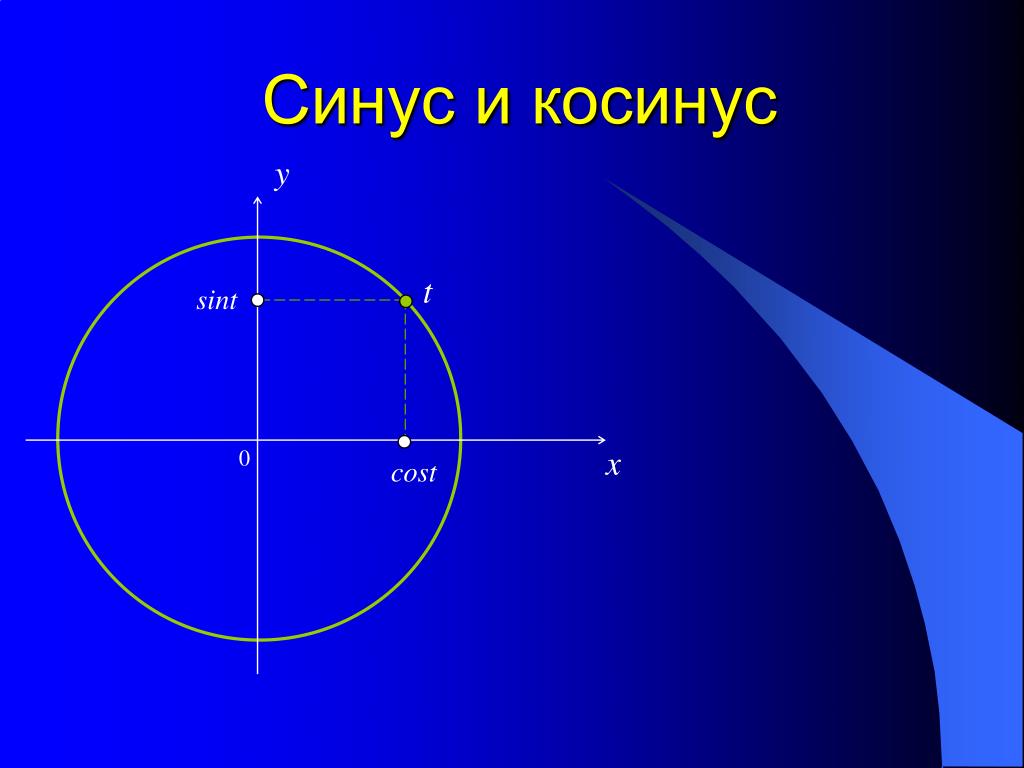
96	Найти точное значение	tan((7pi)/6)
97	Найти точное значение	cos(270)
98	Найти точное значение	sin((7pi)/6)
99	Найти точное значение	arcsin(-( квадратный корень из 2)/2)
100	Преобразовать из градусов в радианы	88 град.

Известно, что sint-cost=1/3. Вычислите 9sint cost.

Решено

Укажите самые древние наречия, которые появились раньше остальных:1) впотьмах 2)опрометью 3)сюда 4)наотмашь 5)всегда 6)рано

Если положительное число a возвести в четвертую степень, то оно увеличится втрое. Во сколько раз увеличится число a, если его возвести в десятую степень?

Алиса и Боб играют в игру. Игра происходит по следующим правилам: — изначально на столе лежит куча из N камней; — за один ход каждый игрок может…

С горизонтальной поверхности земли под углом к горизонту спортсмен бросает мячик. Через 0,9 секунды после броска он упруго ударяется о вертикальную стенку и отскакивает от неё. Через какое время

В стране есть 19 городов. Некоторые пары городов соединены одной двусторонней дорогой. Известно, что из любого города в любой другой можно добраться ровно двумя различными способами (способом

Пользуйтесь нашим приложением

Ответов пока нет

Аревик от 300 p. Читать ответы Михаил Александров от 0 p. Читать ответы Андрей Андреевич от 70 p. Читать ответы

Посмотреть всех экспертов из раздела Учеба и наука

Похожие вопросы

перекрестное произведение — Найдите все функции f(t) такие, что x = (cost, sint, f(t)) является плоской кривой

Задавать вопрос

спросил 2 года, 2 месяца назад

Изменено 2 года, 2 месяца назад

Просмотрено 365 раз

$\begingroup$

Итак, у меня есть вопрос

Как найти все функции f(t) такие, что x = (cost, sint, f(t)) является плоской кривой

Я знаю, что это означает, что кручение равно 0. 2} $$ Таким образом, $\tau=0$, когда $0=r'(t)\times r»(t)\cdot r»'(t)=f'(t)+f»'(t)$, т. е. $ $f»'(t)=-f'(t)$$

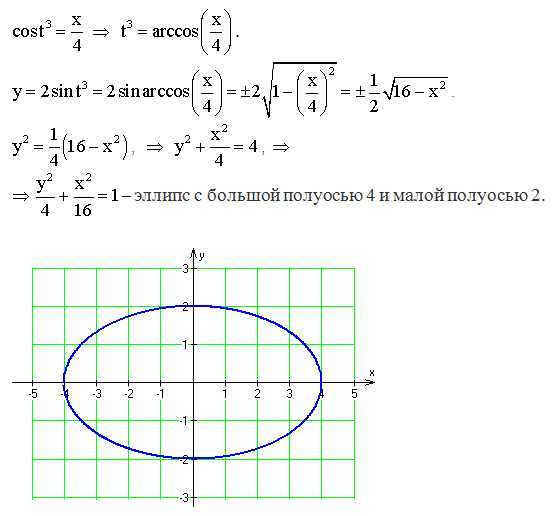
Теперь найдите $f(t)$. Ответ — эллипс, представляющий собой пересечение плоскости с цилиндром.

$\endgroup$

1

$\begingroup$

Другой подход:

Точки $P$ лежат на плоскости с нормалью $n$, когда $n\cdot P=d$ .

Следовательно, при фиксированных константах $n_x,n_y,n_z,d$ должно быть $n_z f(t)=d-n_x \cos(t) -n_y \sin(t)$

$\endgroup$

Зарегистрируйтесь или войдите в систему

Зарегистрируйтесь с помощью Google

Зарегистрироваться через Facebook

Зарегистрируйтесь, используя электронную почту и пароль

Опубликовать как гость

Электронная почта

Требуется, но не отображается

Опубликовать как гость

Электронная почта

Требуется, но не отображается

Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie

.

Если tant=−7/24 и π/2

Тригонометрия

Лова Д.

спросил 01.08.22

Подписаться І 1

Подробнее

Отчет

2 ответа от опытных наставников

Лучший Новейшие Самый старый

Автор: Лучшие новыеСамые старые

Брэндон Т. ответил 01.08.22

Репетитор

5 (13)

Бывший инженер-программист, страстно увлеченный репетиторством по предметам STEM

Об этом репетиторе ›

Об этом репетиторе ›

На основе SOH-CAH-TOA tan(x) = напротив/смежно. Таким образом, это описывает прямоугольный треугольник с противоположной стороной длиной 7, смежной стороной длиной 24 и неизвестной гипотенузой. К счастью, благодаря теореме Пифагора мы можем это понять.

гипотенуза = √ (7 ² + 24 ² ) = 49,497…

Здесь много десятичных знаков, поэтому я буду хранить его в виде √ (7 ² + 24 2 ), поэтому мы не теряем точности.

Еще одна вещь, которую следует иметь в виду, это то, что на единичном круге тангенс представляет собой наклон гипотенузы (подъем/наклон). Таким образом, положительный тангенс означает, что подъем и направление (или противоположное и смежное) должны иметь один и тот же знак. Это означает, что угол должен быть в первом квадранте (оба положительные) или в третьем квадранте (оба отрицательные). У нас здесь отрицательный тангенс, а это значит, что противолежащая и прилежащая стороны должны иметь разные знаки, а это значит, что угол находится либо во второй, либо в четвертой четверти. В ответе указано, что угол должен быть между π/2 и π, что подтверждает, что мы работаем во 2-м квадранте. Это означает, что соседняя сторона (координата x) отрицательна, а противоположная сторона (координата y) положительна. Таким образом, это поясняет, что противоположная сторона равна 7, а прилежащая сторона равна -24. Это важно указать, потому что это было бы -7 и 24, если бы оно было в четвертом квадранте.

Подводя итог, мы знаем следующее:

напротив = 7

рядом = -24

гипотенуза = √ (7 ² + 24 ² )

), так как это всего лишь величина, обратная тангенсу (t), по определению. Итак, раскладушка (t) = -24/7.

Используя определение SOH-CAH-TOA sin(t) = противоположность/гипотенуза, sin(t) = 7/√ (7 ² + 24 ² ). Это можно упростить с помощью умной алгебры.

sin(t) = 7/√ (7 ² + 24 ² )

= 7/√(7 ² (1 + 24 ² /7 ² ))

= 7/(7√7))

= 1/√(1 + 576/49)

= 1/√(49/49 + 576/49)

= 1/√(625/49)

К счастью, 625 — это полный квадрат с квадратным корнем из 25 и 49 является полным квадратом с квадратным корнем из 7, поэтому:

= 1/(25/7)

= 7/25

csc(t) является обратной величиной sin(t) по определению , поэтому csc(t) = 25/7

Используя определение SOH-CAH-TOA cos(t) = смежный/гипотенуза, cos(t) = -24/√ (7 ² + 24 ² ). Это также можно упростить с помощью умной алгебры.

cos (t) = -24 /√ (7 ² + 24 ² )

= -24 /√ 24 ² (7 ² /24 ² + 1)

= — 24 / 24 √(49/576 + 1)

= -24 / 24 √(49/576 + 576/576)

= -1 / √(625/576)

= -1 / √(25 ² /24 ² )

= -24/25

Эта задача действительно проверяет ваше понимание определения длины стороны тригонометрических функций, а также единичного круга.

Голосовать за 0 Понизить

Подробнее

Отчет

Ефим С. ответил 01.08.22

Репетитор

5 (20)

Репетитор по математике с опытом

Смотрите таких репетиторов

Смотрите таких репетиторов

котт = — 24/7; секта = — √(1 + 49/576) = — 25/24; стоимость = — 24/25; sint = tant·cost = — 7/24·(- 24/25) = 7/25;

csct = 25/7

Голосовать за 0 Понизить

Подробнее

Отчет

Все еще ищете помощь? Получите правильный ответ, быстро.