Конспект урока по теме: ”Тригонометрические уравнения. Решение простейших тригонометрических уравнений вида sinx = a. “ | План-конспект урока по алгебре (10 класс) на тему:
Тема: ”Тригонометрические уравнения. Решение простейших тригонометрических уравнений вида sinx = a. “
Эпиграф урока: ”Изучать что-либо и не задумываться над
выученным — абсолютно бесполезно.
Задумываться над чем-либо, не изучив
предварительно предмет раздумий-
опасно.”
Конфуций.
Основные цели: 1) Повторить с учащимися определение и свойства функции
у = sinx и ее график.
2) Сформировать умение решать простейшие
тригонометрические уравнения, а также уравнения,
сводящиеся к простейшим в результате преобразования
тригонометрических выражений.
Оборудование урока:
- Учебная литература:
1) Алгебра: Учеб. для 9 кл. общеобразоват. учреждений/
Ю.Н.Макарычев, Н. Г. Миндюк, К. И.Нешков, С. Б.Суворова;
Под ред. С. А. Теляковского. – 4-е изд. – М.: Прсвещение,1997. –
272 с.: ил. – ISBN 5-09-007514-X.
2) Галицкий М.Л. и др.
Сборник задач по алгебре для 8-9 классов. Учебное пособие для
учащихся школ и классов с углубленным изучением математики/
М.Л. Галицкий, А.М.Гольдман, Л.И.Звавич. – 3-е изд. – М.: 1996. –
271 с.: ил.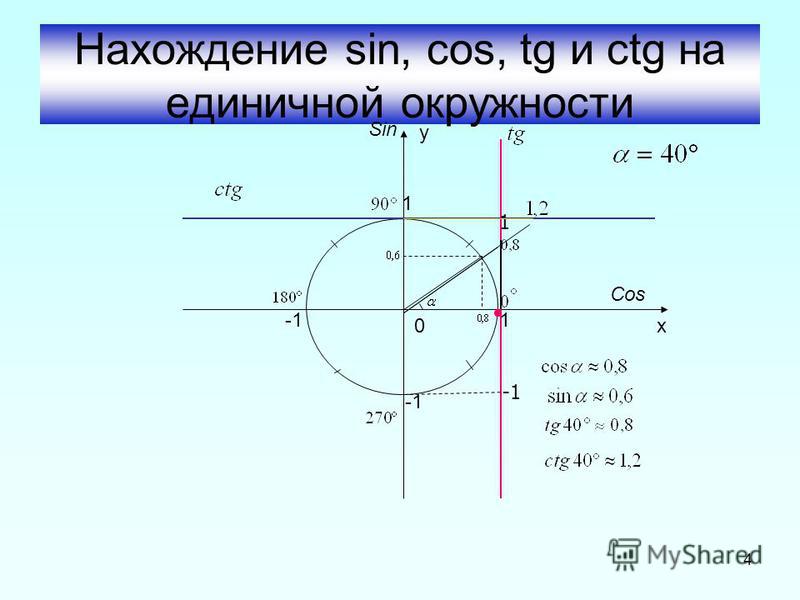 —
—
- Плакаты.
Ход урока.
1.Вводная беседа (о программе, тетрадях, требованиях).
Фронтально проверить домашнее задание.
2.Повторение материала по вопросам.
a) Дать определение sinx.
Чтобы определить понятия тригонометрических функций, рассматривают круг с центром, расположенным в начале координат, и радиусом равным единице (это так называемый тригонометрический круг). Для любого действительного числа х можно провести радиус OQ этого круга, образующий с осью абсцисс угол, радианная мера которого равна числу х (положительным считается направление поворота против хода часовой стрелки).
Пусть конец единичного радиуса OQ, соответствующего углу х,
совпадает с точкой Q(a;b) окружности; тогда координаты (a;b) точки Q называют координатами конца радиуса, соответствующего углу х.
Определение. Число, равное ординате конца единичного радиуса, соответствующего углу х, называется синусом угла х и обозначается sinx.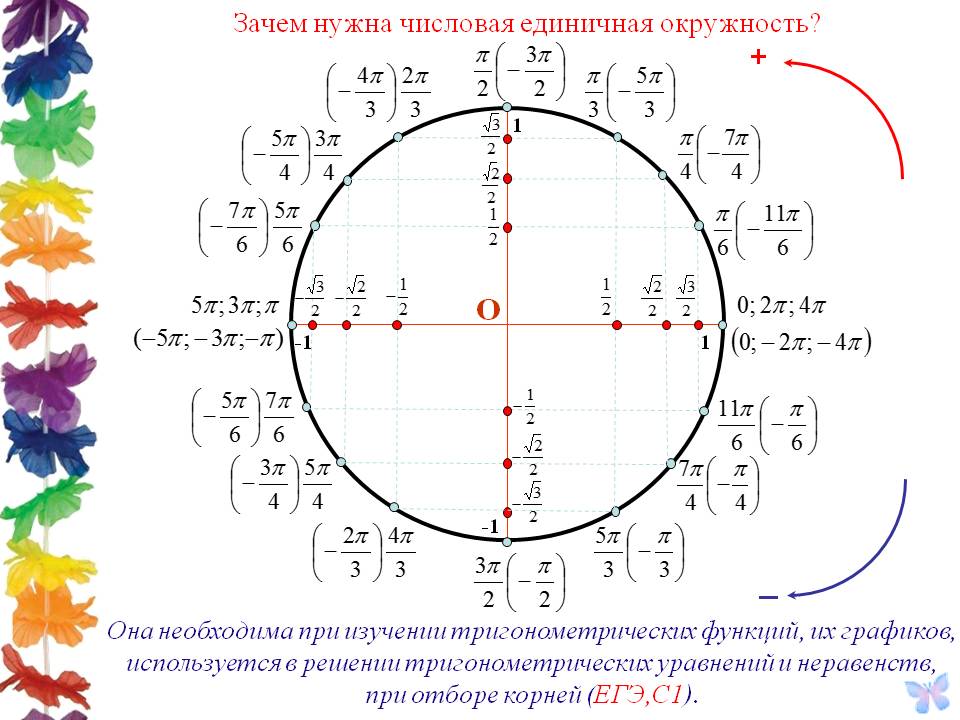
Поскольку каждому значению величины угла х на тригонометрическом круге соответствует единственная точка Q(a;b) такая, что радиус OQ образует угол х с осью абсцисс, то введенное отображение y = sinx является функцией.
б) Область определения функции. Так как для любого значения угла однозначно определена точка, являющаяся концом соответствующего радиуса, то область определения функции y = sinx – множество действительных чисел. Пишут D(sin) = R.
в) Область значений функции. E(sin) = [-1;1]. Действительно, ордината всякой точки, являющейся концом радиуса тригонометрического круга, может принимать лишь значения на отрезке [-1;1]. С другой стороны, для каждого значения ординаты b из этого отрезка можно указать хотя бы одну точку на окружности, имеющую эту ординату. Следовательно, это значение b будет синусом угла, образованного положительным направлением оси абсцисс и радиусом, соединяющим центр окружности и построенную точку.
г) Периодичность. Наименьший положительный период функции равен 2π . Докажем это. Поскольку центральный угол, опирающийся на дугу, совпадающую со всей окружностью, равен 2π , то точки, соответствующие углам х, (х+2π), (х -2π), изображаются на тригонометрическом круге одной и той же точкой, следовательно, синусы этих углов равны. Это означает, что число T=2π является периодом рассматриваемой функции. Докажем, что это наименьший положительный период. Рассмотрим значение функции y = sinx, равное единице. Оно достигается, только если х = π/2 + 2πn, n є Ζ. Следовательно, никакое число, меньшее 2π не может быть периодом.
Наименьший положительный период функции равен 2π . Докажем это. Поскольку центральный угол, опирающийся на дугу, совпадающую со всей окружностью, равен 2π , то точки, соответствующие углам х, (х+2π), (х -2π), изображаются на тригонометрическом круге одной и той же точкой, следовательно, синусы этих углов равны. Это означает, что число T=2π является периодом рассматриваемой функции. Докажем, что это наименьший положительный период. Рассмотрим значение функции y = sinx, равное единице. Оно достигается, только если х = π/2 + 2πn, n є Ζ. Следовательно, никакое число, меньшее 2π не может быть периодом.
д) Четность или нечетность. Рассмотрим (рис.2) точки M и N, соответствующие на тригонометрическом круге углам х и –х. Поскольку всякий круг симметричен относительно любой прямой, проходящей через его центр (а ось Оx является такой прямой), и равные по величине углы при симметрии переходят в равные углы, то точки M и N симметричны относительно оси Оx, следовательно, их ординаты противоположны. Это означает, что для любого значения х выполнено
Это означает, что для любого значения х выполнено
sin(-x) = -sinx, т. е. функция y = sinx является нечетной.
е) Точки пересечения графика с осями координат. График пересекает ось Ох в точках с абсциссами, определяемыми уравнением sinx=0, т. е.
х = πn, n є Ζ; график пересекает ось Оу в точке с ординатой,
определяемой равенством y = sin0, т.е. у = 0.
ж) Промежутки знакопостоянства функции. Так как ординаты точек, лежащих в верхней полуплоскости, положительны, а точек, расположенных в нижней полуплоскости, отрицательны, то sinx > 0 при
х є (2πk; π + 2πk), k є Ζ; sin x
з) Наибольшее и наименьшее значение. Наибольшее значение, равное 1, достигается при х = π/2 + 2πn, n є Ζ ; наименьшее значение, равное -1, достигается при х = — π/2 + 2πn, n є Ζ ;
и) Интервалы возрастания и убывания. Функция не является монотонной на всей области определения; она является монотонной на отрезках: возрастает при х є ( — π /2 +2πk; π /2 + 2πk), k є Ζ; убывает при
х є (π /2+ 2πk; 3π /2 + 2πk ), k є Ζ .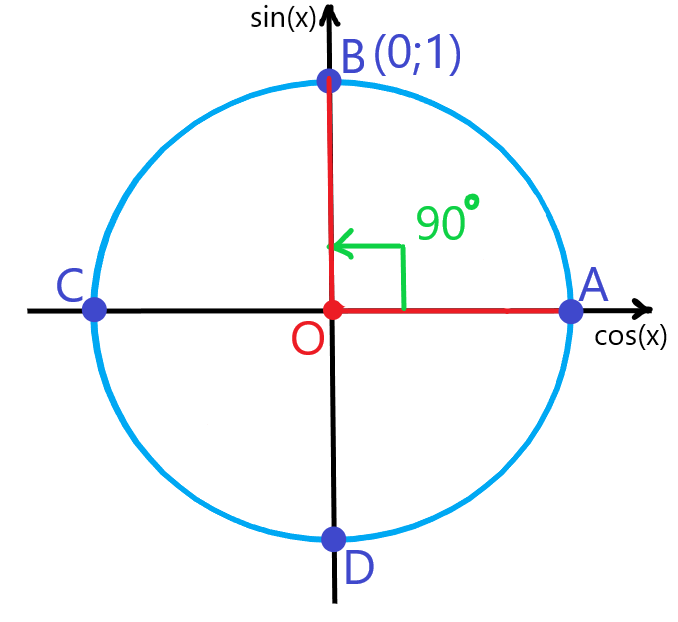
Для исследования функции на возрастание и убывание воспользуемся признаком возрастания и убывания, то есть найдем производную
f ́ (x) = (sinx) ́= cosx. Так как абсциссы точек, лежащих в правой полуплоскости положительны, то cos x >0 при х є ( — π /2 +2πk; π /2 + 2πk),
k є Ζ, следовательно, функция y = sinx будет возрастать на каждом промежутке вида ( — π /2 +2πk; π /2 + 2πk), k є Ζ . Абсциссы точек, лежащих в левой полуплоскости, отрицательны, т.е. cos x
х є (π /2+ 2πk; 3π /2 + 2πk ), k є Ζ ; следовательно, на этих промежутках производная отрицательна и функция y = sinx будет убывать на промежутках вида (π /2+ 2πk; 3π /2 + 2πk ), k є Ζ.
к) Асимптоты. График функции асимптот не имеет.
3. Изложение нового материала.
Решение уравнения sin х = а.
Поскольку по определению синусом угла называется ордината точки, лежащей на окружности единичного радиуса, то для решения уравнения
sin x =a надо найти на окружности все точки имеющие ординату a, т. е. лежащие на прямой y = a, см. рис.4
е. лежащие на прямой y = a, см. рис.4
По теореме о взаимном расположении прямой и окружности на плоскости заключаем, что при |a| > 1 прямая и окружность общих точек не имеют, следовательно и рассматриваемое уравнение не имеет решений. Если |a| = 1, то прямая
y = a касается окружности, т.е. имеет с ней ровно одну общую точку C. Наконец, если |a|
Для записи решения уравнения sin x = a вводят понятие арксинуса числа a. Чтобы однозначно определить угол х0 , соответствующий числу а, приходится требовать выполнения дополнительного условия, например, чтобы этот угол принадлежал интервалу [-π /2; π /2].
Определение. Арксинусом числа а, а є [-1;1], называется такое число х0, принадлежащее отрезку [-π /2; π /2], синус которого равен а. Это число обозначается arcsin a.
Из определения следует, что для каждого числа а, |a| ≤ 1, выполнено
sin(arcsin a) = a и −π /2 ≤ arcsin a ≤ π /2;
и наоборот, если выполнены условия
sinx = a и −π /2 ≤ a ≤ π /2 ,
то x = arcsin a.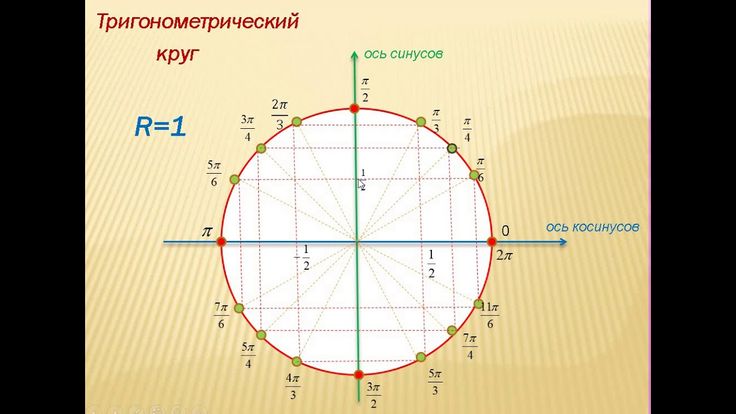
С помощью введенного понятия удобно записать решение уравнения. По определению, точке пересечения A соответствует угол х1 = arcsin a, см. рис.4. Учитывая периодичность функции y = sin x, получим серию решений
x = arcsin a + 2πk, k є Ζ .
Точка В, как отмечалось, симметрична точке А относительно оси Оу, поэтому ей соответствует угол х2 = π − arcsin a, поэтому можно записать вторую серию решений
x = π − arcsin a + 2πk, k є Ζ .
Других решений рассматриваемое уравнение иметь не может, поскольку противное означало бы, что окружность и прямая пересекаются более чем в двух точках.
Для сокращения записи две полученные серии решений обычно объединяют в одну
x = (-1) arcsin a + πk, k є Ζ .
При четных значениях k эта формула соответствует первой серии решений; при нечетных — второй.
4. Решение нескольких примеров на доске.
Пример 1.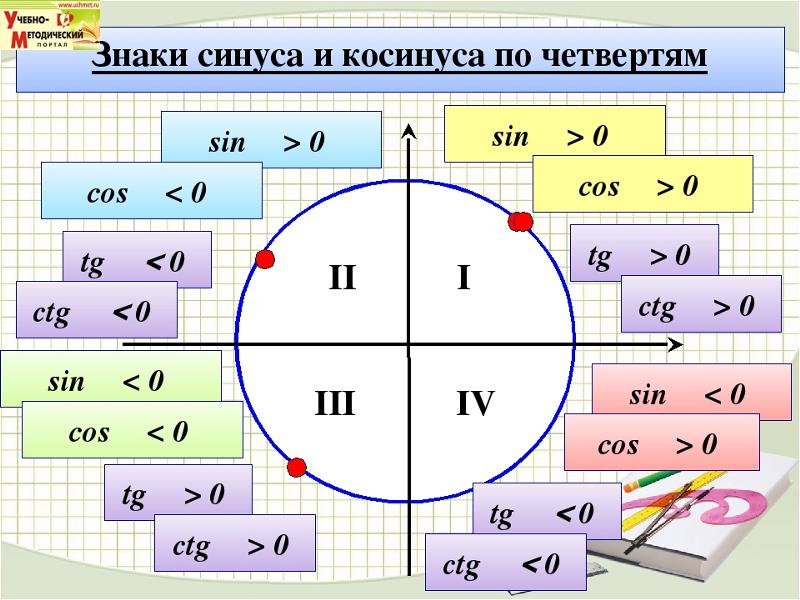 Решить уравнение sin(π /6 – 2x) = √3 /2.
Решить уравнение sin(π /6 – 2x) = √3 /2.
□ Имеем π /6 – 2x = ( — 1) arcsin √3 /2 + πk. Так как arcsin √3 /2 = π /3, то
π /6 – 2x = ( — 1) π /3 + πk, откуда х = — ( — 1) π /6 + π /12 + πk /2, или
х = (-1) π /6 + π /12 (6k + 1), k є Ζ.■
Если уравнение не является простейшим, то с помощью тождественных преобразований его нужно свести к одному или нескольким простейшим уравнениям, совокупность которых равносильна заданному.
При решении тригонометрических уравнений часто используются разложение на множители и введение новой переменной (метод подстановки).
Пример 2. Решить уравнение sin x = sin 2x cos 3x.
□ Применив к sin 2x формулу синуса двойного аргумента, получим
sin x = 2 sin x cos x cos 3x; sin x (1 — 2 cos x cos 3x) = 0.
Так как множители в левой части этого уравнения имеют смысл при любых значениях х, то оно равносильно совокупности двух уравнений: sin x = 0 и
1 — 2 cos x cos 3x = 0.
Первому уравнению удовлетворяют значения x = πn, n є Ζ.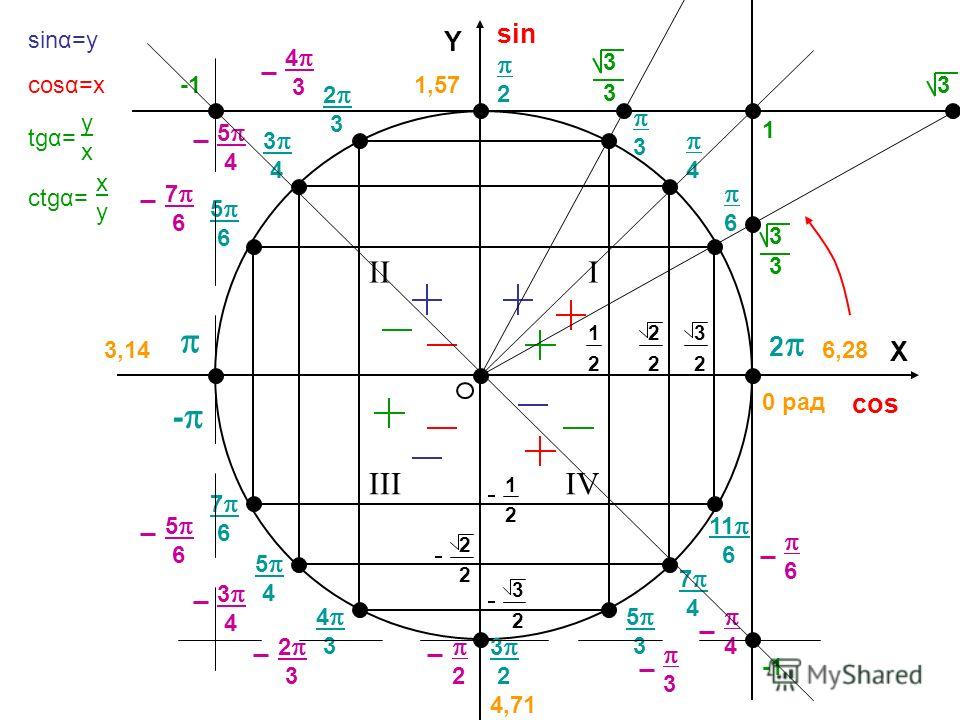
Для решения второго уравнения преобразуем произведение косинусов в сумму; имеем 1 – (cos 4x + cos 2x) = 0. Поскольку 1- cos 4x = 2 sin2x, уравнение принимает вид 2sin2x – cos 2x = 0, или 2(1-cos 2x)-cos 2x = 0, откуда получим 2cos2x + cos 2x – 2 = 0— квадратное уравнение относительно cos 2x. Полагая cos 2x = z , имеем 2z + z – 2 = 0. Решив это уравнение, находим z1 = (-1 + √17) /4, z2 = (-1-√17) /4. Так как
|z2| =|(-1-√17) /4| >1, то уравнение cos 2x = z2 не имеет решений. Остается решить уравнение cos 2x = (-1 + √17) /4. Имеем 2х = ± arccos(√17-1) /4 + 2πk, k є Ζ. Итак получаем ответ: x = πn; х = ± (1 /2)arccos(√17 -1) /4 + πk, k,n є Ζ. ■
При решении уравнения методом разложения на множители оно может не быть равносильным полученной совокупности уравнений, так как возможно появление посторонних корней. Чтобы избежать ошибки в ответе, нужно исключить из найденных значений неизвестного те, для которых заданное уравнение не имеет смысла.
Пример 3. Решить уравнение (1-sinx)(tg x-3) = 0.
□ Найдем значения х, удовлетворяющие каждому из уравнений 1-sinx = 0 и tg x-3 = 0; если sinx = 1,то получим
x = π /2 + 2πk, k є Ζ; (1)
если tg x = 3, т. е. tgx = ±√3, то
x = ±π /3 + πn, n є Ζ. (2)
Однако было бы ошибочным считать ответом объединение решений (1) и (2). Дело в том, что исходное уравнение не имеет смысла для значений
x = π /2 +πn (n є Ζ), поэтому первое из предполагаемых решений непригодно и ответом является только второе решение x = ±π /3 + πn, n є Ζ.■
Пример 4. Решить уравнение cosx cos2x cos4x = 1/8.
□ Наиболее быстрый способ решения – умножение правой и левой частей равенства на 8sinx, хотя при этом возможно появление посторонних корней. Чтобы избежать этого, следует учитывать, что в окончательное решение не должны входить значения х, для которых sinx = 0, т. е. значения x = πn (nєΖ), так как они не удовлетворяют исходному уравнению.
е. значения x = πn (nєΖ), так как они не удовлетворяют исходному уравнению.
После умножения на 8sinx уравнение примет вид
8sinx cosx cos2x cos4x = sinx.
Последовательно трижды применив формулу sin2x = 2 sinx cosx, получим сначала 4sin2x cos2x cos4x = sinx, затем 2sin4x cos4x = sinx и далее
sin8x = sinx, или sin8x — sinx = 0.Преобразуя по формуле
sinx-siny = 2cos(x+y)/2 sin(x-y)/2 разность синусов в произведение, получаем
Пусть sin 7x/2 = 0, тогда 7х/2 = πk (k є Ζ), откуда х = 2πk /7, k є Ζ, причем следует исключить значения х = 2πn (n є Ζ), получающиеся при k = 7n, как посторонние для исходного уравнения. Пусть теперь cos 9x/2 = 0;
тогда 9х/2 = π /2 + πm (m є Ζ), откуда х = π (2m +1) /9 (m є Ζ), причем следует исключить значения х = π(2n +1) (n є Ζ), получающиеся при m=9n+4 (nєΖ),как посторонние для исходного уравнения.
Итак, получаем ответ: х = 2πk /7, где целое k ≠ 7n, n є Ζ; х = π (2m + 1) /9, где целое m ≠ 9n + 4, n є Ζ.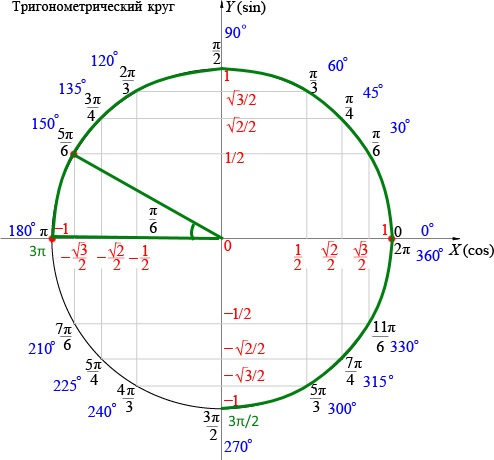 ■
■
5. Заключение урока.
1) теоретико-прикладные итоги урока; дифференцированная оценка
уровня ментального опыта учащихся: уровня усвоения ими темы,
компетентности, качества устной и письменной математической речи;
уровня проявленного творчества; уровня самостоятельности и рефлексии; уровня инициативы, познавательного интереса к отдельным методам математического мышления; уровней сотрудничества, интеллектуальной состязательности, стремления к высоким показателям учебно-математической деятельности и др.;
2) объявление аргументированных отметок, поурочного балла;
3) сбор тетрадей с домашней работой на выборочную или сплошную
проверку.
Спасибо за урок!
Простейшие тригонометрические уравнения
Когда-то я стал свидетелем разговора двух абитуриентов:
– Когда надо прибавить 2πn, а когда – πn? Никак не могу запомнить!
– И у меня такая же проблема.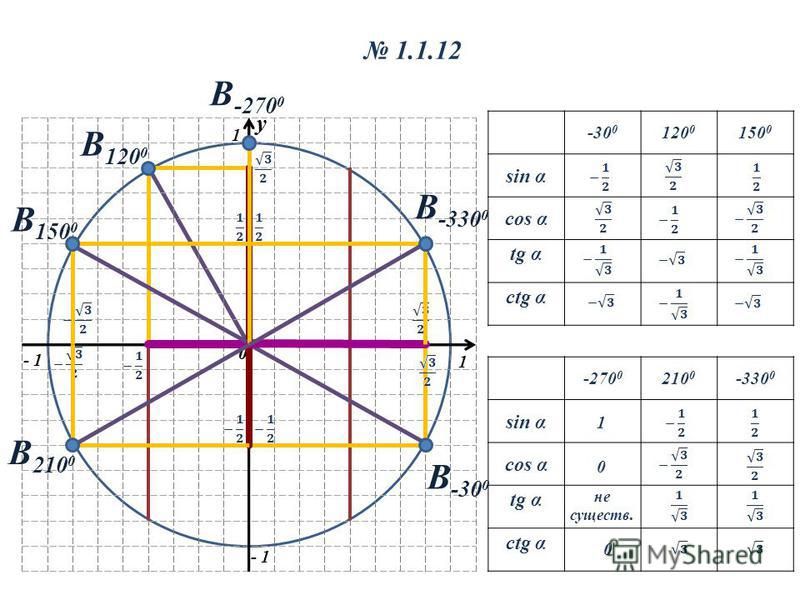
Так и хотелось им сказать: «Не запоминать надо, а понимать!»
Данная статья адресована прежде всего старшеклассникам и, надеюсь, поможет им с «пониманием» решать простейшие тригонометрические уравнения:
1) sinx=a ,
2) cosx=a ,
3) tgx=a и
4) ctgx=a.
Числовая окружность
Наряду с понятием числовой прямой есть еще и понятие числовой окружности. Как мы знаем, в прямоугольной системе координат окружность ,с центром в точке (0;0) и радиусом 1, называется единичной. Вообразим числовую прямую тонкой нитью и намотаем ее на эту окружность : начало отсчета (точку 0), приставим к «правой» точке единичной окружности, положительную полуось обмотаем против движения часовой стрелки, а отрицательную – по направлению (рис. 1). Такую единичную окружность называют числовой.
Свойства числовой окружности
- Каждое действительное число находится на одной точке числовой окружности.
- На каждой точке числовой окружности находятся бесконечно много действительных чисел.
 Так как длина единичной окружности равна 2π, то разность между любыми двумя числами на одной точке окружности равна одному из чисел ±2π ; ±4π ; ±6π ; …
Так как длина единичной окружности равна 2π, то разность между любыми двумя числами на одной точке окружности равна одному из чисел ±2π ; ±4π ; ±6π ; …
Сделаем вывод: зная одно из чисел точки A, мы можем найти все числа точки A.
- Так как длина полуокружности равна π, то разность между любыми двумя числами на диаметрально противоположных точках числовой окружности равна одному из чисел : ±π ; ±3π ; ±5π ; …
Проведем диаметр АС (рис. 2). Так как x_0 – одно из чисел точки А, то числа x_0±π ; x_0±3π; x_0±5π; … и только они будут числами точки C. Выберем одно из этих чисел, скажем, x_0+π, и запишем с его помощью все числа точки C: x_C=x_0+π+2πk ,k∈Z. Отметим, что числа на точках A и C можно объединить в одну формулу: x_(A ; C)=x_0+πk ,k∈Z (при k = 0; ±2; ±4; … получим числа точки A, а при k = ±1; ±3; ±5; … – числа точки C).
Сделаем вывод: зная одно из чисел на одной из точек A или C диаметра АС, мы можем найти все числа на этих точках.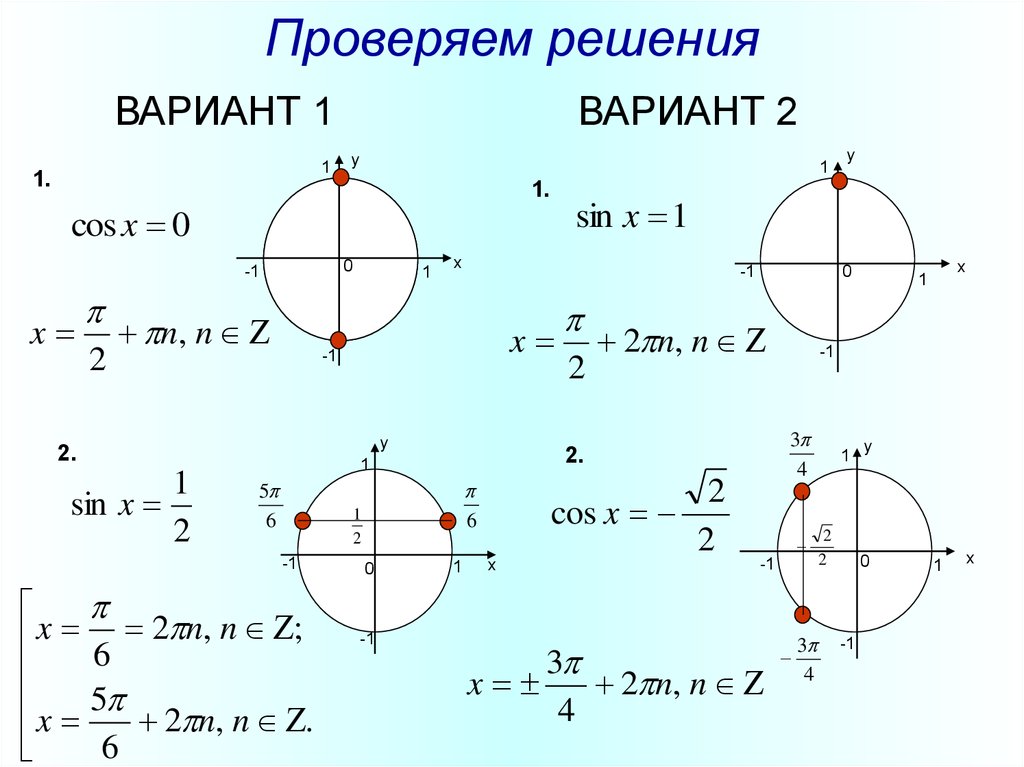 k∙x_0+πk ,k∈Z . (при k= 0; ±2; ±4; … получим числа точки A, а при k = ±1; ±3; ±5; … – числа точки D).
k∙x_0+πk ,k∈Z . (при k= 0; ±2; ±4; … получим числа точки A, а при k = ±1; ±3; ±5; … – числа точки D).
Сделаем вывод: зная одно из чисел на одной из точек A или D горизонтальной хорды AD, мы можем найти все числа на этих точках.
Шестнадцать основных точек числовой окружности
На практике решение большинства простейших тригонометрических уравнений связано с шестнадцатью точками окружности (рис. 3). Что это за точки? Красные, синие и зеленые точки делят окружность на 12 равных частей. Так как длина полуокружности равна π, то длина дуги A1A2 равна π/2, длина дуги A1B1 равна π/6, а длина дуги A1C1 равна π/3.
Теперь можем указать по одному числу на точках:
0 на A1 ,
π/6 на B1 ,
π/3 на С1 и
π/2 на A2 .
Вершины оранжевого квадрата – середины дуг каждой четверти, следовательно, длина дуги A1D1 равна π/4 и, значит, π/4 – одно из чисел точки D1. Воспользовавшись свойствами числовой окружности, мы можем записать с помощью формул все числа на всех отмеченных точках нашей окружности.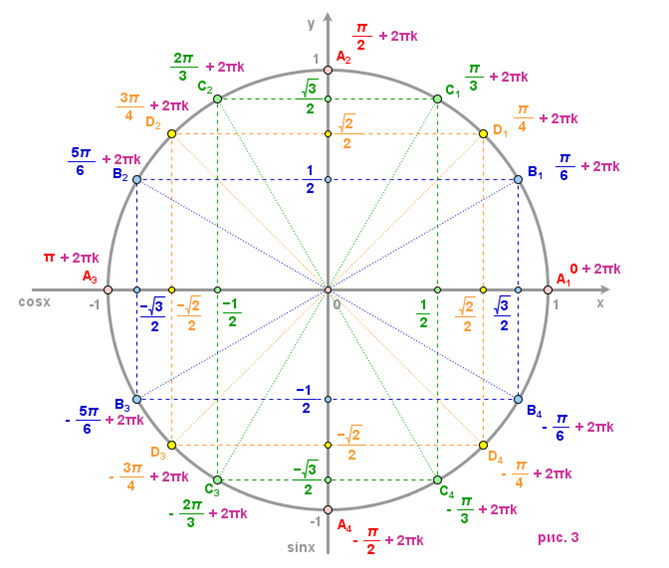 На рисунке отмечены также и координаты этих точек (опустим описание их получения).
На рисунке отмечены также и координаты этих точек (опустим описание их получения).
Усвоив выше сказанное, мы имеем теперь достаточную подготовку для решения частных случаев (для девяти значений числа a)
простейших уравнений.Решить уравнения
1) sinx=1⁄(2 ).
– Что от нас требуется?
– Найти все те числа x, синус которых равен 1/2.
Вспомним определение синуса: sinx – ордината точки числовой окружности, на которой находится число x . На окружности имеем две точки, ордината которых равна 1/2 . Это концы горизонтальной хорды B1B2 . Значит, требование «решить уравнение sinx=1⁄2 » равнозначно требованию «найти все числа на точке B1 и все числа на точке B2».
2) sinx=-√3⁄2 .
Нам надо найти все числа на точках C4 и C3.
3) sinx=1. На окружности имеем только одну точку с ординатой 1 – точка A2 и, значит, нам надо найти только все числа этой точки.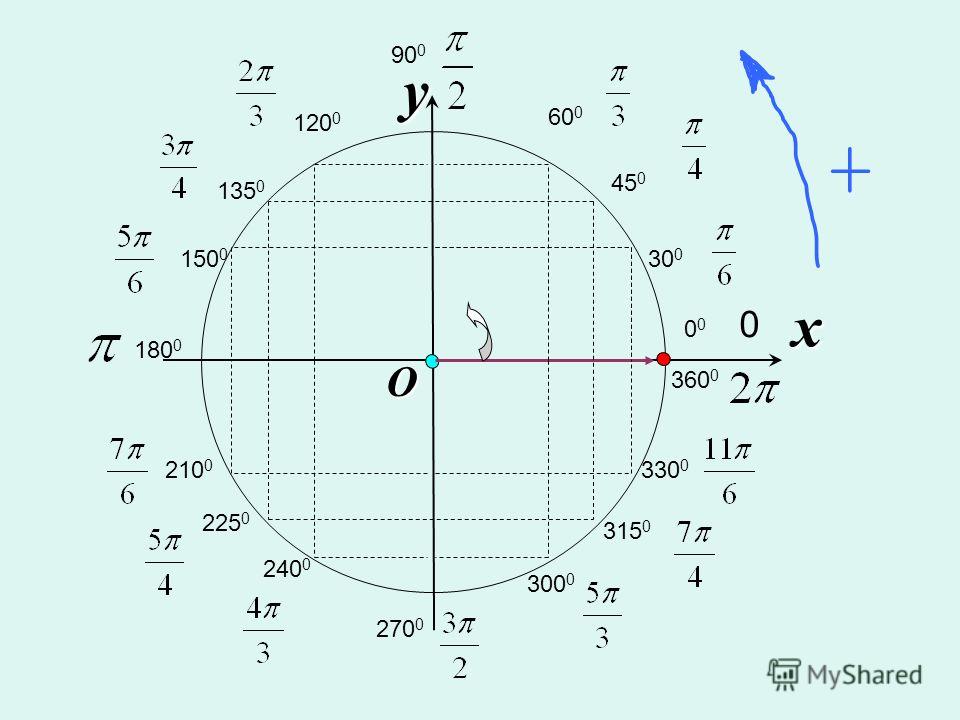
Ответ: x=π/2+2πk , k∈Z .
4) sinx=-1
Только точка A_4 имеет ординату -1. Все числа этой точки и будут конями уравнения.
Ответ: x=-π/2+2πk , k∈Z .
5) sinx=0 .
На окружности имеем две точки с ординатой 0 – точки A1 и A3 . Можно указать числа на каждой из точек по отдельности, но, учитывая, что эти точки диаметрально противоположные, лучше объединить их в одну формулу: x=πk ,k∈Z .
Ответ: x=πk ,k∈Z .
6) cosx=√2⁄2 .
Вспомним определение косинуса: cosx — абсцисса точки числовой окружности на которой находится число x. На окружности имеем две точки с абсциссой √2⁄2 – концы горизонтальной хорды D1D4 . Нам нужно найти все числа на этих точках. Запишем их, объединив в одну формулу.
Ответ: x=±π/4+2πk , k∈Z .
7) cosx=-1⁄2 .
Надо найти числа на точках C_2 и C_3 .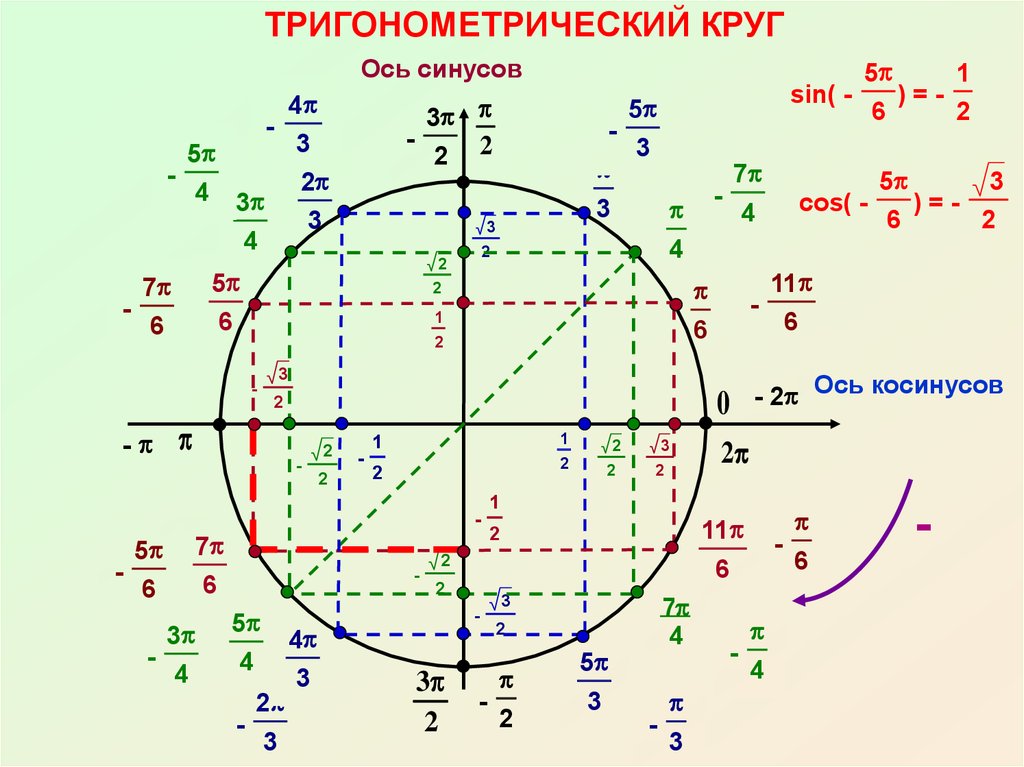
Ответ: x=±2π/3+2πk , k∈Z .
10) cosx=0 .
Только точки A2 и A4 имеют абсциссу 0, значит, все числа на каждой из этих точках и будут решениями уравнения. .
Решениями уравнения системы являются числа на точках B_3 и B_4 .Неравенству cosx<0 удовлетворяют только числа b_3
Ответ: x=-5π/6+2πk , k∈Z .
Заметим,что при любом допустимом значении x второй множитель положителен и, следовательно,уравнение равносильно системе
Решениями уравнения системы являются чила точек D_2 и D_3 . Числа точки D_2 не удовлетворяют неравенству sinx≤0,5 ,а числа точки D_3-удовлетворяют.
© blog.tutoronline.ru, при полном или частичном копировании материала ссылка на первоисточник обязательна.
Единичный круг | Прикладная алгебра и тригонометрия
Чтобы определить наши тригонометрические функции, мы начнем с рисования единичной окружности, окружности с центром в начале координат и радиусом 1, как показано на рисунке 2.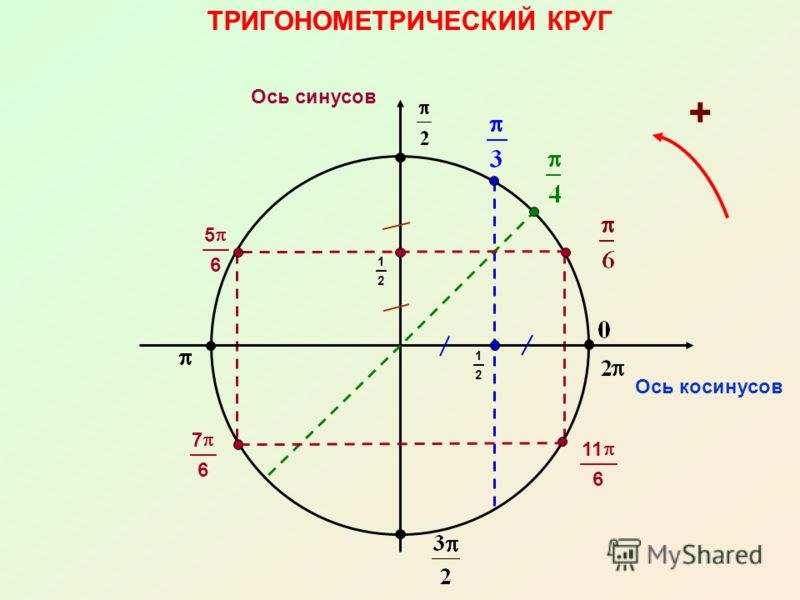 Угол (в радианах), который [латекс]t[/латекс ] образует дугу длиной [latex]s[/latex]. Используя формулу [латекс]s=rt[/латекс] и зная, что [латекс]r=1[/латекс], мы видим, что для окружности единиц [латекс]s=t[/латекс].
Угол (в радианах), который [латекс]t[/латекс ] образует дугу длиной [latex]s[/latex]. Используя формулу [латекс]s=rt[/латекс] и зная, что [латекс]r=1[/латекс], мы видим, что для окружности единиц [латекс]s=t[/латекс].
Напомним, что х- и у- 9Оси 0008 делят координатную плоскость на четыре четверти, называемые квадрантами. Мы помечаем эти квадранты, чтобы имитировать направление положительного угла. Четыре квадранта обозначены I, II, III и IV.
Для любого угла [латекс]t[/латекс] мы можем обозначить пересечение конечной стороны и единичного круга его координатами [латекс]\влево(х,у\вправо)[/латекс]. Координаты [латекс]х[/латекс] и [латекс]у[/латекс] будут выходами тригонометрических функций [латекс]f\left(t\right)=\cos t[/латекс] и [латекс] f\left(t\right)=\sin t[/latex] соответственно. Это означает [латекс]x=\cos t[/латекс] и [латекс]у=\sin t[/латекс].
Рисунок 2. Единичная окружность, центральный угол которой равен [латекс]t[/латекс] радианам
A Общее примечание: Единичная окружность
Единичная окружность имеет центр в точке 0\right)[/latex] и радиус [latex]1[/latex] .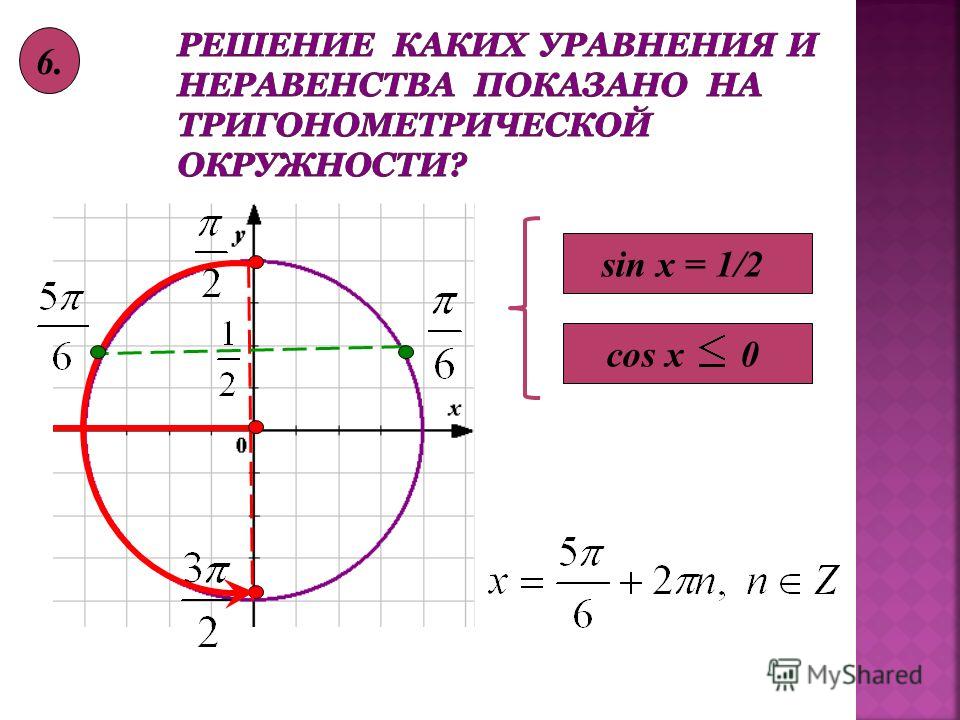 В единичном круге длина пересекаемой дуги равна радианной мере центрального угла [латекс]1[/латекс].
В единичном круге длина пересекаемой дуги равна радианной мере центрального угла [латекс]1[/латекс].
Пусть [латекс]\влево(х,у\вправо)[/латекс] будет концом единичной окружности дуги с длиной дуги [латекс]s[/латекс]. Координаты [латекс]\влево(х,у\вправо)[/латекс] этой точки можно описать как функции угла.
Определение функций синуса и косинуса
Теперь, когда мы пометили нашу единичную окружность, мы можем узнать, как координаты [латекс]\влево(х,у\вправо)[/латекс] соотносятся с длиной дуги и углом . Функция синуса связывает действительное число [latex]t[/latex] с y -координатой точки, где соответствующий угол пересекает единичную окружность. Точнее, синус угла [latex]t[/latex] равен y -значению конечной точки на единичной окружности дуги длины [latex]t[/latex]. На рисунке 2 синус равен [latex]y[/latex]. Как и все функции, синусоидальная функция имеет вход и выход.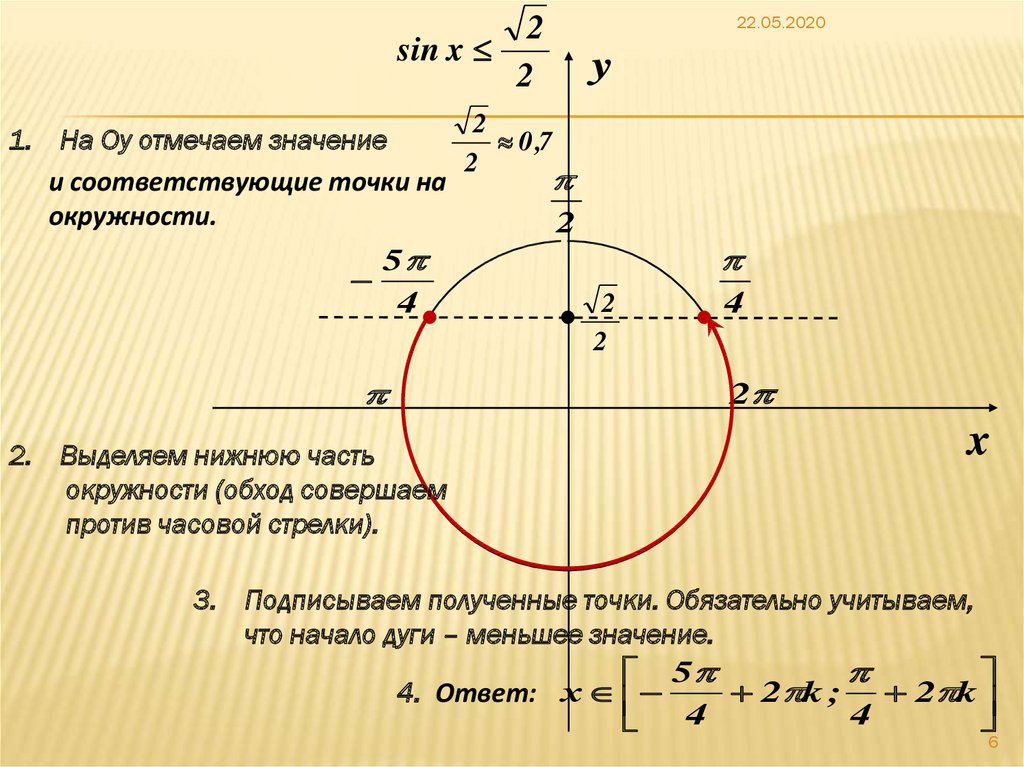 {2} [ /латекс]. Имейте в виду, что многие калькуляторы и компьютеры не распознают стенографию. Если вы сомневаетесь, используйте дополнительные скобки при вводе вычислений в калькулятор или компьютер.
{2} [ /латекс]. Имейте в виду, что многие калькуляторы и компьютеры не распознают стенографию. Если вы сомневаетесь, используйте дополнительные скобки при вводе вычислений в калькулятор или компьютер.
Общее примечание: функции синуса и косинуса
Если [latex]t[/latex] является действительным числом и точка [latex]\left(x,y\right)[/latex] на единичной окружности соответствует угол [латекс]t[/латекс], затем
[латекс]\cos t=x[/латекс]
[латекс]\sin t=y[/латекс]
Как: Дана точка
P [латекс]\влево(х,у\вправо)[/латекс] на единичной окружности, соответствующей углу [латекс]t[/латекс], найдите синус и косинус.- Синус [latex]t[/latex] равен y -координата точки [latex]P:\sin t=y[/latex].
- Косинус [latex]t[/latex] равен x -координате точки [latex]P: \text{cos}t=x[/latex].
Пример 1. Нахождение значений функций для синуса и косинуса
Точка [latex]P[/latex] — это точка на единичной окружности, соответствующая углу [latex]t[/latex], как показано на рисунке 4. Найдите [латекс]\cos\left(t\right)\\[/latex] и [латекс]\text{sin}\left(t\right)\\[/latex].
Найдите [латекс]\cos\left(t\right)\\[/latex] и [латекс]\text{sin}\left(t\right)\\[/latex].
[латекс]\begin{array}{l}\begin{array}{l}\\ x=\cos t=\frac{1}{2}\end{array}\hfill \\ y= \sin t=\frac{\sqrt{3}}{2}\hfill \end{array}\\[/latex]
Попробуйте 1
Некоторый угол [latex]t[/latex] соответствует точка на единичной окружности в точке [латекс]\влево(-\frac{\sqrt{2}}{2},\frac{\sqrt{2}}{2}\right)\\[/latex], как показано на Рисунок 5. Найдите [латекс]\cos t[/латекс] и [латекс]\sin t[/латекс]. 9{2}t=1[/latex], известный как Пифагорейская идентичность .
Мы можем использовать тождество Пифагора, чтобы найти косинус угла, если мы знаем синус, или наоборот. Однако, поскольку уравнение дает два решения, нам нужно дополнительное знание угла, чтобы выбрать решение с правильным знаком. Если мы знаем квадрант, в котором находится угол, мы можем легко выбрать правильное решение.
Общее примечание: Пифагорейская идентичность
Пифагорейская идентичность 9{2}t=1[/latex]
Как сделать: Зная синус некоторого угла [latex]t[/latex] и его положение в квадранте, найдите косинус [latex]t[/latex].
- Подставить известное значение [латекс]\sin\left(t\right)[/латекс] в тождество Пифагора.
- Найдите [латекс]\cos\left(t\right)[/латекс].
- Выберите решение с соответствующим знаком для значений x в квадранте, где находится [латекс]t[/латекс].
Пример 3. Нахождение косинуса по синусу или синуса по косинусу
Если [латекс]\sin \left(t\right)=\frac{3}{7}\\[/latex] и [latex]t[/latex] находится во втором квадранте, найти [latex]\ потому что \влево(т\вправо)\\[/латекс].
Решение
Если мы опустим вертикальную линию из точки на единичной окружности, соответствующей [latex]t[/latex], мы создадим прямоугольный треугольник, из которого мы можем увидеть, что Пифагорейское тождество — это просто один из случаев Теорема Пифагора.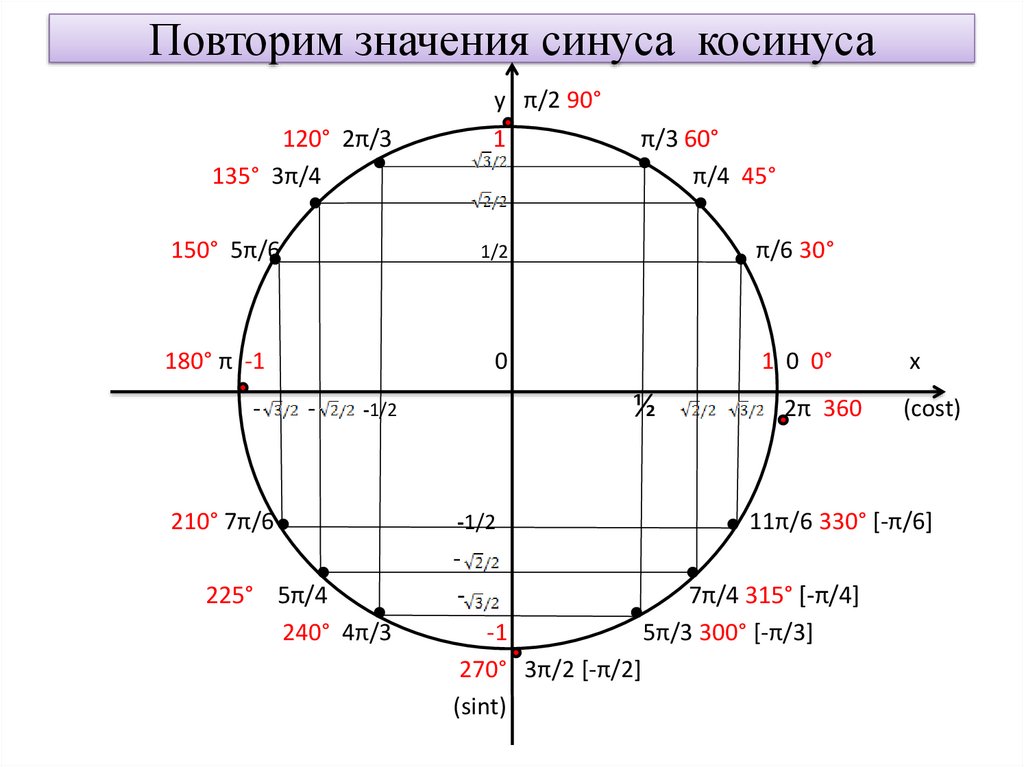
Рисунок 8
Подстановка известного значения синуса в тождество Пифагора, 9{2}\left(t\right)=\frac{40}{49}\hfill \\ \text{cos}\left(t\right)=\pm \sqrt{\frac{40}{49}} =\pm \frac{\sqrt{40}}{7}=\pm \frac{2\sqrt{10}}{7}\hfill \end{array}\\[/latex]
Поскольку угол во втором квадранте мы знаем, что значение x- является отрицательным действительным числом, поэтому косинус также отрицателен. Итак,
[латекс]\текст{cos}\left(t\right)=-\frac{2\sqrt{10}}{7}\\[/latex]
Попробуйте 3
If [латекс]\ потому что \left(t\right)=\frac{24}{25}\\[/latex] и [latex]t[/latex] находится в четвертом квадранте, найдите [latex]\text{sin}\left( т\справа)\\[/латекс]. 9\circ [/latex] треугольник является равнобедренным треугольником, поэтому x- и y -координаты соответствующей точки на окружности совпадают. Поскольку значения x- и y одинаковы, значения синуса и косинуса также будут равны.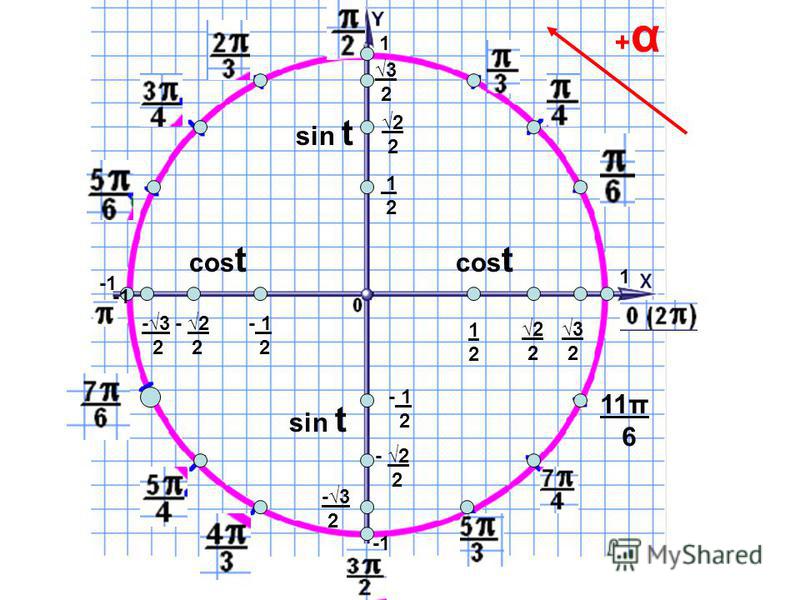 Рис. 9 Это означает, что радиус лежит вдоль линии [латекс]у=х[/латекс]. Радиус единичной окружности равен 1. Итак, прямоугольный треугольник, образованный под линией [latex]y=x[/latex], имеет стороны [latex]x[/latex] и [latex]y\text{ }\left (y=x\right)[/latex], а радиус = 1,9{2}=\frac{1}{2}\\ \text{ }x=\pm \frac{1}{\sqrt{2}}\end{array}\\[/latex]
Рис. 9 Это означает, что радиус лежит вдоль линии [латекс]у=х[/латекс]. Радиус единичной окружности равен 1. Итак, прямоугольный треугольник, образованный под линией [latex]y=x[/latex], имеет стороны [latex]x[/latex] и [latex]y\text{ }\left (y=x\right)[/latex], а радиус = 1,9{2}=\frac{1}{2}\\ \text{ }x=\pm \frac{1}{\sqrt{2}}\end{array}\\[/latex]
В квадранте I , [латекс]x=\frac{1}{\sqrt{2}}\\[/latex].
В [латекс]t=\frac{\pi }{4}[/латекс] или 45 градусов,
[латекс]\begin{array}{l}\left(x,y\right)=\left (x,x\right)=\left(\frac{1}{\sqrt{2}},\frac{1}{\sqrt{2}}\right)\hfill \\ x=\frac{1} {\ sqrt {2}}, y = \ frac {1} {\ sqrt {2}} \ hfill \\ \ cos t = \ frac {1} {\ sqrt {2}}, \ sin t = \ frac { 1}{\sqrt{2}}\hfill \end{array}\\[/latex]
Если мы затем рационализируем знаменатели, то получим 9\circ [/latex], как показано на рисунке 12.
Рисунок 11
Рисунок 12
Поскольку все углы равны, стороны также равны. Вертикальная линия имеет длину [latex]2y[/latex], и поскольку все стороны равны, мы также можем заключить, что [latex]r=2y[/latex] или [latex]y=\frac{1}{2 }р[/латекс]. Так как [латекс]\sin t=y[/латекс] ,
Вертикальная линия имеет длину [latex]2y[/latex], и поскольку все стороны равны, мы также можем заключить, что [latex]r=2y[/latex] или [latex]y=\frac{1}{2 }р[/латекс]. Так как [латекс]\sin t=y[/латекс] ,
[латекс]\sin \left(\frac{\pi }{6}\right)=\frac{1}{2}r\\[/ латекс]
А так как [латекс]r=1[/латекс] в нашем 9\circ [/латекс]. Теперь у нас есть равносторонний треугольник. Поскольку каждая сторона равностороннего треугольника [латекс]ABC[/латекс] имеет одинаковую длину, и мы знаем, что одна сторона является радиусом единичной окружности, все стороны должны иметь длину 1.
Рисунок 13
Угол [латекс]ABD[/латекс] равен 30°. Итак, если число двойное, угол [латекс]АВС[/латекс] равен 60°. [latex]BD[/latex] является серединным перпендикуляром к [latex]AC[/latex], поэтому он делит [latex]AC[/latex] пополам. Это означает, что [latex]AD[/latex] — это [latex]\frac{1}{2}[/latex] радиус, или [latex]\frac{1}{2}[/latex]. Обратите внимание, что [latex]AD[/latex] — это 9\circ [/latex] равны [латекс]\left(\frac{1}{2},\frac{\sqrt{3}}{2}\right)\\[/latex], поэтому мы можем найти синус и косинус.
[латекс]\begin{array}{l}\left(x,y\right)=\left(\frac{1}{2},\frac{\sqrt{3}}{2}\right) \hfill \\ x=\frac{1}{2},y=\frac{\sqrt{3}}{2}\hfill \\ \cos t=\frac{1}{2},\sin t= \frac{\sqrt{3}}{2}\hfill \end{array}\\[/latex]
Теперь мы нашли значения косинуса и синуса для всех наиболее часто встречающихся углов в первом квадранте единичный круг. В таблице ниже приведены эти значения.
| Угол | 0 | [латекс]\frac{\pi }{6}\\[/латекс], или 30 | [латекс]\frac{\pi }{4}\\[/латекс], или 45° | [латекс]\frac{\pi }{3}\\[/латекс], или 60° | [латекс]\frac{\pi }{2}\\[/латекс], или 90° |
| Косинус | 1 | [латекс]\frac{\sqrt{3}}{2}\\[/латекс] | [латекс]\frac{\sqrt{2}}{2}\\[/латекс] | [латекс]\frac{1}{2}\\[/латекс] | 0 |
| Синус | 0 | [латекс]\frac{1}{2}\\[/латекс] | [латекс]\frac{\sqrt{2}}{2}\\[/латекс] | [латекс]\frac{\sqrt{3}}{2}\\[/латекс] | 1 |
На рисунке 14 показаны общие углы в первом квадранте единичной окружности.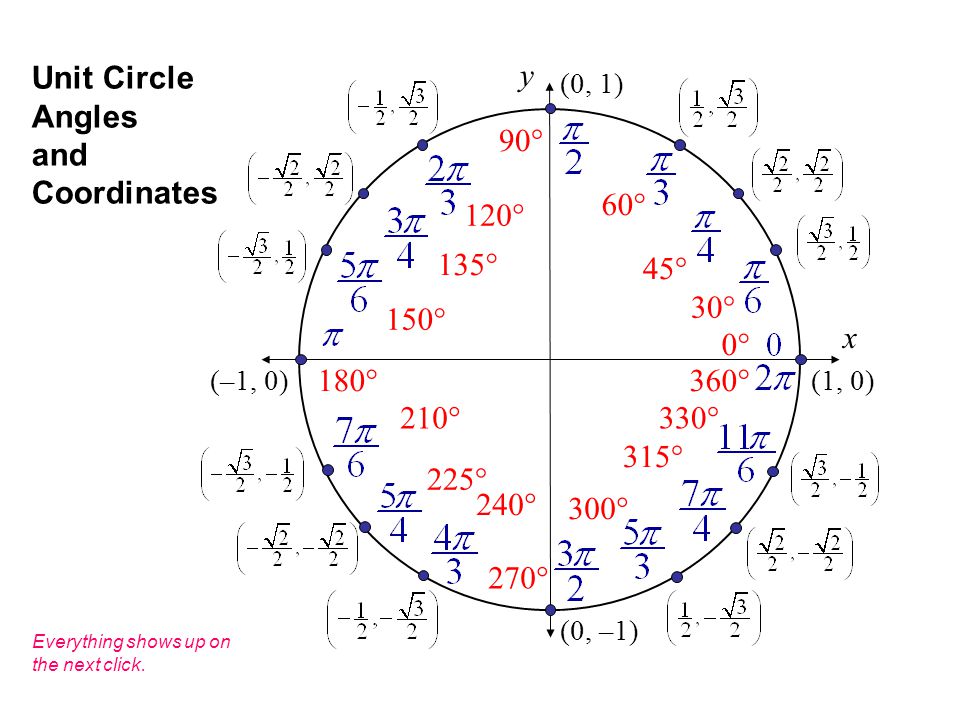
Рис. 14
Использование калькулятора для нахождения синуса и косинуса
Чтобы найти косинус и синус углов, отличных от специальных углов , обратимся к компьютеру или калькулятору. Имейте в виду : Большинство калькуляторов можно установить в режим «градусы» или «радианы», которые сообщают калькулятору единицы измерения для входного значения. Когда мы оцениваем [латекс]\cos \влево(30\вправо)[/латекс] на нашем калькуляторе, он оценивает его как косинус 30 градусов, если калькулятор находится в режиме градусов, или как косинус 30 радиан, если калькулятор находится в радианном режиме.
Как: Зная угол в радианах, используйте графический калькулятор, чтобы найти косинус.
- Если в калькуляторе есть режимы в градусах и в радианах, установите его в режим в радианах.
- Нажмите клавишу COS.
- Введите значение угла в радианах и нажмите клавишу закрытия скобок «)».

- Нажмите ВВОД.
Пример 4. Использование графического калькулятора для нахождения синуса и косинуса . 9\circ [/latex], например, включив коэффициент преобразования в радианы как часть ввода:
SIN( 20 × π ÷ 180 ) ENTER
Попробуйте 4
Оцените [латекс]\sin \left( \frac{\pi }{3}\right)\\[/latex].
Решение
Определение области определения и диапазона функций синуса и косинуса
Теперь, когда мы можем найти синус и косинус угла, нам нужно обсудить их области определения и диапазоны. Каковы области определения функций синуса и косинуса? То есть, каковы наименьшее и наибольшее числа, которые могут быть входными данными функций? Поскольку углы меньше 0 и углы больше [латекс]2\пи [/латекс] все еще могут быть изображены на единичном круге и имеют реальные значения [латекс]x,y[/латекс] и [латекс]r[/ латекс], нет нижнего или верхнего предела углов, которые могут быть входными данными для функций синуса и косинуса. Входными данными для функций синуса и косинуса является вращение от положительной x -ось, и это может быть любое действительное число.
Входными данными для функций синуса и косинуса является вращение от положительной x -ось, и это может быть любое действительное число.
Каковы диапазоны функций синуса и косинуса? Каковы наименьшее и максимальное возможные значения их выхода? Мы можем увидеть ответы, изучив окружность из единиц, как показано на рисунке 15. Границы координаты x равны [латекс]\влево[-1,1\вправо][/латекс]. Границы координаты y также равны [латекс]\влево[-1,1\вправо][/латекс]. Таким образом, диапазон функций синуса и косинуса составляет [латекс]\влево[-1,1\вправо][/латекс].
Рисунок 15
SIN-12-Google SUCE
ALLBILDERVIDEOSSHOPPINGMAPSNEWSBücher
SUCOOPTION
SIN (-120).
www.cuemath.com › тригонометрия › sin-120- градусов
Значение sin 120 градусов равно 0,8660254. . .. Sin 120 градусов в радианах записывается как sin (120° × π/180°), т. е. sin (2π/3) или sin (2,094395…).
е. sin (2π/3) или sin (2,094395…).
Sin 120 — Значение, методы вывода и примеры решений {3}}{2}\]. Способ 2. Другой способ получения значения sineo 120 градусов – это …
Как получить значение Sin 120 градусов? — Byju’s
byjus.com › математика › sin-120
16.07.2020 · Следовательно, sin 120° = √3/2. Здесь для справки приведены значения других важных тригонометрических углов для различных соотношений.
Площади параллелограммов и треугольников Класс 9: Медиана четных чисел
Важные вопросы Класс 11 Математика Глава 11 Конические сечения: сопряжение комплексного числа
Факторы 150: Важные вопросы Класс 8 Математика Глава 1 Рациональные числа Пятиугольная призма
Изображение
Все изображения
Все изображения
sin120 | грех(120)| синус 120 градусов | Первый способ — YouTube
www.youtube.com › смотреть
07.07.2019 · В этом видео учимся находить значение sin120. Здесь я применил sin(90 + x) = cos(x) identity .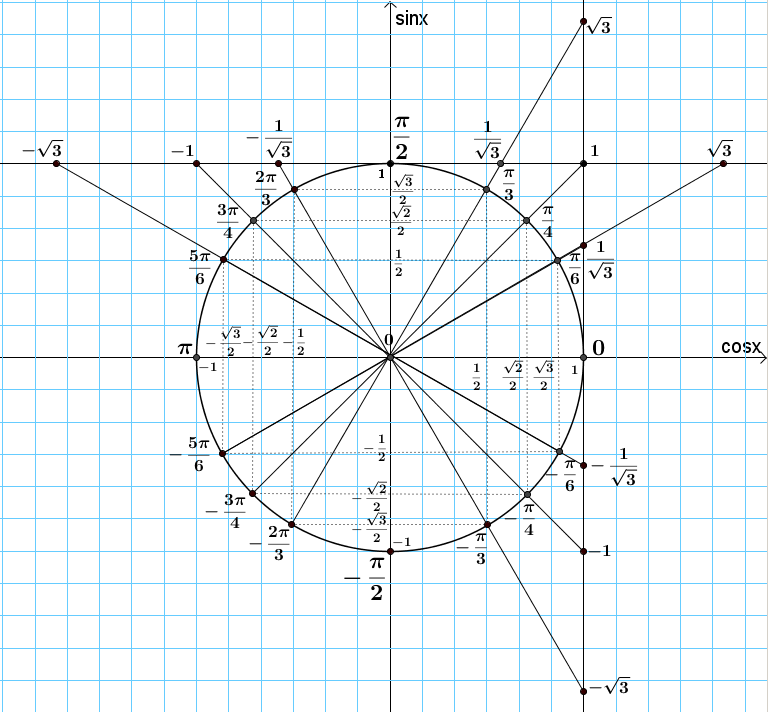 ..
..
Dauer: 1:43
Прислан: 07.07.2019
sin-120 | синус -120 градусов | Способ первый — YouTube
www.youtube.com › смотреть
13.10.2019 · В этом видео учимся находить значение sin(-120). Здесь я применил sin(-x) = -sin(x …
Dauer: 2:28
Прислан: 13.10.2019
sin-120 | синус -120 градусов | Третий метод — YouTube
www.youtube.com › смотреть
20.10.2019 · В этом видео учимся находить значение sin(-120). Здесь я применил sin(-x) = -sin(x …
Dauer: 2:56
Прислан: 20.10.2019
Найдите точное значение sin(120) — Mathway
www.mathway.com › Тригонометрия.о | Вопросы по математике — Toppr
www.toppr.com › … › Тригонометрические функции
sin120∘=sin(180∘−60∘). =sin60∘=23 . Решите любой вопрос о тригонометрических функциях с помощью: — Образцы проблем. > Был ли этот ответ полезен? голосование за 0.
Что такое синус 120 градусов? — Study.

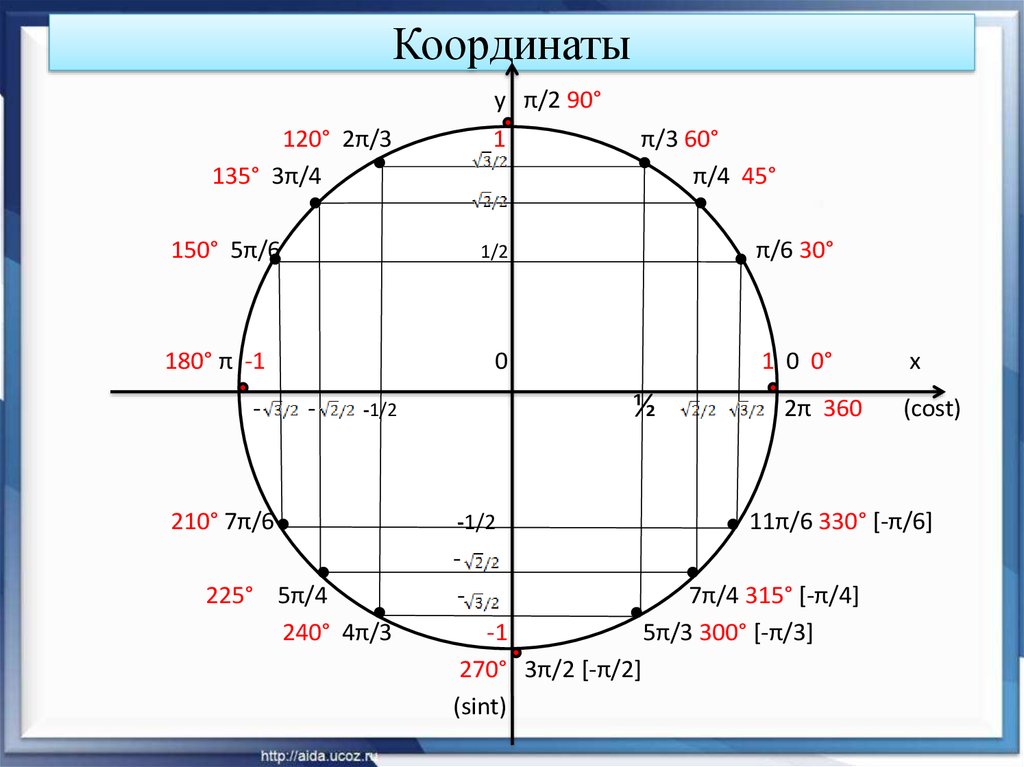 Так как длина единичной окружности равна 2π, то разность между любыми двумя числами на одной точке окружности равна одному из чисел ±2π ; ±4π ; ±6π ; …
Так как длина единичной окружности равна 2π, то разность между любыми двумя числами на одной точке окружности равна одному из чисел ±2π ; ±4π ; ±6π ; … 