Синус 2п: a)+cos(-a) — ответ на Uchi.ru

alexxlab / / Разное

Mathway | Популярные задачи

1Найти точное значениеsin(30)
2Найти точное значениеsin(45)
3Найти точное значениеsin(30 град. )
4Найти точное значениеsin(60 град. )
5Найти точное значениеtan(30 град. )
6Найти точное значениеarcsin(-1)
7Найти точное значениеsin(pi/6)
8
Найти точное значение		cos(pi/4)
9Найти точное значениеsin(45 град. )
10Найти точное значениеsin(pi/3)
11Найти точное значениеarctan(-1)
12Найти точное значениеcos(45 град. )
13Найти точное значениеcos(30 град. )
14Найти точное значениеtan(60)
15
Найти точное значение		csc(45 град. )
16Найти точное значениеtan(60 град. )
17Найти точное значениеsec(30 град. )
18Найти точное значениеcos(60 град. )
19Найти точное значениеcos(150)
20Найти точное значениеsin(60)
21Найти точное значение
cos(pi/2)
22Найти точное значениеtan(45 град. )
23Найти точное значениеarctan(- квадратный корень из 3)
24Найти точное значениеcsc(60 град. )
25Найти точное значениеsec(45 град. )
26Найти точное значениеcsc(30 град. )
27Найти точное значение
sin(0)
28Найти точное значениеsin(120)
29Найти точное значениеcos(90)
30Преобразовать из радианов в градусыpi/3
31Найти точное значениеtan(30)
32Преобразовать из градусов в радианы45
33Найти точное значениеcos(45)
34Упроститьsin(theta)^2+cos(theta)^2
35Преобразовать из радианов в градусыpi/6
36Найти точное значениеcot(30 град. )
37Найти точное значениеarccos(-1)
38Найти точное значениеarctan(0)
39Найти точное значениеcot(60 град. )
40Преобразовать из градусов в радианы30
41Преобразовать из радианов в градусы(2pi)/3
42Найти точное значениеsin((5pi)/3)
43Найти точное значениеsin((3pi)/4)
44Найти точное значениеtan(pi/2)
45Найти точное значениеsin(300)
46Найти точное значениеcos(30)
47Найти точное значениеcos(60)
48Найти точное значениеcos(0)
49Найти точное значениеcos(135)
50Найти точное значениеcos((5pi)/3)
51Найти точное значениеcos(210)
52Найти точное значениеsec(60 град. )
53Найти точное значениеsin(300 град. )
54Преобразовать из градусов в радианы135
55Преобразовать из градусов в радианы150
56Преобразовать из радианов в градусы(5pi)/6
57Преобразовать из радианов в градусы(5pi)/3
58Преобразовать из градусов в радианы89 град.
59Преобразовать из градусов в радианы60
60Найти точное значениеsin(135 град. )
61Найти точное значениеsin(150)
62Найти точное значениеsin(240 град. )
63Найти точное значениеcot(45 град. )
64Преобразовать из радианов в градусы(5pi)/4
65Найти точное значениеsin(225)
66Найти точное значениеsin(240)
67Найти точное значение
cos(150 град. )
68Найти точное значениеtan(45)
69Вычислитьsin(30 град. )
70Найти точное значениеsec(0)
71Найти точное значениеcos((5pi)/6)
72Найти точное значениеcsc(30)
73Найти точное значениеarcsin(( квадратный корень из 2)/2)
74Найти точное значениеtan((5pi)/3)
75Найти точное значениеtan(0)
76Вычислитьsin(60 град. )
77Найти точное значениеarctan(-( квадратный корень из 3)/3)
78Преобразовать из радианов в градусы(3pi)/4
79Найти точное значениеsin((7pi)/4)
80Найти точное значениеarcsin(-1/2)
81Найти точное значениеsin((4pi)/3)
82Найти точное значениеcsc(45)
83Упроститьarctan( квадратный корень из 3)
84Найти точное значениеsin(135)
85Найти точное значениеsin(105)
86Найти точное значениеsin(150 град. )
87Найти точное значение sin((2pi)/3)
88Найти точное значениеtan((2pi)/3)
89Преобразовать из радианов в градусыpi/4
90Найти точное значениеsin(pi/2)
91Найти точное значениеsec(45)
92Найти точное значениеcos((5pi)/4)
93Найти точное значениеcos((7pi)/6)
94Найти точное значение
arcsin(0)
95Найти точное значениеsin(120 град. )
96Найти точное значениеtan((7pi)/6)
97Найти точное значениеcos(270)
98Найти точное значениеsin((7pi)/6)
99Найти точное значениеarcsin(-( квадратный корень из 2)/2)
100Преобразовать из градусов в радианы 88 град.

Контрольная работа по теме «Тригонометрические уравнения» 10 вариантов

Контрольная работа по теме «Тригонометрические уравнения»

10 класс. Варианты 1-14

1 В

1)вычислить а) sin(arccos )-arcsin0

б)cos(3arcctg-arccos(-))

2) решить уравнение

а) 4cos2x+4sinx-1=0

б)cosx*sinx-cos2x=0

3) найти корни уравнения cos(- +3x)=

На промежутке( П; ]

4) решить уравнение sin(П-t)+cos(+t)=-

5)sinx*cosx-5sin2x=-3

2 В

1) вычислить а) cos(arcsin(-)-arcsin1)

Б) arccos(ctg)

2) решить уравнение

а) 2cos2x-3cosx+1=0

б)2x+sinx*cosx=0

3) найти корни уравнения sin(- +2x)=-

Принадлежащих ( 0; ]

4) решить уравнения cos(П+t)+sin( -t)=

5) 3sin2x-3sinxcosx-4cos2x=-2

3 В

1)вычислить а) tg(arccos — arcctg )

б) ctg(arccos(- ))

2) решить уравнение

а) 2cos2t+5sint-4=0

б)sin2x-cosxsinx=0

3)найти корни уравнения sin( +2x)=

На [0;2П]

4)решить уравнения cos(- x)+cos(П — x)=0

5) sinxcosx-5sin2x=-3

4 В

1) вычислить а)arcsin (cos)

б) ctg(arccos + arcsin )

2)решить уравнение а) 2cos2t-3cost+1=0

б) sin2x+cosx*sinx=0

3)найти корни уравнения cos( – x)=

Принадлежащих [-П;П]

4)решить уравнение cos(П+x)-sin( — x)=1

5)3cos2x-sinxcosx-2sin2x=0

5 В

1)вычислить а)arcsin(tg )

б) tg(arccos(-1)+arcsin)

2)решить уравнение а) 2cos2t-3cost+1=0

б) (tgx+1)(2sinx-1)=0

3)найти корни уравнения sin(+x)=-1

На [0;2П]

4)решить уравнение sin(2П+x)-sin(+x)=0

5) 2cos(2x+)=-

6 В

1)вычислить а) cos(arcsin(- ))-arccos 1

б) cos(3arcctg -arccos )

2)решить уравнение а) 4sinx+4cos2x-1=0

б) sin2x+sinx*cosx=0

3)найти корни уравнения cos( – )=

Принадлежащих полуинтервалу [;2П)

4)решить уравнение sin(2П+3x)-sin(+3x)=0

5) 2sin2x-5sinxcosx-cos2x=-2

7 В

1)вычислите а)3arcctg(- )+arccos(- )

б) ctg(arccos + arcsin)

2)решить уравнение а) 5sinx+2cos2x-4=0

б) sinxcosx-2sin2x=0

3)найти корни уравнения sin( +2x)=

На промежутке [-;0]

4)решить уравнение sin(П+)-sin( — )=0

5) 6sin2x+sinxcosx-cos2x=2

8 В

1)вычислить а)arcsin(sin)

б)ctg(6arcctg -arcctg )

2)решить уравнение а)4sin2x+4cosx-1=0

б) 3sin2x+sinxcosx=0

3)решить уравнение 3sin6x-3cos6x=0 и найти его корни

Принадлежащих отрезку [- ; ]

4)решить уравнение cos(2П-x)+cos( — x)=0

5) sinxcosx-5sin2x=-3

9 В

1)вычислите а) cos(3arcctg-arccos(- ))

б) cos(arcsin )-arccos1

2)решить уравнение а)2sin2x-3sinx+1=0

б)5cos2x-sinxcosx=0

3)найти корни уравнения cos( – )=

Принадлежащих полуинтервалу [;2п)

4)решить уравнения cos( + 3x)+cos(2П-3x)=0

5) 2sin2x-5sinxcosx-cos2x=-2

10 В

1)вычислите а)arcctg(-)-arcsin

б) ctg(arccos(-))

2)решить уравнение а)sin2x+sinx-2=0

б) cos*sinx-sin2x=0

3)найти корни уравнения cos(x- )=

Принадлежащих отрезку [0;П]

4)решить уравнение tg2x-tgx=0

5) sin4x+cos4x=0

11 В

1)вычислите а)arcsin(- )+arccos 0

б)arcctg(sinП)

2)решить уравнение а) sin2x=-

б) cos2x-cosx=0

3)найти корни уравнения tgx=

Принадлежащих [0;П]

4)решить уравнение 6sin2x+5cosx-7=0

5) 2sin2x+sinxcosx-3cos2x=0

12 В

1)вычислите а) arcsin0+arccos0

Б)arcctg(cosП)

2)решить уравнения а) 2cosx=-1

б)sin2x-sinx=0

3)найти корни уравнения ctg2x=-1 на интервал (0;)

4)решить уравнение 2sin2t-3sint+1=0

5) 2tgx+ctgx-3=0

13 В

1)вычислите a)arcsin(- )+arcctg 1

б) arcctg(sin )

2)решить уравнения а)sin=-

б)(sinx+1)(cosx-1)=0

3)найти корни уравнения tgx=-1

Принадлежащих отрезку [0;П]

4)решить уравнения sin2x+sinx*cosx=0

5) cos(2П-x)-sin(+x)=1

14 В

1)вычислите а)arcctg(- )+arcctg(-1)-arcctg 0

б) cos(arcctg )

2)решить уравнения а)2sinx+=0

б) tg(x- )=-1

3)найти корни уравнения cos2x+3sinx-3=0

На [0;2П]

4)решить уравнения sin(+x)-cos(П+x)+1=0

5) 3sin2x-4sinxcosx+cos2x=0

Мэтуэй | Популярные задачи

92
1 Найти точное значение грех(30)
2 Найти точное значение грех(45)
3 Найти точное значение грех(30 градусов)
4 Найти точное значение грех(60 градусов)
5 Найти точное значение загар (30 градусов)
6 Найти точное значение угловой синус(-1)
7 Найти точное значение грех(пи/6)
8 Найти точное значение cos(pi/4)
9 Найти точное значение грех(45 градусов)
10 Найти точное значение грех(пи/3)
11 Найти точное значение арктан(-1)
12 Найти точное значение cos(45 градусов)
13 Найти точное значение cos(30 градусов)
14 Найти точное значение желтовато-коричневый(60)
15 Найти точное значение csc(45 градусов)
16 Найти точное значение загар (60 градусов)
17 Найти точное значение сек(30 градусов)
18 Найти точное значение cos(60 градусов)
19 Найти точное значение cos(150)
20 Найти точное значение грех(60)
21 Найти точное значение cos(pi/2)
22 Найти точное значение загар (45 градусов)
23 Найти точное значение arctan(- квадратный корень из 3)
24 Найти точное значение csc(60 градусов)
25 Найти точное значение сек(45 градусов)
26 Найти точное значение csc(30 градусов)
27 Найти точное значение грех(0)
28 Найти точное значение грех(120)
29 Найти точное значение соз(90)
30 Преобразовать из радианов в градусы пи/3
31 Найти точное значение желтовато-коричневый(30)
32
35 Преобразовать из радианов в градусы пи/6
36 Найти точное значение детская кроватка(30 градусов)
37 Найти точное значение арккос(-1)
38 Найти точное значение арктан(0)
39 Найти точное значение детская кроватка(60 градусов)
40 Преобразование градусов в радианы 30
41 Преобразовать из радианов в градусы (2 шт. )/3
42 Найти точное значение sin((5pi)/3)
43 Найти точное значение sin((3pi)/4)
44 Найти точное значение тан(пи/2)
45 Найти точное значение грех(300)
46 Найти точное значение соз(30)
47 Найти точное значение соз(60)
48 Найти точное значение соз(0)
49 Найти точное значение соз(135)
50 Найти точное значение cos((5pi)/3)
51 Найти точное значение cos(210)
52 Найти точное значение сек(60 градусов)
53 Найти точное значение грех(300 градусов)
54 Преобразование градусов в радианы 135
55 Преобразование градусов в радианы 150
56 Преобразовать из радианов в градусы (5 дюймов)/6
57 Преобразовать из радианов в градусы (5 дюймов)/3
58 Преобразование градусов в радианы 89 градусов
59 Преобразование градусов в радианы 60
60 Найти точное значение грех(135 градусов)
61 Найти точное значение грех(150)
62 Найти точное значение грех(240 градусов)
63 Найти точное значение детская кроватка(45 градусов)
64 Преобразовать из радианов в градусы (5 дюймов)/4
65 Найти точное значение грех(225)
66 Найти точное значение грех(240)
67 Найти точное значение cos(150 градусов)
68 Найти точное значение желтовато-коричневый(45)
69 Оценить грех(30 градусов)
70 Найти точное значение сек(0)
71 Найти точное значение cos((5pi)/6)
72 Найти точное значение КСК(30)
73 Найти точное значение arcsin(( квадратный корень из 2)/2)
74 Найти точное значение загар((5pi)/3)
75 Найти точное значение желтовато-коричневый(0)
76 Оценить грех(60 градусов)
77 Найти точное значение arctan(-( квадратный корень из 3)/3)
78 Преобразовать из радианов в градусы (3 пи)/4 
79 Найти точное значение sin((7pi)/4)
80 Найти точное значение угловой синус(-1/2)
81 Найти точное значение sin((4pi)/3)
82 Найти точное значение КСК(45)
83 Упростить арктан(квадратный корень из 3)
84 Найти точное значение грех(135)
85 Найти точное значение грех(105)
86 Найти точное значение грех(150 градусов)
87 Найти точное значение sin((2pi)/3)
88 Найти точное значение загар((2pi)/3)
89 Преобразовать из радианов в градусы пи/4
90 Найти точное значение грех(пи/2)
91 Найти точное значение сек(45)
92 Найти точное значение cos((5pi)/4)
93 Найти точное значение cos((7pi)/6)
94 Найти точное значение угловой синус(0)
95 Найти точное значение грех(120 градусов)
96 Найти точное значение желтовато-коричневый ((7pi)/6)
97 Найти точное значение соз(270)
98 Найти точное значение sin((7pi)/6)
99 Найти точное значение arcsin(-( квадратный корень из 2)/2)
100 Преобразование градусов в радианы 88 градусов

синус в nLab

Пропустить навигационные ссылки | Домашняя страница | Все страницы | Последние версии | Обсудить эту страницу |

Содержание

Контекст

Тригонометрия

Тригонометрия

  • Евклидово пространство

  • треугольник

  • угол, длина дуги

  • тригонометрическая функция

    • косинус

    • синус

    • тангенс

    • котангенс

    • секанс?

    • косеканс?

  • обратная тригонометрическая функция

    • арккос

    • угловых синусов?

    • арктический

    • …

  • тригонометрическое тождество

    • Формула Эйлера

  • гиперболическая функция

  • эллиптическая функция

Analysis

analysis (differential/integral calculus, functional analysis, topology)

epsilontic analysis

infinitesimal analysis

computable analysis

Introduction

Basic concepts

triangle inequality

metric space, normed векторное пространство

открытый шар, открытое подмножество, окрестность

метрическая топология

последовательность, сеть

сходимость, предел последовательности

компактность, секвенциальная компактность

дифференцирование, интегрирование

топологическое векторное пространство

Основные факты

Теоремы

Теорема о промежуточном значении

Теорема об экстремальном значении

Теорема Гейне-Бореля

…

Алгебра

высшая алгебра

универсальная алгебра

Алгебраические теории

  • алгебраическая теория / 2-алгебраическая теория / (∞,1)-алгебраическая теория

  • монада / (∞,1)-монада

  • операда / (∞,1)-операда

Алгебры и модули

  • алгебра над монадой

    ∞-алгебра над (∞,1)-монадой

  • алгебра над алгебраической теорией

    ∞-алгебра над (∞,1)-алгебраической теорией

  • алгебра над операдой

    ∞-алгебра над (∞,1)-операдой

  • действие, ∞-действие

  • представление, ∞-представление

  • модуль

    , ∞-модуль

  • ассоциированный пучок, ассоциированный ∞-пучок

Высшие алгебры

  • моноидальная (∞,1)-категория

    • симметричная моноидальная (∞,1)-категория

    • моноид в (∞,1)-категории

    • коммутативный моноид в (∞,1)-категории

  • симметричная моноидальная (∞,1)-категория спектров

    • разбить произведение спектров

    • симметричное моноидальное произведение спектров

    • кольцевой спектр, модульный спектр, алгебраический спектр

  • А-∞ алгебра

    • Кольцо A-∞, пространство A-∞

  • C-∞ алгебра

  • Кольцо E-∞, алгебра E-∞

    • ∞-модуль, (∞,1)-расслоение модулей

    • теория мультипликативных когомологий

  • L-∞ алгебра

    • теория деформации

Презентации категории моделей

  • модельная структура на симплициальных Т-алгебрах / гомотопических Т-алгебрах

  • структура модели на операдах

    структура модели на алгебрах над операдой

Геометрия на формальных дуальных алгебрах

  • Двойственность Исбелла

  • производная геометрия

Теоремы

  • Гипотеза Делиня

  • гипотеза раскрытия петли

  • моноидальное соответствие Долд-Кан

Изменить эту боковую панель

  • Идея
  • Определения
    • В произвольных архимедовых упорядоченных полях
    • В двойных числах
  • По конструктивной математике
  • Свойства
    • Связь с другими функциями
    • Корни
  • Родственные понятия
  • Каталожные номера

Идея

Функция синуса sin\sin является одной из основных тригонометрических функций.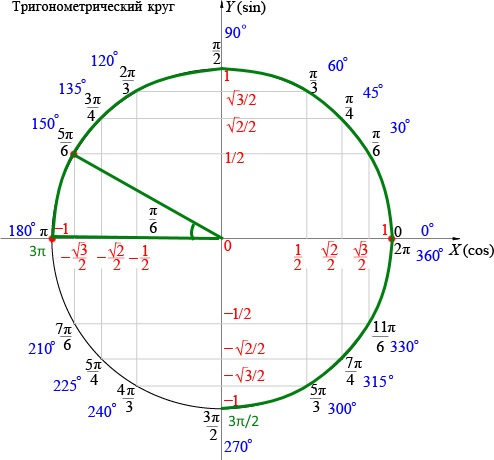

Это можно рассматривать как присвоение любому углу расстояния до выбранной оси точки на единичной окружности с этим углом к ​​этой оси.

Определения

Функция синуса — это функция sin:ℝ→ℝ\sin \;\двоеточие\; \mathbb{R} \to \mathbb{R} из вещественных чисел в самих себя, что характеризуется следующими эквивалентными условиями:

  1. sin\sin — единственное среди гладких функций решение дифференциального уравнения/задачи с начальным значением

    грех″=−грех грех» = -грех

    (где штрих означает производную) при начальных условиях

    sin(0)=0sin'(0)=1. \begin{выровнено} грех(0) &= 0 \\ грех'(0) & = 1 \,. \end{выровнено}

  2. (формула Эйлера) sin\sin — мнимая часть показательной функции с мнимым аргументом

    sin(x)=Im(exp(ix))=12i(exp(ix)−exp(−ix)). \begin{выровнено} \sin(x) & = Im\left( \exp(i x) \right) \\ & = \frac{1}{2 i}\left( \exp(i x) — \exp(- i x)\right) \end{выровнено} \,.

  3. sin\sin — это уникальная функция, которая 9{2 i + 1}}{(2 i + 1)!}

    В произвольных архимедовых упорядоченных полях

    В общем случае архимедово упорядоченные поля, которые не являются последовательно полными по Коши, не имеют функции синуса. Тем не менее синусоидальная карта по-прежнему гарантированно является частичной функцией, потому что каждое архимедово упорядоченное поле является хаусдорфовым пространством и, следовательно, секвенциально хаусдорфовым пространством. Таким образом, к архимедову упорядоченному полю FF можно добавить аксиому, гарантирующую, что частичная функция синуса на самом деле является полной функцией: 92 имеет понятие функции синуса и косинуса, которые являются решениями системы функциональных уравнений sin(x+ϵ)=sin(x)+cos(x)ϵ\sin(x + \epsilon) = \sin(x ) + \cos(x) \epsilon и cos(x+ϵ)=cos(x)−sin(x)ϵ\cos(x + \epsilon) = \cos(x) — \sin(x) \epsilon с sin(0)=1\sin(0) = 1 и cos(0)=1\cos(0) = 1.

    В конструктивной математике

    В классической математике можно доказать, что модулированные действительные числа Кантора ℝC\ mathbb{R}_C последовательно полны по Коши и эквивалентны действительным числам книги HoTT ℝH\mathbb{R}_H. Однако в конструктивной математике сказанное выше не может быть доказано; в то время как вещественные числа ℝH\mathbb{R}_H из книги HoTT все еще являются последовательно полными по Коши, модулированные действительные числа Кантора ℝC\mathbb{R}_C в общем случае не могут быть доказаны как последовательно полные по Коши. В частности, это означает, что последовательность 9{2 i + 1}}{(2 i + 1)!}

    не имеет предела для всех модулированных вещественных чисел Кантора x∈ℝCx \in \mathbb{R}_C. Однако последовательность по определению ℝC\mathbb{R}_C имеет предел для всех рациональных чисел x∈ℚx \in \mathbb{Q}; это означает, что можно ограничить область определения функции синуса рациональными числами sin:ℚ→ℝC\sin:\mathbb{Q} \to \mathbb{R}_C и определить ее обычным образом:

    • Для всех рациональных чисел x∈ℚx \in \mathbb{Q}, существует единственное модулированное канторовское вещественное число sin(x)∈ℝC\sin(x) \in \mathbb{R}_C такое, что для всех положительных рациональных чисел ϵ∈ ℚ+\epsilon \in \mathbb{Q}_+, существует натуральное число N∈ℕN \in \mathbb{N} такое, что для всех натуральных чисел n∈ℕn \in \mathbb{N}, если n≥Nn \geq N, то −ϵ<∑i=0n(−1)ix2i+1(2i+1)!−sin(x)<ϵ-\epsilon \lt \sum_{i = 0}^{n} \frac {(-1)^i x^{2 i + 1}}{(2 i + 1)!} - \sin(x) \lt \epsilon.

      No related posts.

Добавить комментарий

Ваш адрес email не будет опубликован. Обязательные поля помечены *