| 1 | Найти точное значение | sin(30) | |
| 2 | Найти точное значение | sin(45) | |
| 3 | Найти точное значение | sin(30 град. ) | |
| 4 | Найти точное значение | sin(60 град. ) | |
| 5 | Найти точное значение | tan(30 град. ) | |
| 6 | Найти точное значение | arcsin(-1) | |
| 7 | Найти точное значение | sin(pi/6) | |
| 8 | cos(pi/4) | ||
| 9 | Найти точное значение | sin(45 град. ) ) | |
| 10 | Найти точное значение | sin(pi/3) | |
| 11 | Найти точное значение | arctan(-1) | |
| 12 | Найти точное значение | cos(45 град. ) | |
| 13 | Найти точное значение | cos(30 град. ) | |
| 14 | Найти точное значение | tan(60) | |
| 15 | Найти точное значение | csc(45 град. ) | |
| 16 | Найти точное значение | tan(60 град. ) | |
| 17 | Найти точное значение | sec(30 град.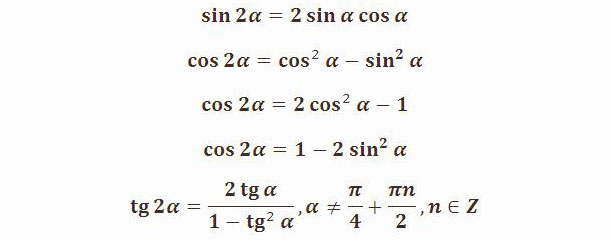 ) ) | |
| 18 | Найти точное значение | cos(60 град. ) | |
| 19 | Найти точное значение | cos(150) | |
| 20 | Найти точное значение | sin(60) | |
| 21 | Найти точное значение | cos(pi/2) | |
| 22 | Найти точное значение | tan(45 град. ) | |
| 23 | Найти точное значение | arctan(- квадратный корень из 3) | |
| 24 | Найти точное значение | csc(60 град. ) | |
| 25 | Найти точное значение | sec(45 град. ) ) | |
| 26 | Найти точное значение | csc(30 град. ) | |
| 27 | Найти точное значение | sin(0) | |
| 28 | Найти точное значение | sin(120) | |
| 29 | Найти точное значение | cos(90) | |
| 30 | Преобразовать из радианов в градусы | pi/3 | |
| 31 | Найти точное значение | tan(30) | |
| 32 | Преобразовать из градусов в радианы | 45 | |
| 33 | Найти точное значение | cos(45) | |
| 34 | Упростить | sin(theta)^2+cos(theta)^2 | |
| 35 | Преобразовать из радианов в градусы | pi/6 | |
| 36 | Найти точное значение | cot(30 град. ) ) | |
| 37 | Найти точное значение | arccos(-1) | |
| 38 | Найти точное значение | arctan(0) | |
| 39 | Найти точное значение | cot(60 град. ) | |
| 40 | Преобразовать из градусов в радианы | 30 | |
| 41 | Преобразовать из радианов в градусы | (2pi)/3 | |
| 42 | Найти точное значение | sin((5pi)/3) | |
| 43 | Найти точное значение | sin((3pi)/4) | |
| 44 | Найти точное значение | tan(pi/2) | |
| 45 | Найти точное значение | sin(300) | |
| 46 | Найти точное значение | cos(30) | |
| 47 | Найти точное значение | cos(60) | |
| 48 | Найти точное значение | cos(0) | |
| 49 | Найти точное значение | cos(135) | |
| 50 | Найти точное значение | cos((5pi)/3) | |
| 51 | Найти точное значение | cos(210) | |
| 52 | Найти точное значение | sec(60 град. ) ) | |
| 53 | Найти точное значение | sin(300 град. ) | |
| 54 | Преобразовать из градусов в радианы | 135 | |
| 55 | Преобразовать из градусов в радианы | 150 | |
| 56 | Преобразовать из радианов в градусы | (5pi)/6 | |
| 57 | Преобразовать из радианов в градусы | (5pi)/3 | |
| 58 | Преобразовать из градусов в радианы | 89 град. | |
| 59 | Преобразовать из градусов в радианы | 60 | |
| 60 | Найти точное значение | sin(135 град. ) ) | |
| 61 | Найти точное значение | sin(150) | |
| 62 | Найти точное значение | sin(240 град. ) | |
| 63 | Найти точное значение | cot(45 град. ) | |
| 64 | Преобразовать из радианов в градусы | (5pi)/4 | |
| 65 | Найти точное значение | sin(225) | |
| 66 | Найти точное значение | sin(240) | |
| 67 | Найти точное значение | cos(150 град. ) | |
| 68 | Найти точное значение | tan(45) | |
| 69 | Вычислить | sin(30 град. ) ) | |
| 70 | Найти точное значение | sec(0) | |
| 71 | Найти точное значение | cos((5pi)/6) | |
| 72 | Найти точное значение | csc(30) | |
| 73 | Найти точное значение | arcsin(( квадратный корень из 2)/2) | |
| 74 | Найти точное значение | tan((5pi)/3) | |
| 75 | Найти точное значение | tan(0) | |
| 76 | Вычислить | sin(60 град. ) | |
| 77 | Найти точное значение | arctan(-( квадратный корень из 3)/3) | |
| 78 | Преобразовать из радианов в градусы | (3pi)/4 | |
| 79 | Найти точное значение | sin((7pi)/4) | |
| 80 | Найти точное значение | arcsin(-1/2) | |
| 81 | Найти точное значение | sin((4pi)/3) | |
| 82 | Найти точное значение | csc(45) | |
| 83 | Упростить | arctan( квадратный корень из 3) | |
| 84 | Найти точное значение | sin(135) | |
| 85 | Найти точное значение | sin(105) | |
| 86 | Найти точное значение | sin(150 град. ) ) | |
| 87 | Найти точное значение | sin((2pi)/3) | |
| 88 | Найти точное значение | tan((2pi)/3) | |
| 89 | Преобразовать из радианов в градусы | pi/4 | |
| 90 | Найти точное значение | sin(pi/2) | |
| 91 | Найти точное значение | sec(45) | |
| 92 | Найти точное значение | cos((5pi)/4) | |
| 93 | Найти точное значение | cos((7pi)/6) | |
| 94 | Найти точное значение | arcsin(0) | |
| 95 | Найти точное значение | sin(120 град. ) ) | |
| 96 | Найти точное значение | tan((7pi)/6) | |
| 97 | Найти точное значение | cos(270) | |
| 98 | Найти точное значение | sin((7pi)/6) | |
| 99 | Найти точное значение | arcsin(-( квадратный корень из 2)/2) | |
| 100 | Преобразовать из градусов в радианы | 88 град. |
Докажите тождество » задачи — страница 1
тождество »
Докажите тождество 1) (a+2)3(степень) -25(а+2) = (а+2)(а+7)(а-3)
2) a2 + 2 ab + b2 — c2 + 2cd -d2 = (a+b+c-d)(a+b-c+d)
Решение: Решение
1) (a+2)3(степень) -25(а+2) = (а+2)(а+7)(а-3)
Упростим левую часть тождества:
(a + 2)³ — 25*(a + 2) = (a + 2)*(a² + 4a + 4 — 25) =
= (a + 2)*(a² + 4a — 21)
a² + 4a — 21 = 0
a₁ = — 7
a₂ = 3
a² + 4a — 21 = (a + 7)*(a — 7)
(a + 2)*(a² + 4a — 21) = (a + 2)*(a + 7)*( a — 3)
(a + 2)*(a + 7)*( a — 3) = (a + 2)*(a + 7)*( a — 3)
доказано
2) a²+ 2 ab + b² — c² + 2cd -d² = (a+b+c-d)(a+b-c+d)
Упростим левую часть тождества:
a² + 2 ab + b² — c² + 2cd -d² = (a² + 2 ab + b²) -(c² — 2cd + d²) =
= (a + b)² — (c — d)² = (a+b+c-d)(a+b-c+d)
(a + b + c — d)*(a + b — c + d) = (a + b + c — d)*(a + b — c + d)
доказаноДокажите тождество an= a1+(n-1)d ( формула n-го члена арифметической прогрессии) методом математической индукции
Решение: При n=1 имеем a(1=a1+d*(1-1)=a(1), так что для n=1 формула верна.
Допустим теперь, что формула верна и для произвольного n=k:
a(k)=a1+d*(k-1) и перейдём теперь к n=k+1:a(k+1)=ak+d=a1+d*(k-1)+d=a1+d*k — формула верна и для n=k+1. А значит, она верна и для любого целого n. Действительно, из справедливости формулы при n=1 (а в этом мы убедились непосредственно) вытекает её справедливость для n=2; из справедливости для n=2 следует справедливость для n=3 и. т. д. Тождество доказано.
Докажите тождество:
sin альфа * cos 3 альфа — cos альфа * sin 3 альфа = cos (3П/2 — 2 альфа)
Решение: по формуле синуса разностиsin альфа * cos 3 альфа — cos альфа * sin 3 альфа =sin(альфа-3альфа)=sin(-2альфа)=
учитывая нечетность синуса -sin(2альфа)
по формуле приведения
cos(3П/2 — 2 альфа)=- sin( 2 альфа)
значит sin альфа * cos 3 альфа — cos альфа * sin 3 альфа = cos (3П/2 — 2 альфа)
Доказано
Докажите тождество:
sin 105° cos 105° = — 1/4
Решение: А вот попроще решение: $$ 105^{0}=60^{0}+45^{0} $$По формулам суммы аргументов получаем: $$ sin(60^0+45^0)*cos(60^0+45^0)= \\ =(sin60^0cos45^0+cos60^0sin45^0)*(cos60^0cos45^0-sin60^0sin45^0) $$
Подставляем известные значения синусов и косинусов:
$$ (\frac{\sqrt3}{2}\frac{\sqrt2}{2}+\frac{1}{2}\frac{\sqrt2}{2})(\frac{1}{2}\frac{\sqrt2}{2}-\frac{\sqrt3}{2}\frac{\sqrt2}{2})=\\=\frac{\sqrt2(\sqrt3+1)}{4}\frac{\sqrt2(1-\sqrt3)}{4}=\frac{2*(-2)}{16}=-\frac{1}{4} $$
докажите тождество (sin⁴α-cos⁴α)/(sin²α)+2ctg²α=1/(sin²α)
Решение: (sin⁴α-cos⁴α)/(sin²α)+2ctg²α=1/(sin²α)чтобы доказать какое-либо дождество надо одну из частей привести к другой.
 2(\frac{x}{2}-\frac{\pi}{8})= \\ =2\sqrt{2}(\frac{1+cos2\cdot (\frac{x}{2}-\frac{\pi}{8})}{2})= \\ =\sqrt{2}(1+cos(x-\frac{\pi}{4})) $$
2(\frac{x}{2}-\frac{\pi}{8})= \\ =2\sqrt{2}(\frac{1+cos2\cdot (\frac{x}{2}-\frac{\pi}{8})}{2})= \\ =\sqrt{2}(1+cos(x-\frac{\pi}{4})) $$Воспользуемся формулой 2. И упростим cos:
$$ \sqrt{2}(1+cos(x-\frac{\pi}{4}))= \\ =\sqrt{2}(1+cosx\cdot cos(\frac{\pi}{4})+sinx \cdot sin(\frac{\pi}{4}))= \\ =\sqrt{2}(1+cosx\cdot \frac{\sqrt{2}}{2}+sinx \cdot \frac{\sqrt{2}}{2}) \\ =\sqrt{2}+cosx+sinx $$
Получаем что левая часть равна правой части:
$$ sinx+cosx+\sqrt{2}=\sqrt{2}+cosx+sinx $$
Что и требовалось доказать
Докажите тождество: sin(45-альфа) / cos(45-альфа)=1
Тема: синус и косинус разности
Решение: sin(45-альфа) / cos(45-альфа)=1
sin45cosA-cos45sinA/cosAcos45+sin45sinA=cosA-sinA/cosA+sinA не равно 1
cos(45+фльфа)=cos45cosA-sin45cosA при таком знаменателе =1Докажите тождество:
1) 1-sin t / cos t=cos t / 1+sin t
2)sin t / 1-cos t=1+ cos t / sin t
Решение: Умножаем крест на крест
cos^2t=(1-sint)(1+sint)
cos^2t=1-sin^2t
cos^2t+sin^2t=1
1=1
2)(1+cost)(1-cost)=sin^2t
1-cos^t=sin^2t
1=sin^2t+cos^2t
1=1.
 2 a $$
2 a $$Доказано
в левой части выносим за скобки sin²a:
sin²a(sin²a+cos²a)=1-cos²a
в правой части применяем основное тригонометрическое тождество:
sin²a(sin²a+cos²a)=sin²a
sin²a сокращается
sin²a+cos²a=1, а это основное тригонометрическое тождество. ч. т. д
1 2 3 > >>
формул тригонометрии.
Тригонометрическая формула — общие математические выражения для тригонометрических функций, выполняемые для всех значений аргумента.
Навигация по страницам Тригонометрические функции Пифагорейская идентичность Формулы суммы-разности Формулы двойного угла Формулы тройного угла Формула снижения мощности Сумма (разность) с формулами произведения Формулы произведения для суммирования (разности) Замена касательной половины угла
Тригонометрические функции
sin α, cos α
| tan α = | sin α | , α ≠ | π | + πn, n є Z |
| cos α | 2 |
| cot α = | cos α | , α ≠ π + πn, n є Z |
| sin α |
| sec α = | 1 | , α ≠ | π | + πn, n є Z |
| cos α | 2 |
| cosec α = | 1 | , α ≠ π + πn, n є Z |
| sin α |
Тождество Пифагора
sin 2 α + cos 2 α = 1
| 1 + TAN 2 α = | 1 |
| COS 2 α |
1 + COT
|


 2(\frac{x}{2}-\frac{\pi}{8})= \\ =2\sqrt{2}(\frac{1+cos2\cdot (\frac{x}{2}-\frac{\pi}{8})}{2})= \\ =\sqrt{2}(1+cos(x-\frac{\pi}{4})) $$
2(\frac{x}{2}-\frac{\pi}{8})= \\ =2\sqrt{2}(\frac{1+cos2\cdot (\frac{x}{2}-\frac{\pi}{8})}{2})= \\ =\sqrt{2}(1+cos(x-\frac{\pi}{4})) $$ 2 a $$
2 a $$ α
α 3 α
3 α + b cos α = r sin (α + φ),
+ b cos α = r sin (α + φ),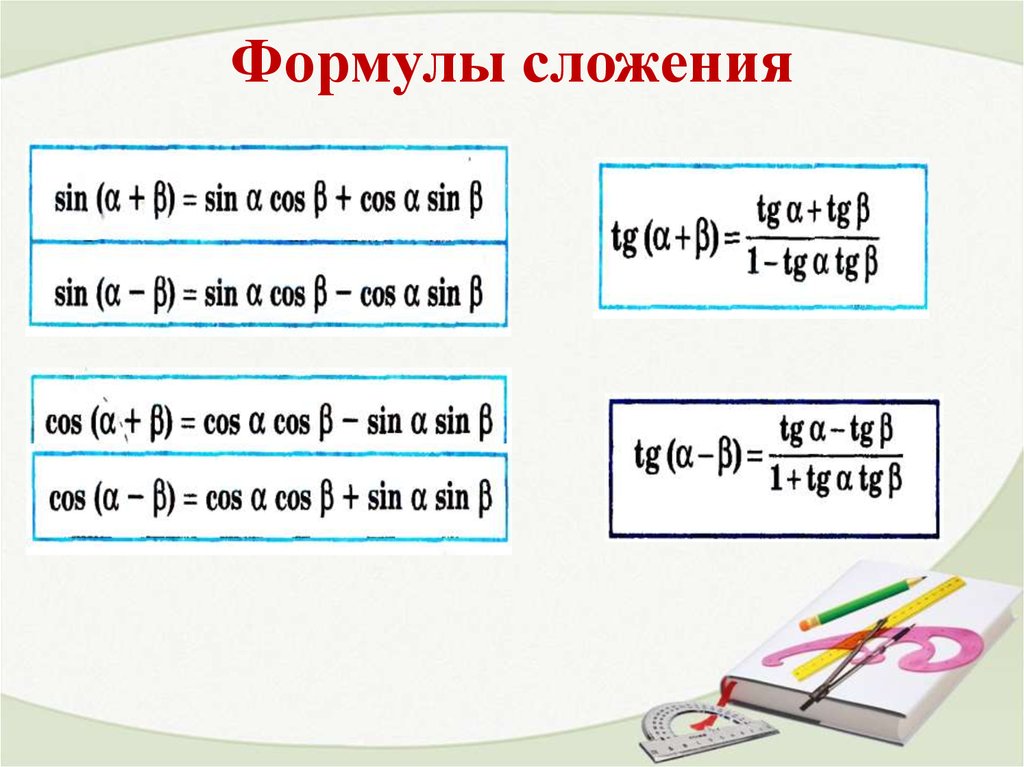 2)
2)


