Вывод производных arctg(x) и arcctg(x)
Вывод производной арктангенса
Здесь мы полагаем, что нам известна производная тангенса:
.
Далее мы выводим формулу производной арктангенса, учитывая, что арктангенс является функцией, обратной к тангенсу.
По формуле производной обратной функции
Рассмотрим функцию арктангенс:
y = arctg x.
Здесь независимая переменная x может принимать любые действительные значения:
.
Зависимая переменная y может принимать значения от – π/2 до + π/2:
.
Арктангенс является функцией, обратной к тангенсу:
x = tg y.
Для определения его производной, применим формулу производной обратной функции:
(1) .
Производная тангенса нам известна:
.
Здесь .
Поменяем местами обозначения переменных x и y. Тогда
,
где .
Подставим в формулу (1):
(2) .
Здесь
y = arctg x;
x = tg y.
Теперь выразим правую часть формулы (2) через переменную x. Для этого воспользуемся формулой и выполним преобразования:
.
Отсюда
.
Подставим в (2):
.
Тем самым мы вывели формулу производной арктангенса:
.
Второй способ
Поскольку арктангенс и тангенс являются взаимно обратными функциями, то
(3) .
Продифференцируем это уравнение по переменной x. То есть найдем производные левой и правой части и приравняем их друг к другу:
(4) .
Из таблицы производных имеем:
.
Производную левой части находим по формуле производной сложной функции:
.
Здесь .
Далее выполним преобразования:
.
Тогда
.
Подставим в (4):
.
Отсюда
.
Вывод производной арккотангенса
Используя связь между арктангенсом и арккотангенсом
Производную арккотангенса можно получить из производной арктангенса, если воспользоваться связью между арктангенсом и арккотангенсом:
.
Отсюда
.
По формуле производной обратной функции
Рассмотрим функцию арккотангенс:
y = arcctg x.
Здесь независимая переменная x может принимать любые действительные значения:
.
Зависимая переменная y может принимать значения от 0 до π:
.
Арккотангенс является функцией, обратной к котангенсу:
x = ctg y.
Для определения его производной, применим формулу производной обратной функции:
(1) .
Считаем, что производная котангенса нам известна:
.
Здесь .
Поменяем местами обозначения переменных x и y. Тогда
,
где .
Подставим в формулу (1):
(5) .
Здесь
y = arcctg x;
x = ctg y.
Выразим правую часть формулы (5) через переменную x. Для этого выполним преобразования:
.
Отсюда
.
Подставим в (5):
.
Таким образом, мы вывели формулу производной арккотангенса:
.
Второй способ
Поскольку арккотангенс и котангенс являются взаимно обратными функциями, то
(6) .
Продифференцируем это уравнение по переменной x:
(7) .
Из таблицы производных находим:
.
Производную левой части находим по формуле производной сложной функции:
.
Здесь .
Далее выполним преобразования:
.
Тогда
.
Подставим в (7):
.
Отсюда
.
Автор: Олег Одинцов. Опубликовано:
1cov-edu.ru
Вывод производных высших порядков arctg(x) и arcctg(x)
Вывод производных высших порядков арктангенса
Пусть . Считаем, что нам известна производная арктангенса первого порядка:
(1) .
Найдем производные высших порядков. Для этого разложим дробь на простейшие:
.
Здесь – мнимая единица, .
Тогда производную арктангенса первого порядка можно записать в следующем виде:
.
Дифференцируем раз и приводим дроби к общему знаменателю:
.
В числителе стоит разность комплексно сопряженных величин. Поэтому числитель является чисто мнимым. Пусть обозначает мнимую часть стоящего следом выражения. Тогда производную арктангенса n-го порядка можно записать в следующем виде:
(2) .
Здесь выражение в числителе является многочленом степени .
Производные арктангенса со второго по пятый порядок
Вычислим производные арктангенса нескольких высших порядков, используя формулу (2). Для этого мы используем формулу бинома Ньютона:
.
Также используем свойства мнимой единицы:
;
;
.
И так далее.
Производная второго порядка.
При имеем:
;
;
.
Производная третьего порядка.
При имеем:
;
;
.
Производная четвертого порядка.
При получаем:
;
;
.
Наконец, вычислим производную пятого порядка.
Подставим :
;
;
.
Другой вид производных арктангенса высших порядков
Оказывается, что формулу производной арктангенса n-го порядка можно представить в удобном виде, если выразить производную не через независимую переменную x, а через сам арктангенс.
Итак, пусть
.
Используем формулу (2) производной n-го порядка:
(2) .
Подставим :
;
;
;
.
Применим формулу Эйлера. Тогда
;
;
;
.
Тем самым мы получили производную арктангенса n-го порядка, выраженную через сам арктангенс:
(3) .
Здесь .
Производные высших порядков арккотангенса
Чтобы получить производные высших порядков арккотангенса, воспользуемся связью между арктангенсом и арккотангенсом:
(4) .
Дифференцируя это уравнение n раз и учитывая, что производная постоянной равна нулю, получим производную арккотангенса n-го порядка:
(5) .
Другой вид производных арккотангенса высших порядков
Пусть
.
Выразим производную n-го порядка арккотангенса через z. Для этого можно подставить в (5) . Но мы используем формулу (3) для n-ой производной арктангенса и формулу (4), связывающую арккотангенс с арктангенсом. Пусть
.
Тогда . Подставим в (3):
(3) ;
.
Далее замечаем, что
;
.
Тогда
(6) .
Это и есть искомая формула производной n-го порядка арккотангенса.
Использованная литература:
Н.М. Гюнтер, Р.О. Кузьмин, Сборник задач по высшей математике, «Лань», 2003.
Автор: Олег Одинцов. Опубликовано:
1cov-edu.ru
Производная сложной функции
Пусть переменная у есть функция от переменной U: y=y(U), а переменная U, в свою очередь есть функция от переменной V: U=U(V), а переменная V – функция независимой переменной х: V=V(x) (эту цепочку можно было бы и продолжить).
— Тогда переменная у является сложной функцией (суперпозиции функций) независимой переменной х: y=y(U(V(x))) («сложена» из различных функций).
— Если все функции в цепочке дифференцируемы, то производная сложной функции по независимой переменной (аргументу) равна произведению производных по промежуточным аргументам:
.
Аналогичную формулу для дифференцирования сложной функции можно получить при любом уровне вложенности и любых обозначениях, если заметить закономерность: производные в произведении вычисляются «по порядку», так, как записаны в выражении для сложной функции.
Схема:
Еще один пример (попробуйте построить формулу сами и сравните):
здесь аргумент – это t.
Таблица производных основных элементарных функций
— Обратите внимание! При вычислении производных сложных функций в роли аргументахиз таблицы производных может выступать любая функция!
Функция | Производная | ||
1 | Степенная |
|
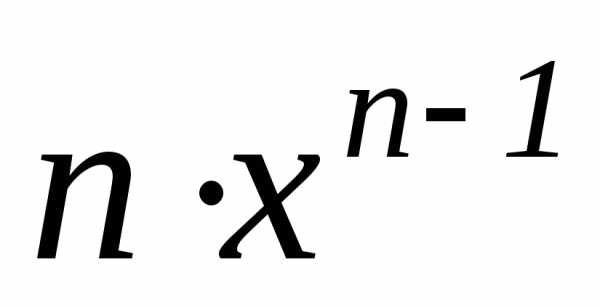 |
Частные случаи |
|
| |
|
| ||
2 | Показательная |
|
|
Экспонента |
|
| |
3 | Логарифмическая |
|
|
Натуральный логарифм |
|
| |
4 | Тригонометрические: | ||
синус |
|
| |
|
| ||
тангенс |
|
| |
котангенс |
|
| |
5 | Обратные тригонометрические | ||
арксинус |
| ||
арккосинус |
| ||
арктангенс |
|
| |
арккотангенс |
| ||
Примеры по вычислению производных различных функций – в разделе « Примеры выполнения обязательных заданий по теме 5 «.
На практике наиболее трудным оказывается дифференцирование сложной функции, когда необходимо правильно оценить порядок вложения функций. Поэтому здесь приведено несколько примеров. Напомним, чтонижний индекс в записи показывает, по какой переменной вычисляется производная.
Примеры
| В этом примере функция «сложена» из показательной (3х), роль х играет sinx, и тригонометрической (sinx) функций. |
Здесь нижний индекс производной показывает, по какой переменной она вычисляется. | |
По таблице производных находим производные соответствующих функций и перемножаем их. |
| Функция
«сложена» из арктангенса (arctg
x), квадратного
корня | ||
По таблице находим производные, учитывая, что в | |||
роли х выступают различные функции (показаны нижним индексом). Перемножаем табличные производные выделенных функций. | |||
После вычисления производных не следует делать никаких алгебраических преобразований.
Производная неявно заданной функции
— Если функция задается общим выражением относительно переменных x и y, то она называется заданной неявно:
F(x,y)=0,
(Сравните с явно заданной функцией: y=y(x)).
— Чтобы
найти производную 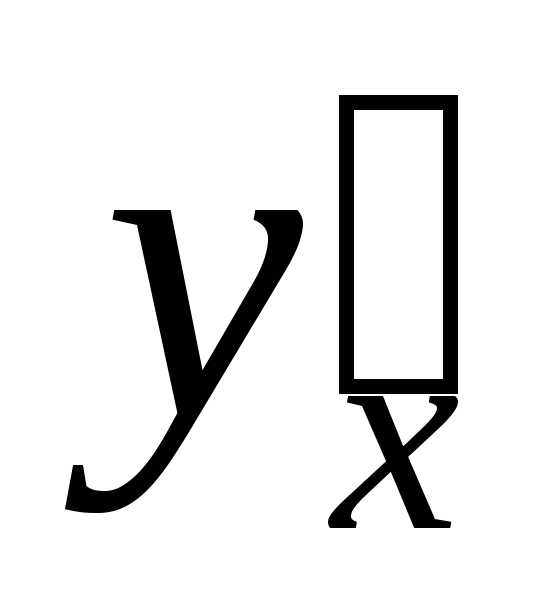
—
При этом следует учитывать, что переменная y зависит от x
(y=y(x)), и
вычислять производную, как от сложной
функции. Затем полученное уравнение
разрешают относительно 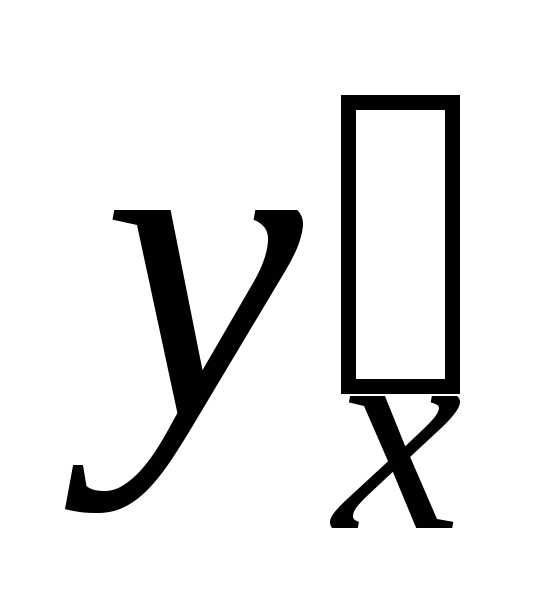 .
.
ПРИМЕР
Найти
производную 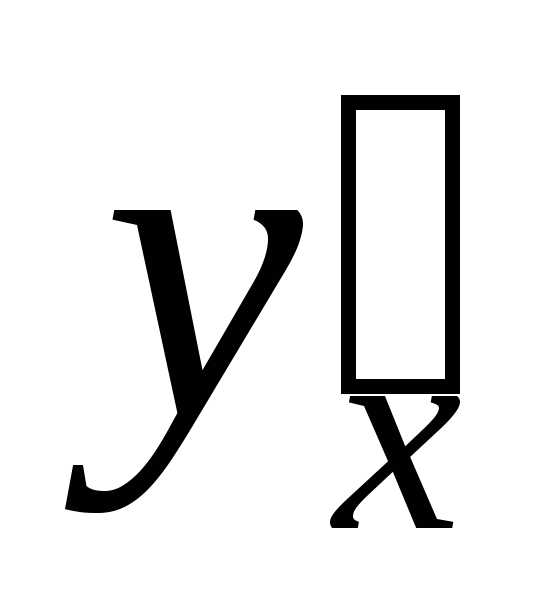 неявно заданной функции:
неявно заданной функции:
.
Найдем производные по х от левой и правой частей равенства, неявно задающего функцию y=y(x).
Здесь использованы правила дифференцирования суммы и вынесения постоянной за знак производной (правила 3 и 5). | |
Первое
слагаемое является произведением
функций: Используем правило дифференцирования произведения (правило 4). Второе и третье слагаемые дифференцируются как сложные функции. | |
Из полученного уравнения с помощью алгебраических преобразований выделяется производная. | |
. | |
studfiles.net
Производная тангенса, формула и примеры
ОПРЕДЕЛЕНИЕПроизводная тангенса равна единице, деленной на косинус того же аргумента в квадрате.
Эту формулу легко получить, зная производные синуса и косинуса:
а также формулу дифференцирования частного:
Согласно тригонометрическим формулам
Тогда
Примеры решения задач по теме «Производная тангенса»
ПРИМЕР 1| Задание | Найти производную функции |
| Решение | Искомая производная:
Перепишем функцию, стоящую под знаком производной, следующим образом:
То есть функция представляем собой степенную функцию. Производная от такой функции находится по формуле:
Так как основание степени представляет собой выражение более сложное, чем просто , то умножаем еще и на производную от основания:
Производная тангенса равна единице деленной на косинус в квадрате, тогда
|
| Ответ |
| Понравился сайт? Расскажи друзьям! | |||
ru.solverbook.com

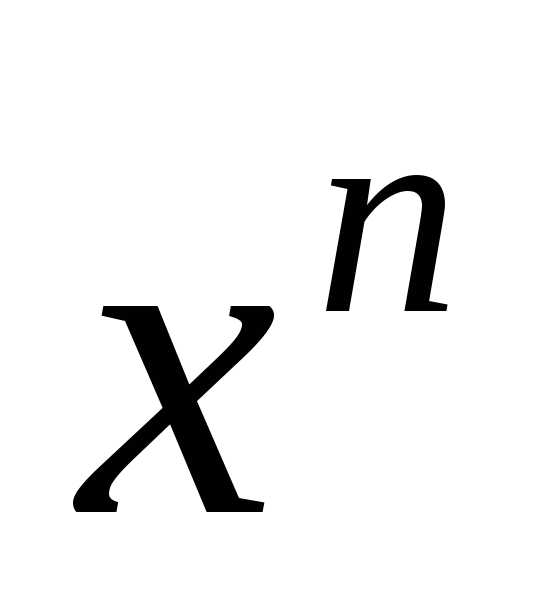
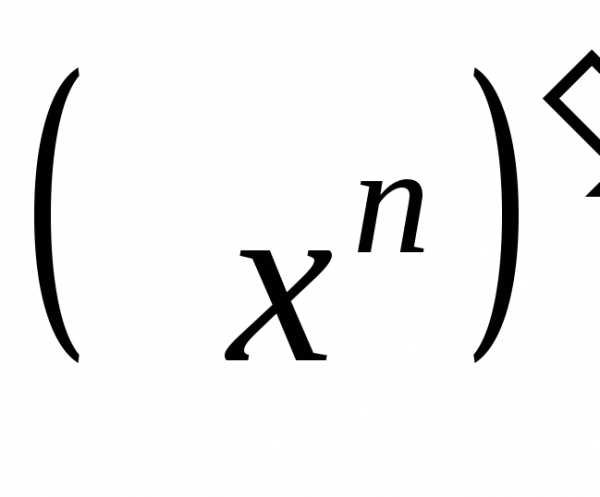
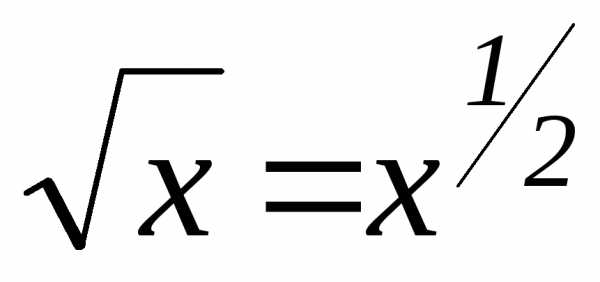
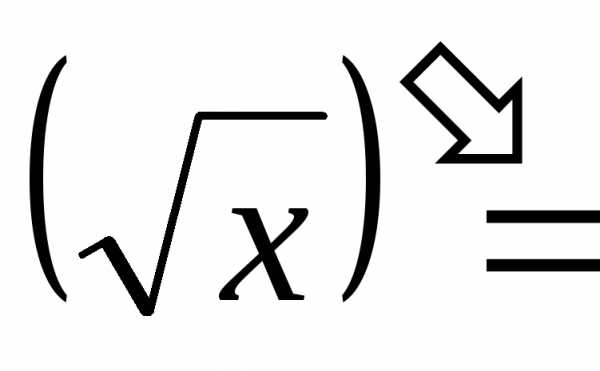
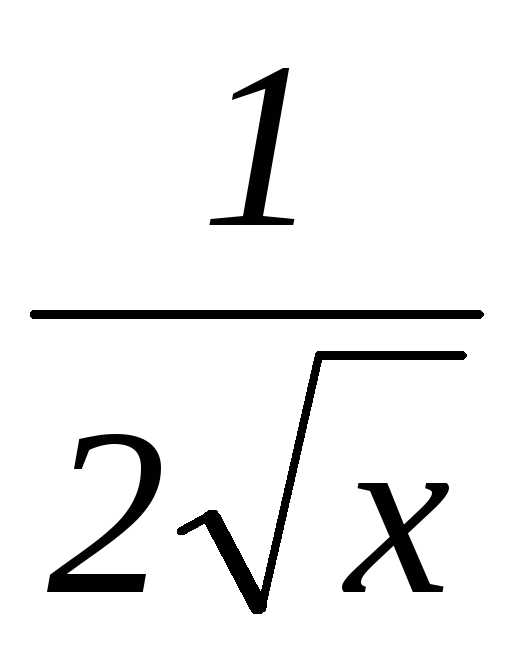
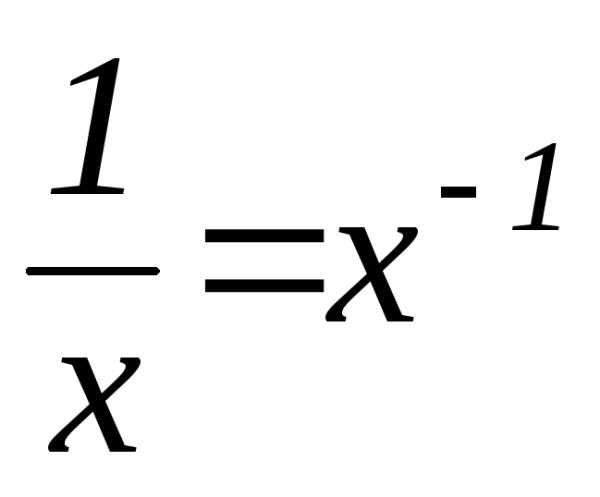
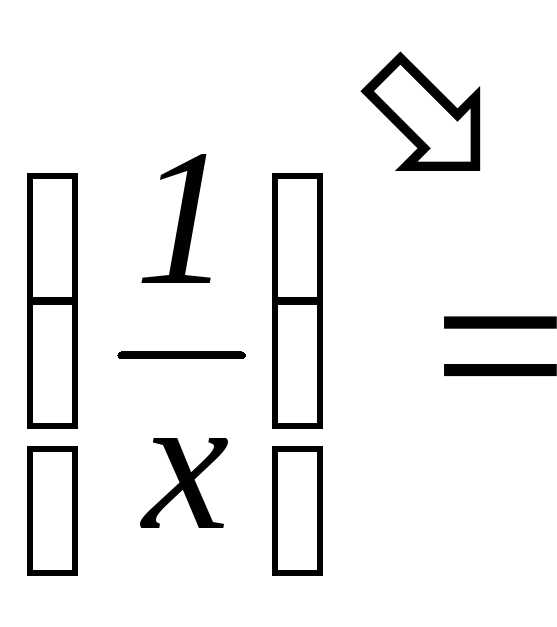
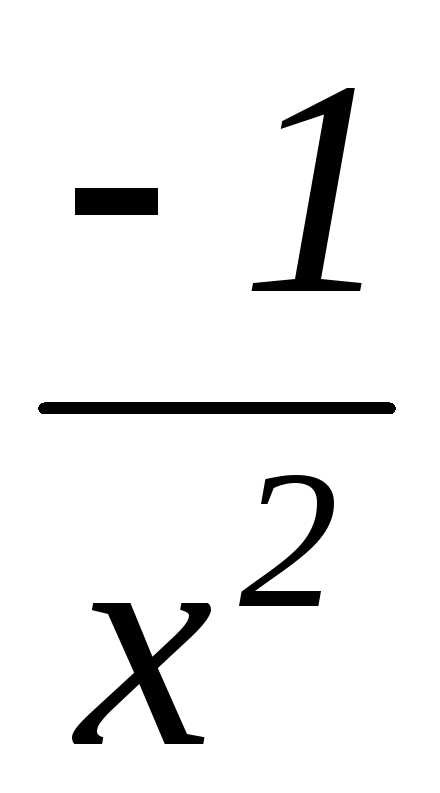
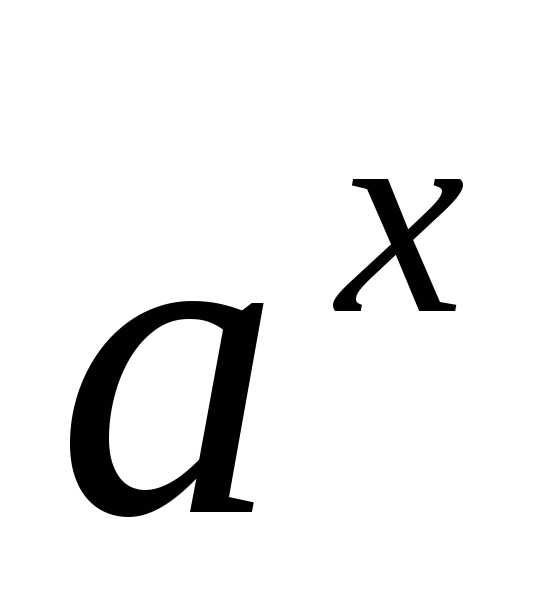
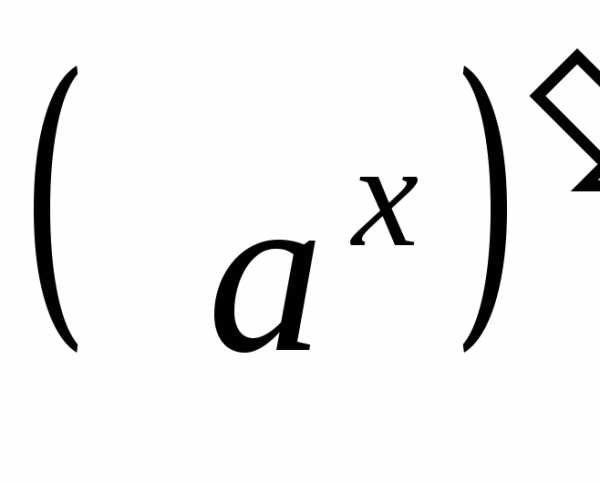 =
=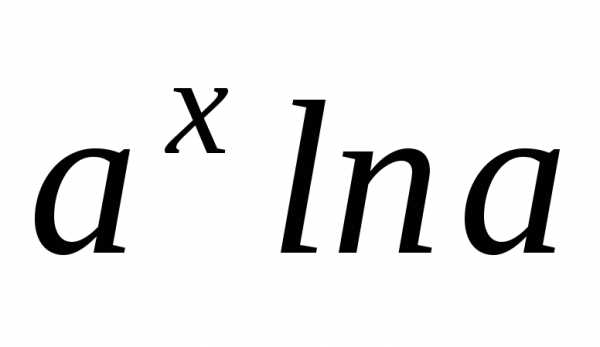
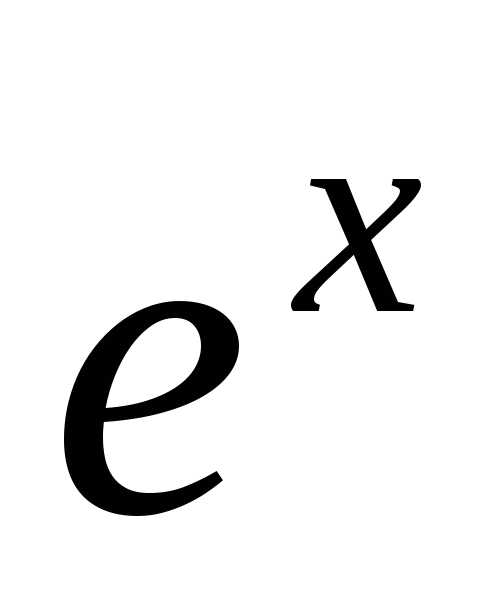
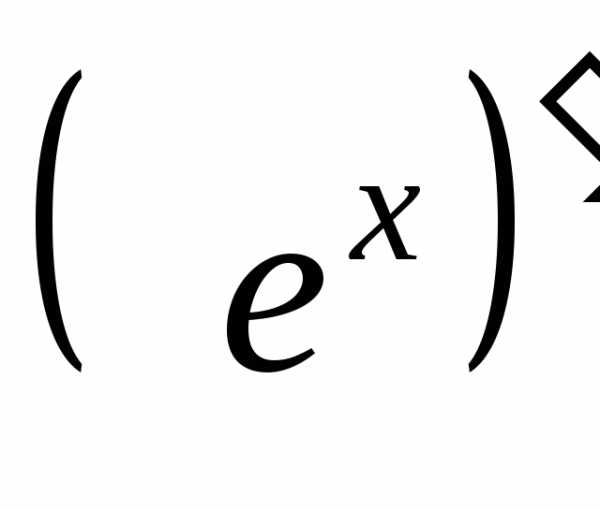 =
=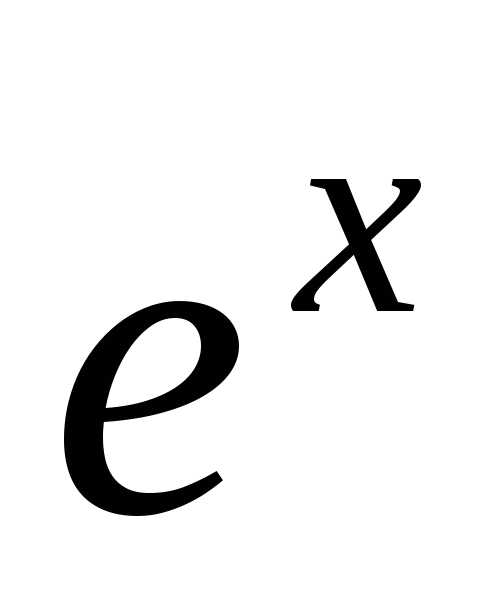
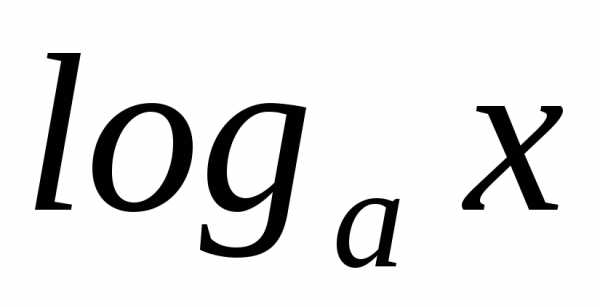
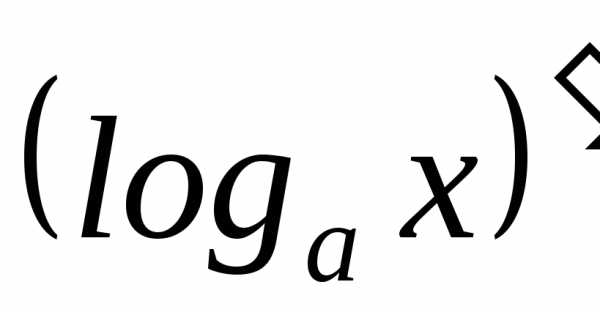 =
=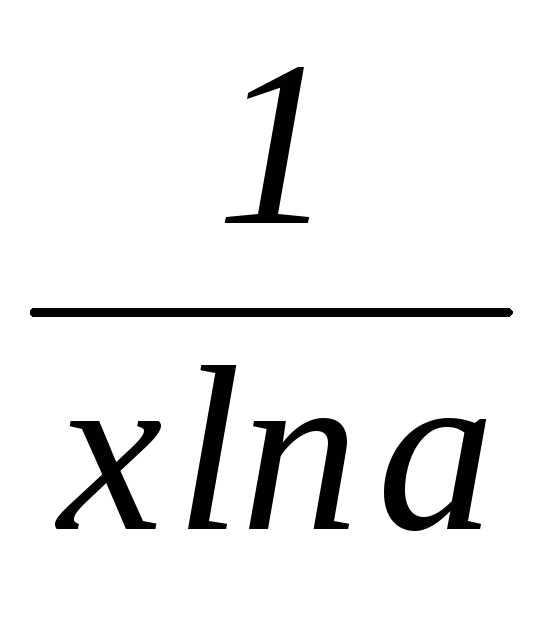
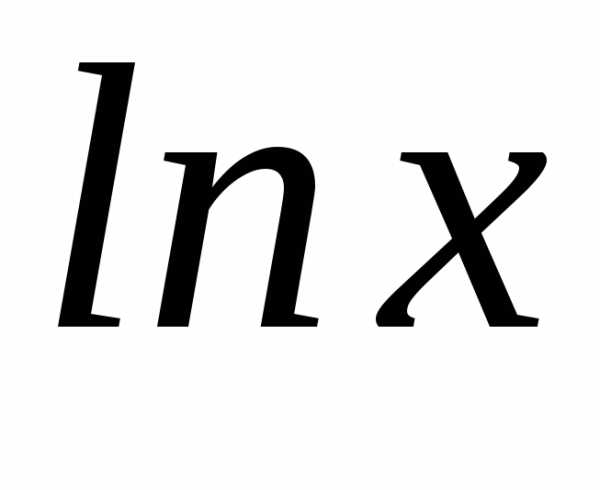
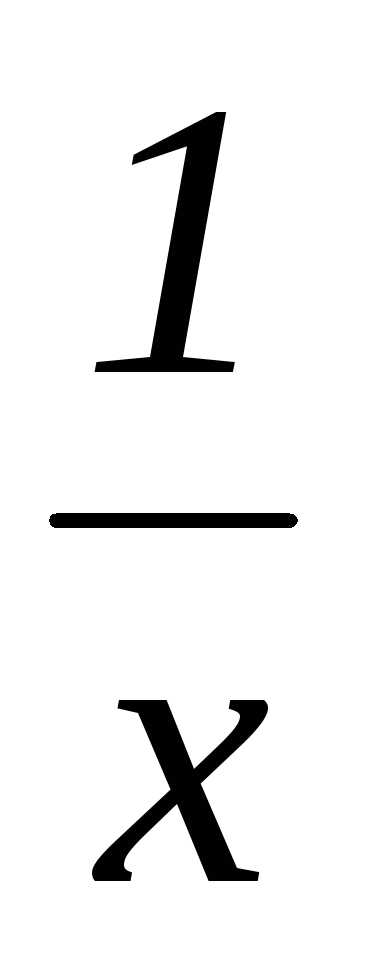
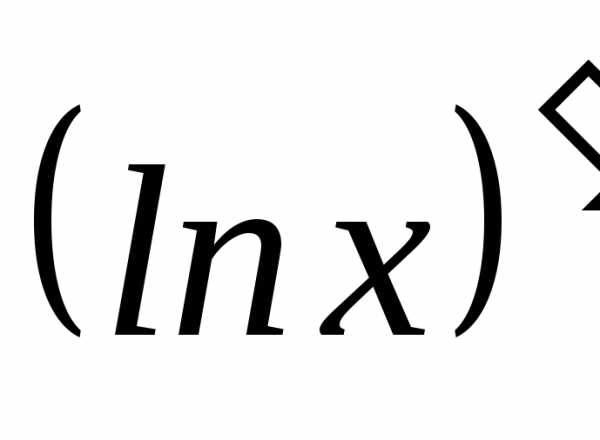 =
=
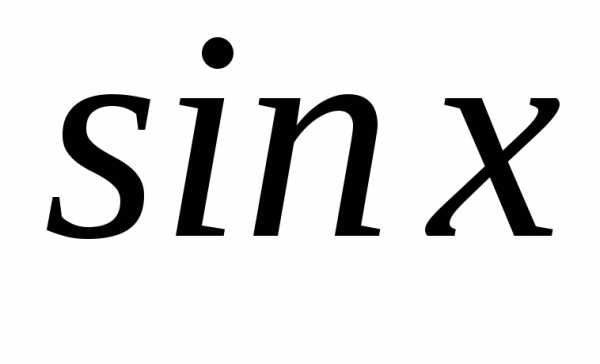
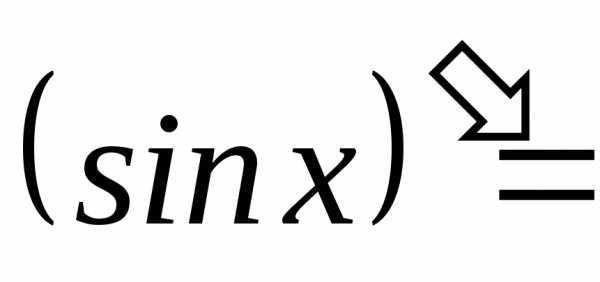
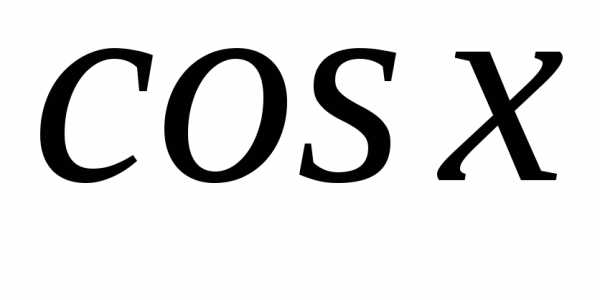
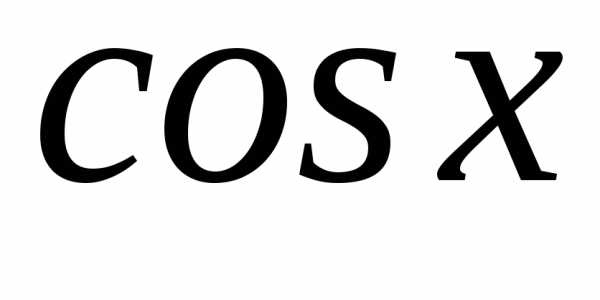
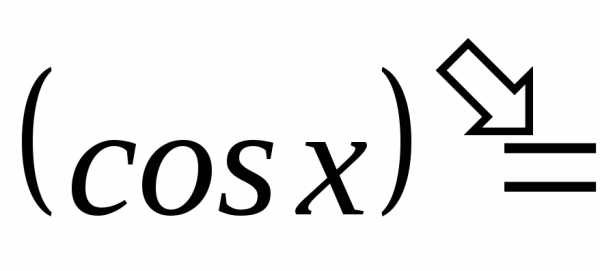
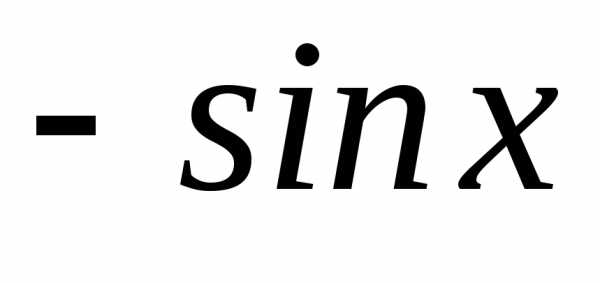
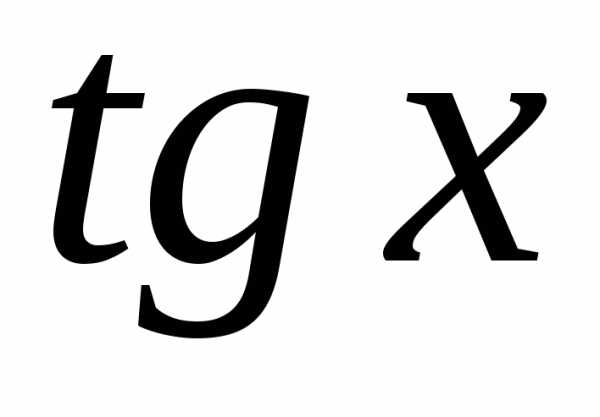
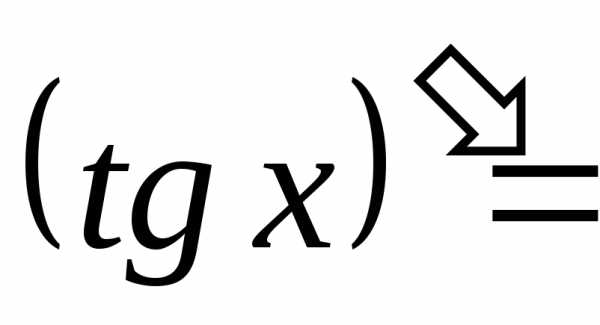
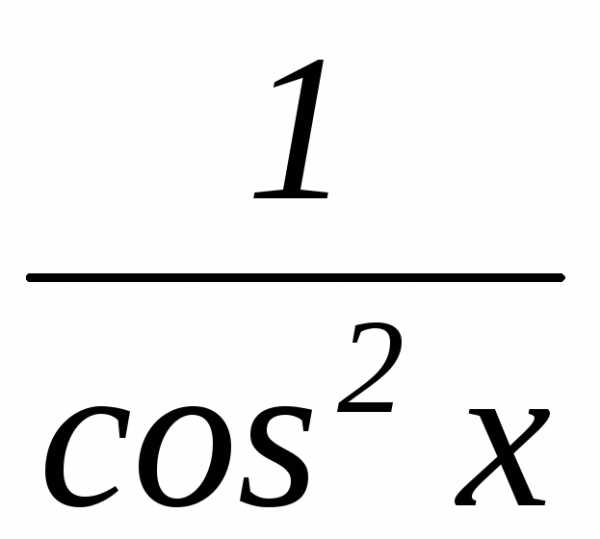
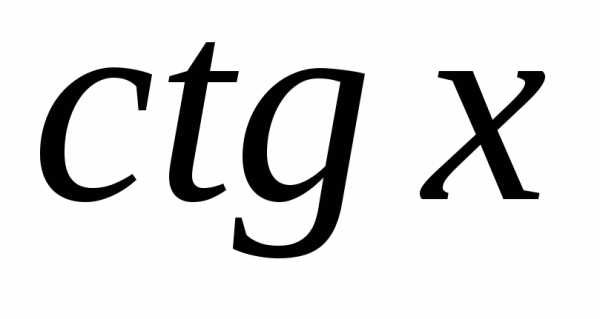
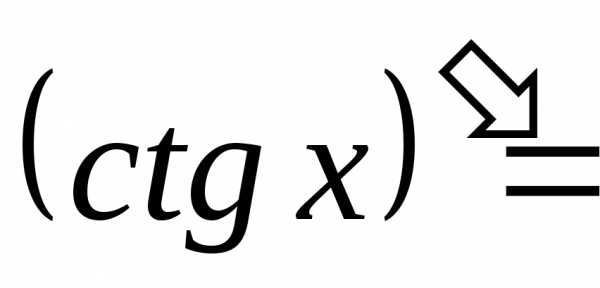
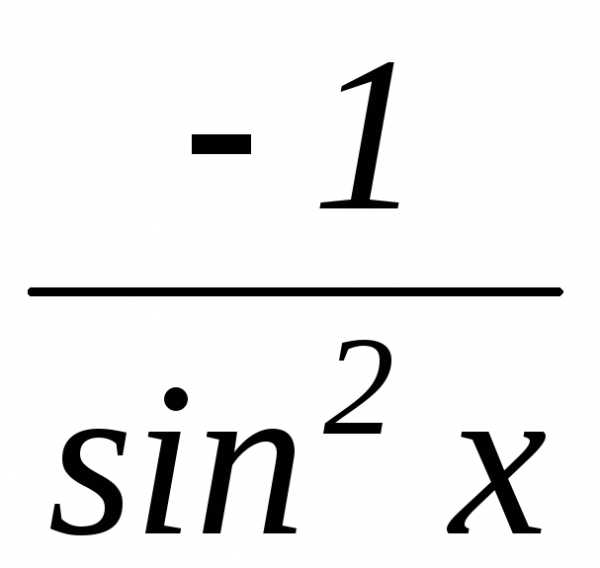
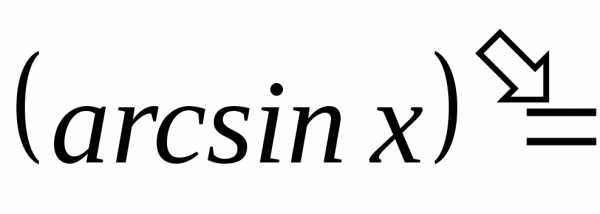
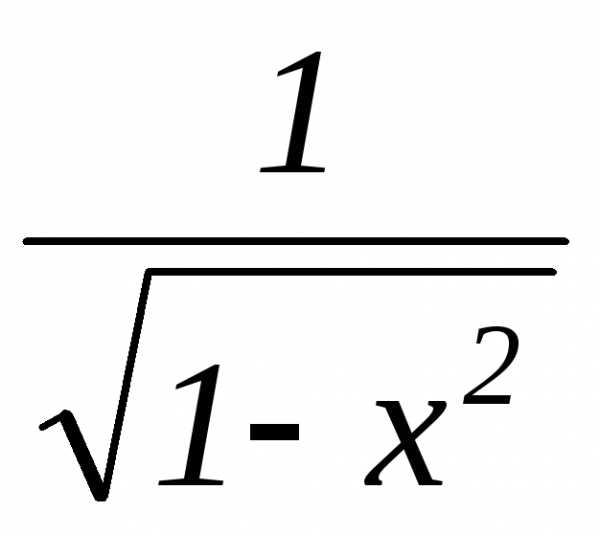
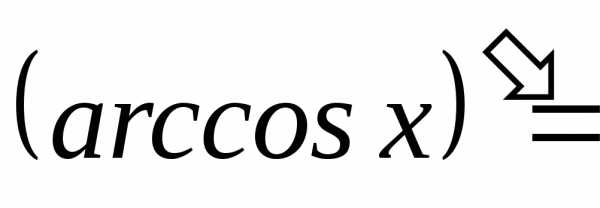
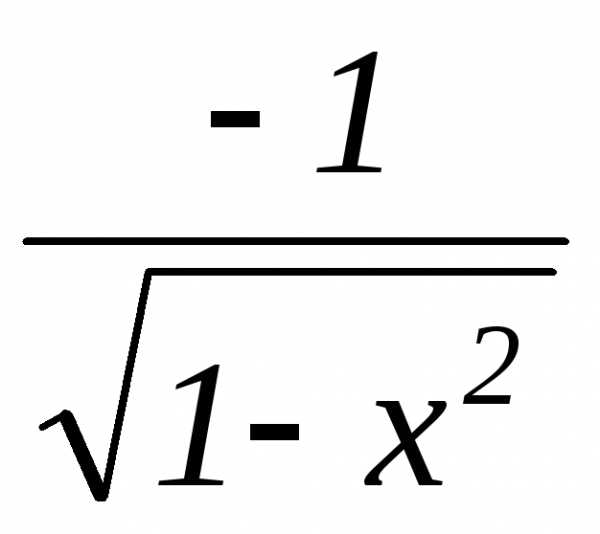
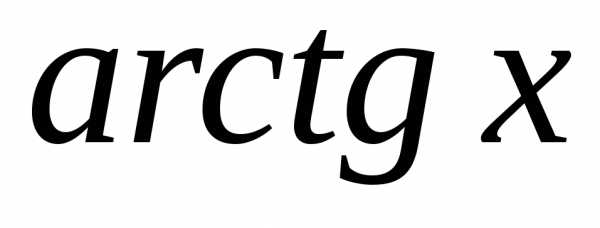
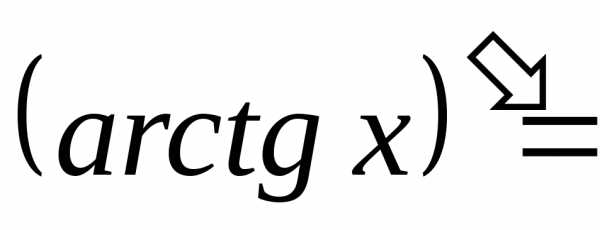
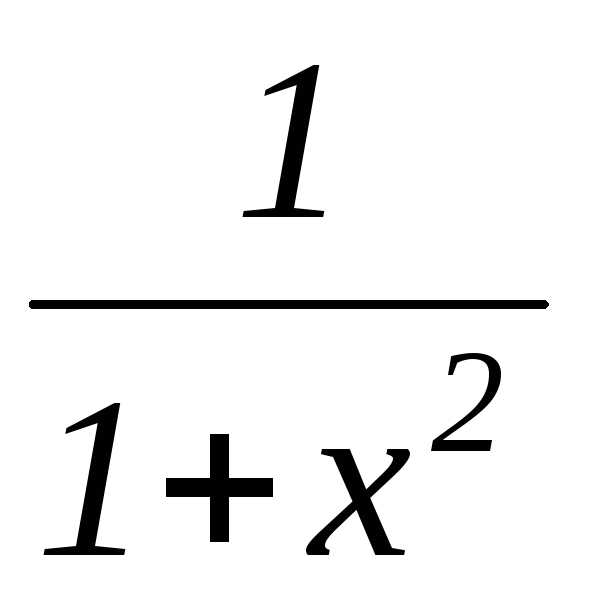
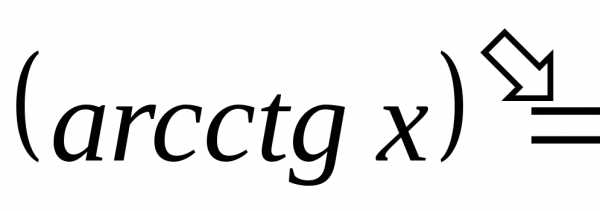
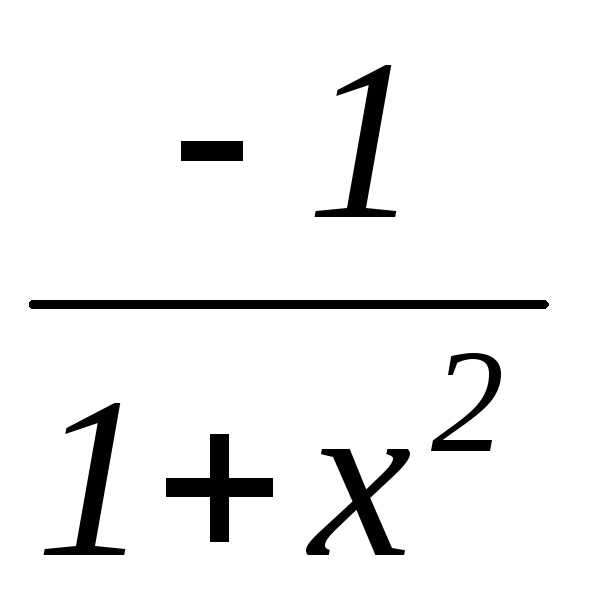
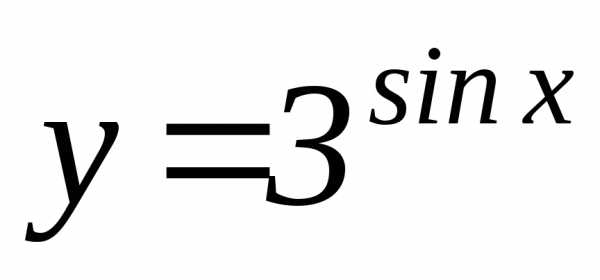 ;
;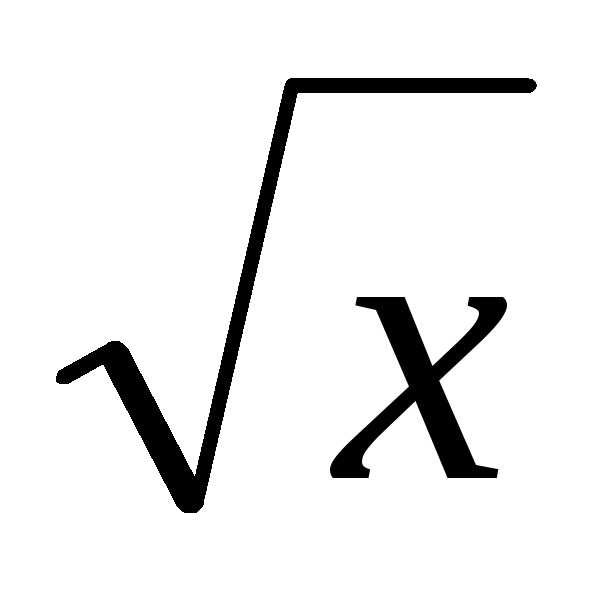
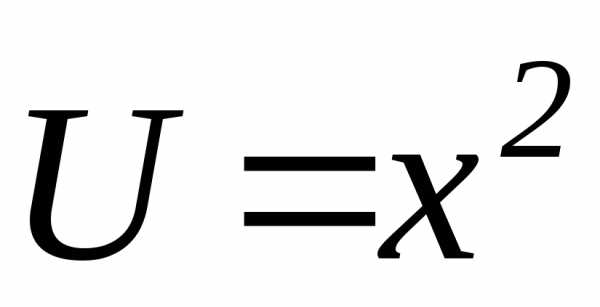 и
и