WolframAlpha по-русски: Определенный интеграл в Wolfram|Alpha
Из предыдущего поста должно быть ясно, как находить неопределенные интегралы в Wolfram|Alpha. Теперь наступил черед узнать, как Wolfram|Alpha вычисляет определенные интегралы.Так же, как и для нахождения неопределенных интегралов, для вычисления определенных интегралов Wolfram|Alpha использует запрос integrate, в котором, после подинтегральной функции, нужно указать пределы интегрирования.
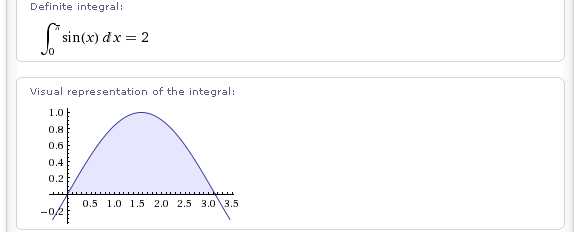
Например,
Как видим, Wolfram|Alpha не только вычисляет определенный интеграл, но и выводит его геометрическую интерпретацию.
Обратите внимание, что при вычислении интеграла в Wolfram|Alpha не обязательно указывать дифференциал переменной интегрирования (dx). Как это было сделано в первом примере. Wolfram|Alpha и без этого прекрасно понимает, что имеется в виду, когда получает запрос integrate. Однако, при вычислении интегралов «вручную», отсутствие dx в подинтегральном выражении считается грубой ошибкой. Поэтому, правильнее будет все же использовать dx. Особенно, если подинтегральная функция содержит другие буквы, кроме «x».
Но все же для Wolfram|Alpha указание dx в подинтегральном выражении не обязательно, если только вы явно указываете для какой переменной устанавливаются пределы интегрирования. Сравните, например, два таких интеграла:
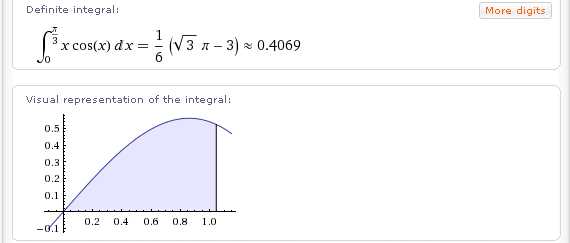
Wolfram|Alpha легко вычисляет определенные интегралы, которые интегрируются «по частям»:
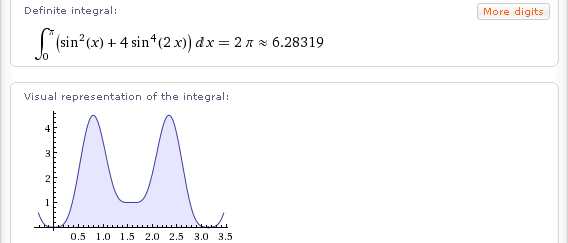
Не составляют проблемы и более сложные интегралы от тригонометрических функций:
В некоторых случаях (по-видимому, достаточно простых) Wolfram|Alpha находит определенные интегралы с параметром:
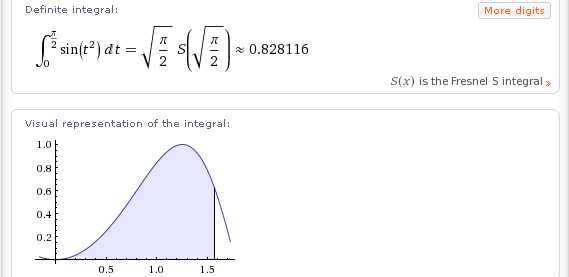
Кроме того, Wolfram|Alpha находит даже такие определенные интегралы, которые не выражаются в элементарных функциях. Например, такие, как:
www.wolframalpha-ru.com
WolframAlpha по-русски: Неопределенный интеграл в Wolfram|Alpha
Для интегрирования функций в Wolfram|Alpha служит запрос integrate. Также можно использовать integral. Иногда Wolfram|Alpha понимает также сокращенную форму int. Однако, лучше ее не использовать, поскольку int традиционно применяется для обозначения целой части числа.Вот несколько примеров на интегрирование функций в Wolfram|Alpha.
Для начала, «самый сложный вопрос»:
Теперь стандартный интеграл от многочлена:

Совет: чтобы получить пошаговое решение, не забывайте о кнопке «Show steps».
Следующий интеграл от рациональной дроби может быть достаточно сложным заданием (посмотрите пошаговое решение):
Пример на интегрирование тригонометрических функций
Интегрирование по частям:

Интегрирование подстановкой (заменой):
Если ввести запрос integrate, не указывая подинтегральную функцию, то Wolfram|Alpha выводит калькулятор интегралов. В окно калькулятора можно ввести любую функцию, и немедленно получить ответ:
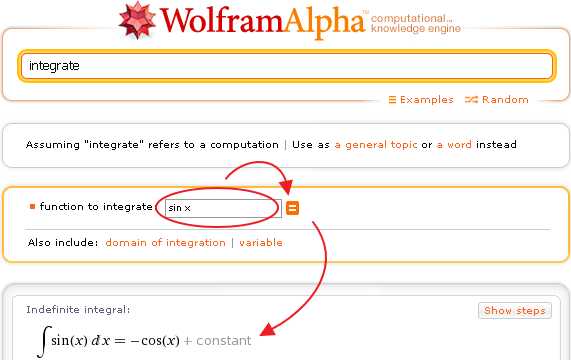
www.wolframalpha-ru.com
WolframAlpha по-русски: Несобственные интегралы в Wolfram|Alpha
При вычислении определенных интеграловпредполагается, что пределы интегрирования a и b конечны, а подынтегральная функция f(x) непрерывна на отрезке интегрирования [a; b]. Если хотя бы одно из этих условий не выполняется, то определенный интеграл называют несобственным интегралом.
Несобственные интегралы бывают двух типов.
Во-первых, это несобственный интеграл 1-го рода (определенный интеграл, в котором один или оба предела интегрирования бесконечны). Его легко узнать по внешнему виду:Во-вторых, это несобственный интеграл 2-го рода (определенный интеграл, в котором подынтегральная функция f (x) имеет одну или несколько точек разрыва на отрезке [a;b] ). Внешне он ничем не отличается от обычного определенного интеграла.
Несобственные интегралы могут быть сходящимися либо расходящимися.
Wolfram|Alpha легко справляется со всеми типами несобственных интегралов.
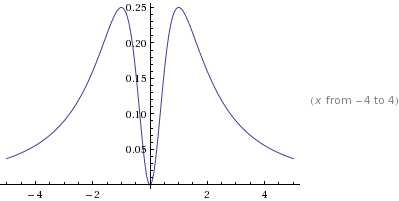
Кстати, можно графически убедиться, что подынтегральная функция в этом интеграле нe имеет разрывов:
Знак бесконечности, который в Wolfram|Alpha вводится, как «infinity», можно также ввести, используя подряд две буквы «о» (в английской раскладке клавиатуры), вот так «оо»:
— интеграл расходится.
Еще пример на вычисление несобственного интеграла 1-го рода, от функции, первообразная которой не выражается в элементарных функциях («неберущийся» интеграл):
— интеграл сходится.
Другие примеры:
Интересно было посмотреть график этой подынтегральной функции:

Примеp несобственного интеграла 2-го рода (подынтегральная функция имеет разрыв в точке x=0):
— интеграл расходится.
www.wolframalpha-ru.com
WolframAlpha по-русски: Калькулятор интегралов в Wolfram|Alpha
Для более удобного нахождения интегралов в Wolfram|Alpha имеется специальное средство — так называемый «калькулятор интегралов».Калькулятор неопределенных интегралов Wolfram|Alpha выводится по запросу
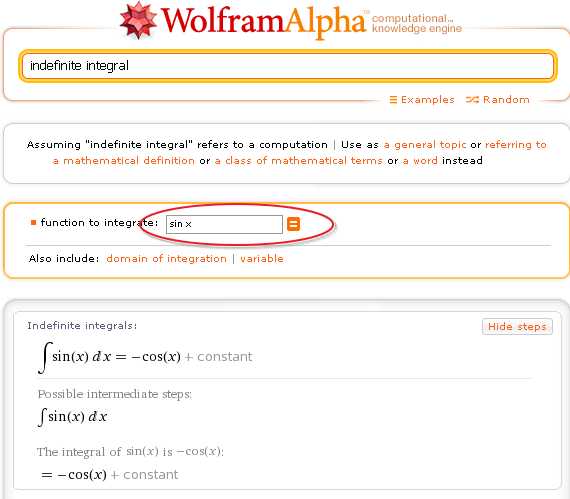
По умолчанию, Wolfram|Alpha выводит, как результат, неопределенный интеграл от функции sin(x). А Вам нужно всего лишь подставить свою подынтегральную функцию и нажать кнопку «=».
Первый способ: находясь в калькуляторе неопределенных интегралов, нажмите ссылку domain of integration:
В результате получите калькулятор определенных интегралов:
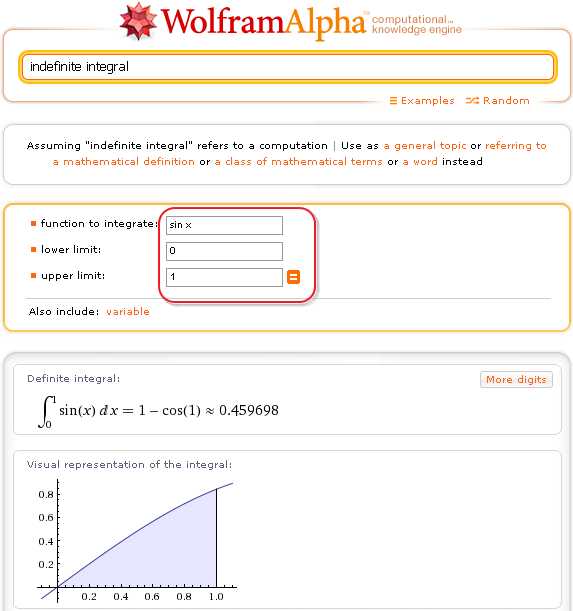
Как и выше, тот Вас требуется лишь ввести свою подынтегральную функцию и пределы интегрирования. Затем жмите кнопку «=», и получите ответ.
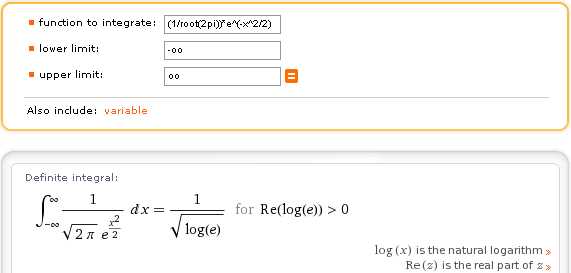
Калькуляторы неопределенных и определенных интегралов в Wolfram|Alpha позволяют решать интегралы с параметрами.
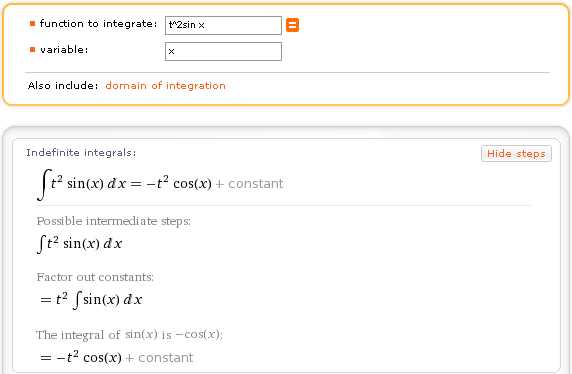
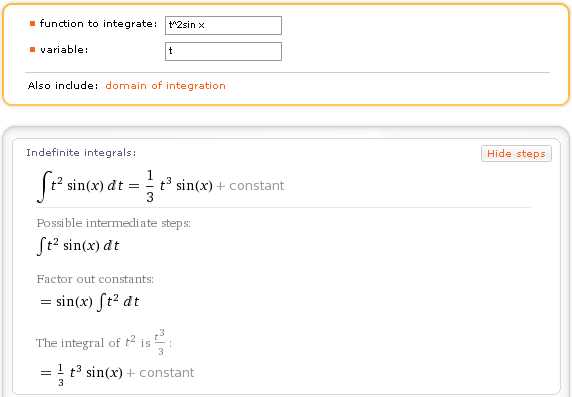
Однако, если нажать ссылку variable, то открывается возможность явно указать переменную интегрирования:
Естественно, результат интегрирования в этом случае будет отличаться от предыдущего:
www.wolframalpha-ru.com
Как вычислять интегралы с помощью Wolfram|Alpha
Вычисление интегралов и их применение — самая популярная на сегодня тема в блоге ”Wolfram|Alpha по-русски”.
В блоге ”Wolfram|Alpha по-русски” на тему интегралов существует отдельный раздел, который называется Интегральное исчисление.
Кроме теоретических аспектов интегрального исчисления, то есть собственно вычисления интегралов, существуют еще и практические, прикладные аспекты применения интегралов. Например, это вычисление площади фигуры, приближеннное вычисление «неберущихся» интегралов и другие, которые отнесены в раздел Прикладная математика.
Далее приводится список основных публикаций блога ”Wolfram|Alpha по-русски” на тему интегралов и их применения. А также на связанную с этим тему решения дифференциальных уравнений из раздела Дифференциальные уравнения.
Вот те публикации, на которые я хочу обратить ваше особое внимание. Здесь они расположены не в хронологическом порядке, а так, как я рекомендую их прочитать. Каждая из них заслуживает вашего внимания, поскольку раскрывает определенный аспект применения Wolfram|Alpha, как инструмента интегрирования:
- Неопределенный интеграл в Wolfram|Alpha
- Определенный интеграл в Wolfram|Alpha
- Несобственные интегралы в Wolfram|Alpha
- Численное интегрирование в Wolfram|Alpha
- Калькулятор интегралов в Wolfram|Alpha
- Как найти площадь плоской фигуры в Wolfram|Alpha
- Как найти площадь фигуры ограниченной кривыми линиями
- Как найти длину дуги кривой линии в Wolfram|Alpha
- Двойной интеграл в Wolfram|Alpha
- Калькулятор двойных интегралов в Wolfram|Alpha
- Тройной интеграл в Wolfram|Alpha
- Решение обыкновенных дифференциальных уравнений в Wolfram|Alpha
Понравилось это:
Нравится Загрузка…
Похожее
wolframalpharu.wordpress.com
