Страница не найдена — 404 ошибка
Инновационный подход к разработке электроники
авторизация
- О компании
- Дистрибьюторы
- Партнеры
- Логотипы
- Продукты
Система автоматизированного проектирования электронных устройств
Узнать больше
модули
- LiBerty
Менеджер библиотек - FlexyS
Схемотехнический редактор - SimOne
Система аналогового моделирования - Simtera
Система цифрового моделирования - DRM
Система управления правилами - RightPCB
Редактор плат - TopoR
Автоматический трассировщик - ЕСКД
Модуль подготовки комплекта конструкторской документации - IPR
Система хранения данных - DeltaCAM
Проверка и редактирование производственных файлов
- LiBerty
ОСРВ для встраиваемых систем
Узнать больше
модули
- Истории успеха
- Учебный центр
- Скачать/Купить
- Delta Design
- Delta ЭКБ
- FX-RTOS
- База знаний
- Сообщество
- Блог
- Мероприятия
- Форум
- Карьера
- Контакты
Будьте в курсе новостей и спецпредложений
НОУ ИНТУИТ | Лекция | Символьные вычисления
Аннотация: Существует мало программ, способных конкурировать с Mathematica при работе с символьными данными. Mathematica позволяет автоматизировать практически все типы символьных вычислений математики. Кроме того, Mathematica является эффективным инструментом проведения численных расчётов любых описанных языком математики задач. В данной лекции мы приведём обзор основных функций, позволяющих осуществлять символьные преобразования и численные расчёты.
Mathematica позволяет автоматизировать практически все типы символьных вычислений математики. Кроме того, Mathematica является эффективным инструментом проведения численных расчётов любых описанных языком математики задач. В данной лекции мы приведём обзор основных функций, позволяющих осуществлять символьные преобразования и численные расчёты.
Ключевые слова: пользователь, компьютер, ПО, массив, операции, подстановка, выражение, функция, аргумент, алгебраические, числитель, производные
Цель лекции: познакомиться с принципами выполнения символьных вычислений и рядом предназначенных для этого встроенных функций Mathematica.
5.0. Введение
Большинство систем компьютерной математики изначально разрабатывалось для выполнения численных расчётов. Пользователь на языке программы задаёт алгебраическую зависимость, вводит набор начальных численных данных и на выходе также получает набор численных данных. Всю рутину вычислений берёт на себя компьютер. По сути, с этой позиции компьютер выступает как очень хороший программируемый калькулятор. В предыдущей лекции мы познакомились с представлением чисел в Mathematica и основами работы с ними. Как мы помним, точными оказываются результаты весьма ограниченного круга вычислений. Большинство результатов оказываются приближёнными. Кроме того, для понимания некоторых моделей может не хватать голых численных данных. Простая алгебраическая зависимость порой может сказать о системе гораздо больше, чем массив подробных численных данных.
Всю рутину вычислений берёт на себя компьютер. По сути, с этой позиции компьютер выступает как очень хороший программируемый калькулятор. В предыдущей лекции мы познакомились с представлением чисел в Mathematica и основами работы с ними. Как мы помним, точными оказываются результаты весьма ограниченного круга вычислений. Большинство результатов оказываются приближёнными. Кроме того, для понимания некоторых моделей может не хватать голых численных данных. Простая алгебраическая зависимость порой может сказать о системе гораздо больше, чем массив подробных численных данных.
Пакет Mathematica — одна из немногих систем, что позволяют аккуратно и качественно выполнять символьные операции и получать результаты вычислений в аналитическом (формульном) виде. Численные результаты в этом случае оказываются развитием и продолжением аналитических. Взяв за основу работу Е. М. Воробьёва [1], познакомимся с основными принципами и встроенными функциями Mathematica для осуществления символьных вычислений и численных расчётов.
5.1. Преобразование выражений
5.1.1.Общие функции для преобразования выражений
Е. М. Воробьёв [1, с. 34] предлагает, не углубляясь в теорию, начать рассмотрение функций преобразования многочленов с простейших примеров. Так же поступим и мы. Присвоим некоторому символу b1 некоторое выражение, например, . Как мы видим в примере Out[1] на рис. 5.1, Mathematica самостоятельно вовсе не старается ни раскрыть скобки в этом выражении, ни упростить его. Для того чтобы раскрыть произведения и положительные степени сумм в выражении expr, используется функция Expand[expr] — пример In[2]. Функция также может задаваться в виде Expand[expr,pattern], где второй аргумент pattern задаёт шаблон для элементов выражения expr, которые следует раскрыть при вычислении, при этом все остальные элементы оказываются нераскрытыми. Так в примере In[3] мы раскрываем только выражения, содержащие , в примере In[4] — содержащие .
intuit.ru/2010/edi»>Подробней о функции Expand см. книгу Е. М. Воробьёва [1, с. 34–35].Рис. 5.1. Раскрытие скобок в выражении
Для упрощения выражений применяется функция Factor[expr], которая раскладывает многочлен expr на множители. Обе функции, и Expand[expr], и Factor[expr], имеют опции – дополнительные аргументы, которые указывать необязательно. Одна их таких опций — Trig. Если активировать её, задав Trig->True, то при раскрытии произведения или упрощении выражения тригонометрические функции будут рассматриваться как функции экспонент. Примеры In[2] и In[3] упрощения выражений при помощи функции Factor см. на рис. 5.2.
Для упрощения выражений также используется функция FactorList[expr], однако вывод результата вычисления имеет достаточно специфический вид. Вычисленное выражение представляет собой вложенный список, элементами которого являются внутренние списки, состоящие из двух элементов. Первым элементом внутреннего списка является множитель полинома expr, а вторым — показатель степени этого множителя, с которым он входит в разложение полинома. Самый первый элемент вложенного списка есть общий числовой множитель: если он равен единице, то список начинается с {1,1}. Пример использования FactorList[expr] — In[4] на рис. 5.2.
Первым элементом внутреннего списка является множитель полинома expr, а вторым — показатель степени этого множителя, с которым он входит в разложение полинома. Самый первый элемент вложенного списка есть общий числовой множитель: если он равен единице, то список начинается с {1,1}. Пример использования FactorList[expr] — In[4] на рис. 5.2.
Рис. 5.2. Упрощение выражений
Функция FactorTerms[expr,x] выносит общий числовой множитель, который не зависит от х. Более полная форма функции FactorTerms[expr,{x1,x2,…}] последовательно выделяет множители, которые не зависят от каждого из x1,x2,…. Выражение FactorTermsList[expr,{x1,x2,…}] возвращает список множителей выражения expr. Первый элемент в списке — общий числовой множитель, второй — множитель, который не зависит ни от одного из заданных x1,x2,…. Следующие элементы — множители, которые не зависят от как можно большего числа x1,x2,. … Примеры вынесения множителей выражения см. на рис. 5.3.
… Примеры вынесения множителей выражения см. на рис. 5.3.
Подробней о функциях упрощения выражений см. книгу Е. М. Воробьёва [1, с. 35].
Рис. 5.3. Вынесение множителей выражения
Mathematica позволяет определять коэффициенты при некотором выражении expr, содержащемся многочлене pol при помощи функции Coefficient[pol,expr], а функция CoefficientList[pol,expr] возвращает список коэффициентов при степенях expr в полиноме pol: первым элементом списка будет коэффициент при нулевой степени выражения expr, а последним — при наибольшей степени expr в полиноме pol. Примеры In[1] – In[3] на рис. 5.4 демонстрируют возможность определения коэффициентов при выражениях в полиноме.
Если в полиноме отсутствует выражение, содержащее expr в какой-то степени, то соответствующий элемент списка коэффициентов принимает значении 0 (пример In[4] на рис.
Подробней о функциях Coefficient и CoefficientList см. книгу Е. М. Воробьёва [1, с. 36].
Рис. 5.4. Определение коэффициентов при конкретных выражениях в полиноме
Ещё одна полезная функция преобразовании выражений — Collect[pol,expr], которая собирает члены с одной и той же степенью expr в многочлене pol. Заданная в расширенной форме Collect[pol,{expr1,expr2,…}] функция группирует члены с одинаковыми степенями expr1,expr2,…. Примеры использования функции Collect — In[1] – In[3] на рис. 5.5.
Подробней о функции Collect см. книгу Е. М. Воробьёва [1, с. 36–37].
увеличить изображение
Функция Variables[expr] возвращает список всех переменных в выражении expr — пример In[6] на рис. 5.6. Как мы видим, встроенные функции Mathematica, задающие математические функции, также могут выступать в роли переменных (в нашем примере это выражение Cos[x]).
Подробней о функциях выяснения структуры полиномов см. книгу Е. М. Воробьёва [1, с. 37].
Рис. 5.6. Использование функций PolinomialQ и Variables в отношении полиномов
При работе с полиномами может возникнуть необходимость в нахождении наибольшего общего делителя и наименьшего общего кратного. Для полиномов expr1 и expr2 НОД находится с помощью функции PolynomialGCD[expr1,expr2], при этом все символьные параметры рассматриваются как переменные, и деление на них невозможно. Функция PolynomialLCM[expr1,expr2] возвращает НОК полиномов expr1 и expr2. См. соответствующие примеры In[3] и In[4] на рис. 5.7.
Рис. 5.7. Нахождение наименьшего общего кратного и наибольшего общего делителя полиномов
6.9: Расчет гиперболических функций
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 2527
- Гилберт Странг и Эдвин «Джед» Герман
- OpenStax
Цели обучения
- Применять формулы для производных и интегралов гиперболических функций.

- Применить формулы для производных обратных гиперболических функций и связанных с ними интегралов.
- Опишите общие прикладные условия контактной кривой.
Ранее мы познакомились с гиперболическими функциями и некоторыми их основными свойствами. В этом разделе мы рассмотрим формулы дифференцирования и интегрирования для гиперболических функций и их обратных функций. 9{−x}] \\[4pt] &=\cosh x. \end{align*} \nonumber \]
Аналогично,
\[\dfrac{d}{dx} \cosh x=\sinh x. \nonumber \]
Мы суммируем формулы дифференцирования для гиперболических функций в таблице \(\PageIndex{1}\).
| \(f(x)\) | \(\dfrac{d}{dx}f(x)\) |
|---|---|
| \(\шп х\) 92\, х\) | |
| \(\text{sech} х\) | \(−\text{sech}\, x \tanh x\) |
| \(\text{csch} х\) | \(−\text{csch}\, x \coth x\) |
Давайте сравним производные гиперболических функций с производными стандартных тригонометрических функций.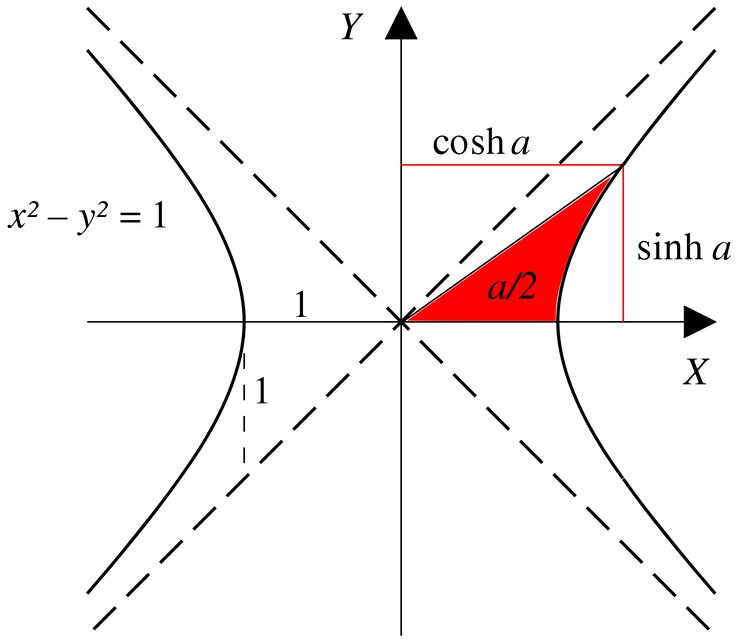 Сходства много, но и различий тоже. Например, производные функций синуса совпадают:
Сходства много, но и различий тоже. Например, производные функций синуса совпадают:
\[\dfrac{d}{dx} \sin x=\cos x \nonumber \]
и
\[\dfrac{d}{dx} \sinx x=\cosh x. \nonumber \]
Производные функций косинуса, однако, отличаются знаком:
\[\dfrac{d}{dx} \cos x=−\sin x, \nonumber \]
но
\ [\dfrac{d}{dx} \cosh x=\sinh x. \nonumber \]
Продолжая изучение гиперболических функций, мы должны помнить об их сходствах и различиях со стандартными тригонометрическими функциями. Эти формулы дифференцирования гиперболических функций непосредственно приводят к следующим интегральным формулам. 92)+С. \end{выравнивание*}\]
б. Пусть \(u=\ch x\). Затем \(du=\sinh x\,dx\) и
\[\begin{align*} \int \tanh x \,dx &=\int \dfrac{\sinh x}{\cosh x}\ ,dx \\[4pt] &=\int \dfrac{1}{u}du \\[4pt] &=\ln|u|+C \\[4pt] &= \ln|\cosh x|+C .\end{align*}\]
Обратите внимание, что \(\cosh x>0\) для всех \(x\), поэтому мы можем убрать знаки абсолютного значения и получить
\[\int \tanh x \ ,dx=\ln(\cosh x)+C.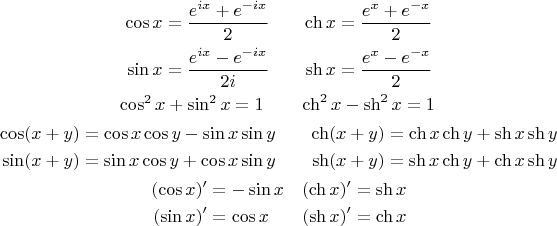 \nonumber \]
\nonumber \]
Упражнение \(\PageIndex{2}\)
Вычислите следующие интегралы: 92(3x) \, dx=\dfrac{\tanh(3x)}{3}+C\)
Вычисление обратных гиперболических функций
Глядя на графики гиперболических функций, мы видим, что при соответствующих ограничениях диапазона все они имеют обратные функции. Большинство необходимых ограничений диапазона можно различить при внимательном рассмотрении графиков. Области и диапазоны обратных гиперболических функций приведены в таблице \(\PageIndex{2}\).


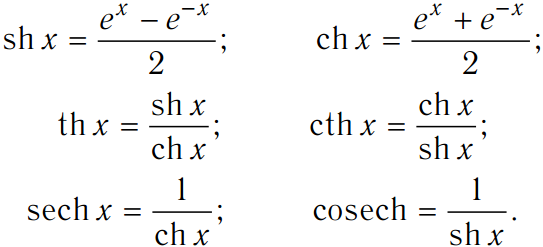 На следующем рисунке показаны цепи, свисающие с ряда столбов.
На следующем рисунке показаны цепи, свисающие с ряда столбов.
 9: Исчисление гиперболических функций распространяется под лицензией CC BY-NC-SA 4.0 и была создана, изменена и/или курирована Гилбертом Стрэнгом и Эдвином «Джедом» Херманом (OpenStax) через исходный контент, который был отредактирован в соответствии со стилем и стандартами платформы LibreTexts; подробная история редактирования доступна по запросу.
9: Исчисление гиперболических функций распространяется под лицензией CC BY-NC-SA 4.0 и была создана, изменена и/или курирована Гилбертом Стрэнгом и Эдвином «Джедом» Херманом (OpenStax) через исходный контент, который был отредактирован в соответствии со стилем и стандартами платформы LibreTexts; подробная история редактирования доступна по запросу. org/details/books/calculus-volume-1
org/details/books/calculus-volume-1 9{-х})}, х\! \нет =\! 0
\end{align*}tanhxcothxsech xcsch x=coshxsinhx=(ex+e-x)(ex-e-x)=sinhxcoshx=(ex-e-x)(ex+e-x),x =0=chx1=(ex+e−x)2=sinhx1=(ex-e−x)2,x=0
9{-х})}, х\! \нет =\! 0
\end{align*}tanhxcothxsech xcsch x=coshxsinhx=(ex+e-x)(ex-e-x)=sinhxcoshx=(ex-e-x)(ex+e-x),x =0=chx1=(ex+e−x)2=sinhx1=(ex-e−x)2,x=0
