sin x = 0 решение
Доброй ночи!
Уравнения вида, которое вы попросили решить — очень часто вызывает различные затруднение у многих людей. Но это, на самом деле, не так страшно и не так сложно, как Вам могло показаться. Прежде, чем разобраться с Вашей уравнением sin x = 0, нужно подумать, в каком виде можно представить данное уравнение, чтоб понять как его решать.
Вот так будет выглядеть Ваше условие на математическом языке:
Да, я понимаю, что это Вам ничем не помогло, но находить будет легче. Для подобных уравнений есть определённое правило решения, которое принимает всегда вот такой общий вид:
Как только мы разобрались с общим решением, то с лёгкостью можем преступить к решению именно Вашего уравнения:
Значение мы найдём при помощи таблицы. И исходя из этого получаем, что , или же . Возьмём с Вами второй вариант.
Так как с основным разобрались, то теперь можем и решить до конца Ваше уравнение:
Ответ:
| 1 | Найти точное значение | sin(30) | |
| 2 | Найти точное значение | sin(45) | |
| 3 | Найти точное значение | sin(60) | |
| 4 | Найти точное значение | sin(30 град. ) | |
| 5 | Найти точное значение | sin(60 град. ) | |
| 6 | Найти точное значение | tan(30 град. ) | |
| 7 | Найти точное значение | arcsin(-1) | |
| 8 | Найти точное значение | sin(pi/6) | |
| 9 | Найти точное значение | cos(pi/4) | |
| 10 | Найти точное значение | sin(45 град. ) | |
| 11 | Найти точное значение | sin(pi/3) | |
| 12 | Найти точное значение | arctan(-1) | |
| 13 | Найти точное значение | cos(45 град. ) | |
| 14 | Найти точное значение | cos(30 град. ) | |
| 15 | Найти точное значение | tan(60) | |
| 16 | Найти точное значение | csc(45 град. ) | |
| 17 | Найти точное значение | tan(60 град. ) | |
| 18 | Найти точное значение | sec(30 град. ) | |
| 19 | Преобразовать из радианов в градусы | (3pi)/4 | |
| 20 | График | y=sin(x) | |
| 21 | Преобразовать из радианов в градусы | pi/6 | |
| 22 | Найти точное значение | cos(60 град. ) | |
| Найти точное значение | cos(150) | ||
| 24 | Найти точное значение | tan(45) | |
| 25 | Найти точное значение | sin(30) | |
| 26 | Найти точное значение | sin(60) | |
| 27 | Найти точное значение | cos(pi/2) | |
| 28 | Найти точное значение | tan(45 град. ) | |
| 29 | График | y=sin(x) | |
| 30 | Найти точное значение | arctan(- квадратный корень 3) | |
| 31 | Найти точное значение | csc(60 град. ) | |
| 32 | Найти точное значение | sec(45 град. ) | |
| 33 | Найти точное значение | csc(30 град. ) | |
| 34 | Найти точное значение | ||
| 35 | Найти точное значение | sin(120) | |
| 36 | Найти точное значение | cos(90) | |
| 37 | Преобразовать из радианов в градусы | pi/3 | |
| 38 | Найти точное значение | sin(45) | |
| 39 | Найти точное значение | tan(30) | |
| 40 | Преобразовать из градусов в радианы | 45 | |
| 41 | Найти точное значение | tan(60) | |
| 42 | Упростить | квадратный корень x^2 | |
| 43 | Найти точное значение | cos(45) | |
| 44 | Упростить | sin(theta)^2+cos(theta)^2 | |
| 45 | Преобразовать из радианов в градусы | pi/6 | |
| 46 | Найти точное значение | cot(30 град. ) | |
| 47 | Найти точное значение | arccos(-1) | |
| 48 | Найти точное значение | arctan(0) | |
| 49 | График | y=cos(x) | |
| 50 | Найти точное значение | cot(60 град. ) | |
| 51 | Преобразовать из градусов в радианы | 30 | |
| 52 | Упростить | ( квадратный корень x+ квадратный корень 2)^2 | |
| 53 | Преобразовать из радианов в градусы | (2pi)/3 | |
| 54 | Найти точное значение | sin((5pi)/3) | |
| 55 | Упростить | 1/( кубический корень от x^4) | |
| 56 | Найти точное значение | sin((3pi)/4) | |
| 57 | Найти точное значение | tan(pi/2) | |
| 58 | Найти угол А | tri{}{90}{}{}{}{} | |
| 59 | Найти точное значение | sin(300) | |
| 60 | Найти точное значение | cos(30) | |
| 61 | Найти точное значение | cos(60) | |
| 62 | Найти точное значение | cos(0) | |
| 63 | Найти точное значение | arctan( квадратный корень 3) | |
| 64 | Найти точное значение | cos(135) | |
| 65 | Найти точное значение | cos((5pi)/3) | |
| 66 | Найти точное значение | cos(210) | |
| 67 | Найти точное значение | sec(60 град. ) | |
| 68 | Найти точное значение | sin(300 град. ) | |
| 69 | Преобразовать из градусов в радианы | 135 | |
| 70 | Преобразовать из градусов в радианы | 150 | |
| 71 | Преобразовать из радианов в градусы | (5pi)/6 | |
| 72 | Преобразовать из радианов в градусы | (5pi)/3 | |
| 73 | Преобразовать из градусов в радианы | 89 град. | |
| 74 | Преобразовать из градусов в радианы | 60 | |
| 75 | Найти точное значение | sin(135 град. ) | |
| 76 | Найти точное значение | sin(150) | |
| 77 | Найти точное значение | sin(240 град. ) | |
| 78 | Найти точное значение | cot(45 град. ) | |
| 79 | Преобразовать из радианов в градусы | (5pi)/4 | |
| 80 | Упростить | 1/( кубический корень от x^8) | |
| 81 | Найти точное значение | sin(225) | |
| 82 | Найти точное значение | sin(240) | |
| 83 | Найти точное значение | cos(150 град. ) | |
| 84 | Найти точное значение | tan(45) | |
| 85 | Вычислить | sin(30 град. ) | |
| 86 | Найти точное значение | sec(0) | |
| 87 | Упростить | arcsin(-( квадратный корень 2)/2) | |
| 88 | Найти точное значение | cos((5pi)/6) | |
| 89 | Найти точное значение | csc(30) | |
| 90 | Найти точное значение | arcsin(( квадратный корень 2)/2) | |
| 91 | Найти точное значение | tan((5pi)/3) | |
| 92 | Найти точное значение | tan(0) | |
| 93 | Вычислить | sin(60 град. ) | |
| 94 | Найти точное значение | arctan(-( квадратный корень 3)/3) | |
| 95 | Преобразовать из радианов в градусы | (3pi)/4 | |
| 96 | Вычислить | arcsin(-1) | |
| 97 | Найти точное значение | sin((7pi)/4) | |
| 98 | Найти точное значение | arcsin(-1/2) | |
| 99 | Найти точное значение | sin((4pi)/3) | |
| 100 | Найти точное значение | csc(45) |
Решите уравнение sin(x)^(2)-sin(x)=0 (синус от (х) в степени (2) минус синус от (х) равно 0)
Дано уравнение$$\sin^{2}{\left (x \right )} — \sin{\left (x \right )} = 0$$
преобразуем
$$\left(\sin{\left (x \right )} — 1\right) \sin{\left (x \right )} = 0$$
$$\sin^{2}{\left (x \right )} — \sin{\left (x \right )} = 0$$
Сделаем замену
$$w = \sin{\left (x \right )}$$
Это уравнение вида
a*w^2 + b*w + c = 0
Квадратное уравнение можно решить
с помощью дискриминанта.
Корни квадратного уравнения:
$$w_{1} = \frac{\sqrt{D} — b}{2 a}$$
$$w_{2} = \frac{- \sqrt{D} — b}{2 a}$$
где D = b^2 — 4*a*c — это дискриминант.
Т.к.
$$a = 1$$
$$b = -1$$
$$c = 0$$
, то
D = b^2 - 4 * a * c =
(-1)^2 - 4 * (1) * (0) = 1
Т.к. D > 0, то уравнение имеет два корня.
w1 = (-b + sqrt(D)) / (2*a)
w2 = (-b - sqrt(D)) / (2*a)
или
$$w_{1} = 1$$
$$w_{2} = 0$$
делаем обратную замену
$$\sin{\left (x \right )} = w$$
Дано уравнение
$$\sin{\left (x \right )} = w$$
— это простейшее тригонометрическое ур-ние
Это ур-ние преобразуется в
$$x = 2 \pi n + \operatorname{asin}{\left (w \right )}$$
$$x = 2 \pi n — \operatorname{asin}{\left (w \right )} + \pi$$
Или
$$x = 2 \pi n + \operatorname{asin}{\left (w \right )}$$
$$x = 2 \pi n — \operatorname{asin}{\left (w \right )} + \pi$$
, где n — любое целое число
подставляем w:
$$x_{1} = 2 \pi n + \operatorname{asin}{\left (w_{1} \right )}$$
$$x_{1} = 2 \pi n + \operatorname{asin}{\left (1 \right )}$$
$$x_{1} = 2 \pi n + \frac{\pi}{2}$$
$$x_{2} = 2 \pi n + \operatorname{asin}{\left (w_{2} \right )}$$
$$x_{2} = 2 \pi n + \operatorname{asin}{\left (0 \right )}$$
$$x_{2} = 2 \pi n$$
$$x_{3} = 2 \pi n — \operatorname{asin}{\left (w_{1} \right )} + \pi$$
$$x_{3} = 2 \pi n — \operatorname{asin}{\left (1 \right )} + \pi$$
$$x_{3} = 2 \pi n + \frac{\pi}{2}$$
$$x_{4} = 2 \pi n — \operatorname{asin}{\left (w_{2} \right )} + \pi$$
$$x_{4} = 2 \pi n — \operatorname{asin}{\left (0 \right )} + \pi$$
$$x_{4} = 2 \pi n + \pi$$
Решите уравнение sin(sin(x))=1 (синус от (синус от (х)) равно 1)
Найду корень уравнения: sin(sin(x))=1
Решение
Вы ввели[TeX]
[pretty]
[text]
$$\sin{\left (\sin{\left (x \right )} \right )} = 1$$
Подробное решение[TeX]
Дано уравнение
$$\sin{\left (\sin{\left (x \right )} \right )} = 1$$
преобразуем
$$\sin{\left (\sin{\left (x \right )} \right )} — 1 = 0$$
$$\sin{\left (\sin{\left (x \right )} \right )} — 1 = 0$$
Сделаем замену
$$w = \sin{\left (\sin{\left (x \right )} \right )}$$
Переносим свободные слагаемые (без w)
из левой части в правую, получим:
$$w = 1$$
Получим ответ: w = 1
делаем обратную замену
$$\sin{\left (\sin{\left (x \right )} \right )} = w$$
подставляем w:
[TeX]
[pretty]
[text]
/ /pi\\ / /pi\\
x1 = pi - re|asin|--|| - I*im|asin|--||
\ \2 // \ \2 //$$x_{1} = — \Re{\left(\operatorname{asin}{\left (\frac{\pi}{2} \right )}\right)} + \pi — i \Im{\left(\operatorname{asin}{\left (\frac{\pi}{2} \right )}\right)}$$
/ /pi\\ / /pi\\
x2 = I*im|asin|--|| + re|asin|--||
\ \2 // \ \2 //$$x_{2} = \Re{\left(\operatorname{asin}{\left (\frac{\pi}{2} \right )}\right)} + i \Im{\left(\operatorname{asin}{\left (\frac{\pi}{2} \right )}\right)}$$
Численный ответ[pretty]
[text]
x1 = 1.5707963267949 + 1.02322747854755*i
x2 = 1.5707963267949 - 1.02322747854755*i
Решите неравенство sin(x)^2-4*sin(x)
Дано неравенство:$$\sin^{2}{\left (x \right )} — 4 \sin{\left (x \right )} Чтобы решить это нер-во — надо сначала решить соотвествующее ур-ние:
$$\sin^{2}{\left (x \right )} — 4 \sin{\left (x \right )} = 0$$
Решаем:
Дано уравнение
$$\sin^{2}{\left (x \right )} — 4 \sin{\left (x \right )} = 0$$
преобразуем
$$\left(\sin{\left (x \right )} — 4\right) \sin{\left (x \right )} = 0$$
$$\sin^{2}{\left (x \right )} — 4 \sin{\left (x \right )} = 0$$
Сделаем замену
$$w = \sin{\left (x \right )}$$
Это уравнение вида
a*w^2 + b*w + c = 0
Квадратное уравнение можно решить
с помощью дискриминанта.
Корни квадратного уравнения:
$$w_{1} = \frac{\sqrt{D} — b}{2 a}$$
$$w_{2} = \frac{- \sqrt{D} — b}{2 a}$$
где D = b^2 — 4*a*c — это дискриминант.
Т.к.
$$a = 1$$
$$b = -4$$
$$c = 0$$
, то
D = b^2 - 4 * a * c =
(-4)^2 - 4 * (1) * (0) = 16
Т.к. D > 0, то уравнение имеет два корня.
w1 = (-b + sqrt(D)) / (2*a)
w2 = (-b - sqrt(D)) / (2*a)
или
$$w_{1} = 4$$
$$w_{2} = 0$$
делаем обратную замену
$$\sin{\left (x \right )} = w$$
Дано уравнение
$$\sin{\left (x \right )} = w$$
— это простейшее тригонометрическое ур-ние
Это ур-ние преобразуется в
$$x = 2 \pi n + \operatorname{asin}{\left (w \right )}$$
$$x = 2 \pi n — \operatorname{asin}{\left (w \right )} + \pi$$
Или
$$x = 2 \pi n + \operatorname{asin}{\left (w \right )}$$
$$x = 2 \pi n — \operatorname{asin}{\left (w \right )} + \pi$$
, где n — любое целое число
подставляем w:
$$x_{1} = 2 \pi n + \operatorname{asin}{\left (w_{1} \right )}$$
$$x_{1} = 2 \pi n + \operatorname{asin}{\left (4 \right )}$$
$$x_{1} = 2 \pi n + \operatorname{asin}{\left (4 \right )}$$
$$x_{2} = 2 \pi n + \operatorname{asin}{\left (w_{2} \right )}$$
$$x_{2} = 2 \pi n + \operatorname{asin}{\left (0 \right )}$$
$$x_{2} = 2 \pi n$$
$$x_{3} = 2 \pi n — \operatorname{asin}{\left (w_{1} \right )} + \pi$$
$$x_{3} = 2 \pi n + \pi — \operatorname{asin}{\left (4 \right )}$$
$$x_{3} = 2 \pi n + \pi — \operatorname{asin}{\left (4 \right )}$$
$$x_{4} = 2 \pi n — \operatorname{asin}{\left (w_{2} \right )} + \pi$$
$$x_{4} = 2 \pi n — \operatorname{asin}{\left (0 \right )} + \pi$$
$$x_{4} = 2 \pi n + \pi$$
$$x_{1} = 0$$
$$x_{2} = \pi$$
$$x_{3} = \pi — \operatorname{asin}{\left (4 \right )}$$
$$x_{4} = \operatorname{asin}{\left (4 \right )}$$
Исключаем комплексные решения:
$$x_{1} = 0$$
$$x_{2} = \pi$$
Данные корни
$$x_{1} = 0$$
$$x_{2} = \pi$$
являются точками смены знака неравенства в решениях.
Сначала определимся со знаком до крайней левой точки:
$$x_{0} Возьмём например точку
$$x_{0} = x_{1} — \frac{1}{10}$$
=
$$- \frac{1}{10}$$
=
$$- \frac{1}{10}$$
подставляем в выражение
$$\sin^{2}{\left (x \right )} — 4 \sin{\left (x \right )}
2 sin (-1/10) - 4*sin(-1/10)2 sin (1/10) + 4*sin(1/10)
но2 sin (1/10) + 4*sin(1/10) > 0
Тогда
$$x не выполняется
значит одно из решений нашего неравенства будет при:
$$x > 0 \wedge x_____ / \ -------ο-------ο------- x1 x2
Решите неравенство sin(x)^2>0 (синус от (х) в квадрате больше 0)
Дано неравенство:$$\sin^{2}{\left (x \right )} > 0$$
Чтобы решить это нер-во — надо сначала решить соотвествующее ур-ние:
$$\sin^{2}{\left (x \right )} = 0$$
Решаем:
Дано уравнение
$$\sin^{2}{\left (x \right )} = 0$$
преобразуем
$$\sin^{2}{\left (x \right )} = 0$$
$$\sin^{2}{\left (x \right )} = 0$$
Сделаем замену
$$w = \sin{\left (x \right )}$$
Это уравнение вида
a*w^2 + b*w + c = 0
Квадратное уравнение можно решить
с помощью дискриминанта.
Корни квадратного уравнения:
$$w_{1} = \frac{\sqrt{D} — b}{2 a}$$
$$w_{2} = \frac{- \sqrt{D} — b}{2 a}$$
где D = b^2 — 4*a*c — это дискриминант.
Т.к.
$$a = 1$$
$$b = 0$$
$$c = 0$$
, то
D = b^2 - 4 * a * c =
(0)^2 - 4 * (1) * (0) = 0
Т.к. D = 0, то корень всего один.
w = -b/2a = -0/2/(1)
$$w_{1} = 0$$
делаем обратную замену
$$\sin{\left (x \right )} = w$$
Дано уравнение
$$\sin{\left (x \right )} = w$$
— это простейшее тригонометрическое ур-ние
Это ур-ние преобразуется в
$$x = 2 \pi n + \operatorname{asin}{\left (w \right )}$$
$$x = 2 \pi n — \operatorname{asin}{\left (w \right )} + \pi$$
Или
$$x = 2 \pi n + \operatorname{asin}{\left (w \right )}$$
$$x = 2 \pi n — \operatorname{asin}{\left (w \right )} + \pi$$
, где n — любое целое число
подставляем w:
$$x_{1} = 2 \pi n + \operatorname{asin}{\left (w_{1} \right )}$$
$$x_{1} = 2 \pi n + \operatorname{asin}{\left (0 \right )}$$
$$x_{1} = 2 \pi n$$
$$x_{2} = 2 \pi n — \operatorname{asin}{\left (w_{1} \right )} + \pi$$
$$x_{2} = 2 \pi n — \operatorname{asin}{\left (0 \right )} + \pi$$
$$x_{2} = 2 \pi n + \pi$$
$$x_{1} = 0$$
$$x_{2} = \pi$$
$$x_{1} = 0$$
$$x_{2} = \pi$$
Данные корни
$$x_{1} = 0$$
$$x_{2} = \pi$$
являются точками смены знака неравенства в решениях.
Сначала определимся со знаком до крайней левой точки:
$$x_{0} Возьмём например точку
$$x_{0} = x_{1} — \frac{1}{10}$$
=
$$- \frac{1}{10}$$
=
$$- \frac{1}{10}$$
подставляем в выражение
$$\sin^{2}{\left (x \right )} > 0$$
$$\sin^{2}{\left (- \frac{1}{10} \right )} > 0$$
2
sin (1/10) > 0
значит одно из решений нашего неравенства будет при:
$$x
_____ _____
\ /
-------ο-------ο-------
x1 x2Другие решения неравенства будем получать переходом на следующий полюс
и т.д.
Ответ:
$$x $$x > \pi$$
грех (х) | функция синуса
sin (x), синусоидальная функция.
Определение синуса
В прямоугольном треугольнике ABC синус α, sin (α) определяется как отношение между стороной, противоположной углу α, и сторона, противоположная прямому углу (гипотенуза):
sin α = a / c
Пример
a = 3 дюйма
c = 5 дюймов
sin α = a / c = 3/5 = 0.6
График синуса
TBD
Синус-правила
| Название правила | Правило |
|---|---|
| Симметрия | sin (- θ ) = -sin θ |
| Симметрия | sin (90 ° — θ ) = cos θ |
| Пифагорейская идентичность | sin 2 α + cos 2 α = 1 |
| sin θ = cos θ × tan θ | |
| sin θ = 1 / csc θ | |
| Уголок двойной | sin 2 θ = 2 sin θ cos θ |
| Сумма углов | sin ( α + β ) = sin α cos β + cos α sin β |
| Разница углов | sin ( α-β ) = sin α cos β — cos α sin β |
| Сумма к продукту | sin α + sin β = 2 sin [( α + β ) / 2] cos [( α — β ) / 2] |
| Отличие от продукта | sin α — sin β = 2 sin [( α-β ) / 2] cos [( α + β ) / 2] |
| Закон синусов | a / sin α = b / sin β = c / sin γ |
| Производная | sin ‘ x = cos x |
| Интегральный | ∫ sin x d x = — cos x + C |
| Формула Эйлера | sin x = ( e ix — e — ix ) / 2 i |
Функция обратной синусоиды
Арксинус x определяется как функция, обратная синусу x, когда -1≤x≤1.
Когда синус y равен x:
sin y = x
Тогда арксинус x равен функции обратного синуса x, которая равна y:
arcsin x = sin -1 ( x ) = y
См .: функция Arcsin
Таблица синусов
| x (°) | x (рад) | грех x |
|---|---|---|
| -90 ° | -π / 2 | –1 |
| -60 ° | -π / 3 | -√3 / 2 |
| -45 ° | -π / 4 | -√2 / 2 |
| -30 ° | -π / 6 | -1/2 |
| 0 ° | 0 | 0 |
| 30 ° | π / 6 | 1/2 |
| 45 ° | π / 4 | √2 / 2 |
| 60 ° | π / 3 | √3 / 2 |
| 90 ° | π / 2 | 1 |
См. Также
,Калькулятор синуса — вычисляет sin (x) для градусов или радианов.
Используйте этот калькулятор, чтобы легко вычислить синус угла в градусах или радианах.
Функция синуса (sin (x))
Синус — это тригонометрическая функция угла, обычно определяемая для острых углов в прямоугольном треугольнике как отношение длины противоположной стороны к самой длинной стороне треугольника. На иллюстрации ниже sin (α) = a / c и sin (β) = b / c.
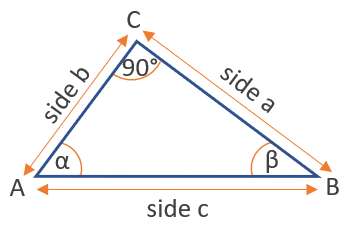
Из cos (α) = a / c следует, что синус любого угла всегда меньше или равен единице.Функция принимает отрицательные значения для углов больше 180 °. Поскольку у прямоугольного треугольника самая длинная сторона — это гипотенуза, а она противоположна прямому углу, синус прямого угла равен отношению гипотенузы к самому себе, т.е. равен 1. Этот калькулятор синусов можно использовать для проверки этот.
Обычно используемый закон в тригонометрии, который тривиально выводится из определения синуса, — это закон синусов : 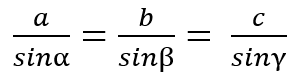
Синусоидальная функция может быть расширена до любого действительного значения на основе длины определенного линейного сегмента в единичной окружности (окружности радиуса один, с центром в начале (0,0) декартовой системы координат.В других определениях синусы выражаются как бесконечный ряд или как дифференциальные уравнения, то есть синус может быть произвольным положительным или отрицательным значением или комплексным числом.
Связанные тригонометрические функции
Синус , обратный синусу , является косекансом: csc (x), иногда записываемым как cosec (x), что дает отношение длины гипотенузы к длине стороны, противоположной углу.
, обратный синусу , является функцией арксинуса: asin (x) или arcsin (x).Функция арксинуса многозначна, например arcsin (0) = 0 или π, или 2π, и так далее. Это полезно для определения угла x, когда известен sin (x).
Как рассчитать синус угла?
Если угол известен, просто воспользуйтесь нашим калькулятором синусов, который поддерживает ввод как в градусах, так и в радианах. После того, как вы измерили угол или просмотрели план или схему, просто введите размер и нажмите «рассчитать». Вот как это просто.
Если сам угол неизвестен, один из способов вычислить синус — это знать измерения длин стороны, противоположной ему, а также гипотенузы (сторона c на рисунке).Например, если нужно вычислить sin (α) и доступны длины a и c, sin (α) = a / c. Другие способы включают использование закона синусов.
Применение синусоидальной функции
Функция синуса обычно используется для моделирования периодических явлений в физике, биологии, социальных науках и т. Д. Например, звуковые и световые волны, изменения продолжительности дня и температуры в течение года могут быть представлены в виде синуса.
Вверху: волна, созданная с помощью синусоидальной функции.Синусоидальная волна — это зеркальное отображение косинусоидальной волны.
Таблица общих значений синуса:
| x (°) | x (рад.) | синус (x) |
|---|---|---|
| 0 ° | 0 | 0 |
| 30 ° | π / 6 | 0,50 |
| 45 ° | π / 4 | 0.707107 |
| 60 ° | π / 3 | 0,866025 |
| 90 ° | π / 2 | 1 |
| 120 ° | 2π / 3 | 0,866025 |
| 135 ° | 3π / 4 | 0,707107 |
| 150 ° | 5π / 6 | 0,50 |
| 180 ° | π | 0 |
Mathway | Популярные задачи
Mathway | Популярные проблемыПопулярные задачи
Основы математики Предварительно Алгебра Алгебра тригонометрия тригонометрия и алгебра Исчисление Конечная математика Линейная алгебра ХимияMathway требует javascript и современного браузера.
Этот веб-сайт использует файлы cookie, чтобы обеспечить вам максимальное удобство работы с ним.
Убедитесь, что ваш пароль состоит не менее чем из 8 символов и содержит каждое из следующих значений:
- номер
- письмо
- специальный символ: @ $ #!% *? &
Интеграл синус Si (x) Калькулятор — расчет высокой точности
- Цель использования
- Физик на пенсии ищу код для создания таблицы комплексного импеданса дипольной антенны в зависимости от длины волны и длины антенны. Это был шаг на этом пути.
- Комментарий / запрос
- Хотелось бы, чтобы код был включен в более сложную оценку функций. Предпочтительнее Fortran или Basic, C, C ++ или Java тоже.
[1] 2018/08/19 23:29 Мужчина / 60 лет и старше / Пенсионер / Полезный /
- Цель использования
- Нормализация качества лазерного луча
[2] 2018/02/28 04:11 Мужчина / 60 лет и старше / Офисный работник / Государственный служащий / Очень /
- Цель использования
- ОБЩИЕ ПРОЦЕНТЫ
[ 3] 2013/12/16 05:28 Мужчина / 60 лет и старше / Средняя школа / Университет / Аспирант / Очень /
- Цель использования
- Спектральный анализ
- Комментарий / Запрос
- Очень хорошая работа.Domo arigoto goziamashita.
[4] 2012/10 / 26 00:50 Мужчина / 50 лет / Офисный работник / Госслужащий / Очень /
- Цель использования
- Знание интегральной функции.
[5] 2011/07/05 02:28 Мужской / 20-летний уровень / Студент / Очень /
- Комментарий / Запрос
- хорошо
[6] 16.09.2010 11:38 Мужчина / Более 60 / Преподаватель / Очень /
- Цель использования
- инженерия
- Комментарий / Запрос
- это хороший сайт.Мне это нужно
[7] 04.07.2010 03:50 Мужской / 30 уровень / Учитель / Очень /
- Цель использования
- Требуется расчет интеграла синуса
- Комментарий / запрос
- Это сайт очень полезный и удобный!
[8] 2009/11/19 06:47 Мужчина / 30 уровень / Исследователь / Очень /
- Цель использования
- для сравнения точного значения интеграла с подходом асимптотического расширения
- Комментарий / Запрос
- впечатляющий сайт! Простой в использовании и все полезные интегралы доступны
[9] 13.10.2009 14:21 Мужчина / 20 уровень / Специализированный студент / Очень /
- Комментарий / Запрос
- Алгоритм могли быть предоставлены, исследователи могут использовать их для научных вычислений.
[10] 2009/09/04 02:25 Мужчина / 30 уровень / Исследователь / Очень /
