Интеграл косинуса
Неопределенный интеграл от косинуса cos (x) равен синусу. Для первоначальной косинуса к правой стороне добавляем постоянную Постоянную определяют с дополнительного условия на первоначальную.
График косинуса имеет вид
Само по себе определение интеграла косинуса достаточно простое. Но как только задают вычислить интеграл косинуса двойного угла, тройного или половины угла, сразу возникают трудности в половины студентов. Выведем формулу интегрирования для функции cos (k*x). Для применения табличной формулы интегрирования надо внести коэффициент под дифференциал, что может привести к изменению самого интеграл. Поэтому одновременно необходимо разделить на этот коэффициент.
.
Зная приведенную формулу, проинтегрировать косинус двойного угла сможет каждый школьник 10, 11 класса. Все что необходимо это подставить 2 или 3 в интеграл
и по индукции следующие интегралы
int(sin(k*x)=-1/k*cos(k*x).
Приведенная формула позволяет вычислить интеграл от косинуса половины угла
и интеграл от косинуса одной трети угла
В этих случаях коэффициент, стоящий при переменной в косинусе при интегрировании становится обратным значением перед синусом.
Пример 1. Найти интеграл от cos(5*x).
Решение: По формуле интегрируем косинус
Пример 2. Вычислить интеграл от cos(7*x).
Решение: Выполняем интегрирование
Пример 3. Проинтегрировать выражение cos (11*x).
Решение: Вычисляем неопределенный интеграл
Пример 4. Найти интеграл функции y= cos (x/5).
Решение: Записываем неопределенный интеграл
Пример 5. Найти интеграл функции y= cos (x/6).
Решение: Проинтегрируем по приведенной выше формуле
Как только Вы освоите методику интегрирования на простых примерах, смело можете переходить к определенным интегралам и первообразным. Для отискания определенного интеграла проводим интегрирование, а дальше подставляем пределы интегрирования и находим изменение первообразной функции.
Пример 6. Проинтегрировать косинус двойного угла y = cos (2 * x) от 0 до 45 градусов.
Решение: Находим указанный интеграл от косинуса
Пример 7.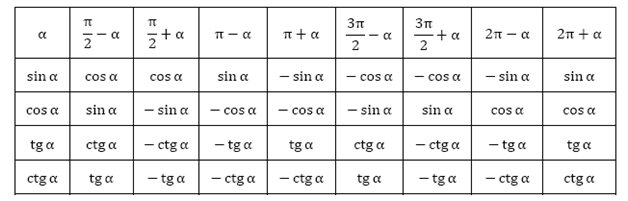
Найти интеграл от косинуса y = cos (x) от 0 до 60 градусов.
Решение: Вычисляем интеграл и подставляем пределы интегрирования
Пример 8. Найти первоначальную от cos (x), которая при 30 градусах равна 1.
Решение: Находим первоначальную
С наложенного условия на первоначальную вычисляем постоянную
sin(Pi/6)+C=1; C=1-
sin(Pi/6)=1-0,5=0,5.
Подставляем полученную постоянную в уравнение
На этом задача решена. На таких простых примерах Вы четко должны знать, чему равный интеграл от косинуса.
Далее полученные знания можно применять для вычисления площадей криволинейных трапеций. Это достаточно абстрактное понятие, но с помощью интегрирования находить площадь фигур достаточно просто и быстро. Следует только помнить, что площадь всегда принимает положительное значение, в то время как определенный интеграл может принимать отрицательное значение.
Например вычислим площадь и интеграл от косинуса, если переменная принадлежит интервалу от 0 до 2*Pi.
По физическому содержанию площадь равна заштрихованным поверхностям.
Находим определенный интеграл в указанных пределах
Он равен нулю. Что касается площади, то сначала следует найти точки пересечения с осью абсцисс на этом интервале
Таким образом площадь необходимо искать на трех промежутках
Ось абсцисс можем записать функцией y = 0. Таким образом на первом промежутке площадь равна интегралу от косинуса,
на втором 0-cos (x) = — cos (x) от минус косинуса и на третьем от косинуса. Все при вычислении площади зависит от того, какая функция принимает большее значение по оси ординат (Oy). Вычисляем площадь интегрированием в указаных пределах
Таким образом искомая площадь равна 4. Если иметь график функции перед глазами, то данное значение можно получить как 4 площади косинус функции, которые периодически повторяются
На этом знакомство с интегрированием косинуса завершается. Приведенная методика интегрирования позволяет вычислить 80% основных задач на интегрирование косинуса.
Остальные 20% Вы научитесь после изучения способов нахождения интегралов от функций вида
Мы научим Вас, какие свертки и замены переменных следует использовать, в каких случаях целесообразно интегрировать по частям.
Интегралы от других тригонометрических и обратных к ним функций Вы найдете в категории «Интегрирование функций».
- Назад
- Вперёд
| 1 | Найти точное значение | грех(30) | |
| 2 | Найти точное значение | грех(45) | |
| 3 | Найти точное значение | грех(30 градусов) | |
| 4 | Найти точное значение | грех(60 градусов) | |
| 5 | Найти точное значение | загар (30 градусов) | |
| 6 | Найти точное значение | угловой синус(-1) | |
| 7 | Найти точное значение | ||
| 8 | Найти точное значение | cos(pi/4) | |
| 9 | Найти точное значение | грех(45 градусов) | |
| 10 | Найти точное значение | грех(пи/3) | |
| 11 | Найти точное значение | арктан(-1) | |
| 12 | Найти точное значение | cos(45 градусов) | |
| 13 | Найти точное значение | cos(30 градусов) | |
| 14 | Найти точное значение | желтовато-коричневый(60) | |
| 15 | Найти точное значение | csc(45 градусов) | |
| 16 | Найти точное значение | загар (60 градусов) | |
| 17 | Найти точное значение | сек(30 градусов) | |
| 18 | Найти точное значение | cos(60 градусов) | |
| 19 | Найти точное значение | cos(150) | |
| 20 | Найти точное значение | грех(60) | |
| 21 | Найти точное значение | cos(pi/2) | |
| 22 | Найти точное значение | загар (45 градусов) | |
| 23 | Найти точное значение | arctan(- квадратный корень из 3) | |
| 24 | Найти точное значение | csc(60 градусов) | |
| 25 | Найти точное значение | сек(45 градусов) | |
| 26 | Найти точное значение | csc(30 градусов) | |
| 27 | Найти точное значение | грех(0) | |
| 28 | Найти точное значение | грех(120) | |
| 29 | Найти точное значение | соз(90) | |
| 30 | Преобразовать из радианов в градусы | пи/3 | |
| 31 | Найти точное значение | желтовато-коричневый(30) | |
| 32 | 92|||
| 35 | Преобразовать из радианов в градусы | пи/6 | |
| 36 | Найти точное значение | детская кроватка(30 градусов) | |
| 37 | Найти точное значение | арккос(-1) | |
| 38 | Найти точное значение | арктический(0) | |
| 39 | Найти точное значение | детская кроватка(60 градусов) | |
| 40 | Преобразование градусов в радианы | 30 | |
| 41 | Преобразовать из радианов в градусы | (2 шт. )/3 | |
| 42 | Найти точное значение | sin((5pi)/3) | |
| 43 | Найти точное значение | sin((3pi)/4) | |
| 44 | Найти точное значение | тан(пи/2) | |
| 45 | Найти точное значение | грех(300) | |
| 46 | Найти точное значение | соз(30) | |
| 47 | Найти точное значение | соз(60) | |
| 48 | Найти точное значение | соз(0) | |
| 49 | Найти точное значение | соз(135) | |
| 50 | Найти точное значение | cos((5pi)/3) | |
| 51 | Найти точное значение | cos(210) | |
| 52 | Найти точное значение | сек(60 градусов) | |
| 53 | Найти точное значение | грех(300 градусов) | |
| 54 | Преобразование градусов в радианы | 135 | |
| 55 | Преобразование градусов в радианы | 150 | |
| 56 | Преобразовать из радианов в градусы | (5 дюймов)/6 | |
| 57 | Преобразовать из радианов в градусы | (5 дюймов)/3 | |
| 58 | Преобразование градусов в радианы | 89 градусов | |
| 59 | Преобразование градусов в радианы | 60 | |
| 60 | Найти точное значение | грех(135 градусов) | |
| 61 | Найти точное значение | грех(150) | |
| 62 | Найти точное значение | грех(240 градусов) | |
| 63 | Найти точное значение | детская кроватка(45 градусов) | |
| 64 | Преобразовать из радианов в градусы | (5 дюймов)/4 | |
| 65 | Найти точное значение | грех(225) | |
| 66 | Найти точное значение | грех(240) | |
| 67 | Найти точное значение | cos(150 градусов) | |
| 68 | Найти точное значение | желтовато-коричневый(45) | |
| 69 | Оценить | грех(30 градусов) | |
| 70 | Найти точное значение | сек(0) | |
| 71 | Найти точное значение | cos((5pi)/6) | |
| 72 | Найти точное значение | КСК(30) | |
| 73 | Найти точное значение | arcsin(( квадратный корень из 2)/2) | |
| 74 | Найти точное значение | загар((5pi)/3) | |
| 75 | Найти точное значение | желтовато-коричневый(0) | |
| 76 | Оценить | грех(60 градусов) | |
| 77 | Найти точное значение | arctan(-( квадратный корень из 3)/3) | |
| 78 | Преобразовать из радианов в градусы | (3 пи)/4 | |
| 79 | Найти точное значение | sin((7pi)/4) | |
| 80 | Найти точное значение | угловой синус(-1/2) | |
| 81 | Найти точное значение | sin((4pi)/3) | |
| 82 | Найти точное значение | КСК(45) | |
| 83 | Упростить | арктан(квадратный корень из 3) | |
| 84 | Найти точное значение | грех(135) | |
| 85 | Найти точное значение | грех(105) | |
| 86 | Найти точное значение | грех(150 градусов) | |
| 87 | Найти точное значение | sin((2pi)/3) | |
| 88 | Найти точное значение | загар((2pi)/3) | |
| 89 | Преобразовать из радианов в градусы | пи/4 | |
| 90 | Найти точное значение | грех(пи/2) | |
| 91 | Найти точное значение | сек(45) | |
| 92 | Найти точное значение | cos((5pi)/4) | |
| 93 | Найти точное значение | cos((7pi)/6) | |
| 94 | Найти точное значение | угловой синус(0) | |
| 95 | Найти точное значение | грех(120 градусов) | |
| 96 | Найти точное значение | желтовато-коричневый ((7pi)/6) | |
| 97 | Найти точное значение | соз(270) | |
| 98 | Найти точное значение | sin((7pi)/6) | |
| 99 | Найти точное значение | arcsin(-( квадратный корень из 2)/2) | |
| 100 | Преобразование градусов в радианы | 88 градусов |
Вычислить lim x → π/4 (sinx-cosx)/(x-π/4)
- Математические сомнения
- Проблемы
- Пределы
- Тригонометрические функции
В этой предельной задаче косинус угла $x$ вычитается из синуса угла $x$ в числителе, а угол сорок пять градусов вычитается из угла $x$ в знаменателе.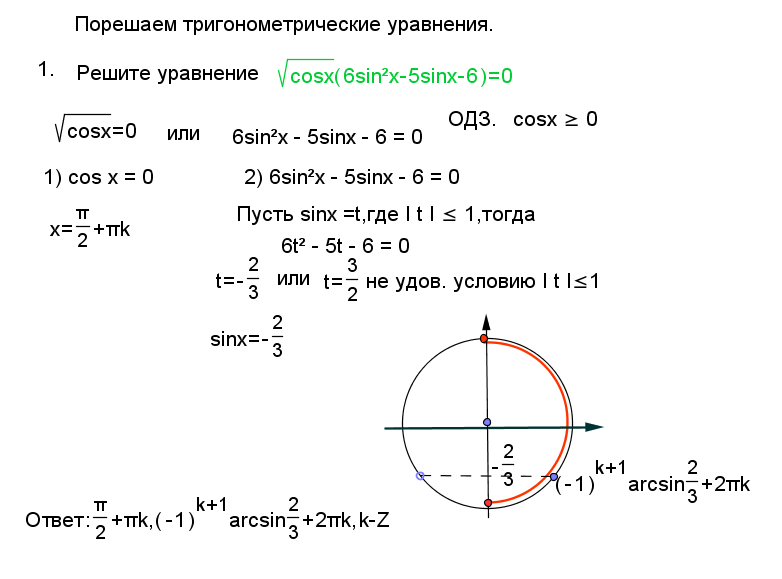
Предел их частного должен быть рассчитан, поскольку значение $x$ стремится к пи на четыре.
Попробуем найти предел $\sin{x}$ минус $\cos{x}$ на $x$ минус $\pi$ на $4$, поскольку значение $x$ ближе к pi на четыре с использованием метода прямой замены.
$ = \, \, \, $ $ \ dfrac {\ sin {\ bigg (\ dfrac {\ pi} {4} \ bigg)} — \ cos {\ bigg (\ dfrac {\ pi} {4} \bigg)}}{\dfrac{\pi}{4}-\dfrac{\pi}{4}}$
$=\,\,\,$ $\dfrac{\dfrac{1}{\sqrt {2}}-\dfrac{1}{\sqrt{2}}}{\dfrac{\pi}{4}-\dfrac{\pi}{4}}$
$=\,\,\, $ $\dfrac{0}{0}$
Отсюда видно, что предел данного рационального выражения не определен. Следовательно, эту предельную задачу следует решать с помощью другого математического подхода.
На самом деле эту предельную тригонометрическую задачу можно решить тремя различными способами. Итак, давайте изучим каждый метод, чтобы узнать, как найти предел заданной рациональной функции, поскольку значение $x$ ближе к pi на четыре.
Логический метод
Выражение в числителе является тригонометрическим выражением, выражающим необходимость вычитания косинуса угла $x$ из синуса угла $x$.
На самом деле обе они являются тригонометрическими функциями, поэтому мы не можем найти между ними разницу, если не знаем значение угла $x$.
$\displaystyle \large \lim_{\Large x\,\to\, \normalsize \dfrac{\pi}{4}}{\normalsize \dfrac{\sin{x}-\cos{x}}{ x-\dfrac{\pi}{4}}}$
Напомним все тригонометрические тождества. Существует только одно тригонометрическое тождество, в котором функции синуса и косинуса участвуют в вычитании, и это тождество разности синусоидальных углов, но тригонометрическое выражение в числителе не совсем совпадает с разложением формулы разности синусоидальных углов. Однако можно привести тригонометрическое выражение в числителе к нужному виду. 9\circ$. Итак, попробуем включить обе функции в тригонометрическое выражение числителя.
$=\,\,\,$ $\displaystyle \large \lim_{\Large x\,\to\, \normalsize \dfrac{\pi}{4}}{\normalsize \bigg(1 \times \ dfrac{\sin{x}-\cos{x}}{x-\dfrac{\pi}{4}}\bigg)}$
$=\,\,\,$ $\displaystyle \large \lim_ {\ Large x \, \ to \, \ normalsize \ dfrac {\ pi} {4}} {\ normalsize \ bigg (\ dfrac {\ sqrt {2}} {\ sqrt {2}} \ times \ dfrac {\ sin{x}-\cos{x}}{x-\dfrac{\pi}{4}}\bigg)}$
$=\,\,\,$ $\displaystyle \large \lim_{\Large x \, \ to \, \ normalsize \ dfrac {\ pi} {4}} {\ normalsize \ bigg (\ dfrac {\ sqrt {2} \ times 1} {\ sqrt {2}} \ times \ dfrac {\ sin{x}-\cos{x}}{x-\dfrac{\pi}{4}}\bigg)}$
$ = \, \, \, $ $ \ displaystyle \ large \ lim _ {\ Large x \, \ to \, \ normalsize \ dfrac {\ pi} {4}} {\ normalsize \ bigg (\ sqrt {2) } \times \dfrac{1}{\sqrt{2}} \times \dfrac{\sin{x}-\cos{x}}{x-\dfrac{\pi}{4}}\bigg)}$
$ = \, \, \, $ $ \ displaystyle \ large \ lim _ {\ Large x \, \ to \, \ normalsize \ dfrac {\ pi} {4}} {\ normalsize \ bigg (\ sqrt {2) } \times \dfrac{\dfrac{1}{\sqrt{2}} \times (\sin{x}-\cos{x})}{x-\dfrac{\pi}{4}}\bigg) }$
Теперь свойство дистрибутивности можно использовать для распределения единицы на квадратный корень из двух при вычитании функций синуса и косинуса.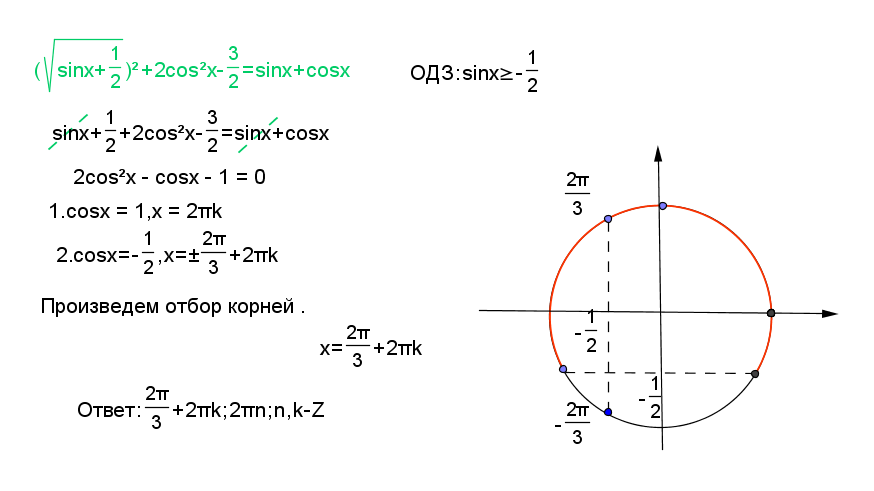
$ = \, \, \, $ $ \ displaystyle \ large \ lim _ {\ Large x \, \ to \, \ normalsize \ dfrac {\ pi} {4}} {\ normalsize \ bigg (\ sqrt {2) } \times \dfrac{\dfrac{1}{\sqrt{2}} \times \sin{x}-\dfrac{1}{\sqrt{2}} \times \cos{x}}{x-\ dfrac{\pi}{4}}\bigg)}$
Согласно тригонометрии, синус угла $45$ градусов и косинус угла сорок пять градусов равны мультипликативной величине, обратной квадратному корню из двух.
$(1).\,\,\,$ $\sin{\bigg(\dfrac{\pi}{4}\bigg)} \,=\, \dfrac{1}{\sqrt{2} }$
$(2).\,\,\,$ $\cos{\bigg(\dfrac{\pi}{4}\bigg)} \,=\, \dfrac{1}{\sqrt{2} }$
Теперь мы можем заменить каждую обратную величину квадратного корня из двух указанными выше тригонометрическими функциями.
$=\,\,\,$ $\displaystyle \large \lim_{\Large x\,\to\, \normalsize \dfrac{\pi}{4}}{\normalsize \bigg(\sqrt{2) } \times \dfrac{\cos{\bigg(\dfrac{\pi}{4}\bigg)} \times \sin{x}-\sin{\bigg(\dfrac{\pi}{4}\bigg )} \times \cos{x}}{x-\dfrac{\pi}{4}}\bigg)}$
Здесь можно использовать свойство коммутативности умножения, чтобы сделать тригонометрическое выражение в числителе в виде разложения правила синусов разности углов.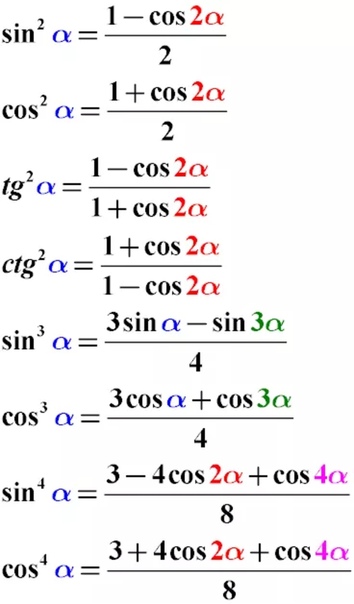
$ = \, \, \, $ $ \ displaystyle \ large \ lim _ {\ Large x \, \ to \, \ normalsize \ dfrac {\ pi} {4}} {\ normalsize \ bigg (\ sqrt {2) } \times \dfrac{\sin{x} \times \cos{\bigg(\dfrac{\pi}{4}\bigg)} — \cos{x} \times \sin{\bigg(\dfrac{\ pi}{4}\bigg)}}{x-\dfrac{\pi}{4}}\bigg)}$
Наконец, тригонометрическое выражение в числителе выражает тождественное разложение синуса разности углов.
$ = \, \, \, $ $ \ displaystyle \ large \ lim _ {\ Large x \, \ to \, \ normalsize \ dfrac {\ pi} {4}} {\ normalsize \ bigg (\ sqrt {2) } \times \dfrac{\sin{\bigg(x-\dfrac{\pi}{4}\bigg)}}{x-\dfrac{\pi}{4}}\bigg)}$
Приведение функции к правилу тригонометрического предела
В исчислении у нас есть правило тригонометрического предела с точки зрения функции синуса. Итак, попробуем приспособить упрощенную функцию к форме тригонометрического предельного правила. Во-первых, давайте отделим мультипликативную константу от функции в соответствии с постоянным кратным правилом пределов.
$=\,\,\,$ $\sqrt{2} \times \displaystyle \large \lim_{\Large x\,\to\, \normalsize \dfrac{\pi}{4}}{\normalsize \dfrac{\sin{\bigg(x-\dfrac{\pi}{4}\bigg)}}{x-\dfrac{\pi}{4}}}$
Если $x\,\to\, \dfrac{\pi}{4}$, то $x-\dfrac{\pi}{4}\,\to\, \dfrac{\pi}{4} -\dfrac{\pi}{4}$, поэтому $x-\dfrac{\pi}{4}\,\to\, 0$, что проясняет, что при приближении $x$ к $\dfrac{\pi} {4}$, значение $x-\dfrac{\pi}{4}$ ближе к нулю.
$=\,\,\,$ $\sqrt{2} \times \displaystyle \large \lim_{\Large x\,-\,\normalsize \dfrac{\pi}{4} \Large \,\ to\, 0}{\normalsize \dfrac{\sin{\bigg(x-\dfrac{\pi}{4}\bigg)}}{x-\dfrac{\pi}{4}}}$
Оценить предел тригонометрической функции
Для удобства возьмем $y \,=\, x-\dfrac{\pi}{4}$ и выразим всю функцию через $y$.
$=\,\,\,$ $\sqrt{2} \times \displaystyle \large \lim_{\Large y \,\to\, 0}{\normalsize \dfrac{\sin{y}}{ y}}$
Согласно правилу тригонометрического предела в синусоидальной функции, частное синуса угла $y$ на $y$ при приближении значения $y$ к нулю равно единице.
$=\,\,\,$ $\sqrt{2} \times 1$
$=\,\,\,$ $\sqrt{2}$
Фундаментальный метод
Мы также можем оценить предел частного вычитания $\cos{x}$ из $\sin{x}$ путем вычитания числа pi на четыре из значения $x$ по мере того, как переменная $x$ приближается к число пи на четыре комбинацией тригонометрических тождеств и правила тригонометрического предела.
Техника разложения тригонометрических функций
Тригонометрические функции $\sin{x}$ и $\cos{x}$ не могут быть разложены. Итак, если мы сделаем некоторые настройки для расширения каждой функции, то мы можем легко упростить тригонометрическое выражение в числителе данного рационального выражения, и это поможет нам легко найти предел этой функции.
$\displaystyle \large \lim_{\Large x\,\to\, \normalsize \dfrac{\pi}{4}}{\normalsize \dfrac{\sin{x}-\cos{x}}{ x-\dfrac{\pi}{4}}}$
Возьмем $y \,=\, x-\dfrac{\pi}{4}$, тогда $x \,=\, \dfrac{ \pi}{4}+y$. Теперь мы можем записать данную функцию в терминах $y$.
$=\,\,\,$ $\displaystyle \large \lim_{\Large y\normalsize \,+\, \dfrac{\pi}{4}\Large \,\to\, \normalsize \dfrac {\ pi} {4}} {\ normalsize \ dfrac {\ sin {\ bigg (\ dfrac {\ pi} {4} + y \ bigg)} — \ cos {\ bigg (\ dfrac {\ pi} {4 }+y\bigg)}}{y}}$
Если $y+\dfrac{\pi}{4} \,\to\, \dfrac{\pi}{4}$, то $y+\dfrac{\pi}{4}-\dfrac{\pi} {4} \,\to\, \dfrac{\pi}{4}-\dfrac{\pi}{4}$. Следовательно, $y \,\to\, 0$. Это означает, что при приближении $y+\dfrac{\pi}{4}$ к $\dfrac{\pi}{4}$ значение $y$ стремится к нулю.
$ = \, \, \, $ $ \ displaystyle \ large \ lim _ {\ Large y \, \ to \, 0} {\ normalsize \ dfrac {\ sin {\ bigg (\ dfrac {\ pi} {4 }+y\bigg)}-\cos{\bigg(\dfrac{\pi}{4}+y\bigg)}}{y}}$
Тригонометрические функции синуса и косинуса появляются с составными углами в числитель. Таким образом, они могут быть расширены с помощью тождества суммы углов sin и формулы суммы углов cos.
$ = \, \, \, $ $ \ displaystyle \ large \ lim _ {\ Large y \, \ to \, 0} {\ normalsize \ dfrac {\ sin {\ bigg (\ dfrac {\ pi} {4 } \ bigg)} \ cos {y} + \ cos {\ bigg (\ dfrac {\ pi} {4} \ bigg)} \ sin {y} — \ Bigg (\ cos {\ bigg (\ dfrac {\ pi }{4}\bigg)}\cos{y}-\sin{\bigg(\dfrac{\pi}{4}\bigg)}\sin{y}\Bigg)}{y}}$
Упростить тригонометрическое выражение в числителе
Тригонометрическое выражение в числителе необходимо упростить, чтобы найти предел функции.
$ = \, \, \, $ $ \ displaystyle \ large \ lim _ {\ Large y \, \ to \, 0} {\ normalsize \ dfrac {\ sin {\ bigg (\ dfrac {\ pi} {4 } \ bigg)} \ cos {y} + \ cos {\ bigg (\ dfrac {\ pi} {4} \ bigg)} \ sin {y} — \ cos {\ bigg (\ dfrac {\ pi} {4 }\bigg)}\cos{y}+\sin{\bigg(\dfrac{\pi}{4}\bigg)}\sin{y}}{y}}$
Теперь подставьте значения синуса числа пи на четыре и косинуса числа пи на четыре в выражение для упрощения тригонометрического выражения.
$=\,\,\,$ $\displaystyle \large \lim_{\Large y\,\to\, 0}{\normalsize \dfrac{\dfrac{1}{\sqrt{2}} \times \cos{y}+\dfrac{1}{\sqrt{2}} \times \sin{y}-\dfrac{1}{\sqrt{2}} \times \cos{y}+\dfrac{1 }{\sqrt{2}} \times \sin{y}}{y}}$
$=\,\,\,$ $\displaystyle \large \lim_{\Large y\,\to\, 0 }{\normalsize \dfrac{\dfrac{1}{\sqrt{2}} \times \cos{y}-\dfrac{1}{\sqrt{2}} \times \cos{y}+\dfrac{ 1}{\sqrt{2}} \times \sin{y}+\dfrac{1}{\sqrt{2}} \times \sin{y}}{y}}$
$=\,\,\,$ $\displaystyle \large \lim_{\Large y\,\to\, 0}{\normalsize \dfrac{\cancel{\dfrac{1}{\sqrt{2} } \times \cos{y}}-\cancel{\dfrac{1}{\sqrt{2}} \times \cos{y}}+2 \times \dfrac{1}{\sqrt{2}} \ раз \sin{y}}{y}}$
$=\,\,\,$ $\displaystyle \large \lim_{\Large y\,\to\, 0}{\normalsize \dfrac{2 \ раз \dfrac{1}{\sqrt{2}} \times \sin{y}}{y}}$
$=\,\,\,$ $\displaystyle \large \lim_{\Large y\, \to\, 0}{\normalsize \dfrac{\dfrac{2 \times 1}{\sqrt{2}} \times \sin{y}}{y}}$ 92}{\sqrt{2}} \times \sin{y}}{y}}$
$=\,\,\,$ $\displaystyle \large \lim_{\Large y\,\to\, 0}{\normalsize \dfrac{\dfrac{\sqrt{2} \times \sqrt{2}}{\sqrt{2}} \times \sin{y}}{y}}$
$=\, \,\,$ $\displaystyle \large \lim_{\Large y\,\to\, 0}{\normalsize \dfrac{\dfrac{\cancel{\sqrt{2}} \times \sqrt{2}} {\cancel{\sqrt{2}}} \times \sin{y}}{y}}$
$=\,\,\,$ $\displaystyle \large \lim_{\Large y\,\to \, 0}{\normalsize \dfrac{\sqrt{2} \times \sin{y}}{y}}$
Вычислить предел тригонометрической функции
Процесс упрощения завершен успешно, пришло время найти предел упрощенной функции.
$=\,\,\,$ $\displaystyle \large \lim_{\Large y\,\to\, 0}{\normalsize \bigg(\sqrt{2} \times \dfrac{\sin{y }}{y}\bigg)}$
Прежде чем вычислять предел, мы должны отделить константы от функции, и это можно сделать с помощью правила множителей констант пределов.
$=\,\,\,$ $\sqrt{2} \times \displaystyle \large \lim_{\Large y\,\to\, 0}{\normalsize \dfrac{\sin{y}}{ г}}$
Мы можем вычислить предел рациональной функции по правилу тригонометрического предела в синусоидальной функции.
$=\,\,\,$ $\sqrt{2} \times 1$
$=\,\,\,$ $\sqrt{2}$
Правило Лопиталя
Предел данное тригонометрическое рациональное выражение является неопределенным, так как значение переменной $x$ стремится к $\pi$ на $4$. Следовательно, для нахождения предела можно использовать правило Лопиталя.
Используйте правило Лопиталя
Согласно правилу Лопиталя предел рационального выражения можно вычислить, найдя предел рационального выражения после дифференцирования тригонометрического выражения $\sin{x}-\cos{x }$ в числителе и алгебраическое выражение в знаменателе.
$\implies$ $\displaystyle \large \lim_{\Large x\,\to\, \normalsize \dfrac{\pi}{4}}{\normalsize \dfrac{\sin{x}-\cos{ x}}{x-\dfrac{\pi}{4}}}$ $\,=\,$ $\displaystyle \large \lim_{\Large x\,\to\, \normalsize \dfrac{\pi} {4}}{\normalsize \dfrac{\dfrac{d}{dx}{\big(\sin{x}-\cos{x}\big)}}{\dfrac{d}{dx}{\bigg (x-\dfrac{\pi}{4}\bigg)}}}$
Дифференцируйте математические выражения
Производная может быть распределена на каждый член каждого выражения в математическом выражении в форме отношения с помощью дистрибутивного свойства умножение вместо вычитания.
$=\,\,\,$ $\displaystyle \large \lim_{\Large x\,\to\, \normalsize \dfrac{\pi}{4}}{\normalsize \dfrac{\dfrac{d }{dx}{\big(\sin{x}\big)}-\dfrac{d}{dx}{\big(\cos{x}\big)}}{\dfrac{d}{dx}{ \big(x\big)}-\dfrac{d}{dx}{\bigg(\dfrac{\pi}{4}\bigg)}}}$
Дифференцирование можно выполнить по производным правилам синуса , косинус, переменная и константа.
$=\,\,\,$ $\displaystyle \large \lim_{\Large x\,\to\, \normalsize \dfrac{\pi}{4}}{\normalsize \dfrac{\cos{x }-\big(-\sin{x}\big)}{1-0}}$
$=\,\,\,$ $\displaystyle \large \lim_{\Large x\,\to\, \normalsize \dfrac{\pi}{4}}{\normalsize \dfrac{\cos{x }+\sin{x}}{1}}$
$=\,\,\,$ $\displaystyle \large \lim_{\Large x\,\to\, \normalsize \dfrac{\pi}{ 4}}{\normalsize \big(\cos{x}+\sin{x}\big)}$
Вычислить предел тригонометрической функции
Данное рациональное выражение становится тригонометрическим выражением путем дифференцирования и его предела можно оценить методом прямой подстановки, когда значение $x$ приближается к pi на $4$.