| 1 | Найти точное значение | sin(30) | |
| 2 | Найти точное значение | sin(45) | |
| 3 | Найти точное значение | sin(30 град. ) | |
| 4 | Найти точное значение | sin(60 град. ) | |
| 5 | Найти точное значение | tan(30 град. ) | |
| 6 | Найти точное значение | arcsin(-1) | |
| 7 | Найти точное значение | sin(pi/6) | |
| 8 | cos(pi/4) | ||
| 9 | Найти точное значение | sin(45 град. ) ) | |
| 10 | Найти точное значение | sin(pi/3) | |
| 11 | Найти точное значение | arctan(-1) | |
| 12 | Найти точное значение | cos(45 град. ) | |
| 13 | Найти точное значение | cos(30 град. ) | |
| 14 | Найти точное значение | tan(60) | |
| 15 | Найти точное значение | csc(45 град. ) | |
| 16 | Найти точное значение | tan(60 град. ) | |
| 17 | Найти точное значение | sec(30 град. ) ) | |
| 18 | Найти точное значение | cos(60 град. ) | |
| 19 | Найти точное значение | cos(150) | |
| 20 | Найти точное значение | sin(60) | |
| 21 | Найти точное значение | cos(pi/2) | |
| 22 | Найти точное значение | tan(45 град. ) | |
| 23 | Найти точное значение | arctan(- квадратный корень из 3) | |
| 24 | Найти точное значение | csc(60 град. ) | |
| 25 | Найти точное значение | sec(45 град. ) ) | |
| 26 | Найти точное значение | csc(30 град. ) | |
| 27 | Найти точное значение | sin(0) | |
| 28 | Найти точное значение | sin(120) | |
| 29 | Найти точное значение | cos(90) | |
| 30 | Преобразовать из радианов в градусы | pi/3 | |
| 31 | Найти точное значение | tan(30) | |
| 32 | Преобразовать из градусов в радианы | 45 | |
| 33 | Найти точное значение | cos(45) | |
| 34 | Упростить | sin(theta)^2+cos(theta)^2 | |
| 35 | Преобразовать из радианов в градусы | pi/6 | |
| 36 | Найти точное значение | cot(30 град. ) ) | |
| 37 | Найти точное значение | arccos(-1) | |
| 38 | Найти точное значение | arctan(0) | |
| 39 | Найти точное значение | cot(60 град. ) | |
| 40 | Преобразовать из градусов в радианы | 30 | |
| 41 | Преобразовать из радианов в градусы | (2pi)/3 | |
| 42 | Найти точное значение | sin((5pi)/3) | |
| 43 | Найти точное значение | sin((3pi)/4) | |
| 44 | Найти точное значение | tan(pi/2) | |
| 45 | Найти точное значение | sin(300) | |
| 46 | Найти точное значение | cos(30) | |
| 47 | Найти точное значение | cos(60) | |
| 48 | Найти точное значение | cos(0) | |
| 49 | Найти точное значение | cos(135) | |
| 50 | Найти точное значение | cos((5pi)/3) | |
| 51 | Найти точное значение | cos(210) | |
| 52 | Найти точное значение | sec(60 град.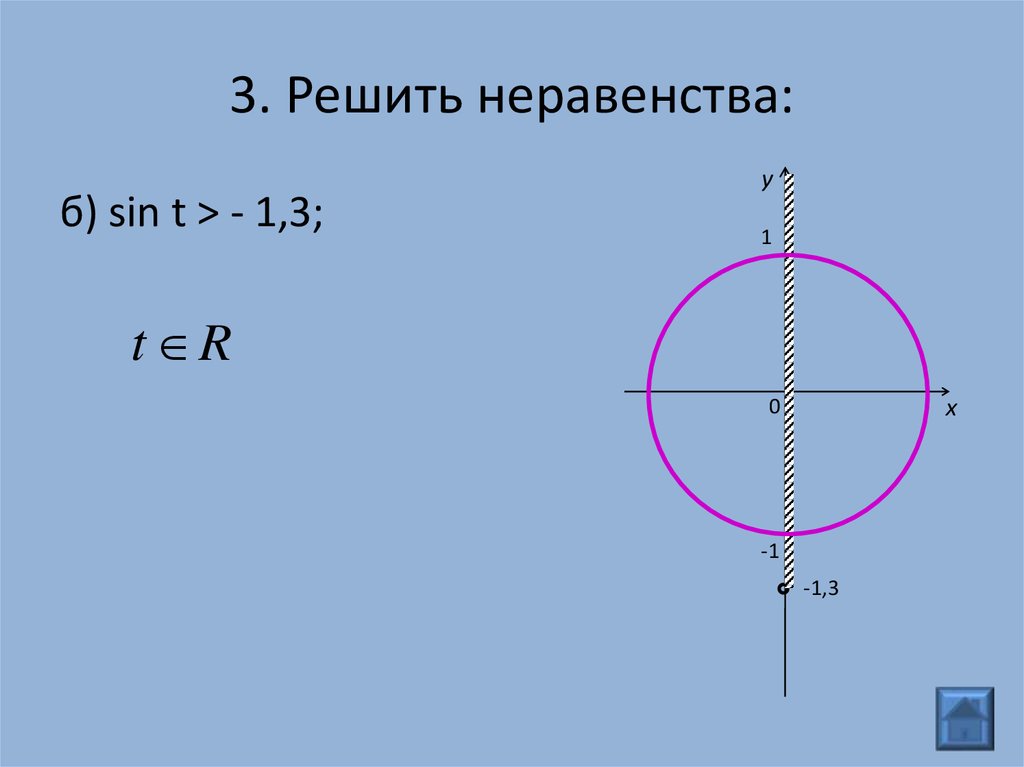 ) ) | |
| 53 | Найти точное значение | sin(300 град. ) | |
| 54 | Преобразовать из градусов в радианы | 135 | |
| 55 | Преобразовать из градусов в радианы | 150 | |
| 56 | Преобразовать из радианов в градусы | (5pi)/6 | |
| 57 | Преобразовать из радианов в градусы | (5pi)/3 | |
| 58 | Преобразовать из градусов в радианы | 89 град. | |
| 59 | Преобразовать из градусов в радианы | 60 | |
| 60 | Найти точное значение | sin(135 град. ) ) | |
| 61 | Найти точное значение | sin(150) | |
| 62 | Найти точное значение | sin(240 град. ) | |
| 63 | Найти точное значение | cot(45 град. ) | |
| 64 | Преобразовать из радианов в градусы | (5pi)/4 | |
| 65 | Найти точное значение | sin(225) | |
| 66 | Найти точное значение | sin(240) | |
| 67 | Найти точное значение | cos(150 град. ) | |
| 68 | Найти точное значение | tan(45) | |
| 69 | Вычислить | sin(30 град. ) ) | |
| 70 | Найти точное значение | sec(0) | |
| 71 | Найти точное значение | cos((5pi)/6) | |
| 72 | Найти точное значение | csc(30) | |
| 73 | Найти точное значение | arcsin(( квадратный корень из 2)/2) | |
| 74 | Найти точное значение | tan((5pi)/3) | |
| 75 | Найти точное значение | tan(0) | |
| 76 | Вычислить | sin(60 град. ) | |
| 77 | Найти точное значение | arctan(-( квадратный корень из 3)/3) | |
| 78 | Преобразовать из радианов в градусы | (3pi)/4 | |
| 79 | Найти точное значение | sin((7pi)/4) | |
| 80 | Найти точное значение | arcsin(-1/2) | |
| 81 | Найти точное значение | sin((4pi)/3) | |
| 82 | Найти точное значение | csc(45) | |
| 83 | Упростить | arctan( квадратный корень из 3) | |
| 84 | Найти точное значение | sin(135) | |
| 85 | Найти точное значение | sin(105) | |
| 86 | Найти точное значение | sin(150 град. ) ) | |
| 87 | Найти точное значение | sin((2pi)/3) | |
| 88 | Найти точное значение | tan((2pi)/3) | |
| 89 | Преобразовать из радианов в градусы | pi/4 | |
| 90 | Найти точное значение | sin(pi/2) | |
| 91 | Найти точное значение | sec(45) | |
| 92 | Найти точное значение | cos((5pi)/4) | |
| 93 | Найти точное значение | cos((7pi)/6) | |
| 94 | arcsin(0) | ||
| 95 | Найти точное значение | sin(120 град. ) ) | |
| 96 | Найти точное значение | tan((7pi)/6) | |
| 97 | Найти точное значение | cos(270) | |
| 98 | Найти точное значение | sin((7pi)/6) | |
| 99 | Найти точное значение | arcsin(-( квадратный корень из 2)/2) | |
| 100 | Преобразовать из градусов в радианы | 88 град. |
Урок 42. уравнение sin x = a — Алгебра и начала математического анализа — 10 класс
Алгебра и начала математического анализа, 10 класс
Урок №42. Уравнение sin x = a.
Перечень вопросов, рассматриваемых в теме:
1) Понятие арксинус числа;
2) Тождества, связанные с арксинусом;
3) Решение тригонометрических уравнений;
Глоссарий по теме
Арксинусом числа m называется такое число α, что: и .
Арксинус числа m обозначают: .
Заметим, что такой промежуток для α берется потому, что синус на отрезке принимает все свои значения ровно по одному разу.
Из определения следует, что для
С другой стороны, если и , то
Таким образом, получаем два простейших тождества для арксинуса.
- для любого m:
- для любого α: .
Основная литература:
Колягин Ю.М., Ткачёва М.В., Фёдорова Н.Е., Шабунин М.И. под ред. Жижченко А.Б. Алгебра и начала математического анализа. 10 класс: учеб. для общеобразоват. учреждений: базовый и профил. Уровни. – 4-е изд. – М.: Просвещение, 2011. – 368 с.: ил. – ISBN 978-5-09-025401-4, с. 310-314.
Открытые электронные ресурсы:
Решу ЕГЭ образовательный портал для подготовки к экзаменам https://ege.sdamgia.ru/
Теоретический материал для самостоятельного изучения
- Так как является абсциссой точки М(α) координатной окружности, то для решения уравнения нужно сначала найти на этой окружности точки, имеющие абсциссу m, то есть точки пересечения окружности с прямой x=m.
 Если , то таких точек нет, если , то такая точка одна, если , то таких точек две.
Если , то таких точек нет, если , то такая точка одна, если , то таких точек две.
После отыскания этих точек нужно найти все такие числа α, которые соответствуют этим точкам. Множество таких чисел и будет решением уравнения .
Примеры и разбор решения заданий тренировочного модуля
Рассмотрим пример на вычисление арксинуса.
Пример.
Вычислить
Решение:
Так как и то
Ответ: .
Задание.
Вычислить .
Ответ: .
На рисунке показано, как связаны друг с другом числа m и
Из рисунка видно, что
Запишем теперь с помощью арксинуса решение уравнения
Одним из решений уравнения является число . Так как , то число также является решением данного уравнения.
Точка соответствует всем числам вида
Точка соответствует всем числам вида
Таким образом, решением уравнения sinα=m являются все числа вида
(*)
Пример.
Решим уравнение
Решение:
Так как , то по формуле (*) получаем:
.
Задание
Решите уравнение
Ответ: .
Рассмотрим решение более сложных уравнений с синусом.
- Рассмотрим решение уравнения .
Решение:
, поэтому
Отсюда , или
Тогда
Ответ: .
- Рассмотрим решение уравнения
Решение:
, поэтому .
Отсюда получаем:
Мы получили два квадратных уравнения с параметром k.
Запишем их решения.
Для того чтобы число х было действительным, дискриминант должен быть неотрицательным. То есть:
(1) и (2)
Неравенство (1) выполняется при , так как k – целое, то .
Неравенство (2) выполняется при , так как k – целое, то .
Таким образом, получаем, что при целых значениях исходное уравнение имеет две серии решений:
При уравнение имеет два решения:
Ответ: а) при ,
б) при ,
в) нет решений при .
- Рассмотрим решение уравнения
Решение:
Так как синусы равны, то их аргументы связаны соотношением:
Отсюда:
Первое уравнение имеет решение при или при .
Второе уравнение имеет решение при или при .
Таким образом:
Ответ:
а) при ,
б) , при при ,
в) нет решений при .
- Рассмотрим решение уравнения
Решение:
Уравнение равносильно совокупности уравнений:
или:
Решение первого уравнения: .
Решение второго уравнения: .
Ответ:
- Рассмотрим решение уравнения
Решение:
Выразим синус:
Имеем две серии решений:
.
Изобразим эти множества на тригонометрической окружности:
Можно записать эти две серии в виде одного равенства:
.
Ответ: .
Заметим, что для краткости решение тригонометрического уравнения sin x=m можно записать в виде:
Пример 1.
Рассмотрим решение уравнения .
Прямая пересекает тригонометрическую окружность в двух точках:
M(π/3) и N(2π/3).
Точка M(π/3) соответствует всем числа вида .
Точка N(2π/3) соответствует всем числа вида .
Таким образом, решение уравнения можно записать так:
.
Ответ: .
Пример 2.
Рассмотрим решение уравнения .
Прямая y=1 имеет с тригонометрической окружностью одну общую точку: .
Этой точке соответствуют все числа вида . Поэтому решение уравнения имеет вид .
Ответ: .
Пример 3.
Рассмотрим решение уравнения .
Прямая y=0 имеет с тригонометрической окружностью две общие точки: С() и К(π).
Поэтому решение уравнения можно записать так: .
Ответ: .
Задание.
Решите уравнение .
Ответ: .
2. Мы можем записать решение уравнение для любых табличных значений m. В тех случаях, когда мы не знаем значения аргумента, соответствующее значению m, чтобы уметь решать уравнение для произвольных значений m, введем понятие арксинуса.
Решение уравнения sin x — cos x = 1. Урок-семинар
Цели урока:
Главная дидактическая цель: рассмотреть все
возможные способы решения данного уравнения.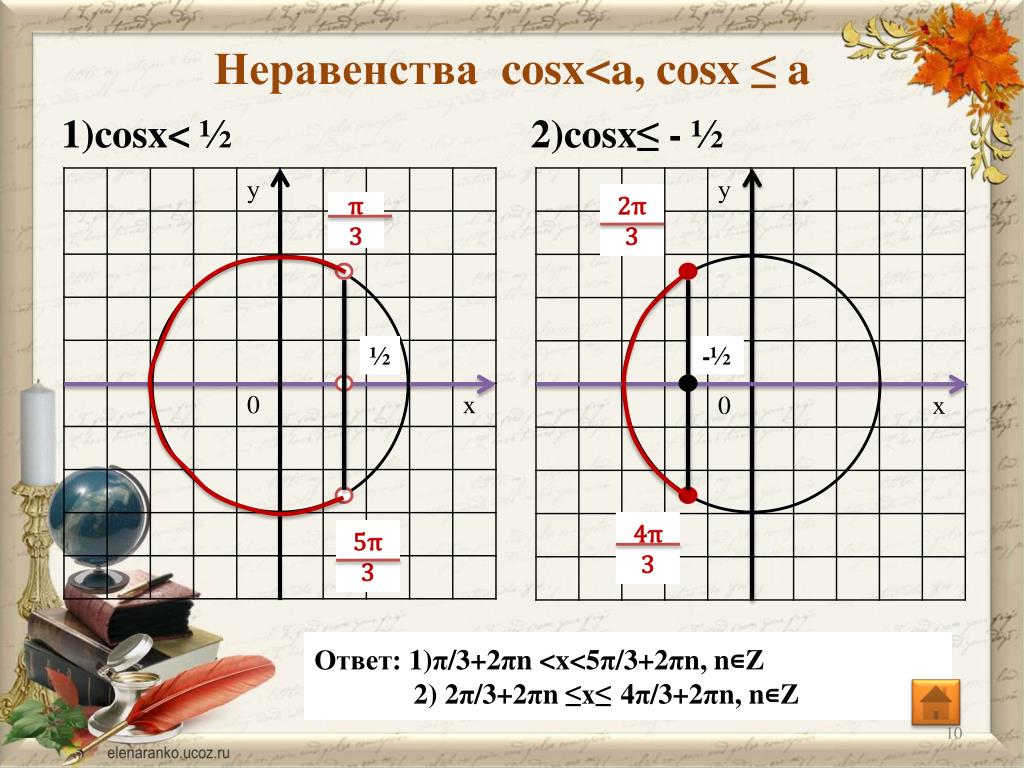
Обучающие: изучение новых приемов решения тригонометрических уравнений на примере данного в творческой ситуации урока-семинара.
Развивающие: формирование общих приемов решения тригонометрических уравнений; совершенствование мыслительных операций учащихся; развитие умений и навыков устной монологической математической речи при изложении решения тригонометрического уравнения.
Воспитывающие: развивать самостоятельность и творчество; способствовать выработке у школьников желания и потребности обобщения изучаемых фактов.
Вопросы для подготовки и дальнейшего обсуждения на семинаре.
- Приведение уравнения к однородному относительно синуса и косинуса.
- Разложение левой части уравнения на множители.
- Введение вспомогательного угла.
- Преобразование разности (или суммы)
тригонометрических функций в произведение.

- Приведение к квадратному уравнению относительно одной из функций.
- Возведение обеих частей уравнения в квадрат.
- Выражение всех функций через tg x (универсальная подстановка).
- Графическое решения уравнения.
Все учащиеся разбиваются на группы (по 2-4 человека) в зависимости от общего количества учащихся и их индивидуальных способностей и желания. Самостоятельно определяют для себя тему для подготовки и выступления на уроке-семинаре. Выступает один человек от группы, а остальные учащиеся принимают участие в дополнениях и исправлениях ошибок, если в этом возникнет необходимость.
Организационный момент.
Учащимся сообщаются:
Тема урока:
“Различные способы решения тригонометрического уравнения sin x — cos x = 1
Форма проведения: урок – семинар.
Эпиграф к уроку:
“Крупное научное открытие дает решение
крупной проблемы, но и в решении любой задачи
присутствует крупица открытия. Задача, которую
вы решаете, может быть скромной, но если она
бросает вызов вашей любознательности и
заставляет вас быть изобретательными и если вы
решаете ее собственными силами, то вы сможете
испытать ведущее к открытию напряжение ума и
насладиться радостью победы”
Задача, которую
вы решаете, может быть скромной, но если она
бросает вызов вашей любознательности и
заставляет вас быть изобретательными и если вы
решаете ее собственными силами, то вы сможете
испытать ведущее к открытию напряжение ума и
насладиться радостью победы”
(Д. Пойа)
Задачи урока:
а) рассмотреть возможность решения одного и
того же уравнения различными способами;
б) познакомиться с различными общими приемами
решения тригонометрических уравнений;
в) изучение нового материала (введение
вспомогательного угла, универсальная
подстановка).
План семинара
- Приведение уравнения к однородному относительно синуса и косинуса.
- Разложение левой части уравнения на множители.
- Введение вспомогательного угла.
- Преобразование разности (или суммы)
тригонометрических функций в произведение.

- Приведение к квадратному уравнению относительно одной из функций.
- Возведение обеих частей уравнения в квадрат.
- Выражение всех функций через tg x (универсальная подстановка).
- Графическое решения уравнения.
Содержание.
1. Слово предоставляется первому участнику.
Приведение уравнения sin x — cos x = 1 к
однородному относительно синуса и косинуса.
Разложим левую часть по формулам двойного
аргумента, а правую часть заменим
тригонометрической единицей, используя основное
тригонометрическое тождество:
2 sin cos — cos + sin = sin + cos ;
2 sin cos — cos =0 ;
cos = 0;
Произведение равно нулю, если хотя бы один из
множителей равен нулю, а другие при этом не
теряют смысла, поэтому следует
cos =0 ; =
= 0 -
однородное уравнение первой степени. Делим обе
части уравнения на cos . (cos 0, так как если
cos = 0 , то sin — 0 = 0 sin = 0, а это противоречит
тригонометрическому тождеству sin + cos = 1).
Делим обе
части уравнения на cos . (cos 0, так как если
cos = 0 , то sin — 0 = 0 sin = 0, а это противоречит
тригонометрическому тождеству sin + cos = 1).
Получим tg -1
= 0 ; tg = 1 ; =
Ответ:
2. Слово предоставляется второму участнику.
Разложение левой части уравнения sin x — cos x = 1 на множители.
sin x – (1+ cos x ) = 1; используем формулы 1+ cos x = 2 , получим ;
далее аналогично:
произведение равно нулю, если хотя бы один из
множителей равен нулю, а другие при этом не
теряют смысла, поэтому следует
cos =0 ; =
= 0 -
однородное уравнение первой степени. Делим обе
части уравнения на cos . (cos 0, так как если
cos = 0 , то sin — 0 = 0 sin = 0, а это противоречит
тригонометрическому тождеству sin + cos = 1)
Получим tg -1
= 0 ; tg = 1 ; =
Ответ:
3. Слово предоставляется третьему участнику.
Решение уравнения sin x — cos x = 1 введением вспомогательного угла.
Рассмотрим уравнение sin x — cos x = 1. Умножим и
разделим каждое слагаемое левой части
уравнения на .
Получим и
вынесем в левой части уравнения за скобку. Получим ; Разделим обе
части уравнения на и используем табличные значения
тригонометрических функций. Получим ; Применим
формулу синус разности.
;
Легко установить(с помощью тригонометрического
круга), что полученное решение распадается на два
случая:
;
Ответ:
4. Слово предоставляется четвертому участнику.
Решение уравнения sin x — cos x = 1 способом преобразования разности (или суммы) тригонометрических функций в произведение.
Запишем уравнение в виде , используя формулу приведения . Применяя формулу разности двух синусов, получим
;
и так далее, аналогично предыдущему способу.
Ответ:
5. Слово предоставляется пятому участнику.
Решение уравнения sin x — cos x = 1 способом приведения к квадратному уравнению относительно одной из функций.
Рассмотрим основное тригонометрическое
тождество ,
откуда следует
подставим
полученное выражение в данное уравнение.
sin x — cos x = 1 ,
Возведем обе части полученного уравнения в квадрат:
В процессе решения обе части уравнения возводились в квадрат, что могло привести к появлению посторонних решений, поэтому необходима проверка. Выполним ее.
Полученные решения эквивалентны объединению трех решений:
Первое и второе решения совпадают с ранее
полученными, поэтому не являются посторонними.
Остается проверить третье решение Подставим.
Левая часть:
Правая часть: 1.
Получили: , следовательно, – постороннее решение.
Ответ:
6. Слово предоставляется шестому участнику.
Слово предоставляется шестому участнику.
Возведение обеих частей уравнения sin x — cos x = 1 в квадрат.
Рассмотрим уравнение sin x — cos x = 1. Возведем обе части данного уравнения в квадрат.
;
;
Используя основное тригонометрическое тождество и формулу синуса двойного угла, получим ; sin 2x = 0 ; .
Полученное решение эквивалентно объединению четырех решений:
(эти решения можно нанести на единичную окружность). Проверка показывает, что первое и четвертое решения — посторонние.
Ответ:
7. Слово предоставляется седьмому участнику.
Использование универсальной подстановки в решении уравнения sin x — cos x = 1. Выражение всех функций через tg x по формулам:
Запишем данное уравнение с учетом приведенных
формул в виде .
,
получим
ОДЗ данного уравнения – все множество R. При
переходе к
из рассмотрения выпали значения, при которых не имеет
смысла, т. е.
или .
е.
или .
Следует проверить, не являются ли решениями данного уравнения. Подставим в левую и правую часть уравнения эти решения.
Левая часть: .
Правая часть: 1.
Получили 1=1. Значит, — решение данного уравнения.
Ответ:
8. Слово предоставляется восьмому участнику.
Рассмотрим графическое решение уравнения sin x — cos x = 1.
Запишем рассматриваемое уравнение в виде sin x = 1 + cos x.
Построим в системе координат Оxy графики функций, соответствующих левой и правой частям уравнения. Абсциссы точек пересечения графиков являются решениями данного уравнения.
y = sin x – график: синусоида.
y = cos x +1 – график: косинусоида y = cos x, смещенная на 1
вверх по оси Oy. Абсциссы точек пересечения
являются решениями данного уравнения.
Ответ:
Итог урока.
- Учащиеся научились решать тригонометрические
уравнения вида , освоили новый материал.

- На примере одного уравнения рассмотрели несколько способов решения.
- Учащиеся были непосредственными участниками урока, была задействована обратная связь в системе ученик-учитель.
- Учащиеся получили навыки самостоятельной работы с дополнительной литратурой.
Список использованной литературы:
- Татарченкова С.С. Урок как педагогический феномен – Санкт-Петербург: Каро, 2005
- Выгодский Н.В. Справочник по элементарной математике.-М.: Наука, 1975.
- Виленкин Н.Я. и др. За страницами учебника математики: Арифметика. Алгебра. Геометрия: Книга для учащихся 10-11 класса – М.: Просвещение, 1996.
- Гнеденко Б.В. Очерки по истории математики в России – М.: ОГИЗ, 1946.
- Депман И.Я. и др. За страницами учебника математики – М.: Просвещение, 1999.
- Дорофеев Г.
 В. и др. Математика: для поступающих в
вузы – М.: Дрофа, 2000.
В. и др. Математика: для поступающих в
вузы – М.: Дрофа, 2000. - Математика: Большой энциклопедический словарь. – М.: БСЭ, 1998.
- Мордкович А.Г. и др. Справочник школьника по математике. 10-11кл. Алгебра и начала анализа. – М.: Аквариум, 1997.
- 300 конкурсных задач по математике. – М.: Рольф, 2000.
- 3600 задач по алгебре и началам анализа. – М.: Дрофа, 1999.
- Школьная программа в таблицах и формулах. Большой универсальный справочник. – М.: Дрофа, 1999.
- Торосян В.Г. История образования и педагогической мысли: учеб. для студентов вузов. - М.: Изд-во ВЛАДОС-ПРЕСС, 2006.- 351 с.
- Крылова Н.Б. Педагогическая, психологическая и нравственная поддержка как пространство личностных изменений ребёнка и взрослого.// Классный руководитель.- 2000.- №3. –С.92-103.
Уравнение sin x = a
Репетиторы ❯ Математика ❯ Уравнение sin x = a
Автор: Валентин В. , онлайн репетитор по математике
, онлайн репетитор по математике
●
02.11.2011
●
Раздел: Математика
Значения синуса заключены в промежутке [-1; 1], т.е. -1 ≤ sin α ≤ 1. Поэтому если |а| > 1, то уравнение sin x = a не имеет корней. Например, уравнение sin x = 2 корней не имеет.
Обратимся к некоторым задачам.
Задача 1.
Решить уравнение sin x = 1/2.
Решение.
Отметим, что sin x – это ордината точки единичной окружности, которая получена в результате поворота точки Р (1; 0) на угол х вокруг начала координат.
Ордината, равная ½, присутствует у двух точек окружности М1 и М2.
Так как 1/2 = sin π/6, то точка М1 получается из точки Р (1; 0) посредством поворота на угол х1 = π/6, а также на углы х = π/6 + 2πk, где k = +/-1, +/-2, …
Точка М2 получается из точки Р (1; 0) в результате поворота на угол х2 = 5π/6, а также на углы х = 5π/6 + 2πk, где k = +/-1, +/-2, …, т.е. на углы х = π – π/6 + 2πk, где k = +/-1, +/-2, ….
Итак, все корни уравнения sin х = 1/2 можно найти по формулам х = π/6 + 2πk, х = π – π/6 + 2πk, где k € Z.
Эти формулы могут объединиться в одну: х = (-1)n π/6 + πn, где n € Z (1).
Действительно, если n – четное число, т.е. n = 2k, то из формулы (1) получаем х = π/6 + 2πk, а если n – нечетное число, т.е. n = 2k + 1, то из формулы (1) получаем х = π – π/6 + 2πk.
Ответ. х = (-1)n π/6 + πn, где n € Z.
Задача 2.
Решить уравнение sin x = -1/2.
Решение.
Ординату -1/2 имеют две точки единичной окружности М1 и М2, где х1 = -π/6, х2 = -5π/6.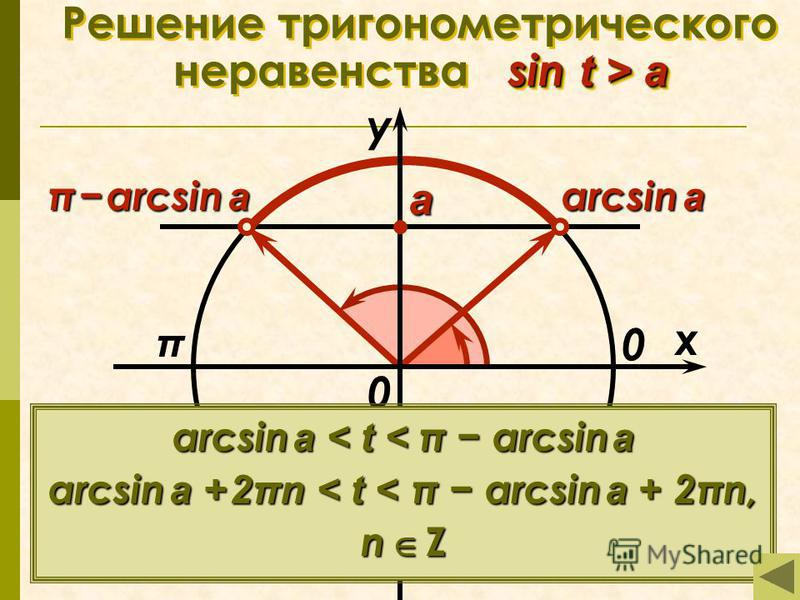 Следовательно, все корни уравнения sin x = -1/2 можно найти по формулам х = -π/6 + 2πk, х = -5π/6 + 2πk, k € Z.
Следовательно, все корни уравнения sin x = -1/2 можно найти по формулам х = -π/6 + 2πk, х = -5π/6 + 2πk, k € Z.
Эти формулы мы можем объединить в одну: х = (-1)n (-π/6) + πn, n € Z (2).
Действительно, если n = 2k, то по формуле (2) получаем х = -π/6 + 2πk, а если n = 2k – 1, то по формуле (2) находим х = -5π/6 + 2πk.
Ответ. х = (-1)n (-π/6) + πn, n € Z.
Таким образом, каждое из уравнений sin x = 1/2 и sin x = -1/2 имеет бесконечное множество корней.
На отрезке -π/2 ≤ х ≤ π/2 каждое из этих уравнений имеет только один корень:
х1 = π/6 – корень уравнения sin x = 1/2 и х1 = -π/6 – корень уравнения sin x = -1/2.
Число π/6 называют арксинусом числа 1/2 и записывают: arcsin 1/2 = π/6; число -π/6 называют арксинусом числа -1/2 и пишут: arcsin (-1/2) = -π/6.
Вообще уравнение sin x = а, где -1 ≤ а ≤ 1, на отрезке -π/2 ≤ х ≤ π/2 имеет лишь один корень. Если а ≥ 0, то корень заключен в промежутке [0; π/2]; если а < 0, то в промежутке [-π/2; 0). Этот корень называют арксинусом числа а и обозначают arcsin а.
Этот корень называют арксинусом числа а и обозначают arcsin а.
Таким образом, арксинусом числа а € [–1; 1] называется такое число а € [–π/2; π/2], синус которого равен а.
аrcsin а = α, если sin α = а и -π/2 ≤ х ≤ π/2 (3).
Например, аrcsin √2/2 = π/4, так как sin π/4 = √2/2 и – π/2 ≤ π/4 ≤ π/2;
аrcsin (-√3/2) = -π/3, так как sin (-π/3) = -√3/2 и – π/2 ≤ – π/3 ≤ π/2.
Аналогично тому, как это сделано при решении задач 1 и 2, можно показать, что корни уравнения sin х = а, где |а| ≤ 1, выражаются формулой
х = (-1)n аrcsin а + πn, n € Z (4).
Также мы можем доказать, что для любого а € [-1; 1] справедлива формула аrcsin (-а) = -аrcsin а.
Из формулы (4) следует, что корни уравнения
sin х = а при а = 0, а = 1, а = -1 можно находить по более простым формулам:
sin х = 0 х = πn, n € Z (5)
sin х = 1 х = π/2 + 2πn, n € Z (6)
sin х = -1 х = -π/2 + 2πn, n € Z (7)
© blog. tutoronline.ru,
при полном или частичном копировании материала ссылка на первоисточник обязательна.
tutoronline.ru,
при полном или частичном копировании материала ссылка на первоисточник обязательна.
Остались вопросы?
Задайте свой вопрос и получите ответ от профессионального преподавателя.
Задать вопрос
Математика
Курсы по математике 10 класс
Математика
Курсы по математике 9 класс
Математика
Математика 11 класс
Математика
Курсы по геометрии 7 класс
Математика
Курсы по алгебре 7 класс
Математика
Алгебра 8 класс
Математика
Курсы по геометрии 8 класс
Французский язык
Курсы французского языка для начинающих
Период функции y sin x.
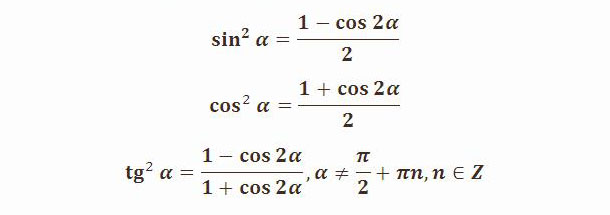 Синус (sin x) и косинус (cos x) – свойства, графики, формулы
Синус (sin x) и косинус (cos x) – свойства, графики, формулыВидеоурок «Периодичность функций у = sin х, у = cos х» раскрывает понятие периодичности функции, рассматривает описание примеров решения задач, в которых используется понятие периодичности функции. Данный видеоурок является наглядным пособием для объяснения темы ученикам. Также данное пособие может стать самостоятельной частью урока, освобождая учителя для проведения индивидуальной работы с учениками.
Наглядность в представлении данной темы очень важна. Чтобы представить поведение функции, построение графика, ее необходимо визуализировать. Произвести построения с помощью классной доски и мела не всегда удается так, чтобы они были понятны всем ученикам. В видеоуроке есть возможность при построении выделять части рисунка цветом, производить преобразования с помощью анимации. Таким образом, построения становятся более понятными большинству учеников. Также возможности видеоурока способствуют лучшему запоминанию материала.
Демонстрация начинается с представления темы урока, а также напоминания ученикам материала, изученного на прошлых уроках. В частности, подытоживается перечень свойств, которые были выявлены в функциях у = sin х, а также у = cos х. Среди свойств рассматриваемых функций отмечены область определения, область значений, четность (нечетность), другие особенности — ограниченность, монотонность, непрерывность, точки наименьшего (наибольшего) значения. Ученикам сообщается, что на данном уроке изучается еще одно свойство функции — периодичность.
Представлено определение периодичной функции y=f(x), где xϵX, в которой выполняется условие f(x-Т)= f(x)= f(x+Т) для некоторого Т≠0. Иначе число Т называют периодом функции.
Для рассматриваемых функций синуса и косинуса выполнение условия проверяется, применяя формулы приведения. Очевидно, что вид тождества sin(x-2π)=sinx=sin(x+2π) соответствует виду выражения определяющего условие периодичности функции. Такое же равенство можно отметить для косинуса cos (x-2π)= cos x= cos (x+2π). Значит, данные тригонометрические функции являются периодическими.
Значит, данные тригонометрические функции являются периодическими.
Далее отмечается, как свойство периодичности помогает строить графики периодичных функций. Рассматривается функция у = sin х. На экране строится координатная плоскость, на которой отмечены абсциссы от -6π до 8π с шагом π. На плоскости строится часть графика синуса, представленный одной волной на отрезке . На рисунке демонстрируется, как график функции формируется на всей области определения сдвигом построенного фрагмента, и получая длинную синусоиду.
Строится график функции у = cos х, используя свойство ее периодичности. Для этого на рисунке строится координатная плоскость, на которой изображается фрагмент графика. Отмечается, что обычно такой фрагмент строится на отрезке [-π/2;3π/2]. Аналогично графику функции синуса, построение графика косинуса выполняется сдвигом фрагмента. В результате построения образуется длинная синусоида.
Построение графика периодичной функции имеет особенности, которые можно использовать. Поэтому они даются в обобщенном виде. Отмечается, что для построения графика такой функции сначала строят ветвь графика на некотором промежутке длиной Т. затем необходимо сдвинуть построенную ветвь вправо и влево на Т, 2Т, 3Т и т.д. при этом указывается еще на одну особенность периода — для любого целого k≠0 число kТ также является периодом функции. Однако Т называется основным периодом, так как он наименьших из всех. Для тригонометрических функций синуса и косинуса основным периодом является 2π. Однако также являются периодами 4π, 6π и т.д.
Поэтому они даются в обобщенном виде. Отмечается, что для построения графика такой функции сначала строят ветвь графика на некотором промежутке длиной Т. затем необходимо сдвинуть построенную ветвь вправо и влево на Т, 2Т, 3Т и т.д. при этом указывается еще на одну особенность периода — для любого целого k≠0 число kТ также является периодом функции. Однако Т называется основным периодом, так как он наименьших из всех. Для тригонометрических функций синуса и косинуса основным периодом является 2π. Однако также являются периодами 4π, 6π и т.д.
Далее предлагается рассмотреть нахождение основного периода функции у = cos 5х. Решение начинается с предположением, что Т — период функции. Значит, необходимо выполнение условия f(x-Т)= f(x)= f(x+Т). В данном тождестве f(x)= cos 5х, а f(x+Т)=cos 5(x+Т)= cos (5x+5Т). При этом cos (5x+5Т)= cos 5х, следовательно 5Т=2πn. Теперь можно найти Т=2π/5. Задача решена.
Во второй задаче необходимо найти основной период функции y=sin(2x/7). Предполагается, что основной период функции Т. для данной функции f(x)= sin(2x/7), а через период f(x+Т)=sin(2x/7)(х+Т)= sin(2x/7+(2/7)Т). после приведения получаем (2/7)Т=2πn. Однако нам необходимо найти основной период, поэтому берем наименьшее значение (2/7)Т=2π, из которого находим Т=7π. Задача решена.
для данной функции f(x)= sin(2x/7), а через период f(x+Т)=sin(2x/7)(х+Т)= sin(2x/7+(2/7)Т). после приведения получаем (2/7)Т=2πn. Однако нам необходимо найти основной период, поэтому берем наименьшее значение (2/7)Т=2π, из которого находим Т=7π. Задача решена.
В конце демонстрации результаты примеров обобщаются, сформировав правило для определения основного периода функции. Отмечается, что для функций у=sinkxи y=coskx основными периодами являются 2π/k.
Видеоурок «Периодичность функций у = sin х, у = cos х» может применяться на традиционном уроке математики для повышения эффективности урока. Также данный материал рекомендуется использовать учителю, осуществляющему дистанционное обучение для повышения наглядности объяснения. Видео может быть рекомендовано отстающему ученику для углубления понимания темы.
ТЕКСТОВАЯ РАСШИФРОВКА:
«Периодичность функций у = cos x, y =sin x».
Для построения графиков функций y =sin x и у = cos x были использованы свойства функций:
1 область определения,
2 область значения,
3 четность или нечетность,
4 монотонность,
5 ограниченность,
6 непрерывность,
7 наибольшее и наименьшее значение.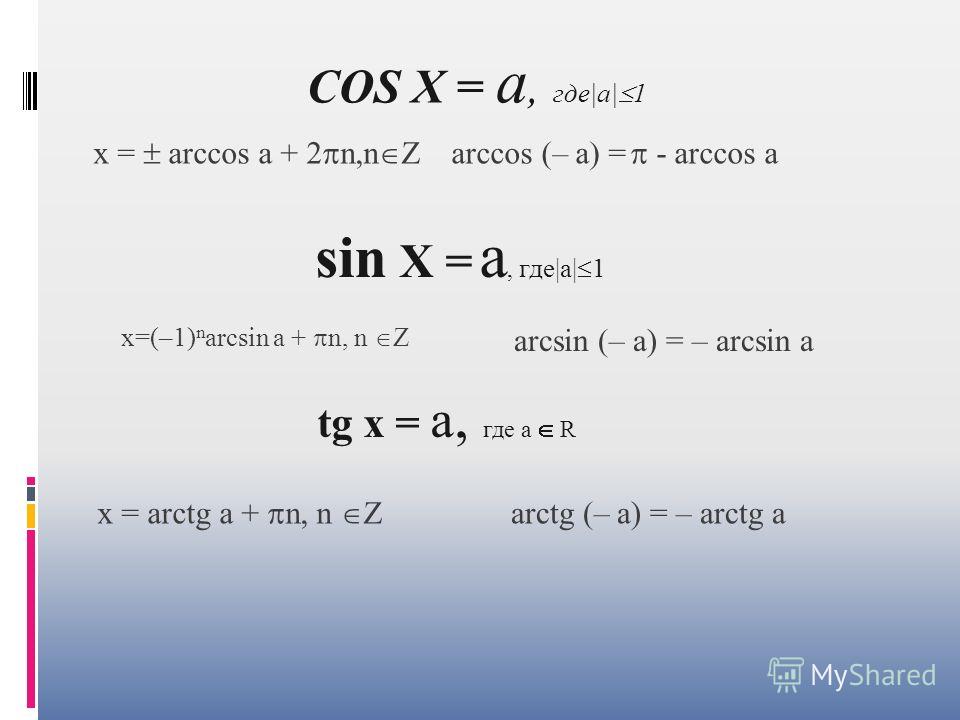
Сегодня мы изучим еще одно свойство: периодичность функции.
ОПРЕДЕЛЕНИЕ. Функцию у = f (x), где х ϵ Х(игрек равно эф от икс, где икс принадлежит множеству икс), называют периодической, если существует отличное от нуля число Т такое, что для любого х из множества Х выполняется двойное равенство: f (x — Т)= f (x) = f (x + Т)(эф от икс минус тэ равно эф от икс и равно эф от икс плюс тэ). Число Т, которое удовлетворяет такому двойному равенству, называют периодом функции
А так как синус и косинус определены на всей числовой прямой и для любого х выполняются равенства sin(x — 2π)= sin x= sin(x+ 2π) (синус от икс минус два пи равен синусу икс и равен синусу от икс плюс два пи) и
cos (x- 2π)= cos x = cos (x+ 2π) (косинус от икс минус два пи равен косинусу икс и равен косинусу от икс плюс два пи), то синус и косинус — это периодические функции с периодом 2π.
Периодичность позволяет быстро построить график функции. Ведь для того, что бы построить график функции y = sin x , достаточно построить одну волну (чаще всего на отрезке (от нуля до двух пи), а затем с помощью сдвига построенной части графика вдоль оси абсцисс вправо и влево на 2π, затем на 4π и так далее получить синусоиду.
(показать сдвиг вправо и влево на 2π, 4π)
Аналогично для графика функции
у = cos x, только строим одну волну чаще всего на отрезке [; ] (от минус пи на два до трех пи на два).
Обобщим выше сказанное и сделаем вывод: для построения графика периодической функции с периодом Т сначала нужно построить ветвь(или волну, или часть) графика на любом промежутке длины Т(чаще всего это промежуток с концами в точках 0 и Т или же — и (минус тэ на два и тэ на два), а затем сдвинуть эту ветвь вдоль оси х(икс) вправо и влево на Т, 2Т, 3Т и т. д.
Очевидно, что если функция периодическая с периодом Т, то при любом целом k0(ка не равном нулю) число вида kT(ка тэ) тоже период этой функции. Обычно стараются выделить наименьший положительный период, который называют основным периодом.
В качестве периода функций у = cos x, y = sin x можно было бы взять — 4π, 4π,- 6π, 6π и т.д.(минус четыре пи, четыре пи, минус шесть пи, шесть пи и так далее). Но число 2π является основным периодом и той, и другой функции.
Рассмотрим примеры.
ПРИМЕР 1.Найти основной период функции у = сos5x (игрек равно косинус пяти икс).
Решение. Пусть Т — основной период функции у = сos5x. Положим
f (x) = сos5x, тогда f (x + Т)= сos5(x + Т)= сos (5x + 5Т) (эф от икс плюс тэ равно косинусу пяти, умноженного на сумму икса и тэ равно косинусу от суммы пяти икс и пяти тэ).
сos (5x + 5Т)= сos5x. Отсюда 5Т= 2πn (пять тэ равно два пи эн), но по условию нужно найти основной период, значит, 5Т= 2π. Получаем Т=
(период данной функции равен два пи, деленное на пять).
Ответ: Т=.
ПРИМЕР 2. Найти основной период функции у = sin (игрек равно синус частного двух икс на семь).
Решение. Пусть Т — основной период функции у = sin . Положим
f (x) = sin , тогда f (x + Т)= sin (x + Т) = sin (x + Т) (эф от икс плюс тэ равно синусу произведения двух седьмых и суммы икса и тэ равно синусу от суммы двух седьмых икс и двух седьмых тэ).
Чтобы число Т было периодом функции, должно выполнятся тождество
sin (x + Т) = sin . Отсюда Т= 2πn (две седьмые тэ равно два пи эн), но по условию нужно найти основной период, значит, Т= 2π. Получаем Т=7
Отсюда Т= 2πn (две седьмые тэ равно два пи эн), но по условию нужно найти основной период, значит, Т= 2π. Получаем Т=7
(период данной функции равен семи пи).
Ответ: Т=7.
Обобщая результаты, полученные в примерах, можно сделать вывод: основной период функций y =sin kx или у = cos kx (игрек равно синус ка икс или игрек равно косинус ка икс) равен (два пи, деленное на ка).
С центром в точке A .
α — угол, выраженный в радианах.
Определение
Синус (sin α) — это тригонометрическая функция, зависящая от угла α между гипотенузой и катетом прямоугольного треугольника, равная отношению длины противолежащего катета |BC| к длине гипотенузы |AC|.
Косинус (cos α) — это тригонометрическая функция, зависящая от угла α между гипотенузой и катетом прямоугольного треугольника, равная отношению длины прилежащего катета |AB| к длине гипотенузы |AC|.
Принятые обозначения
;
;
.
;
;
.
График функции синус, y = sin x
График функции косинус, y = cos x
Свойства синуса и косинуса
Периодичность
Функции y = sin
x
и y = cos
x
периодичны с периодом 2
π
.
Четность
Функция синус — нечетная. Функция косинус — четная.
Область определения и значений, экстремумы, возрастание, убывание
Функции синус и косинус непрерывны на своей области определения, то есть для всех x (см. доказательство непрерывности). Их основные свойства представлены в таблице (n — целое).
| y = sin x | y = cos x | |
| Область определения и непрерывность | — ∞ | — ∞ |
| Область значений | -1 ≤ y ≤ 1 | -1 ≤ y ≤ 1 |
| Возрастание | ||
| Убывание | ||
| Максимумы, y = 1 | ||
| Минимумы, y = -1 | ||
| Нули, y = 0 | ||
| Точки пересечения с осью ординат, x = 0 | y = 0 | y = 1 |
Основные формулы
Сумма квадратов синуса и косинуса
Формулы синуса и косинуса от суммы и разности
;
;
Формулы произведения синусов и косинусов
Формулы суммы и разности
Выражение синуса через косинус
;
;
;
.
Выражение косинуса через синус
;
;
;
.
Выражение через тангенс
; .
При ,
имеем:
;
.
При :
;
.
Таблица синусов и косинусов, тангенсов и котангенсов
В данной таблице представлены значения синусов и косинусов при некоторых значениях аргумента.
Выражения через комплексные переменные
;
Формула Эйлера
Выражения через гиперболические функции
;
;
Производные
; . Вывод формул > > >
Производные n-го порядка:
{ -∞
Секанс, косеканс
Обратные функции
Обратными функциями к синусу и косинусу являются арксинус и арккосинус , соответственно.
Арксинус, arcsin
Арккосинус, arccos
Использованная литература:
И.Н. Бронштейн, К.А. Семендяев, Справочник по математике для инженеров и учащихся втузов, «Лань», 2009.
Инструкция
Чтобы найти период тригонометрической функции, возведенной в степень, оцените четность степени.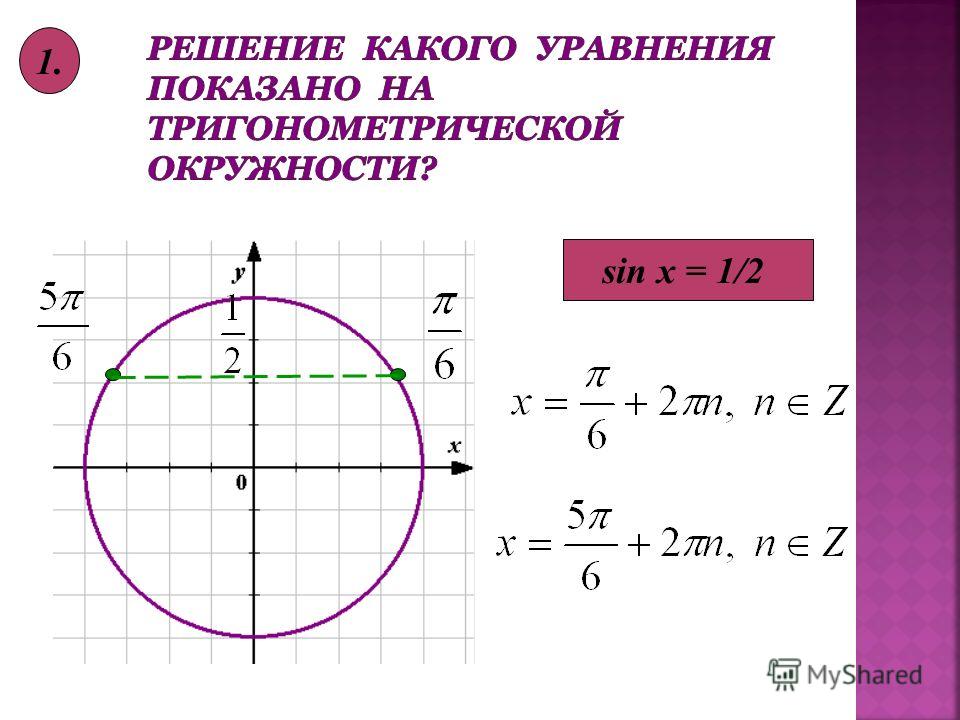 2х, то стандартный период 2П уменьшится в 2 раза, таким образом, период будет равен П. Обратите , функции tg, ctg в любой степени периодичны П.
2х, то стандартный период 2П уменьшится в 2 раза, таким образом, период будет равен П. Обратите , функции tg, ctg в любой степени периодичны П.
Если вам дано уравнение, содержащее или частное двух тригонометрических функций, сначала найдите период для каждой из них отдельно. Затем найдите минимальное число, которое умещало бы в себе целое количество обоих . Например, дана функция у=tgx*cos5x. Для тангенса период П, для косинуса 5х – период 2П/5. Минимальное число, в которое можно уместить оба этих периода, это 2П, таким образом, искомый период – 2П.
Если вы затрудняетесь действовать предложенным образом или сомневаетесь в ответе, попытайтесь действовать по определению. Возьмите в качестве периода функции Т, он больше нуля. Подставьте в уравнение вместо х выражение (х+Т) и решите полученное равенство, как если бы Т было параметром или числом. В результате вы найдете значение тригонометрической функции и сможете подобрать минимальный период. Например, в результате упрощения у вас получилось тождество sin (Т/2)=0.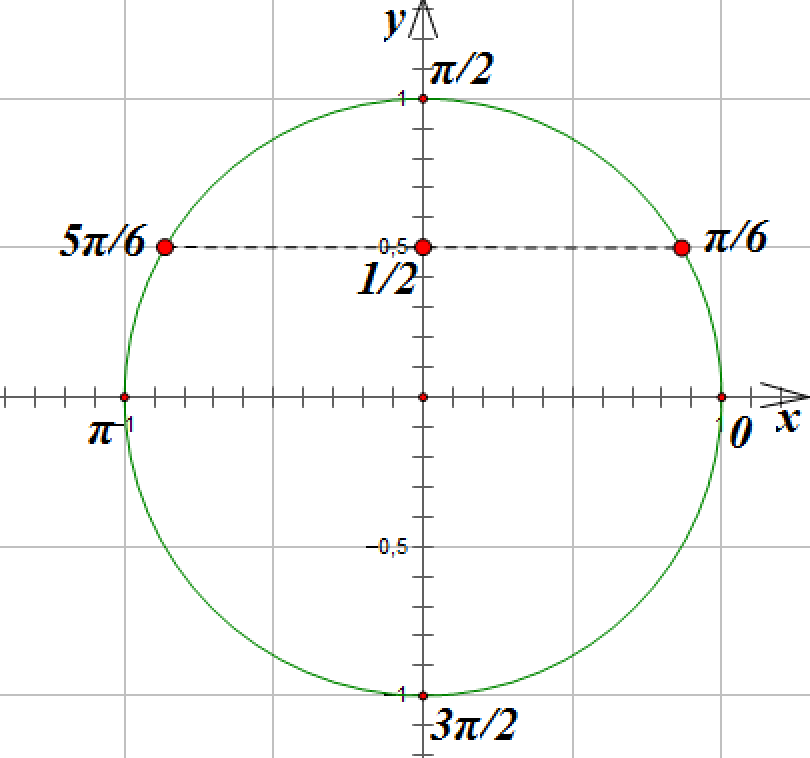 Минимальное значение Т, при котором оно выполняется, 2П, это и будет задачи.
Минимальное значение Т, при котором оно выполняется, 2П, это и будет задачи.
Источники:
- период sin
Периодической функцией называется функция, повторяющая свои значения через какой-то ненулевой период. Периодом функции называется число, при добавление которого к аргументу функции значение функции не меняется.
Вам понадобится
- Знания по элементарной математике и началам анализа.
Инструкция
Видео по теме
Обратите внимание
Все тригонометрические функции являются периодическими, а все полиномиальные со степенью больше 2 — апериодическими.
Полезный совет
Периодом функции, состоящей из двух периодический функций, является Наименьшее общее кратное периодов этих функций.
Тригонометрические уравнения — это уравнения, которые содержат в себе функции неизвестного аргумента (для примера: 5sinx-3cosx =7). Чтобы научиться решать их — нужно знать некоторые для этого методы.
Инструкция
Разложение уравнения на множители. Сначала переносим все члены влево и раскладываем на множители.
Сначала переносим все члены влево и раскладываем на множители.
Важно помнить, что о четности и нечетности функции имеет прямую с областью определения функции. Если, например, четная либо нечетная функция не при х=5, то она не существует и при х=-5, чего нельзя сказать про функцию общего вида. При установлении четности и нечетности обращайте внимание на область определения функции.
Исследование функции на четность и нечетность коррелирует с нахождением множества значений функции. Для нахождения множества значений четной функции достаточно рассмотреть половину функции, правее либо левее нуля. Если при x>0 четная функция y(x) принимает от А до В, то те же значения она будет и при xДля нахождения множества значений, принимаемых нечетной функцией, тоже достаточно рассмотреть только одну функции. Если при x>0 нечетная функция y(x) принимает диапазон значений от А до В, то при x
«Тригонометрическими» когда-то стали называть функции, которые определяются зависимостью острых углов в прямоугольном треугольнике от длин его сторон. К таким функциям относят в первую очередь синус и косинус, во вторую — обратные этим функциям секанс и косеканс, производные от них тангенс и котангенс, а также обратные функции арксинус, арккосинус и др. Правильнее говорить не о «решении» таких функций, а об их «вычислении», то есть о нахождении численного значения.
К таким функциям относят в первую очередь синус и косинус, во вторую — обратные этим функциям секанс и косеканс, производные от них тангенс и котангенс, а также обратные функции арксинус, арккосинус и др. Правильнее говорить не о «решении» таких функций, а об их «вычислении», то есть о нахождении численного значения.
Инструкция
Если аргумент тригонометрической неизвестен, то вычислить ее значение можно косвенным способом исходя из определений этих функций. Для этого требуется знать длины сторон треугольника, тригонометрическую для одного из углов которого требуется вычислить. Например, синус острого угла в прямоугольном треугольнике — это отношение длины противолежащего этому углу катета к длине гипотенузы. Из этого вытекает, что для угла достаточно знать длины этих двух сторон. Аналогичное гласит, что синусом острого угла является отношение длины прилежащего к этому углу катета к длине гипотенузы. Тангенс острого угла можно вычислить, разделив длину противолежащего ему катета на длину прилежащего, а требует деления длины прилежащего катета к длине противолежащего.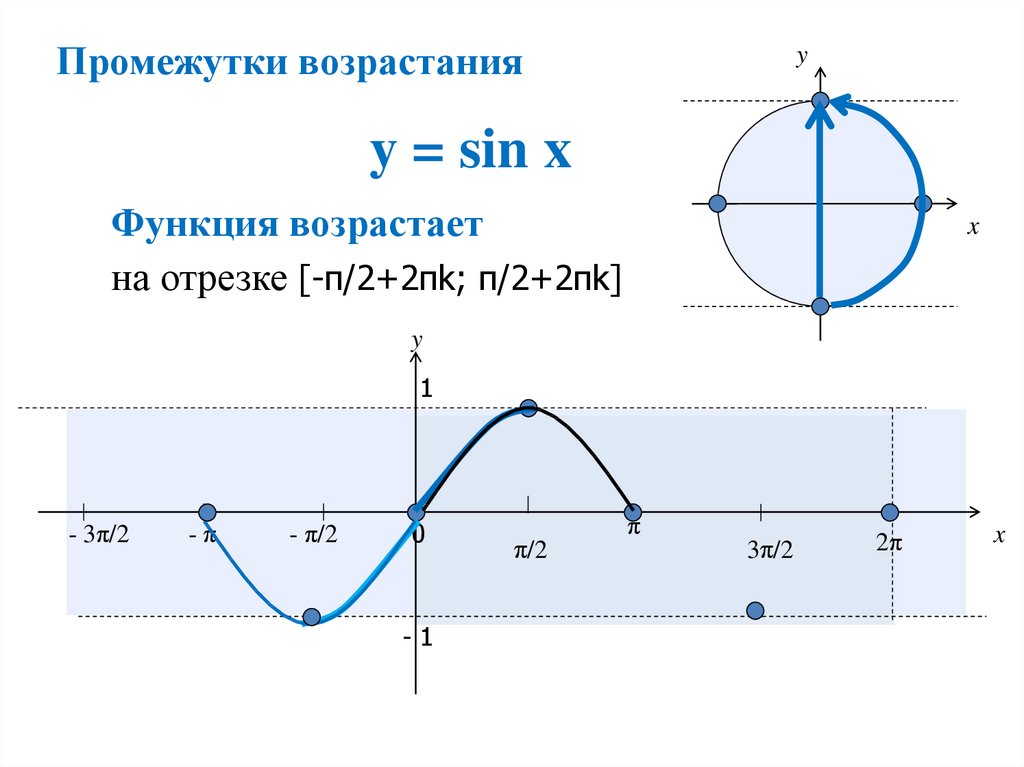 Для вычисления секанса острого угла надо найти отношение длины гипотенузы к длине прилежащего к нужному углу катета, а косеканс определяется отношением длины гипотенузы к длине противолежащего катета.
Для вычисления секанса острого угла надо найти отношение длины гипотенузы к длине прилежащего к нужному углу катета, а косеканс определяется отношением длины гипотенузы к длине противолежащего катета.
Если же аргумент тригонометрической функции известен, то знать длины сторон треугольника не требуется — можно воспользоваться таблицами значений или калькуляторами тригонометрических функций. Такой есть среди стандартных программ операционной системы Windows. Для его запуска можно нажать сочетание клавиш Win + R, ввести команду calc и щелкнуть кнопку «OK». В интерфейсе программы следует раскрыть раздел «Вид» и пункт «Инженерный» или «Научный». После этого можно вводить аргумент тригонометрической функции. Для вычисления функций синус, косинус и достаточно после ввода значения щелкнуть по соответствующей кнопке интерфейса (sin, cos, tg), а для нахождения обратных им арксинуса, арккосинуса и следует предварительно поставить отметку в чекбоксе Inv.
Есть и альтернативные способы. Один из них — перейти на сайт поисковой системы Nigma или Google и ввести в качестве поискового запроса нужную функцию и ее аргумент (например, sin 0.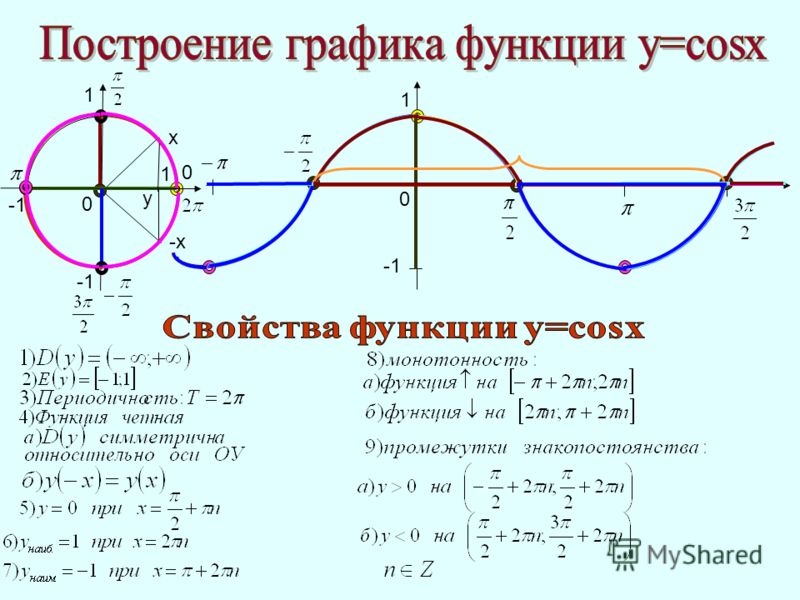 47). Эти поисковики имеют встроенные калькуляторы, поэтому после отправки такого запроса вы получите значение введенной вами тригонометрической функции.
47). Эти поисковики имеют встроенные калькуляторы, поэтому после отправки такого запроса вы получите значение введенной вами тригонометрической функции.
Видео по теме
Тригонометрические функции вначале возникли как инструменты абстрактных математических вычислений зависимостей величин острых углов в прямоугольном треугольнике от длин его сторон. Сейчас они очень широко применяются как в научных, так и в технических областях человеческой деятельности. Для практических вычислений тригонометрических функций от заданных аргументов можно использовать разные инструменты — ниже описано несколько наиболее доступных из них.
Инструкция
Воспользуйтесь, например, устанавливаемой по умолчанию вместе с операционной системой программой-калькулятором. Она открывается выбором пункта «Калькулятор» в папке «Служебные» из подраздела «Стандартные», помещенного в раздел «Все программы». Этот раздел можно , открыв щелчком по кнопке «Пуск» главное меню операционной . Если вы используете версию Windows 7, то имеете возможность просто ввести «Калькулятор» в поле «Найти программы и файлы» главного меню, а затем щелкнуть по соответствующей ссылке в результатах поиска.
Введите угла, для которого надо рассчитать тригонометрическую функцию, а потом кликните по соответствующей этой кнопке — sin, cos или tan. Если вас интересуют обратные тригонометрические функции (арксинус, арккосинус или ), то сначала кликните кнопку с надписью Inv — она меняет присвоенные управляющим кнопкам функции на противоположные.
В более ранних версиях ОС (например, Windows XP) для доступа к тригонометрическим функциям надо раскрыть в меню калькулятора раздел «Вид» и выбрать строку «Инженерный». Кроме того, вместо кнопки Inv в интерфейсе старых версий программы присутствует чекбокс с же надписью.
Можно и без калькулятора, если у вас есть доступ в интернет. В сети много сервисов, которые предлагают по-разному организованные вычислители тригонометрических функций. Один их наиболее удобных встроен в поисковую систему Nigma. Перейдя на ее главную страницу, просто введите в поле поискового запроса интересующее вас значение — например, «арктангенс 30 ». После нажатия кнопки «Найти!» поисковик рассчитает и покажет результат вычисления — 0,482347907101025.
Видео по теме
Тригонометрия – раздел математики для изучения , выражающих различные зависимости сторон прямоугольного треугольника от величин острых углов при гипотенузе. Такие функции получили называние тригонометрических, а для упрощения работы с ними были выведены тригонометрические тождества .
Понятие тождества в означает равенство, которое выполняется при любых значениях аргументов входящих в него функций. Тригонометрические тождества – это равенства тригонометрических функций, доказанные и принятые для облегчения работы с тригонометрическими формулами.Тригонометрическая функция – это элементарная функция зависимости одного из катетов прямоугольного треугольника от величины острого угла при гипотенузе. Чаще всего используются шесть основных тригонометрических функций: sin (синус), cos (косинус), tg (тангенс), ctg (котангенс), sec (секанс) и cosec (косеканс). Эти функции называются прямыми, существуют также
Производная функции y sin x равна.
 Производная синуса: (sin x)′
Производная синуса: (sin x)′Производная
Несмотря на то, что в предыдущих параграфах были рассмотрены два различных примера, между ними есть нечто общее. Для того чтобы это выяснить, нужно стать на функциональную точку зрения.
Пусть дана функция y=f(x).
Чтобы получить задачу о скорости, будем считать, что независимое переменное х есть время, а у- расстояние точки, движущейся по прямой, от начала координат. Уравне- у ние y-f(x) в этом случае называется законом движения.
Чтобы получить задачу о касательной, будем счи-
в
Рис. 47.
тать, что х-абсцисса и у — ордината точки, лежащей на кривой линии, определяемой уравнением у = /(х).
Будем производить над функцией у = /(х) некоторые операции и одновременно выяснять, что эти операции означают в задаче о скорости и в задаче о касательной.
1. Дадим х определенное числовое значение и вычислим соответствующее значение
У» fix). (1)
В задаче о скорости это значит, что для определенного момента времени х мы нашли расстояние у движущейся точки от начала координат (рис, 47). В задаче о касательной это означает, что мы определили координаты точки Р, лежащей на кривой, определенной уравнением у=/(х) (рис. 48).
2. Дадим х приращение h и вычислим соответствующее приращенное значение уу которое отличается от первоначального на величину А у (приращение функции) (см. гл. V, § 4):
у + Ьy=f(x+h). В задаче о скорости тем самым мы определяли положение Р, движущейся точки в момент времени x + h*
В задаче о касательной получена новая точка М. Здесь АВ= PQ= h, OB = x + h, BM = f(x + h).
3. Найдем приращение функции Ду; для этого вычтем почленно из равенства (2) равенство (1):
+ h)-f»=/(*) + Ф»(*), (IV)
т. е. производная суммы двух функций равна сумме их производных.
V. Производная произведения двух функций. Предположим, что нам известны производные функций f{x) и представим ее в виде цепочки функций (см. гл. V, § 3):
Рассмотрим уравнения (*) и (#*) независимо друг от друга. Первое из них дает и как функцию х; ее производная равна ср» (л:). Второе определяет у как функцию независимого переменного и; ее производная равна /» (и).
В задаче о касательной это означает, что мы определили координаты точки Р, лежащей на кривой, определенной уравнением у=/(х) (рис. 48).
2. Дадим х приращение h и вычислим соответствующее приращенное значение уу которое отличается от первоначального на величину А у (приращение функции) (см. гл. V, § 4):
у + Ьy=f(x+h). В задаче о скорости тем самым мы определяли положение Р, движущейся точки в момент времени x + h*
В задаче о касательной получена новая точка М. Здесь АВ= PQ= h, OB = x + h, BM = f(x + h).
3. Найдем приращение функции Ду; для этого вычтем почленно из равенства (2) равенство (1):
+ h)-f»=/(*) + Ф»(*), (IV)
т. е. производная суммы двух функций равна сумме их производных.
V. Производная произведения двух функций. Предположим, что нам известны производные функций f{x) и представим ее в виде цепочки функций (см. гл. V, § 3):
Рассмотрим уравнения (*) и (#*) независимо друг от друга. Первое из них дает и как функцию х; ее производная равна ср» (л:). Второе определяет у как функцию независимого переменного и; ее производная равна /» (и). 1. Представим функцию у в виде цепочки: и-хг + 1, у~еа. Так как (х8 + 1)»= Зх2, (то » =
= —
1. Представим функцию у в виде цепочки: и-хг + 1, у~еа. Так как (х8 + 1)»= Зх2, (то » =
= —
Представлено доказательство и вывод формулы для производной синуса — sin(x). Примеры вычисления производных от sin 2x, синуса в квадрате и кубе. Вывод формулы для производной синуса n-го порядка.
Производная по переменной x от синуса x равна косинусу x:
(sin
x)′ = cos
x
.
Доказательство
Для вывода формулы производной синуса, мы воспользуемся определением производной:
.
Чтобы найти этот предел, нам нужно преобразовать выражение таким образом, чтобы свести его к известным законам, свойствам и правилам. Для этого нам нужно знать четыре свойства.
1) Значение первого замечательного предела:
(1) ;
2) Непрерывность функции косинус:
(2) ;
3) Тригонометрические формулы . Нам понадобится следующая формула:
(3) ;
4) Свойство пределов:
Если и ,
то
(4) .
Применяем эти правила к нашему пределу. Сначала преобразуем алгебраическое выражение
.
Для этого применим формулу
(3) .
В нашем случае
;
.
Тогда
;
;
;
.
Теперь сделаем подстановку .
При ,
.
Применим первый замечательный предел (1):
.
Сделаем такую же подстановку и используем свойство непрерывности (2):
.
Поскольку пределы, вычисленные выше, существуют, то применяем свойство (4):
.
Формула производной синуса доказана.
Примеры
Рассмотрим простые примеры нахождения производных от функций, содержащих синус. Мы найдем производные от следующих функций:
y = sin 2x; y = sin 2
x
и y = sin 3
x
.
Пример 1
Найти производную от sin 2x .
Решение
Сначала найдем производную от самой простой части:
(2x)′ = 2(x)′ = 2 · 1 = 2.
Применяем .
.
Здесь .
Ответ
(sin 2x)′ = 2 cos 2x.
Пример 2
Найти производную от синуса в квадрате:
y = sin 2
x
.
Решение
Перепишем исходную функцию в более понятном виде:
.
Найдем производную от самой простой части:
.
Применяем формулу производной сложной функции.
.
Здесь .
Можно применить одну из формул тригонометрии. Тогда
.
Ответ
Пример 3
Найти производную от синуса в кубе:
y = sin 3
x
.
Производные высших порядков
Заметим, что производную от sin x первого порядка можно выразить через синус следующим образом:
.
Найдем производную второго порядка, используя формулу производной сложной функции :
.
Здесь .
Теперь мы можем заметить, что дифференцирование sin x приводит к увеличению его аргумента на .
Тогда производная n-го порядка имеет вид:
(5) .
Докажем это, применяя метод математической индукции.
Мы уже проверили, что при , формула (5) справедлива.
Предположим, что формула (5) справедлива при некотором значении .
Докажем, что из этого следует, что формула (5) выполняется для .
Выпишем формулу (5) при :
.
Дифференцируем это уравнение, применяя правило дифференцирования сложной функции:
.
Здесь .
Итак, мы нашли:
.
Если подставить ,
то эта формула примет вид (5).
Формула доказана.
Определение. Пусть функция \(y = f(x) \) определена в некотором интервале, содержащем внутри себя точку \(x_0 \). Дадим аргументу приращение \(\Delta x \) такое, чтобы не выйти из этого интервала. Найдем соответствующее приращение функции \(\Delta y \) (при переходе от точки \(x_0 \) к точке \(x_0 + \Delta x \)) и составим отношение \(\frac{\Delta y}{\Delta x} \). Если существует предел этого отношения при \(\Delta x \rightarrow 0 \), то указанный предел называют производной функции \(y=f(x) \) в точке \(x_0 \) и обозначают \(f»(x_0) \).
$$ \lim_{\Delta x \to 0} \frac{\Delta y}{\Delta x} = f»(x_0) $$
Для обозначения производной часто используют символ y».
Отметим, что y» = f(x) — это новая функция, но, естественно, связанная с функцией y = f(x), определенная во всех точках x, в которых
существует указанный выше предел. Эту функцию называют так: производная функции у = f(x) .
Эту функцию называют так: производная функции у = f(x) .
Геометрический смысл производной состоит в следующем. Если к графику функции у = f(x) в точке с абсциссой х=a можно
провести касательную, непараллельную оси y, то f(a) выражает угловой коэффициент касательной:
\(k = f»(a) \)
Поскольку \(k = tg(a) \), то верно равенство \(f»(a) = tg(a) \) .
А теперь истолкуем определение производной с точки зрения приближенных равенств. Пусть функция \(y = f(x) \) имеет
производную в конкретной точке \(x \):
$$ \lim_{\Delta x \to 0} \frac{\Delta y}{\Delta x} = f»(x) $$
Это означает, что около точки х выполняется приближенное равенство \(\frac{\Delta y}{\Delta x} \approx f»(x) \), т.е.
\(\Delta y \approx f»(x) \cdot \Delta x \).
Содержательный смысл полученного приближенного равенства заключается в следующем: приращение функции «почти пропорционально»
приращению аргумента, причем коэффициентом пропорциональности является значение производной в заданной точке х. 2 \) справедливо приближенное равенство \(\Delta y \approx 2x \cdot \Delta x \).
Если внимательно проанализировать определение производной, то мы обнаружим, что в нем заложен алгоритм ее нахождения.
2 \) справедливо приближенное равенство \(\Delta y \approx 2x \cdot \Delta x \).
Если внимательно проанализировать определение производной, то мы обнаружим, что в нем заложен алгоритм ее нахождения.
Сформулируем его.
Как найти производную функции у = f(x) ?
1. Зафиксировать значение \(x \), найти \(f(x) \)
2. Дать аргументу \(x \) приращение \(\Delta x \), перейти в новую точку \(x+ \Delta x \), найти \(f(x+ \Delta x) \)
3. Найти приращение функции: \(\Delta y = f(x + \Delta x) — f(x) \)
4. Составить отношение \(\frac{\Delta y}{\Delta x} \)
5. Вычислить $$ \lim_{\Delta x \to 0} \frac{\Delta y}{\Delta x} $$
Этот предел и есть производная функции в точке x.
Если функция у = f(x) имеет производную в точке х, то ее называют дифференцируемой в точке х. Процедуру нахождения производной функции у = f(x) называют дифференцированием функции у = f(x).
Обсудим такой вопрос: как связаны между собой непрерывность и дифференцируемость функции в точке.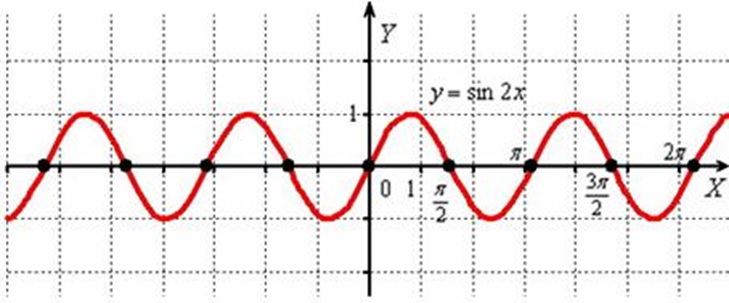
Пусть функция у = f(x) дифференцируема в точке х. Тогда к графику функции в точке М(х; f(x)) можно провести касательную, причем, напомним, угловой коэффициент касательной равен f»(x). Такой график не может «разрываться» в точке М, т. е. функция обязана быть непрерывной в точке х.
Это были рассуждения «на пальцах». Приведем более строгое рассуждение. Если функция у = f(x) дифференцируема в точке х, то выполняется приближенное равенство \(\Delta y \approx f»(x) \cdot \Delta x \). Если в этом равенстве \(\Delta x \) устремить к нулю, то и \(\Delta y \) будет стремиться к нулю, а это и есть условие непрерывности функции в точке.
Итак, если функция дифференцируема в точке х, то она и непрерывна в этой точке .
Обратное утверждение неверно. Например: функция у = |х| непрерывна везде, в частности в точке х = 0, но касательная к графику
функции в «точке стыка» (0; 0) не существует. Если в некоторой точке к графику функции нельзя провести касательную, то в этой
точке не существует производная.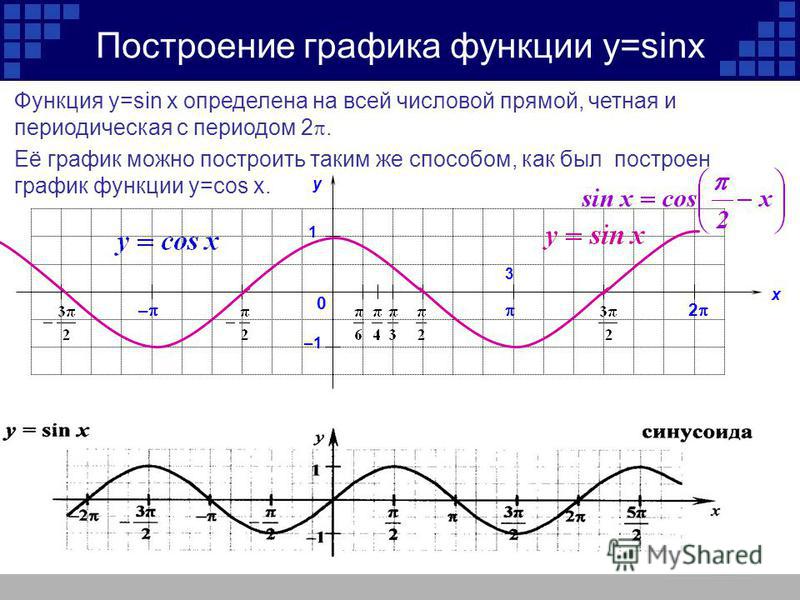
Еще один пример. Функция \(y=\sqrt{x} \) непрерывна на всей числовой прямой, в том числе в точке х = 0. И касательная к графику функции существует в любой точке, в том числе в точке х = 0. Но в этой точке касательная совпадает с осью у, т. е. перпендикулярна оси абсцисс, ее уравнение имеет вид х = 0. Углового коэффициента у такой прямой нет, значит, не существует и \(f»(0) \)
Итак, мы познакомились с новым свойством функции — дифференцируемостью. А как по графику функции можно сделать вывод о ее дифференцируемости?
Ответ фактически получен выше. Если в некоторой точке к графику функции можно провести касательную, не перпендикулярную оси абсцисс, то в этой точке функция дифференцируема. Если в некоторой точке касательная к графику функции не существует или она перпендикулярна оси абсцисс, то в этой точке функция не дифференцируема.
Правила дифференцирования
Операция нахождения производной называется дифференцированием .
При выполнении этой операции часто приходится работать с частными, суммами, произведениями функций, а также с «функциями функций»,
то есть сложными функциями. 2} $$
2} $$
При выводе самой первой формулы таблицы будем исходить из определения производнойфункции в точке. Возьмем , где x – любое действительное число, то есть, x – любое число из области определения функции . Запишем предел отношения приращения функции к приращению аргумента при :
Следует заметить, что под знаком предела получается выражение , которое не являетсянеопределенностью ноль делить на ноль, так как в числителе находится не бесконечно малая величина, а именно ноль. Другими словами, приращение постоянной функции всегда равно нулю.
Таким образом, производная постоянной функции равна нулю на всей области определения .
Производная степенной функции.
Формула производной степенной функции имеет вид , где показатель степени p – любое действительное число.
Докажем сначала формулу для натурального показателя степени, то есть, для p = 1, 2, 3, …
Будем пользоваться определением производной. Запишем предел отношения приращения степенной функции к приращению аргумента:
Для
упрощения выражения в числителе обратимся
к формуле бинома
Ньютона:
Следовательно,
Этим
доказана формула производной степенной
функции для натурального показателя.
Производная показательной функции.
Вывод формулы производной приведем на основе определения:
Пришли к неопределенности. Для ее раскрытия введем новую переменную , причем при . Тогда . В последнем переходе мы использовали формулу перехода к новому основанию логарифма.
Выполним подстановку в исходный предел:
Если
вспомнить второй
замечательный предел, то придем к
формуле производной показательной
функции:
Производная логарифмической функции.
Докажем
формулу производной логарифмической
функции для всех x из
области определения и всех допустимых
значениях основания a логарифма.
По определению производной имеем:
Как Вы заметили, при доказательстве преобразования проводились с использованием свойств логарифма. Равенство справедливо в силу второго замечательного предела.
Производные тригонометрических функций.
Для
вывода формул производных тригонометрических
функций нам придется вспомнить некоторые
формулы тригонометрии, а также первый
замечательный предел.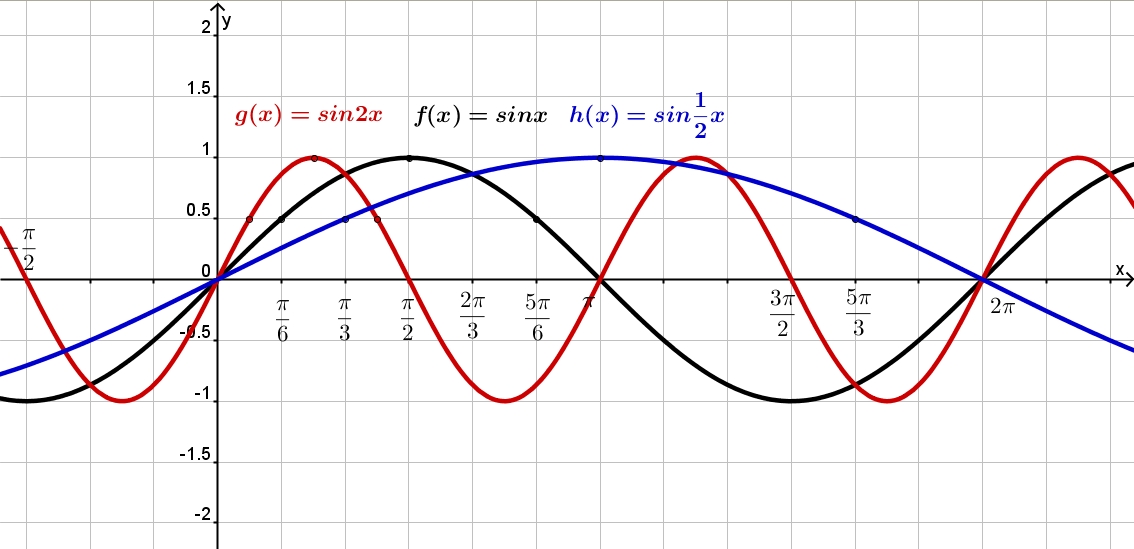
По определению производной для функции синуса имеем .
Воспользуемся
формулой разности синусов:
Осталось обратиться к первому замечательному пределу:
Таким образом, производная функции sin x есть cos x .
Абсолютно
аналогично доказывается формула
производной косинуса.
Следовательно, производная функции cos x есть –sin x .
Вывод
формул таблицы производных для тангенса
и котангенса проведем с использованием
доказанных правил дифференцирования
(производная
дроби).
Производные гиперболических функций.
Правила
дифференцирования и
формула производной показательной
функции из таблицы производных позволяют
вывести формулы производных гиперболического
синуса, косинуса, тангенса и котангенса.
Производная обратной функции.
Чтобы
при изложении не было путаницы, давайте
обозначать в нижнем индексе аргумент
функции, по которому выполняется
дифференцирование, то есть, —
это производная функции f(x) по x .
Теперь сформулируем правило нахождения производной обратной функции.
Пусть функции y = f(x) и x = g(y) взаимно обратные, определенные на интервалах и соответственно. Если в точке существует конечная отличная от нуля производная функции f(x) , то в точке существует конечная производная обратной функции g(y) , причем . В другой записи .
Можно это правило переформулировать для любого x из промежутка , тогда получим .
Давайте проверим справедливость этих формул.
Найдем обратную функцию для натурального логарифма (здесь y – функция, а x — аргумент). Разрешив это уравнение относительно x , получим (здесь x – функция, а y – ее аргумент). То есть, и взаимно обратные функции.
Из таблицы производных видим, что и .
Убедимся, что формулы нахождения производных обратной функции приводят нас к этим же результатам:
Предварительное исчисление алгебры— Есть ли способ решить $\sin(x)=x$?
спросил
Изменено 3 месяца назад
Просмотрено 31к раз
$\begingroup$
Примечание.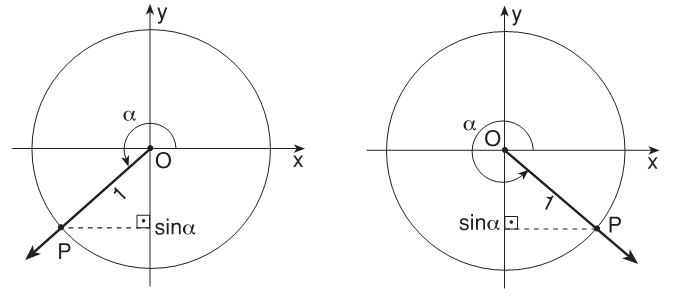 Изначально вопрос должен был решаться алгебраически, но я решил изменить его на аналитический из-за комментариев и ответов.
Изначально вопрос должен был решаться алгебраически, но я решил изменить его на аналитический из-за комментариев и ответов.
При попытке решить $\sin(x)=x$ первым очевидным решением является $x=0$. Однако существует бесконечное количество комплексных значений $x$, которые мы можем попытаться найти. Однако мы собираемся игнорировать их.
Мне интересно, есть ли способ аналитического решения для $x$ в $\sin(x)=x$. Это кажется невозможным, точно так же, как мы не можем решить $\cos(x)=x$ аналитически или легко, но поскольку $\sin(x)=x$ имеет такой простой точный ответ, я подумал, есть ли это способ, которым вы могли бы это сделать.
Итак, существует ли аналитический способ решить эту проблему? Если да, то как? Если нет, то как еще мы могли бы решить это, кроме как графически?
алгебра-предварительный анализ тригонометрия трансцендентальные-уравнения
$\endgroup$
19
$\begingroup$
Если бы проблема могла быть решена чисто алгебраическими средствами (с конечным числом шагов), это означало бы, что $\sin(x)$ можно задать полиномиальное представление, из которого вы могли бы перейти к своей обычной процедуре факторизации к найти нули многочлена. 7}{7!} + \cdots $$ 94}{7!} + \cdots) = 0 $$
7}{7!} + \cdots $$ 94}{7!} + \cdots) = 0 $$
Итак, теперь у нас есть наше «алгебраическое решение», состоящее в том, что $x = 0$.
$\endgroup$
4
$\begingroup$
Подсказка: покажите, что если $x\neq 0$ ($x$ вещественное), $\left|\frac{\sin(x)}{x}\right|<1.$ Я не понимаю, что вы имеете в виду «алгебраически», поэтому я просто оставлю это здесь и позволю вам решить, можно ли найти все решения «алгебраически» или нет.
$\endgroup$
1
$\begingroup$
Поскольку вы рассматриваете только действительные числа, я думаю, что самый простой способ решить эту проблему — разделить случаи и использовать неравенства в каждом случае:
$x=0$ — явное решение, поскольку $\sin 0=0 $.
Если $x\in]0,1[$, то из МВТ следует, что $\exists c\in]0,1[: \cos c=\frac{\sin x-\sin 0}{x-0 }$.
Так как $x,c\in]0,1[$, то $1>\frac{\sin x}{x} \Leftrightarrow x>\sin x$.
Если $x=1$, то $\sin 1 \neq 1$.
Если $x>1$, то очевидно $x>\sin x$.
Теперь ясно, что если $a$ является решением, то $-a$ также является решением (поскольку $\sin(-x) = -\sin x$). Следовательно, нет решений с $x<0$
$\endgroup$
$\begingroup$
Я вижу, что на этот вопрос уже был дан ответ, но я хотел внести свой вклад с очень быстрым интуитивным способом увидеть это просто.
После решения x=0 нам просто нужно убедиться, что наклон $\sin(x)$, равный $\cos(x)$, равен $< 1$ в режиме, когда $x \le 1$ ( после этого очевидно, что решений не будет, так как $\sin(x)$ ограничено от -1 до 1, поэтому любое |x|>1 не будет решением) Проверьте изображение на визуальные эффекты склонов, в x $ \эпсилон$ [0,1]
Итак, нет, кроме x=0 реальных решений больше нет.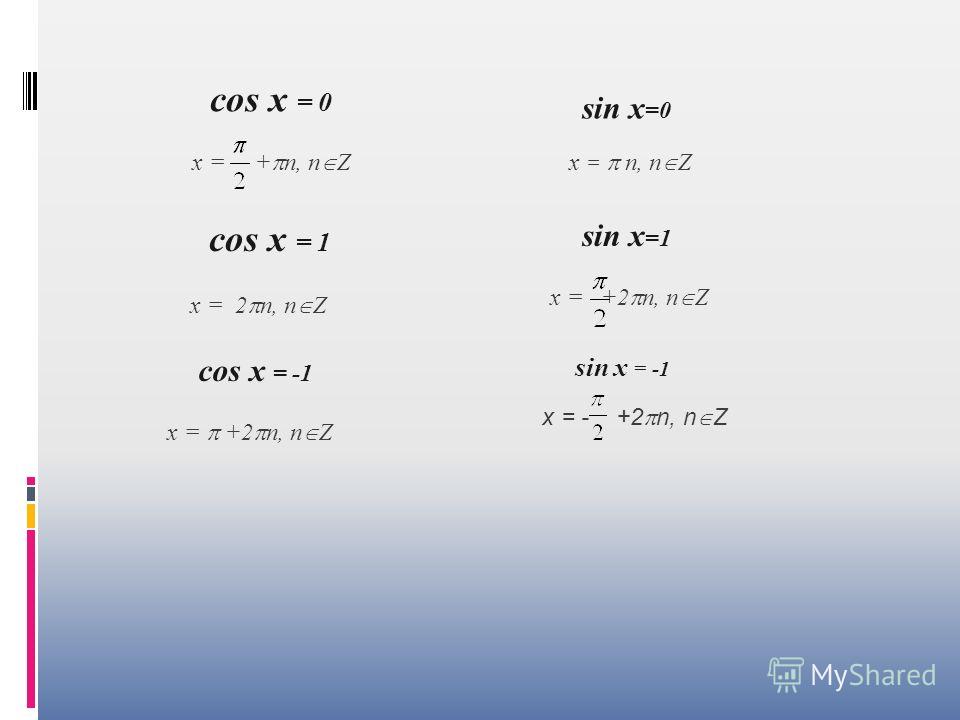
$\endgroup$
1
Твой ответ
Зарегистрируйтесь или войдите в систему
Зарегистрируйтесь с помощью Google
Зарегистрироваться через Facebook
Зарегистрируйтесь, используя электронную почту и пароль
Опубликовать как гость
Электронная почта
Требуется, но никогда не отображается
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie
Расчет— Почему использование приближения $\sin x\приблизительно x$ около $0$ не работает для вычисления этого предела?
Я указывал на это ранее и на MSE (см. ссылка1, ссылка2, ссылка3, ссылка4), но кажется, что этот момент нужно пересказывать и пересказывать, пока он не станет тавтологией типа $1 = 1$.
ссылка1, ссылка2, ссылка3, ссылка4), но кажется, что этот момент нужно пересказывать и пересказывать, пока он не станет тавтологией типа $1 = 1$.
Строгий смысл утверждения «$\sin x \приблизительно x$ для малых $x$» состоит в том, что $$\lim_{x \to 0}\frac{\sin x}{x} = 1\tag{ 1}$$ Таким образом, использование аппроксимации $\sin x \приблизительно x$ при оценке определенных пределов означает использование формулы предела $(1)$ в ваших вычислениях. $\sin x \приблизительно x$ не имеет никакого другого значения, кроме приведенной выше формулы предела, и не следует даже пытаться придавать ей какое-либо значение в том, что касается оценки пределов.
Таким образом, использование $\sin x \ приблизительно x$ в связанном вопросе ОП относительно ограничения $(1/x — 1/\sin x)$ также неверно (хотя по счастливой случайности оно дает правильный ответ).
Более того, принятый здесь ответ (от 2012rcampion) пытается распространить другую ошибку , заключающуюся в том, что приближение $\sin x \ приблизительно x$ недостаточно хорош для в текущем контексте, и, возможно, требуется лучшее приближение. {n} \to 0$ как $h \to 0$. Таким образом, использование разложений в ряд Тейлора типа $(2)$ при вычислении пределов означает использование уравнения $(3), (4)$ в 9{n})$, но тогда теоретическим обоснованием использования бесконечных рядов в предельных процессах является следующая теорема: по срокам
{n} \to 0$ как $h \to 0$. Таким образом, использование разложений в ряд Тейлора типа $(2)$ при вычислении пределов означает использование уравнения $(3), (4)$ в 9{n})$, но тогда теоретическим обоснованием использования бесконечных рядов в предельных процессах является следующая теорема: по срокам
исчисление — как строго доказать $\sin x
спросил
Изменено 3 года, 9 месяцев назад
Просмотрено 40 тысяч раз
$\begingroup$
$$\sin x
ps :
По дифференцированию, монотонности и формуле Тейлора все неверно, потому что $(\sin x)’=\cos x$ должен использовать $\lim_{x \to 0}\frac{ \sin x}{x}=1$, и в этой формуле необходимо использовать $\sin x< x$. Это порочный круг.
Если мы используем ряд Тейлора $\sin x$ для определения $\sin x$, строго доказать $\sin x
неравенство исчисления тригонометрии
$\endgroup$
9
$\begingroup$
Определить функцию $f(x)=x-\sin x.$ Заметим, что $f(0)=0$ и $f'(x)=1-\cos x \geq 0$. Производная равна $0$ только в изолированных точках, поэтому функция возрастает на интервале $[0, \infty)$.
То есть для всех $x>0$ имеем $f(x)>f(0)=0$.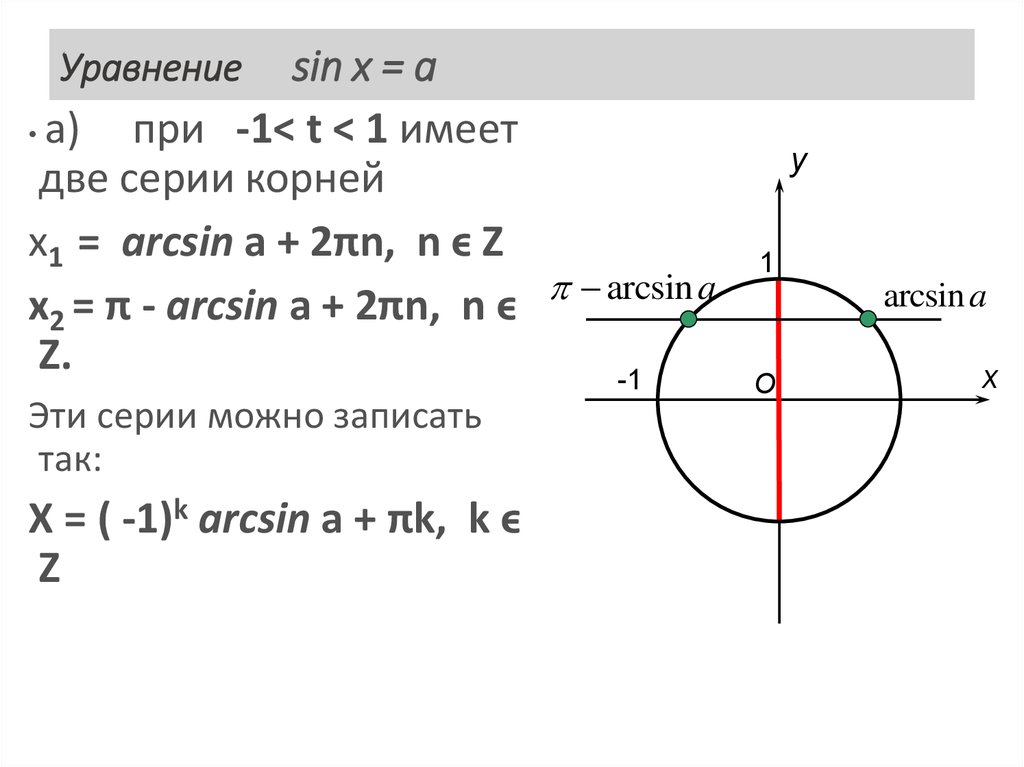 Таким образом, $x>\sin x$ для всех $x>0$.
Таким образом, $x>\sin x$ для всех $x>0$.
$\endgroup$
9{(-1)}(х)$. Ясно, что $f(x)$, заданное в $(1)$, монотонно возрастает при $0=f(0)\le f(x)\le f(1)=\pi/2$. Кроме того, из $(1)$ легко видеть, что $f(x)\ge x$ при $x\ge 0$ с $f(x)>x$ при $0 Поскольку $f$ монотонно возрастает на $(0,1)$, его обратный $\sin(x)$ монотонно возрастает с $0\le \sin(x)\le 1$ при $0\le х\ле\пи/2$. Более того, мы видим, что поскольку $f(x)>x$ при $0 , что завершает доказательство. И это доказательство не апеллировало ни к какому предварительному знанию функции синуса и даже не упоминало функцию косинуса! Вероятно, это самое простое и строгое доказательство. $\endgroup$ 1 $\begingroup$ «В большинстве учебников доказательство этого неравенства основано на геометрической иллюстрации (нарисуйте окружность, сравните длину дуги и хорду), но я думаю, что строгое доказательство должно быть основано на аналитических рассуждениях без геометрической иллюстрации. Традиционное представление круговых функций использует одно из двух вышеприведенных определений (определение площади проще в исполнении), но обычно обоснования длины и площади опускаются, поскольку они требуют понятия интеграла. $\endgroup$ 4 $\begingroup$ Предположим, что для некоторого достаточно малого $\epsilon$ имеем $\sin(\epsilon)\le\epsilon$. (Я вернусь к этому утверждению позже.) Теорема: Предполагая приведенное выше утверждение, мы имеем $\sin(a\epsilon)\le a\epsilon$ для всех $a\ge1$. Нам нужно доказать это только для $a\epsilon\le1$, потому что мы знаем, что $\sin 1\le1$ (поскольку $\sin$ всегда меньше 1). Будем действовать по индукции. Мы знаем (принимая вышеприведенное утверждение), что это верно для $a=1$. Теперь предположим, что это верно для $a$; нам нужно доказать это для $a+1$. Обратите внимание, что для $0 Перемножив их вместе, мы имеем:
$$\cos(a\epsilon)\sin(\epsilon)\le\epsilon$$
$$\sin(a\epsilon)\cos(\epsilon)\le a\epsilon$$
(Нам нужно было знать, что они положительны, потому что тогда мы знаем, что нам не нужно менять местами неравенство.) Складываем их вместе:
$$\cos(a\epsilon)\sin(\epsilon)+\sin(a\epsilon)\cos(\epsilon)\le(a+1)\epsilon$$
$$\sin((a+1)\epsilon)\le(a+1)\epsilon$$
где я использовал формулу суммы для синуса в последней строке. КЭД. Теперь здесь мне придется использовать некоторую схематичность. Вспомните, как в радианах $\sin\epsilon\приблизительно\epsilon$, когда $\epsilon$ мало. Таким образом, если мы допустим, что $\epsilon$ будет бесконечно малым числом (я сказал вам, что мне придется использовать некоторую схематичность), мы фактически получим $\sin\epsilon=\epsilon$. Теперь, поскольку $\epsilon$ бесконечно мало, каждое действительное число $x$ кратно ему. Итак, используя приведенную выше теорему, теперь мы имеем $\sin x\le x$ для всех положительных $x$. Если что-то в этом комментарии несвязно, прошу прощения — я очень устал. $\endgroup$ $\begingroup$ Мы можем определить $\sin x$ как степенной ряд. Применяя знание степенных рядов, получим производную от $\sin x$, и тогда мы легко докажем неравенство. Завершая геометрию $\sin x$, см. здесь. $\endgroup$ $\begingroup$
92) \приблизительно1.23$ Поскольку A1 < A2, мы можем сказать, что: $\sin x $\endgroup$ Примечание: Если вам нужен обзор тригонометрии, нажмите на тригонометрия. Пример 1: Найдите x в следующем уравнении. Существует бесконечное множество решений этой проблемы. Выделите синусоидальный член. Для этого перепишем левую часть уравнения в
эквивалентная факторизованная форма. Произведение двух множителей равно нулю, если хотя бы один из множителей равен
нули. Это означает, что если или же Мы просто превратили сложную задачу в две более простые. Найти
решения исходного уравнения, ,
находим решения уравнений а также Как мы изолируем x? Мы могли бы взять арксинус обеих сторон. Однако функция синуса не является однозначной функцией. Давайте ограничим домен, чтобы функция была взаимно однозначной на ограниченном
домен с сохранением исходного диапазона. График синусоидальной функции
один к одному на интервале Если мы ограничим область определения функции синуса этим интервалом, мы можем взять арксинус обеих частей каждого уравнения. Мы знаем это Следовательно,
если ,
тогда Завершим задачу, найдя второй множитель. С периода
равно ,
эти решения будут повторяться
каждый
единицы. Точные решения Приближенные значения этих решений равны Каждое решение можно проверить алгебраически, подставив каждое решение в
исходное уравнение. Если после подстановки левая часть
исходное уравнение равно правой части исходного уравнения,
решение в силе. Можно также проверить решения графически, построив график функции, образованной левой частью исходного уравнения, и график функции, образованной правой частью исходного уравнения. Координаты x точек пересечения являются решениями. Правая часть уравнения равна 0, а f ( x )=0 — это ось x. Так что на самом деле то, что вы ищете, это
x-пересекает функцию, образованную левой частью уравнения. Алгебраическая проверка: Проверить решение Левая сторона: Правая сторона: 0 Так как левая часть исходного уравнения равна правой части
исходное уравнение при замене -0,52359878 для x, тогда -0,52359878 — это решение. Проверить решение Левая сторона: Правая сторона: 0 Так как левая часть исходного уравнения равна правой части
исходное уравнение при замене 3,665191 вместо x, то 3,665191 — это решение. Проверить решение Левая сторона: Правая сторона: 0 Так как левая часть исходного уравнения равна правой части
исходное уравнение, когда вы заменяете x на 1,5707963, тогда 1,5707963 является решением. Мы только что убедились, что точные решения ,
а также являются решениями, и эти решения повторяются каждые
единицы. Приближенные значения этих решений равны и 1,5707963, и эти решения повторяются каждые единицы. Графическая проверка: Нарисуйте уравнение Обратите внимание, что график пересекает ось x много раз, что указывает на
решения. График пересекает ось x в точке -0,52359878. Так как период ,
вы можете убедиться, что график также пересекает ось x
снова в -0,52359878+6,2831853=5,7595865 и при ,
и т.п. График пересекает ось x в точке .
Так как период ,
график также снова пересекает ось x в точке текс2 html c комментарий m ковчег >
3,665191+6,2831853=9,9483763 и при ,
так далее.. График пересекает ось x в точке .
Так как период ,
график также снова пересекает ось x в точке tex2 html c комментарий m ark >
1,5707963+6,2831853=7,8539816 и при ,
и т.п. Примечание. Если задача состоит в том, чтобы найти решения в интервале ,
затем вы выбираете эти решения из множества бесконечных
решения, принадлежащие множеству ,
а также 5. Если вы хотите проверить себя, решив некоторые задачи, подобные этой
например, щелкните Проблема. Если вы хотите перейти к следующему разделу, нажмите далее. Если вы хотите вернуться к предыдущему разделу, нажмите предыдущий . Если вы хотите вернуться к оглавлению уравнения, нажмите на
Содержание. Домашняя страница S.O.S MATHematics Подход к К А Л К У Л У С Содержание | Дом 12 Производная sin x Производная от cos x Производное загара x Производная кроватки х Производная сек x Производная csc x ПРОИЗВОДНАЯ от sin x равна cos x . sin A − sin B = 2 cos ½( A + B ) sin ½( A − B ). (Тема 20 Тригонометрии.) Проблема 1. Используйте этот идентификатор, чтобы показать: Чтобы увидеть доказательство, наведите указатель мыши на цветную область. Прежде чем перейти к производной sin x , мы должны доказать лемму; которая является предварительной, вспомогательной теоремой, необходимой для доказательства основной теоремы. Задача 2. Показать, что тангенс θ, деленный на sin θ, равен . (См. Тему 20 Тригонометрии.) Лемма, которую мы должны доказать, обсуждается в теме 14 тригонометрии. (Взгляните на него.) Вот он: ЛЕММА.
Если θ измеряется в радианах, то Доказательство. Это невозможно доказать, применяя обычные теоремы о пределах (урок 2). Пусть O будет центром единичной окружности, то есть окружности радиусом 1; и пусть θ будет первым квадрантом центрального угла BOA , измеренным в радианах. Тогда, поскольку длина дуги s = r θ, а r = 1, дуга BA равна θ. (Тема 14 Тригонометрии.) Угол B’OA равен углу θ, что делает дугу AB’ равной дуге BA ; провести прямую линию BB’ , разрезав AO на P ; и проведите прямые линии BC, B’C , касающиеся окружности. Затем BB’ BAB’ BC + CB’ . Теперь в этом единичном круге BP = PB’ = sin θ, (Тема 17 Тригонометрии), , так что BB’ = 2 sin θ; Таким образом, приведенное выше продолжение неравенства принимает вид: 2 sin θ При делении каждого члена на 2 sin θ: (Задача 2.) И взяв обратные значения, таким образом изменив смысл: (Урок 11 алгебры, теорема 5.) При смене знаков смысл снова меняется: (Урок 11 алгебры, теорема 4), и если к каждому члену прибавить 1: Теперь, когда θ становится очень близким к 0 (θ 0), cos θ становится очень близким к 1; следовательно, 1 − cos θ становится очень близким к 0. Что мы и хотели доказать . Учащийся должен иметь в виду, что «приближение» переменной к 0 или любому пределу (определение 2.1) не означает, что переменная когда-либо равна этому пределу. Производная sin x Чтобы доказать это, мы применим определение производной (Урок 5). Сначала вычислим коэффициент разности. Теперь мы возьмем предел как ч 0. Мы установили формулу. Производная от cos x Чтобы установить это, мы будем использовать следующее удостоверение: Функция любого угла равна кофункции своего дополнения. (Тема 3 тригонометрии). Следовательно, при применении цепного правила: Мы установили формулу. Производное загара x  » 9{2} = 1$ является полностью строгим. Это также традиционный подход, используемый в учебниках по тригонометрии. Однако фундаментальным моментом в этом подходе является обоснование одного из следующих двух моментов и соответствующее определение круговых функций:
» 9{2} = 1$ является полностью строгим. Это также традиционный подход, используемый в учебниках по тригонометрии. Однако фундаментальным моментом в этом подходе является обоснование одного из следующих двух моментов и соответствующее определение круговых функций: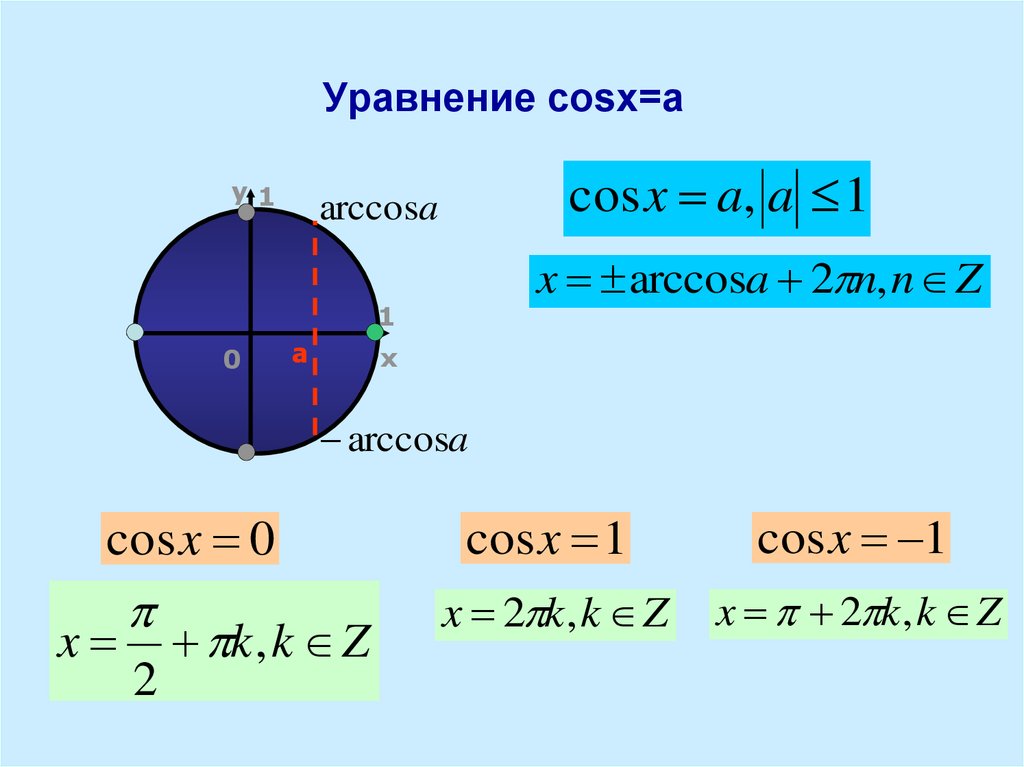 Более того, с помощью интегрального исчисления можно легко установить, что оба приведенных выше определения эквивалентны. Подробнее см. в моем блоге.
Более того, с помощью интегрального исчисления можно легко установить, что оба приведенных выше определения эквивалентны. Подробнее см. в моем блоге.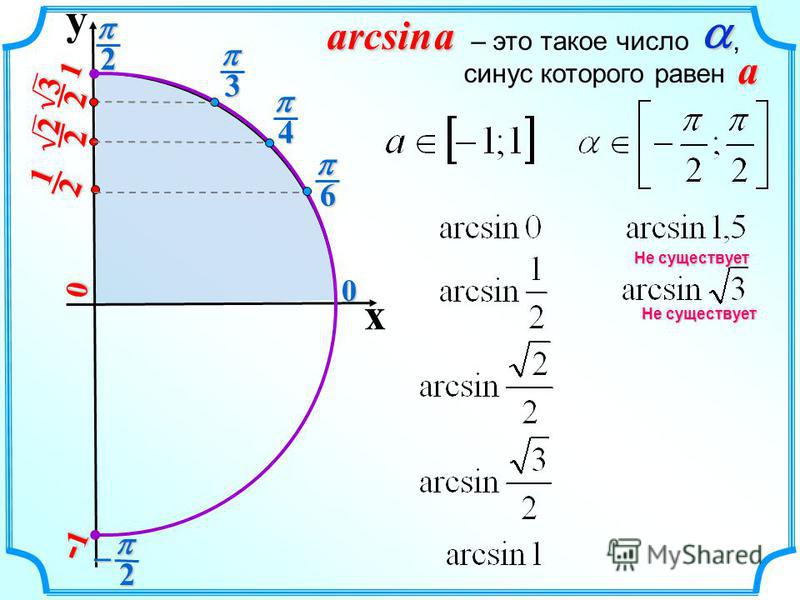 (Схематично) QED.
(Схематично) QED. Мэтуэй | Популярные проблемы
1 Найдите производную — d/dx натуральное бревно х 2 Оценить интеграл интеграл натурального логарифма x относительно x 92) 21 Оценить интеграл интеграл от 0 до 1 кубического корня из 1+7x относительно x 22 Найдите производную — d/dx грех(2x) 23 Найдите производную — d/dx 9(3x) по отношению к x 41 Оценить интеграл интеграл от cos(2x) по x 42 Найдите производную — d/dx 1/(корень квадратный из х) 43 Оцените интеграл 9бесконечность 45 Найдите производную — d/dx х/2 46 Найдите производную — d/dx -cos(x) 47 Найдите производную — d/dx грех(3x) 92+1 68 Оценить интеграл интеграл от sin(x) по x 69 Найдите производную — d/dx угловой синус(х) 70 Оценить предел предел, когда x приближается к 0 из (sin(x))/x 92 по отношению к х 85 Найдите производную — d/dx лог х 86 Найдите производную — d/dx арктан(х) 87 Найдите производную — d/dx бревно натуральное 5х92 РЕШЕНИЕ ТРИГОНОМЕТРИЧЕСКИХ УРАВНЕНИЙ
РЕШЕНИЕ ТРИГОНОМЕТРИЧЕСКИХ УРАВНЕНИЙ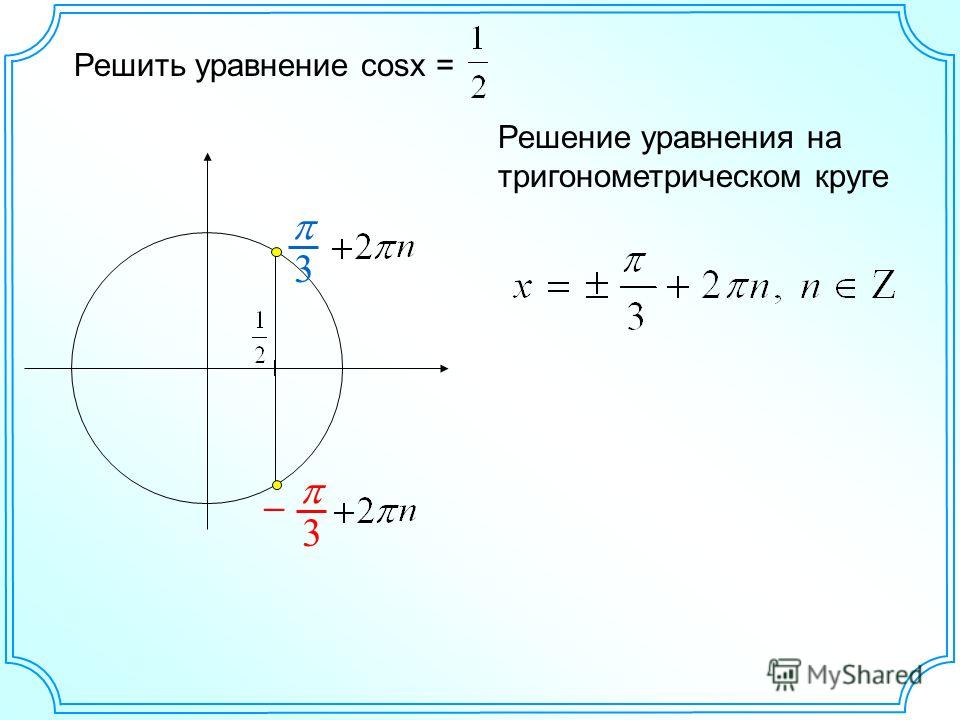
а также

где n — целое число.
где n — целое число.
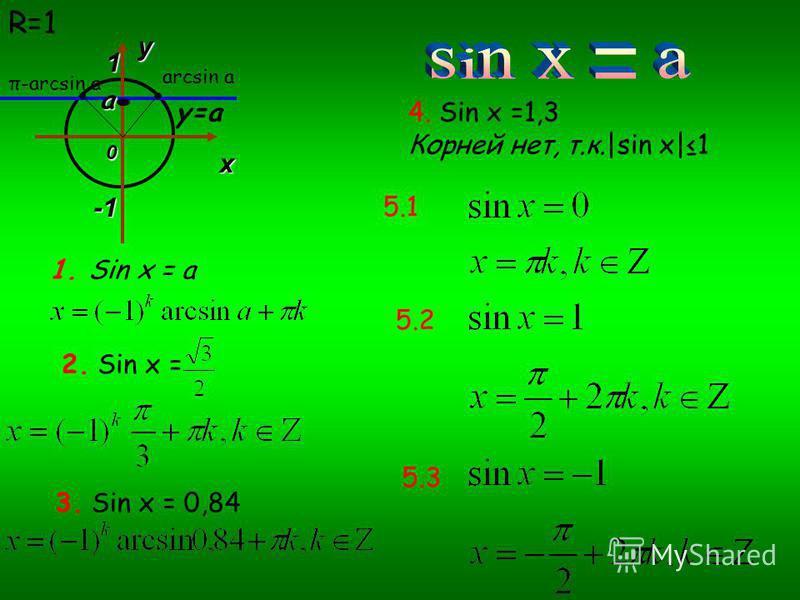
 7595865.
7595865.
Если вы хотите работать с другим примером, нажмите «Пример».
Свяжитесь с нами
Математика Медикс, ООО. — П.О. Box 12395 — Эль-Пасо, Техас 79913 — США
пользователей онлайн за последний час Производная sin x — Подход к исчислению
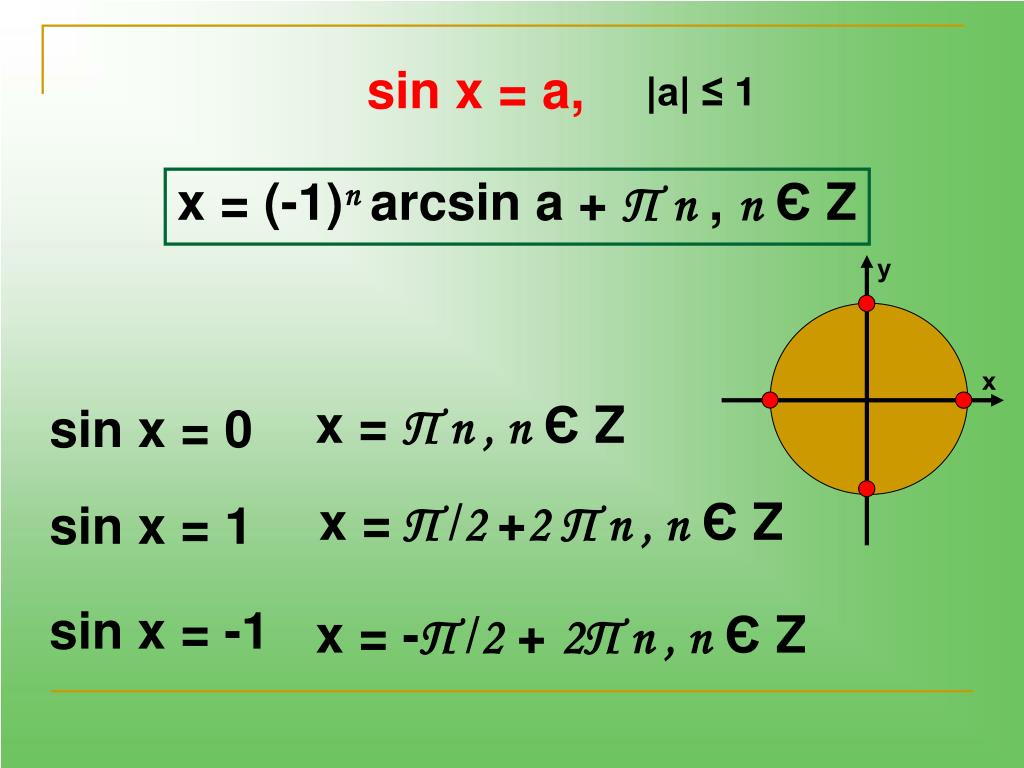 Чтобы доказать это, мы будем использовать следующее тождество:
Чтобы доказать это, мы будем использовать следующее тождество: sin ( x + ч ) − sin x =
Чтобы снова закрыть ответ, нажмите «Обновить» («Reload»).
Сначала решай задачу сам! грех ( x + ч ) — грех х = 2 cos ½( x + h + x ) sin ½( x + h − x ) = 2 cos ½(2 x + h ) sin ½ h =  Эта лемма требует следующего тождества:
Эта лемма требует следующего тождества: тангенс θ
sin θ = 1
cos θ . тангенс θ
sin θ = тан θ · 1
sin θ = sin θ
cos θ · 1
sin θ = 1
cos θ Мы должны обратиться к геометрии и к значениям sin θ и радианам.
Мы должны обратиться к геометрии и к значениям sin θ и радианам. и до н.э. = CB’ = тангенс θ. (Для tan θ = БК
ОБ = БК
1 = г. 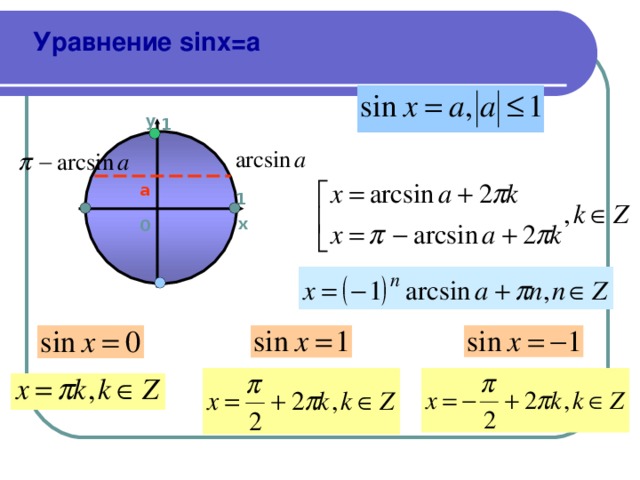 до н.э. г.)
до н.э. г.) 1 θ
sin θ 1
cos θ . 1 > sin θ
θ > cos θ. −1 sin θ
θ −cos θ, 0 1 − sin θ
θ 1 − cos θ.  Выражение в середине, равное меньше , чем 1 − cos θ, становится еще ближе к 0 (и слева ограничено 0), поэтому выражение в середине обязательно будет приближаться к 0. Это означает:
Выражение в середине, равное меньше , чем 1 − cos θ, становится еще ближе к 0 (и слева ограничено 0), поэтому выражение в середине обязательно будет приближаться к 0. Это означает: д
дх грех х = cos x = , Проблема 1, = , при делении числителя
и знаменателя на 2, =  Но предел произведения равен произведению пределов. (Урок 2.) Множитель справа имеет вид sin θ/θ. Поэтому согласно лемме при ч 0 его предел равен 1. Следовательно,
Но предел произведения равен произведению пределов. (Урок 2.) Множитель справа имеет вид sin θ/θ. Поэтому согласно лемме при ч 0 его предел равен 1. Следовательно, д
дх грех х = cos x . д
дх потому что х = −sin x потому что х = грех ( №
2 − x ). 
д
дх тан x = сек 2 x
| Теперь загар x = | sin x cos x | . | (Тема 20 тригонометрии.) |
Следовательно, согласно правилу частных:
| д дх | желтовато-коричневый x | = | г дх | sin x cos x | = | COS x · COS x — SIN x (-Син x ) COS 2 X 9292 | ||
| = | cos 2 x + sin 2 x cos 2 x | |||||||
| = | 1 cos 2 x | |||||||
| = | сек 2 x .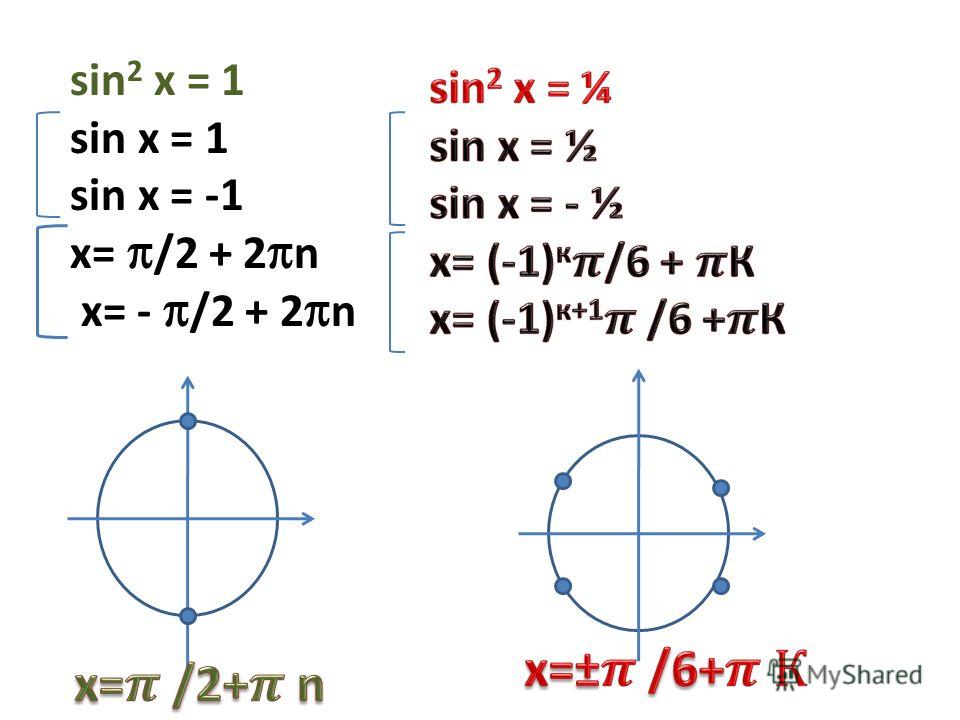 | |||||||
Мы установили формулу.
Задача 3. Производная от кроватки x . Докажите:
| д дх | детская кроватка x = −csc 2 x |
| д дх | детская кроватка x | = | г дх | cos x sin x | ||||
| = | sin x (-sin x ) — cos x · cos x sin 2 x | |||||||
| = | −(sin 2 x + cos 2 x ) sin 2 x | 2|||||||
| = | − | 1 sin 2 x | ||||||
| = | −csc 2 x .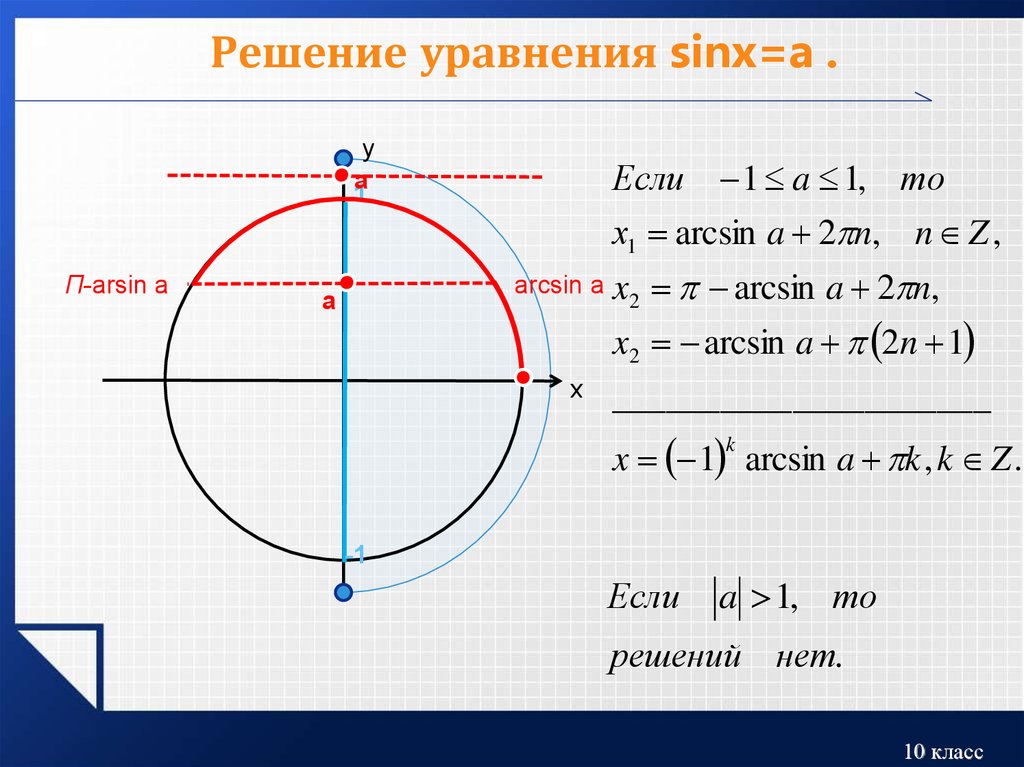 | |||||||
Производная сек x
| д дх | сек х | = сек x загар x |
| С сек x = | 1 потому что x | = | (поскольку х ) −1 | , |
затем при использовании цепного правила и общего правила мощности:
Мы установили формулу.
Задача 4. Производная от csc x . Докажите:
| д дх | csc x | = | −csc x детская кроватка x |
| д дх | csc x | = | г дх | 1 sin x | = | |||
| = | ||||||||
| = | ||||||||
| = | ||||||||
| = | ||||||||
Пример. Вычислить производную от sin x 2 .
Вычислить производную от sin x 2 .
Решение . При применении цепного правила
| д дх | грех топор 2 | = | cos топор 2 · | г дх | топор 2 | = | cos топор 2 · | 2 топор | = | 2 топор cos топор 2 . |
Задача 5. Вычислите эти производные.
| а) | д дх | sin 5 x | = | 5 cos 5 x |
| б) | г дх | ½ sin 2 x | = | грех x потому что x |
| в) | г дх | 2 cos 3 x | = | −6 sin 3 x |
| г) | г дх | x потому что x | = | cos x − x sin x |
| д) | г дх | sin 2 x cos x | = | 2 cos 2 x cos x − sin 2 x sin x |
| е) | г дх | желтовато-коричневый (3 x ) 2 | = | 18 x с 2 (3 x ) 2 |
| г) | д дх | 2 кроватки | x 2 | = | – КСК 2 | x 2 |
| з) | г дх | с 4 x | = | 4 с 4 x желтовато-коричневый 4 x |
| i) | г дх | csc bx | = | − ab csc bx детская кроватка bx |
| к) | = |
Задача 6.

 Если , то таких точек нет, если , то такая точка одна, если , то таких точек две.
Если , то таких точек нет, если , то такая точка одна, если , то таких точек две.
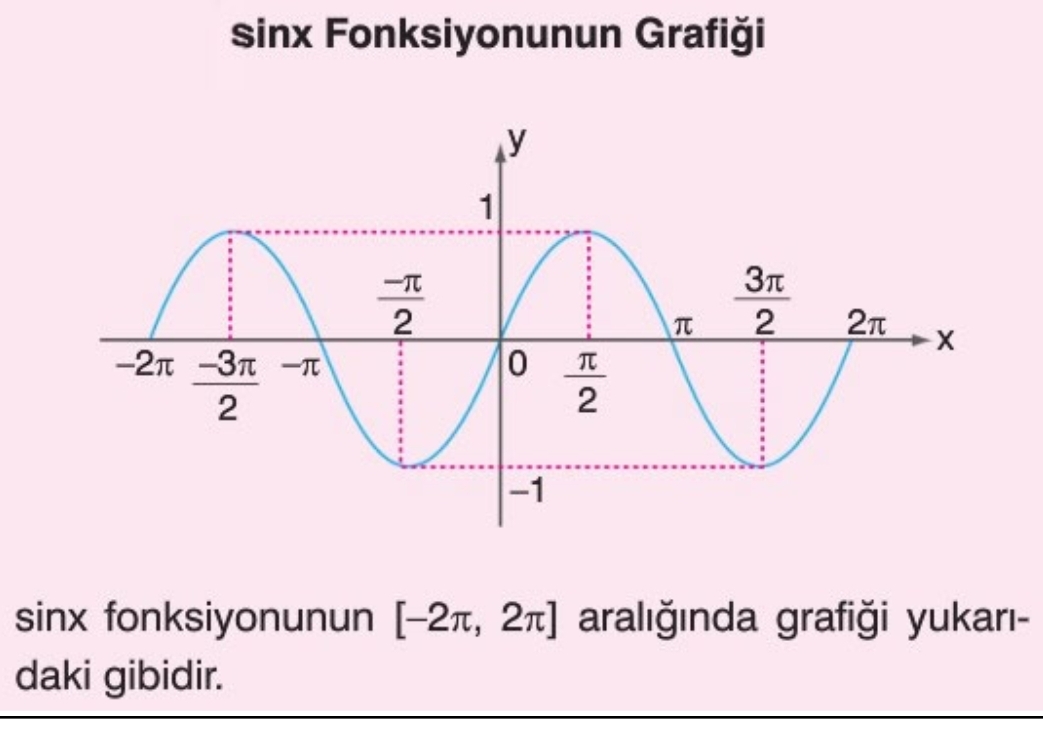
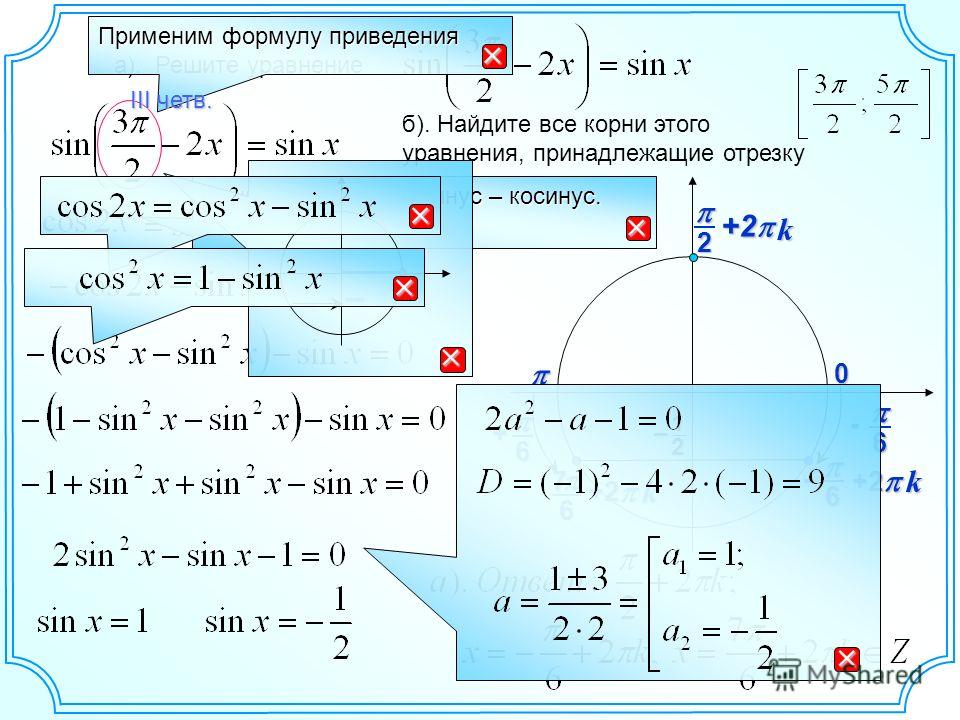
 В. и др. Математика: для поступающих в
вузы – М.: Дрофа, 2000.
В. и др. Математика: для поступающих в
вузы – М.: Дрофа, 2000.