Синус онлайн калькулятор
| 0 | ||||
| AC | +/- | ÷ | ||
| 7 | 8 | 9 | × | |
| 4 | 5 | 6 | — | |
| 1 | 2 | 3 | + | |
| 0 | 00 | , | = | |
Данный калькулятор вычислит синус, косинус, тангенс, котангенс, секанс, косеканс угла как в градусной, так и в радианной мере.
Введите число
синус (sin)косинус (cos)тангенс (tg)котангенс (ctg)секанс (sec)косеканс (cosec)градусырадианы
Что такое синус угла
Пусть задан прямоугольный треугольник ABC с острым углом α, тогда синусом угла α будет отношение противолежащего катета к гипотенузе sin α = BC/AC
Так же для определения синуса угла можно воспользоваться окружностью, построенной в декартовой системе координат, радиуса R и центром в начале координат O.
На окружности отметим точку P с координатами (1;0), теперь повернем луч OP на некоторый угол α. Направление против часовой стрелки считается положительным, по часовой стрелки – отрицательным.
Синусом угла α будет отношение ординаты точки YP к радиусу окружности.
sin α = YP/R, в случае, если окружность единичная (радиус окружности = 1), формула примет вид sin α = YP.
| Вам могут также быть полезны следующие сервисы |
| Калькуляторы (тригонометрия) |
| Калькулятор синуса угла |
| Калькулятор косинуса угла |
| Калькулятор тангенса угла |
| Калькулятор котангенса угла |
| Калькулятор секанса угла |
| Калькулятор косеканса угла |
| Калькулятор арксинуса угла |
| Калькулятор арккосинуса угла |
| Калькулятор арктангенса угла |
| Калькулятор арккотангенса угла |
| Калькулятор арксеканса угла |
| Калькулятор арккосеканса угла |
| Калькулятор нахождения наименьшего угла |
| Калькулятор определения вида угла |
| Калькулятор смежных углов |
| Калькуляторы площади геометрических фигур |
| Площадь квадрата |
| Площадь прямоугольника |
| КАЛЬКУЛЯТОРЫ ЗАДАЧ ПО ГЕОМЕТРИИ |
| Калькуляторы (Теория чисел) |
| Калькулятор выражений |
| Калькулятор упрощения выражений |
| Калькулятор со скобками |
| Калькулятор уравнений |
| Калькулятор суммы |
| Калькулятор пределов функций |
| Калькулятор разложения числа на простые множители |
| Калькулятор НОД и НОК |
| Калькулятор НОД и НОК по алгоритму Евклида |
| Калькулятор НОД и НОК для любого количества чисел |
| Калькулятор делителей числа |
| Представление многозначных чисел в виде суммы разрядных слагаемых |
| Калькулятор деления числа в данном отношении |
| Калькулятор процентов |
| Калькулятор перевода числа с Е в десятичное |
| Калькулятор экспоненциальной записи чисел |
| Калькулятор нахождения факториала числа |
| Калькулятор нахождения логарифма числа |
| Калькулятор квадратных уравнений |
| Калькулятор остатка от деления |
| Калькулятор корней с решением |
| Калькулятор нахождения периода десятичной дроби |
| Калькулятор больших чисел |
| Калькулятор округления числа |
| Калькулятор свойств корней и степеней |
| Калькулятор комплексных чисел |
| Калькулятор среднего арифметического |
| Калькулятор арифметической прогрессии |
| Калькулятор геометрической прогрессии |
| Калькулятор модуля числа |
| Калькулятор абсолютной погрешности приближения |
| Калькулятор абсолютной погрешности |
| Калькулятор относительной погрешности |
| Дроби |
| Калькулятор интервальных повторений |
| Учим дроби наглядно |
| Калькулятор сокращения дробей |
| Калькулятор преобразования неправильной дроби в смешанную |
| Калькулятор преобразования смешанной дроби в неправильную |
| Калькулятор сложения, вычитания, умножения и деления дробей |
| Калькулятор возведения дроби в степень |
| Калькулятор перевода десятичной дроби в обыкновенную |
| Калькулятор перевода обыкновенной дроби в десятичную |
| Калькулятор сравнения дробей |
| Калькулятор приведения дробей к общему знаменателю |
| Калькуляторы систем счисления |
| Калькулятор перевода чисел из арабских в римские и из римских в арабские |
| Калькулятор перевода чисел в различные системы счисления |
| Калькулятор сложения, вычитания, умножения и деления двоичных чисел |
| Системы счисления теория |
| N2 | Двоичная система счисления |
| N3 | Троичная система счисления |
| N4 | Четырехичная система счисления |
| N5 | Пятеричная система счисления |
| N6 | Шестеричная система счисления |
| N7 | Семеричная система счисления |
| N8 | Восьмеричная система счисления |
| N9 | Девятеричная система счисления |
| N11 | Одиннадцатиричная система счисления |
| N12 | Двенадцатеричная система счисления |
| N13 | Тринадцатеричная система счисления |
| N14 | Четырнадцатеричная система счисления |
| N15 | Пятнадцатеричная система счисления |
| N16 | Шестнадцатеричная система счисления |
| N17 | Семнадцатеричная система счисления |
| N18 | Восемнадцатеричная система счисления |
| N19 | Девятнадцатеричная система счисления |
| N20 | Двадцатеричная система счисления |
| N21 |
| N22 | Двадцатидвухричная система счисления |
| N23 | Двадцатитрехричная система счисления |
| N24 | Двадцатичетырехричная система счисления |
| N25 | Двадцатипятеричная система счисления |
| N26 | Двадцатишестеричная система счисления |
| N27 | Двадцатисемеричная система счисления |
| N28 | Двадцативосьмеричная система счисления |
| N29 | Двадцатидевятиричная система счисления |
| N30 | Тридцатиричная система счисления |
| N31 | Тридцатиодноричная система счисления |
| N32 | Тридцатидвухричная система счисления |
| N33 | Тридцатитрехричная система счисления |
| N34 | Тридцатичетырехричная система счисления |
| N 35 | Тридцатипятиричная система счисления |
| N36 | Тридцатишестиричная система счисления |
| Калькуляторы (Комбинаторика) |
| Калькулятор нахождения числа перестановок из n элементов |
| Калькулятор нахождения числа сочетаний из n элементов |
| Калькулятор нахождения числа размещений из n элементов |
| Калькуляторы линейная алгебра и аналитическая геометрия |
| Калькулятор сложения и вычитания матриц |
| Калькулятор умножения матриц |
| Калькулятор транспонирование матрицы |
| Калькулятор нахождения определителя (детерминанта) матрицы |
| Калькулятор нахождения обратной матрицы |
Длина отрезка. Онлайн калькулятор расстояния между точками |
| Онлайн калькулятор нахождения координат вектора по двум точкам |
| Калькулятор нахождения модуля (длины) вектора |
| Калькулятор сложения и вычитания векторов |
| Калькулятор скалярного произведения векторов через длину и косинус угла между векторами |
| Калькулятор скалярного произведения векторов через координаты |
| Калькулятор векторного произведения векторов через координаты |
| Калькулятор смешанного произведения векторов |
| Калькулятор умножения вектора на число |
| Калькулятор нахождения угла между векторами |
| Калькулятор проверки коллинеарности векторов |
| Калькулятор проверки компланарности векторов |
| Генератор Pdf с примерами |
| Тренажёры решения примеров |
| Тренажёр таблицы умножения |
| Тренажер счета для дошкольников |
| Тренажер счета на внимательность для дошкольников |
Тренажер решения примеров на сложение, вычитание, умножение, деление. Найди правильный ответ. |
| Тренажер решения примеров с разными действиями |
| Тренажёры решения столбиком |
| Тренажёр сложения столбиком |
| Тренажёр вычитания столбиком |
| Тренажёр умножения столбиком |
| Тренажёр деления столбиком с остатком |
| Калькуляторы решения столбиком |
| Калькулятор сложения, вычитания, умножения и деления столбиком |
| Калькулятор деления столбиком с остатком |
| Конвертеры величин |
| Конвертер единиц длины |
| Конвертер единиц скорости |
| Конвертер единиц ускорения |
| Цифры в текст |
| Калькуляторы (физика) |
Механика |
| Калькулятор вычисления скорости, времени и расстояния |
| Калькулятор вычисления ускорения, скорости и перемещения |
| Калькулятор вычисления времени движения |
| Калькулятор времени |
Второй закон Ньютона. Калькулятор вычисления силы, массы и ускорения. |
| Закон всемирного тяготения. Калькулятор вычисления силы притяжения, массы и расстояния. |
| Импульс тела. Калькулятор вычисления импульса, массы и скорости |
| Импульс силы. Калькулятор вычисления импульса, силы и времени действия силы. |
| Вес тела. Калькулятор вычисления веса тела, массы и ускорения свободного падения |
Оптика |
| Калькулятор отражения и преломления света |
Электричество и магнетизм |
| Калькулятор Закона Ома |
| Калькулятор Закона Кулона |
| Калькулятор напряженности E электрического поля |
| Калькулятор нахождения точечного электрического заряда Q |
| Калькулятор нахождения силы F действующей на заряд q |
| Калькулятор вычисления расстояния r от заряда q |
| Калькулятор вычисления потенциальной энергии W заряда q |
| Калькулятор вычисления потенциала φ электростатического поля |
| Калькулятор вычисления электроемкости C проводника и сферы |
Конденсаторы |
| Калькулятор вычисления электроемкости C плоского, цилиндрического и сферического конденсаторов |
| Калькулятор вычисления напряженности E электрического поля плоского, цилиндрического и сферического конденсаторов |
| Калькулятор вычисления напряжения U (разности потенциалов) плоского, цилиндрического и сферического конденсаторов |
| Калькулятор вычисления расстояния d между пластинами в плоском конденсаторе |
| Калькулятор вычисления площади пластины (обкладки) S в плоском конденсаторе |
| Калькулятор вычисления энергии W заряженного конденсатора |
Калькулятор вычисления энергии W заряженного конденсатора. Для плоского, цилиндрического и сферического конденсаторов |
| Калькулятор вычисления объемной плотности энергии w электрического поля для плоского, цилиндрического и сферического конденсаторов |
| Калькуляторы по астрономии |
| Вес тела на других планетах |
| Ускорение свободного падения на планетах Солнечной системы и их спутниках |
| Генераторы |
| Генератор примеров по математике |
| Генератор случайных чисел |
| Генератор паролей |
Синус угла – калькулятор онлайн, таблица синусов
Количество комментариев: 0
| sin(0) = 0 | sin(120) = 0.8660254038 | sin(240) = -0.8660254038 |
| sin(1) = 0.01745240644 | sin(121) = 0.8571673007 | sin(241) = -0.8746197071 |
| sin(2) = 0.0348994967 | sin(122) = 0.8480480962 | sin(242) = -0.8829475929 |
| sin(3) = 0.05233595624 | sin(123) = 0. 8386705679 | sin(243) = -0.8910065242 |
| sin(4) = 0.06975647374 | sin(124) = 0.8290375726 | sin(244) = -0.8987940463 |
| sin(5) = 0.08715574275 | sin(125) = 0.8191520443 | sin(245) = -0.906307787 |
| sin(6) = 0.1045284633 | sin(126) = 0.8090169944 | sin(246) = -0.9135454576 |
| sin(7) = 0.1218693434 | sin(127) = 0.79863551 | sin(247) = -0.9205048535 |
| sin(8) = 0.139173101 | sin(128) = 0.7880107536 | sin(248) = -0.9271838546 |
| sin(9) = 0.156434465 | sin(129) = 0.7771459615 | sin(249) = -0.9335804265 |
| sin(10) = 0.1736481777 | sin(130) = 0.7660444431 | sin(250) = -0.9396926208 |
| sin(11) = 0.1908089954 | sin(131) = 0.7547095802 | sin(251) = -0.9455185756 |
| sin(12) = 0.2079116908 | sin(132) = 0.7431448255 | sin(252) = -0.9510565163 |
sin(13) = 0. 2249510543 | sin(133) = 0.7313537016 | sin(253) = -0.956304756 |
| sin(14) = 0.2419218956 | sin(134) = 0.7193398003 | sin(254) = -0.9612616959 |
| sin(15) = 0.2588190451 | sin(135) = 0.7071067812 | sin(255) = -0.9659258263 |
| sin(16) = 0.2756373558 | sin(136) = 0.6946583705 | sin(256) = -0.9702957263 |
| sin(17) = 0.2923717047 | sin(137) = 0.6819983601 | sin(257) = -0.9743700648 |
| sin(18) = 0.3090169944 | sin(138) = 0.6691306064 | sin(258) = -0.9781476007 |
| sin(19) = 0.3255681545 | sin(139) = 0.656059029 | sin(259) = -0.9816271834 |
| sin(20) = 0.3420201433 | sin(140) = 0.6427876097 | sin(260) = -0.984807753 |
| sin(21) = 0.3583679495 | sin(141) = 0.629320391 | sin(261) = -0.9876883406 |
| sin(22) = 0.3746065934 | sin(142) = 0.6156614753 | sin(262) = -0. 9902680687 |
| sin(23) = 0.3907311285 | sin(143) = 0.6018150232 | sin(263) = -0.9925461516 |
| sin(24) = 0.4067366431 | sin(144) = 0.5877852523 | sin(264) = -0.9945218954 |
| sin(25) = 0.4226182617 | sin(145) = 0.5735764364 | sin(265) = -0.9961946981 |
| sin(26) = 0.4383711468 | sin(146) = 0.5591929035 | sin(266) = -0.9975640503 |
| sin(27) = 0.4539904997 | sin(147) = 0.544639035 | sin(267) = -0.9986295348 |
| sin(28) = 0.4694715628 | sin(148) = 0.5299192642 | sin(268) = -0.999390827 |
| sin(29) = 0.4848096202 | sin(149) = 0.5150380749 | sin(269) = -0.9998476952 |
| sin(30) = 0.5 | sin(150) = 0.5 | sin(270) = -1 |
| sin(31) = 0.5150380749 | sin(151) = 0.4848096202 | sin(271) = -0.9998476952 |
| sin(32) = 0.5299192642 | sin(152) = 0.4694715628 | sin(272) = -0. 999390827 |
| sin(33) = 0.544639035 | sin(153) = 0.4539904997 | sin(273) = -0.9986295348 |
| sin(34) = 0.5591929035 | sin(154) = 0.4383711468 | sin(274) = -0.9975640503 |
| sin(35) = 0.5735764364 | sin(155) = 0.4226182617 | sin(275) = -0.9961946981 |
| sin(36) = 0.5877852523 | sin(156) = 0.4067366431 | sin(276) = -0.9945218954 |
| sin(37) = 0.6018150232 | sin(157) = 0.3907311285 | sin(277) = -0.9925461516 |
| sin(38) = 0.6156614753 | sin(158) = 0.3746065934 | sin(278) = -0.9902680687 |
| sin(39) = 0.629320391 | sin(159) = 0.3583679495 | sin(279) = -0.9876883406 |
| sin(40) = 0.6427876097 | sin(160) = 0.3420201433 | sin(280) = -0.984807753 |
| sin(41) = 0.656059029 | sin(161) = 0.3255681545 | sin(281) = -0.9816271834 |
| sin(42) = 0.6691306064 | sin(162) = 0. 3090169944 | sin(282) = -0.9781476007 |
| sin(43) = 0.6819983601 | sin(163) = 0.2923717047 | sin(283) = -0.9743700648 |
| sin(44) = 0.6946583705 | sin(164) = 0.2756373558 | sin(284) = -0.9702957263 |
| sin(45) = 0.7071067812 | sin(165) = 0.2588190451 | sin(285) = -0.9659258263 |
| sin(46) = 0.7193398003 | sin(166) = 0.2419218956 | sin(286) = -0.9612616959 |
| sin(47) = 0.7313537016 | sin(167) = 0.2249510543 | sin(287) = -0.956304756 |
| sin(48) = 0.7431448255 | sin(168) = 0.2079116908 | sin(288) = -0.9510565163 |
| sin(49) = 0.7547095802 | sin(169) = 0.1908089954 | sin(289) = -0.9455185756 |
| sin(50) = 0.7660444431 | sin(170) = 0.1736481777 | sin(290) = -0.9396926208 |
| sin(51) = 0.7771459615 | sin(171) = 0.156434465 | sin(291) = -0.9335804265 |
sin(52) = 0. 7880107536 | sin(172) = 0.139173101 | sin(292) = -0.9271838546 |
| sin(53) = 0.79863551 | sin(173) = 0.1218693434 | sin(293) = -0.9205048535 |
| sin(54) = 0.8090169944 | sin(174) = 0.1045284633 | sin(294) = -0.9135454576 |
| sin(55) = 0.8191520443 | sin(175) = 0.08715574275 | sin(295) = -0.906307787 |
| sin(56) = 0.8290375726 | sin(176) = 0.06975647374 | sin(296) = -0.8987940463 |
| sin(57) = 0.8386705679 | sin(177) = 0.05233595624 | sin(297) = -0.8910065242 |
| sin(58) = 0.8480480962 | sin(178) = 0.0348994967 | sin(298) = -0.8829475929 |
| sin(59) = 0.8571673007 | sin(179) = 0.01745240644 | sin(299) = -0.8746197071 |
| sin(60) = 0.8660254038 | sin(180) = 0 | sin(300) = -0.8660254038 |
| sin(61) = 0.8746197071 | sin(181) = -0.01745240644 | sin(301) = -0. 8571673007 |
| sin(62) = 0.8829475929 | sin(182) = -0.0348994967 | sin(302) = -0.8480480962 |
| sin(63) = 0.8910065242 | sin(183) = -0.05233595624 | sin(303) = -0.8386705679 |
| sin(64) = 0.8987940463 | sin(184) = -0.06975647374 | sin(304) = -0.8290375726 |
| sin(65) = 0.906307787 | sin(185) = -0.08715574275 | sin(305) = -0.8191520443 |
| sin(66) = 0.9135454576 | sin(186) = -0.1045284633 | sin(306) = -0.8090169944 |
| sin(67) = 0.9205048535 | sin(187) = -0.1218693434 | sin(307) = -0.79863551 |
| sin(68) = 0.9271838546 | sin(188) = -0.139173101 | sin(308) = -0.7880107536 |
| sin(69) = 0.9335804265 | sin(189) = -0.156434465 | sin(309) = -0.7771459615 |
| sin(70) = 0.9396926208 | sin(190) = -0.1736481777 | sin(310) = -0.7660444431 |
| sin(71) = 0.9455185756 | sin(191) = -0. 1908089954 | sin(311) = -0.7547095802 |
| sin(72) = 0.9510565163 | sin(192) = -0.2079116908 | sin(312) = -0.7431448255 |
| sin(73) = 0.956304756 | sin(193) = -0.2249510543 | sin(313) = -0.7313537016 |
| sin(74) = 0.9612616959 | sin(194) = -0.2419218956 | sin(314) = -0.7193398003 |
| sin(75) = 0.9659258263 | sin(195) = -0.2588190451 | sin(315) = -0.7071067812 |
| sin(76) = 0.9702957263 | sin(196) = -0.2756373558 | sin(316) = -0.6946583705 |
| sin(77) = 0.9743700648 | sin(197) = -0.2923717047 | sin(317) = -0.6819983601 |
| sin(78) = 0.9781476007 | sin(198) = -0.3090169944 | sin(318) = -0.6691306064 |
| sin(79) = 0.9816271834 | sin(199) = -0.3255681545 | sin(319) = -0.656059029 |
| sin(80) = 0.984807753 | sin(200) = -0.3420201433 | sin(320) = -0.6427876097 |
sin(81) = 0. 9876883406 | sin(201) = -0.3583679495 | sin(321) = -0.629320391 |
| sin(82) = 0.9902680687 | sin(202) = -0.3746065934 | sin(322) = -0.6156614753 |
| sin(83) = 0.9925461516 | sin(203) = -0.3907311285 | sin(323) = -0.6018150232 |
| sin(84) = 0.9945218954 | sin(204) = -0.4067366431 | sin(324) = -0.5877852523 |
| sin(85) = 0.9961946981 | sin(205) = -0.4226182617 | sin(325) = -0.5735764364 |
| sin(86) = 0.9975640503 | sin(206) = -0.4383711468 | sin(326) = -0.5591929035 |
| sin(87) = 0.9986295348 | sin(207) = -0.4539904997 | sin(327) = -0.544639035 |
| sin(88) = 0.999390827 | sin(208) = -0.4694715628 | sin(328) = -0.5299192642 |
| sin(89) = 0.9998476952 | sin(209) = -0.4848096202 | sin(329) = -0.5150380749 |
| sin(90) = 1 | sin(210) = -0.5 | sin(330) = -0.5 |
sin(91) = 0. 9998476952 | sin(211) = -0.5150380749 | sin(331) = -0.4848096202 |
| sin(92) = 0.999390827 | sin(212) = -0.5299192642 | sin(332) = -0.4694715628 |
| sin(93) = 0.9986295348 | sin(213) = -0.544639035 | sin(333) = -0.4539904997 |
| sin(94) = 0.9975640503 | sin(214) = -0.5591929035 | sin(334) = -0.4383711468 |
| sin(95) = 0.9961946981 | sin(215) = -0.5735764364 | sin(335) = -0.4226182617 |
| sin(96) = 0.9945218954 | sin(216) = -0.5877852523 | sin(336) = -0.4067366431 |
| sin(97) = 0.9925461516 | sin(217) = -0.6018150232 | sin(337) = -0.3907311285 |
| sin(98) = 0.9902680687 | sin(218) = -0.6156614753 | sin(338) = -0.3746065934 |
| sin(99) = 0.9876883406 | sin(219) = -0.629320391 | sin(339) = -0.3583679495 |
| sin(100) = 0.984807753 | sin(220) = -0.6427876097 | sin(340) = -0. 3420201433 |
| sin(101) = 0.9816271834 | sin(221) = -0.656059029 | sin(341) = -0.3255681545 |
| sin(102) = 0.9781476007 | sin(222) = -0.6691306064 | sin(342) = -0.3090169944 |
| sin(103) = 0.9743700648 | sin(223) = -0.6819983601 | sin(343) = -0.2923717047 |
| sin(104) = 0.9702957263 | sin(224) = -0.6946583705 | sin(344) = -0.2756373558 |
| sin(105) = 0.9659258263 | sin(225) = -0.7071067812 | sin(345) = -0.2588190451 |
| sin(106) = 0.9612616959 | sin(226) = -0.7193398003 | sin(346) = -0.2419218956 |
| sin(107) = 0.956304756 | sin(227) = -0.7313537016 | sin(347) = -0.2249510543 |
| sin(108) = 0.9510565163 | sin(228) = -0.7431448255 | sin(348) = -0.2079116908 |
| sin(109) = 0.9455185756 | sin(229) = -0.7547095802 | sin(349) = -0.1908089954 |
sin(110) = 0. 9396926208 | sin(230) = -0.7660444431 | sin(350) = -0.1736481777 |
| sin(111) = 0.9335804265 | sin(231) = -0.7771459615 | sin(351) = -0.156434465 |
| sin(112) = 0.9271838546 | sin(232) = -0.7880107536 | sin(352) = -0.139173101 |
| sin(113) = 0.9205048535 | sin(233) = -0.79863551 | sin(353) = -0.1218693434 |
| sin(114) = 0.9135454576 | sin(234) = -0.8090169944 | sin(354) = -0.1045284633 |
| sin(115) = 0.906307787 | sin(235) = -0.8191520443 | sin(355) = -0.08715574275 |
| sin(116) = 0.8987940463 | sin(236) = -0.8290375726 | sin(356) = -0.06975647374 |
| sin(117) = 0.8910065242 | sin(237) = -0.8386705679 | sin(357) = -0.05233595624 |
| sin(118) = 0.8829475929 | sin(238) = -0.8480480962 | sin(358) = -0.0348994967 |
| sin(119) = 0.8746197071 | sin(239) = -0.8571673007 | sin(359) = -0. 01745240644 |
А = угол А
B = угол B
С = угол С
а = сторона а
б = сторона б
с = сторона с
P = периметр
с = полупериметр
К = площадь
r = радиус вписанной окружности
R = радиус описанной окружности
*Единицы длины приведены только для справки, поскольку значения результирующих длин всегда будут одинаковыми, независимо от единиц измерения.
Калькулятор Использование
Использует закон синусов для вычисления неизвестных углов или сторон треугольника. Для расчета неизвестных значений необходимо ввести 3 известных значения.
Некоторые варианты расчета являются избыточными, но все равно включены для точных буквенных обозначений.
Методы расчета
Чтобы вычислить любой угол, A, B или C, скажем, B, введите противоположную сторону b, а затем другую пару угол-сторона, такую как A и a или C и c. Выполненные расчеты следуют метод бокового угла (SSA) и использовать закон синусов только для завершения вычислений для других неизвестных.
Чтобы вычислить любую сторону, a, b или c, скажем, b, введите противоположный угол B, а затем другую пару углов-сторон, например A и a или C и c. Выполненные расчеты следуют угол угол сторона (AAS) и использовать закон синусов только для завершения расчетов для других неизвестных. 9{-1} \left[ \dfrac{c \sin B}{b} \right] \)
Решение уравнений закона синусов для сторон a, b и c
\( a = \dfrac{b \ sin A}{\sin B} \)
\( a = \dfrac{c \sin A}{\sin C} \)
\( b = \dfrac{a \sin B}{\sin A} \)
\( b = \dfrac{c \sin B}{\sin C} \)
\( c = \dfrac{a \sin C}{\sin A} \)
\( c = \dfrac{b \sin C}{\sin B} \)
Характеристики треугольника
Периметр треугольника, P = a + b + c
Полупериметр треугольника, s = 0,5 * (a + b + c)
Площадь треугольника, K = √[ s*(s-a)*(s-b)*(s-c)]
Радиус вписанной окружности в треугольник, r = √[ (s-a)*(s-b)*(s-c) / s ]
Радиус описанной окружности вокруг треугольника, R = (abc) / (4K)
Ссылки/ дополнительная литература
Вайсштейн, Эрик В.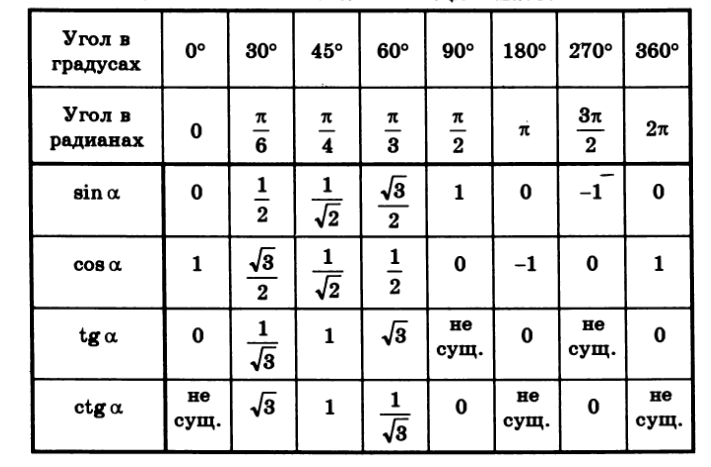
2)*2
Он имеет множество функций, которые вы можете ввести (см. ниже)
числа/изображения/decimal.js, числа/изображения/calc.js
Примеры
- Введите 12+2*3 (=18)
- Выберите «градусы», введите cos(45) (=0,7071067811865476)
- Введите 2/кв.(2) (=1,414213562373095)
Ссылка на функцию
Функция вернет NaN (не число), если вы дадите ей неверные записи, такие как sqrt(−1) 9 Оператор степени/экспоненты/индекса () Скобки
Функции
| кв | Квадратный корень из значения или выражения. | |
|---|---|---|
| грех | синус значения или выражения | |
| потому что | косинус значения или выражения | |
| желтовато-коричневый | тангенс значения или выражения | |
| как | арксинус (арксинус) значения или выражения | |
| акос | арккосинус (arccos) значения или выражения | |
| атан | арктангенс (арктангенс) значения или выражения | |
| синх | Гиперболический арксинус (арксинус) значения или выражения | |
| кош | Гиперболический арккосинус (arccos) значения или выражения | |
| танх | Гиперболический арктангенс (арктангенс) значения или выражения | |
| эксп | e (константа Эйлера), возведенная в степень значения или выражения | |
| п | Натуральный логарифм значения или выражения | |
| журнал | Логарифм по основанию 10 значения или выражения | |
| абс | Абсолютное значение (расстояние от нуля) значения или выражения | |
| град | преобразовать радианы в градусы | |
| рад | перевести градусы в радианы | |
| знак | −1 для значений меньше 0, иначе 1 | |
| круглый | округлить до ближайшего целого числа | |
| этаж | Возвращает наибольшее (ближайшее к положительной бесконечности) значение, которое не больше аргумента и равно математическому целому числу. |