Синус малого угла: Синус малого угла можно приближенно заменить значением самого угла. В результате получим, что

Синус малого угла можно приближенно заменить значением самого угла. В результате получим, что

Откуда

sin= 0,0035 sin cos= 0,0018 sin 2.

(11)

Таким образом, угол изменяется в пределах от нуля (на экваторе, где =0, и на полюсах, где =90°) до 0,0018 рад или 6′ (на ши­роте 45°).

Направление силы Р совпадает с направлением нити, натянутой грузом; которое называется направлением отвеса или вертикаль­ным направлением. Сила Fнаправлена к центру Земли. Следова­тельно, вертикаль направлена к центру Земли только на полюсах и на экваторе, отклоняясь на промежуточных широтах на угол , определяемый выражением (11).

Разность F- Р равна нулю на полюсах и достигает максимума, равного 0,3% силы F, на экваторе. Из-за сплюснутости Земли у полюсов сила Fсама по себе несколько варьирует с широтой, будучи на экваторе примерно на 0,2% меньше, чем у полюсов. В итоге ускорение свободного падения изменяется с широтой в пре­делах от 9,780 м/с² на экваторе до 9,832м/с

2 на полюсах. Значение g =9,80665 м/с² принято в качестве нормального (стандартного) значения.

 

Заметим, что относительно инерциальной, например, гелиоцен­трической» системы отсчета свободно падающее тело движется с ус­корением(а не g). Из рис. 5 видно, что из равенства для разных тел ускорения g вытекает и равенство ускорений w. Действительно, треугольники, построенные на векторах F_g и Р для разных тел, подобны (углы а и > для всех тел в данной точке земной поверхности одинаковы). Следовательно, отношение Fg/P, которое совпадает с отношением ig, для всех тел одно и то же, от­куда вытекает, что при одинаковых g получаются одинаковыми

и .

При движении тела относительно вращающейся системы отсчета, кроме центробежной силы инерции, появляется еще одна сила, на­зываемая силой Кориолис а или кориолисовой силой инерции.

Рис.6(а,б)

Появление кориолисовой силы можно обнаружить на следую­щем примере. Возьмем горизонтально расположенный диск, кото­рый может вращаться вокруг вертикальной оси. Прочертим на ди­ске радиальную прямую ОА (рис. 6,а ). Запустим в направлении от О к А шарик со скоростью v’. Если диск не вращается, шарик будет ка­титься вдоль прочерченной нами пря­мой. Если же диск привести во вра­щение в направлении, указанном стрелкой, то шарик будет катиться по изображенной пунктиром кривой ОВ, причем его скорость относительно диска v’ будет изменять свое направ­ление. Следовательно, по отношению к вращающейся системе отсчета ша­рик ведет себя так, как если бы на него действовала сила F_K, перпендикулярная к скорости v’

Чтобы заставить шарик катиться по вращающемуся диску вдоль радиальной прямой, нужно сделать направляющую, например, в виде ребра

О А (рис. 6,б). При качении шарика направляющее ребро действует на него с некоторой силой F_r. Относительно вра­щающейся системы (диска) шарик движется с постоянной по на­правлению скоростью. Это можно формально объяснить тем, что сила F_r уравновешивается приложенной к шарику силой инерции F_K, перпендикулярной к скорости v’. Сила F_K и есть кориолисова сила инерции.

Найдем сначала выражение силы Кориолиса для частного слу­чая, когда частица т движется относительно вращающейся системы отсчета равномерно по окружности,

Рис.7

лежащей в плоскости, перпендикулярной к оси вращения, с центром, находящимся на этой оси (рис. 7). Скорость частицы относительно вращающейся системы обозначим v’. Скорость частицы относительно неподвижной (инерциальной) системы отсчета v равна по величине +R в случае

(а) и |-Rв случае (б), где — угловая скорость вращающейся системы,R — радиус окружности.

Для того чтобы частица двигалась относительно неподвижной системы по окружности со скоростью на нее должна действовать направленная к центру окружности сила F, например, сила натяжения нити, которой частица привязана к центру окруж­ности (см.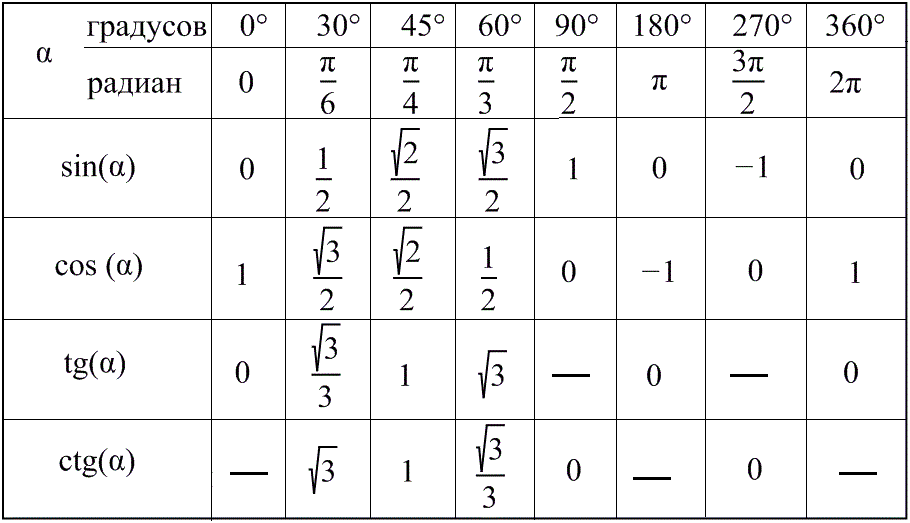 рис. 7 ). Величина этой силы равна

F=m===_+2m+ mR (12)

Относительно вращающейся системы частица в этом случае движется с ускорением т. е. так, как если бы на нее действовала сила

(13)

Таким образом, во вращающейся системе частица ведет себя так, как если бы на нее, кроме направленной к центру окруж­ности силы F, действовали еще две направленные от центра силы: и сила Fk, модуль которой равен

2_m(рис. 7) Cилу F_K можно представить в виде

(14)

Сила (14) и есть кориолисова сила инерции. При v’=0 эта сила отсутствует. Сила F_u6 не зависит от v’ — она, как мы уже отмечали, действует как на покоящиеся, так и на движущиеся тела. В случае, изображенном на рис. 7

F=m===_-2m+ mR

Соответственно

Следовательно, во вращающейся системе частица ведет себя так, как если бы на нее действовали две направленные к центру окружности силы: F и Fk, а также направленная от центра сила F_u6=m²R. Сила Fk и в этом случае может быть представлена в виде (14).

Теперь перейдем к нахождению выражения силы Кориолиса для случая, когда частица движется относительно вращающейся систе­мы отсчета произвольным образом. Свяжем с вращающейся систе­мой координатные оси

х’, y’_, z’, причем ось _, z’ совместим с осью вра­щения (рис. 8). Тогда радиус-вектор частицы можно представить в виде (15)

 

Рис.8

_

 

Положение частицы относительно неподвижной системы следует определять с помощью радиуса-вектора г. Однако символы г’ и г обозначают один и тот же вектор, проведенный из начала координат к частице. Символом г’ обозначил этот вектор наблюдатель, «живу­щий» во вращающейся системе отсчета; по его наблюдениям орты , е’_у, е’_г неподвижны, поэтому при дифференцировании выражения (15) он обращается с этими ортами как с константами.

Символом г пользуется неподвижный наблюдатель; для него орты, е’_у, вра­щаются со скоростью (орт e’_z неподвижен). Поэтому при диффе­ренцировании равного г выражения (15) неподвижный наблюда­тель должен обращаться с и е’_у как с функциями t, производные которых равны:

(16)

| Для вто­рых производных ортов по времени получаются выражения:

(17)

Найдем скорость частицы относительно вращающейся системы отсчета. Для этого продифференцируем радиус-вектор (15) по вре­мени, считая орты константами

Повторное дифференцирование этого выражения даст ускорение ча­стицы относительно вращающейся системы отсчета:

(18)

Теперь найдем скорость частицы относительно неподвижной системы отсчета. Для этого продифференцируем радиус-вектор (15) «с позиций» неподвижного наблюдателя. Воспользовавшись обозначением г вместо г’ (напомним, что г=г’), получим:

(19)

Продифференцировав это выражение еще раз по t, найдем ускорение частицы относительно неподвижной системы. Приняв во внимание формулы (15), (16) и (18), полученное со­отношение можно преобразовать к виду:

(20)

Соотношение (20) можно записать сле­дующим образом:

(21)

Из (21) вытекает, что ускорение частицы относительно непод­вижной системы отсчета можно представить в виде суммы трех ускорений: ускорения относительно вращающейся системы w’,

ускорения, равного — R¹), и ускорения

w_K=2[, v’],которое называется кориолисовым ускорением.

Для того чтобы частица двигалась с ускорением (21), на нее должны действовать какие-то тела с результирующей силой F=mw. Согласно (21)

mw^r = mw — 2m[, v’] + m²R = F + 2m[v’, ] + m²

R (22)

(перестановка сомножителей изменяет знак векторного произведе­ния}. Полученный результат означает, что при составлении уравне­ния второго закона Ньютона во вращающейся системе отсчета,

 

кроме сил взаимодействия, нужно учитывать центробежную силу инер­ции, а также кориолисову силу. Отме­тим, что сила Кориолиса всегда лежит в плоскости, перпендикуляр­ной к оси вращения.

Из сопоставления формул (19), (17), (15), и что с помощью выкладок, аналогичных тем, которые привели нас к со­отношению (21), можно убедиться в том, что

V=v’+[, r’]. (23)

Примеры движений, в которых проявляется кориолисова сила инерции. При истолковании явлений, связанных с движением тел относительно земной поверхности, в ряде случаев необходимо учи­тывать влияние кориолисовых сил. Например, при свободном падении тел на них действует кориолисова сила, обуславливающая отклонение к востоку от линии отвеса (рис.9). Эта сила максимальна на экваторе и обращается в нуль на полюсах.

Рис. 11.

Летящий снаряд также испытывает отклоне­ния, обусловленные кориолисовыми силами инерции (рис.10). При выстреле из орудия, направленного на север, снаряд будет откло­няться к востоку в северном полушарии и к за­паду — в южном.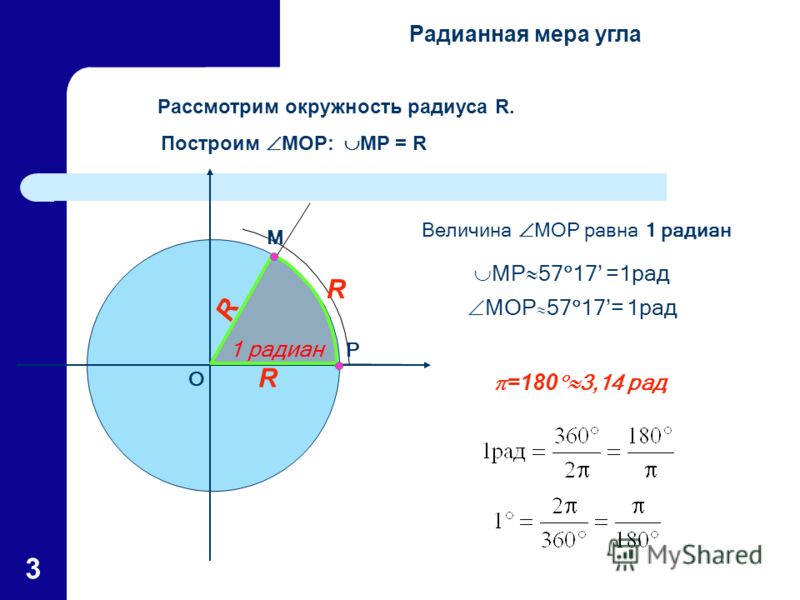 При стрельбе вдоль мериди­ана на юг направления отклонения будут про­тивоположными. При стрельбе вдоль экватора силы Кориолиса будут прижимать снаряд к Зем­ле, если выстрел произведен в направлении на запад, и поднимать его кверху, если выстрел произведен в восточном направлении. Предостав­ляем читателю самому убедиться в том, что сила Кориолиса, действующая на тело, движущееся вдоль меридиана в любом направлении (на се­вер или на юг), направлена по отношению к на­правлению движения вправо в северном полуша­рии и влево в южном полушарии. Это приводит к тому, что у рек под­мывается всегда правый берег в северном полушарии и левый берег в южном полушарии. Эти же причины объясняют неодинаковый износ рельсов при двухколейном движении.

Силы Кориолиса проявляются и при качаниях маятника. На рис. 11 показана траектория груза маятника (для простоты пред­положено, что маятник находится на полюсе). На северном полюсе сила Кориолиса будет все время направлена вправо по ходу маят­ника, на южном полюсе — влево. В итоге траектория имеет вид ро­зетки.

Как следует из рисунка, плоскость качаний маятника поворачи­вается относительно Земли в направлении часовой стрелки, причем за сутки она совершает один оборот. Относительно гелиоцентриче­ской системы отсчета дело обстоит так, что плоскость качаний оста­ется неизменной, а Земля поворачивается относительно нее, делая за сутки один оборот. Можно показать, что на широте ф плоскость ка­чаний маятника поворачивается за сутки на угол 2я sin ф.

Таким образом, наблюдения за вращением плоскости качаний маятника (маятники, предназначенные для этой цели, называются маятниками Фуко) дают непосредственное доказательство враще­ния Земли вокруг своей оси.

 

 

| следующая лекция ==> В то время как Fравна приблизительно 9,8 Н, т. е. почти в 300 раз больше | Циклический (круговой) термодинамический процесс

Поделиться с друзьями:

---

Дата добавления: 2014-01-06; Просмотров: 3344; Нарушение авторских прав?; Мы поможем в написании вашей работы!

---

Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет

---

---

Тригонометрическая окружность. Исчерпывающее руководство (2019)

В принципе можно было бы мерить все углы в радианах. На практике широко используется и градусное измерение углов, хотя с чисто математической точки зрения оно неестественно. При этом для малых углов используются специальные единицы: угловая минута и угловая секунда. Угловая минута — это 1/60 часть градуса; угловая секунда — это 1/60 часть угловой минуты. Если, например, величина угла равна 129 градусам, 34 минутам и 16 секундам, то пишут: 129◦ 340 1600 .

Задача 4.1. На какой угол поворачивается за одну секунду:

а) часовая стрелка часов;

б) минутная стрелка часов;

в) секундная стрелка часов?

Решение. Разберем только пункт а). Полный оборот часовая стрелка делает за 12 часов; стало быть, за час она поворачивается на 360/12 = 30◦ . Следовательно, за минуту часовая стрелка повернется на угол, в 60 раз меньший, чем за час, то есть на 300 ;

в свою очередь, за секунду стрелка повернется на угол, в 60 раз меньший, чем за минуту, то есть на 30 00 . Теперь вы видите, на-

сколько мала угловая секунда: ведь даже угол, в тридцать раз больший (поворот часовой стрелки за секунду времени) мы не

в состоянии заметить.

Представление об угловой минуте дает такой факт: «разрешающая способность» человеческого глаза (при стопроцентном зрении и хорошем освещении) равна примерно одной угловой минуте. Это означает, что две точки, которые видны под углом 10 или меньше, на глаз воспринимаются как одна.

Посмотрим, что можно сказать о синусе, косинусе и тангенсе малых углов. Если на рис. 4.2 угол α мал, то высота BC, дуга BD и отрезок BE, перпендикулярный AB, очень близки. Их длины — это sin α, радианная мера α и tg α. Стало быть, для малых углов синус, тангенс и радианная мера приближенно равны друг другу:

Рис. 4.1. Разрешающая способность.

Если α — малый угол, измеренный в радианах, то sin α ≈ α; tg α ≈ α.

Задача 4.2. Запишите приближенные формулы для синуса и тангенса малых углов, считая, что угол измеряется в градусах.

Ответ. sin α◦ ≈ πα/180.

Видно, что формулы сложнее, чем для радианной меры — еще один довод в ее пользу!

Задача 4.3. Под каким углом видно дерево высотой 10 метров с расстояния в 800 метров? Дайте ответ: а) в радианах; б) в угловых минутах.

Задача 4.4. Чему равно расстояние, равное одной минуте дуги земного меридиана? Радиус Земли равен примерно 6370 .

Расстояние, о котором идет речь в этой задаче, примерно равно морской миле (именно так и появилась эта мера длины).

Рис. 4.3. Парсек.

Рис. 4.4. Формула тысячных.

Задача 4.5. В астрономии применяется единица измерения расстояний, называемая парсек. По определению, расстояние в 1 парсек — это расстояние с которого радиус земной орбиты1 виден под углом 100 (рис.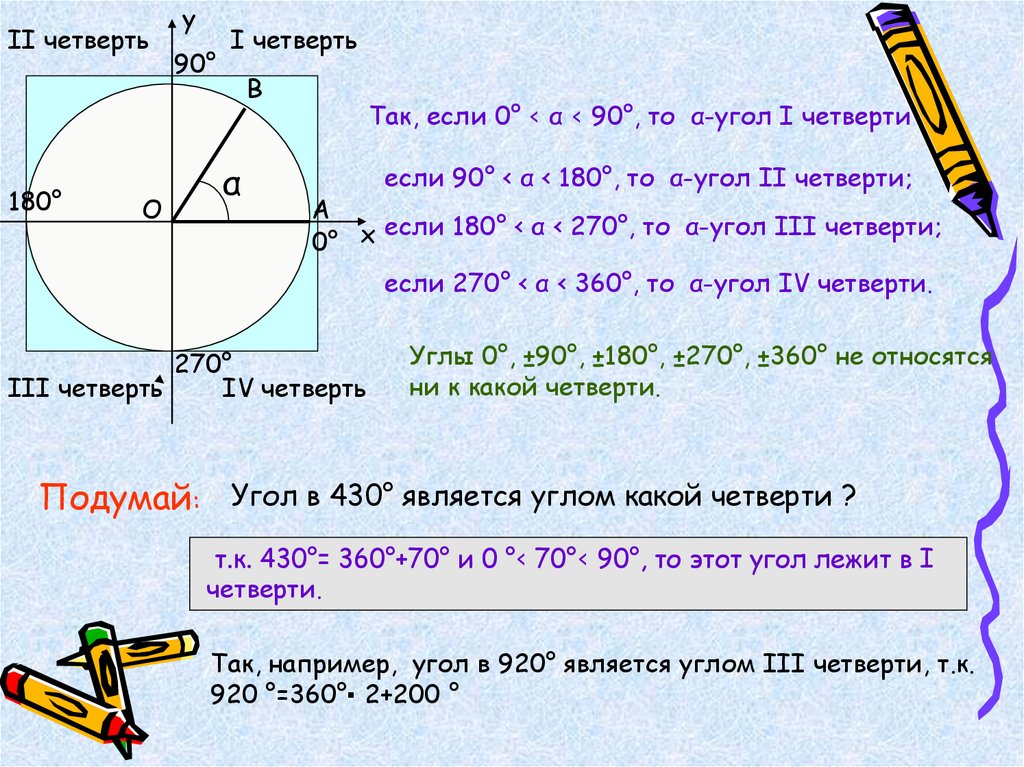 4.3 ). Сколько километров в одном парсеке? (Радиус земной орбиты равен примерно 150 миллионам километров.)

Задача 4.6. Военные пользуются единицей измерения углов, называемой «тысячная». По определению, тысячная — это 1/3000 развернутого угла. Такое измерение углов военные применяют в следующей формуле для определения расстояния до удаленных предметов: = (/) · 1000. Здесь — расстояние до предмета, — его высота, — угол, под которым он виден, измеренный в тысячных (рис. 4.4 ). Точна ли эта формула? Почему ей можно пользоваться на практике? Чему равно число π, по мнению военных?

Мы видим, что формулы sin α ≈ α, tg α ≈ α верны с хорошей точностью для малых углов. Посмотрим, что произойдет,

1 Астрономы поправили бы нас: не радиус (орбита Земли — не круг, а эллипс), а большая полуось (половина расстояния между наиболее удаленными друг от друга точками орбиты).

если угол не столь мал. Для угла в 30◦ точное значение синуса равно 0,5, а радианная мера равна π/6 ≈ 0,52. Ошибка (или, как еще говорят, погрешность), которую дает формула sin α ≈ α, равна примерно 0,02, что составляет 4% от значения синуса. Можно сказать, что относительная погрешность при таком вычислении (отношение погрешности к значению синуса) составляет 4%. Для углов, меньших 10◦ , относительная погрешность формулы sin α ≈ α меньше одного процента. Чем меньше угол α, тем меньше относительная погрешность формулы sin α ≈ α.

Существуют и другие формулы, позволяющие вычислять синусы и тангенсы — и не только малых углов — с хорошей точностью. Например, формула sin α ≈ α − α3 /6 (напоминаем, что α измеряется в радианах!) дает относительную погрешность менее 1% уже для всех углов, не превосходящих 50◦ . Позднее мы увидим, как оценить погрешность наших формул.

Задача 4.7. Пусть α — острый угол, измеренный в радианах. Докажите неравенство cos α > 1 − α2 .

Задача 4.8. Для косинусов малых углов в качестве приближенного значения можно брать 1. Докажите, что при величине угла менее 5◦ относительная погрешность этого приближения будет менее 1%.

Учителя считают, что каждый школьник должен уметь проводить расчёты, знать тригонометрические формулы, но далеко не каждый преподаватель объясняет, что такое синус и косинус. Каков их смысл, где они используются? Почему мы говорим про треугольники, а в учебнике нарисована окружность? Попробуем связать все факты воедино.

Школьный предмет

Изучение тригонометрии начинается обычно в 7-8 классе средней школы. В это время учащимся объясняют, что такое синус и косинус, предлагают решать геометрические задачи с применением этих функций. Позже появляются более сложные формулы и выражения, которые требуется алгебраическим способом преобразовывать (формулы двойного и половинного угла, степенные функции), проводится работа с тригонометрической окружностью.

Однако учителя далеко не всегда могут доходчиво объяснить смысл используемых понятий и применимость формул. Поэтому ученик зачастую не видит смысла в данном предмете, а заученная информация быстро забывается. Однако стоит один раз объяснить старшекласснику, например, связь между функцией и колебательным движением, и логическая связь запомнится на многие годы, а шутки на тему бесполезности предмета уйдут в прошлое.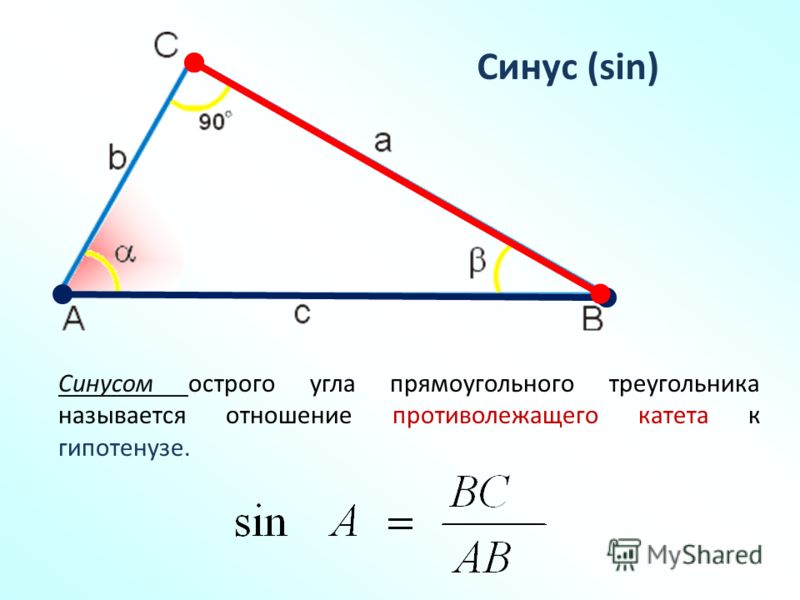

Использование

Заглянем ради любопытства в различные разделы физики. Хотите определить дальность полёта снаряда? Или высчитываете силу трения между объектом и некой поверхностью? Раскачиваете маятник, следите за лучами, проходящими сквозь стекло, высчитываете индукцию? Практически в любой формуле фигурируют тригонометрические понятия. Так что такое синус и косинус?

Определения

Синус угла представляет собой отношение противолежащего катета к гипотенузе, косинус — прилежащего катета всё к той же гипотенузе. Здесь нет совершенно ничего сложного. Возможно, учеников обычно смущают значения, которые они видят в тригонометрической таблице, ведь там фигурируют квадратные корни. Да, получать из них десятичные дроби не очень удобно, но кто сказал, что все числа в математике должны быть ровными?

На самом деле в задачниках по тригонометрии можно найти забавную подсказку: большинство ответов здесь ровные и в худшем случае содержат корень из двух или из трёх. Вывод прост: если у вас в ответе получилась «многоэтажная» дробь, перепроверьте решение на предмет ошибок в расчётах или в рассуждениях. И вы их, скорее всего, найдете.

Что нужно запомнить

Как и в любой науке, в тригонометрии есть такие данные, которые необходимо выучить.

Во-первых, следует запомнить числовые значения для синусов, косинусов прямоугольного треугольника 0 и 90, а также 30, 45 и 60 градусов. Эти показатели встречаются в девяти из десяти школьных задач. Подглядывая эти значения в учебнике, вы потеряете много времени, а на контрольной или экзамене посмотреть и вовсе будет негде.

Нужно помнить, что значение обеих функций не может превышать единицу. Если где-либо в расчетах вы получите значение, выходящее за пределы диапазона 0-1, остановитесь и решите задачу заново.

Сумма квадратов синуса и косинуса равна единице. Если вы уже нашли одно из значений, воспользуйтесь этой формулой для нахождения оставшегося.

Теоремы

В базовой тригонометрии существует две основные теоремы: синусов и косинусов.

Первая гласит, что отношение каждой стороны треугольника к синусу противолежащего угла одинаково. Вторая — что квадрат любой стороны можно получить, если сложить квадраты двух оставшихся сторон и вычесть удвоенное их произведение, умноженное на косинус лежащего между ними угла.

Таким образом, если в теорему косинусов подставить значение угла в 90 градусов, мы получим… теорему Пифагора. Теперь, если требуется высчитать площадь фигуры, не являющейся прямоугольным треугольником, можно больше не переживать — две рассмотренные теоремы существенно упростят решение задачи.

Цели и задачи

Изучение тригонометрии значительно упростится, когда вы осознаете один простой факт: все выполняемые вами действия направлены на достижения всего одной цели. Любые параметры треугольника могут быть найдены, если вы знаете о нём самый минимум информации — это может быть величина одного угла и длины двух сторон или, например, три стороны.

Для определения синуса, косинуса, тангенса любого угла этих данных достаточно, с их же помощью можно легко высчитать площадь фигуры. Практически всегда в качестве ответа требуется привести одно из упомянутых значений, а найти их можно по одним и тем же формулам.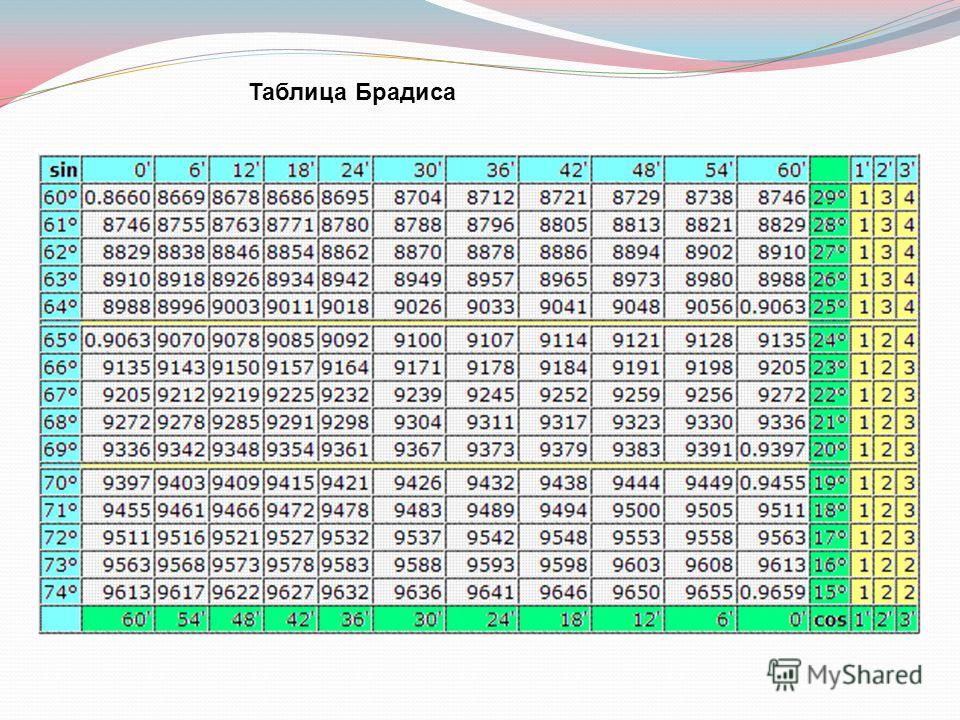

Нестыковки при изучении тригонометрии

Одним из непонятных вопросов, которых школьники предпочитают избегать, является обнаружение связи между различными понятиями в тригонометрии. Казалось бы, для изучения синусов и косинусов углов используются треугольники, но обозначения почему-то часто встречаются на рисунке с окружностью. Кроме того, существует и вовсе непонятный волнообразный график под названием синусоида, не имеющий никакого внешнего сходства ни с окружностью, ни с треугольниками.

Более того, углы измеряются то в градусах, то в радианах, а число Пи, записывающееся просто как 3,14 (без единиц измерения), почему-то фигурирует в формулах, соответствуя 180 градусам. Как всё это связано между собой?

Единицы измерения

Почему число Пи равняется именно 3,14? Помните ли вы, что это за значение? Это количество радиусов, умещающихся в дуге на половине окружности. Если диаметр круга — 2 сантиметра, длина окружности составит 3,14*2, или 6,28.

Второй момент: возможно, вы замечали сходство слов «радиан» и «радиус».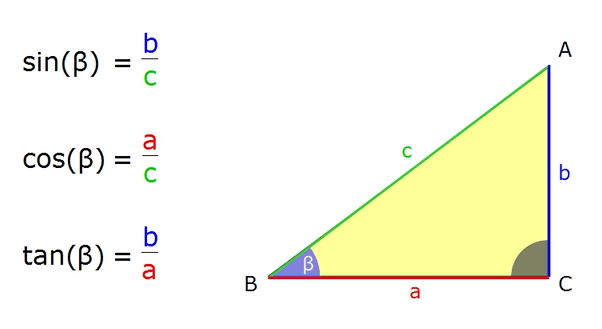 Дело в том, что один радиан численно равен величине угла, отложенного из центра окружности на дугу длиной в один радиус.

Теперь совместим полученные знания и поймем, почему сверху на оси координат в тригонометрии пишется «Пи пополам», а слева — «Пи». Это угловая величина, измеренная в радианах, ведь полукруг — это 180 градусов, или 3,14 радиана. А там, где есть градусы, есть синусы и косинусы. Треугольник же легко провести от нужной точки, отложив отрезки к центру и на ось координат.

Заглянем в будущее

Тригонометрия, изучаемая в школе, имеет дело с прямолинейной системой координат, где, как бы это странно ни звучало, прямая — это прямая.

Но есть и более сложные способы работы с пространством: сумма углов треугольника здесь будет больше 180 градусов, а прямая в нашем представлении будет выглядеть как самая настоящая дуга.

Перейдем от слов к делу! Возьмите яблоко. Сделайте ножом три надреза, чтобы при взгляде сверху получался треугольник. Выньте получившийся кусок яблока и посмотрите на «рёбра», где заканчивается кожура.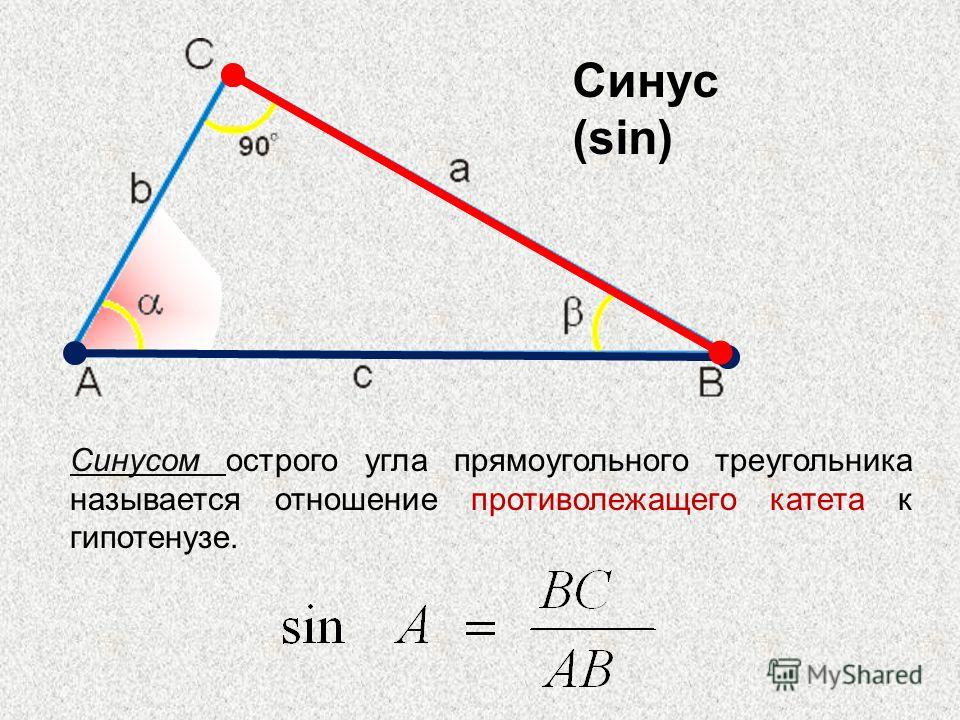 Они вовсе не прямые. Фрукт в ваших руках условно можно назвать круглым, а теперь представьте, какими сложными должны быть формулы, с помощью которых можно найти площадь вырезанного куска. А ведь некоторые специалисты решают такие задачи ежедневно.

Тригонометрические функции в жизни

Обращали ли вы внимание, что самый короткий маршрут самолёта из точки А в точку Б на поверхности нашей планеты имеет ярко выраженную форму дуги? Причина проста: Земля имеет форму шара, а значит, с помощью треугольников многого не вычислишь — здесь приходится использовать более сложные формулы.

Не обойтись без синуса/косинуса острого угла в любых вопросах, связанных с космосом. Интересно, что здесь сходится целое множество факторов: тригонометрические функции требуются при расчётах движения планет по окружностям, эллипсам и различным траекториям более сложных форм; процесса запуска ракет, спутников, шаттлов, отстыковки исследовательских аппаратов; наблюдении за далёкими звёздами и изучении галактик, до которых человек в обозримом будущем добраться не сможет.

В целом поле для деятельности человека, владеющего тригонометрией, очень широко и, по-видимому, со временем будет только расширяться.

Заключение

Сегодня мы узнали или, во всяком случае, повторили, что такое синус и косинус. Это понятия, которых не нужно бояться — стоит захотеть, и вы поймете их смысл. Помните, что тригонометрия — это не цель, а лишь инструмент, который можно использовать для удовлетворения реальных человеческих потребностей: строить дома, обеспечивать безопасность движения, даже осваивать просторы вселенной.

Действительно, сама по себе наука может казаться скучной, но как только вы найдете в ней способ достижения собственных целей, самореализации, процесс обучения станет интересным, а ваша личная мотивация возрастёт.

В качестве домашнего задания попробуйте найти способы применить тригонометрические функции в той сфере деятельности, которая интересна лично вам. Пофантазируйте, включите воображение, и тогда наверняка окажется, что новые знания пригодятся вам в будущем. Да и кроме того, математика полезна для общего развития мышления.

Одним из разделов математики, с которыми школьники справляются с наибольшими трудностями, является тригонометрия. Неудивительно: для того чтобы свободно овладеть этой областью знаний, требуется наличие пространственного мышления, умение находить синусы, косинусы, тангенсы, котангенсы по формулам, упрощать выражения, уметь применять в вычислениях число пи. Помимо этого, нужно уметь применять тригонометрию при доказательстве теорем, а это требует либо развитой математической памяти, либо умения выводить непростые логические цепочки.

Истоки тригонометрии

Знакомство с данной наукой следует начать с определения синуса, косинуса и тангенса угла, однако прежде необходимо разобраться, чем вообще занимается тригонометрия.

Исторически главным объектом исследования данного раздела математической науки были прямоугольные треугольники. Наличие угла в 90 градусов дает возможность осуществлять различные операции, позволяющие по двум сторонам и одному углу либо по двум углам и одной стороне определять значения всех параметров рассматриваемой фигуры. В прошлом люди заметили эту закономерность и стали активно ею пользоваться при строительстве зданий, навигации, в астрономии и даже в искусстве.

Начальный этап

Первоначально люди рассуждали о взаимоотношении углов и сторон исключительно на примере прямоугольных треугольников. Затем были открыты особые формулы, позволившие расширить границы употребления в повседневной жизни данного раздела математики.

Изучение тригонометрии в школе сегодня начинается с прямоугольных треугольников, после чего полученные знания используются учениками в физике и решении абстрактных тригонометрических уравнений, работа с которыми начинается в старших классах.

Сферическая тригонометрия

Позже, когда наука вышла на следующий уровень развития, формулы с синусом, косинусом, тангенсом, котангенсом стали использоваться в сферической геометрии, где действуют иные правила, а сумма углов в треугольнике всегда больше 180 градусов. Данный раздел не изучается в школе, однако знать о его существовании необходимо как минимум потому, что земная поверхность, да и поверхность любой другой планеты, является выпуклой, а значит, любая разметка поверхности будет в трёхмерном пространстве «дугообразной».

Возьмите глобус и нитку. Приложите нитку к двум любым точкам на глобусе, чтобы она оказалась натянутой. Обратите внимание — она обрела форму дуги. С такими формами и имеет дело сферическая геометрия, применяющаяся в геодезии, астрономии и других теоретических и прикладных областях.

Прямоугольный треугольник

Немного узнав про способы применения тригонометрии, вернемся к базовой тригонометрии, чтобы в дальнейшем разобраться, что такое синус, косинус, тангенс, какие расчёты можно с их помощью выполнять и какие формулы при этом использовать.

Первым делом необходимо уяснить понятия, относящиеся к прямоугольному треугольнику. Во-первых, гипотенуза — это сторона, лежащая напротив угла в 90 градусов. Она является самой длинной. Мы помним, что по теореме Пифагора её численное значение равно корню из суммы квадратов двух других сторон.

Например, если две стороны равны 3 и 4 сантиметрам соответственно, длина гипотенузы составит 5 сантиметров. Кстати, об этом знали ещё древние египтяне около четырех с половиной тысяч лет назад.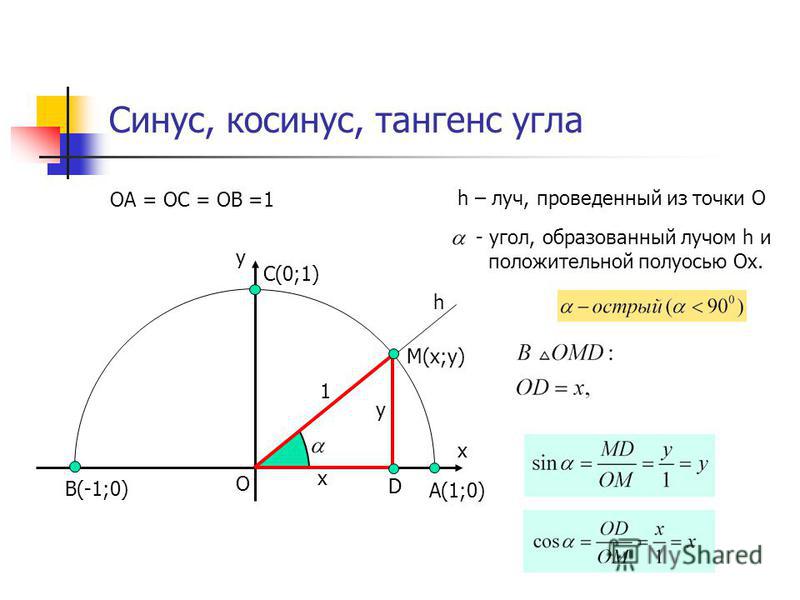

Две оставшиеся стороны, которые образуют прямой угол, носят название катетов. Кроме того, надо помнить, что сумма углов в треугольнике в прямоугольной системе координат равняется 180 градусам.

Определение

Наконец, твердо понимая геометрическую базу, можно обратиться к определению синуса, косинуса и тангенса угла.

Синусом угла называется отношение противолежащего катета (т. е. стороны, располагающейся напротив нужного угла) к гипотенузе. Косинусом угла называется отношение прилежащего катета к гипотенузе.

Запомните, что ни синус, ни косинус не может быть больше единицы! Почему? Потому что гипотенуза — это по умолчанию самая длинная Каким бы длинным ни был катет, он будет короче гипотенузы, а значит, их отношение всегда будет меньше единицы. Таким образом, если у вас в ответе к задаче получился синус или косинус со значением, большим, чем 1, ищите ошибку в расчётах или рассуждениях. Этот ответ однозначно неверен.

Наконец, тангенсом угла называется отношение противолежащей стороны к прилежащей. Тот же самый результат даст деление синуса на косинус. Посмотрите: в соответствии с формулой мы делим длину стороны на гипотенузу, после чего делим на длину второй стороны и умножаем на гипотенузу. Таким образом, мы получаем то же самое соотношение, что и в определении тангенса.

Котангенс, соответственно, представляет собой отношение прилежащей к углу стороны к противолежащей. Тот же результат мы получим, разделив единицу на тангенс.

Итак, мы рассмотрели определения, что такое синус, косинус, тангенс и котангенс, и можем заняться формулами.

Простейшие формулы

В тригонометрии не обойтись без формул — как найти синус, косинус, тангенс, котангенс без них? А ведь именно это требуется при решении задач.

Первая формула, которую необходимо знать, начиная изучать тригонометрию, говорит о том, что сумма квадратов синуса и косинуса угла равна единице. Данная формула является прямым следствием теоремы Пифагора, однако позволяет сэкономить время, если требуется узнать величину угла, а не стороны.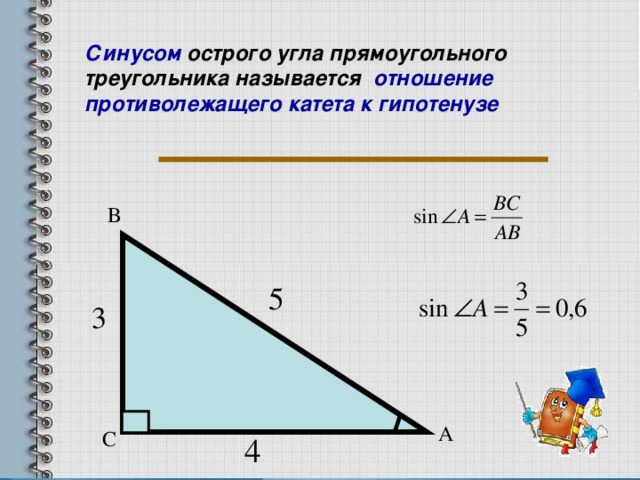

Многие учащиеся не могут запомнить вторую формулу, также очень популярную при решении школьных задач: сумма единицы и квадрата тангенса угла равна единице, деленной на квадрат косинуса угла. Присмотритесь: ведь это то же самое утверждение, что и в первой формуле, только обе стороны тождества были поделены на квадрат косинуса. Выходит, простая математическая операция делает тригонометрическую формулу совершенно неузнаваемой. Помните: зная, что такое синус, косинус, тангенс и котангенс, правила преобразования и несколько базовых формул вы в любой момент сможете сами вывести требуемые более сложные формулы на листе бумаги.

Формулы двойного угла и сложения аргументов

Ещё две формулы, которые требуется выучить, связаны со значениями синуса и косинуса при сумме и разности углов. Они представлены на рисунке ниже. Обратите внимание, что в первом случае оба раза перемножается синус и косинус, а во втором складывается попарное произведение синуса и косинуса.

Также существуют формулы, связанные с аргументами в виде двойного угла.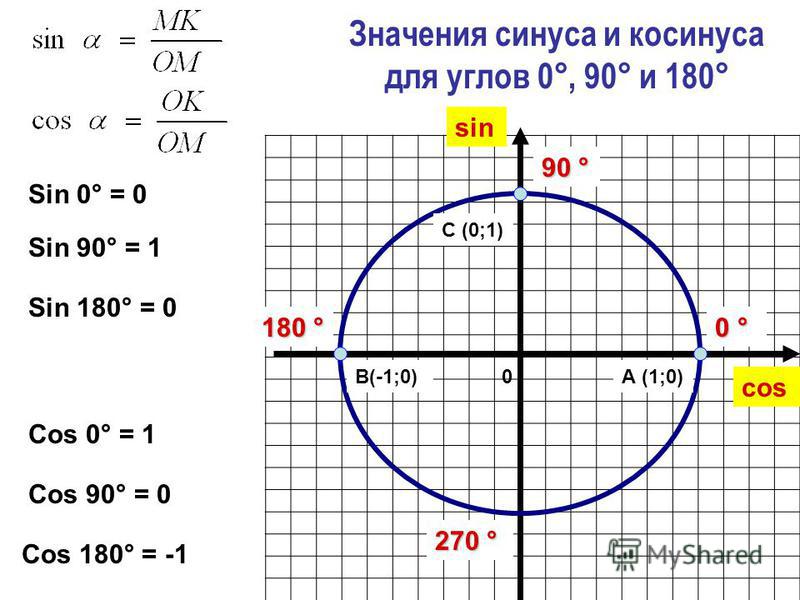 Они полностью выводятся из предыдущих — в качестве тренировки попробуйте получить их самостоятельно, приняв угол альфа равным углу бета.

Наконец, обратите внимание, что формулы двойного угла можно преобразовать так, чтобы понизить степень синуса, косинуса, тангенса альфа.

Теоремы

Двумя основными теоремами в базовой тригонометрии являются теорема синусов и теорема косинусов. С помощью этих теорем вы легко сможете понять, как найти синус, косинус и тангенс, а значит, и площадь фигуры, и величину каждой стороны и т. д.

Теорема синусов утверждает, что в результате деления длины каждой из сторон треугольника на величину противолежащего угла мы получим одинаковое число. Более того, это число будет равно двум радиусам описанной окружности, т. е. окружности, содержащей все точки данного треугольника.

Теорема косинусов обобщает теорему Пифагора, проецируя её на любые треугольники. Оказывается, из суммы квадратов двух сторон вычесть их произведение, умноженное на двойной косинус смежного им угла — полученное значение окажется равно квадрату третьей стороны.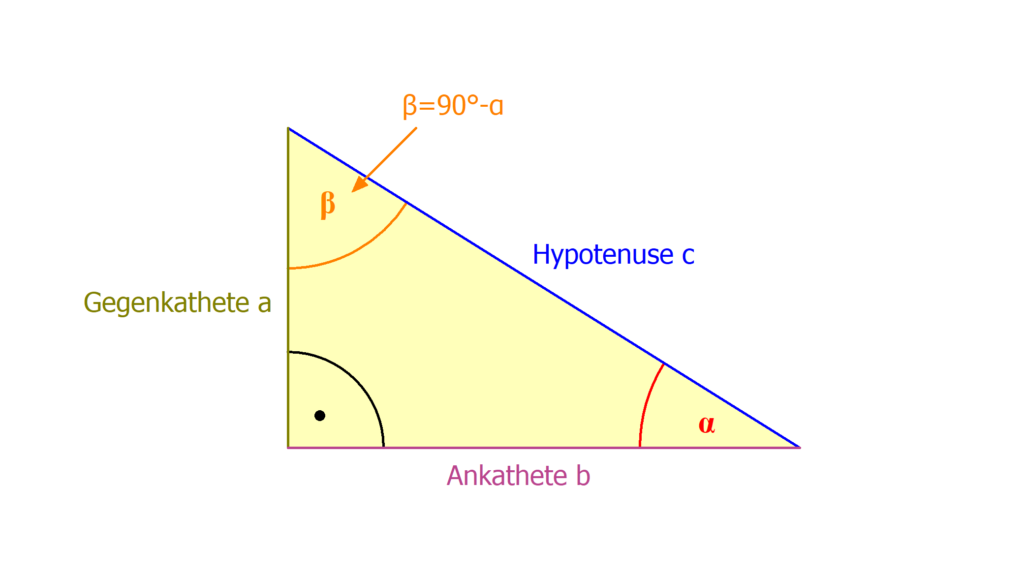 Таким образом, теорема Пифагора оказывается частным случаем теоремы косинусов.

Ошибки по невнимательности

Даже зная, что такое синус, косинус и тангенс, легко совершить ошибку из-за рассеянности внимания или ошибки в простейших расчётах. Чтобы избежать таких ошибок, ознакомимся с наиболее популярными из них.

Во-первых, не следует преобразовывать обыкновенные дроби в десятичные до получения окончательного результата — можно и ответ оставить в виде обыкновенной дроби, если в условии не оговорено обратное. Такое преобразование нельзя назвать ошибкой, однако следует помнить, что на каждом этапе задачи могут появиться новые корни, которые по задумке автора должны сократиться. В этом случае вы напрасно потратите время на излишние математические операции. Особенно это актуально для таких значений, как корень из трёх или из двух, ведь они встречаются в задачах на каждом шагу. То же касается округлений «некрасивых» чисел.

Далее, обратите внимание, что к любому треугольнику применима теорема косинусов, но не теорема Пифагора! Если вы по ошибке забудете вычесть удвоенное произведение сторон, умноженное на косинус угла между ними, вы не только получите совершенно неверный результат, но и продемонстрируете полное непонимание предмета. Это хуже, чем ошибка по невнимательности.

В-третьих, не путайте значения для углов в 30 и 60 градусов для синусов, косинусов, тангенсов, котангенсов. Запомните эти значения, ведь синус 30 градусов равен косинусу 60, и наоборот. Их легко перепутать, вследствие чего вы неизбежно получите ошибочный результат.

Применение

Многие ученики не спешат приступать к изучению тригонометрии, поскольку не понимают её прикладного смысла. Что такое синус, косинус, тангенс для инженера или астронома? Это понятия, благодаря которым можно вычислить расстояние до далёких звёзд, предсказать падение метеорита, отправить исследовательский зонд на другую планету. Без них нельзя построить здание, спроектировать автомобиль, рассчитать нагрузку на поверхность или траекторию движения предмета. И это только самые очевидные примеры! Ведь тригонометрия в том или ином виде используется повсюду, начиная от музыки и заканчивая медициной.

В заключение

Итак, вы синус, косинус, тангенс. Вы можете использовать их в расчётах и успешно решать школьные задачи.

Вся суть тригонометрии сводится к тому, что по известным параметрам треугольника нужно вычислить неизвестные. Всего этих параметров шесть: длины трёх сторон и величины трёх углов. Всё различие в задачах заключается в том, что даются неодинаковые входные данные.

Как найти синус, косинус, тангенс исходя из известных длин катетов или гипотенузы, вы теперь знаете. Поскольку эти термины обозначают не что иное, как отношение, а отношение — это дробь, главной целью тригонометрической задачи становится нахождение корней обычного уравнения либо же системы уравнений. И здесь вам поможет обычная школьная математика.

В этой статье собраны таблицы синусов, косинусов, тангенсов и котангенсов . Сначала мы приведем таблицу основных значений тригонометрических функций, то есть, таблицу синусов, косинусов, тангенсов и котангенсов углов 0, 30, 45, 60, 90, …, 360 градусов (0, π/6, π/4, π/3, π/2, …, 2π радиан). После этого мы дадим таблицу синусов и косинусов, а также таблицу тангенсов и котангенсов В. М. Брадиса, и покажем, как использовать эти таблицы при нахождении значений тригонометрических функций.

Навигация по странице.

Таблица синусов, косинусов, тангенсов и котангенсов для углов 0, 30, 45, 60, 90, … градусов

Список литературы.

• Алгебра: Учеб. для 9 кл. сред. шк./Ю. Н. Макарычев, Н. Г. Миндюк, К. И. Нешков, С. Б. Суворова; Под ред. С. А. Теляковского.- М.: Просвещение, 1990.- 272 с.: ил.- ISBN 5-09-002727-7
• Башмаков М. И. Алгебра и начала анализа: Учеб. для 10-11 кл. сред. шк. — 3-е изд. — М.: Просвещение, 1993. — 351 с.: ил. — ISBN 5-09-004617-4.
• Алгебра и начала анализа: Учеб. для 10-11 кл. общеобразоват. учреждений / А. Н. Колмогоров, А. М. Абрамов, Ю. П. Дудницын и др.; Под ред. А. Н. Колмогорова.- 14-е изд.- М.: Просвещение, 2004.- 384 с.: ил.- ISBN 5-09-013651-3.
• Гусев В. А., Мордкович А. Г. Математика (пособие для поступающих в техникумы): Учеб. пособие.- М.; Высш. шк., 1984.-351 с. , ил.
• Брадис В. М. Четырехзначные математические таблицы: Для общеобразоват. учеб. заведений. — 2-е изд. — М.: Дрофа, 1999.- 96 с.: ил. ISBN 5-7107-2667-2

Приближение малого угла

Когда угол θ (в радианах) мал, мы можем использовать эти приближения для синуса, косинуса и тангенса:

грех θ ≈ θ

cos θ ≈ 1 − θ ² 2

тангенс θ ≈ θ

Если мы очень смелы, мы можем использовать cos θ ≈ 1

Давайте посмотрим некоторые значения! (Примечание: значения приблизительны)

грех θ ≈ θ

θ (радианы)	грех θ	θ − sin θ
0	0	0
0,01	0,0099998	0,0000002
0,1	0,0998	0,0002
0,2	0,1987	0,0013
0,5	0,4794	0,0206
1	0,8415	0,1585

Идеален при нуле, очень хорош при 0,01, хорош при 0,1 и может быть полезен до 0,5, если вы не привередливы.

потому что θ ≈ 1

Можем ли мы просто использовать 1 для аппроксимации cos θ?

θ (радианы)	потому что θ	1 − потому что θ
0	1	0
0,01	0,99995	0,00005
0,1	0,995	0,005
0,2	0,9801	0,0199
0,5	0,8776	0,1224
1	0,5403	0,4597

Ну да, можем, но только для очень малых углов.

cos θ ≈ 1 −

θ ² 2

Итак, давайте попробуем лучшую версию 1 − 9.0009 θ ² 2 :

θ (радианы)	потому что θ	1 − θ 2 2	(1− θ 2 2 ) − cos θ
0	1	1	0
0,01	0,9999500004	0,99995	-0,0000000004
0,1	0,9950042	0,995	-0,0000042
0,2	0,980067	0,98	-0,000067
0,5	0,8776	0,875	-0,0026
1	0,5403	0,5	-0,0403

Вау, это большое улучшение!

тангенс θ ≈ θ

θ (радианы)	загар θ	тангенс θ − θ
0	0	0
0,01	0,0100003	-0,0000003
0,1	0,1003	-0,0003
0,2	0,2027	-0,0027
0,5	0,5463	-0,0463
1	1,5574	-0,5574

Не так уж плохо для небольших значений, верно?

Серия Тейлор

Вы заметили волшебное улучшение для cos, когда мы перешли от 1 к 1 − θ ² 2 ?

Секрет в расширении рядов Тейлора cos:

cos x = 1 − x ² 2! + х ⁴ 4! — . ..

Итак… мы можем использовать больше терминов, если хотим большей точности!

Точно так же мы можем улучшить синус:

sin x = x − x ³ 3! + х ⁵ 5! — …

или tan или другие функции, такие как e ^x

Пример: вы застряли на острове без калькулятора. Вычислите синус 20 градусов.

градусов? Но нам нужно использовать радианы!

Оценим как можно лучше:

20 × π 180 = π 9 ≈ 3,1416 × 0,11 … ≈ 0,35 радиан

Сейчас, используя только один дополнительный термин:

SIN X = X — x ³ 3! …

sin x ≈ 0,35 − 0,35 ³ 3! ≈ 0,35 − 0,35*0,35*0,35 6 ≈ 0,3428 (после долгих усилий)

(позже, когда вы вернетесь домой, вы используете калькулятор, чтобы получить sin(4, 20°) 20 0,30 0,30 неплохо!)

Использует

Эти приближения очень полезны в астрономии , где многие углы очень малы.

Также в некоторых областях техники и оптики тоже.

Формула малого угла | Изображение Вселенной

Размеры наблюдаемых объектов могут быть указаны с точки зрения их углового размера с точки зрения наблюдателя, а не их физического размера. Как показано на рисунке выше, расстояние до наблюдаемого объекта d , физический размер объекта D и угловой размер объекта θ (в радианах) образуют прямоугольный треугольник с тригонометрическим соотношением:

Приближение малого угла для тригонометрии утверждает, что:

Приближение малого угла можно применять, когда θ мало (< 10°), или когда d  >> D ( намного больше — не просто в пару раз больше, а в несколько, 10, даже в 100+ раз больше). Угловые размеры многих объектов в небе малы, и при их изучении можно применять приближение малых углов. Если мы возьмем аппроксимацию малого угла и подставим ее в наше первое уравнение, оно примет вид: 

, которая называется формулой малого угла, где снова θ   должен быть угловым размером в радианах.

θ выражается в радианах, но иногда у нас будут измерения углового размера в градусах. Используя тот факт, что 1 радиан равен 360/2π ≈ 57,3 градуса, мы можем переписать формулу малого угла, чтобы θ можно было ввести как угловой размер в градусах:

При работе с астрономически удаленными объектами угловые размеры чрезвычайно малы, и часто более практично использовать измерения углового размера в угловых секундах («) вместо градусов, где 1 угловая секунда – это 1/3600 градуса. Таким образом, 1 радиан равен (3600 x 360)/2π ≈ 206 265 угловых секунд, и мы можем снова перепишите формулу малого угла, теперь как:

Is легко измерить θ, угловой размер астрономических объектов, поэтому мы часто используем формулу малого угла для решения других неизвестных (либо  D  , либо  d ). Если мы знаем расстояние d до объекта, который наблюдаем, мы можем использовать его с угловым размером θ и формулой малого угла, чтобы найти физический размер D этого небесного объекта. Или, если два объекта находятся примерно на одинаковом расстоянии d от наблюдателя, мы можем использовать это с угловым размером θ и формулой малого угла, чтобы найти расстояние между двумя объектами (где здесь D  – расстояние между двумя объектами). Кроме того, некоторые объекты в космосе имеют «типичный размер», физический диаметр D , который, как мы знаем, является хорошим грубым приближением для размера. Когда мы знаем значения как θ, так и D , мы можем использовать их с формулой малого угла, чтобы найти расстояние d до небесного объекта.

Пример Вопрос

27 августа 2003 года Марс совершил самое близкое сближение с Землей за всю историю наблюдений из-за близкой синхронизации Земли, находящейся в афелии (самая дальняя точка на орбите Солнца), и Марса, находящегося в перигелии ( ближайшая к Солнцу точка на его орбите вокруг Солнца). Расстояние между двумя планетами в тот день составляло всего 55,8 миллиона км (километров).