Синус модуль х: График функции y = sin(x)/sin(|x|)

alexxlab / / Разное

Содержание

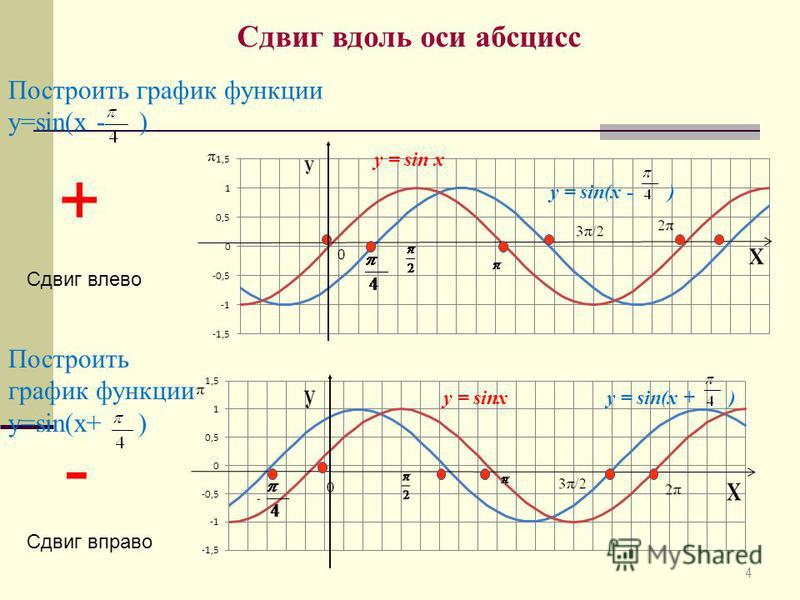
Python. Модуль cmath. Работа с комплексными числами. Тригонометрические функции

Модуль cmath. Работа с комплексными числами. Тригонометрические функции. Гиперболические функции. Функции классификаций

Содержание

  • 1. Тригонометрические функции
    • 1.1. Функции cmath.acos(), cmath.asin(), cmath.atan(). Получить арккосинус, арксинус, арктангенс аргумента
    • 1.2. Функции cmath.cos(), cmath.sin(), cmath.tan(). Получить косинус, синус и тангенс аргумента
  • 2. Гиперболические функции
    • 2.1. Функции cmath.acosh(), cmath.asinh(), cmath.atanh(). Гиперболический арккосинус, арксинус, арктангенс
    • 2.2. Функции cmath.cosh(), cmath.sinh(), cmath.tanh(). Гиперболический косинус, синус, тангенс
  • 3. Функции классификаций
    • 3.1. cmath.isfinite(). Конечность комплексного числа
    • 3.2. cmath.isinf(). Конечность составляющих комплексного числа
    • 3.3. cmath.isnan(). Проверка составляющих комплексного числа на значение Nan
    • 3. 4. cmath.isclose(). Определение близости двух значений между собой
  • Связанные темы

Поиск на других ресурсах:

1. Тригонометрические функции

Модуль cmath содержит 6 тригонометрических функций, которые обрабатывают комплексные числа:

  • cmath.acos(x) — возвращает арккосинус от аргумента x;
  • cmath.asin(x) — возвращает арксинус от аргумента x;
  • cmath.atan(x) — определяет арктангенс от аргумента x;
  • cmath.cos(x) — возвращает косинус от аргумента x;
  • cmath.sin(x) — возвращает синус от аргумента x;
  • cmath.tan(x) — возвращает тангенс от аргумента x.

  ⇑

1.1. Функции cmath.acos(), cmath.asin(), cmath.atan(). Получить арккосинус, арксинус, арктангенс аргумента

Функции

cmath.acos(x)
cmath.asin(x)

возвращают соответственно арккосинус и арксинус от аргумента x. Каждая из функций имеет два разреза разветвления. Первый простирается от 1 до  ∞ вдоль вещественной оси, непрерывный снизу. Второй простирается влево от -1 до -∞ вдоль вещественной оси, непрерывный сверху.

Функция

 cmath.atan(x)

позволяет получить арктангенс от аргумента x.

Функция имеет два разреза разветвления. Первый простирается от 1j вдоль мнимой оси до ∞j непрерывно справа. Второй простирается от -1 до -∞ и является непрерывный слева.

Пример.

# Тригонометрические функции acos(), asin(), atan()

# 1. Подключить модуль cmath
import cmath

# 2. Получить комплексное число с клавиатуры
re = int(input('re = '))
im = int(input('im = '))
z = complex(re, im)

# 3. Вычислить арккосинус аргумента z и вывести его
arc_cos = cmath.acos(z)
print('arc_cos = ', arc_cos)

# 4. Вычислить арксинус от z
arc_sin = cmath.asin(z)
print('arc_sin = ', arc_sin)

# 5. Вычислить арктангенс от z
arc_tan = cmath.atan(z)
print('arc_tan = ', arc_tan)

Тестовый пример

re = 3
im = -4
arc_cos = (0.
 
 9368124611557198+2.305509031243477j)
arc_sin = (0.6339838656391766-2.305509031243477j)
arc_tan = (1.4483069952314644-0.15899719167999918j)

  ⇑

1.2. Функции cmath.cos(), cmath.sin(), cmath.tan(). Получить косинус, синус и тангенс аргумента

Функции

cmath.cos(x)
cmath.sin(x)
cmath.tan(x)

возвращают косинус, синус и тангенс аргумента x.

Пример.

# Функции cos(), sin(), tan()

# Подключить модуль cmath
import cmath

# Создать комплексное число z = 7-8j
z = complex(7, -8)

# Вычислить косинус, синус, тангенс
sin_res = cmath.sin(z)
cos_res = cmath.cos(z)
tan_res = cmath.tan(z)
print('sin_res = ', sin_res)
print('cos_res = ', cos_res)
print('tan_res = ', tan_res)

Тестовый пример

sin_res = (979.2248346123021-1123.6753468137035j)
cos_res = (1123.675599719735+979.2246142178511j)
tan_res = (2.2295633684101687e-07-0.
  9999999692244822j)

  ⇑

2. Гиперболические функции

Модуль cmath содержит реализацию следующих гиперболических функций, которые оперируют комплексными числами:

  • cmath.acosh(x) — возвращает гиперболический арккосинус от аргумента x;
  • cmath.asinh(x) — возвращает гиперболический арксинус от аргумента x;
  • cmath.atanh(x) — возвращает гиперболический арктангенс от аргумента x;
  • cmath.cosh(x) — возвращает гиперболический косинус от аргумента x;
  • cmath.sinh(x) — возвращает гиперболический синус от аргумента x;
  • cmath.tanh(x) — возвращает гиперболический тангенс от аргумента x.

  ⇑

2.1. Функции cmath.acosh(), cmath.asinh(), cmath.atanh(). Гиперболический арккосинус, арксинус, арктангенс

Для вычисления гиперболического арккосинуса от аргумента x используется функция

cmath.acosh(x)

Для данной функции существует один разрез ветви, который простирается слева от -1 вдоль вещественной оси к -∞.

Этот разрез непрерывен сверху.

Для вычисления гиперболического арксинуса от аргумента x используется функция

cmath.asinh(x)

Здесь есть два разветвления. Первое разветвление простирается от 1j вдоль мнимой оси к ∞j.

Это разветвление является непрерывным справа. Второе разветвление простирается от -1j вдоль мнимой оси к -∞j и есть непрерывным справа.

Для вычисления гиперболического арктангенса от аргумента x используется функция

cmath.atanh(x)

Здесь есть два разветвления. Одно разветвление расширяется от 1 вдоль вещественной оси до ∞ и непрерывно снизу. Второе расширяется от -1 вдоль вещественной оси до -∞ и непрерывно сверху.

Пример.

В примере реализовано вычисление гиперболического арккосинуса, гиперболического арксинуса и гиперболического арктангенса. Также демонстрируется вывод результата для гиперболического арккосинуса в удобной форме с точностью 2 знака после запятой.

# Тригонометрические функции acosh(), asinh(), atanh()

# 1.  Подключить модуль cmath
import cmath

# 2. Получить комплексное число с клавиатуры
re = int(input('re = ')) # вещественная часть
im = int(input('im = ')) # мнимая часть
z = complex(re, im)

# 3. Вычислить гиперболический арккосинус аргумента z
# и вывести его с точностью 2 знака после запятой
# 3.1. Получить значение
arc_cosh = cmath.acos(z)

# 3.2. Сформировать составляющие комплексного числа
re_str = '%.2f' % arc_cosh.real # вещественная часть комплексного числа arc_cosh
im_str = '%.2f' % arc_cosh.imag # мнимая часть

# 3.3. Вывести на экран в удобной форме
if arc_cosh.imag>0:
    print('arc_cosh = ' + re_str + '+' + im_str + 'j')
elif arc_cosh.imag==0:
    print('arc_cosh = ' + re_str)
else:
    print('arc_cosh = ' + re_str + im_str + 'j')

# 4. Вычислить и вывести гиперболический арктангенс
arc_tanh = cmath.atanh(z)
print('arc_tanh = ', arc_tanh)

# 5.

  

  
  Вычислить и вывести гиперболический арксинус
arc_sinh = cmath.asinh(z)
print('arc_sinh = ', arc_sinh)

Тестовый пример

re = 3
im = -4
arc_cosh = 0.94+2.31j
arc_tanh = (0.1175009073114339-1.4099210495965755j)
arc_sinh = (2.2999140408792695-0.9176168533514787j)

  ⇑

2.2. Функции cmath.cosh(), cmath.sinh(), cmath.tanh(). Гиперболический косинус, синус, тангенс

Для вычисления гиперболического косинусу, синуса и тангенса соответственно используются функции

cmath.cosh(x)
cmath.sinh(x)
cmath.tanh(x)

Пример.

# Тригонометрические функции cosh(), sinh(), tanh()

# 1. Подключить модуль cmath
import cmath

# 2. Получить комплексное число с клавиатуры
re = int(input('re = ')) # вещественная частина
im = int(input('im = ')) # мнимая частина
z = complex(re, im)

# 3. Вычислить гиперболический косинус аргумента z
# и вывести его с точностью 2 знака после запятой
# 3.
  1. Получить значение
cosh = cmath.cosh(z)

# 3.2. Сформировать составляющие комплексного числа
re_str = '%.2f' % cosh.real # вещественная часть комплексного числа cosh
im_str = '%.2f' % cosh.imag # мнимая часть

# 3.3. Вывести на экран в удобной форме
res_str = re_str
if cosh.imag>0:
    res_str += '+'
res_str += im_str + 'j'
print('cosh = ' + res_str)

# 4. Вычислить и вывести гиперболический тангенс
tanh = cmath.tanh(z)
print('tanh = ', tanh)

# 5. Вычислить и вывести гиперболический синус
sinh = cmath.sinh(z)
print('sinh = ', sinh)

Тестовый пример

re = 4
im = -3
cosh = -27.03-3.85j
tanh = (0.999355987381473+0.0001873462046294784j)
sinh = (-27.016813258003932-3.8537380379193773j)

  ⇑

3. Функции классификаций

К функциям классификаций модуля cmath относятся следующие:

  • cmath.isinfinite(x) — определяет, есть ли конечной вещественная и мнимая часть комплексного числа x;
  • cmath. isinf(x) — определяет, есть ли бесконечной вещественная или мнимая части комплексного числа x;
  • cmath.isnan(x) — определяет, имеют ли значение Nan вещественная или мнимая части комплексного числа x;
  • cmath.isclose(x) — определяет близость двух значений между собой.

  ⇑

3.1. cmath.isfinite(). Конечность комплексного числа

Функция

cmath.isfinite(x)

возвращает True, если вещественная и мнимая части комплексного числа есть конечными. В противном случае функция возвращает False.

Пример.

# Функция isfinite()

# 1. Подключить модуль cmath
import cmath

# 2. Получить комплексное число с клавиатуры
re = int(input('re = ')) # вещественная часть
im = int(input('im = ')) # мнимая часть
z = complex(re, im)

# 3. Использование функции isfinite()
res = cmath.isfinite(z)

if res:
    print('Both parts are finite.')
else:
    print('Both parts are not finite. ')

Тестовый пример

re = 5
im = -2
Both parts are finite.

  ⇑

3.2. cmath.isinf(). Конечность составляющих комплексного числа

Функция

cmath.isinf(x)

возвращает True, если вещественная (x.real) или мнимая (x.imag) части комплексного числа есть бесконечными. В противном случае, возвращается False.

Пример.

# Функция isinf()

# 1. Подключить модуль cmath
import cmath

# 2. Получить комплексное число с клавиатуры
re = int(input('re = ')) # вещественная часть
im = int(input('im = ')) # мнимая часть
z = complex(re, im)

# 3. Использование функции isinf()
res = cmath.isinf(z)

if res:
    print('Both parts are not finite.')
else:
    print('Both parts are finite.')

Тестовый пример

re = 5
im = -3
Both parts are finite.

  ⇑

3.3. cmath.isnan(). Проверка составляющих комплексного числа на значение Nan

Функция

cmath. isnan(x)

возвращает True, если одна из частей (вещественная или мнимая) комплексного числа имеет значение Nan. В противном случае функция возвращает False.

Пример.

# Функция isnan()

# 1. Подключить модуль cmath
import cmath

# 2. Получить комплексное число с клавиатуры
re = int(input('re = ')) # вещественная часть
im = int(input('im = ')) # мнимая часть
z = complex(re, im)

# 3. Использование функции isnan()
res = cmath.isnan(z)

if res:
    print('One of the parts is equal to the Nan value.')
else:
    print('Both parts are not equal to Nan.')

Тестовый пример

re = 2
im = -7
Both parts are not equal to Nan.

  ⇑

3.4. cmath.isclose(). Определение близости двух значений между собой

Функция cmath.isclose() позволяет определить близость двух значений между собой на основе заданной точности. Согласно документации Python синтаксис объявления функции следующий:

cmath. isclose(a, b, rel_tol=1e-09, abs_tol = 0.0)

здесь

  • a, b — комплексные числа, которые сравниваются между собой. Если значения близки (равны с указанной точностью), то функция возвращает True, иначе функция возвращает False;
  • rel_tol — необязательный параметр, задает относительную погрешность при сравнении;
  • abs_tol — необязательный параметр, который определяет абсолютную погрешность между значениями элементов.

Пример.

# Функция isclose()

# Подключить модуль cmath
import cmath

# Случай 1. Два комплексных числа не равны
z1 = complex(2.5, 3.2) # z = 2.5+3.2j
z2 = complex(2.5000001, 3.2) # z = 2.5000001+3.2j

# Использование функции isclose()
res = cmath.isclose(z1, z2) # False
if res:
    print('z1 == z2')
else:
    print('z1 != z2')

# Случай 2. Два комплексных числа равны
z1 = complex(7.2, -1.7) # z1 = 7.2-1.7j
z2 = complex(7.2, -1. 7) # z2 = 7.2-1.7j

# Использование функции isclose()
res = cmath.isclose(z1, z2) # True
if res:
    print('z1 == z2')
else:
    print('z1 != z2')

# Случай 3. Два комплексных числа равны с указанной относительной точностью
z1 = complex(3.001, 2.8)
z2 = complex(3.0, 2.8)

# Использование функции isclose(), указывается относительная точность 0.01
res = cmath.isclose(z1, z2, rel_tol=0.01) # z1 == z2
if res:
    print('z1 == z2')
else:
    print('z1 != z2')

# Случай 4. Два комплексных числа равны с указанной абсолютной точностью
z1 = complex(1.0001, 5.5)
z2 = complex(1.0, 5.5)

# Вызов функции isclose(), указывается абсолютная точность 0.001
res = cmath.isclose(z1, z2, abs_tol=0.001) # z1 == z2
if res:
    print('z1 == z2')
else:
    print('z1 != z2')

Тестовый пример

z1 != z2
z1 == z2
z1 == z2
z1 == z2

  ⇑

Связанные темы

  • Комплексные числа. Модуль cmath. Создание комплексного числа. Класс complex. Функции и константы модуля cmath
  • Функции преобразования в полярные координати и наоборот. Степенные и логарифмические функции
  • Представление чисел разных форматов. Базовые числовые типы. Функции преобразования чисел

  ⇑

 

Модуль Sin x + sin y = 0.5 Sin x • sin y = -0.5

Ответы
13. 02.19

Если модуль относится ко всей сумме sinx + siny:

13. 02.19

Михаил Александров
Читать ответы

Евгений
Читать ответы

Андрей Андреевич
Читать ответы

Посмотреть всех экспертов из раздела Учеба и наука

Пользуйтесь нашим приложением

встроенных математических функций SQL

встроенных математических функций SQL

Маленький. Быстрый. Надежный.
Выберите любые три.

  • Дом
  • Меню
  • О компании
  • Документация
  • Скачать
  • Лицензия
  • Поддержка
  • Покупка

Встроенные математические функции SQL

Математические функции, показанные ниже, являются частью Исходный файл объединения SQLite, но активны только если объединение составлено с использованием -DSQLITE_ENABLE_MATH_FUNCTIONS параметр времени компиляции.

Аргументами математических функций могут быть целые числа, числа с плавающей запятой, или строки или капли, которые выглядят как целые или действительные числа. Если какой-либо аргумент имеет значение NULL или представляет собой строку или большой двоичный объект, который не может быть легко преобразован в число, то функция вернет NULL. Эти функции также возвращают NULL для ошибок домена, таких как попытка извлечь квадратный корень из отрицательного числа или вычислить арккосинус значение больше 1,0 или меньше -1,0.

Значения, возвращаемые этими функциями, часто являются приблизительными. Например, функция pi() возвращает 3.1415926535897931159979634685441851615

171875 который примерно на 1,22465e-16 слишком мало, но это самое близкое доступное приближение для двойников IEEE754.

  • акос(Х)
  • акош(Х)
  • асин(Х)
  • асинх(Х)
  • атан(Х)
  • атан2(Y,X)
  • атан(Х)
  • потолок(Х)
  • потолок(Х)
  • соз(Х)
  • кош(Х)
  • градусов(Х)
  • опыт(Х)
  • этаж(Х)
  • пер(Х)
  • лог(В,Х)
  • лог(Х)
  • лог10(Х)
  • лог2(Х)
  • мод(Х,У)
  • пи()
  • pow(X,Y)
  • мощность(X,Y)
  • радиан(Х)
  • грех(Х)
  • синх(Х)
  • кв.(X)
  • желтовато-коричневый(X)
  • танх(Х)
  • ствол(Х)

акос( X )

Возвращает арккосинус X. Результат в радианах.

акош( X )

Верните гиперболический арккосинус X.

асин( X )

Возвращает арксинус X. Результат в радианах.

asinh( X )

Верните гиперболический арксинус X.

атан( X )

Возвращает арктангенс X. Результат в радианах.

атан2( Y , X )

Возвращает арктангенс Y/X. Результат в радианах. результат помещается в правильный квадрант в зависимости от знаков X и Y.

атанх( х )

Верните гиперболический арктангенс X.

потолок( X )
потолок( X )

Возвращает первое представимое целочисленное значение, большее или равное X. Для положительных значений X эта процедура округляет от нуля. Для отрицательных значений X эта процедура округляет до нуля.

потому что ( х )

Возвратите косинус X. X в радианах.

ш( Х )

Верните гиперболический косинус X.

градусов ( х )

Преобразование значения X из радианов в градусы.

ехр( X )

Вычислить e (число Эйлера, приблизительно 2,71828182845905) поднято в степень Х.

этаж( X )

Возвращает первое представимое целочисленное значение, меньшее или равное X. Для положительных чисел эта функция округляет до нуля. Для отрицательных чисел эта функция округляет от нуля.

лин ( х )

Верните натуральный логарифм X.

журнал( X )
журнал 10( X )
журнал( B , X )

Возвращает логарифм по основанию 10 для X. Или, для версии с двумя аргументами, вернуть логарифм X по основанию B.

Примечание о совместимости: SQLite работает как PostgreSQL в том смысле, что функция log() вычисляет логарифм по основанию 10. Большинство других механизмов баз данных SQL вычисляют натуральный логарифм для log(). В версии log(B,X) с двумя аргументами первый аргумент является основанием, а второй аргумент является операндом. Это то же, что и в PostgreSQL и MySQL, но отличается от SQL Server, который использует второй аргумент в качестве базы и первый аргумент в качестве операнда.

log2( X )

Верните логарифм по основанию 2 для числа X.

мод( X , Y )

Возвращает остаток после деления X на Y. Это похоже на «%» оператор, за исключением того, что он работает для нецелочисленных аргументов.

пи()

Возвращает приближение для π.

pow( X , Y )
power( X , Y )

Вычислите X, возведенное в степень Y.

радиан ( X )

Преобразование X из градусов в радианы.

грех( X )

Возвратите синус X. X в радианах.

синх( X )

Верните гиперболический синус X.

кв.( х )

Возвращает квадратный корень из X. Если X отрицательное значение, возвращается NULL.

желтовато-коричневый( X )

Возвратите тангенс X. X в радианах.

танх( X )

Верните гиперболический тангенс X.

ствол( X )

Возвращает представимое целое число между X и 0 (включительно) что дальше всего от нуля. Или, другими словами, вернуть целая часть X с округлением до нуля. Функция trunc() аналогична функциям потолка(X) и пола(X), за исключением что он всегда округляется до нуля, тогда как потолок (X) и пол (X) округляются вверх и вниз соответственно.

Последнее изменение этой страницы: 20.12.2021, 21:50:59UTC

Математические функции

Математические функции

Следующий список включает встроенные математические функции, которые можно использовать, например, при определении переменных или непосредственно в выражениях в интерфейсе физики или в настройках функций. Имена функций — это зарезервированные имена, которые нельзя использовать для пользовательских функций, но их можно использовать для имен переменных и параметров.

Таблица 5-6: Математические функции

Имя

Описание

Пример синтаксиса

абс

Абсолютное значение

абс(х)

акос

Арккосинус (в радианах)

акос(х)

акош

Арктический гиперболический косинус

акош(х)

или

Арккотангенс (в радианах)

акот(х)

или

Арктический гиперболический котангенс

акот(х)

акск

Арккосеканс (в радианах)

акск(х)

акч

Арктический гиперболический косеканс

акш(х)

аргумент

Фазовый угол (в радианах)

аргумент(х)

асек

Арксеканс (в радианах)

асек(х)

асеч

Арктический гиперболический секанс

асеч(х)

как

Инверсный синус (в радианах)

асин(х)

как

Обратный гиперболический синус

асинх(х)

атан

Арктангенс (в радианах)

атан(х)

атан2

Арктангенс четырех квадрантов (в радианах)

атан2(у,х)

атанх

Арктический гиперболический тангенс

атан(х)

бессель

Функция Бесселя первого рода

бессель(а,х)

Бессели

Функция Бесселя второго рода

бессели (а, х)

бессели

Модифицированная функция Бесселя первого рода

бессели(а,х)

бесселк

Модифицированная функция Бесселя второго рода

бесселк(а,х)

потолок

Ближайшее следующее целое число

потолок(х)

соединение

Комплексно-сопряженный

соединение(х)

потому что

Косинус (аргумент в радианах)

кос(х)

кош

Гиперболический косинус

кош(х)

детская кроватка

Котангенс (аргумент в радианах)

детская кроватка(x)

ткань

Гиперболический котангенс

ткань(х)

КСК

Косеканс (аргумент в радианах)

КСК(х)

чш

Гиперболический косеканс

чш(х)

эрф

Функция ошибки

эрф(х)

erfinv

Обратная функция ошибки

erfinv(x)

опыт

Экспоненциальная функция пр. То есть exp(1) — это математическая константа e (число Эйлера).

ехр(х)

этаж

Ближайшее предыдущее целое число

этаж(х)

гамма

Гамма-функция

гамма(х)

изображение

Мнимая часть

изображение(и)

журнал

Натуральный логарифм

лог(х)

лог10

Десятичный логарифм (основание 10)

лог10(х)

журнал2

Логарифм по основанию 2

лог2(х)

макс.

Максимум два аргумента

макс(а,б)

мин

Минимум два аргумента

мин(а,б)

мод

Оператор по модулю

мод(а,б)

фунтов на квадратный дюйм

Пси-функция и ее производные

фунтов на квадратный дюйм (х, к)

случайный

Случайная функция, равномерное распределение

случайный(х,у)

случайныйнормальный

Случайная функция, нормальное (гауссово) распределение

случайный нормальный (х, у)

диапазон

Создать диапазон чисел

диапазон(а,шаг,б)

реальный

Действительная часть

реальный(у)

раунд

Округлить до ближайшего целого числа

раунд(х)

сек

Секанс (аргумент в радианах)

сек(х)

сек

Гиперболический секанс

сек(х)

знак

Сигнум-функция

знак(и)

грех

Синус (аргумент в радианах)

грех(х)

с

Гиперболический синус

ш(х)

кв

Квадратный корень

кв.

No related posts.

Добавить комментарий

Ваш адрес email не будет опубликован. Обязательные поля помечены *

© 2015 - 2019 Муниципальное казённое общеобразовательное учреждение «Таловская средняя школа»

Карта сайта