Формула координаты середины вектора: Середина отрезка. Координаты середины отрезка

Формулы деления отрезка в данном отношении. Формулы координат середины отрезка

Как найти координаты середины отрезка
Для начала разберемся, что такое середина отрезка.
Серединой отрезка считают точку, которая принадлежит данному отрезку и отстоит на одинаковое расстояние от его концов.

Координаты такой точки несложно найти, если известны координаты концов этого отрезка. В таком случае координаты середины отрезка будут равны половине суммы соответствующих координат концов отрезка.
Координаты середины отрезка часто находят, решая задачи на медиану, среднюю линию и т.п.
Рассмотрим вычисление координат середины отрезка для двух случаев: когда отрезок задан на плоскости и задан в пространстве.
Пусть отрезок на плоскости задан двумя точками с координатами и . Тогда координаты середины отрезка РН рассчитываются по формуле:

Пусть отрезок задан в пространстве двумя точками с координатами и . Тогда координаты середины отрезка РН рассчитываются по формуле:

Пример.

Найти координаты точки К — середины МО, если М (—1; 6) и О (8; 5).

Решение.
Поскольку точки имеют две координаты, значит, отрезок задан на плоскости. Используем соответствующие формулы:

Следовательно, середина МО будет иметь координаты К (3,5; 5,5).

Ответ. К (3,5; 5,5).

Очень часто в задаче C2 требуется работать с точками, которые делят отрезок пополам. Координаты таких точек легко считаются, если известны координаты концов отрезка.

Итак, пусть отрезок задан своими концами — точками A = (x a ; y a ; z a) и B = (x b ; y b ; z b). Тогда координаты середины отрезка — обозначим ее точкой H — можно найти по формуле:

Другими словами, координаты середины отрезка — это среднее арифметическое координат его концов.

· Задача . Единичный куб ABCDA 1 B 1 C 1 D 1 помещен в систему координат так, что оси x, y и z направлены вдоль ребер AB, AD и AA 1 соответственно, а начало координат совпадает с точкой A. Точка K — середина ребра A 1 B 1 .

Найдите координаты этой точки.

Решение . Поскольку точка K — середина отрезка A 1 B 1 , ее координаты равных среднему арифметическому координат концов. Запишем координаты концов: A 1 = (0; 0; 1) и B 1 = (1; 0; 1). Теперь найдем координаты точки K:

Ответ : K = (0,5; 0; 1)

· Задача . Единичный куб ABCDA 1 B 1 C 1 D 1 помещен в систему координат так, что оси x, y и z направлены вдоль ребер AB, AD и AA 1 соответственно, а начало координат совпадает с точкой A. Найдите координаты точки L, в которой пересекаются диагонали квадрата A 1 B 1 C 1 D 1 .

Решение . Из курса планиметрии известно, что точка пересечения диагоналей квадрата равноудалена от всех его вершин. В частности, A 1 L = C 1 L, т.е. точка L — это середина отрезка A 1 C 1 . Но A 1 = (0; 0; 1), C 1 = (1; 1; 1), поэтому имеем:

Ответ : L = (0,5; 0,5; 1)

Простейшие задачи аналитической геометрии.
Действия с векторами в координатах

Задания, которые будут рассмотрены, крайне желательно научиться решать на полном автомате, а формулы запомнить наизусть , даже специально не запоминать, сами запомнятся =) Это весьма важно, поскольку на простейших элементарных примерах базируются другие задачи аналитической геометрии, и будет досадно тратить дополнительное время на поедание пешек. Не нужно застёгивать верхние пуговицы на рубашке, многие вещи знакомы вам со школы.

Изложение материала пойдет параллельным курсом – и для плоскости, и для пространства. По той причине, что все формулы… сами увидите.

Не составляет никакого труда. Для их расчета существует простое выражение, которое легко запомнить. Например, если координаты концов какого-либо отрезка соответственно равняются (х1; у1) и (х2; у2) соответственно, то координаты его середины рассчитываются как среднее арифметическое этих координат, то есть:

Вот и вся сложность.
Рассмотрим расчет координат центра одного из отрезков на конкретном примере, как Вы и просили.

Задача.
Найти координаты некоей точки М, если она является серединой (центром) отрезка КР, концов которого имеют такие координаты: (—3; 7) и (13; 21) соответственно.

Решение.
Используем рассмотренную выше формулу:

Ответ . М (5; 14).

С помощью данной формулы можно также найти не только координаты середины какого-либо отрезка, но и его концов. Рассмотрим пример.

Задача.
Даны координаты двух точек (7; 19) и (8; 27). Найти координаты одного из концов отрезка, если предыдущие две точки являются его концом и серединой.

Решение.
Обозначим концы отрезка К и Р, а его середину S. Перепишем формулу с учетом новых названий:

Подставим известные координаты и вычислим отдельные координаты:

Начальные геометрические сведения

Понятие отрезка, как и понятие точки, прямой, луча и угла, относится к начальным геометрическим сведениям. С перечисленных понятий начинается изучение геометрии.

Под «начальными сведениями» обычно понимают нечто элементарное и простое. В понимании, возможно, это так и есть. Тем не менее, такие простые понятия часто встречаются и оказываются необходимыми не только в нашей повседневной жизни, но и в производстве, строительстве и прочих сферах нашей жизнедеятельности.

Начнём с определений.

Определение 1

Отрезок — часть прямой, ограниченная двумя точками (концами).

Если концы отрезка являются точками $A$ и $B$, то образованный отрезок записывают как $AB$ или $BA$. Такому отрезку принадлежат точки $A$ и $B$, а также все точки прямой, лежащие между этими точками.

Определение 2

Середина отрезка — точка отрезка, которая делит его пополам на два равных отрезка.

Если это точка $C$, то $AC=CB$.

Измерение отрезка происходит сравнением с определённым отрезком, принятым за единицу измерения. Чаще всего используют сантиметр. Если в заданном отрезке сантиметр укладывается ровно четыре раза, то это означает, что длина данного отрезка равна $4$ см.

Введём простое наблюдение. Если точка делит отрезок на два отрезка, то длина всего отрезка равна сумме длин этих отрезков.

Формула нахождения координаты середины отрезка

Формула нахождения координаты середины отрезка относится к курсу аналитической геометрии на плоскости.

Дадим определение координатам.

Определение 3

Координаты — это определённые (или упорядоченные) числа, которые показывают положение точки на плоскости, на поверхности или в пространстве.

В нашем случае, координаты отмечаются на плоскости, определённой координатными осями.

Рисунок 3. Координатная плоскость. Автор24 — интернет-биржа студенческих работ

Опишем рисунок. На плоскости выбрана точка, называемая началом координат. Её обозначают буквой $O$. Через начало координат проведены две прямые (координатные оси), пересекающиеся под прямым углом, причём одна из них строго горизонтальная, а другая — вертикальная. Такое положение считается обычным. Горизонтальная прямая называется осью абсцисс и обозначается $OX$, вертикальная — осью ординат $OY$.

Таким образом, оси определяют плоскость $XOY$.

Координаты точек в такой системе определяются двумя числами.

Существуют разные формулы (уравнения), определяющие те или иные координаты. Обычно в курсе аналитической геометрии изучают разные формулы прямых, углов, длины отрезка и прочие.

Перейдём сразу к формуле координаты середины отрезка.

Определение 4

Если координаты точки $E(x,y)$ — это середина отрезка $M_1M_2$, то:

Рисунок 4. Формула нахождения координаты середины отрезка. Автор24 — интернет-биржа студенческих работ

Практическая часть

Примеры из школьного курса геометрии достаточно просты. Рассмотрим несколько основных.

Для лучшего понимания, рассмотрим для начала элементарный наглядный пример.

Пример 1

Имеем рисунок:

На рисунке отрезки $AC, CD, DE, EB$ равны.

1. Серединой каких отрезков является точка $D$?
2. Какая точка является серединой отрезка $DB$?

1. точка $D$ является серединой отрезков $AB$ и $CE$;
2. точка $E$.

Рассмотрим другой простой пример, в котором нужно вычислить длину.

Пример 2

Точка $B$ — середина отрезка $AC$. $AB = 9$ см. Какая длина $AC$?

Так как т. $B$ делит $AC$ пополам, то $AB = BC= 9$ см. Значит, $AC = 9+9=18$ см.

Ответ: 18 см.

Прочие подобные примеры обычно идентичны и ориентированы на умение сопоставлять значения длин и их представление с алгебраическими действиями. Нередко в задачах встречаются случаи, когда сантиметр не укладывается ровное количество раз в отрезок. Тогда единицу измерения делят на равные части. В нашем случае сантиметр делится на 10 миллиметров. Отдельно измеряют остаток, сравнивая с миллиметром. Приведём пример, демонстрирующий такой случай.

В статье ниже будут освещены вопросы нахождения координат середины отрезка при наличии в качестве исходных данных координат его крайних точек. Но, прежде чем приступить к изучению вопроса, введем ряд определений.

Определение 1

Отрезок – прямая линия, соединяющая две произвольные точки, называемые концами отрезка. В качестве примера пусть это будут точки A и B и соответственно отрезок A B .

Если отрезок A B продолжить в обе стороны от точек A и B , мы получим прямую A B . Тогда отрезок A B – часть полученной прямой, ограниченный точками A и B . Отрезок A B объединяет точки A и B , являющиеся его концами, а также множество точек, лежащих между. Если, к примеру, взять любую произвольную точку K , лежащую между точками A и B , можно сказать, что точка K лежит на отрезке A B .

Определение 2

Длина отрезка – расстояние между концами отрезка при заданном масштабе (отрезке единичной длины). Длину отрезка A B обозначим следующим образом: A B .

Определение 3

Середина отрезка – точка, лежащая на отрезке и равноудаленная от его концов. Если середину отрезка A B обозначить точкой C , то верным будет равенство: A C = C B

Исходные данные: координатная прямая O x и несовпадающие точки на ней: A и B . Этим точкам соответствуют действительные числа x A и x B . Точка C – середина отрезка A B: необходимо определить координату x C .

Поскольку точка C является серединой отрезка А В, верным будет являться равенство: | А С | = | С В | . Расстояние между точками определяется модулем разницы их координат, т.е.

| А С | = | С В | ⇔ x C — x A = x B — x C

Тогда возможно два равенства: x C — x A = x B — x C и x C — x A = — (x B — x C)

Из первого равенства выведем формулу для координаты точки C: x C = x A + x B 2 (полусумма координат концов отрезка).

Из второго равенста получим: x A = x B , что невозможно, т.к. в исходных данных — несовпадающие точки. Таким образом, формула для определения координат середины отрезка A B с концами A (x A) и B (x B):

Полученная формула будет основой для определения координат середины отрезка на плоскости или в пространстве.

Исходные данные: прямоугольная система координат на плоскости О x y , две произвольные несовпадающие точки с заданными координатами A x A , y A и B x B , y B . Точка C – середина отрезка A B . Необходимо определить координаты x C и y C для точки C .

Возьмем для анализа случай, когда точки A и B не совпадают и не лежат на одной координатной прямой или прямой, перпендикулярной одной из осей. A x , A y ; B x , B y и C x , C y — проекции точек A , B и C на оси координат (прямые О х и О y).

Согласно построению прямые A A x , B B x , C C x параллельны; прямые также параллельны между собой. Совокупно с этим по теореме Фалеса из равенства А С = С В следуют равенства: А x С x = С x В x и А y С y = С y В y , и они в свою очередь свидетельствуют о том, что точка С x – середина отрезка А x В x , а С y – середина отрезка А y В y . И тогда, опираясь на полученную ранее формулу, получим:

x C = x A + x B 2 и y C = y A + y B 2

Этими же формулами можно воспользоваться в случае, когда точки A и B лежат на одной координатной прямой или прямой, перпендикулярной одной из осей. Проводить детальный анализ этого случая не будем, рассмотрим его лишь графически:

Резюмируя все выше сказанное, координаты середины отрезка A B на плоскости с координатами концов A (x A , y A) и B (x B , y B) определяются как :

(x A + x B 2 , y A + y B 2)

Исходные данные: система координат О x y z и две произвольные точки с заданными координатами A (x A , y A , z A) и B (x B , y B , z B) . Необходимо определить координаты точки C , являющейся серединой отрезка A B .

A x , A y , A z ; B x , B y , B z и C x , C y , C z — проекции всех заданных точек на оси системы координат.

Согласно теореме Фалеса верны равенства: A x C x = C x B x , A y C y = C y B y , A z C z = C z B z

Следовательно, точки C x , C y , C z являются серединами отрезков A x B x , A y B y , A z B z соответственно. Тогда, для определения координат середины отрезка в пространстве верны формулы:

x C = x A + x B 2 , y c = y A + y B 2 , z c = z A + Z B 2

Полученные формулы применимы также в случаях, когда точки A и B лежат на одной из координатных прямых; на прямой, перпендикулярной одной из осей; в одной координатной плоскости или плоскости, перпендикулярной одной из координатных плоскостей.

Определение координат середины отрезка через координаты радиус-векторов его концов

Формулу для нахождения координат середины отрезка также можно вывести согласно алгебраическому толкованию векторов.

Исходные данные: прямоугольная декартова система координат O x y , точки с заданными координатами A (x A , y A) и B (x B , x B) . Точка C – середина отрезка A B .

Согласно геометрическому определению действий над векторами верным будет равенство: O C → = 1 2 · O A → + O B → . Точка C в данном случае – точка пересечения диагоналей параллелограмма, построенного на основе векторов O A → и O B → , т. е. точка середины диагоналей.Координаты радиус-вектора точки равны координатам точки, тогда верны равенства: O A → = (x A , y A) , O B → = (x B , y B) . Выполним некоторые операции над векторами в координатах и получим:

O C → = 1 2 · O A → + O B → = x A + x B 2 , y A + y B 2

Следовательно, точка C имеет координаты:

x A + x B 2 , y A + y B 2

По аналогии определяется формула для нахождения координат середины отрезка в пространстве:

C (x A + x B 2 , y A + y B 2 , z A + z B 2)

Примеры решения задач на нахождение координат середины отрезка

Среди задач, предполагающих использование полученных выше формул, встречаются, как и те, в которых напрямую стоит вопрос рассчитать координаты середины отрезка, так и такие, что предполагают приведение заданных условий к этому вопросу: зачастую используется термин «медиана», ставится целью нахождение координат одного из концов отрезка, а также распространены задачи на симметрию, решение которых в общем также не должно вызывать затруднений после изучения настоящей темы. Рассмотрим характерные примеры.

Пример 1

Исходные данные: на плоскости – точки с заданными координатами А (- 7 , 3) и В (2 , 4) . Необходимо найти координаты середины отрезка А В.

Решение

Обозначим середину отрезка A B точкой C . Координаты ее буду определяться как полусумма координат концов отрезка, т.е. точек A и B .

x C = x A + x B 2 = — 7 + 2 2 = — 5 2 y C = y A + y B 2 = 3 + 4 2 = 7 2

Ответ : координаты середины отрезка А В — 5 2 , 7 2 .

Пример 2

Исходные данные: известны координаты треугольника А В С: А (- 1 , 0) , В (3 , 2) , С (9 , — 8) . Необходимо найти длину медианы А М.

Решение

1. По условию задачи A M – медиана, а значит M является точкой середины отрезка B C . В первую очередь найдем координаты середины отрезка B C , т.е. точки M:

x M = x B + x C 2 = 3 + 9 2 = 6 y M = y B + y C 2 = 2 + (- 8) 2 = — 3

1. Поскольку теперь нам известны координаты обоих концов медианы (точки A и М), можем воспользоваться формулой для определения расстояния между точками и посчитать длину медианы А М:

A M = (6 — (- 1)) 2 + (- 3 — 0) 2 = 58

Ответ: 58

Пример 3

Исходные данные: в прямоугольной системе координат трехмерного пространства задан параллелепипед A B C D A 1 B 1 C 1 D 1 . Заданы координаты точки C 1 (1 , 1 , 0) , а также определена точка M , являющаяся серединой диагонали B D 1 и имеющая координаты M (4 , 2 , — 4) . Необходимо рассчитать координаты точки А.

Решение

Диагонали параллелепипеда имеют пересечение в одной точке, которая при этом является серединой всех диагоналей. Исходя из этого утверждения, можно иметь в виду, что известная по условиям задачи точка М является серединой отрезка А С 1 . Опираясь на формулу для нахождения координат середины отрезка в пространстве, найдем координаты точки А: x M = x A + x C 1 2 ⇒ x A = 2 · x M — x C 1 = 2 · 4 — 1 + 7 y M = y A + y C 1 2 ⇒ y A = 2 · y M — y C 1 = 2 · 2 — 1 = 3 z M = z A + z C 1 2 ⇒ z A = 2 · z M — z C 1 = 2 · (- 4) — 0 = — 8

Ответ: координаты точки А (7 , 3 , — 8) .

Если вы заметили ошибку в тексте, пожалуйста, выделите её и нажмите Ctrl+Enter

Формула нахождения середины отрезка по координатам. Нахождение координат середины отрезка: примеры, решения

Очень часто в задаче C2 требуется работать с точками, которые делят отрезок пополам.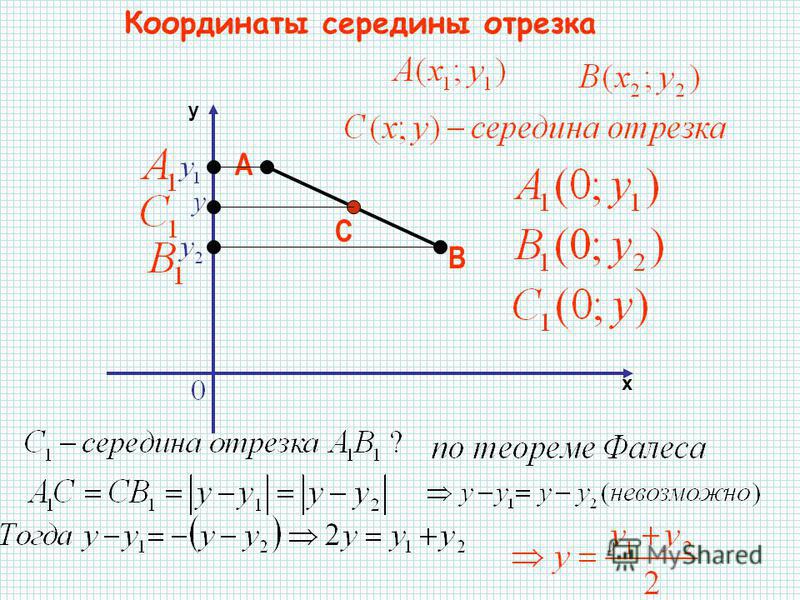 Координаты таких точек легко считаются, если известны координаты концов отрезка.

Итак, пусть отрезок задан своими концами — точками A = (x a ; y a ; z a) и B = (x b ; y b ; z b). Тогда координаты середины отрезка — обозначим ее точкой H — можно найти по формуле:

Другими словами, координаты середины отрезка — это среднее арифметическое координат его концов.

· Задача . Единичный куб ABCDA 1 B 1 C 1 D 1 помещен в систему координат так, что оси x, y и z направлены вдоль ребер AB, AD и AA 1 соответственно, а начало координат совпадает с точкой A. Точка K — середина ребра A 1 B 1 . Найдите координаты этой точки.

Решение . Поскольку точка K — середина отрезка A 1 B 1 , ее координаты равных среднему арифметическому координат концов. Запишем координаты концов: A 1 = (0; 0; 1) и B 1 = (1; 0; 1). Теперь найдем координаты точки K:

Ответ : K = (0,5; 0; 1)

· Задача . Единичный куб ABCDA 1 B 1 C 1 D 1 помещен в систему координат так, что оси x, y и z направлены вдоль ребер AB, AD и AA 1 соответственно, а начало координат совпадает с точкой A. Найдите координаты точки L, в которой пересекаются диагонали квадрата A 1 B 1 C 1 D 1 .

Решение . Из курса планиметрии известно, что точка пересечения диагоналей квадрата равноудалена от всех его вершин. В частности, A 1 L = C 1 L, т.е. точка L — это середина отрезка A 1 C 1 . Но A 1 = (0; 0; 1), C 1 = (1; 1; 1), поэтому имеем:

Ответ : L = (0,5; 0,5; 1)

Простейшие задачи аналитической геометрии.
Действия с векторами в координатах

Задания, которые будут рассмотрены, крайне желательно научиться решать на полном автомате, а формулы запомнить наизусть , даже специально не запоминать, сами запомнятся =) Это весьма важно, поскольку на простейших элементарных примерах базируются другие задачи аналитической геометрии, и будет досадно тратить дополнительное время на поедание пешек. Не нужно застёгивать верхние пуговицы на рубашке, многие вещи знакомы вам со школы.

Изложение материала пойдет параллельным курсом – и для плоскости, и для пространства. По той причине, что все формулы… сами увидите.

В статье ниже будут освещены вопросы нахождения координат середины отрезка при наличии в качестве исходных данных координат его крайних точек. Но, прежде чем приступить к изучению вопроса, введем ряд определений.

Yandex.RTB R-A-339285-1 Определение 1

Отрезок – прямая линия, соединяющая две произвольные точки, называемые концами отрезка. В качестве примера пусть это будут точки A и B и соответственно отрезок A B .

Если отрезок A B продолжить в обе стороны от точек A и B , мы получим прямую A B . Тогда отрезок A B – часть полученной прямой, ограниченный точками A и B . Отрезок A B объединяет точки A и B , являющиеся его концами, а также множество точек, лежащих между. Если, к примеру, взять любую произвольную точку K , лежащую между точками A и B , можно сказать, что точка K лежит на отрезке A B .

Определение 2

Длина отрезка – расстояние между концами отрезка при заданном масштабе (отрезке единичной длины). Длину отрезка A B обозначим следующим образом: A B .

Определение 3

Середина отрезка – точка, лежащая на отрезке и равноудаленная от его концов. Если середину отрезка A B обозначить точкой C , то верным будет равенство: A C = C B

Исходные данные: координатная прямая O x и несовпадающие точки на ней: A и B . Этим точкам соответствуют действительные числа x A и x B . Точка C – середина отрезка A B: необходимо определить координату x C .

Поскольку точка C является серединой отрезка А В, верным будет являться равенство: | А С | = | С В | . Расстояние между точками определяется модулем разницы их координат, т.е.

| А С | = | С В | ⇔ x C — x A = x B — x C

Тогда возможно два равенства: x C — x A = x B — x C и x C — x A = — (x B — x C)

Из первого равенства выведем формулу для координаты точки C: x C = x A + x B 2 (полусумма координат концов отрезка).

Из второго равенста получим: x A = x B , что невозможно, т.к. в исходных данных — несовпадающие точки. Таким образом, формула для определения координат середины отрезка A B с концами A (x A) и B (x B):

Полученная формула будет основой для определения координат середины отрезка на плоскости или в пространстве.

Исходные данные: прямоугольная система координат на плоскости О x y , две произвольные несовпадающие точки с заданными координатами A x A , y A и B x B , y B . Точка C – середина отрезка A B . Необходимо определить координаты x C и y C для точки C .

Возьмем для анализа случай, когда точки A и B не совпадают и не лежат на одной координатной прямой или прямой, перпендикулярной одной из осей. A x , A y ; B x , B y и C x , C y — проекции точек A , B и C на оси координат (прямые О х и О y).

Согласно построению прямые A A x , B B x , C C x параллельны; прямые также параллельны между собой. Совокупно с этим по теореме Фалеса из равенства А С = С В следуют равенства: А x С x = С x В x и А y С y = С y В y , и они в свою очередь свидетельствуют о том, что точка С x – середина отрезка А x В x , а С y – середина отрезка А y В y . И тогда, опираясь на полученную ранее формулу, получим:

x C = x A + x B 2 и y C = y A + y B 2

Этими же формулами можно воспользоваться в случае, когда точки A и B лежат на одной координатной прямой или прямой, перпендикулярной одной из осей. Проводить детальный анализ этого случая не будем, рассмотрим его лишь графически:

Резюмируя все выше сказанное, координаты середины отрезка A B на плоскости с координатами концов A (x A , y A) и B (x B , y B) определяются как :

(x A + x B 2 , y A + y B 2)

Исходные данные: система координат О x y z и две произвольные точки с заданными координатами A (x A , y A , z A) и B (x B , y B , z B) . Необходимо определить координаты точки C , являющейся серединой отрезка A B .

A x , A y , A z ; B x , B y , B z и C x , C y , C z — проекции всех заданных точек на оси системы координат.

Согласно теореме Фалеса верны равенства: A x C x = C x B x , A y C y = C y B y , A z C z = C z B z

Следовательно, точки C x , C y , C z являются серединами отрезков A x B x , A y B y , A z B z соответственно. Тогда, для определения координат середины отрезка в пространстве верны формулы:

x C = x A + x B 2 , y c = y A + y B 2 , z c = z A + Z B 2

Полученные формулы применимы также в случаях, когда точки A и B лежат на одной из координатных прямых; на прямой, перпендикулярной одной из осей; в одной координатной плоскости или плоскости, перпендикулярной одной из координатных плоскостей.

Определение координат середины отрезка через координаты радиус-векторов его концов

Формулу для нахождения координат середины отрезка также можно вывести согласно алгебраическому толкованию векторов.

Исходные данные: прямоугольная декартова система координат O x y , точки с заданными координатами A (x A , y A) и B (x B , x B) . Точка C – середина отрезка A B .

Согласно геометрическому определению действий над векторами верным будет равенство: O C → = 1 2 · O A → + O B → . Точка C в данном случае – точка пересечения диагоналей параллелограмма, построенного на основе векторов O A → и O B → , т. е. точка середины диагоналей.Координаты радиус-вектора точки равны координатам точки, тогда верны равенства: O A → = (x A , y A) , O B → = (x B , y B) . Выполним некоторые операции над векторами в координатах и получим:

O C → = 1 2 · O A → + O B → = x A + x B 2 , y A + y B 2

Следовательно, точка C имеет координаты:

x A + x B 2 , y A + y B 2

По аналогии определяется формула для нахождения координат середины отрезка в пространстве:

C (x A + x B 2 , y A + y B 2 , z A + z B 2)

Примеры решения задач на нахождение координат середины отрезка

Среди задач, предполагающих использование полученных выше формул, встречаются, как и те, в которых напрямую стоит вопрос рассчитать координаты середины отрезка, так и такие, что предполагают приведение заданных условий к этому вопросу: зачастую используется термин «медиана», ставится целью нахождение координат одного из концов отрезка, а также распространены задачи на симметрию, решение которых в общем также не должно вызывать затруднений после изучения настоящей темы. Рассмотрим характерные примеры.

Пример 1

Исходные данные: на плоскости – точки с заданными координатами А (- 7 , 3) и В (2 , 4) . Необходимо найти координаты середины отрезка А В.

Решение

Обозначим середину отрезка A B точкой C . Координаты ее буду определяться как полусумма координат концов отрезка, т.е. точек A и B .

x C = x A + x B 2 = — 7 + 2 2 = — 5 2 y C = y A + y B 2 = 3 + 4 2 = 7 2

Ответ : координаты середины отрезка А В — 5 2 , 7 2 .

Пример 2

Исходные данные: известны координаты треугольника А В С: А (- 1 , 0) , В (3 , 2) , С (9 , — 8) . Необходимо найти длину медианы А М.

Решение

1. По условию задачи A M – медиана, а значит M является точкой середины отрезка B C . В первую очередь найдем координаты середины отрезка B C , т.е. точки M:

x M = x B + x C 2 = 3 + 9 2 = 6 y M = y B + y C 2 = 2 + (- 8) 2 = — 3

1. Поскольку теперь нам известны координаты обоих концов медианы (точки A и М), можем воспользоваться формулой для определения расстояния между точками и посчитать длину медианы А М:

A M = (6 — (- 1)) 2 + (- 3 — 0) 2 = 58

Ответ: 58

Пример 3

Исходные данные: в прямоугольной системе координат трехмерного пространства задан параллелепипед A B C D A 1 B 1 C 1 D 1 . Заданы координаты точки C 1 (1 , 1 , 0) , а также определена точка M , являющаяся серединой диагонали B D 1 и имеющая координаты M (4 , 2 , — 4) . Необходимо рассчитать координаты точки А.

Решение

Диагонали параллелепипеда имеют пересечение в одной точке, которая при этом является серединой всех диагоналей. Исходя из этого утверждения, можно иметь в виду, что известная по условиям задачи точка М является серединой отрезка А С 1 . Опираясь на формулу для нахождения координат середины отрезка в пространстве, найдем координаты точки А: x M = x A + x C 1 2 ⇒ x A = 2 · x M — x C 1 = 2 · 4 — 1 + 7 y M = y A + y C 1 2 ⇒ y A = 2 · y M — y C 1 = 2 · 2 — 1 = 3 z M = z A + z C 1 2 ⇒ z A = 2 · z M — z C 1 = 2 · (- 4) — 0 = — 8

Ответ: координаты точки А (7 , 3 , — 8) .

Если вы заметили ошибку в тексте, пожалуйста, выделите её и нажмите Ctrl+Enter

Как найти середину отрезка с помощью циркуля?Элементарная задачка о нахождении середины отрезка при помощи циркуля была сформулирована еще в античности. Часто ее приписывают древнегреческим мудрецам, однако, скорее всего, она присутствовала и в других культурах, в которых была развита математика и геометрия (например, в древнеегипетской). В древности эта задача имела и вполне практическое применение, ведь знание того, как найти середину отрезка при помощи простейших измерительных приборов, было полезно, например, в землемерстве, землеустройстве и строительстве. Сегодня, при наличии сложной измерительной техники, такое задание скорее представляет упражнение для развития интеллектуальных способностей и пространственной фантазии школьников.

Как же на самом деле решается данная задача? Берем циркуль и открываем его таким образом, чтобы радиус предполагаемой окружности был очевидно больше половины заданного отрезка. Теперь, ставим основание (иглу) циркуля в одну из точек, ограничивающих отрезок, и рисуем окружность выбранного радиуса. В принципе, решая задачу о том, как построить середину отрезка, достаточно нарисовать и полукруг, располагающийся «внутри» отрезка. Затем устанавливаем иглу циркуля в другой конец отрезка и повторяем процедуру очерчивания полукруга.Проделав описанную процедуру, видим, что наши окружности пересекаются в двух точках. Берем линейку и соединяем эти две точки прямой линией. Получаем линию перпендикулярную исходному отрезку. Именно точка пересечения этой линии и отрезка и является серединой последнего.

Конечно, здесь важно понять саму сущность данной задачи. Почему центр отрезка получится именно там, где пересекутся линии? Знание смысла данной задачи может, например пригодиться, при поиска ответа на вопрос о том, как найти середину треугольника, а также при решении других, более сложных геометрических задач.Итак, если соединить крайние точки исходного отрезка с точками пересечения наших окружностей, то получим четырехугольник. Но какой четырехугольник? Все его стороны являются радиусами наших окружностей, а значит равными по длине (ведь мы использовали одинаковый радиус). Любой четырехугольник с равными сторонами представляет собой ромб, диагонали которого всегда пересекаются под прямым углом и, что более важно для нашей задачи, делят друг друга пополам. Именно в этом и состоит логика подобного решения задачи о построении середины отрезка при помощи циркуля.

Если же вопрос формулируется иначе, а именно о том, как найти координаты середины отрезка, то для его решения необходимо знать координаты его конечных точек. Координаты же середины будут равны полусуммам координат точек окончания отрезка. Конечно, здесь уже используется декартова система координат, в связи с чем данные задачи имеют разную сущность, хотя и решают одну проблему.

В любом случае, решение разных формулировок геометрических задач очень полезно для развития интеллекта и образного мышления ребенка. Поэтому не стоит пренебрегать этими инструментами личностного развития.

Инструкция

Если интервал является участком непрерывной числовой последовательности, то для нахождения ее середины используйте математические методы вычисления среднеарифметического значения. Минимальное значение (его начало) сложите с максимальным () и разделите результат пополам — это один из способов вычисления среднеарифметического значения. Например, это применимо, когда речь идет о возрастных интервала х. Скажем, серединой возрастного интервала в диапазоне от 21 года до 33 лет будет отметка в 27 лет, так как (21+33)/2=27.

Иногда удобнее использовать другой метод вычисления среднеарифметического значения между верхней и нижней границами интервала . В этом варианте сначала определите ширину диапазона — отнимите от максимального значения минимальное. Затем поделите полученную величину пополам и прибавьте результат к минимальному значению диапазона. Например, если нижняя соответствует значению 47,15, а верхняя — 79,13, то ширина диапазона составит 79,13-47,15=31,98. Тогда серединой интервала будет 63,14, так как 47,15+(31,98/2) = 47,15+15,99 = 63,14.

Если интервал не является участком обычной числовой последовательности, то вычисляйте его середину в соответствии с цикличностью и размерностью используемой измерительной шкалы. Например, если речь идет об историческом периоде, то серединой интервала будет являться определенная календарная дата. Так для интервала с 1 января 2012 года по 31 января 2012 серединой будет дата 16 января 2012.

Кроме обычных (закрытых) интервалов статистические методы исследований могут оперировать и «открытыми». У таких диапазонов одна из границ не определена. Например, открытый интервал может быть задан формулировкой «от 50 лет и старше». Середина в этом случае определяется методом аналогий — если все остальные диапазоны рассматриваемой последовательности имеют одинаковую ширину, то предполагается, что и этот открытый интервал такую же . В противном случае вам надо определить динамику ширины интервалов, предшествующих открытому, и его условную ширину, исходя из полученной тенденции изменения.

Источники:

• что такое открытый интервал

При изучении вариации – различий индивидуальных значений признака у единиц изучаемой совокупности – рассчитывают ряд абсолютных и относительных показателей. На практике наибольшее применение среди относительных показателей нашел коэффициент вариации. 2/N. Иными словами дисперсия – это средний квадрат отклонения от среднего арифметического значения. определяет, насколько в среднем отклоняются конкретные показатели ряда от их среднего значения. Оно является абсолютной мерой колеблемости признака, а потому четко интерпретируется.

Формула средней точки

Горячая математика

В одном измерении

На числовая линия , число на полпути между Икс 1 а также Икс 2 является

Икс 1 + Икс 2 2

Пример 1:

Найдите середину между − 1 а также 4 .

Используйте формулу. Середина

− 1 + 4 2 знак равно 3 2 знак равно 1,5 .

Пример 2:

Если 0,5 это середина п р ¯ и координата п является − 4 , найти координату р .

Используйте формулу.

− 4 + Икс 2 2 знак равно 0,5

Для начала умножьте обе части на 2 .

− 4 + Икс 2 знак равно 1

Затем добавьте 4 в обе стороны.

Икс 2 знак равно 5

Итак, координата р является 5 .

В двух измерениях

Предположим, вам даны две точки на плоскости ( Икс 1 , у 1 ) а также ( Икс 2 , у 2 ), и попросили найти точку на полпути между ними. Координаты этой средней точки будут:

( Икс 1 + Икс 2 2 , у 1 + у 2 2 )

Простой способ подумать об этом состоит в том, что Икс -координата середины — это среднее значение Икс -координаты двух точек, а также с у -координата.

Пример 1:

Найдите середину между ( − 2 , 5 ) а также ( 7 , 7 ) .

Используйте формулу. Координаты середины:

( − 2 + 7 2 , 5 + 7 2 )

Упрощать.

( 2,5 , 6 )

Пример 2:

Если Вопрос ( 2 , − 2 ) это середина п р ¯ а также п имеет координаты ( − 6 , − 6 ) , найти координаты р .

С помощью формулы напишите и решите два уравнения для координат точки. р .

Вопрос ( 2 , − 2 ) знак равно ( − 6 + Икс 2 2 , − 6 + у 2 2 )

Сначала найдите Икс -координата.

2 знак равно − 6 + Икс 2 2 4 знак равно − 6 + Икс 2 10 знак равно Икс 2

Затем найдите у -координата.

− 2 знак равно − 6 + у 2 2 − 4 знак равно − 6 + у 2 2 знак равно у 2

Итак, координаты г. р находятся ( 10 , 2 ) .

В трех измерениях

Это довольно легко догадаться, основываясь на формуле для двух измерений!

В 3 -мерное пространство, середина между ( Икс 1 , у 1 , г 1 ) а также ( Икс 2 , у 2 , г 1 ) является

( Икс 1 + Икс 2 2 , у 1 + у 2 2 , г 1 + г 2 2 )

Алгебра: формула средней точки

• Главная

• Узнать

• Алгебра

• Что такое алгебра
• Алгебра в повседневной жизни
• Основные алгебраические термины
• Методы решения по алгебре
• Линейные, нелинейные уравнения
• Алгебра Формулы
• Коммутативные ассоциативные законы
• Формула расстояния
• Фольга Метод
• Формула средней точки
• Скобки Правила
• Квадратичное уравнение
• Квадратичная формула
• Полиномиальные операции
• Полиномиальное сложение
• Полиномиальное вычитание
• Полиномиальное умножение
• Многочлен длинного деления
• Графики полиномиальных функций

Формула средней точки используется для нахождения точки (значения ее координат), которая расположена точно между двумя другими точками на плоскости. Эта формула находит огромное применение в геометрии.

Координаты точки (x, y), которая находится точно посередине между двумя точками (x ₁ , y ₁ ) и (x ₂ , y ₂ ), определяются как:

` x = ( x_(1 )+ x_2)/2 , y = ( y_(1 )+ y_2)/2 `

Аналогично, если мы хотим найти середину отрезка в трехмерном пространстве, мы можем определить середина использования:

`x = (x_(1)+ x_2)/2, y = (y_(1)+ y_2)/2, z = (z_(1)+ z_2)/2`

На приведенном ниже рисунке показана формула средней точки.

Объяснение:

При вычислении средней точки между двумя наборами координат отрезка, если предположить, что точка A равна x ₁ , y ₁ и x ₂ , y ₂ . Используя приведенную выше формулу средней точки, среднее значение координат x и координат y дает середину точек A и B.