Область определения функции
Каждая функция имеет свою собственную область определения. Целью этого материала является объяснение этого понятия и описание способов ее вычисления. Сначала мы введем основное определение, а потом на конкретных примерах покажем, как выглядит область определения основных элементарных функций (степенной, постоянной и др.) Разбирать случаи с более сложными функциями мы пока не будем.
В рамках данной статьи мы рассмотрим область определения функций, включающих в себя только одну переменную.
Понятие и обозначение области определения функции
Самое простое определение этого понятия дается в учебниках тогда, когда впервые вводится понятие функции как таковой. На этом этапе термином «область определения» обозначают множество всех возможных значений аргумента.
По мере углубления знаний о функциях определение сужается и усложняется. Так, в одном из учебников можно встретить следующую формулировку:
Определение 1Числовая функция с областью определения D – это соответствие значений переменной x некоторому числу y, которое находится в зависимых отношениях с x.
Используя это определение, охарактеризуем нужное нам понятие более четко:
Определение 2Областью определения функции называется множество значений аргумента, на котором можно задать эту функцию.
Теперь рассмотрим, как правильно обозначать ее на письме. Ранее мы договорились, что для записи самих функций будем использовать маленькие латинские буквы, например, g, f и др. Чтобы указать на наличие функциональной зависимости, используется запись вида y=f(x). Таким образом, функция f представляет собой некоторое правило, согласно которому каждому значению переменной x можно поставить в соответствие значение другой переменной y, которая находится в зависимых отношениях от x.
Возьмем для примера функцию y=x2. Можно записать ее как f(x)=x2. Это функция возведения в квадрат, которая ставит в соответствие каждому значению переменной x=x0 некоторое значение y=x02. Так, если мы возьмем число 3, то функция поставит ему в соответствие 9, поскольку 32=9.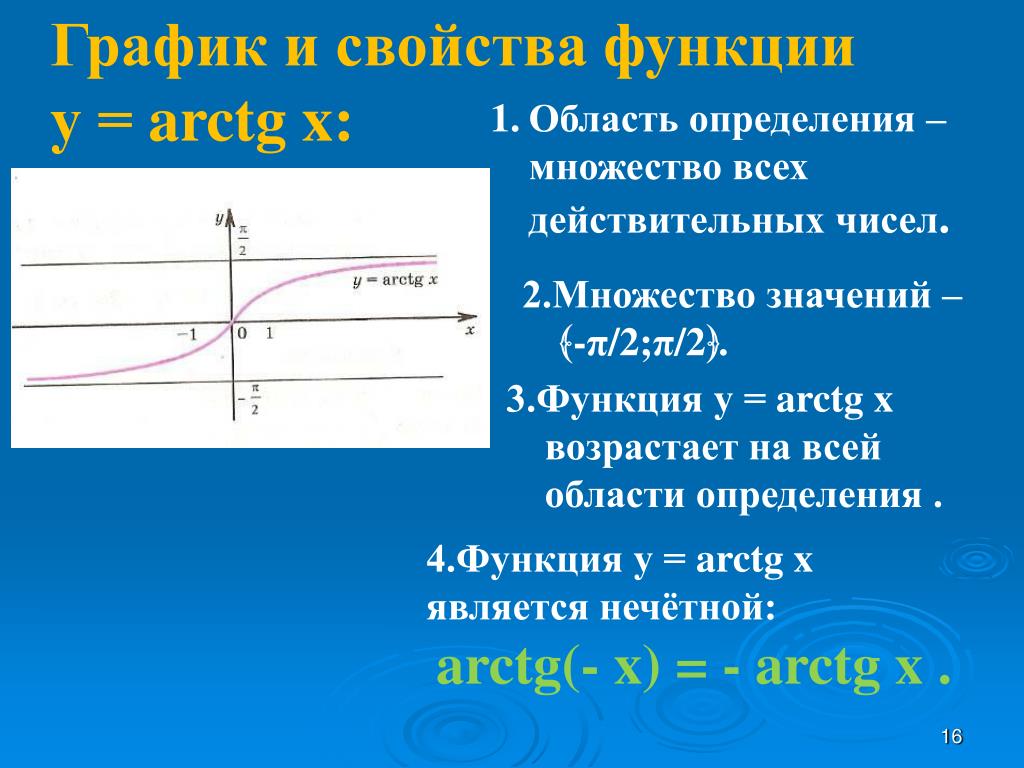
Чтобы обозначить область определения некоторой функции f, используется запись D(f). Однако нужно помнить, что у некоторых функций есть собственные обозначения, например, у тригонометрических. Поэтому в учебниках иногда встречаются записи вида D(sin) или D(arcsin). Их следует понимать как области определения синуса и арксинуса соответственно. Допустима и запись вида D(f), где f – функция синуса или арксинуса.
Если мы хотим записать, что функция f определена на множестве значений x, то используем формулировку D(f)=X. Так, для того же арксинуса запись будет выглядеть как D(arcsin)= [−1, 1] (подробнее об области определения арксинуса мы расскажем далее.)
Как найти области определения для основных элементарных функций
Прочитав определения выше, легко понять, что понятие области определения очень важно для любой функции. Это ее неотъемлемая часть, которую задают вместе с самой функцией. То есть когда мы вводим какую-либо функцию, то мы сразу указываем и область ее определения. Обычно в рамках школьного курса основные функции изучаются последовательно: сначала прямые пропорциональности, затем линейные функции, потом y=x2 и т.д., а их области определения указываются в качестве основных свойств.
Обычно в рамках школьного курса основные функции изучаются последовательно: сначала прямые пропорциональности, затем линейные функции, потом y=x2 и т.д., а их области определения указываются в качестве основных свойств.
В этом пункте мы расскажем, какие области определения имеют основные элементарные функции.
Область определения постоянной функции
Определение 3Вспомним формулу, которой задается постоянная функция: y=C, или f(x)=C. Переменная C может быть любым действительным числом.
Смысл функции в том, что каждому значению аргумента будет соответствовать значение, равное C, следовательно, областью определения данной функции будет множество всех действительных чисел. Обозначим его R.
Пример 2Так, если у нас есть функция y=−3 (или в другой записи f(x)=−3), то (D(f)= (−∞, +∞) или D(f)=R).
Если же мы возьмем функцию y=73, то для нее, как и для любой постоянной функции, область определения будет равна R.
Область определения функции с корнем
С помощью знака корня, или радикала, мы можем задать функцию извлечения квадратного корня y=x, либо в обобщенном виде функцию корня степени N, которую можно записать в виде формулы y=xn. В этих случаях n может быть любым натуральным числом, которое больше 1.
В этих случаях n может быть любым натуральным числом, которое больше 1.
Область определения таких функций будет зависеть от того, является ли показатель четным или нечетным числом.
Определение 4- Возьмем сначала случай, когда n – четное число, т.е. n=2·m, где m∈N. Тогда областью определения станет множество всех неотрицательных действительных чисел: D2·m=[0; +∞).
- Если же n представляет из себя нечетное число, которое больше 1, т.е. n=2·m+1, то областью определения будет множество всех действительных чисел: D2·m+1=(-∞; +∞).
Таким образом, область определения функций с корнем y=x, y=x4, y=x6 – это числовое множество [0, +∞), а функций y=x3, y=x5, y=x7 – множество (−∞, +∞).
Область определения степенной функции
Запись степенной функции выглядит как y=xa или f(x)=xa, где x является переменной, которая лежит в основании степени, и a представляет из себя определенное число в ее показателе. Мы берем область определения степенной функции в зависимости от значения ее показателя.
Перечислим возможные варианты.
Определение 5- Допустим, что a будет положительным целым числом. Тогда областью определения степенной функции будет множество действительных чисел (−∞, +∞).
- Если a является нецелым положительным числом, то D(f)= [0, +∞).
- В случае, когда a относится к целым отрицательным числам, областью определения такой функции становится множество (−∞, 0)∪(0, +∞).
- В остальных случаях, т.е. когда a будет отрицательным нецелым числом, область определения будет числовым промежутком (0, +∞).
- Если a имеет нулевое значение, то такая степенная функция будет определена для всех действительных x, кроме нулевого. Это связано с неопределенностью 00. Мы знаем, что любое число, кроме 1, при возведении в нулевую степень будет равно 1, тогда при a=0 у нас получится функция y=x0=1, область определения которой (−∞, 0) ∪ (0, +∞).
Поясним нашу мысль несколькими примерами.
Пример 4Для функций y=x5, y=x12 область определения представляет собой множество всех действительных чисел R, поскольку показатели степени являются целыми положительными числами.
Для степенных функций y=x63, y=xπ, y=x74, y=x23 будут определены на интервале [0, +∞), поскольку показатели являются положительными, но не целыми числами.
Пример 63. Для функции y=x−5 с целыми отрицательными показателями областью определения будет множество (−∞, 0)∪(0, +∞).
Пример 74. Для степенных функций y=x-19, y=x-3e, y=x-98, y=x-311 область определения будет представлять из себя открытый числовой луч (0, +∞), т.к. их показателями являются нецелые отрицательные числа.
Область определения показательной функции
Определение 6Такую функцию принято записывать как y=ax, причем переменная будет располагаться в показателе функции. Основанием степени здесь является число a, которое больше 0 и не равно 1.
Область определения такой функции есть множество всех действительных чисел, т.е. R.
Пример 8Например, если у нас есть показательные функции y=14x, y=ex, y=13x, y=15x, то они будут определены на промежутке от минус бесконечности до плюс бесконечности.
Область определения логарифмической функции
Определение 7Функция логарифма задается как y=logax
Так, для логарифмических функций y=log23x, y=log3x, y=log7x, y=lnx областью определения будет множество (0, +∞).
Область определения тригонометрических функций
Чтобы узнать, на каком промежутке будут определены тригонометрические функции, нужно вспомнить, как именно они задаются и как называются.
Определение 8- Формула y=sin x обозначает функцию синуса (sin). Она будет определена на множестве всех действительных чисел. Можно записать, что D(sin)=R.
- Формула y=cos x означает функцию косинуса (cos). Она также будет определена на множестве всех действительных чисел, т.е. D(cos)=R.

- Формула y=tg x означает функцию тангенса (tg), а y=ctg x– котангенса. Областью определения тангенса будет множество всех действительных чисел, за исключением π2+π·k, k∈Z.
Областью определения котангенса будет также множество R, за исключением π·k, k∈Z.
Иными словами, если мы знаем, что x является аргументом функций тангенса и котангенса, то нужно помнить, что данные функции определены при x∈R, x≠π2+π·k, k∈Z и x∈R, x≠π·k, k∈Z.
Область определения тригонометрических функций
К обратным тригонометрическим относятся функции арксинуса, арккосинуса, арктангенса и арккотангенса.
Определение 9- Формула y=arcsin x обозначает функцию арксинуса. Обычно она рассматривается на отрезке [−1, 1]] и обозначается arcsin. Промежуток [−1, 1] и будет нужной нам областью определения данной функции. Можно записать, что D(arcsin)=[−1, 1].
- Формула y=arccos x выражает функцию арккосинуса (обозначается arccos). Она рассматривается на том же отрезке, что и арксинус.

- Функции y=arctg x и y=arcctg x означают арктангенс и арккотангенс. Они рассматриваются на множестве всех действительных чисел, значит, областью их определения является R. Можем записать, что D(arctg)=R и D(arcctg)=R.
Области определения основных функций в табличном виде
Чтобы запомнить или легко найти нужные нам области, правила вычисления которых мы объяснили выше, представим всю информацию в табличном виде. Не лишним будет оформить ее на отдельном листе и держать под рукой, так же, как и таблицу простых чисел, квадратов и др. Она очень пригодится при работе с функциями, пока вы не выучите ее содержимое наизусть.
| Области определения функций | |
| Функиця | Ее область определения |
| Постоянная y=C | R |
| Корень y=xn | [0; +∞), если n — четное |
| Степенная y=xa | -∞; +∞, если a>0, a∈Z |
| Показательная y=ax | R |
| Логарифмическая y=logax | 0; +∞ |
Тригонометрические y=sin xy=cos xy=tg xy=ctg x |
RRx∈R, x≠π2+π·k, k∈Zx∈R, x≠π·k, k∈Z |
Обратные тригонометрические y=arcsin xy=arccos xy=arctg xy=arcctg x |
-1; 1-1; 1RR |
Подводя итоги статьи, следует отметить, что в рамках школьного курса изучаются не только основные элементарные функции, но и их различные сочетания.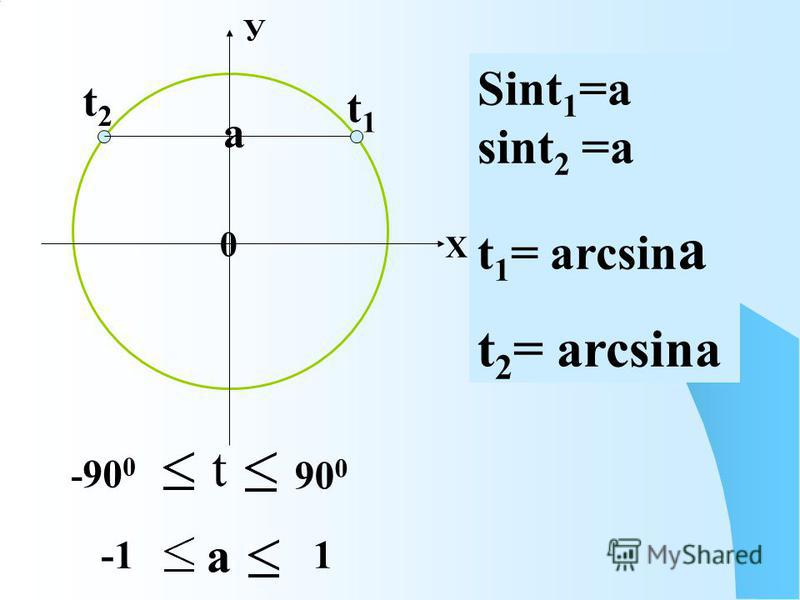 Задачи такого типа встречаются очень часто. Области определения таких комбинированных функций указываются далеко не всегда. Авторы задач подразумевают, что в таких случаях областью определения функции можно считать множество таких значений аргумента, при которых она будет иметь смысл. Это позволяет нам приблизиться к ответу на вопрос, как именно вычисляется область определения функции в подобных случаях.
Задачи такого типа встречаются очень часто. Области определения таких комбинированных функций указываются далеко не всегда. Авторы задач подразумевают, что в таких случаях областью определения функции можно считать множество таких значений аргумента, при которых она будет иметь смысл. Это позволяет нам приблизиться к ответу на вопрос, как именно вычисляется область определения функции в подобных случаях.
Решение задач
от 1 дня / от 150 р.
Курсовая работа
от 5 дней / от 1800 р.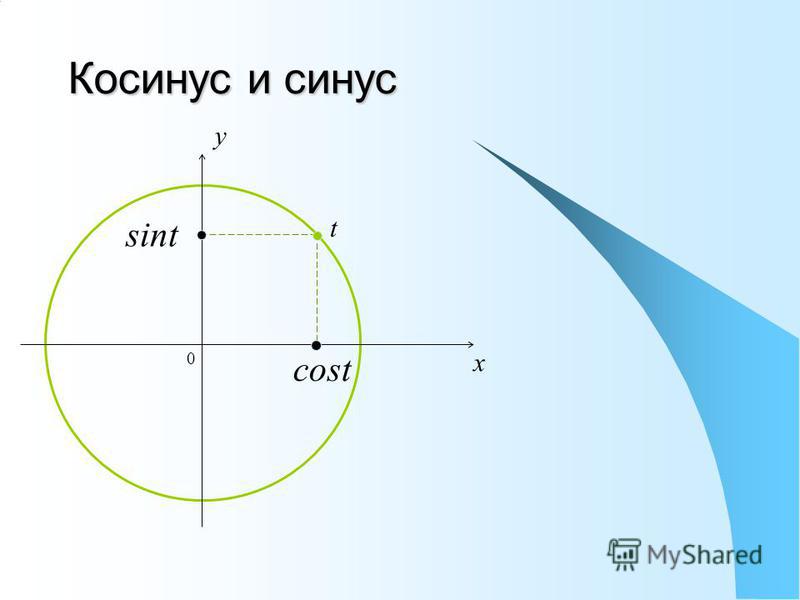 Реферат
от 1 дня / от 700 р.
Реферат
от 1 дня / от 700 р.
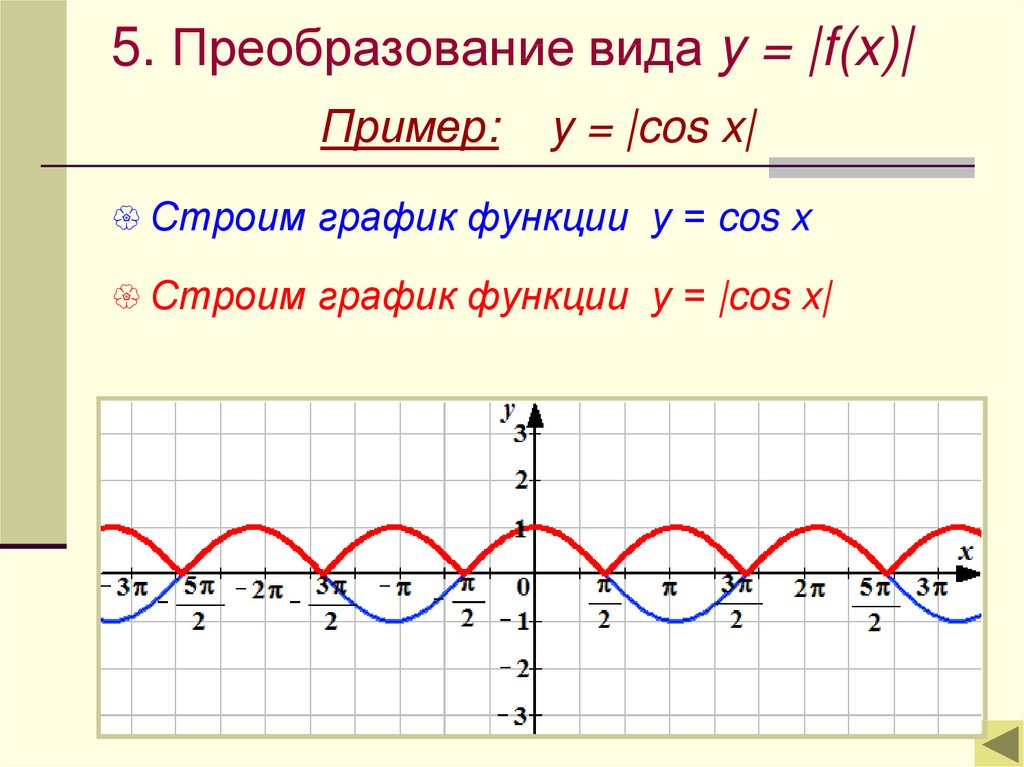
Определение функции y sin x. Синус (sin x) и косинус (cos x) – свойства, графики, формулы
ГРАФИКИ ФУНКЦИЙ
Функция синус
— множество R всех действительных чисел.
Множество значений функции — отрезок [-1; 1], т.е. синус функция — ограниченная .
Функция нечетная: sin(−x)=−sin x для всех х ∈ R .
Функция периодическая
sin(x+2π·
k) = sin x, где k ∈ Z для всех х ∈ R .
sin x = 0 при x = π·k , k ∈ Z .
sin x > 0 (положительная) для всех x ∈ (2π·k , π+2π·k ), k ∈ Z .
sin x (отрицательная) для всех x ∈ (π+2π·k , 2π+2π·k ), k ∈ Z .
Функция косинус
Область определения функции — множество R всех действительных чисел.
Множество значений функции — отрезок [-1; 1], т.е. косинус функция — ограниченная .
Функция четная: cos(−x)=cos x для всех х ∈ R .
Функция периодическая с наименьшим положительным периодом 2π :
cos(x+2π· k ) = cos x, где k ∈ Z для всех х ∈ R .
| cos x = 0 при | |
| cos x > 0 для всех | |
| cos x для всех | |
| Функция возрастает от −1 до 1 на промежутках: | |
| Функция убывает от −1 до 1 на промежутках: | |
| Наибольшее значение функции sin x = 1 в точках: | |
| Наименьшее значение функции sin x = −1 в точках: |
Множество значений функции — вся числовая прямая, т. е. тангенс — функция неограниченная .
е. тангенс — функция неограниченная .
Функция нечетная: tg(−x)=−tg x
График функции симметричен относительно оси OY.
Функция периодическая с наименьшим положительным периодом π , т.е. tg(x+π· k ) = tg x, k ∈ Z для всех х из области определения.
Функция котангенс
Множество значений функции — вся числовая прямая, т.е. котангенс — функция неограниченная .
Функция нечетная: ctg(−x)=−ctg x для всех х из области определения.
График функции симметричен относительно оси OY.
Функция периодическая с наименьшим положительным периодом π , т.е. ctg(x+π· k )=ctg x, k ∈ Z для всех х из области определения.
Функция арксинус
Область определения функции — отрезок [-1; 1]
Множество значений функции — отрезок -π
/2 arcsin x π
/2, т.е. арксинус — функция ограниченная .
Функция нечетная: arcsin(−x)=−arcsin x для всех х ∈ R .
График функции симметричен относительно начала координат.
На всей области определения.
Функция арккосинус
Область определения функции — отрезок [-1; 1]
Множество значений функции — отрезок 0 arccos x π , т.е. арккосинус — функция ограниченная .
Функция является возрастающей на всей области определения.
Функция арктангенс
Область определения функции — множество R всех действительных чисел.
Множество значений функции — отрезок 0 π, т.е. арктангенс — функция ограниченная .
Функция нечетная: arctg(−x)=−arctg x для всех х ∈ R .
График функции симметричен относительно начала координат.
Функция является возрастающей на всей области определения.
Функция арккотангенс
Область определения функции — множество R всех действительных чисел.
Множество значений функции — отрезок 0 π, т.е. арккотангенс — функция ограниченная .
Функция не является ни четной, ни нечетной.
График функции несимметричен ни относительно начала координат, ни относительно оси Оy.
Функция является убывающей на всей области определения.
С центром в точке A .
α — угол, выраженный в радианах.
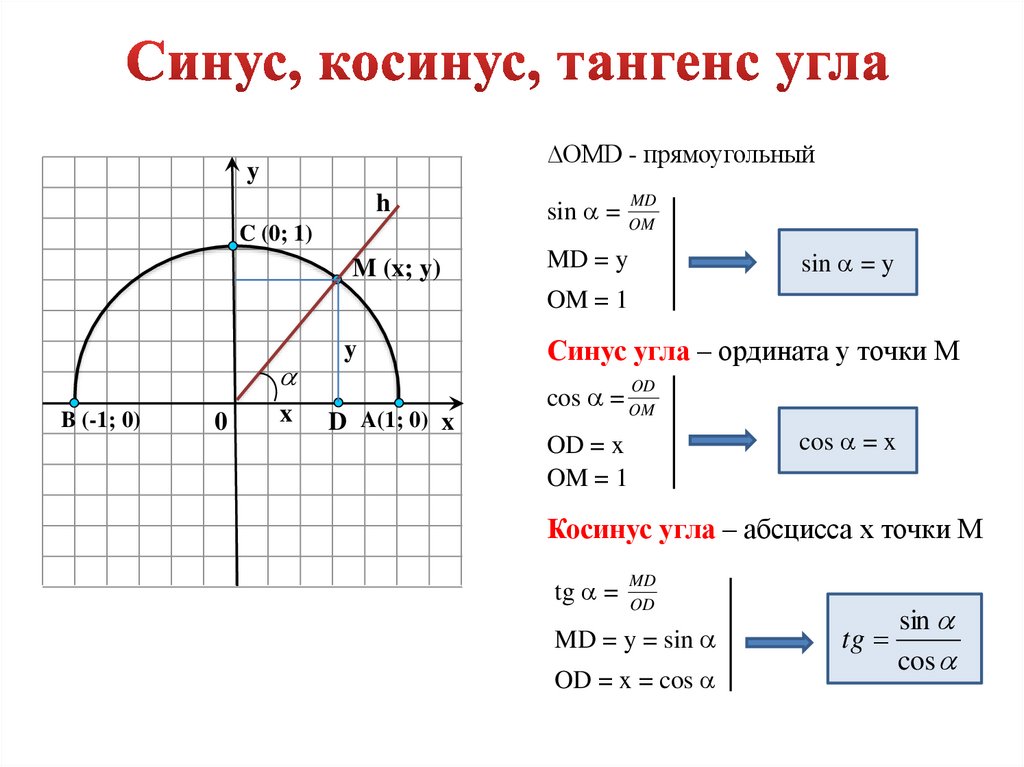
Определение
Синус (sin α) — это тригонометрическая функция, зависящая от угла α между гипотенузой и катетом прямоугольного треугольника, равная отношению длины противолежащего катета |BC| к длине гипотенузы |AC|.
Косинус (cos α) — это тригонометрическая функция, зависящая от угла α между гипотенузой и катетом прямоугольного треугольника, равная отношению длины прилежащего катета |AB| к длине гипотенузы |AC|.
Принятые обозначения
;
;
.
;
;
.
График функции синус, y = sin x
График функции косинус, y = cos x
Свойства синуса и косинуса
Периодичность
Функции y = sin
x
и y = cos
x
периодичны с периодом 2
π
.
Четность
Функция синус — нечетная. Функция косинус — четная.
Область определения и значений, экстремумы, возрастание, убывание
Функции синус и косинус непрерывны на своей области определения, то есть для всех x (см. доказательство непрерывности). Их основные свойства представлены в таблице (n — целое).
| y = sin x | y = cos x | |
| Область определения и непрерывность | — ∞ | — ∞ |
| Область значений | -1 ≤ y ≤ 1 | -1 ≤ y ≤ 1 |
| Возрастание | ||
| Убывание | ||
| Максимумы, y = 1 | ||
| Минимумы, y = -1 | ||
| Нули, y = 0 | ||
| Точки пересечения с осью ординат, x = 0 | y = 0 | y = 1 |
Основные формулы
Сумма квадратов синуса и косинуса
Формулы синуса и косинуса от суммы и разности
;
;
Формулы произведения синусов и косинусов
Формулы суммы и разности
Выражение синуса через косинус
;
;
;
.
Выражение косинуса через синус
;
;
;
.
Выражение через тангенс
; .
При ,
имеем:
;
.
При :
;
.
Таблица синусов и косинусов, тангенсов и котангенсов
В данной таблице представлены значения синусов и косинусов при некоторых значениях аргумента.
Выражения через комплексные переменные
;
Формула Эйлера
Выражения через гиперболические функции
;
;
Производные
; . Вывод формул > > >
Производные n-го порядка:
{ -∞
Секанс, косеканс
Обратные функции
Обратными функциями к синусу и косинусу являются арксинус и арккосинус , соответственно.
Арксинус, arcsin
Арккосинус, arccos
Использованная литература:
И.Н. Бронштейн, К.А. Семендяев, Справочник по математике для инженеров и учащихся втузов, «Лань», 2009.
На этом уроке мы подробно рассмотрим функцию у = sin х, ее основные свойства и график. В начале урока дадим определение тригонометрической функции у = sin t на координатной окружности и рассмотрим график функции на окружности и прямой. Покажем периодичность этой функции на графике и рассмотрим основные свойства функции. В конце урока решим несколько простейших задач с использованием графика функции и ее свойств.
В начале урока дадим определение тригонометрической функции у = sin t на координатной окружности и рассмотрим график функции на окружности и прямой. Покажем периодичность этой функции на графике и рассмотрим основные свойства функции. В конце урока решим несколько простейших задач с использованием графика функции и ее свойств.
Тема: Тригонометрические функции
Урок: Функция y=sinx, её основные свойства и график
При рассмотрении функции важно каждому значению аргумента поставить в соответствие единственное значение функции. Этот закон соответствия и называется функцией.
Определим закон соответствия для .
Любому действительному числу соответствует единственная точка на единичной окружности У точки есть единственная ордината, которая и называется синусом числа (рис. 1).
Каждому значению аргумента ставится в соответствие единственное значение функции.
Из определения синуса вытекают очевидные свойства.
На рисунке видно, что т. к. это ордината точки единичной окружности.
к. это ордината точки единичной окружности.
Рассмотрим график функции . Вспомним геометрическую интерпретацию аргумента. Аргумент — это центральный угол, измеряемый в радианах. По оси мы будем откладывать действительные числа или углы в радианах, по оси соответствующие значения функции.
Например, угол на единичной окружности соответствует точке на графике (рис. 2)
Мы получили график функции на участке Но зная период синуса мы можем изобразить график функции на всей области определения (рис. 3).
Основным периодом функции является Это значит, что график можно получить на отрезке а затем продолжить на всю область определения.
Рассмотрим свойства функции :
1) Область определения:
2) Область значений:
3) Функция нечетная:
4) Наименьший положительный период:
5) Координаты точек пересечения графика с осью абсцисс:
6) Координаты точки пересечения графика с осью ординат:
7) Промежутки, на которых функция принимает положительные значения:
8) Промежутки, на которых функция принимает отрицательные значения:
9) Промежутки возрастания:
10) Промежутки убывания:
11) Точки минимума:
12) Минимум функции:
13) Точки максимума:
14) Максимум функции:
Мы рассмотрели свойства функции и её график.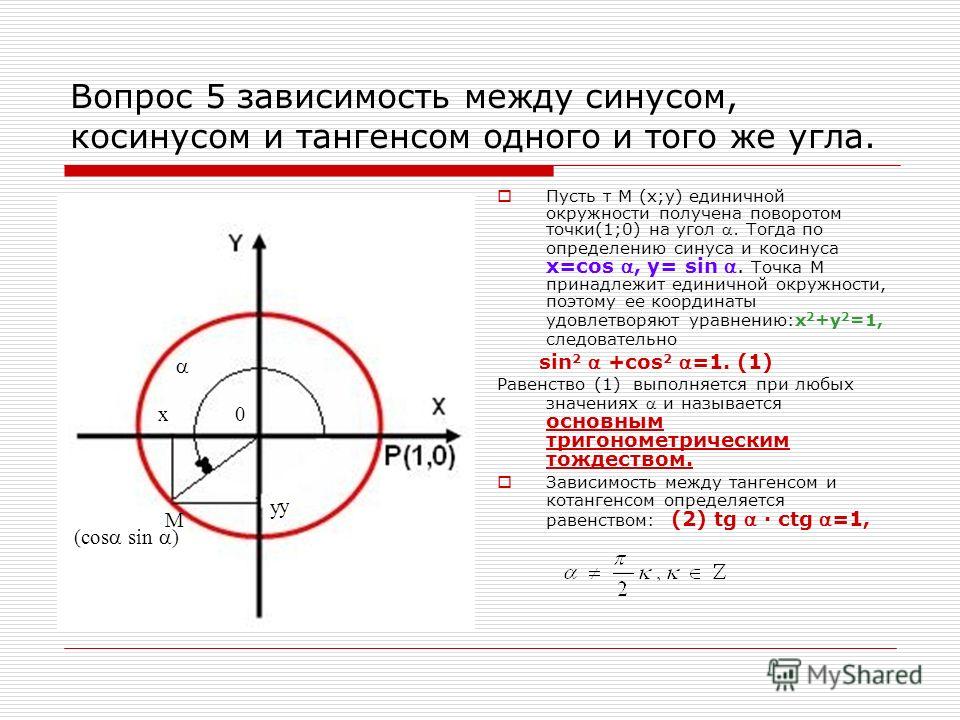 Свойства неоднократно будут использоваться при решении задач.
Свойства неоднократно будут использоваться при решении задач.
Список литературы
1. Алгебра и начала анализа, 10 класс (в двух частях). Учебник для общеобразовательных учреждений (профильный уровень) под ред. А. Г. Мордковича. -М.: Мнемозина, 2009.
2. Алгебра и начала анализа, 10 класс (в двух частях). Задачник для общеобразовательных учреждений (профильный уровень) под ред. А. Г. Мордковича. -М.: Мнемозина, 2007.
3. Виленкин Н.Я., Ивашев-Мусатов О.С., Шварцбурд С.И. Алгебра и математический анализ для 10 класса (учебное пособие для учащихся школ и классов с углубленным изучением математики).-М.: Просвещение, 1996.
4. Галицкий М.Л., Мошкович М.М., Шварцбурд С.И. Углубленное изучение алгебры и математического анализа.-М.: Просвещение, 1997.
5. Сборник задач по математике для поступающих во ВТУЗы (под ред. М.И.Сканави).-М.:Высшая школа, 1992.
6. Мерзляк А.Г., Полонский В.Б., Якир М.С. Алгебраический тренажер.-К.: А.С.К., 1997.
7. Саакян С. М., Гольдман А.М., Денисов Д.В. Задачи по алгебре и началам анализа (пособие для учащихся 10-11 классов общеобразов. учреждений).-М.: Просвещение, 2003.
М., Гольдман А.М., Денисов Д.В. Задачи по алгебре и началам анализа (пособие для учащихся 10-11 классов общеобразов. учреждений).-М.: Просвещение, 2003.
8. Карп А.П. Сборник задач по алгебре и началам анализа: учеб. пособие для 10-11 кл. с углубл. изуч. математики.-М.: Просвещение, 2006.
Домашнее задание
Алгебра и начала анализа, 10 класс (в двух частях). Задачник для общеобразовательных учреждений (профильный уровень) под ред.
А. Г. Мордковича. -М.: Мнемозина, 2007.
№№ 16.4, 16.5, 16.8.
Дополнительные веб-ресурсы
3. Образовательный портал для подготовки к экзаменам ().
Функция y = sin x
Графиком функции является синусоида.
Полную неповторяющуюся часть синусоиды называют волной синусоиды.
Половину волны синусоиды называют полуволной синусоиды (или аркой).
Свойства функции y = sin x :
3) Это нечетная функция. 4) Это непрерывная функция.
6) На отрезке [-π/2; π/2] функция возрастает, на отрезке [π/2; 3π/2] – убывает. 7) На промежутках функция принимает положительные значения. 8) Промежутки возрастания функции: [-π/2 + 2πn; π/2 + 2πn]. 9) Точки минимума функции: -π/2 + 2πn. |
Для построения графика функции y = sin x удобно применять следующие масштабы:
На листе в клетку за единицу отрезка примем длину в две клетки.
На оси x отмерим длину π. При этом для удобства 3,14 представим в виде 3 – то есть без дроби. Тогда на листе в клетку π составит 6 клеток (трижды по 2 клетки). А каждая клетка получит свое закономерное имя (от первой до шестой): π/6, π/3, π/2, 2π/3, 5π/6, π.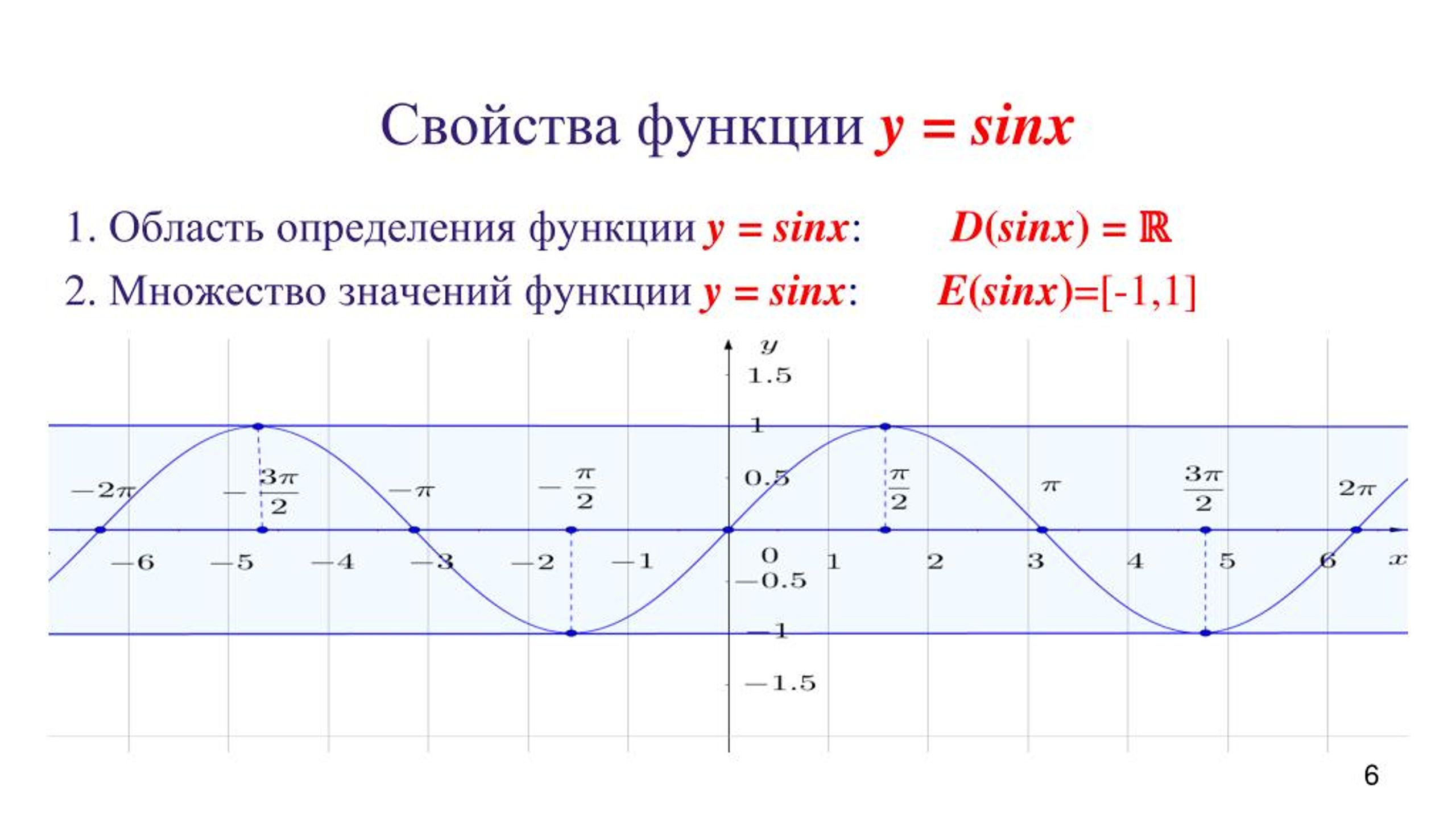 Это значения x .
Это значения x .
На оси y отметим 1, включающий две клетки.
Составим таблицу значений функции, применяя наши значения x :
√3 | √3 |
Далее составим график. Получится полуволна, наивысшая точка которой (π/2; 1). Это график функции y = sin x на отрезке . Добавим к построенному графику симметричную полуволну (симметричную относительно начала координат, то есть на отрезке -π). Гребень этой полуволны – под осью x с координатами (-1; -1). В результате получится волна.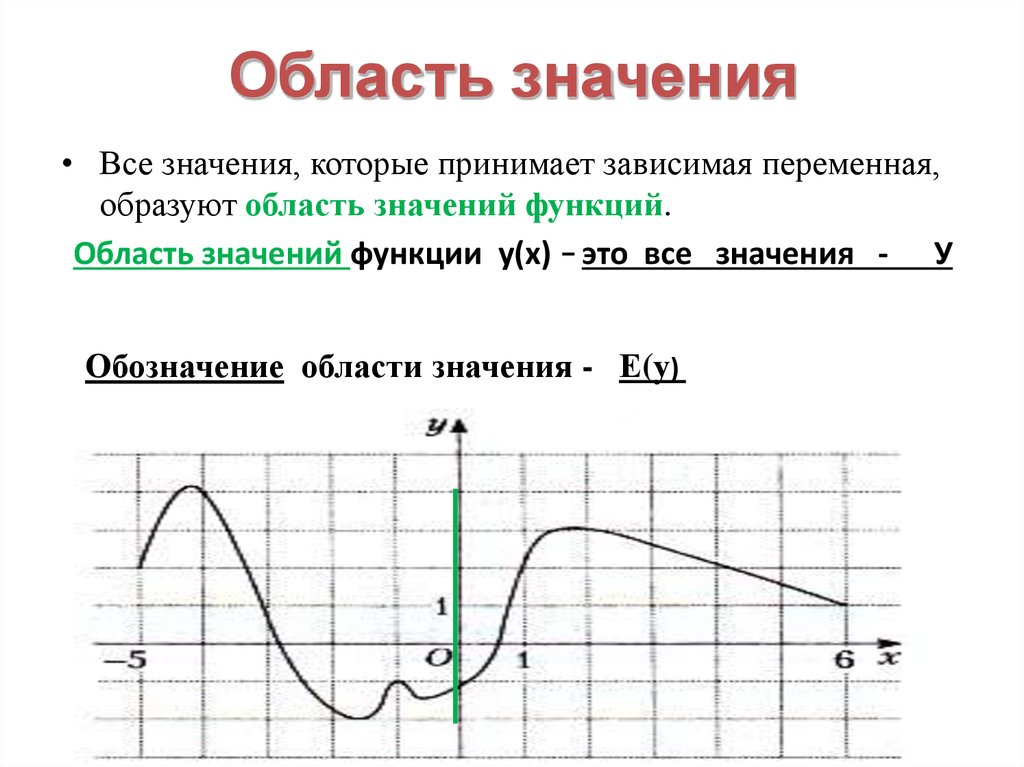 Это график функции y = sin x на отрезке [-π; π].
Это график функции y = sin x на отрезке [-π; π].
Можно продолжить волну, построив ее и на отрезке [π; 3π], [π; 5π], [π; 7π] и т.д. На всех этих отрезках график функции будет выглядеть так же, как на отрезке [-π; π]. Получится непрерывная волнистая линия с одинаковыми волнами.
Функция y = cos x .
Графиком функции является синусоида (ее иногда называют косинусоидой).
Свойства функции y = cos x :
1) Область определения функции – множество действительных чисел. 2) Область значений функции – отрезок [–1; 1] 3) Это четная функция. 4) Это непрерывная функция. 5) Координаты точек пересечения графика: 6) На отрезке функция убывает, на отрезке [π; 2π] – возрастает. 7) На промежутках [-π/2 + 2πn; π/2 + 2πn] функция принимает положительные значения. 8) Промежутки возрастания: [-π + 2πn; 2πn]. 9) Точки минимума функции: π + 2πn. 10) Функция ограничена сверху и снизу. Наименьшее значение функции –1, 11) Это периодическая функция с периодом 2π (Т = 2π) |
Функция y = mf (x ).
Возьмем предыдущую функцию y = cos x . Как вы уже знаете, ее графиком является синусоида. Если мы умножим косинус этой функции на определенное число m, то волна растянется от оси x (либо сожмется, в зависимости от величины m).
Эта новая волна и будет графиком функции y = mf(x), где m – любое действительное число.
Таким образом, функция y = mf(x) – это привычная нам функция y = f(x), умноженная на m.
Если m x на коэффициент m.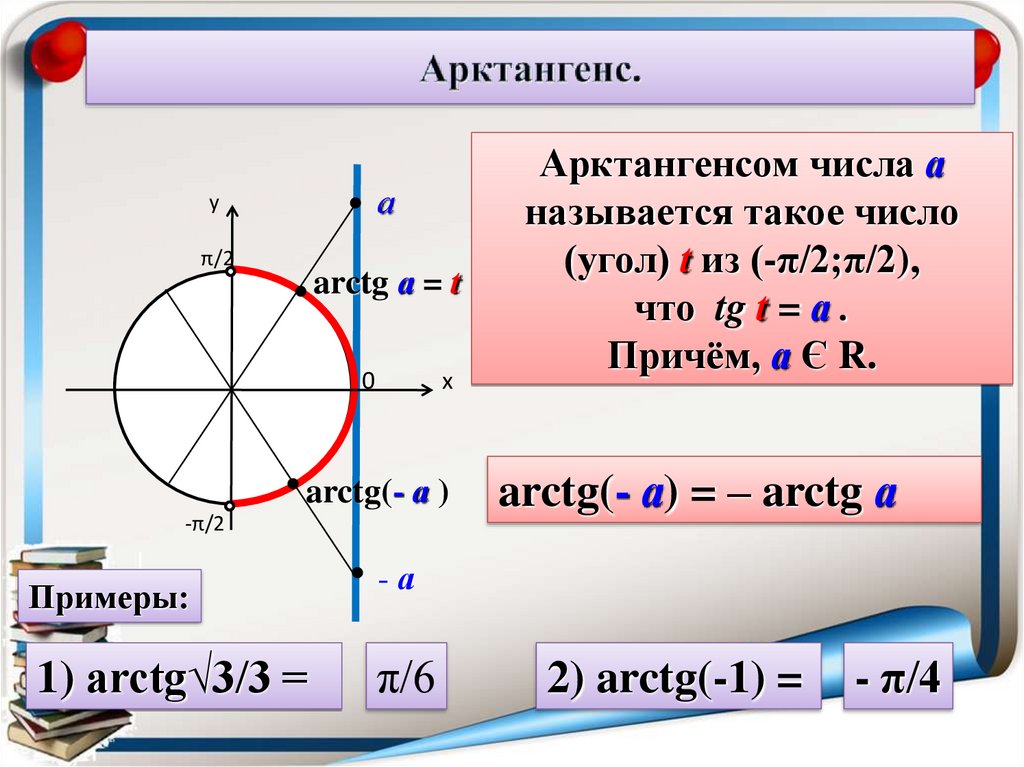 Если m > 1, то синусоида растягивается от оси x на коэффициент m.
Если m > 1, то синусоида растягивается от оси x на коэффициент m.
Выполняя растяжение или сжатие, можно сначала построить лишь одну полуволну синусоиды, а затем уже достроить весь график.
Функция y = f (kx ).
Если функция y = mf (x ) приводит к растяжению синусоиды от оси x либо сжатию к оси x , то функция y = f(kx) приводит к растяжению от оси y либо сжатию к оси y .
Причем k – любое действительное число.
При 0 k y на коэффициент k. Если k > 1, то синусоида сжимается к оси y на коэффициент k.
Составляя график этой функции, можно сначала построить одну полуволну синусоиды, а по ней достроить затем весь график.
Функция y = tg x .
Графиком функции y = tg x является тангенсоида.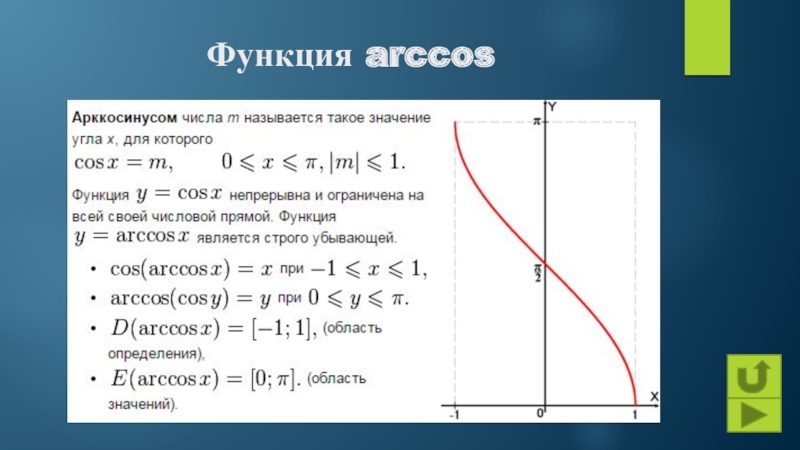
Достаточно построить часть графика на промежутке от 0 до π/2, а затем можно симметрично продолжить ее на промежутке от 0 до 3π/2.
Свойства функции y = tg x :
Функция y = ctg x
Графиком функции y = ctg x также является тангенсоида (ее иногда называют котангенсоидой).
Свойства функции y = ctg x :
Назад
Вперёд
Внимание! Предварительный просмотр слайдов используется исключительно в ознакомительных целях и может не давать представления о всех возможностях презентации. Если вас заинтересовала данная работа, пожалуйста, загрузите полную версию.
Железо ржавеет, не находя себе применения,
стоячая вода гниет или на холоде замерзает,
а ум человека, не находя себе применения, чахнет.
Леонардо да Винчи
Используемые технологии: проблемного обучения, критического мышления, коммуникативного общения.
Цели:
- Развитие познавательного интереса к обучению.
- Изучение свойств функции у = sin x.
- Формирование практических навыков построения графика функции у = sin x на основе изученного теоретического материала.
Задачи:
1. Использовать имеющийся потенциал знаний о свойствах функции у = sin x в конкретных ситуациях.
2. Применять осознанное установление связей между аналитической и геометрической моделями функции у = sin x.
Развивать инициативу, определенную готовность и интерес к поиску решения; умение принимать решения, не останавливаться на достигнутом, отстаивать свою точку зрения.
Воспитывать у учащихся познавательную
активность, чувство ответственности, уважения
друг к другу, взаимопонимания, взаимоподдержки,
уверенности в себе; культуру общения.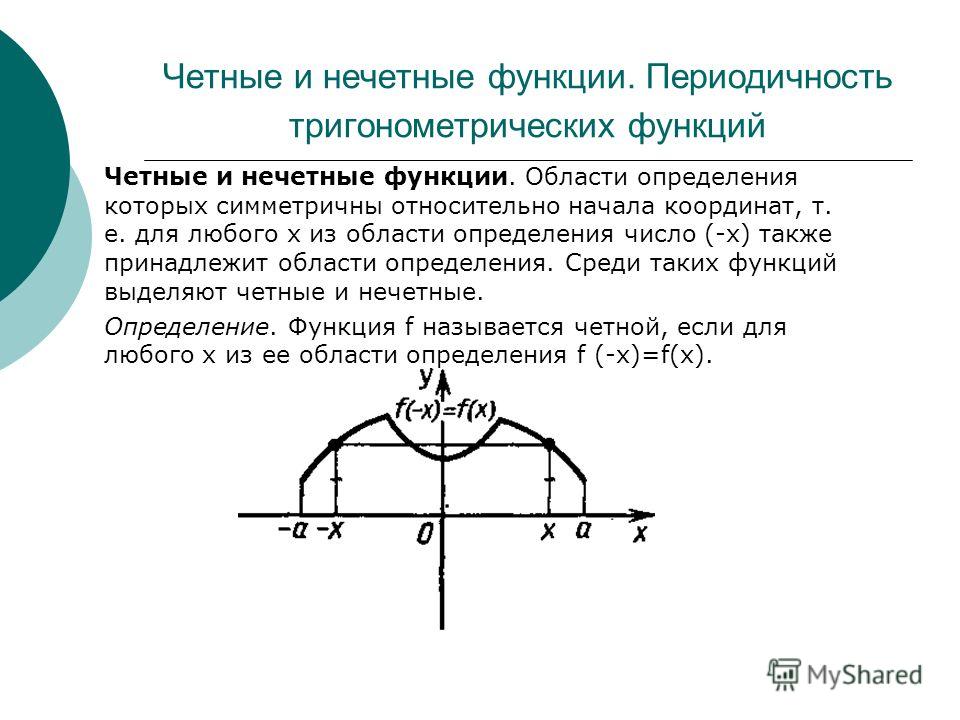
Ход урока
1 этап. Актуализация опорных знаний, мотивация изучения нового материала
«Вход в урок».
На доске написаны 3 утверждения:
- Тригонометрическое уравнение sin t = a всегда имеет решения.
- График нечетной функции можно построить с помощью преобразования симметрии относительно оси Оу.
- График тригонометрической функции можно построить, используя одну главную полуволну.
Учащиеся обсуждают в парах: верны ли утверждения? (1 минута). Затем результаты первоначального обсуждения (да, нет) вносятся в таблицу в столбец «До».
Учитель ставит цели и задачи урока.
2. Актуализация знаний (фронтально на модели тригонометрического круга ).
Мы уже познакомились с функцией s = sin t.
1) Какие значения может принимать переменная t. Какова область определения этой функции?
2) В каком промежутке заключены значения
выражения sin t. Найти наибольшее и наименьшее
значения функции s = sin t.
3) Решите уравнение sin t = 0.
4) Что происходит с ординатой точки при ее движении по первой четверти? (ордината увеличивается). Что происходит с ординатой точки при ее движении по второй четверти? (ордината постепенно уменьшается). Как это связано с монотонностью функции? (функция s = sin t возрастает на отрезке и убывает на отрезке ).
5) Запишем функцию s = sin t в привычном для нас виде у = sin x (строить будем в привычной системе координат хОу) и составим таблицу значений этой функции.
| х | 0 | ||||||
| у | 0 | 1 | 0 |
2 этап.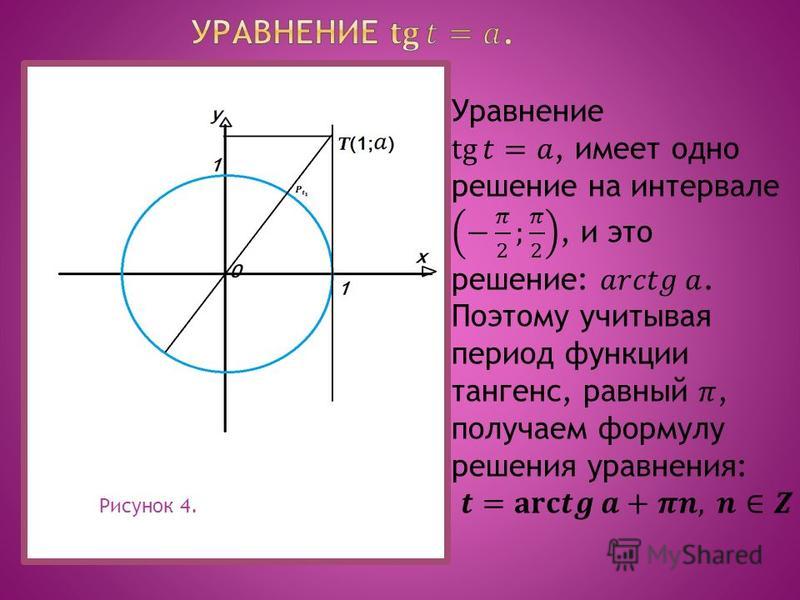 Восприятие, осмысление, первичное
закрепление, непроизвольное запоминание
Восприятие, осмысление, первичное
закрепление, непроизвольное запоминание
4 этап. Первичная систематизация знаний и способов деятельности, их перенос и применение в новых ситуациях
6. № 10.18 (б,в)
5 этап. Итоговый контроль, коррекция, оценка и самооценка
7. Возвращаемся к утверждениям (начало урока), обсуждаем, используя свойства тригонометрической функции у = sin x, и заполняем в таблице столбец «После».
8. Д/з: п.10, №№ 10.7(а), 10.8(б), 10.11(б), 10.16(а)
2.4.3. Обратные тригонометрические функции
Глава 2. Алгебраические выражения
2.4.
2.4.3.
Вернемся к определению функции, данному в § 2. 2.1. Отметим, что в этом определении функция f не обязана разным элементам
и
множества X ставить в соответствие разные элементы множества Y.
2.1. Отметим, что в этом определении функция f не обязана разным элементам
и
множества X ставить в соответствие разные элементы множества Y.
Если Y – множество значений функции f (x) и для любого элемента
существует единственный элемент
такой, что f (x) = y, то говорят, что функция осуществляет взаимнооднозначное соответствие между множествами X и Y. Другими словами, соответствие называется взаимнооднозначным, если каждому элементу соответствует единственный элемент
и наоборот, каждому элементу
соответствует единственный элемент Функция, осуществляющая взаимнооднозначное соответствие, называется обратимой; ещё говорят, что у функции f существует обратная функция. Такая функция обозначается
и каждому элементу
ставит в соответствие такой элемент
что f (x) = y; этот факт записывают так:
Однако нам непривычна запись функции как зависимости x от y. Поэтому сделаем формальную замену переменных
что соответствует отражению относительно биссектрисы первого и третьего координатных углов. Тогда получим, что
− обратная функция, график которой получается из графика исходной функции y = f (x) отражением относительно биссектрисы первого и третьего координатных углов. Область определения обратной функции совпадает с областью значений самой функции:
Область значений обратной функции совпадает с множеством определения самой функции:
Тогда получим, что
− обратная функция, график которой получается из графика исходной функции y = f (x) отражением относительно биссектрисы первого и третьего координатных углов. Область определения обратной функции совпадает с областью значений самой функции:
Область значений обратной функции совпадает с множеством определения самой функции:
Рассмотрим функцию f (x) = sin x для Тогда При этом область определения выбрана так, что соответствие является взаимнооднозначным. Следовательно, существует обратная функция с областью определения и областью значений Эта обратная функция называется арксинусом. Её обозначение: y = arcsin x. График функции y = arcsin x изображён на рисунке.
|
|
| Рисунок 2.4.3.1. Арксинус |
|
Модель 2. |
Аналогично, на промежутке D (f–1) = E (f) = [–1; 1] можно определить функцию, обратную cos x, c областью значений E (f–1) = D (f) = [0; π] Эта обратная функция называется арккосинусом. Её обозначение: y = arccos x. График функции y = arccos x изображён на рисунке.
|
|
| Рисунок 2.4.3.2. Арккосинус |
|
Модель 2.12. Функция y = arccos x |
Рассмотрим функцию f (x) = tg x для
Тогда
При этом область определения выбрана так, что соответствие является взаимнооднозначным. Следовательно, существует обратная функция с областью определения
и областью значений
Эта обратная функция называется арктангенсом.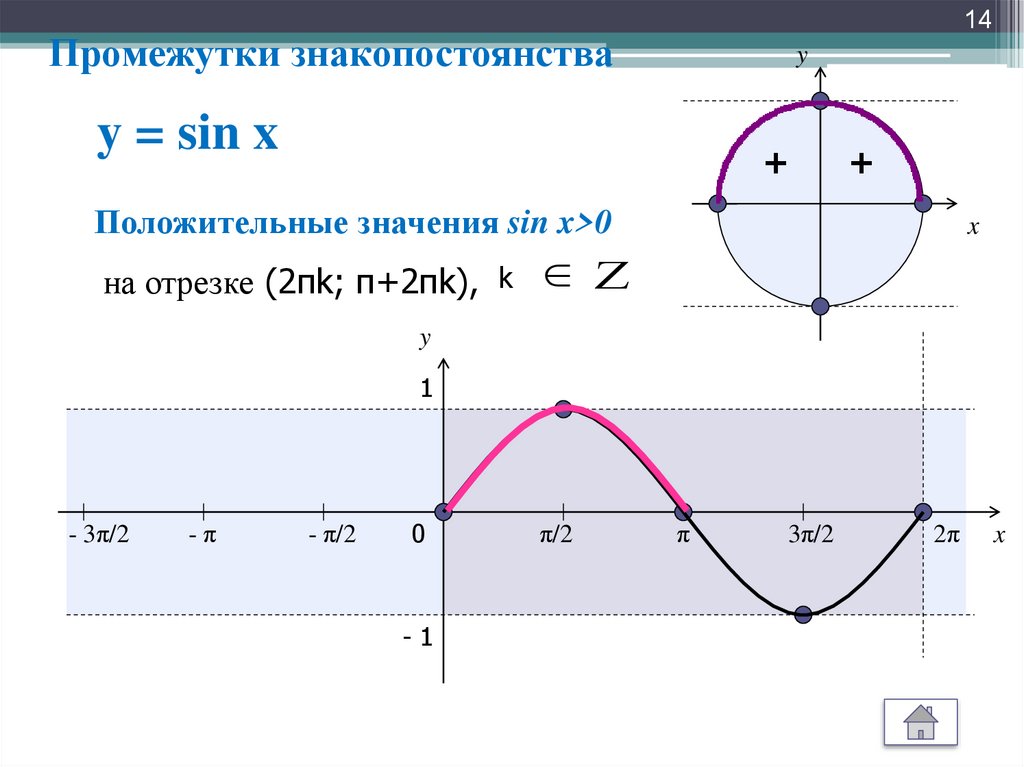 Её обозначение y = arctg x. График функции y = arctg x изображён на рисунке.
Её обозначение y = arctg x. График функции y = arctg x изображён на рисунке.
|
|
| Рисунок 2.4.3.3. Арктангенс |
|
Модель 2.13. Функция y = arctg x |
Для построения арккотангенса выберем промежуток x (0; π). Тогда Построим обратную функцию с областью определения и областью значений Эта обратная функция называется арккотангенсом. Её обозначение y = arcctg x. График функции y = arcctg x изображён на рисунке.
|
|
| Рисунок 2.4.3.4. Арккотангенс |
|
Модель 2. |
Итак, запись b = arcsin a обозначает, что и sin b = a. Аналогичные соотношения справедливы и для остальных обратных тригонометрических функций.
Пример 1
Докажите тождество
Показать решение
Пример 2
Найти соотношение между A (x) = arcsin (cos (arcsin x)) и B (x) = arccos (sin (arccos x)).
Показать решение
Главная Онлайн учебники База репетиторов России Тренажеры по математике Подготовка к ЕГЭ 2017 онлайн |
||||||||
|
||||||||
|
|
||||||||
Найти область определения функции у lg sin x
Обновлено: 28.09.2022
Данный калькулятор позволит найти область определения функции онлайн.
Область определения функции y=f(x) – это множество всех значений аргумента x, на котором задана функция. Другими словами, это все x, для которых могут существовать значения y. На графике областью определения функции является промежуток, на котором есть график функции.
Область определения функции f(x), как правило, обозначается как D(f). Принадлежность к определенному множеству обозначается символом ∈, а X – область определения функции. Таким образом, формула x∈X означает, что множество всех значений x принадлежит к области определения функции f(x).
Таким образом, формула x∈X означает, что множество всех значений x принадлежит к области определения функции f(x).
Приведем примеры определения основных элементарных функций. Областью определения постоянной функции y=f(x)=C является множество всех действительных чисел. Когда речь идет о степенной функции y=f(x)=xa, область определения зависит от показателя степени данной функции. При нахождении области определения функции y=f(x)= √(n&x) (корень n-ой степени) следует обращать внимание на четность или нечетность n.
Областью определения логарифмической функции являются все положительные действительные числа, и она не зависит от основания логарифма. Областью определения показательной функции, также как и у постоянной функции, является множество всех действительных чисел.
Областью определения сложных функций y=f1(f2(x)) является пересечение двух множеств: x∈D(f2) и множества всех x, для которых f2(x) ∈ D(f1). Следовательно, для того чтобы найти область определения сложной функции, необходимо решить систему неравенства.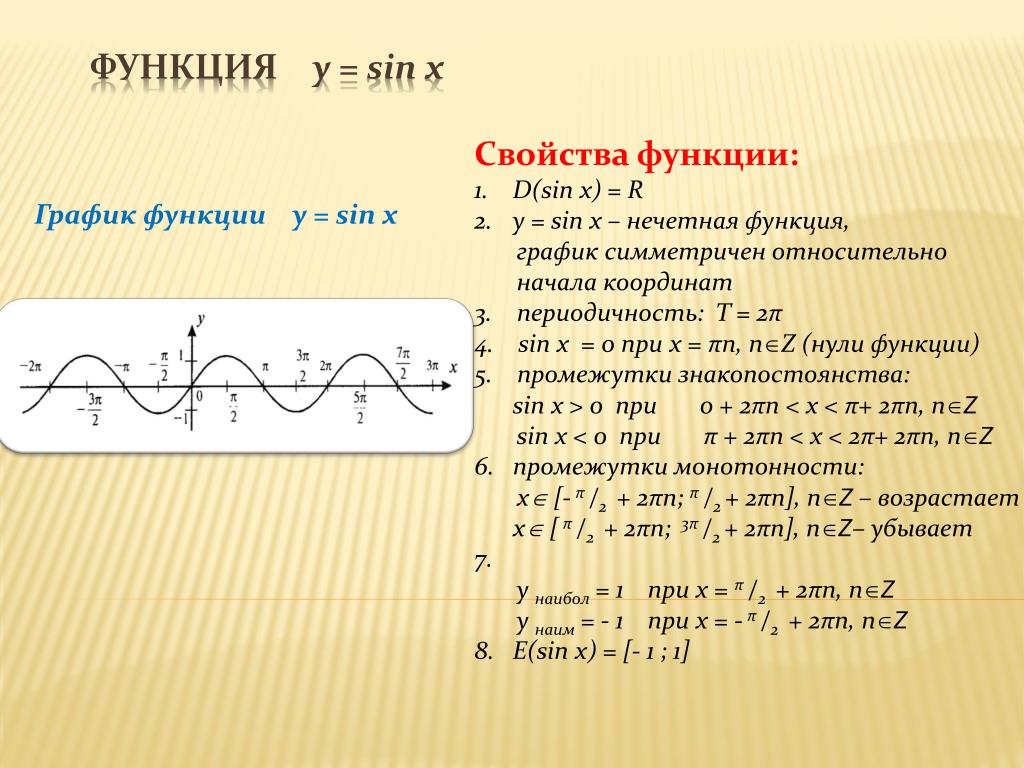 4)
4)
Впервые школьники знакомятся с термином «функция» на алгебре в 7 классе, и с каждой четвертью, с каждой новой темой это понятие раскрывается с новых сторон. И, конечно же, усложняются задачки. Сейчас дадим определения ключевым словам и будем находить область определения функции заданной формулой и по графику.
Если каждому значению x из некоторого множества соответствует число y, значит, на этом множестве задана функция. При этом х называют независимой переменной или аргументом, а у — зависимой переменной или функцией.
Зависимость переменной у от переменной х называют функциональной зависимостью. Записывают так: y = f(x).
Функция — это соответствие между двумя множествами, причем каждому элементу первого множества соответствует один элемент второго множества.
Из понятия функции сформулируем определение области определения функции.
Область определения функции — это множество всех значений аргумента (переменной x). Геометрически — это проекция графика функции на ось Ох.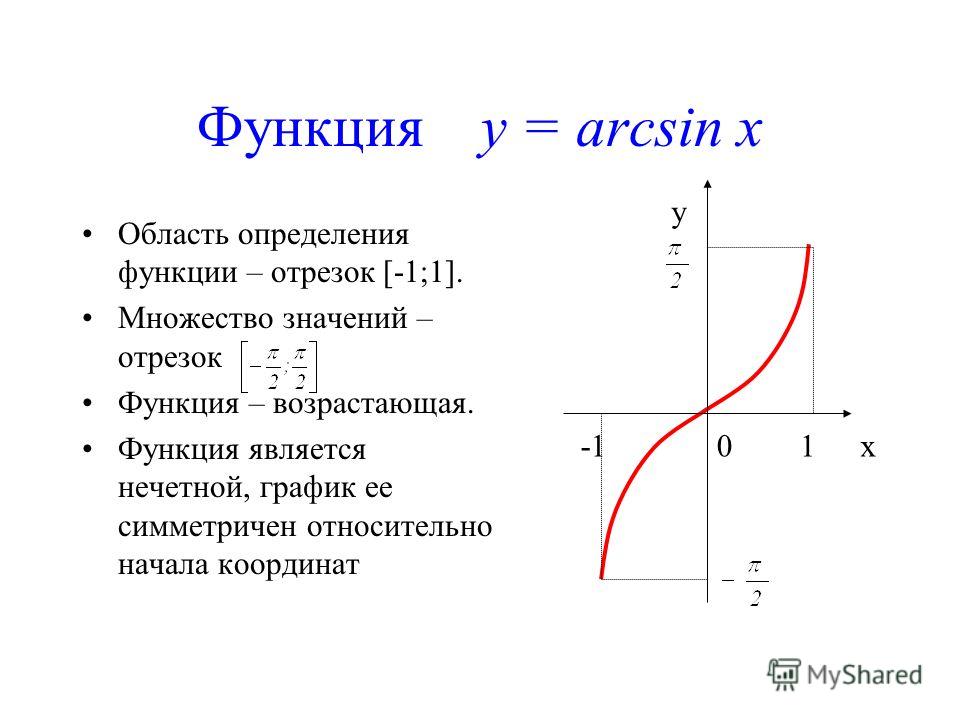
Множество значений функции — множество всех значений, которые функция принимает на области определения. Геометрически — это проекция графика функции на ось Оy.
- Например, область значений функции y = x2 — это все числа больше либо равные нулю. Это можно записать так: Е (у): у ≥ 0.
Чтобы обозначить область определения некоторой функции f, используют запись D(f). При этом нужно помнить, что у некоторых функций есть собственные обозначения. Например, у тригонометрических. Поэтому в учебниках можно встретить такие записи: D(sin) — область определения функции синус, D(arcsin) — область определения функции арксинус.
Можно также записать D(f), где f — функция синуса или арксинуса. Если функция f определена на множестве значений x, то можно использовать формулировку D(f) = X. Так, например, для того же арксинуса запись будет выглядеть так: D (arcsin) = [-1, 1].
Область определения можно описывать словами, но часто ответ получается громоздким. Поэтому используют специальные обозначения.
Если мы хотим указать на множество чисел, которые лежат в некотором промежутке, то делаем так:
- Через точку с запятой указываем два числа: левую и правую границы промежутка.
- Если граница входит в промежуток, ставим возле нее квадратную скобку, если не входит — круглую.
- Если у промежутка нет правой границы, записываем так: ∞ или +∞. Если нет левой границы, пишем -∞.
- Если нужно описать множество, состоящее из нескольких промежутков, ставим между ними знак объединения: ∪.
Например, все действительные числа от 2 до 5 включительно можно записать так:
Все положительные числа можно описать так:
Ноль не положительное число, поэтому скобка возле него круглая.
Области определения основных элементарных функций
Область определения функции — неотъемлемая часть самой функции. Когда мы вводим какую-либо функцию, то сразу указываем ее область определения.
На уроках алгебры мы последовательно знакомимся с каждой функцией: прямая пропорциональность, линейная функция, функция y = x2 и другие. А области их определения изучаем, как свойства.
А области их определения изучаем, как свойства.
Рассмотрим области определения основных элементарных функций.
Область определения постоянной функции
Постоянная функция задается формулой y = C, то есть f(x) = C, где C — некоторое действительное число. Ее еще называют константа.
Смысл функции — в том, что каждому значению аргумента соответствует значение, которое равно C. Поэтому, область определения этой функции — множество всех действительных чисел R.
Константная функция — функция, которая для любого элемента из области определения возвращает одно и то же заданное значение. Множество значений такой функции состоит из одного единственного элемента.
- Область определения постоянной функции y = -3 — это множество всех действительных чисел: D(f) = (−∞, +∞) или D(f) = R.
- Область определения функции y = 3 √9 является множество R.
Область определения функции с корнем
Функцию с корнем можно определить так: y = n √x, где n — натуральное число больше единицы.
Рассмотрим две вариации такой функции.
Область определения корня зависит от четности или нечетности показателя:
Значит, область определения каждой из функций y = √x, y = 4 √x, y = 6 √x,… есть числовое множество [0, +∞). А область определения функций y = 3 √x, y = 5 √x, y = 7 √x,… — множество (−∞, +∞).
Пример
Найти область определения функции:
Так как подкоренное выражение должно быть положительным, то решим неравенство x 2 + 4x + 3 > 0.
Разложим квадратный трёхчлен на множители:
D = 16 — 12 = 4 > 0
Дискриминант положительный. Ищем корни:
Значит парабола a(x) = x 2 + 4x + 3 пересекает ось абсцисс в двух точках. Часть параболы расположена ниже оси (неравенство x 2 + 4x + 3 < 0), а другая часть — выше оси (неравенство x 2 + 4x + 3 > 0).
Поскольку коэффициент a = 1 > 0, то ветви параболы смотрят вверх. Можно сделать вывод, что на интервалах (−∞, -3) ∪ (−1, +∞) выполнено неравенство x 2 + 4x + 3 > 0 (ветви параболы уходят вверх на бесконечность), а вершина параболы расположена на промежутке (-3; -1) ниже оси абсцисс, что соответствует неравенству x 2 + 4x + 3 < 0.
Ответ: область определения: D(f) = (−∞, -3) ∪ (−1, +∞).
Область определения степенной функции
Степенная функция выглядит так: y = x a , то есть, f(x) = x a , где x — переменная в основании степени, a — некоторое число в показателе степени.
Область определения степенной функции зависит от значения показателя степени.
Перечислим возможные случаи:
- Если a — положительное целое число, то область определения функции есть множество действительных чисел: (−∞, +∞).
- Для нецелых действительных положительных показателей степени: D(f) = [0, +∞).
- Если a — отрицательное целое число, то область определения функции представляет собой множество (−∞, 0) ∪ (0, +∞).
- Для остальных действительных отрицательных a область определения степенной функции — числовой промежуток (0, +∞).
При a = 0 степенная функция y = x a определена для всех действительных значений x, кроме x = 0. Это связано с тем, что мы не определяли 0 0 . А любое отличное от нуля число в нулевой степени равно единице. То есть, при a = 0 функция приобретает вид y = x 0 = 1 на области определения (−∞, 0) ∪ (0, +∞).
А любое отличное от нуля число в нулевой степени равно единице. То есть, при a = 0 функция приобретает вид y = x 0 = 1 на области определения (−∞, 0) ∪ (0, +∞).
Рассмотрим несколько примеров.
- Область определения функций y = x 5 , y = x 12 — множество R, так как показатели степени целые положительные.
- Степенные функции определены на интервале [0, +∞), так как их показатели положительные, но не целые.
- Область определения функции y = x −2 , как и функции y = x −5 — это множество (−∞, 0) ∪ (0, +∞), так как показатели степени целые отрицательные.
- Область определения степенных функций y = x -√19 , y = x -3e , — открытый числовой луч (0, +∞), так как их показатели не целые и отрицательные.
Область определения показательной функции
Показательную функцию можно задать формулой y = a x , где переменная x — показатель степени, а — больше нуля и не равно единице.
Область определения показательной функции — это множество R.
Примеры показательных функций:
Область определения каждой из них (−∞, +∞).
Область определения логарифмической функции
Логарифмическая функция выглядит так: y = logax, где где число a > 0 и a ≠ 1. Она определена на множестве всех положительных действительных чисел.
Область определения логарифмической функции или область определения логарифма — это множество всех положительных действительных чисел. То есть, D (loga) = (0, +∞).
Например:
Рассмотрим примеры логарифмических функций:
Область определения этих функций есть множество (0, +∞).
Пример
Укажите, какова область определения функции:
Составим и решим систему:
Ответ: область определения: D(f) = (−3, -2) ∪ (−2, +∞).
Область определения тригонометрических функций
Сначала вспомним, как задавать тригонометрические функции и как увидеть их области определения.
- Функция, которая задается формулой y = sinx, называется синусом, обозначается sin и определяется на множестве всех действительных чисел.
 Область определения синуса — это множество всех действительных чисел, то есть, D(sin) = R.
Область определения синуса — это множество всех действительных чисел, то есть, D(sin) = R. - Функция, которая задана формулой y = cosx, называется косинусом, обозначается cos и определяется на множестве R. Область определения функции косинус — множество всех действительных чисел: D(cos) = R.
- Функции, которые заданы формулами y = tgx и y = ctgx, называются тангенсом и котангенсом и обозначаются tg и ctg. Область определения тангенса — это множество всех действительных чисел, кроме чисел . Область определения котангенса — это множество всех действительных чисел, кроме чисел πk, k ∈ Z.
Поэтому, если x — аргумент функций тангенс и котангенс, то области определения тангенса и котангенса состоят из всех таких чисел x, что и x ∈ r, x ≠ πk, k ∈ Z соответственно.
Пример
Найдите область определения функции f(x) = tg2x.
Так как a(x) = 2x, то в область определения не войдут следующие точки:
Перенесем 2 из левой части в знаменатель правой части:
В результате . Отразим графически:
Отразим графически:
Ответ: область определения: .
Область определения обратных тригонометрических функций
Вспомним обратные тригонометрические функции: арксинус, арккосинус, арктангенс и арккотангенс.
-
Функция, которая задается формулой y = arcsinx и рассматривается на отрезке [−1, 1], называется арксинусом и обозначается arcsin.
Таблица областей определения функций
Области определения основных функций в табличном виде можно распечатать и использовать на уроках, чтобы быстрее решать задачки.
И, помните: чем чаще вы практикуетесь в решении задач — тем быстрее все запомните.
Читайте также:
- Ассасин тихое место
- Simcity новые регионы
- Fallout 4 самый лучший дом
- Назови имя своего бога dark souls 3
- Щит храмовника dark souls 3
Тригонометрические функции
Репетиторы ❯ Математика ❯ Тригонометрические функции
Автор: Валентин В.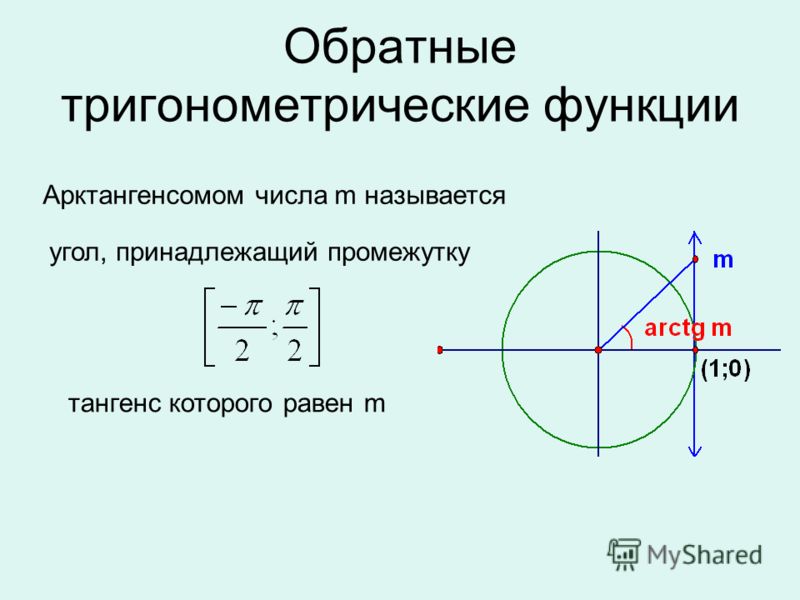 , онлайн репетитор по математике
, онлайн репетитор по математике
●
10.10.2011
●
Раздел: Математика
Предположим, что на нашей координатной плоскости есть некий отрезок ОА, который называется начальным радиусом и лежит на оси абсцисс. В результате поворотов радиуса ОА получается радиус ОВ.
Синусом угла α называется отношение ординаты точки В к радиусу. Синус обозначается sin α.
Косинусом угла α называют отношение абсциссы точки В к радиусу и обозначают cos α.
Тангенс угла α – это отношение ординаты точки В к ее абсциссе. Тангенс угла записывается так: tg α.
Отношение абсциссы точки В к ее ординате называется котангенсом угла α и записывается как ctg α.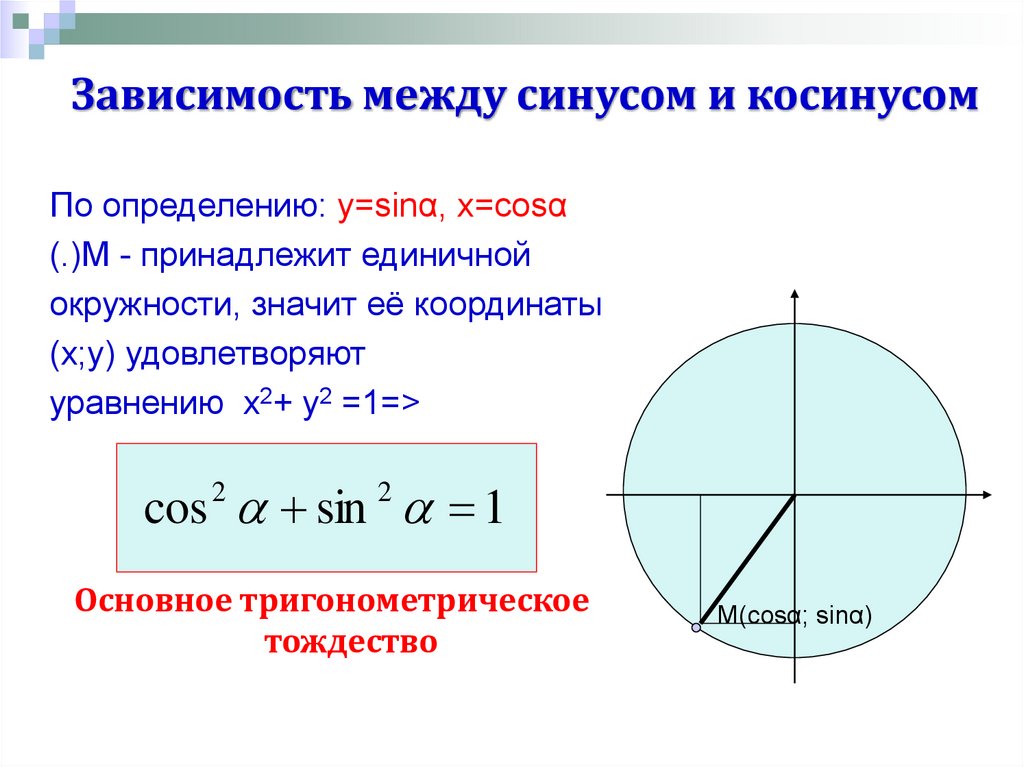
Тригонометрическими называются функции у = sin x, у = cos x, у = tg x, у = ctg x.
Как и ранее рассматриваемые функции, тригонометрические функции могут быть четными и нечетными:
cos (-x) = cos x
sin (-x) = -sin x
tg (-x) = -tg x
ctg (-x) = -сtg x.
Исходя из данных равенств, получаем, что функции у = sin x, у = tg x, у = ctg x являются нечетными, а функция у = cos x – четной.
Рассмотрим графики и свойства этих функций.
Функция у = sin x обладает набором следующих характеристик:
1. Область определения – множество всех действительных чисел.
2. Область значений – отрезок [-1; 1].
3. Функция периодическая; основной период – 2n.
Чтобы построить график функции, нужно выбрать отрезок, например, [0; n] и построить график на нем. Затем симметрично «достроить» график относительно начала координат, воспользовавшись периодичностью функции. График функции у = sin x называется синусоидой.
Свойства функции у = cos x во многом повторяют свойства функции у = sin x. Итак, у = cos x:
Итак, у = cos x:
1. Область определения – множество всех действительных чисел.
2. Область значений – отрезок [-1; 1].
3. Функция периодическая; основной период – 2n.
График функции у = cos x – это косинусоида. Этот график похож на синусоиду, но отличается тем, что он симметричен не относительно начала координат, а относительно оси y, т.е. оси ординат.
Функция у = tg x отличается от предыдущих функций следующими свойствами:
1. Область определения: х ≠ n/2 + πk, где k € Z.
2. Область значений – вся числовая прямая.
3. Функция периодическая; основной период — n.
4. Функция нечетная.
Для того чтобы построить график функции у = tg x, нужно:
1. Выбрать несколько «опорных» точек : (0; 0), (n/4; 1) и др.
2. Построить график функции на промежутке [0; n/2).
3. На основании нечетностью функции построить график на интервале (-π/2; π/2).
4. На основании периодичности функции «достроить» график на всей области определения.
График рассматриваемой функции называется тангенсоидой.
Функция у = ctg x обладает следующими свойствами:
1. Область определения: х ≠ nk, где k € Z.
2. Область значений – вся числовая прямая.
3. Функция периодическая; основной период – n.
4. Функция нечетная.
Чтобы построить график функции у = ctg x, необходимо:
1. Воспользоваться тождеством ctg x = -tg (x = n/2).
2. Сдвинуть тангенсоиду влево по оси абсцисс на расстояние n/2.
3. Полученную кривую отобразить симметрично относительно оси х.
Построенный график и будет нашей котангенсоидой.
© blog.tutoronline.ru, при полном или частичном копировании материала ссылка на первоисточник обязательна.
Остались вопросы?
Задайте свой вопрос и получите ответ от профессионального преподавателя.
Задать вопрос
Математика
Курсы по математике 10 класс
Математика
Курсы по математике 9 класс
Математика
Математика 11 класс
Математика
Курсы по геометрии 7 класс
Математика
Курсы по алгебре 7 класс
Математика
Алгебра 8 класс
Математика
Курсы по геометрии 8 класс
Французский язык
Курсы французского языка для начинающих
Область определения и диапазон тригонометрических функций
Перейти к основному содержанию
Домашняя страница Технологического института Онтарио
nool
Область определения функции — это определенный набор значений, которые может принимать независимая переменная в функции.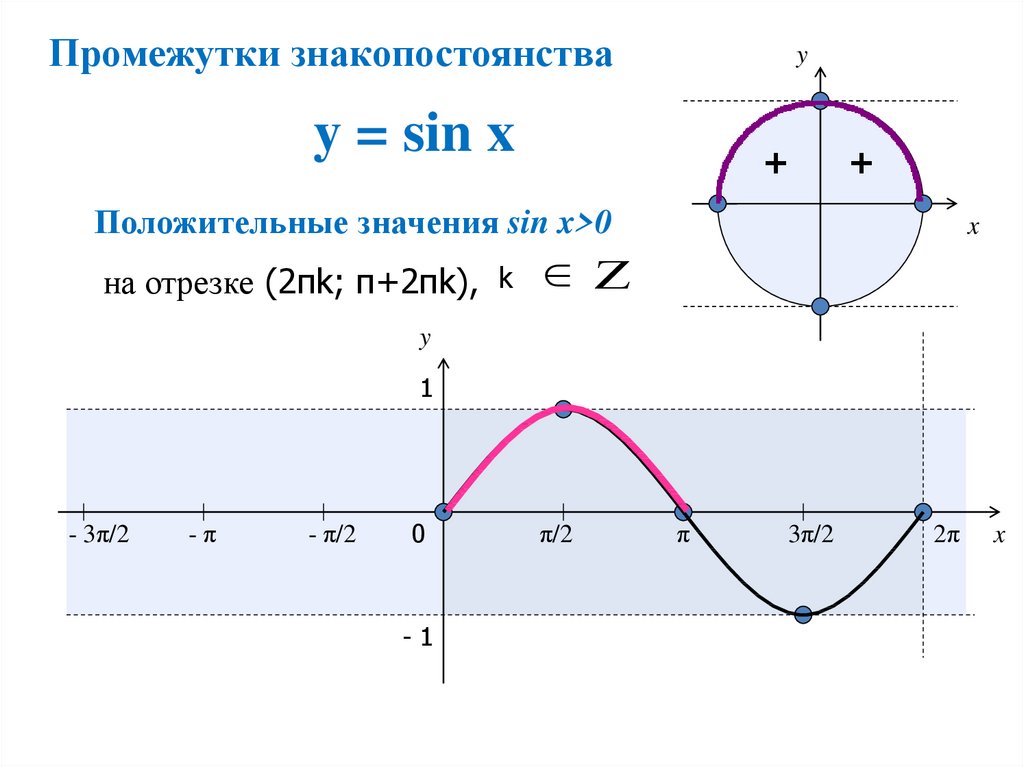 Диапазон — это результирующие значения, которые зависимая переменная может иметь при изменении x в пределах домена.
Диапазон — это результирующие значения, которые зависимая переменная может иметь при изменении x в пределах домена.
Домен и диапазон функций синуса и косинуса
На область определения функций синуса и косинуса ограничений нет; следовательно, их область определения такова, что x ∈ R. Обратите внимание, однако, что диапазон как для y = sin(x), так и для y = cos(x) находится между -1 и 1. Следовательно, преобразования этих функций в виде сдвиги и растяжения повлияют на диапазон, но не на домен.
Область определения и диапазон для функций тангенса
Обратите внимание, что y = tan(x) имеет вертикальные асимптоты при . Следовательно, его домен таков, что . Однако ее область значений такова при y ∈ R, поскольку функция принимает все значения y. В этом случае преобразования коснутся домена, но не диапазона.
Пример: Найти область определения и диапазон y = cos(x) – 3
Решение:
Область: x ∈ R
Диапазон: — 4 ≤ y ∈ R ≤ — 2, y
Обратите внимание, что диапазон просто сдвинут вниз на 3 единицы.
Пример: Найдите домен и диапазон y = 3 tan(x)
Решение:
Домен: , x ∈ R
Обратите внимание, что домен тот же, что и домен для y = tan(x) x), потому что график был растянут по вертикали, что не меняет места расположения вертикальных асимптот.
Диапазон: y ∈ R
Пример 1:
Пример 2:
Область и диапазон тригонометрических функций
Существует шесть тригонометрических функций sin θ, cos θ, tan θ, cot θ, tan θ, cosec θ и sec θ. Область и диапазон тригонометрических функций задаются углом θ и результирующим значением соответственно. Область определения тригонометрических функций — это углы в градусах или радианах, а диапазон — действительное число. Некоторые значения исключаются из области определения и диапазона тригонометрических функций в зависимости от области, в которой тригонометрическая функция не определена.
Область и диапазон тригонометрических функций задаются углом θ и результирующим значением соответственно. Область определения тригонометрических функций — это углы в градусах или радианах, а диапазон — действительное число. Некоторые значения исключаются из области определения и диапазона тригонометрических функций в зависимости от области, в которой тригонометрическая функция не определена.
В этой статье мы рассмотрим область и диапазон тригонометрических функций, используя таблицу и график, а также область и диапазон обратных тригонометрических функций, а также примеры для лучшего понимания.
| 1. | Что такое область определения и область значений тригонометрических функций? |
| 2. | Область определения и диапазон тригонометрических функций Таблица |
| 3. | Область определения и область значений обратных тригонометрических функций |
4. | Область определения и диапазон тригонометрических функций с использованием графика |
| 5. | Часто задаваемые вопросы по домену и диапазону тригонометрических функций |
Что такое область определения и область значений тригонометрических функций?
Область определения и диапазон тригонометрических функций — это входные значения и выходные значения тригонометрических функций соответственно. Область определения тригонометрических функций обозначает значения углов, в которых определены тригонометрические функции, а диапазон тригонометрических функций дает результирующее значение тригонометрической функции, соответствующее конкретному углу в области. Существует шесть основных тригонометрических функций, а именно: sin θ, cos θ, tan θ, cot θ, tan θ, cosec θ и sec θ.
Область и диапазон тригонометрической функции: синус
Мы знаем, что функция синуса представляет собой отношение перпендикуляра к гипотенузе прямоугольного треугольника. Область определения и область значений синуса тригонометрической функции задаются формулой:
Область определения и область значений синуса тригонометрической функции задаются формулой:
- Область определения = все действительные числа, т. е. (−∞, ∞)
- Диапазон = [-1, 1]
Область определения и диапазон тригонометрической функции: косинус
Мы знаем, что функция косинуса представляет собой отношение прилежащей стороны и гипотенузы прямоугольного треугольника. Область определения и область значений косинуса тригонометрической функции определяются как:
- Домен = все действительные числа, т. е. (−∞, ∞)
- Диапазон = [-1, 1]
Область определения и диапазон тригонометрической функции: тангенс
Мы знаем, что тангенс представляет собой отношение противолежащих и прилежащих сторон прямоугольного треугольника. Его также можно записать как отношение функции синуса и косинуса, поэтому область значений tan x не содержит значений, при которых cos x равен нулю. Мы знаем, что cos x равен 0 при нечетных целых числах, кратных π/2, поэтому область определения и область значений тангенса тригонометрической функции определяются выражением:
- Домен = R — (2n + 1)π/2
- Диапазон = (−∞, ∞)
Область определения и область значений тригонометрической функции: котангенс
Мы знаем, что функция котангенса представляет собой отношение прилежащей стороны к противолежащей стороне в прямоугольном треугольнике. Это также может быть записано как отношение функции косинуса и синуса, а cot x является обратной величиной tan x. Поэтому область определения ctg x не содержит значений, при которых sin x равен нулю. Мы знаем, что sin x равен 0 при целых кратных π, следовательно, область определения и область значений котангенса тригонометрической функции определяются как:
Это также может быть записано как отношение функции косинуса и синуса, а cot x является обратной величиной tan x. Поэтому область определения ctg x не содержит значений, при которых sin x равен нулю. Мы знаем, что sin x равен 0 при целых кратных π, следовательно, область определения и область значений котангенса тригонометрической функции определяются как:
- Домен = R — nπ
- Диапазон = (−∞, ∞)
Область определения и диапазон тригонометрической функции: секущая
Мы знаем, что секущая функция представляет собой отношение гипотенузы к прилежащей стороне в прямоугольном треугольнике. Его также можно записать как обратную функцию косинуса. Поэтому область определения sec x не содержит значений, при которых cos x равен нулю. Мы знаем, что cos x равен 0 при нечетных целых числах, кратных π, следовательно, область определения и область значений секанса тригонометрической функции определяются как:
- Домен = R — (2n + 1)π/2
- Диапазон = (-∞, -1] U [+1, +∞)
Область определения и диапазон тригонометрической функции: косеканс
Мы знаем, что косеканс представляет собой отношение гипотенузы к противолежащему катету в прямоугольном треугольнике.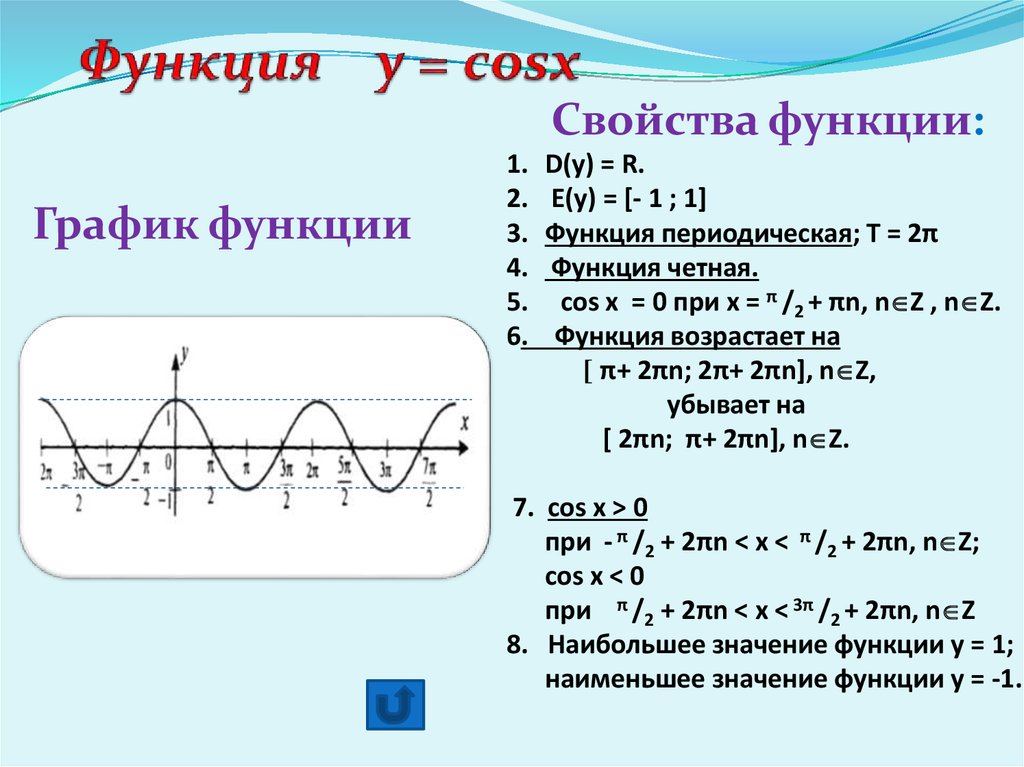 Его также можно записать как обратную функцию синуса. Поэтому область определения тригонометрической функции cosec x не содержит значений, при которых sin x равен нулю. Мы знаем, что sin x равен 0 при целых числах, кратных π, следовательно, область определения и область значений косеканса тригонометрической функции определяются выражением:
Его также можно записать как обратную функцию синуса. Поэтому область определения тригонометрической функции cosec x не содержит значений, при которых sin x равен нулю. Мы знаем, что sin x равен 0 при целых числах, кратных π, следовательно, область определения и область значений косеканса тригонометрической функции определяются выражением:
- Домен = R — nπ
- Диапазон = (-∞, -1] U [+1, +∞)
Таблица
Область определения и диапазон тригонометрических функций
Итак, мы изучили область определения и область значений тригонометрических функций. В приведенной ниже таблице дается ее краткое изложение, которое поможет лучше понять и использовать для решения различных задач:
| Тригонометрические функции | Домен | Диапазон |
| Синθ | (-∞, + ∞) | [-1, +1] |
| Cosθ | (-∞ +∞) | [-1, +1] |
| Танθ | Р — (2n + 1)π/2 | (-∞, +∞) |
| Кот θ | Р — номер | (-∞, +∞) |
| сек θ | Р — (2n + 1)π/2 | (-∞, -1] U [+1, +∞) |
| Косекθ | Р — номер | (-∞, -1] U [+1, +∞) |
Область определения и диапазон обратных тригонометрических функций
Функция обратима тогда и только тогда, когда она биективна. Обратные тригонометрические функции являются обратными по отношению к тригонометрическим функциям, и, чтобы сделать тригонометрические функции обратимыми, мы ограничиваем их область определения ветвью главного значения. В таблице ниже представлены область определения и диапазон обратных тригонометрических функций:
Обратные тригонометрические функции являются обратными по отношению к тригонометрическим функциям, и, чтобы сделать тригонометрические функции обратимыми, мы ограничиваем их область определения ветвью главного значения. В таблице ниже представлены область определения и диапазон обратных тригонометрических функций:
| Обратные тригонометрические функции | Домен | Диапазон |
| Грех -1 х | [-1, +1] | [-π/2, π/2] |
| Кос -1 x | [-1, +1] | [0, π] |
| Желто-коричневый -1 x | (-∞, + ∞) | (-π/2, π/2) |
| Детская кроватка -1 x | (-∞, + ∞) | (0, π) |
| сек -1 x | (−∞,−1] U [1,∞) | [0, π/2) U (π/2, π] |
| Косек -1 x | (−∞,−1] U [1,∞) | [-π/2, 0) U (0, π/2] |
Область определения и диапазон тригонометрических функций с использованием графика
Далее мы исследуем область и диапазон тригонометрических функций, используя графики тригонометрических функций.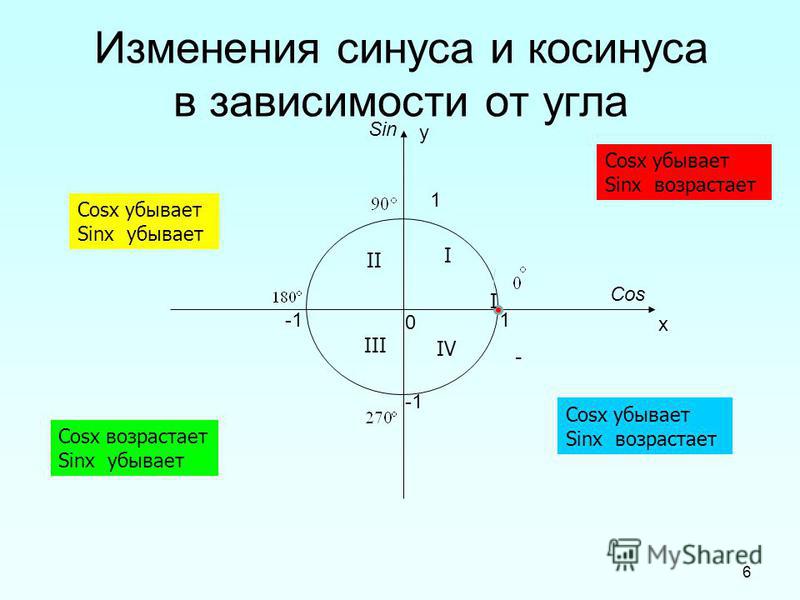 Ниже приведены графики шести тригонометрических функций. Как мы видим на графиках, область определения и диапазон тригонометрических функций представлены осью x и осью y соответственно.
Ниже приведены графики шести тригонометрических функций. Как мы видим на графиках, область определения и диапазон тригонометрических функций представлены осью x и осью y соответственно.
Советы и рекомендации по области определения и диапазону тригонометрических функций
- Проверьте значение ввода, если функция не определена. Значение, в котором функция не определена, может быть исключено из домена.
- Диапазон тригонометрической функции задается выходными значениями для каждого из входных значений (область).
Похожие темы
- Тригонометрия
- Тригонометрические формулы
- Тригонометрические тождества
Часто задаваемые вопросы по домену и диапазону тригонометрических функций
Что такое область и диапазон тригонометрических функций в тригонометрии?
область и диапазон тригонометрических функций являются входными значениями и выходными значениями тригонометрических функций соответственно.
- Для sin θ, домен = (-∞, + ∞), диапазон = [-1, 1]
- Для cos θ, домен = (-∞, + ∞), диапазон = [-1, 1]
- Для тангенса θ, домен = R — (2n + 1)π/2, диапазон = (-∞, +∞)
- Для кроватки θ, домен = R — nπ , диапазон = (-∞, +∞)
- Для сек θ, домен = R — (2n + 1)π/2, диапазон = (-∞, -1] U [+1, +∞)
- Для cosec θ, домен = R — nπ , диапазон = (-∞, -1] U [+1, +∞)
Как найти область определения и диапазон тригонометрических функций?
Домен и диапазон тригонометрических функций можно найти, проверив, где определена функция, и выходные значения функции для каждого входного значения.
Каков диапазон теты Cos Square?
Мы знаем, что диапазон cos θ равен [-1, 1], а cos 2 θ всегда положителен, поэтому диапазон cos квадрат тета равен [0, 1].
Как найти область определения и область значений обратных тригонометрических функций?
Обратные тригонометрические функции являются обратными по отношению к тригонометрическим функциям, и чтобы сделать тригонометрические функции обратимыми, мы ограничиваем их область определения ветвью главного значения.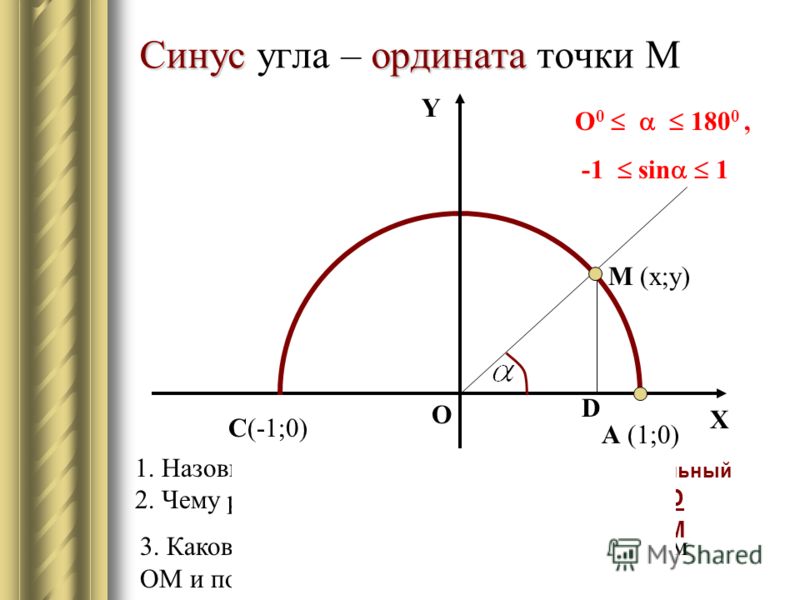
Что такое домен и диапазон Sec Theta?
Область определения sec θ равна R — (2n + 1)π/2, а диапазон равен (-∞, -1] U [+1, +∞), где n — целое число.
Видео-урок: Область определения и область значений тригонометрических функций
Расшифровка видео
В этом видео мы узнаем, как
определить область определения и область значений тригонометрических функций. Мы начнем с того, что вспомним
определения домена и диапазона функции. Область определения функции 𝑓 из 𝑥
это набор всех возможных значений 𝑥, таких что выражение 𝑓 для 𝑥 есть
определенный. Диапазон функции 𝑓 от 𝑥 равен
набор всех возможных значений, которые может принимать выражение 𝑓 из 𝑥, где 𝑥 — любое
число из домена функции. В частности, мы можем найти
область и область значений функции по ее графику. Учитывая график функции,
домен — это часть горизонтальной оси, где существует график, а диапазон
часть вертикальной оси, где находится график.
Начнем с рассмотрения график 𝑦 равен sin 𝑥 для значений 𝑥 от отрицательных 360 до 360 градусов. Мы видим, что функция определено для каждого 𝑥-значения. Это означает, что область греха 𝑥 — все действительные числа. Это также может быть записано как множество чисел на открытом интервале от отрицательных ∞ до ∞. Мы видим, что график колеблется между отрицательным единицей и единицей. Максимальное значение графика равно единица, а минимальное значение отрицательное. Это означает, что возможные значения sin 𝑥 находятся между этими двумя значениями. И диапазон этой функции множество значений на замкнутом интервале от отрицательной единицы до единицы. То же самое и с косинусом функция. Это, еще раз, имеет домен все действительные числа и диапазон от отрицательной единицы до единицы включительно.
Мы можем резюмировать это как
следует. Область определения функций sin 𝑥
а cos 𝑥 — все действительные числа, обозначенные, как показано. Обратите внимание, что они часто пишутся
как sin 𝜃 и cos 𝜃, где функция будет 𝑓 от 𝜃. Диапазон функций sin 𝑥
а cos 𝑥 — множество чисел на отрезке, отрицательных один к одному. Теперь давайте рассмотрим, как мы можем найти
область определения и область значений любой периодической функции по ее графику.
Область определения функций sin 𝑥
а cos 𝑥 — все действительные числа, обозначенные, как показано. Обратите внимание, что они часто пишутся
как sin 𝜃 и cos 𝜃, где функция будет 𝑓 от 𝜃. Диапазон функций sin 𝑥
а cos 𝑥 — множество чисел на отрезке, отрицательных один к одному. Теперь давайте рассмотрим, как мы можем найти
область определения и область значений любой периодической функции по ее графику.
Следующий график показывает функция 𝑓 от 𝜃. Предположим, что функция имеет период два 𝜋. Каков домен 𝑓 из 𝜃? Каков диапазон 𝑓 из 𝜃?
Мы знаем, что все
характеристики периодической функции содержатся на интервале этого
длина. В этом вопросе нам говорят
период равен двум 𝜋. Поэтому нам остается только рассмотреть
график между нулем и двумя 𝜋. Область определения любой функции есть множество
всех возможных входных значений. И мы можем видеть из графика, что
функция корректно определена при всех значениях 𝜃. Таким образом, мы можем сделать вывод, что
домен 𝑓 из 𝜃 — это все действительные числа, записанные в виде открытого интервала от отрицательного ∞
до ∞.
И мы можем видеть из графика, что
функция корректно определена при всех значениях 𝜃. Таким образом, мы можем сделать вывод, что
домен 𝑓 из 𝜃 — это все действительные числа, записанные в виде открытого интервала от отрицательного ∞
до ∞.
Диапазон любой функции набор всех выходных значений. Из графика мы видим, что функция колеблется и непрерывна между отрицательными семью и тремя. Максимальное значение графика равно три, а минимальное значение отрицательное семь. Таким образом, мы можем сделать вывод, что диапазон 𝑓 of 𝜃 — это множество значений на замкнутом интервале от минус семи до три. Два ответа на этот вопрос — открытый интервал от отрицательного ∞ до ∞ и закрытый интервал от отрицательного с семи до трех.
Теперь рассмотрим, как
преобразование тригонометрических функций влияет на область определения и диапазон.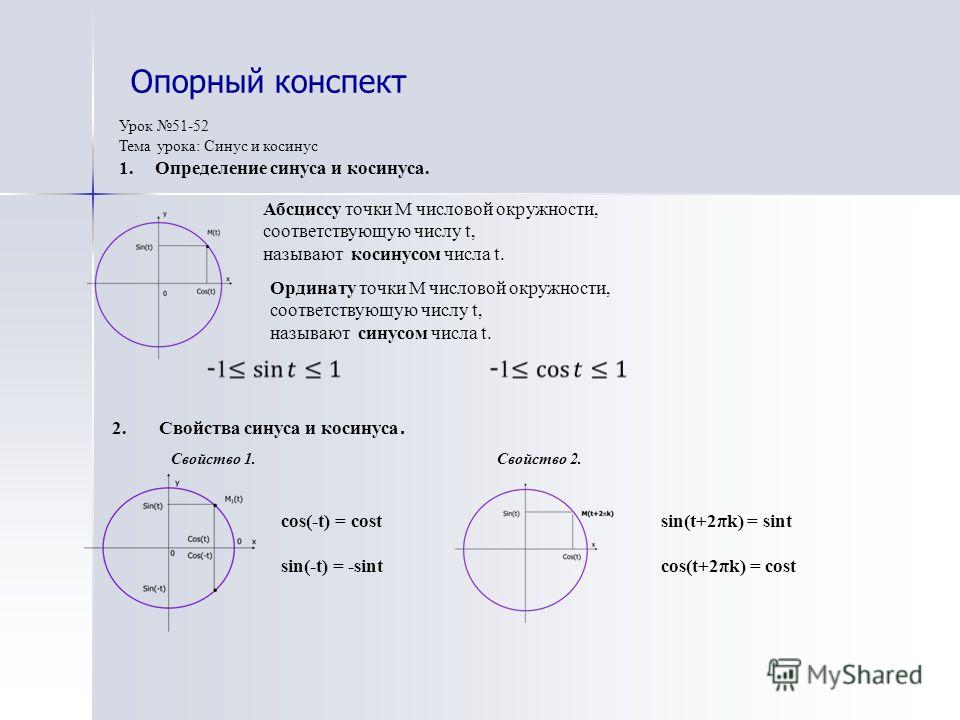 Напомним, что синусоидальная функция
имел домен и диапазон, как показано. Любое преобразование этой функции
не изменит своего домена. Однако определенные преобразования
повлияет на диапазон нашей функции.
Напомним, что синусоидальная функция
имел домен и диапазон, как показано. Любое преобразование этой функции
не изменит своего домена. Однако определенные преобразования
повлияет на диапазон нашей функции.
Рассмотрим функцию 𝑓 от
𝑥, что равно 𝑎 sin 𝑥 плюс 𝑏, где 𝑎 и 𝑏 — вещественные константы. Умножение функции на
положительная константа 𝑎 приводит к вертикальному расширению или растяжению на масштабный коэффициент
𝑎. Это изменит диапазон
функция от отрезка отрицательная единица, от единицы к отрезку отрицательная
𝑎, 𝑎. Однако умножение функции на
отрицательная константа приводит к отражению по оси 𝑥 и растяжению на
масштабный коэффициент абсолютного значения 𝑎. Это означает, что диапазон
функция 𝑎 sin 𝑥 равна отрезку от отрицательного абсолютного значения
𝑎 к положительному абсолютному значению 𝑎.
Далее, мы знаем, что добавление 𝑏 к функция приводит к вертикальному сдвигу вверх, если 𝑏 больше нуля и вниз, если 𝑏 меньше нуля. Таким образом, мы можем сделать вывод, что диапазон функции 𝑎 sin 𝑥 plus 𝑏 — замкнутый интервал от отрицательных абсолютное значение 𝑎 плюс 𝑏 к положительному абсолютному значению 𝑎 плюс 𝑏. Давайте теперь рассмотрим, как это работает на практике.
Рассмотрим функцию 𝑓 от 𝑥 равно четырем из семи 𝑥 плюс 𝜋 плюс пять. Каков домен 𝑓 из 𝑥? Каков диапазон 𝑓 из 𝑥?
Начнем с того, что вспомним, что
область определения любой функции — это множество всех возможных входных значений, и область определения
из cos 𝜃 все действительные значения. В этом вопросе выражение
семь 𝑥 плюс 𝜋 находятся внутри функции косинуса. Поскольку это выражение корректно определено
для любого действительного числа домен 𝑓 of 𝑥 — это все действительные числа, которые могут быть
записывается как открытый интервал от отрицательного ∞ до ∞. Мы знаем, что диапазон — это множество
выходных значений. Поскольку диапазон семь 𝑥 плюс 𝜋
все действительные числа, это выражение может принимать любое действительное значение. Поэтому мы примем это равным 𝜃
так что у нас есть четыре cos 𝜃 плюс пять.
Мы знаем, что диапазон — это множество
выходных значений. Поскольку диапазон семь 𝑥 плюс 𝜋
все действительные числа, это выражение может принимать любое действительное значение. Поэтому мы примем это равным 𝜃
так что у нас есть четыре cos 𝜃 плюс пять.
Мы знаем, что у cos 𝜃 есть диапазон
на замкнутом интервале от отрицательной единицы до единицы. Поэтому нам необходимо рассмотреть, как
преобразования этой функции в четыре cos 𝜃 плюс пять влияют на диапазон. Во-первых, мы умножили
на четыре, что приводит к растяжению диапазона по вертикали в
четыре. Это дает нам закрытый интервал
от отрицательной четвёрки до четвёрки. Добавление пяти к этому выражению
сдвигает функцию вверх на пять. Минус четыре плюс пять равно
один, а четыре плюс пять равно девяти. Это означает, что диапазон 𝑓 из
𝑥 — закрытый интервал от одного до девяти.
Мы могли решить вторую часть алгебраически, используя наши знания о неравенствах. Мы знаем, что cos 𝜃 больше больше или равно отрицательной единице и меньше или равно единице. Умножая на четыре, мы есть четыре, потому что 𝜃 больше или равно отрицательному четырем и меньше или равно четыре. Добавляя пять к каждому члену в неравенство, имеем четыре потому что 𝜃 плюс пять больше или равно единице и меньше больше или равно девяти. Это соответствует закрытому интервал от одного до девяти. Область определения функции четыре cos из семи 𝑥 плюс 𝜋 плюс пять — это открытый интервал от отрицательного ∞ до ∞, и его диапазон — закрытый интервал от одного до девяти.
Прежде чем перейти к последнему
Например, давайте рассмотрим область определения и область значений касательной функции. В отличие от синуса и косинуса
функции, касательная функция имеет ограничения области. Учитывая график загара 𝜃
в интервале от минус 360 градусов до 360 градусов или минус два 𝜋
радиан до двух 𝜋 радиан, мы отмечаем, что график не определен при 90 градусах, 270
градусов, минус 90 градусов и минус 270 градусов. Так как касательная функция
периодическое, это поведение повторяется бесконечно каждые 180 градусов. Таким образом, мы можем сделать вывод, что 𝑥
не определен и график имеет асимптоту при значениях 𝑥, равных 90 градусов
плюс 180 градусов, умноженное на 𝑛, где 𝑛 — любое целое число.
Учитывая график загара 𝜃
в интервале от минус 360 градусов до 360 градусов или минус два 𝜋
радиан до двух 𝜋 радиан, мы отмечаем, что график не определен при 90 градусах, 270
градусов, минус 90 градусов и минус 270 градусов. Так как касательная функция
периодическое, это поведение повторяется бесконечно каждые 180 градусов. Таким образом, мы можем сделать вывод, что 𝑥
не определен и график имеет асимптоту при значениях 𝑥, равных 90 градусов
плюс 180 градусов, умноженное на 𝑛, где 𝑛 — любое целое число.
Таким образом, домен загара 𝑥 может
быть записано, как показано. Это все действительные числа, кроме
𝑥 равно 90 градусов плюс 180 градусов, умноженное на 𝑛. Это также может быть записано в радианах
так как 𝑥 равно 𝜋 больше двух плюс 𝜋𝑛. Еще раз, 𝑛 — любое целое число
ценность. Диапазон касательной функции
все действительные значения, которые можно записать в виде открытого интервала от отрицательного ∞ до
∞. В нашем последнем примере мы будем
идентифицируйте входные значения, где функция тангенса не определена.
В нашем последнем примере мы будем
идентифицируйте входные значения, где функция тангенса не определена.
Найти значение 𝜃 в радианах такая, что функция 𝑓 от 𝜃 равна тангенсу трех 𝜃, не определена.
Начнем с того, что вспомним, что
область определения функции тангенса в радианах исключает значения вида 𝜃 равна
𝜋 больше двух плюс 𝑛𝜋, где 𝑛 — целое число. В этом вопросе нам дается
функция 𝑓 от 𝜃 равна тангенсу трех 𝜃, и мы хотим найти значения
где это не определено. Поэтому мы можем положить три 𝜃 равными
𝜋 больше двух плюс 𝑛𝜋, где 𝑛 — целое число. Разделив обе стороны этого
уравнение на три, мы имеем 𝜃 равно 𝜋 больше шести плюс 𝑛𝜋 больше трех. Еще раз, это для всех целых
значения 𝑛. Таким образом, загар трех 𝜃 равен
undefined для всех значений 𝜃, равных 𝜋 более шести плюс 𝑛𝜋 более трех, где 𝑛
целое число.
Теперь мы закончим это видео, резюмируя ключевые моменты. Область определения функций sin 𝜃 а cos 𝜃 — все действительные числа. И круг этих функций набор чисел на замкнутом интервале от отрицательной единицы до единицы. Для любых констант 𝑎 и 𝑏 диапазон функций 𝑎 sin 𝜃 plus 𝑏 или 𝑎 cos 𝜃 plus 𝑏 — замкнутый интервал от отрицательного абсолютного значения 𝑎 плюс 𝑏 к абсолютному значению 𝑎 плюс 𝑏. Домен загара 𝜃 написан в радианах все действительные числа, кроме 𝜃, равно 𝜋 больше двух плюс 𝑛𝜋, где 𝑛 — целое число. Мы также можем записать это в градусах, где 𝜋 больше двух равно 90 градусов, а 𝜋 равно 180 градусам. Наконец, диапазон касательной функция tan 𝜃 состоит из действительных чисел.
Обратные тригонометрические функции | Предварительное исчисление
Результаты обучения
- Понимать и использовать функции арксинуса, косинуса и тангенса.

- Найдите точное значение выражений, включающих функции арксинуса, косинуса и тангенса.
- Используйте калькулятор для вычисления обратных тригонометрических функций.
- Используйте обратные тригонометрические функции для решения прямоугольных треугольников.
- Найдите точные значения сложных функций с помощью обратных тригонометрических функций.
Понимание и использование функций арксинуса, косинуса и тангенса
Чтобы использовать обратные тригонометрические функции, мы должны понимать, что обратная тригонометрическая функция «отменяет» то, что «делает» исходная тригонометрическая функция, как в случае с любая другая функция и ее обратная. Другими словами, область определения обратной функции — это область значений исходной функции и наоборот, как показано на рис. 1.9.{−1}(b)=a[/латекс].
Имейте в виду, что функции синуса, косинуса и тангенса не являются взаимно однозначными функциями. График каждой функции не прошел бы тест горизонтальной линии. На самом деле никакая периодическая функция не может быть взаимно однозначной, потому что каждый выход в ее диапазоне соответствует по крайней мере одному входу в каждом периоде, а периодов бесконечное количество. Как и в случае с другими функциями, которые не являются взаимно однозначными, нам потребуется ограничить домен каждой функции, чтобы получить новую функцию, которая является взаимно однозначной. Мы выбираем область определения для каждой функции, которая включает число 0. На рисунке 2 показан график синусоидальной функции, ограниченный [латекс]\left[\frac{−\pi}{2}\text{, }\frac{\pi }{2}\right][/latex] и график функции косинуса, ограниченной [0, π].
На самом деле никакая периодическая функция не может быть взаимно однозначной, потому что каждый выход в ее диапазоне соответствует по крайней мере одному входу в каждом периоде, а периодов бесконечное количество. Как и в случае с другими функциями, которые не являются взаимно однозначными, нам потребуется ограничить домен каждой функции, чтобы получить новую функцию, которая является взаимно однозначной. Мы выбираем область определения для каждой функции, которая включает число 0. На рисунке 2 показан график синусоидальной функции, ограниченный [латекс]\left[\frac{−\pi}{2}\text{, }\frac{\pi }{2}\right][/latex] и график функции косинуса, ограниченной [0, π].
Рис. 2. (a) Синусоидальная функция на ограниченной области [латекс]\left[−\frac{\pi}{2}\text{, }\frac{\pi}{2}\right] [/латекс]; (b) Функция косинуса в ограниченной области [0, π]
На рисунке 3 показан график функции тангенса, ограниченной [латекс]\left(−\frac{\pi}{2}\text{, }\ frac{\pi}{2}\right)[/latex].
Рис. 3. Касательная функция на ограниченной области [латекс]\left(−\frac{\pi}{2}\text{, }\frac{\pi}{2}\right)[/latex ]
Эти обычные варианты ограниченного домена несколько произвольны, но у них есть важные и полезные характеристики. Каждый домен включает в себя начало координат и некоторые положительные значения, и, что наиболее важно, каждый из них приводит к взаимно однозначной функции, которая является обратимой. Традиционный выбор для ограниченной области касательной функции также имеет полезное свойство, состоящее в том, что он расширяется от одного 9{−1}x[/latex] имеет область определения всех действительных чисел и диапазон [latex]\left(−\frac{\pi}{2}\text{, }\frac{\pi}{2}\right) [/латекс]. Чтобы найти домен и диапазон обратных тригонометрических функций, поменяйте местами домен и диапазон исходных функций. Каждый график обратной тригонометрической функции является отражением графика исходной функции относительно прямой [латекс]у=х[/латекс].
Рис. 4. Функция синуса и функция обратного синуса (или арксинуса) 9{−1}x=y[/латекс].
Пример 1. Запись отношения для обратной функции синус.
Показать решение
Попробуй
Учитывая [латекс]\cos(0,5)\приблизительно 0,8776[/латекс], напишите соотношение, включающее арккосинус.
Показать решение
Нахождение точного значения выражений, включающих функции арксинуса, косинуса и тангенса 9\circ)[/latex] и их отражение в других квадрантах.
Как: При наличии «специального» входного значения вычислить обратную тригонометрическую функцию.
- Найдите угол x , для которого исходная тригонометрическая функция имеет выход, равный заданному входу для обратной тригонометрической функции.
- Если x не входит в заданный диапазон обратной величины, найдите другой угол y , который находится в заданном диапазоне и имеет тот же синус, косинус или тангенс, что и 9{−1}(\frac{1}{2})[/латекс]
Показать раствор
Попробуйте
Использование калькулятора для вычисления обратных тригонометрических функций
Чтобы вычислить обратных тригонометрических функций , которые не включают специальные углы, обсуждавшиеся ранее, нам потребуется использовать калькулятор или другую технику. Большинство научных калькуляторов и приложений, имитирующих калькулятор, имеют специальные клавиши или кнопки для функций обратного синуса, косинуса и тангенса. Они могут быть помечены, например, SIN-1, ARCSIN или ASIN.
Большинство научных калькуляторов и приложений, имитирующих калькулятор, имеют специальные клавиши или кнопки для функций обратного синуса, косинуса и тангенса. Они могут быть помечены, например, SIN-1, ARCSIN или ASIN.
В предыдущей главе мы работали с тригонометрией над прямоугольным треугольником, чтобы найти стороны треугольника по одной стороне и дополнительному углу. Используя обратные тригонометрические функции, мы можем найти углы прямоугольного треугольника с двумя сторонами, и мы можем использовать калькулятор, чтобы найти значения с точностью до нескольких знаков после запятой.
В этих примерах и упражнениях ответы будут интерпретироваться как углы, и мы будем использовать θ как независимую переменную. Значение, отображаемое на калькуляторе, может быть в градусах или радианах, поэтому обязательно установите режим, соответствующий приложению. 9{−1}\left(\frac{p}{a}\right)[/latex].
Пример 4. Применение арккосинуса к прямоугольному треугольнику
Решите треугольник на рисунке 8 для угла θ.
Рисунок 8
Показать решение
Попробуйте
Решите треугольник на рисунке 9 для угла θ.
Рисунок 9
Показать решение
Попробуйте
Нахождение точных значений составных функций с помощью обратных тригонометрических функций
Бывают случаи, когда нам нужно составить тригонометрическую функцию с обратной тригонометрической функцией. В этих случаях мы обычно можем найти точные значения результирующих выражений, не прибегая к помощи калькулятора. Даже когда входными данными для составной функции являются переменная или выражение, мы часто можем найти выражение для вывода. Чтобы помочь разобраться в различных случаях, пусть f ( x ) и g ( x ) будут двумя разными тригонометрическими функциями, принадлежащими множеству {sin( 9{−1}(g(x))[/латекс]. Для специальных значений x мы можем точно вычислить внутреннюю функцию, а затем внешнюю, обратную функцию.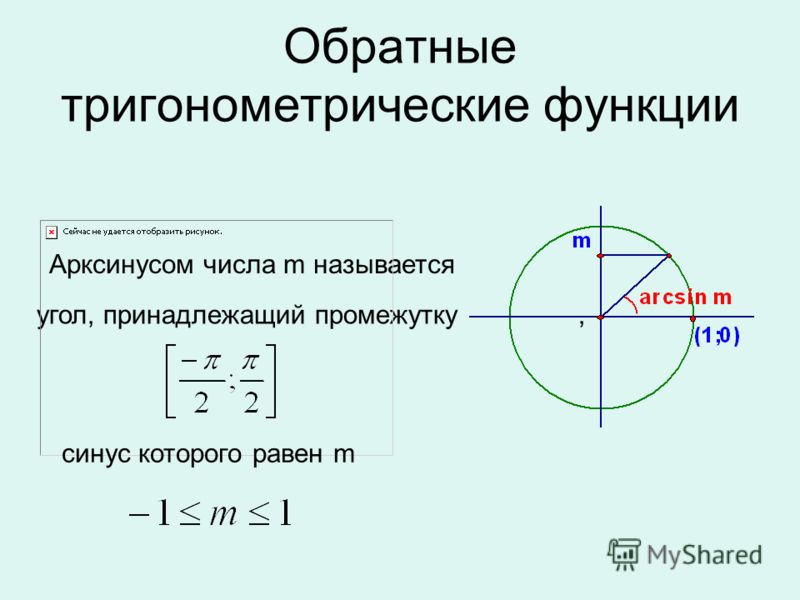 Однако мы можем найти более общий подход, рассмотрев отношение между двумя острыми углами прямоугольного треугольника, где один равен θ, что делает другой [латекс]\фракция{\пи}{2}-\тета[/латекс]. Рассмотрим синус и косинус каждого угла прямоугольного треугольника на рисунке 10.
Однако мы можем найти более общий подход, рассмотрев отношение между двумя острыми углами прямоугольного треугольника, где один равен θ, что делает другой [латекс]\фракция{\пи}{2}-\тета[/латекс]. Рассмотрим синус и косинус каждого угла прямоугольного треугольника на рисунке 10.
Рисунок 10. Прямоугольный треугольник, иллюстрирующий кофункциональные отношения 9{−1}\left(4x\right)\right)\\[/latex] для [латекса]−\frac{1}{4}\leq x \leq\frac{1}{4}[/latex] .
Показать решение
Попробуйте
Ключевые понятия
- Обратная функция — это функция, которая «отменяет» другую функцию. Область определения обратной функции — это область определения исходной функции, а область определения обратной функции — область определения исходной функции.
- Поскольку тригонометрические функции не являются взаимно однозначными в своих естественных областях, обратные тригонометрические функции определены для ограниченных областей.
 9{−1}\left(\sin x\right)=\frac{\pi}{2}-x[/latex], если [латекс]-\frac{\pi}{2}\leq x \leq\frac {\pi}{2}[/латекс].
9{−1}\left(\sin x\right)=\frac{\pi}{2}-x[/latex], если [латекс]-\frac{\pi}{2}\leq x \leq\frac {\pi}{2}[/латекс]. - При оценке композиции тригонометрической функции с обратной тригонометрической функцией нарисуйте опорный треугольник, чтобы помочь в определении отношения сторон, которое представляет результат тригонометрической функции.
- При оценке композиции тригонометрической функции с обратной тригонометрической функцией вы можете использовать тригонометрические тождества, чтобы помочь в определении отношения сторон. 9{−1}x[/latex], обратная функции тангенса и углу, тангенс которого равен заданному числу.
Область определения и область значений обратных тригонометрических функций
В этом разделе вы узнаете, как найти область определения и область значений обратных тригонометрических функций.
Чтобы вы могли понять область определения и область значений обратной тригонометрической функции, мы привели таблицу, в которой четко указаны область определения и область значений обратных тригонометрических функций.

Правило определения области определения обратных тригонометрических функций
Для любой тригонометрической функции мы можем легко найти область определения, используя приведенное ниже правило.
То есть,
Домен (y -1 ) = Диапазон (y)
Точнее, из области значений тригонометрических функций мы можем получить область значений обратных тригонометрических функций. Это было ясно объяснено ниже.
Область обратных тригонометрических функций
Мы уже знаем диапазон sin(x).
То есть диапазон sin(x) равен
[-1, 1]
А также, мы знаем, что
Область обратной функции = Диапазон функции.
Итак, область определения sin -1 (x) равна
[-1, 1] или -1 ≤ x ≤ 1
В приведенной выше таблице указаны диапазоны всех тригонометрических функций.
Из факта,
«Область обратной функции = диапазон функции»,
мы можем получить область определения всех обратных тригонометрических функций.

Домен sin -1 (x) = [-1, 1]
Домен cos -1 (x) = [-1, 1]
Домен csc -1 (x ) = (-∞, -1] или [1, +∞)
Домен sec -1 (x) = (-∞, -1] или [1, +∞)
Домен tan — 1 (x) = Все действительные числа
Область определения кроватки -1 (x) = Все действительные числа
Правило поиска диапазона обратных тригонометрических функций
Несмотря на то, что существует много способов ограничить диапазон обратных тригонометрических функций, используется согласованный интервал.
То есть ,
[-π/2 , π]
Мы должны разделить вышеуказанный интервал на части, и каждая часть будет рассматриваться как диапазон, который зависит от заданной обратной тригонометрической функции.
Длина каждой части должна быть π или 180° .
Когда мы пытаемся получить диапазон обратных тригонометрических функций, мы можем начать либо с -π/2, либо с 0 (но не с обоих).

Если мы начинаем с -π/2, диапазон должен быть ограничен интервалом
[-π/2, π/2], Length = 180°
Если мы начинаем с 0, диапазон должен быть ограничен в интервале
[0, π], длина = 180°
В общем интервале диапазона [-π/2, π] покрываются три квадранта.
Квадрант IV, квадрант I и квадрант II.
Для любой обратной тригонометрической функции нужно выбрать только два квадранта в интервале [-π/2, π]. В одном из двух квадрантов тригонометрическая функция должна быть положительной, а в другом — отрицательной.
Для всех обратных тригонометрических функций мы должны рассматривать только первый квадрант как положительный. (Не любой другой квадрант)
Исходя из этого, мы должны выбрать начальную точку.
Это либо -π/2, либо 0.
Диапазон sin⁻¹(x)
Как объяснялось выше, sin x положителен в первом квадранте (учитывается только первый квадрант) и отрицателен в четвертом квадранте общего интервала [-π/2, π].

Эти два квадранта покрываются интервалом
[-π/2, π/2]
Итак, диапазон y = sin -1 (x) равен
[-π/2, π/2]
Точнее, диапазон y = sin -1 (x) is ,
-π/2 ≤ y ≤ π/2
Диапазон cos⁻¹(x)
Как объяснялось выше, cos x положителен в первом квадранте (только рассматриваемого квадранта) и отрицательно во втором квадранте общего интервала [-π/2, π] .
Эти два квадранта покрываются интервалом [0, π]
Итак, диапазон y = cos -1 (x) равен
[0, π]
Точнее, диапазон y = cos -1 (x) равен
0 ≤ y ≤ π
Диапазон csc⁻¹(x)
Как объяснялось выше, csc x положителен в первом квадранте (учитывается только первый квадрант) и отрицателен в четвертом квадранте общего интервала [-π/2, π] .
Эти два квадранта покрываются интервалом
[-π/2, π/2]
Мы можем рассматривать [-π/2, π/2] как диапазон y = csc -1 (х). Но в интервале [-π/2, π/2] есть значение 0, для которого мы имеем
csc (0) = 1 / sin(0) = 1/0 = Undefined.

Итак, «0» не может рассматриваться как часть диапазона
y = csc -1 (x)
Итак, диапазон y = csc⁻¹(x) равен
[-π /2, π/2] — {0}
Точнее, диапазон y = csc -1 (x) равен ,
-π/2 ≤ y ≤ π/2, y ≠ 0
Диапазон of sec⁻¹(x)
Как объяснялось выше, sec x положителен в первом квадранте (рассматривается только первый квадрант) и отрицателен во втором квадранте общего интервала [-π/2, π].
Эти два квадранта покрываются интервалом [0, π]
Мы можем рассматривать [0, π] как диапазон y = с -1 (x).
Но есть значение π/2 в интервале [0, π], для которого мы имеем
с (π/2) = 1 / cos (π/2) = 1/0 = Undefined.
Таким образом, «π/2» не может рассматриваться как часть диапазона
y = sec -1 (x)
Итак, диапазон y = sec -1 (x) равен
[0, π] — {π/2}
Точнее, диапазон y = сек -1 (x) равно
0 ≤ y ≤ π, y ≠ π/2
Диапазон значений tan⁻¹(x)
учитываться) и отрицательными как во втором, так и в четвертом квадранте общего интервала [-π/2, π].

Случай 1:
Если мы рассмотрим первый квадрант для положительного и второй квадрант для отрицательного, мы получим интервал [0, π] как диапазон y = tan -1 (x).
Примечание. Начальная точка — 0,9.0949
Случай 2:
Если мы рассмотрим первый квадрант как положительный и четвертый квадрант как отрицательный, мы получим интервал [-π/2, π/2] как диапазон y = tan -1 (x) .
Примечание: Начальная точка -π/2.
При рассмотрении первого случая мы получим интервал [0, π] как диапазон y = tan -1 (x). Но есть значение π/2 в середине интервала [0, π], для которого мы имеем
tan (π/2) = undefined
Таким образом, мы не можем рассматривать π/2 как часть диапазона
y = tan -1 (x)
Таким образом, мы можем игнорировать случай 1 и рассмотреть случай 2.
как диапазон y = tan -1 (x).
Несмотря на то, что мы получаем интервал [-π/2, π/2] как диапазон
y = tan -1 (x),
tan x становится неопределенным для двух угловых значений -π/2 и π/2.

Таким образом, -π/2 и π/2 не могут рассматриваться как части диапазона
г = тангенс -1 (х).
Итак, диапазон y = tan -1 (x) равен
(-π/2, π/2)
Точнее, диапазон y = tan -1 (x) равен ,
-π/2 < y < π/2
Диапазон cot⁻¹(x)
Как объяснялось выше, cot x положителен в первом квадранте (учитывается только первый квадрант) и отрицателен во втором и четвертые квадранты общего интервала [-π/2, π].
Случай 1 :
Если мы рассмотрим первый квадрант для положительного и второй квадрант для отрицательного, мы получим интервал [0, π] как диапазон y = cot -1 (x).
Примечание. Начальная точка — 0.
Случай 2:
Если мы рассмотрим первый квадрант для положительных значений и четвертый квадрант для отрицательных, мы получим интервал [-π/2, π/2] как диапазон
y = кроватка -1 (x).
Примечание: Начальная точка -π/2.

Когда мы рассмотрим второй случай, мы получим интервал [-π/2, π/2] как диапазон y = cot -1 (х).
Но в интервале [-π/2, π/2] есть значение 0, для которого мы имеем
cot (0) = undefined
Таким образом, мы не можем рассматривать 0 как часть диапазона
у = кроватка -1 (х).
Таким образом, мы можем проигнорировать случай 2 и рассмотреть случай 1.
При рассмотрении случая 1 мы получаем интервал [0, π] как диапазон получить интервал [0, π] как диапазон
y = кроватка -1 (x),
кроватка x становится неопределенной для двух угловых значений 0 и π.
Таким образом, 0 и π не могут рассматриваться как части диапазона
y = кроватка -1 (x).
Итак, диапазон y = кроватка -1 (x) равен
(0, π)
Точнее, диапазон y = кроватка -1 (x) равен
0 < y < π
Пожалуйста, отправьте свой отзыв по адресу v4formath@gmail.
 com
comМы всегда ценим ваши отзывы.
©Все права защищены. onlinemath5all.com
Регулируемая развитием активация повтора SINE B2 в качестве границы домена в органогенезе
. 2007 г., 13 июля; 317 (5835): 248-51.
doi: 10.1126/science.1140871.
Виктория В Луняк 1 , Гратьен Дж. Префонтен, Эсперанса Нуньес, Торстен Крамер, Бонг-Гун Джу, Кеннет А. Оги, Кейси Хатт, Роза Рой, Анхель Гарсия-Диас, Сяоян Чжу, Юн Юн, Луис Монтолиу, Кристофер К. Гласс, Майкл Г. Розенфельд
Принадлежности
принадлежность
- 1 Медицинский институт Говарда Хьюза, Медицинский факультет Калифорнийского университета, Сан-Диего, 9500 Gilman Drive, Room 345, La Jolla, CA 92093-0648, США. vlunyak@uscd.
 edu
edu
- PMID: 17626886
- DOI: 10.1126/науч.1140871
Виктория В. Луняк и др. Наука. .
. 2007 г., 13 июля; 317 (5835): 248-51.
doi: 10.1126/science.1140871.
Авторы
Виктория В Луняк 1 , Гратьен Дж. Префонтен, Эсперанса Нуньес, Торстен Крамер, Бонг-Гун Джу, Кеннет А. Оги, Кейси Хатт, Роза Рой, Анхель Гарсия-Диас, Сяоян Чжу, Юн Юн, Луис Монтолиу, Кристофер К. Гласс, Майкл Г. Розенфельд
принадлежность
- 1 Медицинский институт Говарда Хьюза, Медицинский факультет Калифорнийского университета, Сан-Диего, 9500 Gilman Drive, Room 345, La Jolla, CA 92093-0648, США.
 [email protected]
[email protected]
- PMID: 17626886
- DOI: 10.1126/науч.1140871
Абстрактный
Временная и пространственная регуляция экспрессии генов в развитии млекопитающих связана с установлением функциональных доменов хроматина. Здесь мы сообщаем, что для активации гена необходима тканеспецифическая транскрипция повтора ретротранспозона в локусе гормона роста мыши. Этот повтор служит границей для блокирования влияния репрессивных модификаций хроматина. Повторяющийся элемент способен генерировать короткие перекрывающиеся транскрипты, управляемые Pol II и Pol III, оба из которых необходимы и достаточны для реструктуризации регулируемого локуса в ядерные компартменты. Эти данные указывают на то, что транскрипция вкрапленных повторяющихся последовательностей может представлять стратегию развития для установления функционально различных доменов в геноме млекопитающих для контроля активации генов.

Похожие статьи
Транскрипционная активация коротких вкрапленных элементов агентами, повреждающими ДНК.
Рудин С.М., Томпсон С.Б. Рудин С.М. и соавт. Гены Хромосомы Рак. 2001 Январь; 30 (1): 64-71. Гены Хромосомы Рак. 2001. PMID: 11107177
Эпигенетический временной контроль Hox-генов мыши in vivo.
Сошникова Н., Дюбул Д. Сошникова Н., и соавт. Наука. 2009 5 июня; 324 (5932): 1320-3. doi: 10.1126/наука.1171468. Наука. 2009. PMID: 19498168
Рецептор диоксина и факторы транскрипции SLUG регулируют инсуляторную активность ретротранспозонов B1 SINE посредством переключателя РНК-полимеразы.

Роман А.С., Гонсалес-Рико Ф.Дж., Молто Э., Эрнандо Х., Нето А., Висенте-Гарсия К., Баллестар Э., Гомес-Скармета Х.Л., Ваврова-Андерсон Х., Уайт Р.Дж., Монтолиу Л., Фернандес-Сальгеро П.М. Роман А.С. и др. Геном Res. 2011 март; 21(3):422-32. doi: 10.1101/гр.111203.110. Epub 2011 3 февраля. Геном Res. 2011. PMID: 21324874 Бесплатная статья ЧВК.
Границы доменов хроматина: инсуляторы и не только.
Вэй Г.Х., Лю Д.П., Лян К.К. Вэй Г.Х. и соавт. Сотовый рез. 2005 г., 15 апреля (4): 292–300. doi: 10.1038/sj.cr.72. Сотовый рез. 2005. PMID: 15857584 Обзор.
Повышенные уровни транскриптов B1 и B2 SINE в клетках фибробластов мыши из-за заражения мышей мельчайшим вирусом.
Williams WP, Tamburic L, Astell CR.
 Уильямс В.П. и др.
Вирусология. 1 октября 2004 г .; 327 (2): 233–41. doi: 10.1016/j.virol.2004.06.040.
Вирусология. 2004.
PMID: 15351211
Уильямс В.П. и др.
Вирусология. 1 октября 2004 г .; 327 (2): 233–41. doi: 10.1016/j.virol.2004.06.040.
Вирусология. 2004.
PMID: 15351211
Посмотреть все похожие статьи
Цитируется
Происхождение, эволюция и тканеспецифические функции свиного повторяющегося элемента 1.
Чжэн М., Го Т., Ян Б., Чжан З., Хуан Л. Чжэн М. и др. Генет Сель Эвол. 2022 27 июля; 54 (1): 54. doi: 10.1186/s12711-022-00745-3. Генет Сель Эвол. 2022. PMID: 35896967 Бесплатная статья ЧВК.
Роль мобильных элементов генома человека в функционировании и патологии нейронов.
Чеснокова Е, Белецкий А, Колосов П. Чеснокова Е и др. Int J Mol Sci. 2022 23 мая; 23 (10): 5847.
 дои: 10.3390/ijms23105847.
Int J Mol Sci. 2022.
PMID: 35628657
Бесплатная статья ЧВК.
Обзор.
дои: 10.3390/ijms23105847.
Int J Mol Sci. 2022.
PMID: 35628657
Бесплатная статья ЧВК.
Обзор.Роль мобильных элементов в регуляции транскрипции млекопитающих.
Фуэйо Р., Джадд Дж., Фешотт С., Высоцкая Дж. Фуэйо Р. и др. Nat Rev Mol Cell Biol. 2022 июль; 23 (7): 481-497. doi: 10.1038/s41580-022-00457-y. Epub 2022 28 февраля. Nat Rev Mol Cell Biol. 2022. PMID: 35228718 Обзор.
Новые роли эндогенных ретровирусов в эпигенетической регуляции иммунитета.
Баттлер, Калифорния, Чуонг, Э.Б. Батлер К.А. и соавт. Immunol Rev. 2022 Jan; 305(1):165-178. doi: 10.1111/imr.13042. Epub 2021 23 ноября. Иммунол Ред. 2022. PMID: 34816452 Обзор.
SINEUPs: новый набор инструментов для РНК-терапии.

- 1 Медицинский институт Говарда Хьюза, Медицинский факультет Калифорнийского университета, Сан-Диего, 9500 Gilman Drive, Room 345, La Jolla, CA 92093-0648, США. vlunyak@uscd.


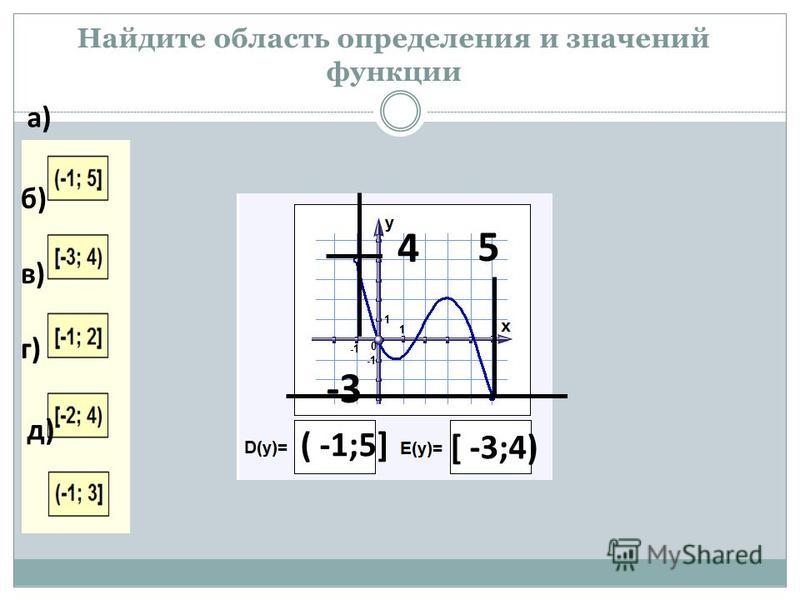



 11.
Функция y = arcsin x
11.
Функция y = arcsin x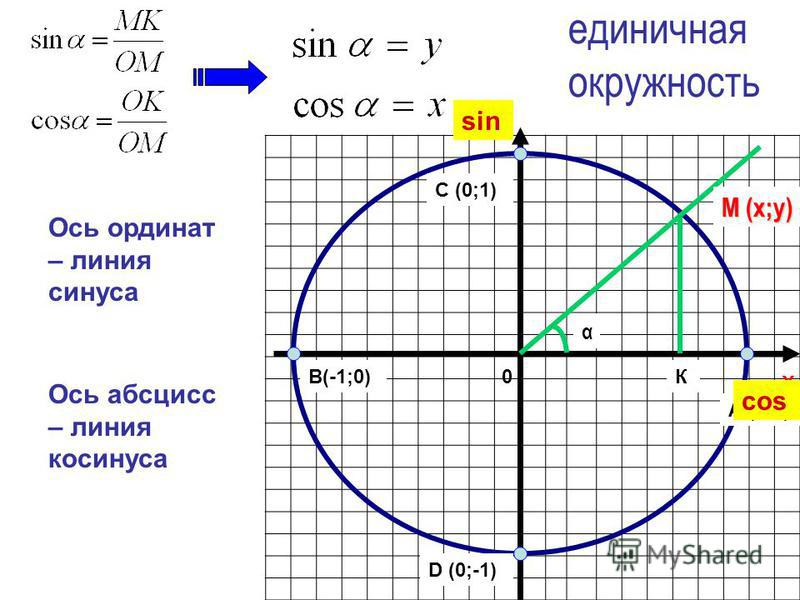 14.
Функция y = arcctg x
14.
Функция y = arcctg x ru
ru Область определения синуса — это множество всех действительных чисел, то есть, D(sin) = R.
Область определения синуса — это множество всех действительных чисел, то есть, D(sin) = R.
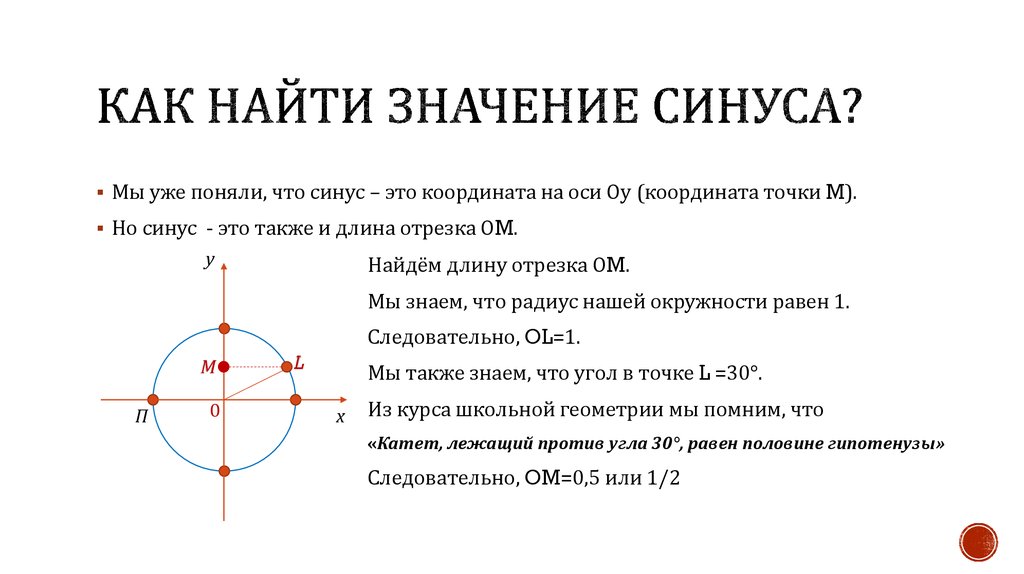 9{−1}\left(\sin x\right)=\frac{\pi}{2}-x[/latex], если [латекс]-\frac{\pi}{2}\leq x \leq\frac {\pi}{2}[/латекс].
9{−1}\left(\sin x\right)=\frac{\pi}{2}-x[/latex], если [латекс]-\frac{\pi}{2}\leq x \leq\frac {\pi}{2}[/латекс].