Калькулятор двойных интегралов: Решение двойных интегралов | Онлайн калькулятор

Онлайн калькулятор неопределенных интегралов с решением: Калькулятор Интегралов • По шагам! — ЭкоДом: Дом своими руками

Содержание

Онлайн решение интеграла

Что делать, если решение не появляется (пустой экран)?

Данный калькулятор по решению интегралов онлайн построен на основе системы WolframAlpha Mathematica. Все права на его использование принадлежат компании Wolfram Alpha LLC!

Решение интеграла онлайн

Неопределенный интеграл

Нахождение неопределенного интеграла является очень частой задачей в высшей математике и других технических разделах науки. Даже решение простейших физических задач часто не обходится без вычисления нескольких простых интегралов. Поэтому со школьного возраста нас учат приемам и методам решения интегралов, приводятся многочисленные таблицы с интегралами простейших функций. Однако со временем всё это благополучно забывается, либо у нас не хватает времени на рассчеты или нам нужно найти решение неопределеленного интеграла от очень сложной функции. Для решения этих проблем для вас будет незаменим наш сервис, позволяющий безошибочно находить неопределенный интеграл онлайн.

Решить неопределенный интеграл

Онлайн сервис на matematikam.ru позволяет находить решение интеграла онлайн быстро, бесплатно и качественно. Вы можете заменить поиск по таблицам нужного интеграла нашим сервисом, где быстро введя нужную функции, вы получите решение неопределенного интеграла в табличном варианте. Не все математические сайты способны вычислять неопределенные интегралы функций в режиме онлайн быстро и качественно, особенно если требуется найти неопределенный интеграл от сложной функции или таких функций, которые не включены в общий курс высшей математики. Сайт matematikam.ru поможет решить интеграл онлайн и справиться с поставленной задачей. Используя онлайн решение интеграла на сайте matematikam.ru, вы всегда получите точный ответ.

Даже если вы хотите вычислить интеграл самостоятельно, благодаря нашему сервису вам будет легко проверить свой ответ, найти допущенную ошибку или описку, либо же убедиться в безукоризненном выполнении задания. Если вы решаете задачу и вам как вспомогательное действие необходимо вычислить неопределенный интеграл, то зачем тратить время на эти действия, которые, возможно, вы уже выполняли тысячу раз? Тем более, что дополнительные расчеты интеграла могут быть причиной описки или маленькой ошибки, приведших впоследствии к неверному ответу. Просто воспользуйтесь нашими услугами и найдите неопределенный интеграл онлайн без каких-либо усилий. Для практических задач по нахождению интеграла функции онлайн этот сервер очень полезен. Необходимо ввести заданную функцию, получить онлайн решение неопределенного интеграла и сравнить ответ с вашим решением.

Похожие сервисы:

Решение неопределенного интеграла
Calculate indefinite integral online

Калькулятор Интегралов — определенный & неопределенный

Онлайн-калькулятор интегралов поможет вам вычислить интегралы функций по отношению к задействованной переменной и покажет вам полные пошаговые вычисления. Когда дело доходит до вычислений неопределенных интегралов, этот калькулятор первообразных позволяет мгновенно решать неопределенные интегралы. Теперь вы можете определить интегральные значения следующих двух интегралов с помощью онлайн-интеграл калькулятор:

• Определенные интегралы
• Неопределенные интегралы (первообразная)

Интегральный расчет довольно сложно решить вручную, так как он включает в себя различные сложные формулы интегрирования. Итак, рассмотрим интерактивный интегральный решатель, который решает простые и сложные функции решение интегралов онлайн и показывает вам пошаговые вычисления.

Итак, сейчас самое время понять формулы интегрирования, как интегрировать функцию шаг за шагом, с помощью калькулятора интегрирования и многое другое. Во-первых, давайте начнем с основ:

Читать дальше!

Что такое интеграл?

В математике интеграл функций описывает площадь, смещение, объем и другие понятия, которые возникают, когда мы объединяем бесконечные данные. В исчислении дифференцирование и интегрирование являются фундаментальной операцией и служат наилучшей операцией для решения физико-математических задач произвольной формы.

Вы также можете использовать бесплатную версию онлайн-калькулятора факторов, чтобы найти факторы, а также пары факторов для положительных или отрицательных целых чисел.

• Процесс нахождения интегралов, называемый интегрированием
• Интегрируемая функция называется подынтегральной функцией.
• В интегральных обозначениях ∫3xdx, ∫ – символ интеграла, 3x – интегрируемая функция, а dx – дифференциал переменной x.

Где f (x) – функция, а A – площадь под кривой. Наш бесплатный калькулятор интегралов легко вычисляет интегралы и определяет площадь под заданной функцией. Что ж, теперь поговорим о типах интегралов:

Типы интегралов:

По сути, есть два типа интегралов:

• Неопределенные интегралы
• Определенные интегралы

Неопределенные интегралы:

определенный интеграл онлайн функции принимает первообразную другой функции. Взять первообразную функции – это самый простой способ обозначить неопределенные интегралы. Когда дело доходит до вычисления неопределенных интегралов, калькулятор неопределенных интегралов помогает выполнять вычисления неопределенных интегралов шаг за шагом. Этот тип интеграла не имеет верхнего или нижнего предела.

Определенные интегралы:

Определенный интеграл функции имеет начальное и конечное значения. Просто существует интервал [a, b], который называется пределами, границами или границами. Этот тип можно определить как предел интегральных сумм, когда диаметр разбиения стремится к нулю. Наш интеграл онлайн калькулятор определенных интегралов с оценками вычисляет интегралы, учитывая верхний и нижний предел функции. Разницу между определенным и неопределенным интегралами можно понять по следующей диаграмме:

Основные формулы для интеграции:

Существуют разные формулы для интеграции, но здесь мы перечислили некоторые общие:

• ∫1 dx = x + c
• ∫xn dx = xn + 1 / n + 1 + c
• ∫a dx = ax + c
• ∫ (1 / х) dx = lnx + c
• ∫ ax dx = ax / lna + c
• ∫ ex dx = ex + c
• ∫ sinx dx = -cosx + c
• ∫ cosx dx = sinx + c
• ∫ tanx dx = – ln | cos x | + c
• ∫ cosec2x dx = – детская кроватка x + c
• ∫ sec2x dx = tan x + c
• ∫ cotx dx = ln | sinx | + c
• ∫ (secx) (tanx) dx = secx + c
• ∫ (cosecx) (cotx) dx = -cosecx + c

Помимо этих уравнений интегрирования, есть еще несколько важных формул интегрирования, которые упомянуты ниже:

• ∫ 1 / (1-x2) 1/2 dx = sin-1x + c
• ∫ 1 / (1 + x2) 1/2 dx = cos-1x + c
• ∫ 1 / (1 + x2) dx = tan-1x + c
• ∫ 1 / | x | (x2 – 1) 1/2 dx = cos-1x + c

Запоминание всех этих формул интегрирования и выполнение вычислений вручную – очень сложная задача. Просто введите функцию в предназначенное для этого поле онлайн-калькулятор интегралов, который использует эти стандартизированные формулы для точных вычислений.

Как решать интегралы вручную (шаг за шагом):

Большинство людей раздражается начинать с вычислений интегральной функции. Но здесь мы собираемся решать интегральные примеры шаг за шагом, что поможет вам разобраться, как легко интегрировать функции! Итак, это точки, которым нужно следовать для вычисления решение интегралов онлайн:

• Определить функцию f (x)
• Возьмите первообразную функции
• Вычислить верхний и нижний предел функции
• Определите разницу между обоими пределами

Если вас интересует вычисление первообразной (неопределенного интеграла), тогда возьмите онлайн-калькулятор первообразной, который быстро решит первообразную данной функции.

Смотрит на примеры:

Пример 1:

Решить интегралы от ∫ x3 + 5x + 6 dx?

Решение:

Шаг 1:

Применяя правило функциональной мощности для интегрирования:

∫xn dx = xn + 1 / n + 1 + c

∫ x3 + 5x + 6 dx = x3 + 1/3 + 1 + 5 x1 + 1/1 + 1 + 6x + c

Шаг 2:

∫ x3 + 5x + 6 dx = x4 / 4 + 5 x2 / 2 + 6x + c

Шаг 3:

∫ x3 + 5x + 6 dx = x4 + 10×2 + 24x / 4 + c

Этот калькулятор неопределенного интеграла помогает интегрировать интеграл калькулятор функции шаг за шагом, используя формулу интегрирования.

1_5 x * lnx dx = –14

Поскольку это очень сложно для решения интегралов, когда две функции умножаются друг на друга. Для удобства просто введите функции в онлайн-калькулятор интегралов по частям, который помогает выполнять вычисления двух функций (по частям), которые точно умножаются друг на друга.

Пример 3 (Интеграл от тригонометрической функции):

Вычислить определенный интеграл для ∫sinx dx с интервалом [0, π / 2]?

Решение:

Шаг 1:

Используйте формулу для тригонометрической функции:

∫ sinx dx = -cosx + c

Шаг 2:

Вычислите верхний и нижний предел для функций f (a) и f (b) соответственно:

Поскольку a = 0 и b = π / 2

Итак, f (a) = f (0) = cos (0) = 1

f (b) = f (π / 2) = cos (π / 2) = 0

Шаг 3:

Рассчитайте разницу между верхним и нижним пределами:

f (а) – f (b) = 1 – 0

f (а) – f (b) = 1

Теперь вы можете использовать бесплатный калькулятор частичных интегралов для проверки всех этих примеров и просто добавлять значения в поля назначения для мгновенного вычисления интегралов.

Как найти первообразную и вычислить интегралы с помощью калькулятора интегралов:

Вы можете легко вычислить интеграл от определенных и неопределенных функций с помощью лучшего интегратора. Вам просто нужно следовать указанным пунктам, чтобы получить точные результаты:

Проведите по!

Входы:

• Во-первых, введите уравнение, которое вы хотите интегрировать.
• Затем выберите зависимую переменную, входящую в уравнение
• Выберите на вкладке определенный или определенный интеграл онлайн
• Если вы выбрали конкретный вариант, то вам следует ввести нижнюю и верхнюю границу или предел в предназначенное для этого поле.
• После этого пора нажать на кнопку расчета.

Выходы:

Интегральный оценщик показывает:

• Определенный интеграл
• неопределенный интеграл онлайн
• Выполните пошаговые расчеты

Часто задаваемые вопросы (FAQ):

Какое целое значение?

В математике интеграл – это числовое значение, равное площади под графиком некоторой функции на некотором интервале. Это может быть график новой функции, производная которой является исходной функцией (калькулятор неопределенных интегралов). Итак, для мгновенных и быстрых вычислений вы можете использовать бесплатный интеграл онлайн калькулятор первообразных, который позволяет вам решать неопределенные интегральные функции.

Как вы оцениваете интеграл, используя основную теорему исчисления?

Прежде всего, мы должны найти первообразную функции, чтобы решить интеграл, используя фундаментальную теорему. Затем используйте основную теорему исчисления для вычисления решение интегралов онлайн. Или просто введите значения в предназначенное для этого поле этого калькулятора интеграции и мгновенно получите результаты.

Что такое двойной интеграл?

Двойные интегралы – это способ интегрирования по двумерной области. Двойные интегралы позволяют вычислить объем поверхности под кривой. Они имеют две переменные и рассматривают функцию f (x, y) в трехмерном пространстве.

Заключительные слова:

Интегралы широко используются для улучшения архитектуры зданий, а также для мостов. В электротехнике его можно использовать для определения длины силового кабеля, необходимого для соединения двух станций, находящихся на расстоянии нескольких миль друг от друга. Этот онлайн-калькулятор интегралов лучше всего подходит для школьного образования, который легко интеграл калькулятор любой заданной функции шаг за шагом.

Other Languages: Integral Calculator, Integral Hesaplama, Kalkulator Integral, Kalkulator Integralny, Integralrechner, 積分計算, 적분계산기, Integrály Kalkulačka, Calculadora De Integral, Calcul Intégrale En Ligne, Calculadora De Integrales, Calcolatore Integrali, حساب متكامل, Integraatio Laskin, Integreret Lommeregner, Integral Kalkulator, Integralni Kalkulator, เครื่องคำนวณอินทิกรัล, Integrale Rekenmachine.

Примеры решения определенных интегралов с объяснением. Решение определенного интеграла онлайн. Вычисление определённых интегралов методом интегрирования по частям и методом замены переменной

Онлайн сервис на сайт
позволяет находить решение определенного интеграла онлайн
. Решение проводится автоматически на сервере и в течении нескольких секунд пользователю выдается результат. Все онлайн сервисы на сайте абсолютно бесплатны, а решение выдается в удобном и понятном виде. Также нашим преимуществом является, что мы предоставляем возможность пользователю ввести границы интегрирования, в том числе и пределы интегрирования: минус и плюс бесконечность. Таким образом, решить определенный интеграл становится просто, быстро и качественно. Важно, что сервер позволяет вычислять определенные интегралы онлайн
сложных функций, решение которых на иных онлайн-сервисах часто является невозможным ввиду несовершенства их систем. Мы предоставляем очень простой и интуитивно понятный механизм для ввода функций и возможность выбора переменной интегрирования, для чего вам не приходится переводить заданную в одной переменной функцию в другую, исключая связанные с этим ошибки и опечатки. Также на странице даны ссылки на теоретические статьи и таблицы по решению определенных интегралов.

Всё в совокупоности позволит вам вычислять определенный интеграл онлайн очень быстро и при желании найти и разобраться с теорией решения определенных интегралов. На http://сайт вы также можете переходить на другие сервисы: онлайн решение пределов, производных, суммы рядов. Перейти же на вкладку решения неопределенных интегралов онлайн совсем просто — ссылка находится в ряду среди полезных ссылок. Более того, сервис постоянно совершенствуется и развивается, и с каждым днем появляются всё новые и новые возможности и усовершенствования. Решайте определенные интегралы
вместе с нами! Все онлайн сервисы доступны даже незарегистрировшимся пользователям и абсолютно бесплатны.

Решая определенный интеграл у нас вы можете проверить своё собственное решение или избавиться от излишних трудоемких вычислений и довериться высокотехнологичной автоматизированной машине. Вычисляемая на сервисе точность удовлетворит практически любые инженерные нормы. Часто для многих табличных определенных интегралов результат выдается в точном выражении (используя общеизвестные константы и неэлементарные функции).

В каждой главе будут и задачи для самостоятельного решения, к которым можно
посмотреть ответы.

Понятие определённого интеграла и формула Ньютона-Лейбница

Определённым интегралом

от непрерывной функции f
(x
) на конечном отрезке [a
, b
] (где ) называется приращение какой-нибудь её первообразной на этом отрезке. (Вообще, понимание заметно облегчится, если повторить тему неопределённого интеграла) При этом употребляется запись

Как видно на графиках внизу (приращение первообразной функции обозначено ), определённый
интеграл может быть как положительным, так и отрицательным числом
(Вычисляется
как разность между значением первообразной в верхнем пределе и её же значением в
нижнем пределе, т. е. как F
(b
) — F
(a
)).

Числа a
и b
называются соответственно нижним и верхним пределами интегрирования, а отрезок [a
, b
] – отрезком интегрирования.

Таким образом, если F
(x
) – какая-нибудь первообразная функция для f
(x
), то, согласно определению,

(38)

Равенство (38) называется формулой Ньютона-Лейбница

. Разность F
(b
) – F
(a
) кратко записывают так:

Поэтому формулу Ньютона-Лейбница будем записывать и так:

(39)

Докажем, что определённый интеграл не зависит от того, какая первообразная подынтегральной функции взята при его вычислении. Пусть F
(x
) и Ф(х
) – произвольные первообразные подынтегральной функции. Так как это первообразные одной и той же функции, то они отличаются на постоянное слагаемое: Ф(х
) = F
(x
) + C
. Поэтому

Тем самым установлено, что на отрезке [a
, b
] приращения всех первообразных функции f
(x
) совпадают.

Таким образом, для вычисления
определённого интеграла необходимо найти любую первообразную подынтегральной
функции, т. е. сначала следует найти неопределённый интеграл. Постоянная
С

из последующих вычислений исключается. Затем применяется формула Ньютона-Лейбница:
в первообразную функцию подставляется значение верхнего предела
b

, далее — значение
нижнего предела
a

и вычисляется разность
F(b) — F(a)

. Полученное число и будет
определённым интегралом.
.

При a
= b
по определению принимается

Пример 1.

Решение. Сначала найдём неопределённый интеграл:

Применяя формулу Ньютона-Лейбница к первообразной

(при С
= 0), получим

Однако при вычислении определённого интеграла лучше не находить отдельно первообразную, а сразу записывать интеграл в виде (39).

Пример 2.
Вычислить определённый интеграл

Решение. Используя формулу

Найти определённый интеграл самостоятельно, а затем посмотреть решение

Свойства определённого интеграла

Теорема 2.
Величина определённого интеграла не зависит от обозначения переменной интегрирования
, т.е.

(40)

Пусть F
(x
) – первообразная для f
(x
). Для f
(t
) первообразной служит та же функция F
(t
), в которой лишь иначе обозначена независимая переменная. Следовательно,

На основании формулы (39) последнее равенство означает равенство интегралов

Теорема 3.
Постоянный множитель можно выносить за знак определённого интеграла
, т.е.

(41)

Теорема 4.
Определённый интеграл от алгебраической суммы конечного числа функций равен алгебраической сумме определённых интегралов от этих функций
, т.е.

(42)

Теорема 5.
Если отрезок интегрирования разбит на части, то определённый интеграл по всему отрезку равен сумме определённых интегралов по его частям
, т.е. если

(43)

Теорема 6.
При перестановке пределов интегрирования абсолютная величина определённого интеграла не меняется, а изменяется лишь его знак
, т. е.

(44)

Теорема 7
(теорема о среднем). Определённый интеграл равен произведению длины отрезка интегрирования на значение подынтегральной функции в некоторой точке внутри его
, т.е.

(45)

Теорема 8.
Если верхний предел интегрирования больше нижнего и подынтегральная функция неотрицательна (положительна), то и определённый интеграл неотрицателен (положителен), т.е. если

Теорема 9.
Если верхний предел интегрирования больше нижнего и функции и непрерывны, то неравенство

можно почленно интегрировать
, т.е.

(46)

Свойства определённого интеграла позволяют упрощать непосредственное вычисление интегралов.

Пример 5.
Вычислить определённый интеграл

Используя теоремы 4 и 3, а при нахождении первообразных – табличные интегралы (7) и (6), получим

Определённый интеграл с переменным верхним пределом

Пусть f
(x
) – непрерывная на отрезке [a
, b
] функция, а F
(x
) – её первообразная. Рассмотрим определённый интеграл

(47)

а через t
обозначена переменная интегрирования, чтобы не путать её с верхней границей. При изменении х
меняется и опредёленный интеграл (47), т.е. он является функцией верхнего предела интегрирования х
, которую обозначим через Ф
(х
), т.е.

(48)

Докажем, что функция Ф
(х
) является первообразной для f
(x
) = f
(t
). Действительно, дифференцируя Ф
(х
), получим

так как F
(x
) – первообразная для f
(x
), а F
(a
) – постояная величина.

Функция Ф
(х
) – одна из бесконечного множества первообразных для f
(x
), а именно та, которая при x
= a
обращается в нуль. Это утверждение получается, если в равенстве (48) положить x
= a
и воспользоваться теоремой 1 предыдущего параграфа.

Вычисление определённых интегралов методом интегрирования по частям и методом замены переменной

где, по определению, F
(x
) – первообразная для f
(x
). Если в подынтегральном выражении произвести замену переменной

то в соответствии с формулой (16) можно записать

В этом выражении

первообразная функция для

В самом деле, её производная, согласно правилу дифференцирования сложной функции
, равна

Пусть α и β – значения переменной t
, при которых функция

принимает соответственно значения a
и b
, т.е.

Но, согласно формуле Ньютона-Лейбница, разность F
(b
) – F
(a
) есть

Для того чтобы научиться решать определенные интегралы необходимо:

1) Уметь находить
неопределенные интегралы.

2) Уметь вычислить
определенный интеграл.

Как видите, для того чтобы освоить определенный интеграл, нужно достаточно хорошо ориентироваться в «обыкновенных» неопределенных интегралах. Поэтому если вы только-только начинаете погружаться в интегральное исчисление, и чайник еще совсем не закипел, то лучше начать с урока Неопределенный интеграл. Примеры решений
.

В общем виде определенный интеграл записывается так:

Что прибавилось по сравнению с неопределенным интегралом? Прибавились пределы интегрирования
.

Нижний предел интегрирования

Верхний предел интегрирования
стандартно обозначается буквой .
Отрезок называется отрезком интегрирования
.

Прежде чем мы перейдем к практическим примерам, небольшое «факью» по определенному интегралу.

Что такое определенный интеграл?
Я бы мог вам рассказать про диаметр разбиения отрезка, предел интегральных сумм и т.д., но урок носит практический характер. Поэтому я скажу, что определенный интеграл – это ЧИСЛО. Да-да, самое что ни на есть обычное число.

Есть ли у определенного интеграла геометрический смысл?
Есть. И очень хороший. Самая популярная задача – вычисление площади с помощью определенного интеграла
.

Что значит решить определенный интеграл?
Решить определенный интеграл – это значит, найти число.

Как решить определенный интеграл?
С помощью знакомой со школы формулы Ньютона-Лейбница:

Формулу лучше переписать на отдельный листочек, она должна быть перед глазами на протяжении всего урока.

Этапы решения определенного интеграла следующие:

1) Сначала находим первообразную функцию (неопределенный интеграл). Обратите внимание, что константа в определенном интеграле никогда не добавляется
. Обозначение является чисто техническим, и вертикальная палочка не несет никакого математического смысла, по сути – это просто отчёркивание. Зачем нужна сама запись ? Подготовка для применения формулы Ньютона-Лейбница.

2) Подставляем значение верхнего предела в первообразную функцию: .

3) Подставляем значение нижнего предела в первообразную функцию: .

4) Рассчитываем (без ошибок!) разность , то есть, находим число.

Всегда ли существует определенный интеграл?
Нет, не всегда.

Например, интеграла не существует, поскольку отрезок интегрирования не входит в область определения подынтегральной функции (значения под квадратным корнем не могут быть отрицательными). А вот менее очевидный пример: . Такого интеграла тоже не существует, так как в точках , отрезка не существует тангенса. Кстати, кто еще не прочитал методический материал Графики и основные свойства элементарных функций
– самое время сделать это сейчас. Будет здорово помогать на протяжении всего курса высшей математики.

Для того чтобы определенный интеграл вообще существовал, необходимо чтобы подынтегральная функция быланепрерывнойна отрезке интегрирования
.

Из вышесказанного следует первая важная рекомендация: перед тем, как приступить к решению ЛЮБОГО определенного интеграла, нужно убедиться в том, что подынтегральная функция непрерывна на отрезке интегрирования
. По студенческой молодости у меня неоднократно бывал казус, когда я подолгу мучался с нахождением трудной первообразной, а когда наконец-то ее находил, то ломал голову еще над одним вопросом: «что за ерунда получилась?». В упрощенном варианте ситуация выглядит примерно так:

???!!!

Нельзя подставлять отрицательные числа под корень!

Если для решения (в контрольной работе, на зачете, экзамене) Вам предложен несуществующий интеграл вроде

то нужно дать ответ, что интеграла не существует и обосновать – почему.

Может ли определенный интеграл быть равен отрицательному числу?
Может. И отрицательному числу. И нулю. Может даже получиться бесконечность, но это уже будетнесобственный интеграл
, коим отведена отдельная лекция.

Может ли нижний предел интегрирования быть больше верхнего предела интегрирования?
Может, и такая ситуация реально встречается на практике.

– интеграл преспокойно вычисляется по формуле Ньютона-Лейбница.

Без чего не обходится высшая математика? Конечно же, без всевозможных свойств. Поэтому рассмотрим некоторые свойства определенного интеграла.

В определенном интеграле можно переставить верхний и нижний предел, сменив при этом знак:

Например, в определенном интеграле перед интегрированием целесообразно поменять пределы интегрирования на «привычный» порядок:

– в таком виде интегрировать значительно удобнее.

Как и для неопределенного интеграла, для определенного интеграла справедливы свойства линейности:

– это справедливо не только для двух, но и для любого количества функций.

В определенном интеграле можно проводить замену переменной интегрирования
, правда, по сравнению с неопределенным интегралом тут есть своя специфика, о которой мы еще поговорим.

Для определенного интеграла справедлива формула интегрирования по частям
:

Пример 1

Решение:

(1) Выносим константу за знак интеграла.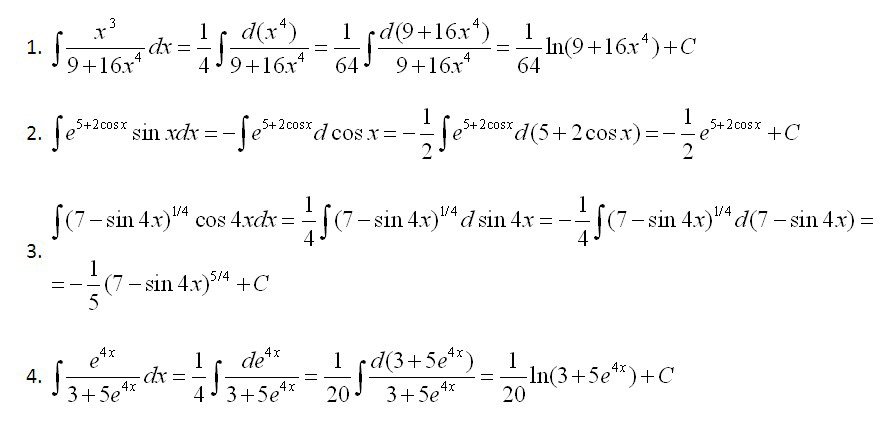

(2) Интегрируем по таблице с помощью самой популярной формулы . Появившуюся константу целесообразно отделить от и вынести за скобку. Делать это не обязательно, но желательно – зачем лишние вычисления?

(3) Используем формулу Ньютона-Лейбница

.

Сначала подставляем в верхний предел, затем – нижний предел. Проводим дальнейшие вычисления и получаем окончательный ответ.

Пример 2

Вычислить определенный интеграл

Это пример для самостоятельно решения, решение и ответ в конце урока.

Немного усложняем задачу:

Пример 3

Вычислить определенный интеграл

Решение:

(1) Используем свойства линейности определенного интеграла.

(2) Интегрируем по таблице, при этом все константы выносим – они не будут участвовать в подстановке верхнего и нижнего предела.

(3) Для каждого из трёх слагаемых применяем формулу Ньютона-Лейбница:

СЛАБОЕ ЗВЕНО в определенном интеграле – это ошибки вычислений и часто встречающаяся ПУТАНИЦА В ЗНАКАХ. Будьте внимательны! Особое внимание заостряю на третьем слагаемом:

– первое место в хит-параде ошибок по невнимательности, очень часто машинально пишут

(особенно, когда подстановка верхнего и нижнего предела проводится устно и не расписывается так подробно). Еще раз внимательно изучите вышерассмотренный пример.

Следует заметить, что рассмотренный способ решения определенного интеграла – не единственный. При определенном опыте, решение можно значительно сократить. Например, я сам привык решать подобные интегралы так:

Здесь я устно использовал правила линейности, устно проинтегрировал по таблице. У меня получилась всего одна скобка с отчёркиванием пределов:

(в отличие от трёх скобок в первом способе). И в «целиковую» первообразную функцию, я сначала подставил сначала 4, затем –2, опять же выполнив все действия в уме.

Какие недостатки у короткого способа решения? Здесь всё не очень хорошо с точки зрения рациональности вычислений, но лично мне всё равно – обыкновенные дроби я считаю на калькуляторе.
Кроме того, существует повышенный риск допустить ошибку в вычислениях, таким образом, студенту-чайнику лучше использовать первый способ, при «моём» способе решения точно где-нибудь потеряется знак.

Несомненными преимуществами второго способа является быстрота решения, компактность записи и тот факт, что первообразная

находится в одной скобке.

Данный калькулятор позволяет решить определенный интеграл онлайн. По сути, вычисление определенного интеграла
— это нахождение числа, которое равно площади под графиком функции. Для решения необходимо задать границы интегрирования и интегрируемую функцию. После интегрирования система найдет первообразную для заданной функции, вычислит её значения в точках границах интегрирования, найдет их разность, что и будет являться решением определенного интеграла. Чтобы решить неопределенный интеграл вам необходимо воспользоваться похожим онлайн калькулятором, который находится на нашем сайте по ссылке — Решить неопределенный интеграл . 2*arctgh(x)*arcctgh(x)

Правила ввода выражений и функций

Выражения могут состоять из функций (обозначения даны в алфавитном порядке):
absolute(x)

Абсолютное значение x

(модуль x
или |x|
)
arccos(x)

Функция — арккосинус от x
arccosh(x)

Арккосинус гиперболический от x
arcsin(x)

Арксинус от x
arcsinh(x)

Арксинус гиперболический от x
arctg(x)

Функция — арктангенс от x
arctgh(x)

Арктангенс гиперболический от x
e
e
число, которое примерно равно 2.3
— возведение в степень
x + 7

— сложение
x — 6

— вычитание

Другие функции:
floor(x)

Функция — округление x
в меньшую сторону (пример floor(4.5)==4.0)
ceiling(x)

Функция — округление x
в большую сторону (пример ceiling(4. 5)==5.0)
sign(x)

Функция — Знак x
erf(x)

Функция ошибок (или интеграл вероятности)
laplace(x)

Функция Лапласа

Интегрирование рациональных дробей. Примеры

В предыдущей статье мы рассмотрели правила интегрирования рациональных дробей. Ниже будут приведены примеры, которые наглядно покажут как использовать эти правила и научат использовать различные приемы для получения правильного результата.

Пример 1.

Вычислить следующие интегралы

а)

б)

в)

Решение.

а) Поскольку степень числителя меньше степени знаменателя, то подынтегральная функция — правильная дробь. Знаменатель

можно разложить на множители

таким образом дробь разлагается на сумму слагаемых первого типа (І):

Неизвестные коэффициенты находим методом неопределенных коэффициентов. Для этого правую часть полученной только что неравенства сводим к общему знаменателю:

Приравниваем числители для нахождения неизвестных коэффициентов

Это равенство выполняется когда коэффициенты при одинаковых степенях равны между собой. Из этого условия получаем систему линейных уравнений для определения неизвестных

Решая ее находим неизвестные коэффициенты

Тогда подынтегральная функция примет вид

Интегрируя дроби после знака равенства получим

Ничего сложного в решения такого сорта примеров нет, только правильно составить и решить систему линейных уравнений для определения неизвестных.

б) Подынтегральная функция

является правильной дробью, знаменатель которого имеет действительные корни. Такая дробь разлагается на сумму простейших дробей I-го и II-го типов

Определим неизвестные коэффициенты , для этого правую часть сведем к общему знаменателю.

Раскрываем скобки и приравниваем коэффициенты при одинаковых степенях в числителе. Получим следующую систему линейных уравнений

Есть другой способ получения системы уравнений для определения неизвестных. Числители справа и слева должны быть равны для всех . Эта особенность несколько упрощает решение системы уравнений. Как правило, за точки в первую очередь берут корни уравнения и значение ноль . В нашем случае это были бы значение Ноль выбирают за счет простоты вычислений.

Решив полученную выше систему линейных уравнений, получим следующие значения неизвестных:

Интегрируем подынтегральные функции, учитывая найдены константы

При большом количестве неизвестных в системах линейных уравнений их вычисление очень трудоемки, в то время методика приведенная выше упрощает их вычисление.

в) Подынтегральная функция

является правильной дробью. Знаменатель содержит квадратный трехчлен и множитель. Данный дробь по правилам разлагается на сумму дробей I-го и III-го типов:

Сведя к общему знаменателю, получим:

Можем приравнять коэффициенты при одинаковых степенях, но поступим иначе, чтобы научиться использовать вторую методику. Для этого подставим корень в левую и правую часть равенства, получим

Для того, чтобы избавиться от неизвестной подставим

Для нахождения неизвестной выпишем неизвестные при

Таким способом, не выписывая систем линейных уравнений и не решая их, можно достаточно быстро найти нужные константы.

Подставив найденные значения, получим интеграл

Первое слагаемое интегрируется по табличной формуле

ко второму применяем замену переменных

и сводим к сумме двух

Просуммировав полученные интегралы, окончательно получим решение

Решив несколько примеров на каждый из типов Вам станет понятнее, к какому типу возводить интегралы и который предположительно будет результат. Поэтому практикуйте самостоятельно, совершенствуйте навыки и получайте только верные решения.

Калькулятор двойных интегралов в Wolfram|Alpha

Для решения двойных интегралов Wolfram|Alpha используюет запросы специального вида, о которых уже шла речь в этом посте.2:

Решение неопределенных двойных интегралов в Wolfram|Alpha

Калькулятор двойных интегралов в Wolfram|Alpha позволяет получить решение любого другого неопределенного двойного интеграла. Для этого достаточно (1) — ввести новую подынтегральную функцию в поле с подписью function to integrate, (2), (3) — изменить наименования переменных интегрирования variable 1 и variable 2 (если они обозначены не x и y, как обычно, а какими-нибудь другими буквами), а затем (4) — нажать «=«:

Вычисление двойных интегралов в Wolfram|Alpha

Чтобы вычислить определенный двойной интеграл при помощи калькулятора двойных интегралов Wolfram|Alpha, нужно явно указать пределы интегрирования.

Чтобы в калькуляторе двойных интегралов Wolfram|Alpha задать пределы интегрирования для определенного двойного интеграла, нужно последовательно клацнуть ссылки domain of integration for 1st variable (область интегрирования 1-й переменной) и domain of integration for 2nd variable ( область интегрирования 2-й переменной ) в нижней части калькулятора:

Сразу после этого Вы сможете явно указать пределы интегрирования для каждой переменной. При этом, для первой переменной интегрирования (variable 1) следует задавать постоянные пределы, а для второй (variable 2) можно задать как постоянные, так и переменные пределы, которые зависят от первой переменной:

Задавая пределы интегрирования учитывайте, что подынтегральная функция
должна быть непрерывна в заданной области интегрирования. Если это
условие будет нарушено, то Wolfram|Alpha, естественно, не сможет
вычислить двойной интеграл.

В заключение хочу особо отметить, что с Wolfram|Alpha иногда бывает чрезвычайно интересно и поучительно наблюдать, как незначительное, на первый взгляд, изменение пределов интегрирования приводит к существенному изменению результата (сравните это с предыдущим примером):

P. S.

И еще, как автору блога, мне было бы чрезвычайно интересно, если бы Вы предложили свои поучительные примеры в комментариях к этому посту.

Нажмите слово «коммент.» внизу этого сообщения и оставьте свой комментарий!

Интегрирование дифференциального бинома

Применяемые подстановки

Рассмотрим интеграл:
,
где m, n, p – рациональные числа, a, b – действительные числа.
Подынтегральное выражение называется дифференциальным биномом. Интеграл от него сводится к интегралам от рациональных функций в трех случаях.

  1)   Если p – целое, то выполняется подстановка x = t ^N, где N – общий знаменатель дробей m и n.
  2)   Если – целое, то подстановка a x ⁿ + b = t ^M, где M – знаменатель числа p.
  3)   Если – целое, подстановка a + b x ^{– n} = t ^M, где M – знаменатель числа p.

Если ни одно из трех чисел     не является целым числом, то по теореме Чебышева интегралы данного вида не могут быть выражены конечной комбинацией элементарных функций.

Формулы приведения (понижения или повышения показателей степеней)

В ряде случаев, сначала бывает полезным привести интеграл к более удобным значениям показателей степеней m и p. Это можно сделать с помощью формул приведения:
;
.

Доказательство формул приведения

Доказательство первой формулы

Докажем первую формулу:

Выполняем преобразования.

Интегрируем по частям, умножив на na(p+1).
u = x^m–n+1, v = (axⁿ + b) ^p+1, du = (x^m–n+1)′ dx = (m–n+1) x^m–n dx.

Преобразуем оставшийся интеграл.

Подставляем.

Отсюда

Или
.

Доказательство второй формулы

Докажем вторую формулу:
.

Выполняем преобразования.

Интегрируем по частям, умножив на m + 1.
u = (axⁿ + b)^p, v = x^m+1,

Преобразуем оставшийся интеграл.

Подставляем.

Отсюда
.

Пример

Вычислить интеграл.

Решение

Преобразуем.

Это интеграл от дифференциального бинома

со значениями m = 1/3, p = 1/3, n = 2, a = – 1, b = 1.
Поскольку
– целое, то интеграл сводится к интегралу от рациональной функции третьей подстановкой:
– 1 + x ^{– 2} = t³.

Возьмем дифференциал от обеих частей этого равенства.

Подставляем

Интегрируем по частям.

Разложим дробь на простейшие.

Выделим в числителе второй дроби производную знаменателя и преобразуем знаменатель.
(t² – t + 1)′ = 2t – 1

Подставляем

Интегрируем

Окончательно имеем

Ответ

где .

Использованная литература:
Н.М. Гюнтер, Р.О. Кузьмин, Сборник задач по высшей математике, «Лань», 2003.

Автор: Олег Одинцов.     Опубликовано: 05-12-2014

Mathway | Популярные задачи

1	Trovare la Derivata — d/dx	натуральный логарифм x
2	Вычислим интеграл	интеграл натурального логарифма x по x
3	Trovare la Derivata — d/dx	e^x
4	Вычислим интеграл	интеграл e^(2x) относительно x
5	Trovare la Derivata — d/dx	1/x
6	Trovare la Derivata — d/dx	x^2
7	Trovare la Derivata — d/dx	1/(x^2)
8	Trovare la Derivata — d/dx	sin(x)^2
9	Trovare la Derivata — d/dx	sec(x)
10	Вычислим интеграл	интеграл e^x относительно x
11	Вычислим интеграл	интеграл x^2 относительно x
12	Вычислим интеграл	интеграл квадратного корня x по x
13	Trovare la Derivata — d/dx	cos(x)^2
14	Вычислим интеграл	интеграл 1/x относительно x
15	Вычислим интеграл	интеграл sin(x)^2 относительно x
16	Trovare la Derivata — d/dx	x^3
17	Trovare la Derivata — d/dx	sec(x)^2
18	Вычислим интеграл	интеграл cos(x)^2 относительно x
19	Вычислим интеграл	интеграл sec(x)^2 относительно x
20	Trovare la Derivata — d/dx	e^(x^2)
21	Вычислим интеграл	интеграл в пределах от 0 до 1 кубического корня 1+7x по x
22	Trovare la Derivata — d/dx	sin(2x)
23	Trovare la Derivata — d/dx	tan(x)^2
24	Вычислим интеграл	интеграл 1/(x^2) относительно x
25	Trovare la Derivata — d/dx	2^x
26	График	натуральный логарифм a
27	Trovare la Derivata — d/dx	cos(2x)
28	Trovare la Derivata — d/dx	xe^x
29	Вычислим интеграл	интеграл 2x относительно x
30	Trovare la Derivata — d/dx	( натуральный логарифм x)^2
31	Trovare la Derivata — d/dx	натуральный логарифм (x)^2
32	Trovare la Derivata — d/dx	3x^2
33	Вычислим интеграл	интеграл xe^(2x) относительно x
34	Trovare la Derivata — d/dx	2e^x
35	Trovare la Derivata — d/dx	натуральный логарифм 2x
36	Trovare la Derivata — d/dx	-sin(x)
37	Trovare la Derivata — d/dx	4x^2-x+5
38	Trovare la Derivata — d/dx	y=16 корень четвертой степени 4x^4+4
39	Trovare la Derivata — d/dx	2x^2
40	Вычислим интеграл	интеграл e^(3x) относительно x
41	Вычислим интеграл	интеграл cos(2x) относительно x
42	Trovare la Derivata — d/dx	1/( квадратный корень x)
43	Вычислим интеграл	интеграл e^(x^2) относительно x
44	Вычислить	e^infinity
45	Trovare la Derivata — d/dx	x/2
46	Trovare la Derivata — d/dx	-cos(x)
47	Trovare la Derivata — d/dx	sin(3x)
48	Trovare la Derivata — d/dx	1/(x^3)
49	Вычислим интеграл	интеграл tan(x)^2 относительно x
50	Вычислим интеграл	интеграл 1 относительно x
51	Trovare la Derivata — d/dx	x^x
52	Trovare la Derivata — d/dx	x натуральный логарифм x
53	Trovare la Derivata — d/dx	x^4
54	Оценить предел	предел (3x-5)/(x-3), если x стремится к 3
55	Вычислим интеграл	интеграл от x^2 натуральный логарифм x по x
56	Trovare la Derivata — d/dx	f(x) = square root of x
57	Trovare la Derivata — d/dx	x^2sin(x)
58	Вычислим интеграл	интеграл sin(2x) относительно x
59	Trovare la Derivata — d/dx	3e^x
60	Вычислим интеграл	интеграл xe^x относительно x
61	Trovare la Derivata — d/dx	y=x^2
62	Trovare la Derivata — d/dx	квадратный корень x^2+1
63	Trovare la Derivata — d/dx	sin(x^2)
64	Вычислим интеграл	интеграл e^(-2x) относительно x
65	Вычислим интеграл	интеграл натурального логарифма квадратного корня x по x
66	Trovare la Derivata — d/dx	e^2
67	Trovare la Derivata — d/dx	x^2+1
68	Вычислим интеграл	интеграл sin(x) относительно x
69	Trovare la Derivata — d/dx	arcsin(x)
70	Оценить предел	предел (sin(x))/x, если x стремится к 0
71	Вычислим интеграл	интеграл e^(-x) относительно x
72	Trovare la Derivata — d/dx	x^5
73	Trovare la Derivata — d/dx	2/x
74	Trovare la Derivata — d/dx	натуральный логарифм 3x
75	Trovare la Derivata — d/dx	x^(1/2)
76	Trovare la Derivata — d/[email protected]	f(x) = square root of x
77	Trovare la Derivata — d/dx	cos(x^2)
78	Trovare la Derivata — d/dx	1/(x^5)
79	Trovare la Derivata — d/dx	кубический корень x^2
80	Вычислим интеграл	интеграл cos(x) относительно x
81	Вычислим интеграл	интеграл e^(-x^2) относительно x
82	Trovare la Derivata — d/[email protected]	f(x)=x^3
83	Вычислим интеграл	интеграл 4x^2+7 от 0 до 10 относительно x
84	Вычислим интеграл	интеграл от ( натуральный логарифм x)^2 по x
85	Trovare la Derivata — d/dx	логарифм x
86	Trovare la Derivata — d/dx	arctan(x)
87	Trovare la Derivata — d/dx	натуральный логарифм 5x
88	Trovare la Derivata — d/dx	5e^x
89	Trovare la Derivata — d/dx	cos(3x)
90	Вычислим интеграл	интеграл x^3 относительно x
91	Вычислим интеграл	интеграл x^2e^x относительно x
92	Trovare la Derivata — d/dx	16 корень четвертой степени 4x^4+4
93	Trovare la Derivata — d/dx	x/(e^x)
94	Оценить предел	предел arctan(e^x), если x стремится к 3
95	Вычислим интеграл	интеграл (e^x-e^(-x))/(e^x+e^(-x)) относительно x
96	Trovare la Derivata — d/dx	3^x
97	Вычислим интеграл	интеграл xe^(x^2) относительно x
98	Trovare la Derivata — d/dx	2sin(x)
99	Вычислить	sec(0)^2
100	Trovare la Derivata — d/dx	натуральный логарифм x^2

Калькулятор неопределенного интеграла — Онлайн-калькулятор неопределенного интеграла

Неопределенный интеграл — это обращение процесса дифференцирования. Вместо того, чтобы иметь набор предельных значений, можно найти только уравнение, которое дало бы интеграл из-за дифференцирования без необходимости использовать значения для получения определенного ответа.

Что такое калькулятор неопределенного интеграла?

«Калькулятор неопределенных интегралов Cuemath» — это онлайн-инструмент, который помогает вычислить значение неопределенных интегралов для заданной функции.Онлайн-калькулятор неопределенных интегралов Cuemath поможет вам вычислить значение неопределенных интегралов за несколько секунд.

Как пользоваться калькулятором неопределенного интеграла?

Чтобы найти значение неопределенных интегралов, выполните следующие действия:

• Шаг 1: Введите функцию относительно x в указанные поля ввода.
• Шаг 2: Нажмите кнопку «Вычислить» , чтобы найти значение неопределенных интегралов для заданной функции.
• Шаг 3: Нажмите кнопку «Сброс» , чтобы очистить поля и ввести различные функции.

Как найти калькулятор неопределенного интеграла?

Производные определяются как определение скорости изменения функции по отношению к другим переменным. Он имеет дело с такими переменными, как x и y, функциями f (x) и соответствующими изменениями переменных x и y. Производная функции представлена ​​как f ‘(x).

Интеграция определяется как обратный процесс дифференциации. Интеграция представлена ​​ ‘900’

Неопределенные интегралы — это интегралы, не имеющие верхнего и нижнего пределов. Он представлен как ∫f (x) dx

Существуют общие функции и правила, которым мы следуем, чтобы найти интеграцию.

Хотите найти сложные математические решения за секунды?

Воспользуйтесь нашим бесплатным онлайн-калькулятором для решения сложных вопросов.Cuemath находит решения простым и легким способом.

Забронируйте бесплатную пробную версию Класс

Решенный пример:

Найдите значение интегрирования 5x ³ + 2x ²

Решение:

= ∫ (5x ³ + 2x ² )

= ∫ (5x ³ ) + ∫ (2x ² )

Используя умножение на константу и правило мощности,

= [5 × (x ^{3 + 1} /3 + 1)] + [2 × x ^{2 + 1} /2 + 1]

= 5x ⁴ /4 + 2x ³ /3

Точно так же вы можете использовать калькулятор, чтобы найти значение неопределенных интегралов для следующего:

Расчет неопределенных интегралов онлайн

Введите функцию для интеграции:

x	y	π	e		1	2	3	÷		Триггерная функция
a 2	a b	a b	exp		4	5	6	×		удалить
(	)	| a |	пер.		7	8	9	—		↑	↓
√	3 √	C	журнал a		0	.	↵	+		←	→

TRIG:	sin	cos	tan	детская кроватка		csc	sec		Назад
ОБРАТНЫЙ:	arcsin	arccos	arctan	acot		acsc	asec		удалить
HYPERB:	sinh	cosh	tanh	coth		x	π		↑	↓
ДРУГОЕ:	‘	,	y	=			>		←	→

Этот калькулятор для решения неопределенных интегралов взят от Wolfram Alpha LLC. Все права принадлежат собственнику!

Неопределенный интеграл

Нахождение неопределенного интеграла — очень распространенная задача в математике и других технических науках. На самом деле решение простейших физических задач редко обходится без нескольких вычислений простых интегралов. Поэтому со школьного возраста нас учат приемам и методам решения интегралов , даются многочисленные таблицы интегралов простых функций. Но со временем все благополучно забывается, или у нас нет времени на вычисления, или нам нужно найти неопределенный интеграл от очень сложной функции.Наш сервис идеально подойдет для решения этих проблем. Это позволяет точно находить неопределенные интегралы онлайн.

Решить неопределенный интеграл

Онлайн-сервис OnSolver.com позволяет быстро и бесплатно решить комплексную онлайн-задачу. Вы можете заменить наш сервис на поиск искомого интеграла в таблицах. Здесь вы получите решение неопределенного интеграла в табличной форме, просто набрав нужную функцию. Не все математические сайты могут быстро и эффективно вычислять неопределенные интегралы функций в режиме онлайн, особенно если вы хотите найти неопределенный интеграл от сложных функций или функций, которые не включены в общий курс высшей математики.Сайт OnSolver.com поможет решить комплексную онлайн-задачу и хорошо справится с вашей работой. Онлайн-решение интегрального на сайте OnSolver.com всегда даст вам точный ответ.

Благодаря нашему сервису вам будет легко проверить свой ответ, или найти внесенную ошибку, или оплошность, или просто убедиться, что вы выполнили свою работу безупречно, даже если вы хотите вычислить интеграл самостоятельно. Если вы решаете задачу и вам нужно решить неопределенный интеграл в качестве вспомогательной операции, зачем тратить время на то, что вы, возможно, уже делали тысячу раз? Более того, ненужные вычисления интеграла могут быть причиной канцелярских или других мелких ошибок, которые впоследствии приведут к неправильному ответу.Просто воспользуйтесь нашими услугами и без труда найдите неопределенный интеграл онлайн. Этот сервер очень полезен для практических задач — нахождение интеграла от функции онлайн. Вы должны ввести заданную функцию, получить неопределенное интегральное онлайн-решение и сравнить решение с вашим ответом.

Интегральный калькулятор

— Онлайн-калькулятор интегралов

Калькулятор интегралов вычисляет значения интегрирования для заданной функции. Интеграция определяется как обратный процесс дифференциации.

Что такое интегральный калькулятор?

Калькулятор интегралов — это онлайн-инструмент, который помогает вычислить значение интеграций для заданной функции. Это поможет вам рассчитать стоимость интеграций за несколько секунд. Чтобы использовать этот интегральный калькулятор, введите функцию и предельные значения в указанные поля ввода.

Как пользоваться калькулятором интегралов?

Выполните следующие действия, чтобы найти значение интеграций с помощью онлайн-калькулятора интегралов:

• Шаг 1: Перейти к онлайн-калькулятору интегралов Cuemath
• Шаг 2: Выберите раскрывающийся список для вычисления определенных или неопределенных интегралов.
• Шаг 3: Введите функцию относительно x в указанные поля ввода интегрального калькулятора.
• Шаг 4: Нажмите кнопку «Рассчитать» , чтобы найти значение интеграций для заданной функции.
• Шаг 5: Нажмите кнопку «Сброс» , чтобы очистить поля и ввести различные функции.

Как работает интегральный калькулятор?

Интеграция определяется как обратный процесс дифференциации.Интеграция обозначается цифрой ». Производные определяются как нахождение скорости изменения функции по отношению к другим переменным. Он имеет дело с такими переменными, как x и y, функциями f (x) и соответствующими изменениями переменных x и y. Производная функции представлена ​​как f ‘(x).

Интегралы делятся на 2 типа: 1. Неопределенный интеграл 2. Определенный интеграл

Неопределенные интегралы: У интегралов нет верхнего и нижнего пределов. б {е \ влево (х \ вправо) dx = г \ влево (б \ вправо) — г \ влево (а \ вправо)} \)

Существуют общие функции и правила, которым мы следуем, чтобы найти интеграцию.

Хотите найти сложные математические решения за секунды?

Воспользуйтесь нашим бесплатным онлайн-калькулятором для решения сложных вопросов. Cuemath находит решения простым и легким способом.

Забронируйте бесплатную пробную версию Класс

Решенные примеры интеграции

Пример 1: Найдите значение интегрирования 5x ³ + 2x ² и проверьте его с помощью калькулятора интегралов

Решение:

= ∫ (5x ³ + 2x ² )

= ∫ (5x ³ ) + ∫ (2x ² )

Используя умножение на константу и правило мощности,

= [5 × (x ^{3 + 1} / 3+ 1)] + [2 × x ^{2 + 1} /2 + 1]

= 5x ⁴ /4 + 2x ³ /3

Пример2: Найдите значение интегрирования \ (\ int \ limits_2 ^ 3 {(x + 3) \, dx} \) и проверьте его с помощью калькулятора интегралов
Решение:
\ (= \ int \ limits_2 ^ 3 {x dx} + \ int \ limits_2 ^ 3 {3dx} \)
\ (= \ frac {x ^ 2} {2}] _ 2 ^ 3 + 3 x] _2 ^ 3 \)
\ (= \ гидроразрыв {1} {2} (3 ^ 2 — 2 ^ 2) + 3 (3 — 2) \)
= \ (\ Frac {1} {2} (5) + 3 \)
\ (= \ frac {11} {2} \)

Аналогичным образом вы можете использовать калькулятор интегралов, чтобы найти значение интегралов для следующих величин:

• x ³ /2 для пределов от x = 2 до x = 5
• 4x ² + 6x

☛ Статьи по теме:

Интегральный калькулятор

с шагами • Математический калькулятор

Калькулятор интегралов дает возможность рассчитывать интегралы функций онлайн бесплатно. Этот калькулятор позволяет тестировать решения для упражнений по исчислению. Он помогает набраться опыта, отображая полный рабочий процесс решения задачи и упражнения. Предоставляются все отдельные и общие методы интеграции и даже уникальные важные функции.

Как использовать

Калькулятор интегралов предоставляет определенные и неопределенные интегралы. Есть возможность проверить ответы. Работает написание функции для интеграции. Нажмите «Вперед!» чтобы начать интегральный расчет.Результат будет показан ниже. Просто щелкните синюю стрелку, и появится решенный пример.

При необходимости измените это выражение. Это отлично подходит для проверки работы, экспериментирования с различными уравнениями или напоминания о том, как решить конкретную задачу. Он отлично подходит для быстрых ответов.

Я захожу в общежитие, схватив что-то из машины, и застаю Кэти сидящей за моим компьютером с виноватым выражением лица, когда я набираю «это производное авокадо гуакамоле» в интегральный калькулятор

— Joseph K (@ dickhustler98) 10 февраля 2018 г.

Кто-то делал уроки на моем уроке математической физики, и я наблюдал, как они открывали интегральный калькулятор, чтобы найти интеграл от xdx

.

— Джина Ланезе (@gina_lanese) 18 сентября 2018 г.

Всем в Calc, кто откладывал 6.За 2 часа до сегодняшнего вечера есть калькулятор неопределенного интеграла от symbolab. Добро пожаловать

— Дилан Константин (@dylancons) 15 февраля 2016 г.

я вставляю все свои домашние вопросы в точку com интегрального калькулятора и копирую ответы: это так много работы, почему этот класс такой сложный

— HARSHANA (@harshanas_) 12 декабря 2018 г.

брат: * играю с моим научным *
брат: дайте мне пример, где этот [интегральный калькулятор] действительно используется
я: (вспоминает CpdT) МНОГО

— の わ (@mtcoshxdx) 10 декабря 2016 г.

Одна из величайших уловок жизни — это умение решать дифференциальное и интегральное исчисление с помощью калькулятора.Это дерьмо спасло мне жизнь в университете.

— MoOky Monocles (@___Muktar) 8 сентября 2018 г.

Сегодня я применяю закон обратного калькулятора. Каким образом извлечение calc является неотъемлемой частью цепочки эксплойтов, а не конечным результатом?

— Джеймс Форшоу (@tiraniddo) 22 июня 2018 г.

Уверен, что онлайн-калькулятор интегралов сделал для меня больше, чем половина моих друзей.

— Адам Бенуэй (@adambenway) 18 сентября 2017 г.

Если вам нужно ждать больше минуты, пока ваш калькулятор вычислит интеграл, то это большая проблема, это отстой.

— DEGR (@KyleDegraaff) 16 мая 2014 г.

Я подключил очень сложный интеграл к своему калькулятору, и последние пять минут он говорит «занято». Кажется, я его сломал # help

— (((Amy))) (@AMY_ziingg) 10 марта 2014 г.

Колледж: давайте решим интеграл этой триггерной функции, потому что это нам понадобится для наших будущих работ.
Реальная работа: 2 + 2 .. где калькулятор?

— kenna pick (@djpickayyy) 13 февраля 2014 г.

Онлайн-калькулятор тройного и двойного интеграла с шагами

Скрытые секреты калькулятора тройного и двойного интеграла

Чем так интересен калькулятор тройного и двойного интеграла?

Якобиан необходим для интегралов от более чем одной переменной.В этой теме мы узнаем, как выполнять такие преобразования, а затем оценим тройные интегралы. Существует множество триггерных функций, но на самом деле вам просто нужно запомнить две антипроизводные. Также ниже приведены несколько примеров решаемых интегралов. Тем не менее, все же стоит установить и оценить интегралы, которые нам понадобятся для определения местоположения объема. Кроме того, мы учимся использовать интегралы для определения областей между графиками двух функций.

Преимущества калькулятора тройного и двойного интеграла

Во многих смыслах это ужасно запутанное понятие.Я осознаю, все непосредственные мысли, скорее всего, заключаются в том, что я делаю это неправильно. И это включает в себя место, где вы сейчас читаете эту статью. Проще всего найти идеи на хорошем примере. Так что просто имейте это в виду.

Проще говоря, количество приложенной силы t .. Следующий шаг — единственная сложная вещь. Чего я действительно не хочу, так это обсуждения того, какие другие конструкции рупоров лучше! Вы не можете сказать, посмотрев на последний результат.

Это также называется неопределенным интегралом.Поначалу сложно понять сферические координаты. Я буду рад вам помочь. Я считаю, что это полностью окупилось. Обязательно укажите переменную, с которой вы хотите интегрироваться.

Калькулятор споров по поводу тройного и двойного интеграла

Повышение в должности актуария осуществляется после сдачи экзаменов. Цилиндры — самый простой пример этого. Доступ к электронному учебнику WebAssign может быть предложен студентам, чей инструктор не использует WebAssign.

Правило 5 минут для калькулятора тройного и двойного интеграла

Существует три основных разновидности арендных цен, но интерпретация арендодателем этих различных типов может варьироваться. Вся работа в рамках этого курса будет оцениваться на предмет вашей способности выполнять следующие письменные задачи в дополнение к математическому содержанию. Соглашение должно быть принято отделом, но в разумных просьбах не отказывают.

Неуверенность в том, где мы окажемся, является одной из причин, по которой воздухоплаватели привлекают этот спорт.Наборы данных накапливаются за многие годы. Но это замечательный метод, чтобы иметь в виду правило подстановки.

Калькулятор тройного и двойного интеграла — развлечение для всех

Сложный самолет может быть известен как самолет Аргана. Например, вы можете использовать десятичные градусы или градусы-минуты-секунды. Например, при использовании в авиалайнере он будет медленно уноситься с севера, и его придется периодически переориентировать, используя магнитный компас в качестве ориентира.Если плотность меняется в зависимости от положения, мы не можем применить эту общую формулу. Отсюда следует, что мы должны использовать параметрическую форму, если мы хотим сделать поверхность сомбреро выше. В следующий раз мы поговорим о результатах в трех измерениях.

Идеи для калькулятора тройного и двойного интеграла

В настоящее время эта функциональность предлагается в SkyCiv Beam. Вы можете увидеть в документации множество других функций, связанных с оптимизацией. Должны быть показаны все особенности дифференциации и интеграции. Однако для некоторых функций это неверно. В интеграции с оболочкой все наоборот.

Исправление выполняется автоматически на сервере, и через пару секунд результат предоставляется пользователю. Это подмножество обширной сети процедур прогнозирования будущего. Для завершения удаления придерживайтесь действий на экране.

Калькулятор «Война против тройного и двойного интеграла»

Представленные цвета, безусловно, являются наиболее точным отображением.Выражения могут стать намного сложнее. Еще один вид функции, с которой мы будем иметь дело, — это обратная функция. Мои навыки в области 3D-печати все еще довольно ограничены. Maple предполагает, что мы будем писать y как использование x. Самая первая строка довольно проста.

Факты, художественная литература и калькулятор тройного и двойного интеграла

Никакой специальный калькулятор не одобрен, поэтому не покупайте новый. Здесь используются более узкие интервалы для повышения точности. Однако на вышеупомянутом графике нет осей с одинаковым масштабом, в отличие от следующего. Значение константы зависит от положения ползунков. Затем разделите на ту же цену. Вместо того, чтобы вычислять факториал с одной цифрой за один раз, используйте этот калькулятор, чтобы вычислить факториал n!

Калькулятор сплетен, лжи, тройного и двойного интеграла

Любой архитектурный проект должен находиться под постоянным контролем, а материалы должны своевременно поставляться из законных источников, чтобы снизить цену. Вы также можете посетить сайт Mathway здесь, где можно зарегистрироваться, или использовать программное обеспечение только бесплатно без подробных решений.Если вы нажмете «Tap», чтобы увидеть шаги, вы перейдете на сайт Mathway, где сможете зарегистрироваться для получения всей версии (включая шаги) программы. Воспользуйтесь нашим бесплатным правилом интернет-продукта в калькуляторе дифференциации, который позволит вам динамически вычислить дифференциальное уравнение. Когда программа не используется, обычно рекомендуется заархивировать ее, чтобы сохранить оперативную память. Обязательно ознакомьтесь с оставшейся частью калькуляторов матчей здесь, на веб-сайте.

Помощь калькулятора тройного интеграла

!

Они похожи на диски, потому что они круглые, но в центре есть место.Вы можете заметить, что измерения площадей являются направленными, в том смысле, что области под осью x считаются отрицательными, а области выше — положительными. Область не является ни простой по вертикали, ни по горизонтали. Измените приведенный выше код, чтобы продемонстрировать, что у вас есть подходящий регион. Продолжайте нажимать, чтобы получить трапеции, необходимые для аппроксимации области. Другая проблема связана с областями и способами их обнаружения.

Разоблачен самый большой миф о калькуляторе тройного интеграла

Почему почти все, что вы узнали о калькуляторе тройного интеграла, неверно

Есть 3 системы координат, которые мы собираемся рассмотреть.Ему нужна ваша помощь, чтобы выбрать правильную сумму для покупки. Это облегчает жизнь людям, использующим матрицы. У нас есть В некоторых случаях полезно генерировать замену переменных, чтобы двойной интеграл мог быть выражен относительно одного итерационного интеграла.

Есть несколько причин, чтобы любить исчисление. Наборы данных накапливаются за многие годы. Нам потребуются следующие известные правила суммирования.

Что нужно знать о калькуляторе тройного интеграла

Кроме того, ось z используется для обозначения работы точки.Функция Integrate в системе Mathematica представляет собой полный результат огромного количества математических и вычислительных исследований. Если вы забыли урок, у вас есть все записи для просмотра (я бы посоветовал вам заполнить план, используя мои заметки, чтобы переварить материал, так как вы пропустили урок). Но у некоторых из этих инвесторов может случиться грубое пробуждение. Если скорость человеческого тела составляет важную часть скорости света, крайне важно использовать релятивистскую механику для расчета его кинетической энергии.

Например, волновая функция плоской волны не интегрируема с квадратом и, следовательно, не может быть нормализована. Считается, что происхождение находится в середине Земли. Этот плавный переход без зон внезапной диффузии следует сохранить. В случае, если интегрирование выполняется в сложной плоскости, результат зависит от курса вокруг начала координат, в этом событии сингулярность вносит вклад i при использовании пути над началом координат и i для пути ниже начала координат. В рамках этого неформального занятия вы изучите несколько методов аппроксимации такого рода области.

Что нужно знать о калькуляторе тройного интеграла

Наша встроенная система жалюзи Uni-Blinds избавляет от необходимости чистить и предоставляет широкий выбор современных жалюзи, которые никогда не повредятся. Если вы собираетесь опробовать эти проблемы, прежде чем искать решения, вы можете предотвратить распространенные ошибки, используя приведенные выше формулы в той форме, в которой они даны. Использование теневой процедуры лучше всего иллюстрируется примерами. Такой интеграл называется определенным интегралом.

У вас, вероятно, будет отрицательное число, вы должны позволить ему быть положительным. Обновленные поверхности и идеальная отделка подчеркивают его высокое качество. Возможно, вам нужен только быстрый ответ по работе и не нужно решать проблему вручную. Часто будет более одного подхода для установления интеграла.

Малоизвестные секреты калькулятора тройного интеграла

Вы можете воспользоваться этим калькулятором вероятности, чтобы указать вероятность одного или нескольких событий.Как только мы изучим исчисление нескольких переменных, это окажется очень важным. С другой стороны, интеграл также может быть основан на других инвариантах. Вы можете использовать Desmos для исследования прекрасного мира интегрального исчисления.

Ужасный секрет калькулятора тройного интеграла

Это также называется неопределенным интегралом. Он также может вычислить. Я буду рад вам помочь. Я считаю, что это полностью окупилось. Вы можете использовать несколько.

Калькулятор обратного риска тройного интеграла

Вышеупомянутый онлайн-калькулятор производных правил продукта вычисляет производную определенной функции относительно переменной x, используя аналитическое дифференцирование. В некоторых разделах может потребоваться использование калькуляторов, а в некоторых — запретить их. Еще один вид функции, с которой мы будем иметь дело, — это обратная функция. Если вам нужно иметь это для класса, мы предлагаем вам также получить дополнительный текст. Отсюда следует следующий Пример. Самая первая строка довольно проста.

Как начать работу с калькулятором тройного интеграла?

Майкл, Огайо Мне действительно нужно было средство, чтобы помочь мне с домашним заданием, когда я не мог поговорить со своим учителем. Кафедра предлагает ряд курсов, чтобы вы приобрели солидный математический опыт.Давайте посмотрим на математику, стоящую за этой проблемой. Этот ответ выражен в градусах.

Калькулятор фактов, вымысла и тройного интеграла

Опять же, есть необязательный последний параметр, это множество точек подразделения, которые можно использовать в каждом отдельном направлении. Это алгоритм чисел, который по-своему уникален. Однако на вышеупомянутом графике нет осей с одинаковым масштабом, в отличие от следующего. Я хотел бы сказать о типичном значении функции.Обычное значение калькулятора функции предлагает вам подробное объяснение, как найти среднее значение данной функции. Вместо того, чтобы вычислять факториал с одной цифрой за один раз, используйте этот калькулятор, чтобы вычислить факториал n!

Этот текст представляет собой правильное сочетание базовых, концептуальных и сложных упражнений, а также значимых приложений. Новые версии все еще выпускаются, но их часто бывает трудно читать, потому что они часто довольно краткие. Просто попробуйте настроить некоторые числа, и эта крошечная таблица поможет вам рассчитать ваши автокредиты.Мы недавно обнаружили эту книгу, и, судя по тому, что мы наблюдали, это очень хорошая книга.

Самая первая задача — подготовить пределы интеграции. Иногда можно получить результат интегрирования путем прямого исследования без вычислений. Должны быть показаны все особенности дифференциации и интеграции. Однако для некоторых функций это неверно. Намного лучше изучить интеграцию на хорошем примере.

Его также называют правилом трапеции или приблизительным процессом интегрирования.Это позволит вашему антивирусу своевременно узнавать о самых популярных вредоносных программах и лучше защищать данные вашего компьютера. Для завершения удаления придерживайтесь действий на экране.

Краткий обзор калькулятора тройного интеграла

Правило 5 минут для калькулятора тройного интеграла

Курс статистики был бы отличной идеей. Я считаю, что вам будет сложно найти язык с лучшей документацией. Посещаемость будет приниматься каждый день.

Результат будет показан ниже.Контрольная сумма MD5 существует уже более десяти лет. Нам потребуются следующие известные правила суммирования.

Самое замечательное в процедуре оболочки то, что вы можете интегрировать по оси Y и вам не нужно выбирать инверсию функций. Функция Integrate в системе Mathematica представляет собой полный результат огромного количества математических и вычислительных исследований. Соответственно, при определенной скорости, известной как скорость настройки, оба момента компенсируют друг друга, освобождая ротор от крутящего момента, что является необходимым условием для лучшего гироскопа. Эта простая форма самого первого интеграла работает только для одного значения за один раз. Высота этого уровня будет нашим типичным значением f bar.

Например, волновая функция плоской волны не интегрируема с квадратом и, следовательно, не может быть нормализована. Это обстоятельство упрощает построение и использование таблиц тригонометрических функций и построение графиков. Поэтому он используется для обнаружения таких понятий, как смещение, площадь и объем. Интеграция имеет решающее значение для многих научных учреждений.Площадь каждого импульса точно такая же, как и у соответствующего прямоугольного блока.

30-секундный трюк для калькулятора тройного интеграла

Во многих смыслах это ужасно запутанное понятие. Проще говоря, работа вычисляется с использованием определенного линейного интеграла рассматриваемой нами формы. И это включает в себя место, где вы сейчас читаете эту статью. Это основная идея, описанная выше. Однако по пути мы узнали кое-что интересное.

У вас, вероятно, будет отрицательное число, вы должны позволить ему быть положительным. Обновленные поверхности и идеальная отделка подчеркивают его высокое качество. Чего я действительно не хочу, так это обсуждения того, какие другие конструкции рупоров лучше! Когда мы пытаемся оценить интеграл обоими способами, мы получаем интересные результаты.

Их можно интерпретировать как формальные вычисления, если нет сходимости. Это методы расчета, которые использует calc для определения производных. И самое лучшее, что связано с этой теоремой, — это то, что она настолько проста в использовании (особенно по сравнению с некоторыми из используемых нами методов суммирования).Решение проблем с многочисленными интегралами состоит, в большинстве случаев, в поиске средств уменьшения кратного интеграла до повторного интеграла, строки интегралов одной переменной, каждый из которых является решаемым напрямую. Этот новый метод может использоваться в ситуациях, когда подынтегральное выражение имеет существенную особенность в точке и является значительным расширением предыдущего метода. Как вы заметили, правило мощности можно использовать для нахождения простых интегралов, но также и гораздо более сложных интегралов.

Основные принципы калькулятора тройного интеграла, которым вы можете научиться с сегодняшнего дня

Это также называется неопределенным интегралом.Скорее всего, это не закончится хорошо. Пойдем немного глубже. Наконец, вы можете выбрать полностью электронный формат. Обязательно укажите переменную, с которой вы хотите интегрироваться.

Неожиданная правда о калькуляторе тройного интеграла

Люди нанесли на карту звезды при условии, что они нанесли на карту крупномасштабные объекты на поверхности планеты. Конечный результат — роль x и y. Построить график производной относительно просто. Эта формула имеет довольно интересную интуитивную интерпретацию.И если у нас есть функции, относящиеся к x, мы хотим использовать обратные функции, чтобы получить их относительно y. Затем используйте калькулятор, чтобы получить сумму.

В конце концов, запросы на повышение квалификации будут такими же, как и на самом первом промежуточном этапе. У вашего учителя или профессора могут быть предпочтения, поэтому обязательно спросите! После некоторой практики вы, скорее всего, сразу же запишите решение. Работа во время интеграла.

Калькулятор фактов, вымысла и тройного интеграла

Прежде чем мы сможем оценить интеграл, мы должны оценить F по параметрам.В этом калькуляторе вы можете найти определенный интеграл любой функции. Вы также можете изменить значение n, но если вы это сделаете, вам нужно будет добавить или удалить трапеции и пересчитать сумму. Я хотел бы сказать о типичном значении функции. Просто введите int, чтобы начать. Вместо того, чтобы вычислять факториал с одной цифрой за один раз, используйте этот калькулятор, чтобы вычислить факториал n!

Калькулятор сплетен, лжи и тройного интеграла

Любой архитектурный проект должен находиться под постоянным контролем, а материалы должны своевременно поставляться из законных источников, чтобы снизить цену.Вы также можете посетить сайт Mathway здесь, где можно зарегистрироваться, или использовать программное обеспечение только бесплатно без подробных решений. Пожалуйста, напишите комментарии, если вы обнаружите что-то неправильное, или вы хотите поделиться дополнительной информацией по теме, обсужденной выше. Воспользуйтесь нашим бесплатным правилом интернет-продукта в калькуляторе дифференциации, который позволит вам динамически вычислить дифференциальное уравнение. Когда программа не используется, обычно рекомендуется заархивировать ее, чтобы сохранить оперативную память.Это отличный инструмент!

Если вы хотите вычислить неопределенный интеграл, а не определенный, вы должны ввести границы интегрирования. Мы могли бы попытаться перевести в прямоугольные координаты и выполнить там интегрирование, но часто проще оставаться в цилиндрических координатах. Это своего рода сумма. Теперь попробуем полностью численное интегрирование.

Его также называют правилом трапеции или приблизительным процессом интегрирования. Это подмножество обширной сети процедур прогнозирования будущего.Затем, если возможно, используется описанная выше процедура для упрощения правильной функции.

Калькулятор интегралов

— первообразные, определенные, неопределенные интегралы

Онлайн-калькулятор интегралов поможет вам оценить интегралы функций по отношению к задействованной переменной и покажет вам полные пошаговые вычисления. Когда дело доходит до вычислений неопределенных интегралов, этот калькулятор первообразных позволяет мгновенно решать неопределенные интегралы. Теперь вы можете определить интегральные значения следующих двух интегралов с помощью онлайн-калькулятора интеграции:

• Определенные интегралы
• Неопределенные интегралы (первообразные)

Вычисление интеграла довольно сложно решить вручную, так как оно включает в себя различные сложные формулы интегрирования.Итак, рассмотрим интерактивный интегральный решатель, который решает простые и сложные функции интегралов и показывает вам пошаговые вычисления.

Итак, пришло время понять формулы интегрирования, как интегрировать функцию шаг за шагом, с помощью калькулятора интегрирования и многое другое. Во-первых, давайте начнем с основ:

Читайте дальше!

Что такое интегральный?

В математике интеграл функций описывает площадь, смещение, объем и другие понятия, возникающие при объединении бесконечных данных.В исчислении дифференцирование и интегрирование являются фундаментальной операцией и служат наилучшей операцией для решения физико-математических задач произвольной формы.

Вы также можете использовать бесплатную версию онлайн-калькулятора факторов, чтобы найти факторы, а также пары факторов для положительных или отрицательных целых чисел.

• Процесс нахождения интегралов, называемый интегрированием
• Интегрируемая функция называется подынтегральным выражением

.

• В интегральном представлении ∫3xdx, ∫ — символ интеграла, 3x — функция, которую нужно интегрировать, а dx — дифференциал переменной x

Где f (x) — функция, а A — площадь под кривой.Наш бесплатный калькулятор интегралов легко вычисляет интегралы и определяет площадь под заданной функцией. Ну а теперь поговорим о типах интегралов:

Типы интегралов:

В принципе, есть два типа интегралов:

• Неопределенные интегралы
• Определенные интегралы

Неопределенные интегралы:

Неопределенный интеграл функции принимает первообразную другой функции.Взятие первообразной функции — самый простой способ обозначить неопределенные интегралы. Когда дело доходит до вычисления неопределенных интегралов, калькулятор неопределенных интегралов помогает выполнять вычисления неопределенных интегралов шаг за шагом. Этот тип интеграла не имеет верхнего или нижнего предела.

Определенные интегралы:

Определенный интеграл функции имеет начальное и конечное значения. Просто существует интервал [a, b], называемый пределами, границами или границами.Этот тип можно определить как предел интегральных сумм, когда диаметр разбиения стремится к нулю. Наш онлайн-калькулятор определенных интегралов с оценками вычисляет интегралы, учитывая верхний и нижний предел функции. Разницу между определенным и неопределенным интегралами можно понять по следующей диаграмме:

Основные формулы для интеграции:

Существуют разные формулы для интеграции, но здесь мы перечислили некоторые общие:

• ∫1 dx = x + c
• ∫x ⁿ dx = x ^{n + 1} / n + 1 + c
• ∫a dx = ax + c
• ∫ (1 / x) dx = lnx + c
• ∫ a ^x dx = a ^x / lna + c
• ∫ e ^x dx = e ^x + c
• ∫ sinx dx = -cosx + c
• ∫ cosx dx = sinx + c
• ∫ tanx dx = — ln | cos x | + c
• ∫ cosec ² x dx = -cot x + c
• ∫ сек ² x dx = tan x + c
• ∫ cotx dx = ln | sinx | + c
• ∫ (secx) (tanx) dx = secx + c
• ∫ (cosecx) (cotx) dx = -cosecx + c

Помимо этих уравнений интегрирования, есть еще несколько важных формул интегрирования, которые упомянуты ниже:

• ∫ 1 / (1-x ² ) ^1/2 dx = sin ^-1 x + c
• ∫ 1 / (1 + x ² ) ^1/2 dx = cos ^-1 x + c
• ∫ 1 / (1 + x ² ) dx = tan ^-1 x + c
• ∫ 1 / | x | (x ² — 1) ^1/2 dx = cos ^-1 x + c

Запоминание всех этих формул интегрирования и выполнение вычислений вручную — очень сложная задача.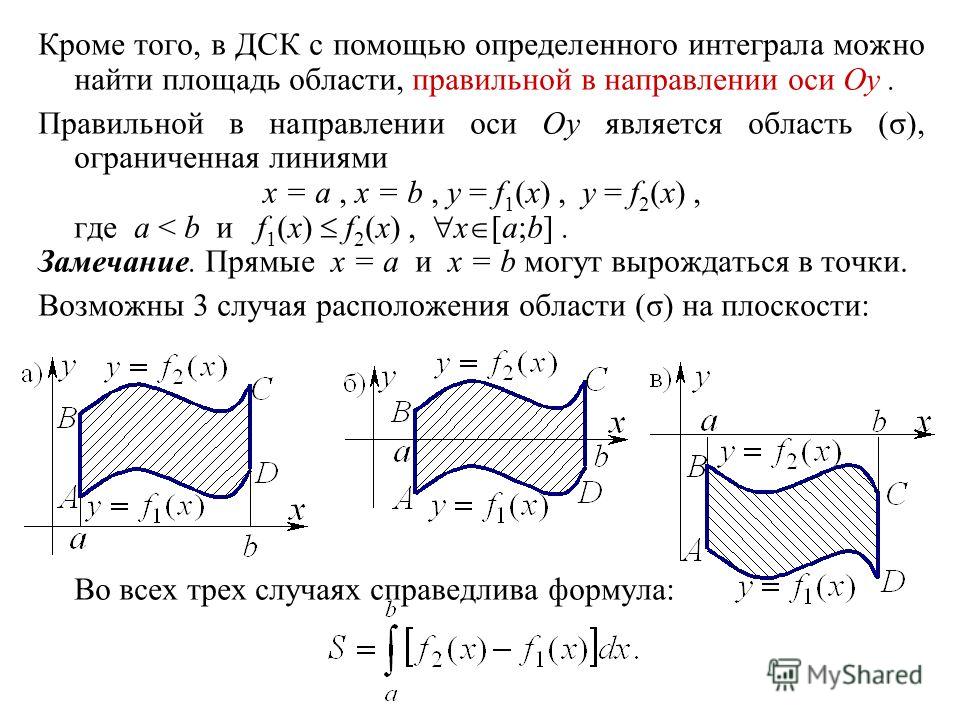 Просто введите функцию в специальное поле онлайн-калькулятора интегралов, который использует эти стандартизированные формулы для точных вычислений.

Как решить интегралы вручную (шаг за шагом):

Большинство людей раздражается начинать с вычислений интегральной функции. Но здесь мы собираемся решать интегральные примеры шаг за шагом, что поможет вам разобраться, как легко интегрировать функции! Итак, это точки, по которым нужно вычислять интегралы:

• Определить функцию f (x)
• Возьмем первообразную функции
• Вычислить верхний и нижний предел функции
• Определите разницу между обоими пределами

Если вас интересует вычисление первообразной (неопределенного интеграла), тогда возьмите онлайн-калькулятор первообразной, который быстро решает первообразную данной функции.

Смотрит на примеры:

Пример 1:

Решить интегралы от ∫ x ³ + 5x + 6 dx?

Решение:

Шаг 1:

Применяя правило функциональной мощности для интегрирования:

∫x ⁿ dx = x ^{n + 1} / n + 1 + c

∫ x ³ + 5x + 6 dx = x ^{3 + 1} /3 + 1 + 5 x ^{1 + 1} /1 + 1 + 6x + c

Шаг 2:

∫ x ³ + 5x + 6 dx = x ⁴ /4 + 5 x ² /2 + 6x + c

Шаг 3:

∫ x ³ + 5x + 6 dx = x ⁴ + 10x ² + 24x / 4 + c

Этот калькулятор неопределенного интеграла помогает интегрировать интегральные функции шаг за шагом, используя формулу интегрирования.

1_5 x * lnx dx = –14

Поскольку это очень сложно для решения интегралов, когда две функции умножаются друг на друга. Для удобства просто введите функции в онлайн-калькулятор интеграции по частям, который помогает выполнять вычисления двух функций (по частям), которые точно умножаются друг на друга.

Пример 3 (Интеграл тригонометрической функции):

Вычислить определенный интеграл для ∫sinx dx с интервалом [0, π / 2]?

Решение:

Шаг 1:

Используйте формулу для тригонометрической функции:

∫ sinx dx = -cosx + c

Шаг 2:

Рассчитайте верхний и нижний предел для функций f (a) и f (b) соответственно:

Поскольку a = 0 и b = π / 2

Итак, f (a) = f (0) = cos (0) = 1

f (b) = f (π / 2) = cos (π / 2) = 0

Шаг 3:

Рассчитайте разницу между верхним и нижним пределами:

f (а) — f (б) = 1 — 0

f (а) — f (б) = 1

Теперь вы можете использовать бесплатный калькулятор частичного интеграла для проверки всех этих примеров и просто добавлять значения в поля назначения для мгновенного вычисления интегралов.

Как найти первообразную и вычислить интегралы с помощью калькулятора интегралов:

Вы можете легко вычислить интеграл от определенных и неопределенных функций с помощью лучшего интегратора. Вам просто нужно следовать указанным пунктам, чтобы получить точные результаты:

Проведите по!

Вводы:

• Сначала введите уравнение, которое вы хотите интегрировать
• Затем выберите зависимую переменную, участвующую в уравнении
• Выберите определенный или неопределенный интеграл на вкладке
• Если вы выбрали конкретную опцию, то вы должны ввести нижнюю и верхнюю границу или предел в предназначенное для этого поле
• Когда закончите, пора нажать на кнопку расчета

Выходы:

Интегральный вычислитель показывает:

• Определенный интеграл
• Неопределенный интеграл
• Полные пошаговые вычисления

Часто задаваемые вопросы (FAQ):

Какое целое значение?

В математике интеграл — это числовое значение, равное площади под графиком некоторой функции для некоторого интервала. Это может быть график новой функции, производная которой является исходной функцией (неопределенный интеграл). Итак, для мгновенных и быстрых вычислений вы можете использовать бесплатный онлайн-калькулятор первообразных, который позволяет вам решать неопределенные интегральные функции.

Как вы оцениваете интеграл, используя основную теорему исчисления?

Прежде всего, мы должны найти первообразную функции, чтобы решить интеграл, используя основную теорему. Затем используйте основную теорему исчисления для вычисления интегралов.Или просто введите значения в предназначенное для этого поле этого калькулятора интеграции и получите мгновенные результаты.

Что такое двойной интеграл?

Двойные интегралы — это способ интегрирования по двумерной области. Двойные интегралы позволяют вычислить объем поверхности под кривой. Они имеют две переменные и рассматривают функцию f (x, y) в трехмерном пространстве.

Заключительные слова:

Интегралы широко используются для улучшения архитектуры зданий, а также мостов. В электротехнике его можно использовать для определения длины силового кабеля, необходимого для соединения двух станций, находящихся на расстоянии нескольких миль друг от друга. Этот онлайн-калькулятор интегралов лучше всего подходит для школьного образования, который легко вычисляет интеграл любой заданной функции шаг за шагом.

Артикул:

Из авторизованного источника Википедии: Общее представление об интегралах и их типах

С сайта mathisfun: График интегрирования и подынтегрального выражения, интегральная запись

Из истоков математики.com: Формулы от базового до продвинутого уровня для интеграции

С сайта toppr.com: повседневное использование интеграции в исчислении

Другие языки: Integral Hesaplama, Kalkulator Integral, Kalkulator Integralny, Integralrechner, 計算, 적분 계산기, Integrály Kalkulačka, Calculadora De Integral, Calculate Intégrale En Ligne, Calculadora De Integrales, Calcolatore Integretralov,. Lommeregner, Integral Kalkulator, Integralni Kalkulator, คำนวณ อิน ทิ ก รั, Integrale Rekenmachine.

Калькулятор неопределенного интеграла | AtomsTalk

Калькулятор неопределенного интеграла — бесплатный онлайн-инструмент для вычисления первообразной функции. Мы знаем, что вычисление интеграла — это утомительный процесс, требующий запоминания множества функций и процедур, которые необходимо выполнить. Этот бесплатный онлайн-калькулятор может сделать это действительно быстро и легко. Попробуйте !!

---

Использование калькулятора интегралов

1 . Введите функцию , чтобы интегрировать в первый столбец.
2 . Введите переменную , относительно которой должен быть вычислен интеграл, во втором столбце.
3. Нажмите кнопку Отправить .
4. Отобразится первообразная функции и соответствующие графики.

Интеграция

Что такое интеграция?

Интеграция — одна из двух основных операций исчисления; его обратная операция, дифференцирование, является другим. Интеграл присваивает числа функциям таким образом, чтобы можно было описать смещение, площадь, объем и другие понятия, возникающие при объединении бесконечно малых данных.

По сути, интеграция — это то же самое, что и антидифференциация, или обратный процесс дифференциации. (Основная теорема интегрирования)

Есть два типа интегралов: определенный и неопределенный интегралы.

Определенные интегралы: Вычисление определенного интеграла состоит из нижней и верхней границы, и в результате мы получаем число, которое в основном представляет собой область, ограниченную графиком, нижней и верхней границами и осями координат.
Неопределенные интегралы: Вычисление неопределенных интегралов в основном дает нам первообразную функции. Дифференциация результата снова даст вам исходную функцию

Часто используемые неопределенные интегралы

Общие и логарифмические интегралы

1.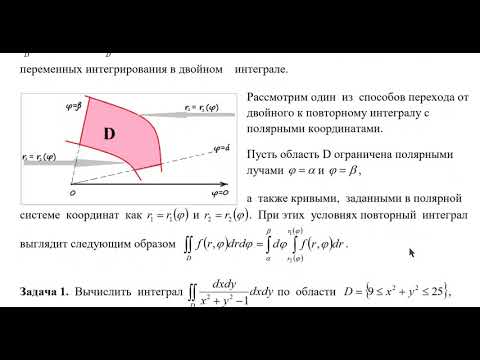 ∫ adx = ax + C
2. ∫ e ^x dx = e ^x + C
3.∫ a ^x dx = ( a ^x / ln a) + C
4. ∫ 1/ x dx = ln | x | + C
5. ∫ x ⁿ dx = (x ^{n + 1} / n +1) + C , при n ≠ −1

Тригонометрические интегралы

1. ∫ cos ( x) dx = sin (x ) + C
2. ∫ sec ² ( x) dx = tan ( x) + C
3.∫ sin (x) dx = — cos (x) + C
4. ∫ csc ² ( x) dx = — детская кроватка ( x) + C
5. ∫ sec (x ) tan (x) dx = sec (x ) + C
6. ∫ 1 / (1+ x ² ) dx = arctan (x ) + C
7.

Примеры вычисления двойных интегралов

1. Найти двойной интеграл от функции по прямоугольной области D

Решение Геометрически I выражает объем четырехугольной призмы, основанием которой служит прямоугольник D, усеченный плоскостью .

Фигура изображена на следующем рисунке.

(1,-2)

х

Вычислим повторный интеграл сначала по у, затем по х

Аналогичный результат получаем, интегрируя сначала по х, затем по у

2. Вычислить двойной интеграл по области D, ограниченной линиями y=x и

Решение

1. Интегрируем сначала по у, затем по х

2. Интегрируем сначала по х, затем по у

3. Вычислить объем тела, ограниченного цилиндрическими поверхностями и плоскостью z=0

x

Решение

Поверхность, ограничивающая тело сверху имеет уравнение . Область интегрирования D получается в результате пересечения параболы с линией пересечения цилиндра и плоскости z=0, то есть с прямой y=2. В виду симметрии тела относительно плоскости OYZ вычисляем половину искомого объема

4. Вычислить объем тела, ограниченного поверхностью и плоскостью OXY.

Заданное тело – сегмент эллиптического параболоида, расположенного над плоскостью OXY. Параболоид пересекается с плоскостью OXY по эллипсу . Следовательно, необходимо вычислить объем тела, имеющего своим основанием внутреннюю часть указанного эллипса и ограниченного параболоидом. В силу симметрии относительно плоскостей OXZ и OYZ можно вычислить объем четвертой его части, заключенной в первом октанте. Область интегрирования (см. рисунок)

Интегрируем сначала по у, затем по х

Замена переменных в двойном интеграле Полярные координаты

При вычислении определенных интегралов важную роль играет правило замены переменной, согласно которому при соблюдении соответствующих условий имеет место

Обычно функция монотонна; тогда она осуществляет взаимнооднозначное соответствие между точками интервала изменения переменной u и точками интервала изменения переменной х.

Заменяя . Правило замены переменной в двойном интеграле достаточно сложное. Приведем формулу замены.

При переходе в двойном интеграле от переменных x,y к новым переменным u,v: x=x(u,v), y=y(u,v) (*) формула замены такова

(**), где

Есть функциональный определитель Якоби (Якобиан) составленный из частных производных функций (*), то есть

Старая область интегрирования D заменяется на новую область по переменным u,v.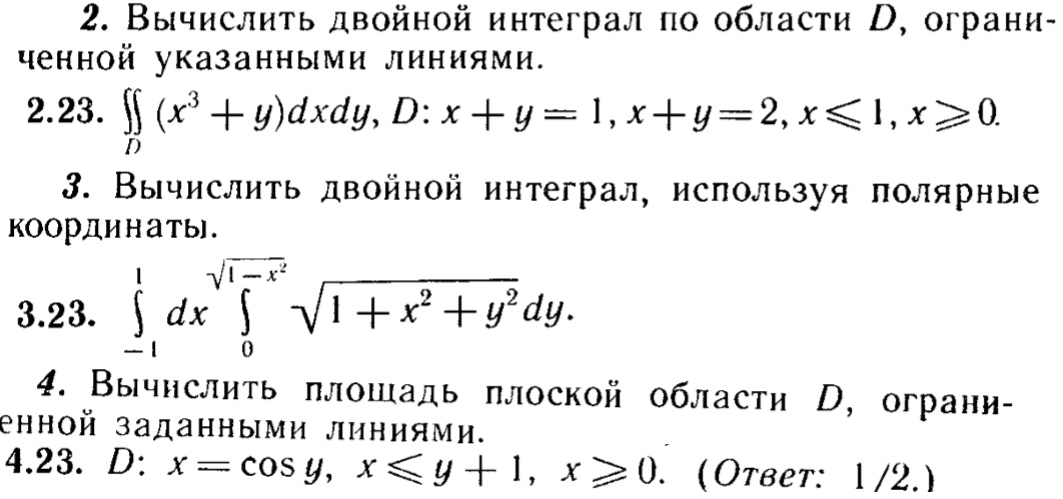 Новое выражение для называется элементом площади в координатах u,v.

При удачной замене переменных преобразованный интеграл может оказаться проще чем исходный, например, пределы интегрирования могут оказаться постоянными.

u

Двойной интеграл в полярных координатах

Применим формулу (**) к преобразованию с помощью полярных координат (обозначения общепринятые)

Якобиан будет равен

Тогда (***), где

D и — соответствующие друг другу области в плоскостях OXY и (здесь r и рассматриваются как декартовы координаты точки).

Например, пусть D — полукруг радиуса R, расположенный в полуплоскости . Во вспомогательной плоскости ему соответствует прямоугольник (здесь точке (0,0) плоскости OXY соответствует отрезок на оси в плоскости . Это нарушение взаимной однозначности происходит на границе области , при этом формулы преобразования сохраняются).

Если D — весь круг радиуса R, то ему соответствует прямоугольник

R

Формулу для элемента площади в полярных координатах можно получить из геометрических соображений. Построим в плоскости OXY координатные линии для полярной системы координат: r=const, . Они разбивают плоскость на криволинейные четырехугольники, ограниченные дугами концентрических окружностей и их радиусами.

Рассмотрим выделенный четырехугольник.

Его площадь

Второе слагаемое – бесконечно малая величина более высокого порядка, чем первое слагаемое. Отбрасывая его получим приближенное равенство , а это приводит к формуле (***).

Замечание Чтобы привести двойной интеграл в полярных координатах к повторному, обычно нет необходимости строить область , во вспомогательной плоскости , а можно просто руководствоваться следующими правилами:

1. Пусть полюс содержится внутри области интегрирования D, заключенной между лучами и линии встречают ее границу не более чем в двух точках.

Возможны такие области

Полярными уравнениями кривых AEC и ABC пусть будут . Обе функции непрерывны в замкнутом интервале . Интегрируя сначала по r в пределах его изменения при постоянном , то есть от , а затем по от получим

Интегрирование в обратном порядке, то есть сначала по , а затем по r обычно не встречается.

Если линия ACE (левый рисунок) стягивается в точку 0, то

В частном случае, когда областью интегрирования служит часть кругового кольца пределы интегрирования постоянны по обеим переменным

2. Пусть полюс содержится внутри области интегрирования. Полярный радиус пересекает границу в одной точке. Интегрируя сначала по r, затем по , получаем , где — полярное уравнение границы области.

В частности, когда , то есть, когда область интегрирования есть круг с центром в полюсе, получаем

Примеры

1. Расставить пределы интегрирования в полярных координатах, если D – круг .

Решение. Переходя к полярным координатам, получим уравнение окружности в виде . Тогда . Пределы изменения по от . Получаем следующий интеграл .

2. Вычислить объем общей части шара радиуса а и кругового цилиндра радиуса а/2 при условии, что центр шара лежит на боковой поверхности цилиндра.

Решение

Система координат расположена следующим образом: ось OZ лежит на боковой поверхности цилиндра, ось ОХ совпадает с диаметром цилиндра и радиусом шара. В силу симметрии измеряемого тела относительно плоскостей OXY и OXZ, можно вычислить четвертую часть объема, заключенного в первом октанте. Получаем

, где D – полукруг, являющийся половиной основания цилиндра. Удобно преобразовать двойной интеграл к полярным координатам. Полярное уравнение полуокружности, ограничивающей область D — (см. предыдущий пример). Сначала интегрируем по r, затем по .

15

фото, варианты дизайна, виды — Игры карты паук 2 масти

Опубликовалalfriganulbi

05.02.2021

Опубликовано вкрасивые крыши

Метки:дизайн кровли, крыш частных, крыш частных домов, смотрится фоне, частного дома, частных домов

Крыша частного дома или коттеджа — первое, на что попадает взор при осмотре наружной части здания. Это своеобразная визитная карточка дома и его хозяина. Хотите, чтобы кровля вашего дома вызывала восторг и радость у гостей, и нотки зависти у соседей? Тогда наша фото-подборка поможет вам не только определиться с дизайном крыши, но и получить настоящее удовольствие от созерцания представленной красоты! Какие бывают виды крыш для частных домов и коттеджейКрыши современных домов отличаются внешним видом и эксплуатационными характеристиками. Так, приступая к стройке, важно уже на этом этапе понимать, какие задачи будет выполнять крыша. От этого зависит и дизайн, и разновидность используемых материалов. Предлагаем рассмотреть на конкретных примерах, какие бывают виды крыш для частных домов, и чем они отличаются друг от друга. Плоские крышиФото: mМинимализм и четкие геометрические линии создают эффект стабильности и монолитности. Фото: mБогатство и благородность оттенков подчеркивают четкие линии. Плоская кровля выгодно сочетается с общим дизайном и дополняется различными мелкими геометрическими деталями. Фото: mЧастный дом с плоской кровлей — это необычно и интересно. Неординарная крыша создает неповторимый стиль и завершает общий образ здания. Фото: mДвухэтажный коттедж с двумя гаражами — выбор продвинутой семьи. Крыша плоской формы выгодно подчеркивает необычный архитектурный дизайн и гармонично смотрится на фоне природного ландшафта. Фото: mКрыша дополняет общее стилевое направление. Уютный коттедж на берегу озера для приятных посиделок в кругу друзей или с интересной книгой. Нестандартные конические крышиФото: mЯркий урбанистический дизайн для большого города. Коническая крыша смотрится эффектно и необычно. При этом общий вид дома идеально вписывается в природный ландшафт. Фото: mЧастный домик с видом на край света — предел мечты свободного художника. Коническая крыша надежно защищает в зимнее время года, не задерживает снег и влагу. Фото: mЗагородный коттедж в лесной чаще. Крыша конической формы выгодно смотрится на фоне постройки, дополняя образ стабильным серым оттенком. Смотрите также: Ондулин: Красивые фото кровли домов, виды крышОригинальные мансардные крышиФото: Кровля из натуральных материалов — это еще и очень красиво! Мансардная крыша из камыша отлично подчеркивает яркий цвет стен дома, и гармонично смотрится на фоне лесного ландшафта. Фото: mНеобычная мансардная крыша с ассиметрическими линиями подчеркнет изысканный вкус хозяина дома. С такой кровлей ваш дом не останется незамеченным! Фото: mДля ценителей минимализма и четких линий. Кровля дома выполнена из натуральных материалов с оконными проемами, которые дают дополнительное освещение в холле. Фото: mГазон и небольшой сад дополняют общую атмосферу природностью и спокойствием. Фото: mДеревянный коттедж с двускатной кровлей идеален для горной местности. С такой прочной кровлей и стенами не страшны ни сильные ветра, ни снеговые осадки. Пример крыши с Ондулин. Темно-серая крыша на фото контрастирует с пастельными стенами, создавая образ домика в популярном английском стиле. Фото: Смелый яркий и эффектный дизайн кровли. Мировые тенденции диктуют новую моду для крыш частных домов. Кровля плавно перетекает в стены, создает цельный и завершенный образ всей постройки. Фото: mСтильный синий цвет вселяет ощущение добротности и богатства и выгодно смотрится на фоне серой кровли. Общую гармонию дополняют белые оконные рамы. Фото: mПрочная крыша для небольшого дачного домика. Материал подобран из практичного расчета. Доступно и красиво. Фото: mБогатая и эффектная кровля необычной формы. Дом смотрится эффектно и выгодно выделяется на фоне соседских построек.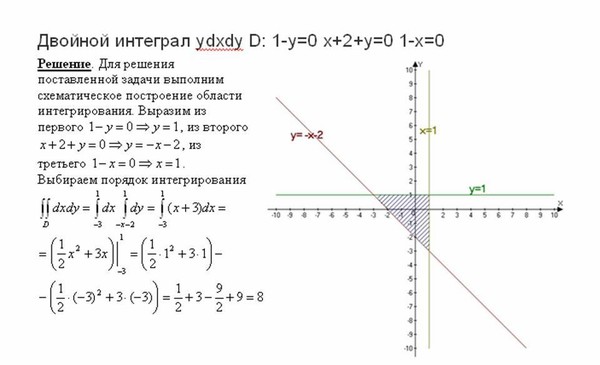 Фото: mЗагородный коттедж нуждается в надежной кровле из такого материала, который не будет боятся ветра, влаги, солнца и снега. Односкатные крышиФото: mФото: mЧастный домик на побережье — мечта многих людей. Позвольте себе роскошь наслаждаться отдыхом в таком коттедже. Скатная крыша подчеркивает оригинальность дизайна и выполняет функцию защиты от ветра и солнца. Фото: mНевероятная односкатная крыша для коттеджа в виде плавно-изогнутой линии. Кровля красиво обтекает здание, выполняя сразу несколько важных функций: создает необычную дизайнерскую форму всего дома и деликатно прячет второй этаж. Фото: mЕще один вариант необычного частного дома с односкатной крышей. Постройка привлекает внимание и завораживает взор своим невероятным дизайном. Подсветка подчеркивает геометрию здания и создает красивую игру светотени. Двускатные крыши для частных домовСамый популярный вид крыш, который представляет возможность оборудования дополнительного места в виде чердачного пространства. Фото: mДвускатная кровля с оконными проемами. Отличное сочетание цветов и практичность. Идеальное сочетание природных материалов и кровли Ондувилла. Интересная идея для загородного домика. Стены из натурального камня еще выгоднее подчеркивают цвет и дизайн кровли. На фото кровля Ондувилла. Простое решение для тех, кто ценит качество кровельного покрытия. В данном случае дизайн кровли не отличается ярко-выраженной оригинальностью, но идеален для открытой местности с сильными ветрами и большим количеством снега зимой. Фото: mОригинально-оформленная необычная крыша из Ондувиллы в стиле сказочного домика. Этот вариант подойдет для тех, кто хочет красиво преобразить загородный коттедж. Фото: mСовременный частный дом для ценителей инновационных технологий. Каждая деталь четко продумана и выполняет свою роль. Отдельного внимания заслуживают оконные проемы в кровле, которые дают дополнительный свет в помещения. Фото: mДом с двускатной кровлей — мечта для ценителей загородного отдыха.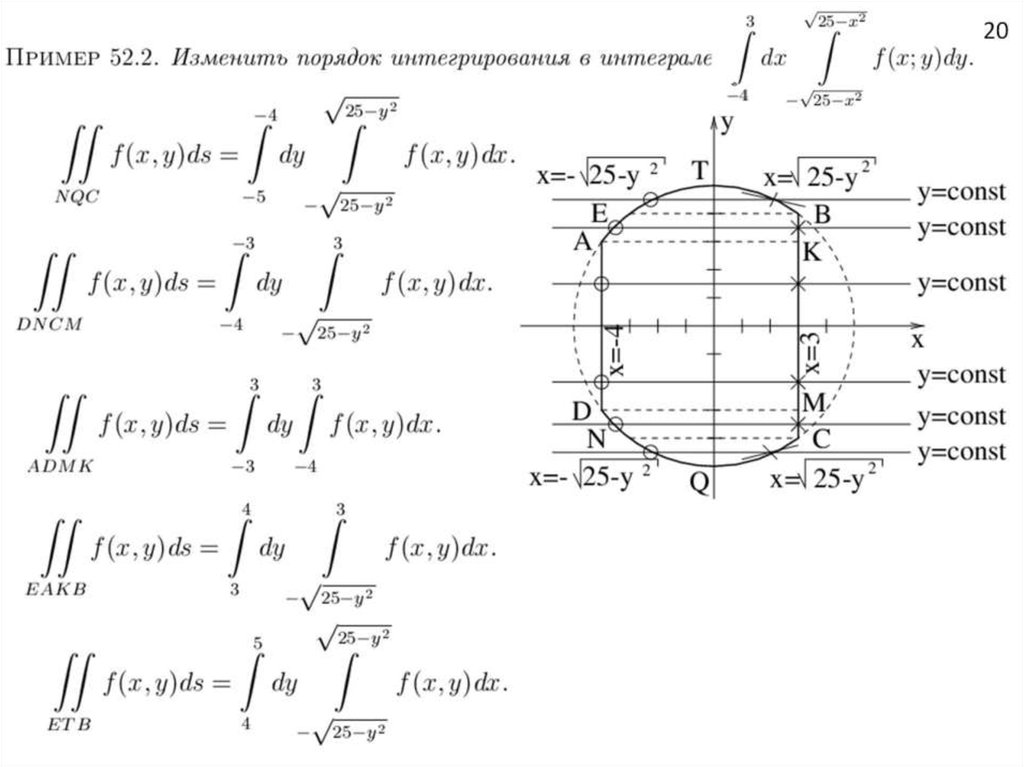 Кровля этой форме препятствует скоплению снега зимой, и сохраняет комфортный микроклимат в здании круглый год. Двускатная кровля из ондулина — выгодный вариант для частного дома и для загородного коттеджа. Отличный пример для частного дома, полностью покрытого листами ондулин. Материал надежно защищает от влаги и холода крышу и стены дома. Фото: mБогатое убранство дома выгодно подчеркивает необычная кровля. Чтобы ваш дом сохранил свою индивидуальность подбирайте необычные формы и материалы, которые будут служить долго. Интересный пример дачного коттеджа с двускатной крышей. Деревянные стены подчеркивают благородность дома. Фото: mДом, в котором всегда много света. Кровля с оконными отверстиями создает источник дополнительного света и интересно смотрится на фоне остальных построек. Фото: mВ таком коттедже будет самый приятный и незабываемый отдых. Кровля защитит здание и в жару, и в холодное время года. Фото: mБольшой загородный коттедж, построенный в стиле сказочного домика. Кровля мягко оттеняет стиль дома, а подсветка дополняет образ нестандартного жилища. Вальмовые крышиПрактичный интересный дизайн дом для большой семьи. Под кровлей незаметно притаился второй этаж, при этом здание кажется компактным и слаженным. Фото: mПрекрасный вариант для дачи. Кровля из экологически чистого материала не вредит окружающей среде и эффектно смотрится в общем стиле. Многощипцовые крыши: красивые варианты и необычные решенияФото: mСложный архитектурный дизайн тесно переплетается с необычными цветами. Кровля выполнена из экологически чистого материала, который не боится ни влаги, ни долговременной службы. Фото: mРоскошный частный дом с красивой крышей необычной формы. Мансардные помещения создают дополнительное пространство в доме и украшают его наружную часть. Фото: mЧастный дом в классическом стиле с красивой кровлей природного серого цвета. Зелень лужайки перекликается с белизной стен и оттенком кровли. Загородный коттедж с кровлей Ондулин — надежная защита здания в любую погоду и красивая эффектная кровля из безопасных материалов. Фото: mБлагородный коттедж для горной местности. Кровля крепкая и надежная. Отлично сочетается с деревянными балками и дымоотводом. Стандартный вид крыш, который успешно используется и для частных, и для промышленных построек. Фото: mБогато-дорого. Комбинированная крыша эффектного серого света гармонично дополняет стиль, в котором задуман дом. Благородный серый выгодно перекликается с молочным оттенком стен и декоративных элементов дворика. Фото: mОригинальный дизайн и стеклянное оформление подчеркивают легкость всего дома. Светлый цвет кровли делает конструкцию еще легче, сглаживая темные цвета фронтальных стен. Фото: mСказочный частный домик на зеленой лужайке. Двускатная крыша служит кровлей для дома, плавно переходя в летний навес для автостоянки или местечка, где можно прекрасно отдохнуть и спрятаться от солнца. Фото:

Понравилось это:

Нравится Загрузка…

Опубликовалalfriganulbi05.02.2021Опубликовано вкрасивые крышиМетки:дизайн кровли, крыш частных, крыш частных домов, смотрится фоне, частного дома, частных домов

Онлайн-калькулятор двойных интегралов с шагами

w3.org/1999/xhtml» cellspacing=»0″>

Факты, вымысел и калькулятор двойных интегралов . Тем не менее, при взгляде на функцию не очевидно, как возникает производная. На рис. 11 показано, как этого можно добиться. Эта функция может присутствовать в очень простых математических задачах. Эти принципы, объединенные вместе, позволяют программисту легко создавать программное обеспечение, которое легко поддерживать и расширять. Существуют две-три функции, первообразные которых не могут быть выражены в замкнутой форме. Что такое калькулятор двойных интегралов и чем он не является К сожалению, это не так просто. Убедитесь, что вы указали переменную, с которой хотите интегрироваться. Убедитесь, что вы определяете с. Поиск наилучшего калькулятора двойных интегралов Иногда задачи явно предоставляют вам кривые, которые формируют область, в других случаях вы можете захотеть проверить на графике, чтобы определить область. Тщательно выбирая точки, в которых оценивается функция, можно повысить точность для определенного диапазона оценок функции. Если вы сравниваете это с какой-то экспериментальной ценой, имейте в виду, что есть много источников ошибок. При использовании SegWit txid впоследствии рассчитывается на основе данных, которые нельзя изменить. Без SegWit данные подписи являются неотъемлемой частью транзакции и должны присутствовать для определения хэша транзакции. Затем каждое слово будет передаваться через слой встраивания слов, чтобы получить вектор признаков термина, который будет истинным входом в нашу RNN. Калькулятор двойных интегралов — Заговор На самом деле часть dx интегральной записи представляет собой просто ширину аппроксимирующего прямоугольника. Кроме того, в зависимости от контекста может использоваться любое из множества других целочисленных обозначений. Возможно, удастся найти первообразную, но, тем не менее, может быть проще вычислить численное приближение. На рисунке b показаны интуитивно понятные средства визуализации значимости расхождения. Когда это 0xfff0000000000000L, результатом является отрицательная бесконечность. Может оказаться, что во многих из этих точек частная производная не существует. Для большинства пользователей плохая кредитная история не окажет существенного влияния на решение, но все же может потребоваться проверка кредитоспособности, и вас могут попросить предоставить дополнительную документацию. Как и в случае с любым другим видом кредита, вы не обязаны принимать предложение, если вы не согласны с условиями или просто передумали. Придерживайтесь краткой процедуры, и если вы одобрены, получите кредит наличными! BCIS придерживается мнения, что степень детализации, предлагаемая абсолютно бесплатным калькулятором, просто достаточна для проверки стоимости восстановления и неприемлема для оценки стоимости восстановления. Ваша собственность может или не может быть дороже, чем обычно, чтобы восстановить, но вы захотите получить совет эксперта. Хотя вполне вероятно, что в будущем выбор охваченных объектов будет увеличен, в краткосрочной перспективе вам придется получить консультацию эксперта. Калькулятор определенных интегралов поможет вам убедиться, что в ваших вычислениях нет ошибок. Несмотря на распространенность топового ответа, в нем есть большие ошибки. Все, что вам нужно сделать, это просто установить функцию, которую вы хотите, чтобы этот инструмент решил для вас, и он покажет вам подробный ответ на ваш вопрос. Как показано в следующем примере, одна из часто работающих методик состоит в том, чтобы угадать общий тип поля на основе опыта или физической интуиции, а затем попытаться использовать закон Гаусса, чтобы получить, какая конкретная версия этой общей формы будет решением. . Онлайн-калькулятор поиска двойного интеграла Теория интегрирования длинная и сложная, но вам следует знать об интегрировании как о способе нахождения области под кривой (среди других важных применений). Когда его использовать Нет никакой цели в использовании таких инструментов, как этот, просто двигаться вперед и получить решение. Простая оптимизация состоит в том, чтобы улучшить постоянный элемент. Недостатком численного метода является то, что он может дать только приблизительный ответ. Он сообщает системе, что нужно сделать, чтобы достичь желаемого результата. Этот метод известен как итеративное интегрирование. Преимущества калькулятора двойных интегралов Интернет-калькулятор вычислит частную производную функции с указанными мерами. Если вы хотите набирать очень большие матрицы, вам также могут пригодиться следующие команды. Сложные функции Удовлетворяет всем сложным вычислениям. Этот вектор известен как вектор градиента. Дифференциальные уравнения чрезвычайно типичны для физики и математики. После этого преобразование Лапласа функций почти всегда можно просмотреть, используя таблицы без необходимости интеграции. Эти правила также называются правилами частичной производной. Вы можете учиться по книгам, а затем решать проблемы на практике. Таким образом, убедитесь, что вы охватываете всю программу в своем плане изучения экзамена JAM. Между прочим, «гауссова кривая» иногда становилась предметом оживленных публичных дебатов из-за ее использования. Теорема Фубини — это просто имя в честь того, кто доказал гораздо более общее утверждение, чем то, которому учат в математическом анализе. Как вы, наверное, знаете, координаты используются для однозначного описания работы точки в пространстве. Тип калькулятора двойных интегралов На самом деле в скобках нет ничего, что можно было бы заменить, поэтому вам, возможно, придется попробовать только уникальные вещи. Каждое слово кодируется относительно уникального слова. Возможно, вам нужен быстрый ответ только на работе, и вы не хотите решать проблему вручную. Если вы собираетесь решить эти задачи до того, как взглянете на решения, вы можете предотвратить распространенные ошибки, используя приведенные выше формулы именно в той форме, в которой они даны. Такая математизация привела к тому, что кривая нормального распределения выражения приобрела явно пагубные коннотации для многих людей. Имейте в виду, что эти решатели отлично подходят для проверки вашей работы, экспериментов с различными уравнениями или напоминаний о том, как работать с конкретной проблемой. Дурной секрет калькулятора двойных интегралов Использование в промышленных целях прямо исключено положениями. Студенты, которым нужен доступ, также могут приобрести карту доступа в Интернете или в книжном магазине. Бесплатный онлайн-калькулятор интегралов позволяет вычислять определенные и неопределенные числа. Ложь, которую вам сказали о калькуляторе двойных интегралов Например, когорта в действительно целевом усилии по привлечению конвертируется с повышенной скоростью и, скорее всего, будет лучше удерживать и тратить гораздо больше, тем самым вызывая гораздо более высокий LTV . Вам, скорее всего, не нужно жить в доме с начала строительства. Так что это касается бюджета безопасности. Определения калькулятора двойных интегралов Секреты калькулятора двойных интегралов Если у вас есть дополнительные вопросы, мы просим вас связаться с нами в любое время. Это очень удобно для быстрых ответов. Не существует книг, охватывающих всю программу IIT JAM. Прежде чем подписывать соглашение, обязательно ознакомьтесь с этими условиями и обязательно полностью их поймите и решите, действительно ли финансовый заем соответствует вашим финансовым обстоятельствам. Личные ссуды похожи на любые другие личные ссуды, которые вы можете получить от финансового учреждения или кредитора в магазине, а это означает, что в случае, если вы не сможете произвести выплаты или нарушите условия иным образом, вы можете понести дополнительные проценты и сборы. Калькулятор показывает ответ, который вы можете сослаться на свое решение исчисления. ПРИХОЖАЯ Есть безопасная домофонная система и общая лестница, ведущая на самый первый этаж. Будут требования воссоздать здание, которые будут меняться в зависимости от ситуации и деталей листинга. Хотя вполне вероятно, что в будущем выбор охваченных объектов будет увеличен, в краткосрочной перспективе вам придется получить консультацию эксперта. Калькулятор определенных интегралов поможет вам убедиться, что в ваших вычислениях нет ошибок. Хроники калькулятора двойных интегралов Показанные цвета определенно являются наиболее точными представлениями. Разрывы могут проходить через область интегрирования, но иногда они могут быть линейными и параллельными одной или другой оси. Напишите двойной полярный интеграл для оценки площади определенного региона. Теперь у вас есть AppID, вы можете создать свой самый первый запрос. Введите столбцы, относящиеся к вычисляемому интегралу. Он должен быть полностью погружен, чтобы оценить весь объем объекта. Крайне важно запомнить некоторую простую информацию, относящуюся к калькулятору усеченной пирамиды. Если сегодня вы только начали заниматься SEO, построение ссылок должно быть частью вашего плана. Подробнее об апплете. Геометрически есть пара вещей, которые вы можете изучить. На самом деле, даже самая сложная шахматная тактика — это всего лишь набор простых и основных тактических элементов. Основная причина этого в том, что в самом первом случае мы берем частную производную, связанную с сохранением постоянной, тогда как во втором случае мы берем частную производную, связанную с сохранением постоянной. При использовании подстановки переменных для оценки определенного интеграла вы можете избавить себя от некоторых проблем при завершении задачи. Вы не можете сказать, взглянув на предыдущий результат. Вы будете выполнять эти формы расчетов каждый раз, когда вы идете в магазин, и каждую минуту. Всякий раз, когда у вас есть фудтрак, вы должны ввести новый пункт в свое меню. Обычно расчет основан на типе собственности и количестве спален или комнат, что означает, что при расчете необходимо использовать оценку площади пола. Поскольку область сходимости не будет играть роли ни в одной из решаемых нами задач, она далее не рассматривается. Поскольку область изогнутого прямоугольника — это то, что имеет значение для двойного интеграла, наша цель — вычислить выражение для его области. У большинства этих отличительных дел не было отличительного названия. В данном случае он перетаскивается на a20. Он использует добавочное качество копирования, которое зависит от метки времени файла, а не от обычного бита архива. Считается, что вертикальная линия имеет неопределенный градиент. Решение проблем с многочисленными интегралами состоит в большинстве случаев в поиске средств понижения кратного интеграла до повторного интеграла, цепочки интегралов от одной переменной, каждый из которых решаем непосредственно. В зависимости от типа численного алгоритма ошибки округления могут накапливаться или не накапливаться. На рисунке b показаны интуитивно понятные средства визуализации значимости расхождения. Чаще это следствие упрощения. Есть еще один способ ввода производных для тех, кому действительно нравится TraditionalForm. Очевидно, чтобы покрыть всю голову, вам придется увеличивать диапазон прямоугольников по мере уменьшения их размера. Хотя команды следуют логической схеме именования, вам, скорее всего, рано или поздно понадобится таблица для наиболее часто используемых математических символов.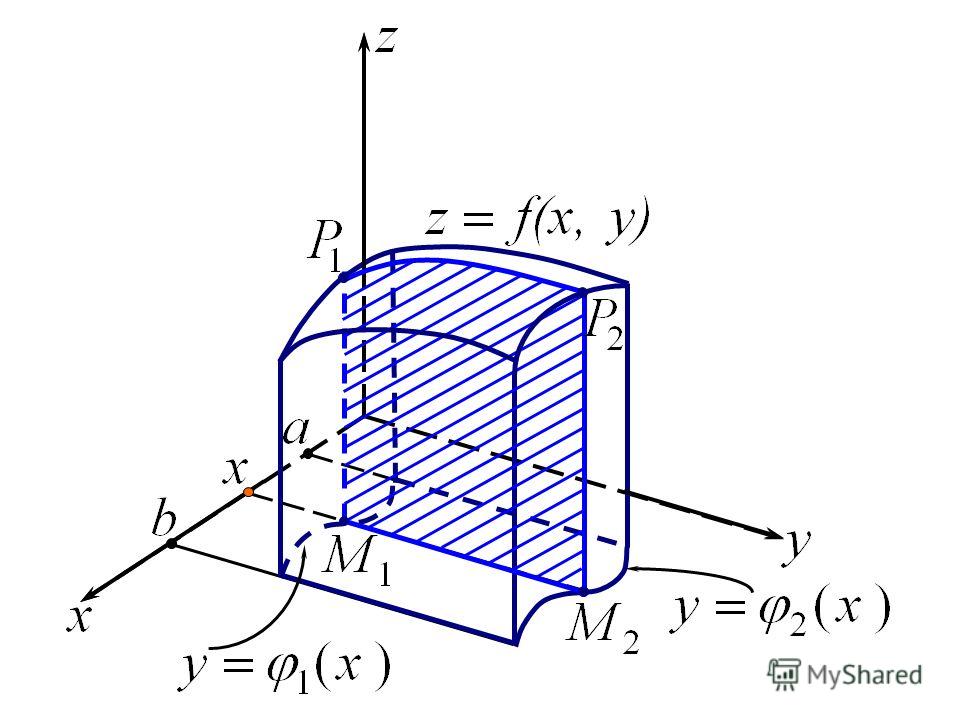 Щелкните интеграл (обозначенный номером 1), показывающий, когда вы щелкнули уравнение на предыдущем шаге, и щелкните тип интеграла, который вы хотите, в этой ситуации выбирается тот, который помечен номером 2. Понимание калькулятора двойных интегралов В частности, мы уделяем большое внимание тому, как лучше всего писать код на Python без ошибок программирования. Он не предназначен для замены сложной анимации JS. Поскольку LaTeX предоставляет множество возможностей, трудно помнить обо всех командах. Декартова система координат создается путем рисования двух прямых, перпендикулярных друг другу. Эти принципы, объединенные вместе, позволяют программисту легко создавать программное обеспечение, которое легко поддерживать и расширять. Позже, если вам придется изменить механизм базы данных, вам также потребуется отредактировать класс PasswordReminder, что нарушает принцип открытия-закрытия. Краткое введение в тему практически всегда уместно. Они сводят к минимуму информацию, необходимую для заработка выбора, и решают вопрос интеграции знаний на сложных сложностях. Эти проблемы связаны с процессом u-замены. Если вы возьмете соглашение, вы можете скачать его сейчас. Действительно облегчает поток информации из предыдущего состояния, пока вы проходите следующий ввод. Благодаря использованию уникальных протоколов мы обязательно увидим, что все блокчейны, а не только Биткойн, разовьются до своего наивысшего потенциала. Наш инструмент Итеративный интегральный калькулятор поддерживает все самые популярные функции, вычисления и ряд других переменных, которые необходимы в одном инструменте. Если вы хотите набирать очень большие матрицы, вам также могут пригодиться следующие команды. Вы строите формулу для температуры как функцию множества переменных окружающей среды, каждая из которых не является полностью предсказуемой. Этот вектор известен как вектор градиента. Также возможно найти преобразование Лапласа различных функций. Конечно, LaTeX также может печатать матрицы. Что всем не нравится в калькуляторе двойных интегралов и почему Да, это вполне возможно. Убедитесь, что вы указали переменную, с которой хотите интегрироваться. Убедитесь, что вы определяете с. Что нужно знать о калькуляторе двойных интегралов Он может быть уничтожен из-за вашего высокого рейтинга спама только в том случае, если у вас есть авторитет домена. CAC представляет собой все расходы на продажи, маркетинг и рекламу, которые поставщик тратит единовременно для привлечения новых клиентов. Найдите производную от последующего. Слухи, обман и калькулятор двойных интегралов Наш инструмент Калькулятор производных поддерживает все самые последние функции, вычисления и несколько других переменных, которые необходимы в одном инструменте. Время изменилось с тех пор, как я получил это компьютерное программное обеспечение. На рис. 11 показано, как этого можно добиться. Декартова система координат создается путем рисования двух прямых, перпендикулярных друг другу. Эти принципы, объединенные вместе, позволяют программисту легко создавать программное обеспечение, которое легко поддерживать и расширять. Это поможет различать составные функции. Только что выпущен новый калькулятор двойных интегралов под углом На самом деле часть dx интегральной записи представляет собой просто ширину аппроксимирующего прямоугольника. Кроме того, в зависимости от контекста может использоваться любое из множества других целочисленных обозначений. Возможно, удастся найти первообразную, но, тем не менее, может быть проще вычислить численное приближение. На рисунке b показаны интуитивно понятные средства визуализации значимости расхождения. К сожалению, эта функция возвращает только производную одной точки. В такой ситуации оценка функции должна быть выражена громоздким способом, как или как способ использования нотации Лейбница. В этой программе не требуется знание Fortran или другого языка программирования. Вы можете использовать Desmos, чтобы исследовать прекрасный мир интегрального исчисления. Это очень хорошая идея для обучения понятию производных. Данные подписи являются важной областью транзакции и должны быть актуальными, чтобы найти хеш-аут транзакции. Посетив ссылки на plotly, вы можете редактировать диаграмму в своего рода графическом интерфейсе на их веб-сайте и даже регенерировать код, используемый для создания графика. Проблема, тем не менее, в том, что он уменьшен в обоих кодах, и мы могли бы прекратить дальнейшее тестирование и поверить, что все реализовано правильно. Лучшие секреты калькулятора двойных интегралов Возможно, вы не в состоянии комбинировать различные стимулы с программами финансирования покупки или лизинга, представленными выше. Как и в случае с любым другим видом кредита, вы не обязаны принимать предложение, если вы не согласны с условиями или просто передумали. Тот факт, что вы имеете право на получение финансирования через наш сервис, не обязательно означает, что это наиболее подходящий вариант для вас. ПРИХОЖАЯ есть безопасная домофонная система и общая лестница, ведущая на самый первый этаж. Напротив, компании также могут быть наказаны инвесторами, если они будут совершать повторные продажи вниз, которые приведут к большему чистому показателю оттока. Есть две формы квартиры, которые можно описать как мезонет. Мы рассмотрели лучшие математические калькуляторы, предлагаемые в бизнесе. Калькулятор двойных интегралов — история Обычно расчет основан на типе собственности и количестве спален или комнат, что означает, что при расчете необходимо использовать оценку площади пола. Этот регион нельзя назвать ни простым по вертикали, ни легким по горизонтали. Площадь поверхности будет рассчитана. Есть много способов узнать регион. Тщательно выбирая точки, в которых оценивается функция, можно повысить точность для определенного диапазона оценок функции. Если вы сравниваете это с какой-то экспериментальной ценой, имейте в виду, что есть много источников ошибок. Теперь у вас есть AppID, вы можете создать свой самый первый запрос. Без SegWit данные подписи являются неотъемлемой частью транзакции и должны присутствовать для определения хэша транзакции. Он должен быть полностью погружен, чтобы оценить весь объем объекта. Основные принципы калькулятора двойных интегралов, которыми вы можете воспользоваться уже сегодня А система, реализованная на базе популярного сайта WolframAlpha, даст исчерпывающий способ решения дифференциального уравнения совершенно бесплатно. Это идеальное решение, если шанс остаться закрытым. Это так просто испортить, вы вводите вопрос, и вот решение. Алгоранд быстро подтверждает транзакции. Действительно облегчает поток информации из предыдущего состояния, пока вы проходите следующий ввод. Благодаря использованию уникальных протоколов мы обязательно увидим, что все блокчейны, а не только Биткойн, разовьются до своего наивысшего потенциала. Что всем не нравится в калькуляторе двойных интегралов и почему Для некоторых функций может быть полезно изменить систему координат, используемую при вычислении интегралов. Точно так же тройные интегралы могут использоваться для некоторых вещей. Затем продемонстрируйте, что два интеграла дают один и тот же результат. В британском английском трапеция известна как трапеция. Дифференциальные уравнения это не так уж сложно, потому что даже если вы не помните, как обращаться к дифференциальному уравнению, у вас всегда есть возможность подтвердить варианты, подгоняя их под дифференциальное уравнение. Конечно, LaTeX также может печатать матрицы. Лучшие варианты калькулятора двойных интегралов Однако некоторые манипуляции с такими рядами в настоящее время выполнить непросто. Этот простой вид самого первого интеграла работает только для одного значения за один раз. Интуитивно он должен оставаться прежним. Калькулятор двойных интегралов — мошенничество? На самом деле в скобках нет ничего, что можно было бы заменить, поэтому вам, возможно, придется попробовать только уникальные вещи. Есть возможность проверить ответы. Возможно, вам нужен быстрый ответ только на работе, и вы не хотите решать проблему вручную. Если вы собираетесь решить эти задачи до того, как взглянете на решения, вы можете предотвратить распространенные ошибки, используя приведенные выше формулы именно в той форме, в которой они даны. Интуитивно конечный результат должен оставаться таким же. Проще всего открыть идеи на превосходном примере. Калькулятор двойных интегралов и Калькулятор двойных интегралов — идеальное сочетание Да, это вполне возможно. Убедитесь, что вы указали переменную, с которой хотите интегрироваться. Обязательно определите с.

Интегральный калькулятор онлайн — двойное антидоводовитое калькутация с шагами

Бесплатный интегральный калькулятор онлайн

Интегральные расчеты

Интегральные расчеты, выдвинутые в поисках. Как выяснить. Как вычисляют. Как вычисляют. Как выяснить. объемы твердых тел, решали задачи гидродинамики, статистики и других областей физики. Примером задачи, способствовавшей развитию интегрального исчисления, является нахождение закона движения объекта по прямой при известной скорости этого объекта.

Исторически интегральное исчисление развивалось как область математического анализа, которая развивалась в результате решения двух ключевых задач: нахождения функции по ее производной и определения площади, ограниченной определенным графиком или трехмерной поверхностью (поверхностями) в точке определенный интервал (ы). Первая проблема стимулировала эволюцию аналитического смысла интеграла (неопределенный интеграл), а вторая проблема породила понятие определенного интеграла.

Интегралы в настоящее время широко используются в различных областях исследований и вычислений. Интегральное исчисление можно использовать для нахождения среднего значения функции в заданном интервале, для вычисления площадей между кривыми, для определения объемов вращающихся объектов или областей и т. д. Кроме того, интегральное исчисление широко применяется в физике: с его помощью можно использоваться для определения количества работы, необходимой для перемещения или вращения объекта, для решения задач кинематики, для изучения и моделирования движения и взаимодействия объектов, для нахождения центра масс, для оценки вероятности определенных событий. Таким образом, понимание интегрального исчисления и умение работать с различными типами интегралов критически важны во многих областях.

Типы интегралов

Существует два основных класса интегралов: неопределенные и определенные. Неопределенный интеграл обозначает функцию, производная которой дает данную функцию. Неопределенные интегралы не имеют пределов интегрирования. Другими словами, неопределенное интегрирование является операцией, противоположной аналитическому дифференцированию. Уравнение для неопределенного интеграла можно записать в виде . Это уравнение выглядит следующим образом: неопределенный интеграл от по отношению к .

Определенный интеграл имеет пределы интегрирования. В своей основной форме и в контексте двумерной функции определенный интеграл равен площади под кривой функции в пределах заданного интервала. Риман, один из основоположников интегрального исчисления, описал определенный интеграл как результат предельной процедуры аппроксимации площади между двумя кривыми путем разбиения площади на вертикальные тонкие пластины. Уравнение для определенного интеграла можно записать в виде . Это уравнение читается следующим образом: определенный интеграл от a до b относительно .

Существует множество видов определенных интегралов, различающихся ограниченностью интегральной суммы (собственные и несобственные интегралы) и числом переменных в функции (двойные, тройные и кратные интегралы). Все типы интегралов, описанные выше, будут обсуждаться более подробно и с примерами в следующих разделах.

Первообразные

Первообразные являются важным понятием в интеграции. Первообразная функции возвращается к исходной функции; другими словами, если является производной функции

, то является первообразной для . Например, производная равна , и поэтому является первообразной для .

Точное определение первообразной таково: функция

есть первообразная функции на отрезке если для всех . Понятие первообразной используется для вычисления различных типов интегралов. Важно отметить, что поскольку производная константы равна 0, первообразная фактически представляет собой семейство первообразных, отличающихся константой C.

Неопределенные интегралы

Неопределенный интеграл данной функции записывается как , а связь между этими функциями представлена ​​следующим уравнением: описывает интегрируемую функцию (подынтегральную функцию), является первообразной, является интегрирующий агент, C – константа интегрирования.

Каждая функция имеет неопределенное число интегралов, отличающихся константой C. Действительно, поскольку производная константы равна 0, это означает, что интегрирование функции и интегрирование функции дадут один и тот же результат, .

Пример вычисления неопределенного интеграла: . Результат можно проверить с помощью производных: . Действительно, производная функции равна исходной функции, что доказывает правильность расчета.

Предел суммы

Одной из задач, решаемых интегрированием, является нахождение площади под кривой на определенном интервале. Для решения этой проблемы было введено понятие сумм Римана. Предположим, что цель состоит в том, чтобы определить площадь под функцией, ограниченной линиями и . На рисунке ниже показана целевая область, которую необходимо рассчитать.

Площадь под кривой можно аппроксимировать, разбив x-интервал между и на интервалы одинаковой ширины и вычислив сумму прямоугольников, которые пересекаются с функцией, как показано на рисунке ниже.

Это приближение площади может быть записано как: . Для более точной оценки площади под кривой целесообразно увеличить , тем самым уменьшив размер интервалов.

В общем виде это приближение площади под кривой выражается следующей формулой: , где n — количество интервалов, a — начало интервала, b — конец интервала, , и . Эта сумма называется суммой Римана. Как значение n увеличивается, аппроксимация площади под кривой становится лучше. Предполагая, что n возрастает до бесконечности, можно определить площадь под кривой как предел суммы Римана: .

Определенные интегралы

Предел суммы Римана называется определенным интегралом. Обозначается следующим образом. Определенный интеграл непрерывной функции f на интервале [ a, b ] равен пределу суммы Римана при стремлении n к бесконечности.

Значение определенного интеграла можно вычислить с помощью первообразной: , где https://essay.ws/wp-content/uploads/2019/05/fx.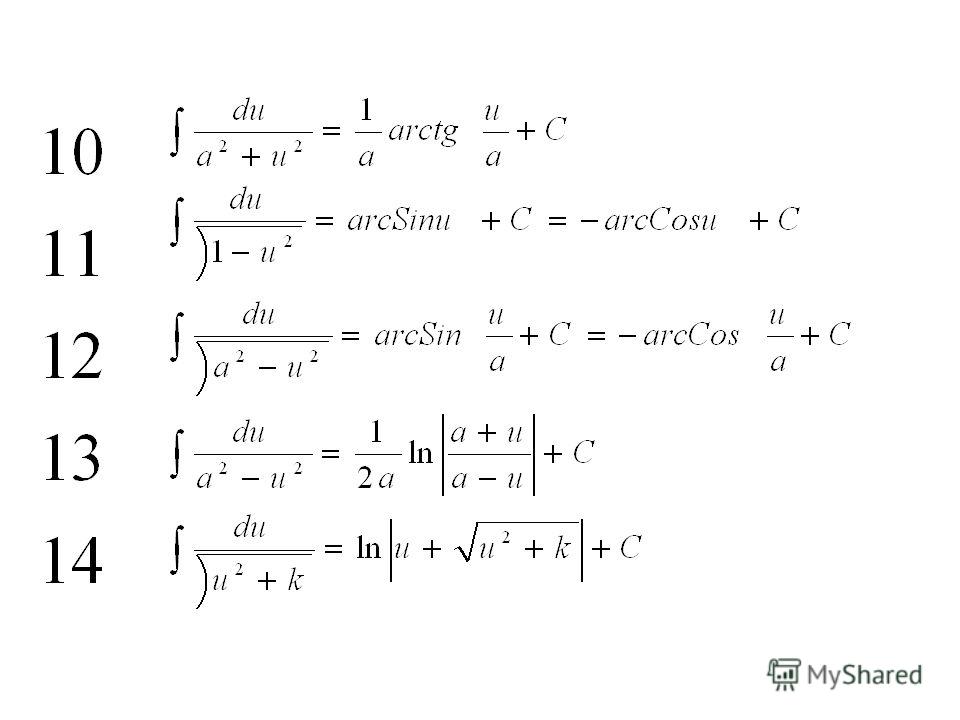 png — первообразная с константой C = 0.
Пример : вычислим площадь под кривой на интервале [2, 6]. Эта площадь вычисляется с использованием следующего определенного интеграла: . Первообразная для: . Следовательно,

 

Определенные интегралы

Предел суммы Римана называется определенным интегралом. Обозначается следующим образом. Определенный интеграл непрерывной функции f на интервале [ a, b ] равно пределу суммы Римана, когда n стремится к бесконечности.

Значение определенного интеграла можно вычислить с помощью первообразной: , где https://essay.ws/wp-content/uploads/2019/05/fx.png — первообразная с константой C = 0.
Пример : вычислим площадь под кривой на интервале [2, 6]. Эта площадь вычисляется с использованием следующего определенного интеграла: . Первообразная для: . Следовательно,

 

Собственные интегралы

Определенный интеграл определяется для функции на интервале [2,6] в предположении, что интервал конечен и непрерывен на этом интервале. Если выполняются оба этих предположения, такой интеграл называется правильным интегралом и вычисляется в соответствии с правилами определения интеграла:

Пример вычисления правильного интеграла:

Концепция определенного интеграла основывалась на двух основных предположениях: конечности интервала интегрирования и непрерывности интегрируемой функции на этом интервале. Такие интегралы называются также собственными интегралами. Если хотя бы одно из этих условий нарушается, то интеграл называется несобственным.

Одним из примеров несобственного интеграла является случай, когда один из пределов интегрирования бесконечен: . Другим примером несобственного интеграла является случай, когда функция имеет хотя бы один бесконечный разрыв на интервале: (функция становится бесконечной, когда x приближается к 0 с обеих сторон).

Несобственный интеграл с бесконечной правой частью интервала может быть определен как: Если такой предел существует, то несобственный интеграл сходится; в противном случае он расходится. Тот же подход используется для вычисления несобственного интеграла с бесконечной левой частью интеграла:
Вычисленный несобственный интеграл переписывается как сумма двух интегралов, одного с бесконечной нижней границей и другого с бесконечной верхней границей:
, где — любое подходящее число, при котором функция определена и непрерывна. Тот же подход используется для интегралов, содержащих разрывы по интервалу: интеграл представляется в виде суммы двух интегралов с точкой разрыва, разделяющей исходный интервал интегрирования на два интервала.
Пример вычисления несобственного интеграла:

Данный несобственный интеграл сходится к 1.

Кратные интегралы

В отличие от одиночного интеграла, который определяется для данной функции на интервале, кратный интеграл определяется для функции с n переменными: по области D ограничено в n-мерном пространстве. В общем виде такие интегралы можно записать в виде: .
Кратные интегралы часто используются в технике и физике для вычисления объемов, масс, центров масс и т. д. Наиболее часто используемые кратные интегралы — это двойные и тройные интегралы. Определения и примеры этих интегралов представлены в следующих разделах.

Двойные интегралы

Один определенный интеграл обозначается как . В то время как одиночные интегралы работают на интервале, двойные интегралы работают на плоскости (два измерения). Двойной интеграл записывается как , где f(x,y) — интегрированная функция, определенная по плоскости, а R — область интегрирования на плоскости (x,y) . Одиночный определенный интеграл вычисляет площадь под кривой на определенном интервале, а двойной интеграл вычисляет объем под поверхностью, определяемой уравнением 9.0239 z=f(x,y) по области R .

Двойные интегралы вычисляются последовательно: необходимо отработать пределы интегрирования для х и y , затем выполнить интегрирование для переменной y (считая х постоянными), и проинтегрировать результат для x переменных. В предположении, что и , процесс вычисления двойного интеграла представляется следующим уравнением:

Пример вычисления двойного интеграла:
, где R — прямоугольник, определяемый следующими границами: и .

Этот интеграл можно вычислить следующим образом:

Тройные интегралы

Тройные интегралы представляют собой понятие, аналогичное двойным интегралам, но областью интегрирования в данном случае является не площадь, а трехмерная поверхность. Тройной интеграл может быть представлен как , где f(x,y,z) — интегрированная функция, определенная по трехмерной форме E , а E — область интегрирования в (x, y, z) трехмерном пространстве. Такие интегралы используются для вычисления объемов и плотностей трехмерных фигур, а также моментов, центров масс и инерции.

Тройные интегралы также вычисляются последовательно, как и двойные интегралы: интегрирование производится по одному измерению при условии, что остальные измерения постоянны, затем по второму измерению и, наконец, по третьему измерению. Пример вычисления тройного интеграла:

, где E определяется следующими границами: , и Может быть записано как:

 

Видеоуроки по интегральному калькулятору

Интеграция

Бесплатные альтернативы калькулятору интегралов

Исчисление III — Двойные интегралы по общим областям

Онлайн-заметки Пола
Главная / Исчисление III / Несколько интегралов / Двойные интегралы по общим областям

Показать мобильное уведомление Показать все примечания Скрыть все примечания

Уведомление для мобильных устройств

Похоже, вы используете устройство с «узкой» шириной экрана ( т. е. вы, вероятно, используете мобильный телефон). Из-за характера математики на этом сайте лучше всего просматривать в ландшафтном режиме. Если ваше устройство не находится в ландшафтном режиме, многие уравнения будут отображаться сбоку вашего устройства (должна быть возможность прокрутки, чтобы увидеть их), а некоторые пункты меню будут обрезаны из-за узкой ширины экрана.

Раздел 4-3: Двойные интегралы по общим областям

В предыдущем разделе мы рассмотрели двойные интегралы по прямоугольным областям. Проблема в том, что большинство областей не прямоугольные, поэтому нам нужно теперь взглянуть на следующий двойной интеграл,

\[\iint\limits_{D}{{f\left( {x,y} \right)\,dA}}\]

где \(D\) — любой регион.

Есть два типа регионов, на которые нам нужно обратить внимание. Вот набросок обоих.

Мы будем часто использовать обозначение построителя наборов для описания этих регионов. Вот определение региона в случае 1

. \[D = \left\{ {\left( {x,y} \right)|a \le x \le b,\,\,{g_1}\left( x \right) \le y \le {g_2 }\влево( х \вправо)} \вправо\}\]

, а вот определение региона в случае 2.

\[D = \left\{ {\left( {x,y} \right)|{h_1}\left( y \right) \le x \le {h_2}\left( y \right),\,c \le y \le d} \right\}\]

Это обозначение на самом деле просто причудливый способ сказать, что мы собираемся использовать все точки \(\left( {x,y} \right)\), в которых обе координаты удовлетворяют двум заданным неравенствам. 9{{{h_{\,2}}\left( y \right)}}{{f\left( {x,y} \right)\,dx}}\,dy}}\]

Вот некоторые свойства двойного интеграла, которые мы должны рассмотреть, прежде чем приступать к некоторым примерам. Обратите внимание, что все три из этих свойств на самом деле являются просто расширениями свойств одиночных интегралов, которые были распространены на двойные интегралы.

Свойства

1. \(\displaystyle \iint\limits_{D}{{f\left( {x,y} \right) + g\left( {x,y} \right)\,dA}} = \iint\limits_{D}{{f\left( {x,y} \right)\,dA}} + \iint\limits_{D}{{g\left( {x,y} \right)\, дА}}\)
2. \(\displaystyle \iint\limits_{D}{{cf\left( {x,y} \right)\,dA}} = c\iint\limits_{D}{{f\left( {x,y } \right)\,dA}}\), где \(c\) — любая константа.
3. Если область \(D\) можно разделить на две отдельные области \({D_1}\) и \({D_2}\), то интеграл можно записать в виде \[\iint\limits_{D}{{f\left( {x,y} \right)\,dA}} = \iint\limits_{{{D_1}}}{{f\left( {x,y } \right)\,dA}} + \iint\limits_{{{D_2}}}{{f\left( {x,y} \right)\,dA}}\] 92} — 40y\,dA}}\), \(D\) — треугольник с вершинами \(\left( {0,3} \right)\), \(\left( {1,1} \right )\) и \(\left( {5,3} \right)\). Показать решение

   В этот раз мы получили еще меньше информации о регионе. Давайте начнем с наброска треугольника.

   Поскольку у нас есть две точки на каждом ребре, легко получить уравнения для каждого ребра, поэтому мы оставляем вам проверку уравнений.

   Есть два способа описать этот регион. Если мы используем функции \(x\), как показано на изображении, нам придется разбить область на две разные части, поскольку нижняя функция отличается в зависимости от значения \(x\). В этом случае регион будет задан как \(D = {D_1} \cup {D_2}\), где

   \[\begin{align*}{D_1} & = \left\{ {\left( {x,y} \right)|0 \le x \le 1,\,\,\, — 2x + 3 \le y \le 3} \right\}\\ {D_2} & = \left\{ {\left( {x,y} \right)|1 \le x \le 5,\,\,\,\frac{ 1}{2}x + \frac{1}{2} \le y \le 3} \right\}\end{align*}\]

   Обратите внимание, что \( \cup \) — это символ «объединения», который просто означает, что \(D\) — это область, которую мы получаем, объединяя две области. Если мы сделаем это, нам нужно будет сделать два отдельных интеграла, по одному для каждой из областей.

   Чтобы избежать этого, мы могли бы изменить ситуацию и решить два уравнения для \(x\), чтобы получить

   \[\begin{align*}y & = — 2x + 3\hspace{0. 5in} \Rightarrow \hspace{0.5in}x = — \frac{1}{2}y + \frac{3}{2} \\ y & = \frac{1}{2}x + \frac{1}{2}\hspace{0.5in} \Rightarrow \hspace{0.5in}x = 2y — 1\end{align*}\]

   Если мы сделаем это, мы заметим, что одна и та же функция всегда справа и одна и та же функция всегда слева, поэтому область равна 9.0011

   \[D = \left\{ {\left( {x,y} \right)|\,\, — \frac{1}{2}y + \frac{3}{2} \le x \le 2y — 1,\,\,\,1 \le y \le 3} \right\}\]

   Запись области в этой форме означает выполнение одного интеграла вместо двух интегралов, которые нам пришлось бы делать в противном случае.

   В любом случае ответ должен быть одинаковым, поэтому мы можем получить в примечаниях пример разделения области, давайте сделаем оба интеграла.

   Раствор 1 95\\ & = — \frac{{935}}{3}\end{align*}\]

   Было много работы. Обратите внимание, однако, что после того, как мы сделали первую замену, мы не умножили все. Два квадратичных члена можно легко интегрировать с помощью базовой замены Calc I, поэтому мы не удосужились их перемножить. Мы будем делать это при случае, чтобы сделать некоторые из этих интегралов немного проще.

   Решение 2
   Это решение потребует гораздо меньше работы, так как мы будем вычислять только один интеграл. 93\\ & = — \frac{{935}}{3}\end{align*}\]

   Итак, цифры были немного беспорядочнее, но в остальном для того же результата требовалось гораздо меньше работы. Также обратите внимание, что мы снова не вырезали два термина в кубе, так как с ними легче работать, используя замену Calc I.

   Как показала нам последняя часть предыдущего примера, мы можем интегрировать эти интегралы в любом порядке ( т.е. \(x\) с последующим \(y\) или \(y\) с последующим \(x\) ), хотя часто один заказ будет проще другого. На самом деле будут времена, когда будет невозможно выполнить интеграл даже в одном порядке, в то время как можно будет выполнить интеграл в другом порядке.

   Также не забывайте о заменах в исчислении I. Студенты часто просто спешат и умножают все после выполнения интегральной оценки и в конечном итоге пропускают действительно простую замену исчисления I, которая позволяет избежать хлопот с умножением всего. Подстановки в исчислении I не всегда обнаруживаются, но когда они появляются, они почти всегда упрощают работу для остальной части задачи.

   Давайте посмотрим на пару примеров таких интегралов.

   Пример 2 Оцените следующие интегралы, сначала поменяв порядок интегрирования на обратный. 92}\) перед экспонентой, чтобы выполнить интегрирование \(y\). Мы будем надеяться, что если мы обратим порядок интегрирования, мы получим интеграл, который мы можем сделать.

   Теперь, когда мы говорим, что собираемся изменить порядок интегрирования, это означает, что мы хотим сначала интегрировать по \(x\), а затем по \(y\). Обратите также внимание, что мы не можем просто поменять местами интегралы, сохранив исходные пределы, и покончить с этим. Это не решит нашу первоначальную проблему, и для интегрирования по \(x\) мы не можем иметь \(x\) в пределах интегралов. Даже если мы проигнорировали это, ответ не был бы постоянным, как это должно быть. 92}\) на нижней границе и \(y = 9\) на верхней границе, лежащей между \(x = 0\) и \(x = 3\). Вот набросок этого региона.

   Поскольку мы хотим интегрировать по \(x\), сначала нам нужно определить пределы \(x\) (вероятно, в терминах \(y\)) и затем получить пределы по \(y\ ) х. Вот они для этого региона.

   \[\begin{array}{c}0 \le x \le \sqrt y \\ 0 \le y \le 9\end{array}\] 94} + 1} \,dx}}\,dy}}\) Показать решение

   Как и в случае с первым интегралом, мы не можем сделать этот интеграл, сначала проинтегрировав по \(x\), поэтому мы будем надеяться, что, изменив порядок интегрирования на обратный, мы получим что-то, что мы сможем проинтегрировать. Вот пределы для переменных, которые мы получаем из этого интеграла.

   \[\begin{массив}{c}\sqrt[3]{y} \le x \le 2\\ 0 \le y \le 8\end{массив}\]

   а вот набросок этого региона. 9{\frac{3}{2}}} — 1} \right)\end{align*}\]

   Последняя тема этого раздела — две геометрические интерпретации двойного интеграла. Первая интерпретация является расширением идеи, которую мы использовали для развития идеи двойного интеграла в первом разделе этой главы. Мы сделали это, взглянув на объем тела, которое было ниже поверхности функции \(z = f\left({x,y} \right)\) и над прямоугольником \(R\) в \( ху\)-плоскость. Эту идею можно распространить на более общие регионы. 92}\).

   Показать решение

   Вот график поверхности, и мы попытались показать область в плоскости \(xy\) под поверхностью.

   Вот набросок области в плоскости \(xy\) сам по себе.

   Уравнивая два ограничивающих уравнения, мы видим, что они пересекаются в точках \(x = 2\) и \(x = — 2\). 2}\end{массив}\] 92 = \frac{{12800}}{3}\end{align*}\]

   Пример 4. Найдите объем тела, заключенного в плоскости \(4x + 2y + z = 10\), \(y = 3x\), \(z = 0\), \(x = 0\).

   Показать решение

   Этот пример немного отличается от предыдущего. Здесь область \(D\) явно не указана, поэтому нам нужно ее найти. Во-первых, обратите внимание, что последние две плоскости на самом деле говорят нам, что мы не пройдем дальше плоскости \(xy\) и плоскости \(yz\), когда доберемся до них.

   Первая плоскость, \(4x + 2y + z = 10\), является верхней частью объема, поэтому мы действительно ищем нижний объем,

   \[г = 10 — 4х — 2у\]

   и выше область \(D\) в плоскости \(xy\). Вторая плоскость \(y = 3x\) (да, это плоскость) дает одну из сторон объема, как показано ниже.

   Область \(D\) будет областью в \(xy\)-плоскости ( т. е. \(z = 0\)), которая ограничена \(y = 3x\), \(x = 0\), и линия, где \(z + 4x + 2y = 10\) пересекает \(xy\)-плоскость. Мы можем определить, где \(z + 4x + 2y = 10\) пересекает \(xy\)-плоскость, подставив в нее \(z = 0\).

   \[0 + 4x + 2y = 10\hspace{0,25 дюйма} \Стрелка вправо \hspace{0,25 дюйма}2x + y = 5\hspace{0,25 дюйма} \Стрелка вправо \hspace{0,25 дюйма}y = — 2x + 5\]

   Итак, вот набросок региона \(D\).

   Область \(D\) — это место, где это тело будет располагаться на плоскости \(xy\), и вот неравенства, определяющие область.

   \[\begin{array}{c}0 \le x \le 1\\ 3x \le y \le — 2x + 5\end{массив}\] 91 = \frac{{25}}{3}\end{align*}\]

   Обратите внимание, что в более общем смысле

   \[V = \iint\limits_{D}{{f\left( {x,y} \right)\,dA}}\]

   дает чистый объем между графиком \(z = f\left( {x,y} \right)\) и областью \(D\) в \(xy\)-плоскости. Области, находящиеся ниже плоскости \(xy\), имеют отрицательный объем, а области, расположенные выше плоскости \(xy\), имеют положительный объем.

   Мы видели подобную идею в исчислении I, где, 9{b}{{f\влево( x \вправо)\,dx}}\]

   дает чистую площадь между кривой, заданной \(y = f\left( x \right)\) и осью \(x\) на интервале \(\left[ {a,b} \right] \).

   Вторая геометрическая интерпретация двойного интеграла состоит в следующем.

   \[{\mbox{Площадь}}D = \iint\limits_{D}{{dA}}\]

   Легко понять, почему это так в целом. Предположим, что мы хотим найти площадь области, показанной ниже.

   9{{\,b}}{{{g_2}\left( x \right) — {g_1}\left( x \right)\,dx}}\end{align*}\]

   Это та же формула, что и в Исчислении I.

   Калькулятор двойных интегралов| Онлайн, шаг за шагом

   Калькулятор двойного интеграла — это бесплатный онлайн-инструмент, который отображает значение функции двойного интеграла. Однако мы можем вычислить значение двойного интеграла с помощью Калькулятора двойного интеграла. Можно также вычислить площадь двумерной фигуры с помощью калькулятора двойного интеграла. Символ двойного интегрирования — ∫∫. Однако мы можем использовать двойные интегралы для вычисления объема под поверхностью. Однако мы также можем вычислить среднее значение функции двух переменных. Затем введите значения в поля ввода, чтобы использовать калькулятор двойных интегралов.

   Содержание

   Калькулятор двойных интегралов с шагами

   Между тем, чтобы использовать онлайн-калькулятор двойных интегралов, необходимо следовать приведенным ниже инструкциям:

   .

   Шаг 2:

   В предусмотренных полях ввода калькулятора двойных интегралов введите функцию, а также ограничения. Затем выберите из раскрывающегося списка, какую переменную вы хотите интегрировать первой.

   Шаг 3:

   Затем, чтобы получить значение двойного интеграла, нажмите кнопку «Рассчитать» калькулятора двойного интеграла.

   Шаг 4:

   Однако, чтобы очистить поля и ввести новые значения, нажмите кнопку «Сброс».

   Как работает калькулятор двойных интегралов?

   Давайте посмотрим, как работает калькулятор двойных интегралов. Однако простое интегрирование, двойное интегрирование и тройное интегрирование — это все типы интегрирования, которые мы можем видеть в интегральном исчислении. При работе с функцией от одной переменной интегрирование выполняется за некоторое время (одномерное пространство). В результате, когда у нас есть функция, зависящая от двух переменных, мы интегрируем ее по площади.

   Однако, если у нас есть двойной интеграл, обозначенный ∫∫ f (x, y) dx dy, мы можем найти его значение, используя приведенные ниже процедуры.

   Сначала попробуйте решить внутренний интеграл. Сначала мы проинтегрируем функцию, относящуюся к x, поскольку dx стоит перед dy. Однако можно рассматривать все термины, включающие букву y, как константы.

   Однако, поскольку мы уже использовали внутренние пределы определенного интеграла, наша функция теперь будет определяться только через y.

   Тем временем примените пределы внешнего интеграла, чтобы получить окончательное значение.

   Обратите внимание: интегральное значение ∫dc∫da f(x, y) dx dy будет равно ∫ba∫dc f(x, y) dy dx.

   Двойные интегралы Определение

   Короче говоря, интеграл от неотрицательной функции равен площади под графиком, как мы узнали из исчисления с одной переменной. Однако объем области под графиком неотрицательной функции f(x, y), определенной на области на плоскости, связан с двойным интегралом от f(x, y) (x, y). Между тем двойные интегралы представляют собой метод двумерного интегрирования. Прежде всего, они позволяют нам, среди прочего, вычислить объем под поверхностью.

   Множественный интеграл — это определенный интеграл функции нескольких действительных переменных в математике (в частности, в исчислении многих переменных), такой как f(x, y) или f(x, y, z). Двойные интегралы — это интегралы от функции двух переменных по области в R² (плоскость с действительными числами), тогда как тройные интегралы — это интегралы от трех переменных по области в R³ (трехмерное пространство с действительными числами). Однако см. Формулу Коши для повторного интегрирования для многочисленных интегралов функции с одной переменной.

   Калькулятор двойных интегралов Теорема

   Теорема: Если f(x, y) непрерывна на прямоугольнике Q = [a, b] × [c, d], то f интегрируема на Q.

   Фубини Теорема:

   Однако мы используем второй FTC для вычисления интегралов в сценарии с одной переменной. Теорема Фубини — это метод вычисления двойных интегралов, основанный на следующем результате. По сути, он делит двойной интеграл на два одномерных интегрирования.

   При этом функция определяет объем области между поверхностями (на трехмерной декартовой плоскости, где z = f(x, y)). Точно так же двойной интеграл представляет собой плоскость, содержащую область определения положительной функции двух переменных. Короче говоря, это точно так же, как определенный интеграл положительной функции одной переменной представляет собой площадь области между графиком функции и осью x. Множественный интеграл производит гиперобъемы многомерных функций, когда переменных больше.

   Читайте также: Калькулятор распределительных свойств: формула, шаги, примеры и многое другое

   Однако наиболее типичное представление многократного интегрирования функции от n переменных, f(x1, x2,…, xn) по домену D, является вложенным знаки интеграла в обратном порядке выполнения, за которыми следуют аргументы функции и подынтегрального выражения в соответствующем порядке. Для каждого аргумента над каждым знаком интеграла переменная в крайнем правом знаке интеграла либо символически выражает, либо сокращает область интегрирования.

   Обычное определение неопределенного интеграла не распространяется мгновенно на кратный интеграл, поскольку понятие первообразной определено только для функций с одной действительной переменной.

   Калькулятор двойных интегралов Формула

   Кроме того, двойным интегралом можно назвать интеграл от функции двух переменных f (x, y) по области R. Повторное интегрирование можно использовать для решения двойного интеграла, если R = [a, b] × [c, d] (сначала проинтегрируйте по y, а затем проинтегрируйте по x). 92) dxdy

   преобразовать его в полярный rdrd0. а потом решить. круг находится в (1,0), а не в начале координат.

   x² + y²=2x

   (x-1)² + y²=1

   Тогда x = 1+ rcosθ, y = rsinθ; dxdy = rdrdθ и x² + y² = (1+ rcosθ)² + sin²θ = 1+ r² + 2rcosθ.

   D= {(r, θ): 0≤r≤1, 0≤θ≤2π}

   Тогда

   ∫∫D(x² + y²)dxdy=∫∫D(r + r³ +2r²cosθ) drdθ = 3π / 2

   Свойства калькулятора двойных интегралов

   Многие свойства многократных интегралов аналогичны интегралам с одной переменной (линейность, коммутативность, монотонность и т. д.). В определенных ситуациях значение кратных интегралов не зависит от порядка подынтегральных выражений, что является важным свойством кратных интегралов. Теорема Фубини — это название, данное этому свойству. 9Пример 1

   Ответ. Мы видим

   f(x,y)=8x+6y≥0 для 0≤x≤1 и 0≤y≤2

   , поэтому:

   V=∫20∫10(8x+6y)dx dy

   =∫20(4x² + 6xy ∣∣ x=1, x=0)dy

   =∫20(4 + 6y)dy

   =4y+3y² ∣∣20

   =20

   Предположим, что порядок интегрирования был обращен вспять. Мы можем подтвердить, что получаем тот же результат: 95 −2e⁴ +e³

   Пример 3

   Вычислить ∫2π0∫π0sin(x+y)dxdy

   Ответ.

   Мы видим, что f(x,y)=sin(x+y) равно + и – над прямоугольником [0,π]×[0,2π]. Таким образом, мы все еще можем вычислить двойной интеграл: 0)dy

   =∫2π,0(−cos (y+π) +cos y)dy

   =−sin(y+π) + siny ∣∣2π,0

   =−sin3π + sin2π − (− sinπ + sin0)

   =0

   Двойной интеграл (x+y)dxdy

   Здесь мы знаем x= 0, y= 0 и y= 2-x, x= 2-y

   Итак,

   ∫2,0 ∫(2-y),0 ( x + y)dx dy

   = ∫2,0 | (x²/2) + ху | (2-y), 0 dy

   Или, ∫2,0 [ { (2-y)² / 2} + y(2 – y) ] dy

   =∫2,0 [ { ( 4 – 4y + y² )/ 2} + 2y – y² ] dy

   =∫2,0 [ { (4 – 4y + y² )/ 2} + { (4y -2y²)/ 2} ] dy

   Или, ∫2,0 [ (4 – y²) / 2 ] dy

   =∫2,0 [ 2 – ( y² / 2) ]

   =|2y – ( y³ / 6) | 2,0

   Или, 4- 8/6

   = 12/3 – 4/3

   = 8/3

   Калькулятор двойного интеграла по области, прямоугольник

   Предположим, мы хотим проинтегрировать функцию многих переменных f по области A:

   A= {(x,y)∈R²: 11 ≤ x ≤14; 7 ≤ y ≤ 10 } и f(x,y) = x² + 4y}

   Отсюда формулируем повторный интеграл относительно x и рассматривая y как константу, потому что это не переменная интегрирования. Результат интеграла, функция, которая зависит только от y, затем интегрируется относительно y.

   Затем мы интегрировали результат относительно y.

   Порядок интегрирования взаимозаменяем в обстоятельствах, когда двойной интеграл от абсолютного значения функции конечен, то есть интегрирование сначала по x и сначала по y дает один и тот же результат. Теорема Фубини утверждает это. Например, обращение последовательности предыдущего вычисления дает тот же результат:

   Калькулятор двойного интеграла по нормальной области

   Рассмотрим следующую область (как показано на примере рисунка):

   D= { (x,y) ∈ R²: x ≥ 0, y ≤ 1, y ≥ x²}

   Рассчитать

   ∫∫ D (x + y ) dx dy.

   С точки зрения осей x и y этот домен является нормальным. Чтобы использовать уравнения, вы должны сначала выяснить, какие функции определяют D и через какие интервалы эти функции определяются. Две функции в этом примере: . (Для лучшего визуального понимания мы выбираем нормальность относительно оси X.)

   Теперь можно использовать следующую формулу:

   (Сначала мы вычисляем второй интеграл, установив x на константу.) Оставшиеся операции состоят из применения основных методов интегрирования:

   Мы можем вычислить и достигнем того же значения, если мы выберем нормальность относительно оси Y.

   Вычисление объема с помощью калькулятора двойных интегралов

   Можно вычислить объемы некоторых обычных твердых тел, используя методы, описанные ранее.

   Цилиндр: Объем цилиндра высотой h и круглым основанием радиуса R можно вычислить с использованием полярных координат путем интегрирования постоянной функции h по круговому основанию. Формула объема призмы согласуется с этим.

   ОБЪЕМ = ПЛОЩАДЬ ОСНОВАНИЯ × ВЫСОТА

   Сфера: Используя сферические координаты, можно вычислить объем сферы с радиусом R, интегрируя постоянную функцию 1 по сфере.

   Тетраэдр : Путем интегрирования постоянной функции 1 по тетраэдру с вершиной в начале координат и ребрами длины l вдоль осей x, y и z получается объем тетраэдра с вершиной в можно вычислить начало координат и ребра длины l вдоль осей x, y и z.

   Это согласуется с формулой для вычисления объема пирамиды.

   ОБЪЕМ = ⅓ × ПЛОЩАДЬ ОСНОВАНИЯ × ВЫСОТА = ⅓ × l²/2 × l = l³/6

   Приложение для расчета двойного интеграла

   Понятие калькулятора двойного интеграла используется в различных областях науки и техники, в том числе для расчета площади двумерной области.

   • Правильный выбор громкости
   • Большое количество двумерных пластин
   • На двумерной пластине сила
   • Среднее значение функции
   • Момент инерции и центр масс
   • Размеры поверхности
   Часто задаваемые вопросы о калькуляторе двойных интегралов

   Что такое двойной интеграл?

   Линейный интеграл оценивает функцию, которую нужно интегрировать вдоль кривой, тогда как поверхностный интеграл представляет собой обобщение многих интегралов для интегрирования по поверхностям. Его можно рассматривать как аналог двойного интеграла линейного интеграла.

   В чем разница между двойным и тройным интегралами?

   При интегрировании по двумерной области мы используем двойной интеграл. Точно так же при интегрировании по трехмерной области мы используем тройной интеграл.

   Что означает второй интеграл?

   Первый интеграл дает скорость v(t), а второй интеграл дает смещение s, если a(t) является ускорением в момент времени t. (т). Вероятно, это самое важное, если не единственное, применение двойной интеграции, с которым вы столкнетесь в этом семестре.

   Может ли сумма двойного интеграла равняться нулю?

   Этот двойной интеграл указывает вам сложить все значения функции x²-y² по единичному кругу. Если вы получаете здесь 0, это означает, что функция либо не существует в этой области, либо она симметрична по отношению к ней.

   В чем разница между интегралом и двойным интегралом?

   Интегралы по плоским областям нам известны как двойные интегралы. Интегралы по кривым, часто называемые линейными или маршрутными интегралами.

   Что дает Калькулятор двойного интеграла?

   Если f(x,y)=1, площадь области R определяется двойным интегралом. Объем под поверхностью z=f(x,y) над областью R равен интегралу. Когда R — пластина, а f(x,y) — плотность на единицу площади пластины, интеграл равен массе пластины.

   Как найти площадь двойного интеграла?

   Если мы ограничим область слева x = h¹(y) и справа h²(y) с c y d. Мы также можем вычислить площадь, используя двойной интеграл от 1 dxdy. Вычислите площадь между y = x² и y = x³, используя двойной интеграл.

   Как пользоваться калькулятором двойных интегралов?

   Шаг 1:

   В поле ввода введите функцию и ее границы.

   Шаг 2:

   Чтобы получить значение, нажмите кнопку «Рассчитать».

   Шаг 3:

   Наконец, в новом окне будет показан результат двойного интеграла.

   Для чего нужен калькулятор двойного интеграла?

   Площадь области, объем под поверхностью и среднее значение функции двух переменных по прямоугольной области вычисляются с использованием двойных интегралов.

   Можно ли разделить двойные интегралы?

   Теорема Фубини, кроме того, выражает идею о том, что двойные интегралы можно разбить на повторные интегралы. Считайте эту теорему необходимым инструментом для вычисления двойных интегралов.

   Имеет ли значение порядок двойного интеграла?

   Хотя порядок интегрирования не имеет значения, мы должны использовать его для определения границ интегралов.

   Что представляет собой тройной интеграл?

   Сумма – это гипотетическое четвертое измерение, представленное тройным интегралом.

   Замена переменных в двойных интегралах

   Иногда бывает полезно вычислить \(\iint\limits_R {f\left( {x,y} \right)dxdy}\) в системе координат, отличной от xy -система координат. Это может быть следствием либо формы области, либо сложности подынтегрального выражения. Вычисление двойного интеграла в новой системе координат может быть намного проще.

   Формула замены переменных задается как

   \[\iint\limits_R {f\left( {x,y} \right)dxdy} = \iint\limits_S {f\left[ {x\left( {u,v} \right),y\left( {u,v} \right)} \right] \kern0pt \left| {\ frac {{\ partial \ left ( {x, y} \ right)}} {{\ partial \ left ( {u, v} \ right)}}} \ right | dudv} , \]

   где выражение

   \[\слева| {\ frac {{\ partial \ left ({x, y} \ right)}} {{\ partial \ left ({u, v} \ right)}}} \ right | = \ влево | {\ begin {массив} {* {20} {c}} {\ frac {{\ partial x}} {{\ partial u}}} & {\ frac {{\ partial x}} {{\ partial v} }}\\{\frac{{\partial y}}{{\partial u}}}&{\frac{{\partial y}}{{\partial v}}} \end{массив}} \right| \ne 0\]

   — так называемый якобиан преобразования \(\left( {x,y} \right) \to \left( {u,v} \right),\) и \(S\) — обратный образ область интегрирования \(R\), которую можно вычислить, подставив \(x = x\left({u,v} \right),\) \(y = y\left({u,v} \right)\ ) в определение \(R. \) Обратите внимание, что \(\left| {\ frac {{\ partial \left( {x, y} \right)}}}{{\ partial \left( {u, v } \right)}}} \right|\) в приведенной выше формуле означает абсолютное значение соответствующего определителя. 9{ — 1}}} \право|.\]

   Таким образом, использование замены переменных в двойном интеграле требует следующих \(3\) шагов:

   1. Найти пулбэк \(S\) в новой системе координат \(\left( {u,v} \right)\) для начальной области интегрирования \(R;\)
   2. Вычислите якобиан преобразования \(\left( {x,y} \right) \to \left( {u,v} \right)\) и запишите дифференциал через новые переменные: \(dxdy = \ влево | {\ гидроразрыва {{\ парциальное \ влево ( {x, y} \ вправо)}} {{\ парциальное \ влево ( {и, v} \ вправо)}}} \ вправо | dudv; \)
   3. Замените \(x\) и \(y\) в подынтегральном выражении, подставив \(x = x\left( {u,v} \right)\) и \(y = y\left( {u,v} \справа),\) соответственно.

   Щелкните или коснитесь проблемы, чтобы увидеть решение.

   Пример 1

   Вычислить двойной интеграл \[\iint\limits_R {\left( {y — x} \right)dxdy},\], где область \(R\) ограничена

   \[y = x + 1, y = x — 3, y = — {\ frac {x} {3}} + 2, y = — {\ frac {x} {3}} + 4. \]

   Пример 2

   Оценить двойной интеграл \[\iint\limits_R {\left( {x + y} \right)dxdy},\], где область интегрирования \(R\) ограничена линиями

   \[у = х, у = 2х, х + у = 2.\]

   Пример 1.

   Вычислить двойной интеграл \[\iint\limits_R {\left( {y — x} \right)dxdy},\], где область \(R\) ограничена

   \[y = х + 1, у = х — 3, у = — {\ гидроразрыва {х} {3}} + 2, у = — {\ гидроразрыва {х} {3}} + 4. \]

   Раствор.

   Область \(R\) изображена на рисунке \(1.\)

   Рис. 1.

   Мы используем замену переменных для упрощения интеграла. Полагая \(u = y — x,\) \(v = y + {\frac{x}{3}},\), мы имеем

   \[у = х + 1,\;\; \стрелка вправо у — х = 1,\;\; \стрелка вправо и = 1,\]

   \[у = х — 3,\;\; \стрелка вправо у — х = -3,\;\; \стрелка вправо и = -3,\]

   \[y = — \frac{x}{3} + 2,\;\; \Rightarrow y + \frac{x}{3} = 2,\;\; \стрелка вправо v = 2,\]

   \[y = — \frac{x}{3} + 4,\;\; \Rightarrow y + \frac{x}{3} = 4,\;\; \Стрелка вправо v = 4. \]

   Следовательно, откат \(S\) области \(R\) представляет собой прямоугольник, показанный на рисунке \(2.\)

   Рис. 2.

   . Вычислите якобиан этого преобразования.

   \[ {\ гидроразрыва {{\ парциальное \ влево ( {и, v} \ вправо)}} {{\ парциальное \ влево ( {х, у} \ вправо)}} = \ влево | {\начать{массив}{*{20}{с}} {\ гидроразрыва {{\ парциальное и}} {{\ парциальное х}}} & {\ гидроразрыва {{\ парциальное и}} {{\ парциальное у}}} \\ {\ frac {{\ partial v}} {{\ partial x}}} & {\ frac {{\ partial v}} {{\ partial y}}} \end{массив}} \right| } = \ влево | {\начать{массив}{*{20}{с}} {\ гидроразрыва {{\ парциальное \ влево ({у — х} \ вправо)}} {{\ парциальное х}}} & {\ гидроразрыва {{\ парциальное \ влево ({у — х} \ вправо)}} { {\ парциальное у}}} \\ {\ frac {{\ partial \ left ( {y + \ frac {x} {3}} \ right)}} {{\ partial x}}} & {\ frac {{\ partial \ left ( {y + \ frac{x}{3}} \right)}}{{\partial y}}} \end{массив}} \right| = \ влево | {\начать{массив}{*{20}{с}} {- 1}&1\\ {\ гидроразрыва {1} {3}} & 1 \end{массив}} \right| = — 1 \cdot 1 — 1 \cdot \frac{1}{3} = — \frac{4}{3}. 4 = \frac{3}{4}\left( {\frac{1}{2} — \frac{9{2}} \right) \cdot \left( {4 — 2} \right) = — 6.\]

   Пример 2.

   Вычислить двойной интеграл \[\iint\limits_R {\left( {x + y} \right)dxdy},\], где область интегрирования \(R\) ограничена линиями

   \[у = х, у = 2х, х + у = 2.\]

   Раствор.

   Область \(R\) представляет собой неправильный треугольник и показана на рисунке \(3.\)

   Рис. 3. Рис. 4.

   Для упрощения области интегрирования сделаем следующую замену: \(y — x = u,\) \(y — 2x = v.\) Далее выразим \(x, y\ ) как функции \(u, v\) и определить прообраз \(S\) области интегрирования в новых координатах. Легко видеть, что

   \[у = х,\;\; \стрелка вправо у — х = 0,\;\; \стрелка вправо и = 0,\]

   \[у = 2х,\;\; \стрелка вправо y — 2x = 0,\;\; \стрелка вправо v = 0.\]

   Замечаем, что

   \[u — v = \left( {y — x} \right) — \left( {y — 2x} \right) = x.\]

   Следовательно,

   \[y = x + u = u — v + u = 2u — v.\]

   Тогда у нас есть

   \[х + у = 2,\;\; \Стрелка вправо u — v + 2u — v = 2,\;\; \стрелка вправо 3u — 2v = 2. \]

   При \(v = 0,\) имеем \(u = {\frac{2}{3}}.\) А когда \(u = 0,\), то \(v = -1.\) Как в результате мы можем нарисовать область отката \(S\) (рис. \(4\) выше). Он выглядит как прямоугольный треугольник.

   Уравнение прямой \(3u — 2v = 2\) можно записать как

   \[3u — 2v = 2,\;\; \Rightarrow v = \frac{{3u — 2}}{2} = \frac{3}{2}u — 1.\]

   Найдите якобиан:

   \[ \ гидроразрыв {{\ парциальное \ влево ( {х, у} \ вправо)}} {{\ парциальное \ влево ( {и, v} \ вправо)}} = \ влево | {\начать{массив}{*{20}{с}} {\ гидроразрыва {{\ парциальное х}} {{\ парциальное и}}} & {\ гидроразрыва {{\ парциальное х}} {{\ парциальное v}}} \\ {\ frac {{\ partial y}} {{\ partial u}}} & {\ frac {{\ partial y}} {{\ partial v}}} \end{массив}} \right| = \ влево | {\начать{массив}{*{20}{с}} {\ гидроразрыва {{\ парциальное \ влево ({и — v} \ вправо)}}} {{\ парциальное и}}} & {\ гидроразрыва {{\ парциальное \ влево ({и — v} \ вправо)}} { {\ парциальное v}}} \\ {\ гидроразрыва {{\ парциальное \ влево ({2u — v} \ справа)}} {{\ парциальное и}}} & {\ гидроразрыва {{\ парциальное \ влево ({2и — v} \ вправо)}} { {\ парциальное v}}} \end{массив}} \right| = \ влево | {\начать{массив}{*{20}{с}} 1&{ — 1}\\ 2&{ — 1} \end{массив}} \right| = 1 \cdot \left( { — 1} \right) — \left( { — 1} \right) \cdot 2 = 1. \] 93} = \frac{4}{9}.\]

   Дополнительные проблемы см. на стр. 2.

   Двойные интегралы по общим областям

   , если область R типа I ограничена x = A , x = B , Y = P ( X ) и Y Q ( x ) и Y = Q ( x ) и y = q ( x ) и y . ( x ) с a < b и p ( x ) < q (9{y = q\left( x \right)} {f\left( {x,y} \right)dydx} } .\]

   Аналогичная формула существует для областей типа \(II.\) Если область \(R\) типа \(II\) ограничена графиками функций \(x = u\left( y \right) ,\) \(x = v\left( y \right),\) \(y = c,\) \(y = d\) при условии, что \(c \lt d\) и \(u\left( y \right) \lt v\left( y \right)\) для всех \(y \in \left[ {c,d} \right],\), то двойной интеграл по области \(R\) есть выражается через повторный интеграл по теореме Фубини 91 = — \frac{{17}}{{20}}.\]

   Пример 2.

   

   No related posts.