Синус онлайн калькулятор: Найти синус угла. Онлайн калькулятор

Содержание

Функция синуса: онлайн калькулятор, формулы, график

Тригонометрия – это раздел математики, изначально изучающий соотношения углов и сторон в прямоугольном треугольнике. Со временем тригонометрические функции расширились на числовую ось и вышли за переделы геометрии.

Из истории вопроса

Ученые полагают, что основы тригонометрии заложили древние астрономы. Еще в Древних государствах Египта, Вавилона и Китая встречались задачи на поиск углов и сторон прямоугольного треугольника. Именно тогда были введены градусы, минуты и секунды для характеристик величины углов, а также выведено знаменитое выражение, связывающее стороны прямоугольного треугольника. Позднее выражение a² + b² = c² получило название теоремы Пифагора в честь самосского математика, впервые доказавшего данное утверждение.

Систематизация разрозненных знаний и гипотез о свойствах прямоугольного треугольника произошла в Древней Греции, когда впервые были четко выделены основные тригонометрические определения. В книге «Начала» Евклида приведены первые теоремы о соотношениях углов и сторон в прямоугольном треугольнике, а также выведен словесный аналог теоремы косинусов. Тригонометрия планомерно развивалась даже во времена Средневековья, а современный вид этой науке придал знаменитый ученый Леонард Эйлер, который расширил влияние тригонометрических функций на другие разделы математики.

Определение синуса

Две стороны, образующие прямой угол треугольника, называются катетами. Обозначим их буквами a и b. Самая длинная сторона треугольника носит название гипотенузы и обозначается литерой c. Пусть у нас есть прямоугольный треугольник со сторонами a = 3, b = 4, c = 5, при этом гипотенуза и катет образуют некий угол cb. Мы можем найти соотношение катетов к гипотенузе, которые будут равны a/c = 3/5 или b/c= 4/5. Или соотношение катетов a/b = 3/4 и b/a = 4/3. На первый взгляд эти рациональные числа не дают нам ровно никакой информации.

Но попробуем увеличить стороны так, чтобы угол cb остался неизменным. Для этого нам потребуется подобный треугольник, но больше исходного. Пусть наш новый треугольник имеет стороны m = 9, n = 12 иk = 15. Это увеличенный в три раза треугольник, угол которого nk равен углу cb. Посмотрим на те же соотношения сторон, например, катета к гипотенузе m/k = 9/15 = 3/5 и n/k = 12/15 = 4/5. Удивительно, но при неизменном угле соотношения сторон прямоугольного треугольника совершенно не изменяются, а потому они заслужили собственные названия в пантеоне математических терминов.

Синус – это отношение противолежащего катета к гипотенузе. Противолежащему чему? Углу, для которого он рассчитывается. В этом кроется весь смысл тригонометрии. Как только мы изменим угол, все наши соотношения также изменятся. Неважно, какого размера катеты и гипотенузы при угле cb и равном ему nk, так как отношение сторон для него всегда будет фиксированным и равным 3/5. Это утверждение легко проверить на практике, вычисляя отношение сторон угла, равного приблизительно 37 градусов.

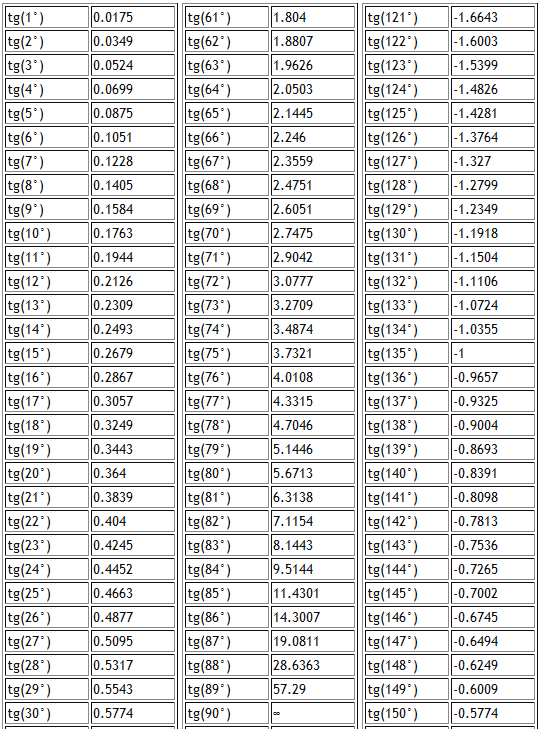
Угол – всему голова. Несмотря на то, что каждая тригонометрическая функция – это соотношение сторон, рассчитывает такое соотношение всегда и только для угла. Изменяется угол – изменяется и его синус. Для каждого целого градуса от 0 до 360 градусов известны значения соответствующих синусов, которые легко отыскать в известной четырехзначной таблице, созданной советским математиком Владимиром Брадисом. Можно не заморачиваться поиском значений в таблице и посчитать прямо на калькуляторе.

Применение функции

Прежде всего тригонометрические функции используются в геометрии для расчета углов или длин сторон. Например, мы знаем, что синус некоторого угла равен единице. Это важное значение, и его помнят школьники и студенты, которые сразу могут сказать, что синус, равный единице, имеет только прямой угол, равный 90 градусов. Однако синусы находят применение и в куда более интересных областях науки. Когда Леонард Эйлер расширил тригонометрию до алгебры, синусы появились в физике и механике. Волновые процессы – наиболее известная тема школьных уроков физики. Любое волновое движение описывается при помощи тригонометрических функций.

Представьте себе маятник, который пока еще находится в состоянии покоя, то есть в нулевой точке. Толчок приводит маятник в движение. Теперь мы легко можем описать это движение при помощи синусоидальной функции вида y = sinx. Однако наш маятник не может колебаться по идеальной синусоиде, у него наверняка есть амплитуда или размах колебаний, а также частота или скорость. Как это выразить математически?

Наша функция стартовала с нуля, поэтому мы можем записать y = 0 + sinx, что излишне, поэтому оставим y= sinx. Пусть маятник при движении делает 10 см то в одну сторону, то в другую. Это амплитуда, а значит наша функция преобразится в y = 10 sinx. Кроме того, маятник делает 20 шагов в обе стороны в минуту, следовательно, это частота, которая запишется как y = 10sin20x. При помощи такой простой функции мы описали движение маятника, но синусоидой легко описать любые волновые процессы.

Наша программа позволяет вычислять синусы углов или определять величину угла по известному синусу.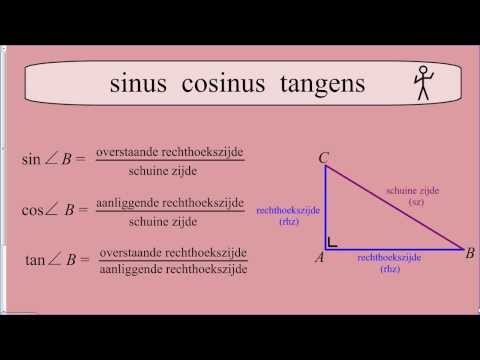 Для этого достаточно ввести в соответствующие ячейки значение синуса или величину угла в радианах или градусах, после чего калькулятор выдаст результат. Рассмотрим пример работы программы на простой школьной задаче по тригонометрии.

Пример из жизни

Школьная задача

Существует несколько особенных значений углов, которые чаще всего встречаются не только в задачах, но и в инженерных расчетах. Прежде всего это прямой угол, равный 90 градусов, а также углы величиной 30, 45, 60, 180, 270 и 360. Давайте вычислим эти значения при помощи нашего онлайн-калькулятора:

sin0 = 0
sin30 = 0,5
sin45 = 0,7071
sin60 = 0,8660
sin90 = 1
sin180 = 0
sin270 = -1
sin360 = 0.

Естественно, данные значения рассчитаны для углов, измеренных в градусах. Для углов больше 360 градусов значения синусов циклически повторяются.

Заключение

Тригонометрия – важный раздел математической науки, который находит применение не только в геометрии или физике, но и в астрономии, экономике, механике и даже биологии. Используйте наш калькулятор для вычисления синусов любых углов.

Инженерный калькулятор степеней онлайн ? арктангенс (arctg), косинус, синус и прочие варианты возведения

Для расчета котангенса, тангенса, косинуса и синуса угла теперь можно воспользоваться данным видом калькулятора.

Инженерный калькулятор для сложных расчетов онлайн

Кстати! У нас на сайте есть множество разных удобных сервисов, например калькулятор ндс, а также калькулятор процентов. Пользуйтесь!

Чтобы произвести сложные математические расчеты с использованием тригонометрических функций используйте инженерный калькулятор. Все команды вводятся с помощью клавиатуры или мыши. Для расчета котангенса, тангенса, косинуса и синуса угла теперь можно воспользоваться данным видом калькулятора. Кроме того, с его помощью можно исчислять логарифм числа, а также возводить число в степень.

Основные команды инженерного калькулятора: деление, умножение, ввод цифр, вычитание, сложение, сброс, равенство.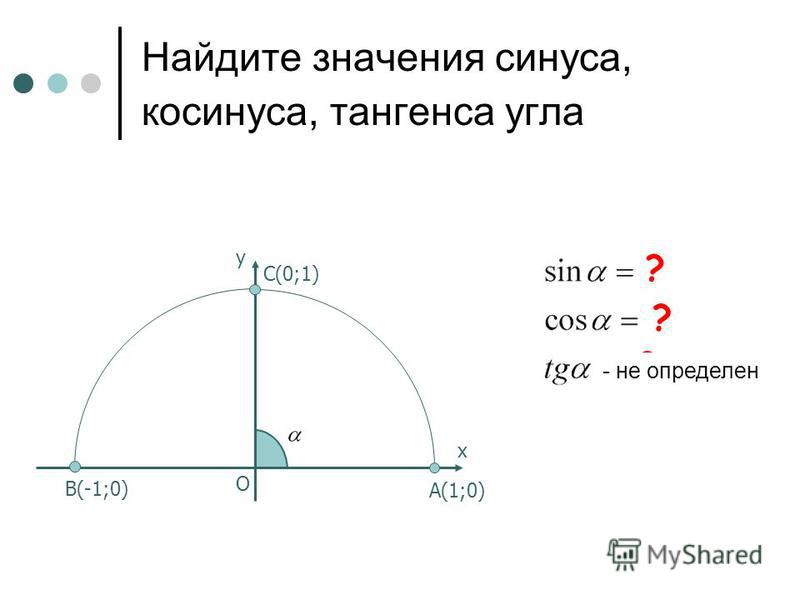 Данные команды можно вводить с помощью клавиатуры или используя мышку.

Внимание! Данная версия калькулятора находится в тестовом режиме и может содержать ошибки при выполнении расчетов с использованием тригонометрических функций.

Инструкция для работы с калькулятором

Основные функции кнопок

[ 0 ], [ 1 ],… [ 8 ], [ 9 ] — цифровые клавиши;
[ 00 ] — клавиша для одновременного ввода двух нулей;
[ → ] — удаление последнего введенного Вами знака на экране;
[ +/- ] – смена знака числового выражения на экране на противоположный;
[ X^Y ] — возведение числа X в степень Y;
[ + ] — сложение, [ — ] — вычитание, [ х ] — умножение, [ ÷ ] — деление;
[ √ ] — вычисление квадратного корня;
[ % ] — определение процентов;
[ M+ ] — сохранение в памяти калькулятора числа со знаком [ + ];
[ M- ] — сохранение в памяти калькулятора числа со знаком [ — ];
[ MR ] — отображение содержимого памяти на дисплей;
[ MC ] — очистка содержимого памяти;
[ AC ] — сброс калькулятора включая память;
[ C ] — сброс калькулятора, без сброса памяти.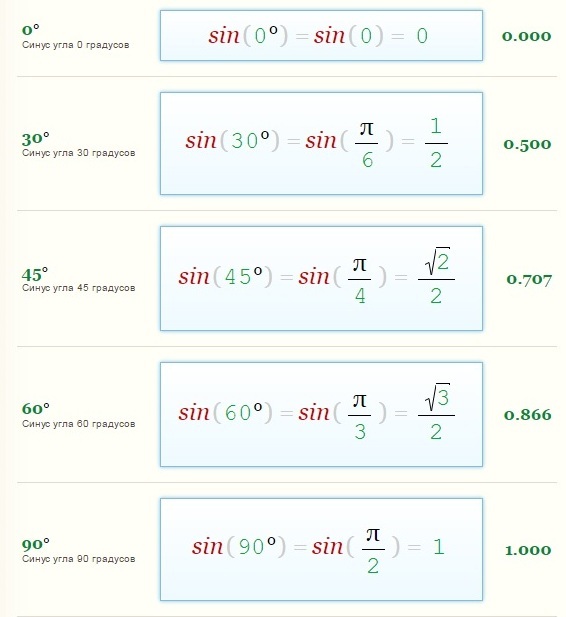

Для работы с тригонометрическими функциями используются функции кнопок

[ cos ] — косинус угла, [ ctg ] — котангенс угла, [ sin ] — синус угла, [ tg ] — тангенс угла;
[ atg ] — арктангенс угла, [ asin ] — арксинус угла, [ actg ] — арккотангенс угла, [ acos ] — арккосинус угла;
[ e ] — математическая костанта, число Эйлера;
[ π ] — математическая константа, отношение длины окружности к диаметру этой окружности;
[ √ ] — вычисление квадратного корня;
[ Xʸ ] — возведение числа X в степень Y.

Примеры вычислений на инженерном калькуляторе

Возвести число 2 в степень 3: 2 [ X^Y ]3. Результат — 8.
Вычисление квадратного корня числа 625: 625 [ √ ]. Результат — 25.
Вычисление процента от числа:    1000 [ х ] 20 [ % ]. Результат — 200.
Прибавление процента к числу:   800 [ + ] 25 [ % ]. Результат — 1000.
Вычитание процента из числа:   800 [ — ] 25 [ % ]. Результат — 600.

Ввод команд на калькулятор с клавиатуры ПК

Работа с калькулятором довольно проста и не вызовет сложностей ни у кого. Для ввода цифр используются клавиши компьютерной клавиатуры с цифрами или цифровые клавиши справа на дополнительной панели.

Чтобы стереть неправильно введенный символ используйте клавишу [Backspace].

Чтобы получить результат сложения или вычитания, жмите клавишу равно – используйте для этого [Enter].

Чтобы использовать знак «плюс», жмите на клавиатуре клавишу [ + ]. Она расположена на дополнительной клавиатуре справа вверху.

Чтобы использовать знак «минус», жмите на клавиатуре клавишу [ — ]. Она расположена сверху или на дополнительной клавиатуре.
Для умножения или деления используйте знаки [ * ] и [ / ] соответственно, которые расположены на боковой клавиатуре.

Чтобы обнулить все расчеты или начать подсчет сначала, нажмите [Del], [Esc] на верхней клавиатуре или же используйте кнопку [End] на боковой клавиатуре.

{-1} \left[ \dfrac{a \sin B}{b} \right]\)

А = угол А
B = угол B
С = угол С
а = сторона а
б = сторона б
с = сторона с
P = периметр
с = полупериметр
К = площадь
r = радиус вписанной окружности
R = радиус описанной окружности

*Единицы длины приведены только для справки, поскольку значения результирующих длин всегда будут одинаковыми, независимо от единиц измерения.

Калькулятор Использование

Использует закон синусов для вычисления неизвестных углов или сторон треугольника. Для расчета неизвестных значений необходимо ввести 3 известных значения.

Некоторые варианты расчета являются избыточными, но все равно включены для точных буквенных обозначений.

Методы расчета

Чтобы вычислить любой угол, A, B или C, скажем, B, введите противоположную сторону b, а затем другую пару углов-сторон, например A и a или C и c. Выполненные расчеты следуют метод бокового угла (SSA) и использовать закон синусов только для завершения вычислений для других неизвестных.

Чтобы вычислить любую сторону, a, b или c, скажем, b, введите противоположный угол B, а затем другую пару углов-сторон, например A и a или C и c. Выполненные расчеты следуют угол угол сторона (AAS) и использовать закон синусов только для завершения расчетов для других неизвестных.

9{-1} \left[ \dfrac{c \sin B}{b} \right] \)

Решение уравнений закона синусов для сторон a, b и c

\( a = \dfrac{b \ sin A}{\sin B} \)

\( a = \dfrac{c \sin A}{\sin C} \)

\( b = \dfrac{a \sin B}{\sin A} \)

\( b = \dfrac{c \sin B}{\sin C} \)

\( c = \dfrac{a \sin C}{\sin A} \)

\( c = \dfrac{b \sin C}{\sin B} \)

Характеристики треугольника

Периметр треугольника, P = a + b + c

Полупериметр треугольника, s = 0,5 * (a + b + c)

Площадь треугольника, K = √[ s*(s-a)*(s-b)*(s-c)]

Радиус вписанной окружности в треугольник, r = √[ (s-a)*(s-b)*(s-c) / s ]

Радиус описанной окружности вокруг треугольника, R = (abc) / (4K)

Ссылки/ дополнительная литература

Вайсштейн, Эрик В. «Закон синусов» Из MathWorld — Веб-ресурс Wolfram. Закон синусов.

Цвиллингер, Даниэль (главный редактор). CRC Standard Mathematical Tables and Formulae, 31st Edition New York, NY: CRC Press, p. 512, 2003.

http://hyperphysics.phy-astr.gsu.edu/hbase/lcos.html

http://hyperphysics.phy-astr.gsu.edu/hbase/lsin.html

Калькулятор синусоидального стержня и синусоидальных тисков

Меню калькулятора

Межцентровое расстояние — это межцентровое расстояние между цилиндрами на синусоиды барные или синусоидальные тиски.

Введите межосевое расстояние и угол или высоту блока.

Высота блока – это высота калибровочных блоков или пространственных блоков. под верхний цилиндр.