Tg arctg 5: Ответы: Вычислить: tg(arctg 5/6)…

alexxlab / / Разное

Открытая Математика. Алгебра. Тригонометрические уравнения

Тригонометрические уравнения

Найдём условие, при котором будут равны синусы двух углов. Пусть sin a = sin b. Тогда sin a – sin b = 0, и по известной формуле разности синусов имеем 2sina-b2cosa+b2=0. Значит, либо sina-b2=0, то есть a-b2=πn,  n∈ℤ, либо cosa+b2=0, то есть a+b2=π2+πn,  n∈ℤ. Итак, sin a = sin b тогда и только тогда, когда либо a – b = 2πn, либо a + b = (2n + 1)π, n∈ℤ.

Рассмотрим решение простейшего уравнения sin x = a. Если |a| > 1, то решений нет, если |a| ≤ 1, то в силу периодичности синуса решений будет бесконечно много. По определению обратных тригонометрических функций, одно из решений − это arcsin a. Следовательно, наше уравнение можно переписать в виде sin x = sin (arcsin a). Тогда либо x – arcsin a = 2πn, n∈ℤ, либо x + arcsin a = 2(n + 1)π, n∈ℤ. Оба эти равенства могут быть объединены в одно: x=(-1)narcsina+πn, n∈ℤ. Это равенство называется формулой общего решения уравнения 

sin x = a, |a| ≤ 1.

Аналогично можно показать, что формула общего решения уравнения cos x = a при |a| ≤ 1 имеет вид x=±arccos a+2πn, n∈ℤ.

Формула общего решения уравнения tg x = a при любом действительном a имеет вид x = arctg a + πn, n∈ℤ.

Формула общего решения уравнения ctg x = a при любом действительном a имеет вид x = arcctg a + πn, n∈ℤ.

Рассмотренные уравнения называются простейшими тригонометрическими уравнениями.

Простейшие тригонометрические уравнения

Решите уравнение sin 2x = cos 3x.

Воспользуемся формулой приведения sin2x=cos(π2-2x), получаем cos(π2-2x)-cos3x=0. По формуле разности синусов имеем 2sinπ2-2x+3x2sin3x-π2+2×2=0.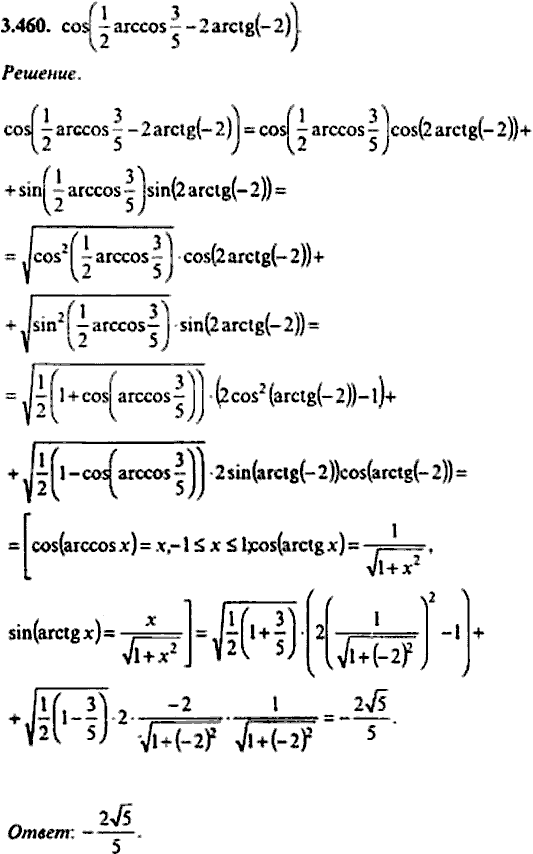

Следовательно, либо π4+x2=πk, то есть x=-π2+2πk, k∈ℤ, либо 5×2-π4=πk, то есть x=π10+2πk5, k∈ℤ.

Ответ. x=-π2+2πk, k∈ℤ, x=π10+2πk5, k∈ℤ.

Решите уравнение sin x – 2 cos x = 0.

Преобразуем уравнение sin x = 2 cos x. Рассмотрим те x, для которых cos x = 0. Для этих x sin x = ±1. Следовательно, эти x не являются корнями исходного уравнения, так как при их подстановке получается неверное числовое равенство 0 = ±1. Значит, cos x ≠ 0. Разделим обе части уравнения на cos x ≠ 0, имеем tg x = 2, x = arctg 2 + πn, n∈ℤ.

Ответ.  x = arctg 2 + πn, n∈ℤ.

Решите уравнение sin2 x – 6 sin x cos x + 5 cos2 x = 0.

Те значения переменной
x, для которых cos x = 0, не являются решениями, в чём можно убедиться непосредственной подстановкой. Разделим обе части уравнения на cos2 x, получим tg2x – 6 tg x + 5 = 0.

Это уравнение является квадратным относительно переменной t = tg x: t2 – 6t + 5 = 0. Корни этого уравнения: t1=1 и t2=5. Уравнение tgx=1 имеет решения x=π4+πn, n∈ℤ. Уравнение tg x = 5 имеет решения x=arctg 5+πn, n∈ℤ.

Ответ. x=π4+πn, x=arctg 5+πn, n∈ℤ.

Только что рассмотренные уравнения называются однородными уравнениями соответственно 1-го и 2-го порядка. Вспомним определение многочлена n-ной степени, данное в § 2.1.1. Однородным многочленом n-ного порядка относительно переменных u и v называется многочлен, у которого сумма степеней переменных постоянна у всех членов.

Аналогично, уравнения au + bu = 0 и au2 + bvu + cv2 = 0 также называются однородными уравнениями 1-го и 2-го порядка. В нашем случае было u = sin x и v = cos x.

Уравнение 1-го порядка делением на v сводится к линейному относительно новой переменной t=uv. Уравнения 2-го порядка делением на v2 сводятся к квадратному относительно t=uv.

Уравнения с обратными тригонометрическими функциями, как правило, удаётся решить, применяя одну и ту же тригонометрическую функцию к обеим частям данного уравнения.

Решите уравнение arccos x = arctg x.

Применим функцию косинус к обеим частям данного уравнения. Имеем x=cos(arctg x). Так как область определения данного уравнения − множество x∈[-1; 1], то: x∈[-1; 1]⇒{arccosx∈[0; π]arctgx∈[-π4; π4]⇒{arccosx∈[0; π4]arctgx∈[0; π4]⇒x>0⇒x=cos(arctg x)=11+tg2 (arctg x)=11+x2. Значит,

x > 0. Решаем полученное иррациональное уравнение: x2=11+x2⇔x4+x2-1=0⇔x2=-1±52. Так как x > 0, то x=5-12.

Ответ. 5-12.





 

Смотрите также: Математика, Английский язык, Химия, Биология, Физика, География, Астрономия.
А также: библиотека ЭОРов и образовательный онлайн-сервис с тысячами интерактивных работ «Облако знаний».

Mathway | Популярные задачи

1Найти точное значениеsin(30)
2Найти точное значениеsin(45)
3Найти точное значениеsin(30 град. )
4Найти точное значениеsin(60 град. )
5Найти точное значениеtan(30 град. )
6Найти точное значениеarcsin(-1)
7Найти точное значениеsin(pi/6)
8Найти точное значениеcos(pi/4)
9Найти точное значениеsin(45 град. )
10Найти точное значениеsin(pi/3)
11Найти точное значениеarctan(-1)
12Найти точное значениеcos(45 град. )
13Найти точное значениеcos(30 град. )
14Найти точное значениеtan(60)
15Найти точное значениеcsc(45 град. )
16Найти точное значениеtan(60 град. )
17Найти точное значениеsec(30 град. )
18Найти точное значениеcos(60 град. )
19Найти точное значениеcos(150)
20Найти точное значениеsin(60)
21Найти точное значениеcos(pi/2)
22Найти точное значениеtan(45 град. )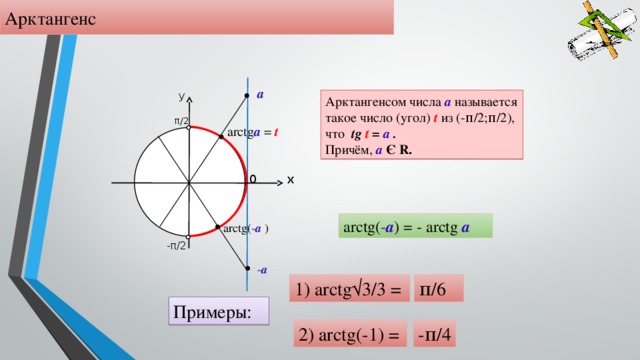
23Найти точное значениеarctan(- квадратный корень из 3)
24Найти точное значениеcsc(60 град. )
25Найти точное значениеsec(45 град. )
26Найти точное значениеcsc(30 град. )
27Найти точное значениеsin(0)
28
Найти точное значение		sin(120)
29Найти точное значениеcos(90)
30Преобразовать из радианов в градусыpi/3
31Найти точное значениеtan(30)
32Преобразовать из градусов в радианы45
33Найти точное значениеcos(45)
34Упроститьsin(theta)^2+cos(theta)^2
35Преобразовать из радианов в градусыpi/6
36Найти точное значениеcot(30 град. )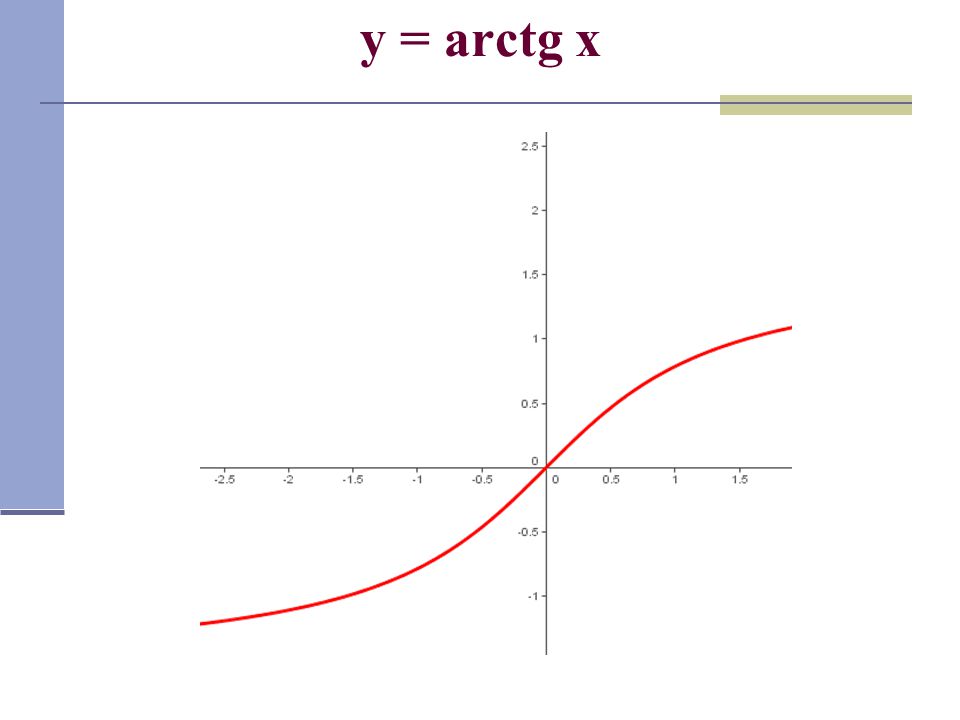
37Найти точное значениеarccos(-1)
38Найти точное значениеarctan(0)
39Найти точное значениеcot(60 град. )
40Преобразовать из градусов в радианы30
41Преобразовать из радианов в градусы(2pi)/3
42Найти точное значениеsin((5pi)/3)
43Найти точное значениеsin((3pi)/4)
44Найти точное значениеtan(pi/2)
45Найти точное значениеsin(300)
46Найти точное значениеcos(30)
47Найти точное значениеcos(60)
48Найти точное значениеcos(0)
49Найти точное значениеcos(135)
50Найти точное значениеcos((5pi)/3)
51Найти точное значениеcos(210)
52Найти точное значениеsec(60 град. )
53Найти точное значениеsin(300 град. )
54Преобразовать из градусов в радианы135
55Преобразовать из градусов в радианы150
56Преобразовать из радианов в градусы(5pi)/6
57Преобразовать из радианов в градусы(5pi)/3
58Преобразовать из градусов в радианы89 град.
59Преобразовать из градусов в радианы60
60Найти точное значениеsin(135 град. )
61Найти точное значениеsin(150)
62Найти точное значениеsin(240 град. )
63Найти точное значениеcot(45 град. )
64Преобразовать из радианов в градусы(5pi)/4
65Найти точное значениеsin(225)
66Найти точное значениеsin(240)
67Найти точное значениеcos(150 град. )
68Найти точное значениеtan(45)
69Вычислитьsin(30 град. )
70Найти точное значениеsec(0)
71Найти точное значениеcos((5pi)/6)
72Найти точное значениеcsc(30)
73Найти точное значениеarcsin(( квадратный корень из 2)/2)
74Найти точное значениеtan((5pi)/3)
75Найти точное значениеtan(0)
76Вычислитьsin(60 град. )
77Найти точное значениеarctan(-( квадратный корень из 3)/3)
78Преобразовать из радианов в градусы(3pi)/4
79Найти точное значениеsin((7pi)/4)
80Найти точное значениеarcsin(-1/2)
81Найти точное значениеsin((4pi)/3)
82Найти точное значениеcsc(45)
83Упроститьarctan( квадратный корень из 3)
84Найти точное значениеsin(135)
85Найти точное значениеsin(105)
86Найти точное значениеsin(150 град. )
87Найти точное значениеsin((2pi)/3)
88Найти точное значениеtan((2pi)/3)
89Преобразовать из радианов в градусыpi/4
90Найти точное значениеsin(pi/2)
91Найти точное значениеsec(45)
92Найти точное значениеcos((5pi)/4)
93Найти точное значениеcos((7pi)/6)
94Найти точное значениеarcsin(0)
95Найти точное значениеsin(120 град. )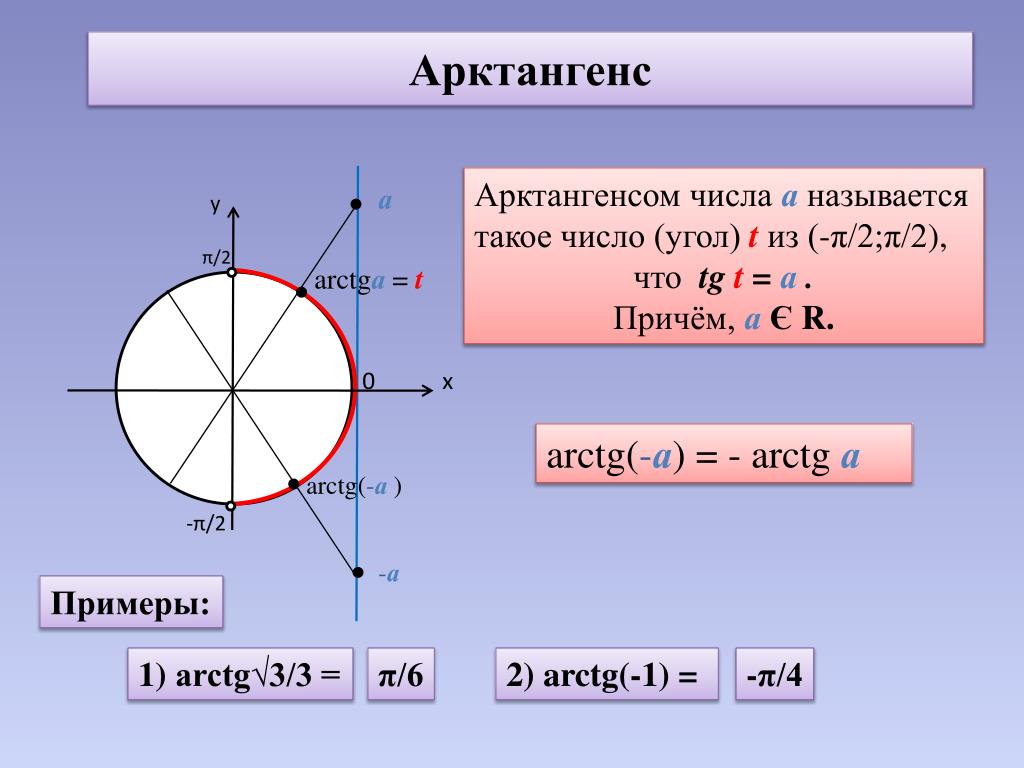
96Найти точное значениеtan((7pi)/6)
97Найти точное значениеcos(270)
98Найти точное значениеsin((7pi)/6)
99Найти точное значениеarcsin(-( квадратный корень из 2)/2)
100Преобразовать из градусов в радианы88 град.

Arkus tangens — Wikipedia

Iz Wikipedije, slobodne enciklopedije

Idi na navigacijuIdi na pretragu

9008 9008 9008
Arkus tangens
Osnovne osobine
Parnost непарна
Домен (-∞,∞)
Кодомен (-π/2,π/2)
Specifične vrednosti
Nule 0
Vrednost u +∞ π/2
Vrednost u -∞ -π/2
Specifične osobine
ASIMPTOTE — {y} — = ± π/2
Prevoji (0,0)
Ulazak U Nul Pod Uglom
Ulazak U Nulu Pod Uglom		 Ulazak U Nul{-1}x={\frac {i}{2}}\left(\log(1-ix)-\log(ix+1)\right)}

Следуй за формулой koje se vezuju za arkus касательные:

arctgx=π2−arcctgx{\displaystyle\operatorname{arctg}\;x={\frac {\pi}{2}}-\operatorname{arcctg}\;x} (правило дополнительных углов)
arctg⁡(-x)=-arctgx{\displaystyle \operatorname {arctg} (-x)=-\operatorname{arctg} \;x\!} (непарность f-je)
arctg1x = π2-arctgx = arctgx, {\ displaystyle \ operatorname {arctg} \; {\ frac {1} {x}} = {\ frac {\ pi} {2}} — \ operatorname {arctg} \; x =\operatorname {arcctg} \;x,\ }x>0{\displaystyle x>0} 9{2n+1}}{2n+1}};\qquad |x|\leq 1\qquad x\neq i,-i\end{выровнено}}}
  • Функция -{arctg}- na -{ wolfram. com}-
Тригонометрические и гиперболические функции
9 кош(х)
Синус Косинус Тангенс Котангенс Секанс Косеканс
Функция sin(x) cos(x) tg(x) ctg(x) sec(x) cosec(x)
Inverzna arcsin(x) arccos(x) arctg(x) arcctg(x) arcsec(x) arccosec4 arccosec
Гиперболическая шв(х) щ(х) тгх(х) ктгх(х) сеч(х)
Инв. гиперболическая угл(х)арккош(х) арктгх(х) arcctgh(x) арксек(х) арккосех(х)

Jaký je rozdil mezi cotangens a arcustangens? | Odpovědi.

cz
Положите новую отазку
  • Категория
  • Взделани…
  • Стредни…
  • Деталь отазки

P70

Добрый день, arctg je tangens na minus prvou. A cotg je jedna lomeno tangens, není to ve vysledku to same? Декуйи

Одповедет

Диск: напиште првни пршиспевек

Nejlepší odpověď

cochee

Není. Pleteš си числовых и логических вычислений. Máš pravdu, že cotg x = 1/(tg x), avšak numerický vztah arctg x = 1/(tg x) neplatí. Správné vyjádření je, že arctg je funkce inverzní k tg, nikoliv je je jeho numerickou převrácenou hodnotou. To znamená, že definujeme-li velikost úhlu jako x a jeho tangens (tedy tg x) jako y, pak platí, že arctg y = x. Значения слов и конкретных значений pro x = 0,5 рад: tg x ≐ 0,546302 и заполнение: arctg 0,546302 ≐ 0,5 (рад). Почополь? (Заокрухлил йсем, протоже до числа 0,546302… мá неконечной десeтинной розвой.)

To tangens na minus prvou je zřejmě z anglického prostředí, protože tam místo zkratky arctg x používají buď atan x anebo tan⁻¹ x. Opakuji, že to ale numericky není pravda.

Управ/а: кочи

Další odpovědi

orwell

Je to tak, jak píše cochee. Jednoduše řečeno funkce tg přiřazuje nějakému úhlu číslo a arctg přiřazuje číslu zase úhel. Platí-li tedy y = tg x, pak x = arctg y.
V tomto smyslu lze v zápisu formálně (symbolicky) nahradit arctg y výrazem tan⁻¹ y.
Также 1/( tg x) = (tg x)⁻¹ = cotg x a není to tudíž inverzní funkce k funkci tg x.
Je třeba rozlišovat tan⁻¹ x a (tg x)⁻¹ !!!
Koukni se ještě sem: https://matematika.cz/…

Zaimavé otázky в категории Vzdělání práce

  • Co Vás motivuje se učit? (9 повторений)
  • Взпоменете си на нектерa пржислови чи джина услови, ктера се указала ве ваше животэ яко правдива? (14 повторений)
  • Jaký je váš názor na školní systém známek? Мыслите, же дети мотивируют небо наопак? (5 повторений)
  • Co си myslíte или povinné maturitě u matematiky? (7 повторений)
  • Co je mezigenerační propast? А каковы все проблемы в родине? (5 повторений)
  • Kam psát addressu odesilatele, příjemce na poštovní balík (4 подсказки)
  • Готовы ли вы к учебе? Maturita Solutions Pre-Intermediate? (5 повторений)
  • Přepočet jednotek. Kolik gramů je 150 mililitrů? (3 подсказки)
  • Взпомел небо взпомнил (3 подсказки)
  • Význam Slova hrdobec (3 подсказки)
  • Co jsou to слова заклад, словотворный заклад и словотворный prostředek? (2 подсказки)
  • кечи небо кеси? (7 повторений)
  • Выпочет относительной одчылки (1 раз)
  • Jak spočítat průměr z vysvědčení ? (1 раз)
  • co znamená zkratka ZPS (1 раз)
  • Co je to IZO? (1 раз)
  • Jak má vypadat odvolání na střední školu? (1 раз)
  • Dobré ráno, chtěla bych se zeptat, píše se jakoukoli nebo jakoukoliv.

    No related posts.

    Добавить комментарий

    Ваш адрес email не будет опубликован. Обязательные поля помечены *

    © 2015 - 2019 Муниципальное казённое общеобразовательное учреждение «Таловская средняя школа»

    Карта сайта