Синус онлайн в радианах: Онлайн калькулятор: Обратные тригонометрические функции

mathmatic PHP functions — functions-online (русский)

Math

abs
acos
acosh
asin
asinh
atan2
atan
atanh
base_convert
bindec
calculate
ceil
cos
cosh
decbin
dechex
decoct
deg2rad
exp
expm1
floor
fmod
hexdec
hypot
is_finite
is_infinite
is_nan
log10
log1p
log
max
min
mt_rand
octdec
pow
rad2deg
rand
round
sin
sinh
sqrt
tan
tanh

Наиболее используемое

dns_get_record
preg_match
unserialize
preg_replace
json_decode
strlen
preg_match_all
json_encode
date
serialize

deenesfritjaptrutrzh

Execute and test PHP functions with an mathmatic background. These functions use and except only float and integer values.

abs

Возвращает абсолютное значение $number.

acos

Возвращает арккосинус числа $arg в радианах. acos() — обратная тригонометрическая функция к cos(), т.е. a==cos(acos(a)) для каждого значения а, входящего в область значений функции acos().

acosh

Возвращает гиперболический арккосинус $arg, т.е. значение, чей гиперболический косинус равен $arg.

asin

Возвращает арксинус числа $arg в радианах. asin() — обратная тригонометрическая функция к sin(), т.е. a==sin(asin(a)) для каждого значения a, входящего в область значений функции asin().

asinh

Возвращает гиперболический арксинус $arg, т.е. значение, чей гиперболический синус равен $arg.

atan2

Функция вычисляет арктангенс переменных $x и $y. Это подобно вычислению арктангенса $y / $x, за исключением того, что знаки обоих аргументов используются для вычисления квадранта результата.

atan

Возвращает арктангенс числа $arg в радианах. atan() — обратная тригонометрическая функция к tan(), т.е. a==tan(atan(a)) для каждого значения a, входящего в область значений функции atan().

atanh

Возвращает гиперболический арктангенс $arg, т.е. значение, чей гиперболический тангенс равен $arg.

base_convert

Возвращает строку, содержащую число $number представленное в системе счисления $tobase. Система счисления, в которой дано число $number указана в $frombase. Значения $frombase и $tobase должны быть между 2 и 36 (включительно). Цифры в числах, представленных в системе счисления выше десятичной, будут представлены буквами a-z, гда a обозначает 10, b обозначает 11 и z — 35.

bindec

Возвращает десятичный эквивалент двоичного числа $binary_string.

calculate

This function calculates a mathmatic formula. It is somewhat like a calculator, but without an usable frontend. Often you have the problem, that you just want write down the complete formular, but on GUI-based calculators you can’t, here you can! Allowed are the usual operators (+, -, *, /, %) and the following functions:

exp($arg) (exp(1) = 2,718. ..)
log($arg, $basis) (log(2, 8) = 1/3)
pow($basis, $exponent) (pow(4, 2) = 16)
sqrt($arg) (sqrt(16) = 4)

Attention: The comma (,) is reserved to devide the parameters of function. The comma in this way is represented by the dot (.).

ceil

Возвращает ближайшее большее целое от $value.

cos

cos() возвращает косинус параметра $arg . Параметр $arg задаётся в радианах.

cosh

Возвращает гиперболический косинус $arg, определяемый как (exp(arg) + exp(-arg))/2.

decbin

Возвращает строку, содержащую двоичное представление указанного аргумента $number.

dechex

Возвращает строку, содержащую шестнадцатеричное представление указанного аргумента $number. Наибольшее число, которое может быть преобразовано — 4294967295, в шестнадцатеричном представлении — «ffffffff».

decoct

Возвращает строку, содержащую восьмеричное представление указанного аргумента $number. Наибольшее число, которое может быть преобразовано — 4294967295, в восьмеричном представлении «37777777777».

deg2rad

Функция преобразует $number из градусов в радианы.

exp

Возвращает e в степени $arg.

expm1

expm1() возвращает эквивалент выражения ‘exp(arg) — 1’, рассчитанный таким образом, что результат точен, даже если значение $arg близко к нулю, тогда как ‘exp (arg) — 1’ будет неточно из-за вычитания двух почти равных чисел.

floor

Возврашает ближайшее целое число, округляя $value в меньшую сторону.

fmod

Возвращает дробный остаток от деления делимого ($x) и делителя ($y). Остаток (r) определяется так: x = i * y + r, где i — некоторое целое. Если $y не равен нулю, то r имеет такой же знак, как $x и величину, меньшую или равную величине $y.

hexdec

Возвращает десятичный эквивалент шестнадцатеричного числа, содержащегося в аргументе $hexString. hexdec() преобразует шестнадцатеричную строку в десятичное число.

hypot

hypot() возвращает длину гипотенузы прямоугольного треугольника с длинами сторон $x и $y, или расстояние точки ($x, $y) до начала координат Эквивалентно sqrt(x*x + y*y).

is_finite

Проверяет, является ли $val допустимым конечным числом на данной платформе.

is_infinite

Возвращает TRUE, если $val является бесконечностью (положительной или отрицательной), например, как результат вычисления log(0) или любые другие значения, слишком большие, чтобы уместиться в float на данной платформе.

is_nan

Проверяет, является ли val «не числом» (NaN), например, как результат выполнения функции acos(1.01).

log10

Возвращает десятичный логарифм $arg.

log1p

log1p() возвращает log(1 + $number), рассчитанное таким образом, что результат точен, даже когда значение $number близко к нулю. Из-за недостатка точности log() в этом случае может вернуть просто log(1).

log

Если указан необязательный параметр $base, log() возвращает log_base от $arg, иначе log() возвращает натуральный логарифм числа $arg.

max

Если в качестве единственного аргумента передан массив, max() вернет значение наибольшее значение из этого массива. Если передано 2 или более аргумента, функция max() вернет наибольший из них.

min

Если в качестве аргументов передан только один — массив чисел, min() возвращает наименьшее из них. Если первый аргумент — integer или float, то обязательно должен быть хотя бы ещё один. В этом случае функция min() вернёт наименьшее из них.

mt_rand

Многие генераторы случайных чисел в старых библиотеках имеют сомнительные или неизвестные характеристики, а также работают довольно медленно. По умолчанию, PHP использует генератор случайных чисел libc с помощью функции rand(). Функция mt_rand() представляет собой удобную замену этой функции. Она использует генератор случайных чисел с известными характеристиками, основанный на «? Вихре Мерсенна», который генерирует случайные числа в среднем в четыре раза быстрее, чем libc rand().

Вызванная без необязательных параметров $min и $max, функция mt_rand() возвращает псевдослучайное значение между 0 и mt_getrandmax(). Если вам нужно, например, случайное число между 5 и 15 (включительно), используйте вызов mt_rand(5,15)

octdec

Возвращает десятичный эквивалент восьмеричного числа, указанного в аргументе $octal_string.

pow

Возвращает $base, возведенное в степень $exp.

rad2deg

Функция преобразует значение $number из радианов в градусы.

rand

При вызове без параметров $min и $max, возвращает псевдослучайное целое в диапазоне от 0 до getrandmax(). Например, если вам нужно случайное число между 5 и 15 (включительно), вызовите rand(5, 15).

round

Возвращает округлённое значение $val с указанной точностью $precision (количество цифр после запятой). Последняя может быть отрицательной или нулём (по умолчанию).

sin

sin() возвращает синус параметра $arg . Параметр $arg задаётся в радианах.

sinh

Возвращает гиперболический синус $arg, определяемый как (exp($arg) — exp(-$arg))/2.

sqrt

Возвращает квадратный корень из $arg.

tan

tan() возвращает тангенс параметра $arg. Параметр $arg задаётся в радианах.

tanh

Возвращает гиперболический тангенс $arg, определяемый как sinh(arg)/cosh(arg).

Обзор алгебраических триггеров

Онлайн-заметки Пола

Главная / Обзор алгебраических триггеров / Тригонометрия / Оценка функции триггера

Показать мобильное уведомление Показать все примечания Скрыть все примечания

Уведомление для мобильных устройств

Похоже, вы используете устройство с «узкой» шириной экрана ( т. е. вы, вероятно, используете мобильный телефон). Из-за характера математики на этом сайте лучше всего просматривать в ландшафтном режиме. Если ваше устройство не находится в ландшафтном режиме, многие уравнения будут отображаться сбоку вашего устройства (должна быть возможность прокрутки, чтобы увидеть их), а некоторые пункты меню будут обрезаны из-за узкой ширины экрана.

Раздел 2.1: Оценка функции запуска

Одна из проблем с большинством классов триггеров заключается в том, что они имеют тенденцию концентрироваться на прямоугольном треугольнике и делать все в терминах градусов. Затем вы попадаете на курс исчисления, где почти все делается в радианах, а единичный круг — очень полезный инструмент.

Итак, сначала давайте посмотрим на следующую таблицу, чтобы соотнести градусы и радианы.

Степень	0	30	45	60	90	180	270	360
Радиан	0	$\displaystyle \frac{\pi} {6}$	$\displaystyle \frac{\pi}}{4}$	$\displaystyle \frac{\pi}{3}$	$\displaystyle \frac{\pi}}{2}$	$\displaystyle\pi$	$\displaystyle \frac{{3\pi}}{2}$	$\displaystyle 2\pi $

Знай эту таблицу! Конечно, есть много других углов в радианах, которые мы увидим на этом уроке, но большинство из них будет связано с этими несколькими углами.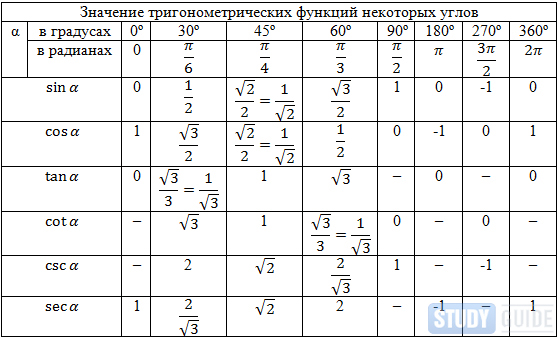 Таким образом, если вы справитесь с этими углами, вы сможете справиться и с большинством других.

Предупреждаем, все в большинстве классов исчисления будет сделано в радианах!

Теперь давайте посмотрим на единичный круг. Ниже приведен единичный круг с заполненным только первым квадрантом. Принцип работы единичного круга заключается в том, чтобы провести линию из центра круга наружу, соответствующую заданному углу. Затем посмотрите координаты точки пересечения прямой и окружности. Первая координата — это косинус этого угла, а вторая координата — это синус этого угла. Есть пара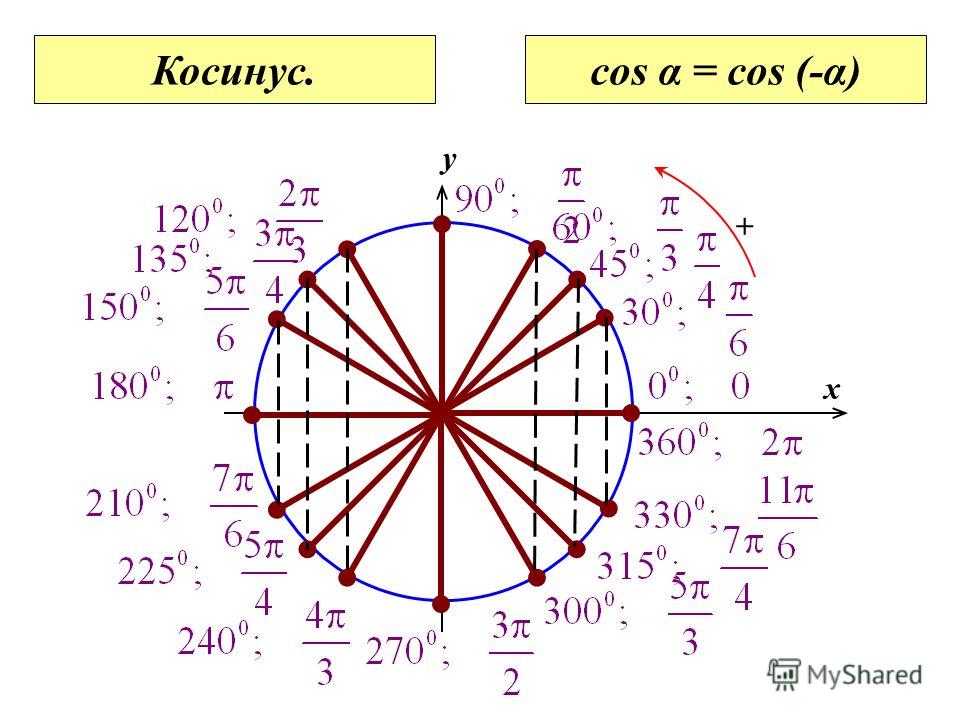

основные углы , которые обычно используются. Это $0,\frac{\pi }{6},\frac{\pi }{4},\frac{\pi }{3},\frac{\pi }{2},\pi ,\ frac{{3\pi }}{2}$ и $2\pi $ и показаны ниже вместе с координатами пересечений. Итак, из единичного круга ниже мы можем видеть, что $\cos \left( {\frac{\pi }{6}} \right) = \frac{{\sqrt 3}}{2}$ и $ \ грех \ влево ( {\ гидроразрыва {\ пи {6}} \ вправо) = \ гидроразрыва {1} {2} $.

Вспомните, как работают знаки углов. При вращении против часовой стрелки угол положительный, при вращении по часовой стрелке угол отрицательный.

Напомним также, что один полный оборот равен $2\pi $, поэтому положительная ось $x$ может соответствовать либо углу 0, либо $2\pi $ (или $4\ pi $, или $6\pi $, или $- 2\pi $, или $- 4\pi $, и т.д. . в зависимости от направления вращения). Точно так же угол $\frac{\pi }{6}$ (чтобы выбрать угол совершенно случайно) также может быть любым из следующих углов:

$\displaystyle \frac{\pi }{6} + 2\pi = \frac{{13\pi}}{6}$ (начните с $\displaystyle \frac{\pi }{6}$, затем поверните один раз против часовой стрелки)

$\displaystyle \frac{\pi }{6} + 4\pi = \frac{{25\pi}}{6}$ (начать с $\displaystyle \frac{\pi }{6} $ затем дважды поверните против часовой стрелки)

$\displaystyle \frac{\pi }{6} — 2\pi = — \frac{{11\pi}}{6}$ (начните с $\ displaystyle \frac{\pi }{6}$ затем поверните один раз по часовой стрелке)

$\displaystyle \frac{\pi }{6} — 4\pi = — \frac{{23\pi }}{6 }$ (начать с $\displaystyle \frac{\pi }{6}$ затем повернуть дважды по часовой стрелке)

и т.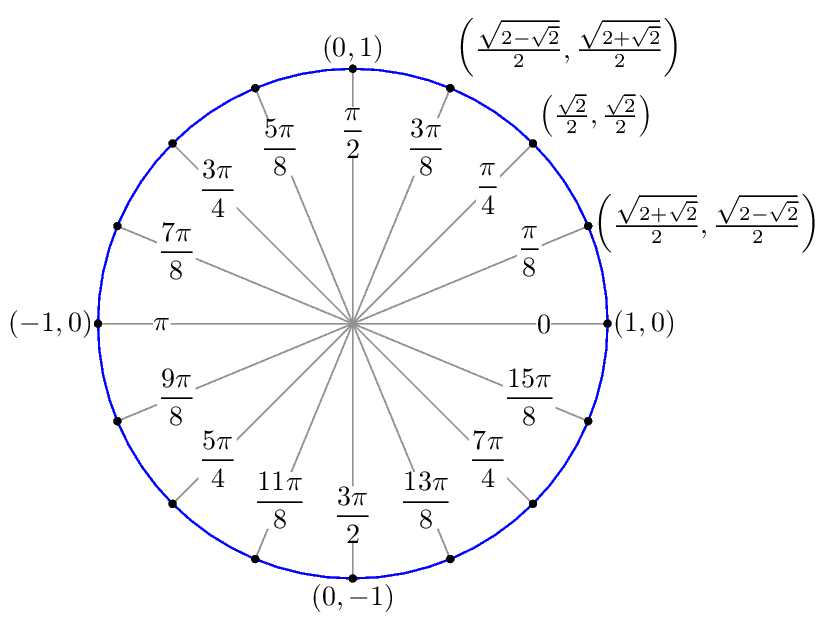 д.

Фактически, $\frac{\pi }{6}$ может быть любым из следующих углов $\frac{\pi }{6} + 2\pi \,n\,\;\; n = 0,\, \pm 1,\, \pm 2,\, \pm 3,\, \ldots $ В этом случае $n$ — это количество полных оборотов, которые вы делаете по единичному кругу, начиная с $\ гидроразрыва {\pi} {6}$. Положительные значения $n$ соответствуют вращениям против часовой стрелки, а отрицательные значения $n$ соответствуют вращениям по часовой стрелке.

Итак, почему я указал только первый квадрант? Ответ прост. Если вы знаете первый квадрант, то вы можете получить все остальные квадранты из первого. Вы увидите это в следующих примерах.

Найдите точное значение каждого из следующих. Другими словами, не используйте калькулятор. Показать все решенияСкрыть все решения пи }}{3}} \справа)\)
Показать решение

Первая оценка здесь использует угол $\frac{{2\pi }}{3}$. Обратите внимание, что $\frac{{2\pi }}{3} = \pi — \frac{\pi }{3}$. Таким образом, $\frac{{2\pi}}{3}$ находится путем вращения $\frac{\pi }{3}$ вверх от отрицательной оси $x$.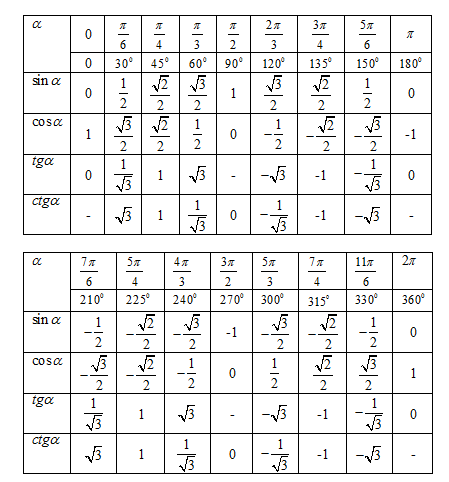

Это означает, что линия для $\frac{{2\pi}}{3}$ будет зеркальным отображением линии для $\frac{\pi }{3}$ только во втором квадранте. Координаты для $\frac{{2\pi}}{3}$ будут координатами для $\frac{\pi }{3}$, за исключением того, что координата $x$ будет отрицательной.

Аналогично, для $ — \frac{{2\pi }}{3}$ мы можем заметить, что $ — \frac{{2\pi }}{3} = — \pi + \frac{\ pi }{3}$, поэтому этот угол можно найти, повернув $\frac{\pi }{3}$ вниз от отрицательной оси $x$. Это означает, что линия для $ — \frac{{2\pi}}{3}$ будет зеркальным отображением линии для $\frac{\pi }{3}$ только в третьем квадранте. и координаты будут такими же, как координаты для $\frac{\pi }{3}$, за исключением того, что обе они будут отрицательными.

Оба этих угла вместе с их координатами показаны на следующем единичном круге.

Из этого единичного круга видно, что $\sin \left( {\frac{{2\pi}}{3}} \right) = \frac{{\sqrt 3}}{2}$и $\sin\left( { — \frac{{2\pi}}{3}} \right) = — \frac{{\sqrt 3}}{2}$.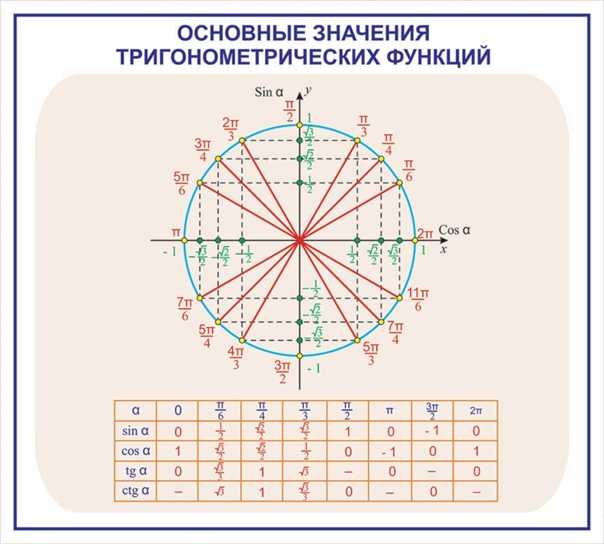

Это приводит к приятному факту о синусоидальной функции. Функция синуса называется нечетной функцией , поэтому для ЛЮБОГО угла мы имеем

\[\sin \left( { — \theta } \right) = — \sin \left( \theta \right)\]

$\cos \left( {\frac{{7\pi}}{6}} \right)$ и $\cos \left({ — \frac{{7\pi}}}{6}} \верно)$
Показать решение

В этом примере обратите внимание, что $\frac{{7\pi}}{6} = \pi + \frac{\pi }{6}$, так что это означает, что мы будем вращать вниз $\frac{\pi {6}$ от отрицательной оси $x$, чтобы получить этот угол. Также $ — \frac{{7\pi }}{6} = — \pi — \frac{\pi }{6}$ так что это означает, что мы будем вращаться вверх $\frac{\pi }{6} $ от отрицательной оси $x$, чтобы добраться до этого угла. Оба они показаны на следующем единичном круге вместе с соответствующими координатами точек пересечения.

Из этой единичной окружности видно, что $\cos \left({\frac{{7\pi}}{6}} \right) = — \frac{{\sqrt 3}}{2}$ и $\cos\left( { — \frac{{7\pi}}{6}} \right) = — \frac{{\sqrt 3}}{2}$. В этом случае функция косинуса называется функцией даже , и поэтому для ЛЮБОГО угла мы имеем

\[\cos \left( { — \theta } \right) = \cos \left( \theta \right)\]

$\tan \left( { — \frac{\pi }{4}} \right)$ и $\tan \left({\frac {{7\pi}}{4}} \right) $
Показать решение

Здесь следует отметить, что $\frac{{7\pi}}{4} = 2\pi — \frac{\pi }{4}$, поэтому $\frac{{7\pi}}{4 }$ и $ — \frac{\pi }{4}$ на самом деле являются одним и тем же углом! Единичная окружность для этого угла равна

Теперь, если мы вспомним, что $\tan \left( x \right) = \frac{{\sin \left( x \right)}}{{\cos \left( x \right)}}$ мы можем использовать единичный круг, чтобы найти значения функции касательной. Итак,

\[\ tan \left( \frac{7\pi }{4} \right)=\tan \left( -\frac{\pi }{4} \right)=\frac{\sin \left( -{ \pi}/{4}\;\right)}{\cos\left(-{\pi}/{4}\;\right)}=\frac{-{\sqrt{2}}/{2} \;}{{\sqrt{2}}/{2}\;}=-1\]

Кстати, обратите внимание, что $\tan \left( {\frac{\pi }{4}} \right) = 1$, и мы видим, что функция тангенса также называется нечетной функция и поэтому для ЛЮБОГО угла мы будем иметь

\[\tan \left( { — \theta } \right) = — \tan \left( \theta \right)\]

$\ грех \ влево ( {\ гидроразрыва {{9 \ пи}} {4}} \ вправо) $
Показать решение

Для этой задачи заметим, что $\frac{{9\pi}}{4} = 2\pi + \frac{\pi}{4}$. Теперь вспомним, что один полный оборот равен $2\pi $. Итак, это означает, что $\frac{{9\pi }}{4}$ и $\frac{\pi }{4}$ находятся в одной и той же точке единичной окружности. Следовательно,

\[\ грех \ влево ( {\ гидроразрыва {{9 \ пи}} {4}} \ справа) = \ грех \ влево ( {2 \ пи + \ гидроразрыва {\ пи} {4}} \ справа) = \ грех \ влево ( {\ гидроразрыва {\ пи} {4}} \ вправо) = \ гидроразрыва {{\ sqrt 2}} {2} \]

Это приводит нас к очень интересному факту о синусоидальной функции. Синусоидальная функция является примером периодическая функция . Периодические функции — это функции, которые повторяются снова и снова. «Расстояние», которое вам нужно пройти вправо или влево, прежде чем функция начнет повторяться, называется периодом функции.

В случае синуса период равен $2\pi $. Это означает, что синусоидальная функция будет повторяться каждые $2\pi $. Это приводит к хорошей формуле для функции синуса.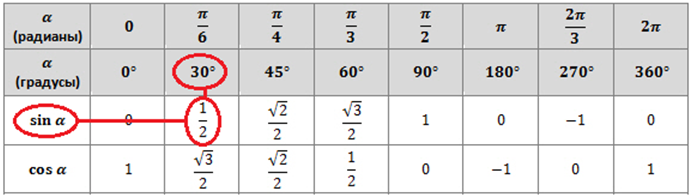

\[\sin \left( {x + 2\pi n} \right) = \sin \left( x \right)\hspace{0.25in}\,\,\,\,\,\,\,\, n = 0,\, \pm 1,\,\, \pm 2,\, \ldots\]

Обратите внимание, что поскольку

\[csc \ влево ( х \ вправо) = \ гидроразрыва {1} {{\ грех \ влево ( х \ вправо)}} \]

то же самое можно сказать и о косекансе.

\[\csc \left( {x + 2\pi n} \right) = \csc \left( x \right)\hspace{0.25in}\,\,\,\,\,\,\,\, n = 0,\, \pm 1,\,\, \pm 2,\, \ldots\]

Вообще-то тут надо быть осторожным. Мы можем сказать, что это при условии $x \ne n\pi $, так как синус будет равен нулю в этих точках и, следовательно, там не будет косеканса!

\ (\ сек \ влево ( {\ гидроразрыва {{25 \ пи}} {6}} \ вправо) \)
Показать решение

Здесь мы должны заметить, что $\frac{{25\pi }}{6} = 4\pi + \frac{\pi }{6}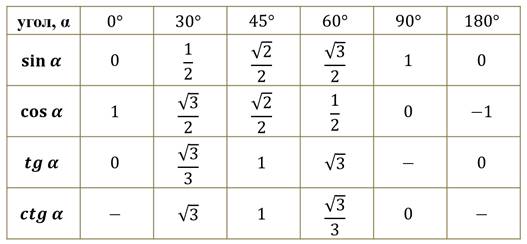$. Другими словами, мы начали с $\frac{\pi }{6}$ и дважды повернулись, чтобы вернуться в ту же точку на единичной окружности. Это означает, что

\[\ сек \ влево ( {\ гидроразрыва {{25 \ пи}} {6}} \ вправо) = \ сек \ влево ( {4 \ пи + \ гидроразрыва {\ пи {6}} \ вправо) = \ сек \ влево ( {\ гидроразрыва {\ pi} {6}} \ вправо) \] 9{\ sqrt {3}}/{} _ {2}} = \ frac {2} {\ sqrt {3}} \]

Следует также отметить, что косинус и секанс являются периодическими функциями с периодом $2\pi $. Итак,

\[\begin{align*}\begin{align}\cos \left( {x + 2\pi n} \right) & = \cos \left( x \right)\\ \sec \left( {x + 2\pi n} \right) & = \sec \left( x \right) \end{aligned}& \hspace{0.5in}n = 0, \pm 1, \pm 2,\, \ldots \end{ выровнять*}\]

\ (\ загар \ влево ( {\ гидроразрыва {{4 \ пи}} {3}} \ вправо) \)
Показать решение

Для решения этой задачи полезно знать, что тангенс (и, следовательно, котангенс) также является периодической функцией, но в отличие от синуса и косинуса имеет период $\pi $.

\[\begin{align*}\begin{aligned}\tan \left( {x + \pi n} \right) & = \tan \left( x \right)\\ \cot \left( {x + \ pi n} \right) & = \cot \left( x \right) \end{aligned}& \hspace{0.5in}n = 0, \pm 1, \pm 2,\, \ldots \end{align* }\]

Итак, для решения этой задачи заметим, что $\frac{{4\pi }}{3} = \pi + \frac{\pi }{3}$. Следовательно,

\[\ tan \left( {\frac{{4\pi}}{3}} \right) = \tan \left({\pi + \frac{\pi}{3}} \right) = \tan \left( {\frac{\pi} {3}} \right) = \sqrt 3 \]

Оценка триггера Заключительные мысли

Как мы видели в предыдущих примерах, если вы знаете первый квадрант единичной окружности, вы можете найти значение ЛЮБОЙ триггерной функции (не только синуса и косинуса) для ЛЮБОГО угла, который может быть связан обратно с один из тех, что показаны в первом квадранте. Это хорошая идея для запоминания, так как это означает, что вам нужно запомнить только первый квадрант и как получить углы в оставшихся трех квадрантах!

В этих задачах я использовал только «базовые» углы, но многие из представленных здесь идей можно применить и к углам, отличным от этих «базовых» углов, как мы увидим в разделе «Решение триггерных уравнений».

Radians -Quiz — Google Suce

AllebildershoppingVideoSmapsNewsbücher

Sucoptionen

Quick Pick: Radians Quiz — By Mhershfield — Sporcle

WWW.Sporcle.com. углы в градусах, если они заданы в радианах? Проверьте свои знания в этом научном тесте и сравните свой результат с …

Единица измерения круга: викторина для измерения радиана — PurposeGames

www.purposegames.com › игра › викторина в радианах

Определите положение радиана. Радианная мера дается через π (вместо «пи»). Этот тест подается в следующих категориях.

Углы единичной окружности — Радианы Викторина — PurposeGames

www.purposegames.com › игра › Углы-в-единице…

От автора викторины. Найдите углы единичной окружности в радианах. Этот тест подается в следующих категориях. единица.

Практическая викторина по преобразованию градусов в радианы — Quizizz

quizizz. com › admin › преобразование в градусы и радианы пр…

Вопрос 1 · В. Сколько радианов в окружности? · 360 градусов. 2пи радиан. пи радианы; Вопрос 2 · Q. Переведите π радиан в градусы. · 90⁰. 180⁰. 360⁰.

Градусы и радианы Викторина | Предварительное исчисление — Quizizz

quizizz.com › admin › градусы-и-радианы-quiz

Q. Положительный угол между 0 и 2 π 2\pi 2π, котерминальный углу 17 π 6 \frac{17 \pi}{6} 617π ? варианты ответа. 11 π 11\pi 11π / 6 радиан.

Градусы в радианы Круг — ThatQuiz

www.thatquiz.org › preview

Преобразование градусов в радианы … Создано с помощью That Quiz — сайта для создания тестов по математике с ресурсами для других предметных областей.

Викторина по измерению радиана — Вопросы с решениями — Vedantu

www.vedantu.com › викторина › викторина по измерению радиана

Попробуйте пройти эти тесты по измерению радиана, в которых есть вопросы с подсказками и ответами. Лучше понять концепции, решая эти практические задачи на …

Радианы Викторина Флэшкарточки — Quizlet

quizlet.com › Математика › Геометрия › Тригонометрия

Изучайте с помощью Quizlet и запоминайте карточки, содержащие такие термины, как радиан 0 градусов, радиан 30 градусов, радиан 45 градусов и другие.

Единица окружности Градусы в радианах Карточки с викториной | Quizlet