Конспект урока «Синус, косинус, тангенс острого угла прямоугольного треугольника»
8г.41
Урок № 41
Дата _____
Класс 8-Б, 8-В
Учитель Туманова И.Н
Тема: «Синус, косинус и тангенс острого угла прямоугольного треугольника»
Цели: Исследовать новые связи и зависимости, вывести соотношения между сторонами и углами прямоугольного треугольника и научиться их применять при решении задач
УУД предметные:
— определения синуса, косинуса, тангенса и котангенса острого угла прямоугольного треугольника
-умение записывать синус, косинус, тангенс и котангенс для острого угла
-умение устанавливать логические отношения
Коммуникативные УУД:
— строить рассуждение и доказательство своей точки зрения;
— формулировать и аргументировано отстаивать свою точку зрения;
— учитывать разные мнения и стремиться к координации различных позиций в сотрудничестве.
Личностные результаты:
— оценивать и осознавать свой вклад в общий результат урока;
— связывать свои успехи с усилием, трудолюбием;
ответственно относиться к учению;
Тип урока: урок усвоения знаний.
Оборудование: карточки, учебник, проектор, экран
Ход урока
Проверка домашнего задания (1 ученик у доски)
Опрос определений
-А какие треугольники называются подобными?
-Сколько существует признаков подобия треугольников? Давайте вспомним каждый из них
-Среднее геометрическое ( отрезок ХУ= )
— Катет прямоугольного треугольника есть среднее пропорциональное между гипотенузой и отрезком гипотенузы, заключенным между катетом и высотой, проведенной из этой вершины
-Высота прямоугольного треугольника, проведенная из вершины прямого угла, есть среднее пропорциональное для отрезков , на которые делится гипотенуза этой выстой
Закрепление изученного материала.
Самостоятельная работа с взаимопроверкой
Самостоятельная работа
АС и ВС — ____________________________
АВ — _________________________________
CD -_________________________________
C
А D B
вар | Катет АС | Катет ВС | Гипотенуза АВ | Высота СD | АD | BD | |||
1 | 10 | 10 | 5 | ||||||
2 | 6 |
Катет прямоугольного треугольника есть среднее пропорциональное между____________ __________________________________________________________________________________________________________________________________________________________
Высота прямоугольного треугольника, проведенная из вершины прямого угла, есть среднее пропорциональное между________________________________________________ _____________________________________________________________________________
ОТВЕТЫ
АС и ВС — _катеты______
АВ — __гипотенуза_________
CD -___высоты______
C
А D B
вар | Катет АС | Катет ВС | Гипотенуза АВ | Высота СD | АD | BD | |||
1 | 10 | 10 | 10 | 5 | 5 | 5 | 5 | 10 | 10 |
2 | 6 | 6 | 6 | 6 |
Катет прямоугольного треугольника есть среднее пропорциональное между гипотенузой и отрезком гипотенузы, заключенным между катетом и высотой, проведенной из этой вершины
Высота прямоугольного треугольника, проведенная из вершины прямого угла, есть среднее пропорциональное для отрезков , на которые делится гипотенуза этой выстой
III Изучение нового материала
Для изучения нового материала формулируйте соотношение между гипотенузой и катетами прямоугольного треугольника:
Т еорема Пифагора: В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.
Термин «гипотенуза» происходит от греческого слова «ипонейноуза», обозначающее «тянущаяся над чем-либо», «стягивающая». Слово берет начало от образа древнегреческих арф, на которых струны натягиваются на концах двух взаимно-перпендикулярных подставок. Термин «катет» происходит от греческого слова «катетос», которое означает начало «отвес», «перпендикуляр».
Евклид говорил: «Катеты – это стороны, заключающие прямой угол».
1.Введем понятия противолежащего и прилежащего катетов в прямоугольном треугольнике.
Пусть АВС – прямоугольный треугольник с прямым углом С и острым углом при вершине А, равным.
В
С А
Выделите красным цветом угол А и катет ВС.
Выделите зеленым цветом катет АС и угол В, а синим гипотенузу АВ.
АВ – гипотенуза
ВС – катет, противолежащий углу А ВС – катет, прилежащий углу В
АС – катет, прилежащий углу А АС – катет, противолежащий углу В
Катет, лежащий против острого угла, называется противолежащим
Катет, выходящий из острого угла, называется прилежащим.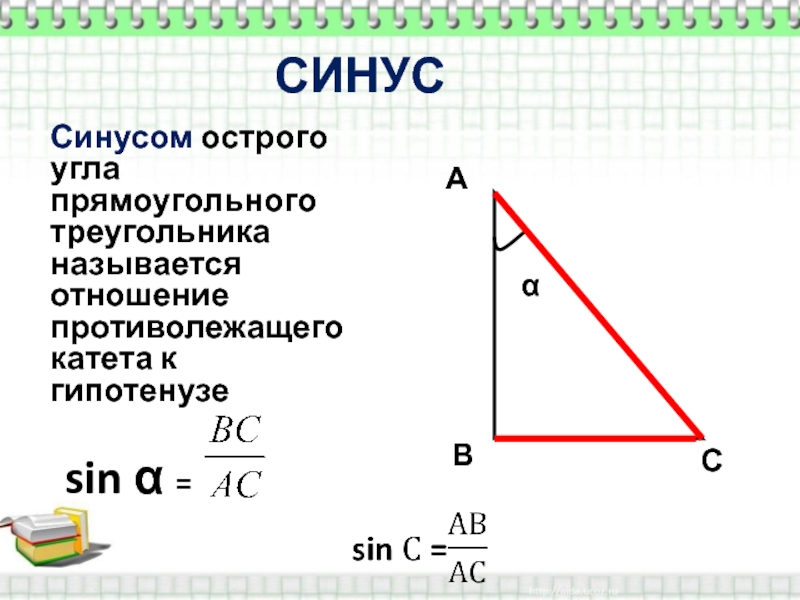
Устно:
Назовите катет, прилежащий к углу О и катет, противолежащий углу О.
Назовите катет, прилежащий к углу Т и катет, противолежащий углу Т.
Назовите катет, прилежащий к углу А1 и катет, противолежащий углу А1.
Назовите катет, прилежащий к углу В1 и катет, противолежащий углу В1.
2.Теперь введем понятие синуса, косинуса, тангенса острого угла прямоугольного треугольника, и их обозначения.
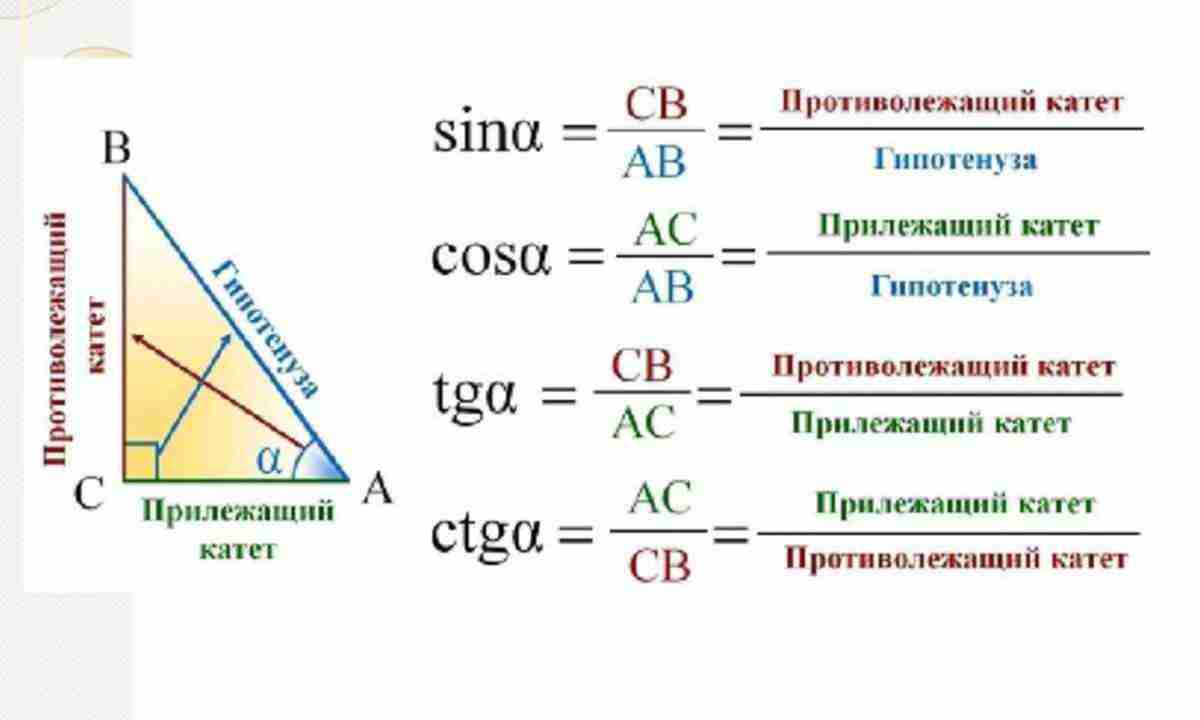
Синусом острого угла в прямоугольном треугольнике называется отношение противолежащего катета к гипотенузе.
Косинусом острого угла в прямоугольном треугольнике называется отношение прилежащего катета к гипотенузе.
Т ангенсом острого угла в прямоугольном треугольнике называется отношение противолежащего катета к прилежащему.
Найдем отношение синуса угла А к его косинусу:
Тангенс угла равен отношению синуса к косинусу этого угла.
IV. Физкультминутка для глаз.
V. Первичная проверка понимания.
Найти:
sin A = 0,8 sin В = 0,6 sin О = 5/13 sin A1 = 0,8
cos A = 0,6 cos В = 0,8 cos О = 12/13 cos A1 = 0,6
tg A = 4/3 tg В = 3/4 tg О = 5/12 tg A1 = 8/6 = 4/3
Сравните значения синуса, косинуса и тангенса углов и сделайте вывод.
sin A = cos В cos A = sin В tg A = 1 / tg В
Эти правила позволяют, зная одну из сторон прямоугольного треугольника и острый угол, находить две другие стороны:
a = c sin α b = c cos α a = b tg α
Выполнить № 591а, 592а по учебнику
№592а (построить треугольник с катетами в отношении 1:2 (4 и 8 ; 5 и 10)
V. Рефлексия.
-Что нового вы узнали сегодня?
Синусом острого угла в прямоугольном треугольнике называется отношение противолежащего катета к гипотенузе.
Косинусом острого угла в прямоугольном треугольнике называется отношение прилежащего катета к гипотенузе.
Тангенсом острого угла в прямоугольном треугольнике называется отношение противолежащего катета к прилежащему
-Что вызвало затруднения?
Домашнее задание: п 68 выучить теорию № 591бв., 593
5
Формула нахождения площади прямоугольного треугольника через синус. Игры с линейкой и карандашом
В жизни нам часто придется сталкиваться с математическими задачами: в школе, в университете, а затем помогая своему ребенку с выполнением домашнего задания. Люди определенных профессий будут сталкиваться с математикой ежедневно. Поэтому полезно запоминать или вспоминать математические правила. В этой статье мы разберем одно из них: нахождение катета прямоугольного треугольника.
Что такое прямоугольный треугольник
Для начала вспомним, что такое прямоугольный треугольник. Прямоугольный треугольник – это геометрическая фигура из трех отрезков, которые соединяют точки, не лежащие на одной прямой, и один из углов этой фигуры равен 90 градусам. Стороны, образующие прямой угол, называются катетами, а сторона, которая лежит напротив прямого угла – гипотенузой.
Прямоугольный треугольник – это геометрическая фигура из трех отрезков, которые соединяют точки, не лежащие на одной прямой, и один из углов этой фигуры равен 90 градусам. Стороны, образующие прямой угол, называются катетами, а сторона, которая лежит напротив прямого угла – гипотенузой.
Находим катет прямоугольного треугольника
Существует несколько способов, позволяющих узнать длину катета. Хотелось бы рассмотреть бы их подробнее.
Теорема Пифагора, чтобы найти катет прямоугольного треугольника
Если нам известны гипотенуза и катет, то мы можем найти длину неизвестного катета по теореме Пифагора. Звучит она так: “Квадрат гипотенузы равен сумме квадратов катетов”. Формула: c²=a²+b², где c – гипотенуза, a и b – катеты. Преобразовываем формулу и получаем: a²=c²-b².
Пример. Гипотенуза равна 5 см, а катет – 3 см. Преобразовываем формулу: c²=a²+b² → a²=c²-b². Далее решаем: a²=5²-3²; a²=25-9; a²=16; a=√16; a=4 (см).
Тригонометрические соотношения, чтобы найти катет прямоугольного треугольника
Также можно найти неизвестный катет, если известны любая другая сторона и любой острый угол прямоугольного треугольника. Есть четыре варианта нахождения катета при помощи тригонометрических функций: по синусу, косинусу, тангенсу, котангенсу. Для решения задач нам поможет таблица, которая находится чуть ниже. Рассмотрим эти варианты.
Есть четыре варианта нахождения катета при помощи тригонометрических функций: по синусу, косинусу, тангенсу, котангенсу. Для решения задач нам поможет таблица, которая находится чуть ниже. Рассмотрим эти варианты.
Найти катет прямоугольного треугольника при помощи синуса
Синус угла (sin) – это отношение противолежащего катета к гипотенузе. Формула: sin=a/c, где а – катет, лежащий против данного угла, а с – гипотенуза. Далее преобразуем формулу и получаем: a=sin*c.
Пример. Гипотенуза равна 10 см, угол А равен 30 градусов. По таблице вычисляем синус угла А, он равен 1/2. Затем по преобразованной формуле решаем: a=sin∠А*c; a=1/2*10; a=5 (см).
Найти катет прямоугольного треугольника при помощи косинуса
Косинус угла (cos) – это отношение прилежащего катета к гипотенузе. Формула: cos=b/c, где b – катет, прилежащий к данному углу, а с – гипотенуза. Преобразуем формулу и получим: b=cos*c.
Пример. Угол А равен 60 градусов, гипотенуза равна 10 см. По таблице вычисляем косинус угла А, он равен 1/2. Далее решаем: b=cos∠A*c; b=1/2*10, b=5 (см).
По таблице вычисляем косинус угла А, он равен 1/2. Далее решаем: b=cos∠A*c; b=1/2*10, b=5 (см).
Найти катет прямоугольного треугольника при помощи тангенса
Тангенс угла (tg) – это отношение противолежащего катета к прилежащему. Формула: tg=a/b, где а – противолежащий к углу катет, а b – прилежащий. Преобразуем формулу и получаем: a=tg*b.
Пример. Угол А равен 45 градусов, гипотенуза равна 10 см. По таблице вычисляем тангенс угла А, он равен Решаем: a=tg∠A*b; a=1*10; a=10 (см).
Найти катет прямоугольного треугольника при помощи котангенса
Котангенс угла (ctg) – это отношение прилежащего катета к противолежащему. Формула: ctg=b/a, где b – прилежащий к углу катет, а – противолежащий. Иначе говоря, котангенс – это “перевернутый тангенс”. Получаем: b=ctg*a.
Пример. Угол А равен 30 градусов, противолежащий катет равен 5 см. По таблице тангенс угла А равен √3. Вычисляем: b=ctg∠A*a; b=√3*5; b=5√3 (см).
Итак, теперь вы знаете, как находить катет в прямоугольном треугольнике.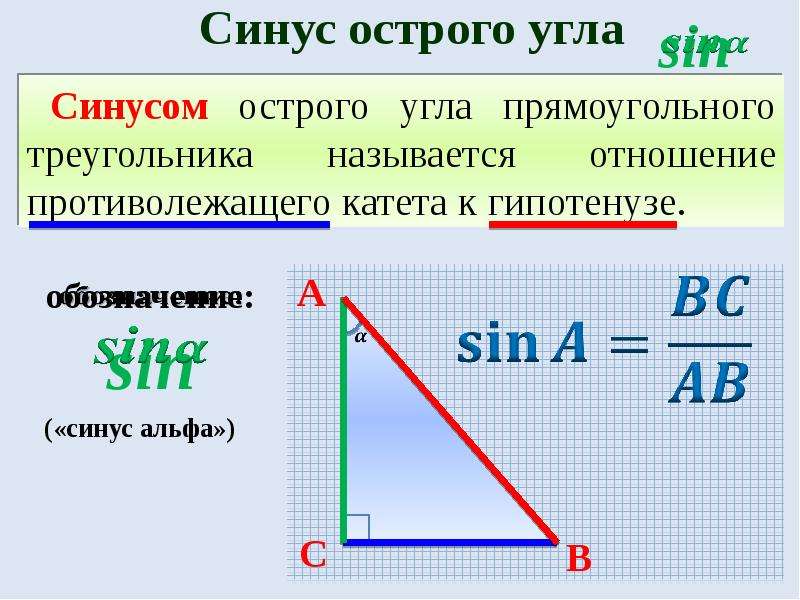 Как видите, это не так уж и сложно, главное – запомнить формулы.
Как видите, это не так уж и сложно, главное – запомнить формулы.
Синус является одной из основных тригонометрических функций, применение которой не ограничено одной лишь геометрией. Таблицы вычисления тригонометрических функций, как и инженерные калькуляторы, не всегда под рукой, а вычисление синуса порой нужно для решения различных задач. Вообще, вычисление синуса поможет закрепить чертёжные навыки и знание тригонометрических тождеств.
Игры с линейкой и карандашом
Простая задача: как найти синус угла, нарисованного на бумаге? Для решения понадобится обычная линейка, треугольник (или циркуль) и карандаш. Простейшим способом вычислить синус угла можно, разделив дальний катет треугольника с прямым углом на длинную сторону — гипотенузу. Таким образом, сначала нужно дополнить острый угол до фигуры прямоугольного треугольника, прочертив перпендикулярную одному из лучей линию на произвольном расстоянии от вершины угла. Потребуется соблюсти угол именно 90°, для чего нам и понадобится канцелярский треугольник.
Использование циркуля немного точнее, но займёт больше времени. На одном из лучей нужно отметить 2 точки на некотором расстоянии, настроить на циркуле радиус, примерно равный расстоянию между точками, и прочертить полуокружности с центрами в этих точках до получения пересечений этих линий. Соединив точки пересечения наших окружностей между собой, мы получим строгий перпендикуляр к лучу нашего угла, остаётся лишь продлить линию до пересечения с другим лучом.
В полученном треугольнике нужно линейкой измерить сторону напротив угла и длинную сторону на одном из лучей. Отношение первого измерения ко второму и будет искомой величиной синуса острого угла.
Найти синус для угла больше 90°
Для тупого угла задача не намного сложнее. Нужно прочертить луч из вершины в противоположную сторону с помощью линейки для образования прямой с одним из лучей интересующего нас угла. С полученным острым углом следует поступать как описано выше, синусы смежных углов, образующих вместе развёрнутый угол 180°, равны.
Вычисление синуса по другим тригонометрическим функциям
Также вычисление синуса возможно, если известны значения других тригонометрических функций угла или хотя бы длины сторон треугольника. В этом нам помогут тригонометрические тождества. Разберём распространённые примеры.
Как находить синус при известном косинусе угла? Первое тригонометрическое тождество, исходящее из теоремы Пифагора, гласит, что сумма квадратов синуса и косинуса одного и того же угла равна единице.
Как находить синус при известном тангенсе угла? Тангенс получают делением дальнего катета на ближний или делением синуса на косинус. Таким образом, синусом будет произведение косинуса на тангенс, а квадратом синуса будет квадрат этого произведения. Заменяем косинус в квадрате на разность между единицей и квадратным синусом согласно первому тригонометрическому тождеству и путём нехитрых манипуляций приводим уравнение к вычислению квадратного синуса через тангенс, соответственно, для вычисления синуса придётся извлечь корень из полученного результата.
Как находить синус при известном котангенсе угла? Значение котангенса можно вычислить, разделив длину ближнего от угла катета на длину дальнего, а также поделив косинус на синус, то есть котангенс — функция, обратная тангенсу относительно числа 1. Для расчёта синуса можно вычислить тангенс по формуле tg α = 1 / ctg α и воспользоваться формулой во втором варианте. Также можно вывести прямую формулу по аналогии с тангенсом, которая будет выглядеть следующим образом.
Как находить синус по трём сторонам треугольника
Существует формула для нахождения длины неизвестной стороны любого треугольника, не только прямоугольного, по двум известным сторонам с использованием тригонометрической функции косинуса противолежащего угла. Выглядит она так.
Ну, а синус можно далее рассчитать по косинусу согласно формулам выше.
Площадь треугольника равна половине произведения его сторон на синус угла между ними.
Доказательство:
Рассмотрим произвольный треугольник ABC. Пусть в нем сторона BC = a, сторона CA = b и S — площадь этого треугольника. Необходимо доказать, что S = (1/2)*a*b*sin(C) .
Пусть в нем сторона BC = a, сторона CA = b и S — площадь этого треугольника. Необходимо доказать, что S = (1/2)*a*b*sin(C) .
Для начала введем прямоугольную систему координат и поместим начало координат в точку С. Расположим нашу систему координат так, чтобы точка B лежала на положительном направлении оси Сх, а точка А имела бы положительную ординату.
Если все выполнить правильно, то должен получится следующий рисунок.
Площадь данного треугольника можно вычислить по следующей формуле: S = (1/2)*a*h , где h — это высота треугольника. В нашем случае высота треугольника h равна ординате точки А, то есть h = b*sin(C).
Учитывая полученные результат, формулу площади треугольника можно переписать следующим образом: S = (1/2)*a*b*sin(C). Что и требовалось доказать.
Решение задач
Задача 1. Найти площадь треугольника ABC, если а) AB = 6*√8 см, АС = 4 см, угол А = 60 градусов б) BC = 3 см, AB = 18*√2 см, угол B= 45 градусов в) AC = 14 см, CB = 7 см, угол C= 48 градусов. 2. Найдите сторону AB, если AC = 15 см, угол А = 30˚.
2. Найдите сторону AB, если AC = 15 см, угол А = 30˚.
Положим S — площадь треугольника ABC. По теореме о площади треугольника имеем:
S = (1/2)*AB*AC*sin(A).
Подставим в неё имеющиеся у нас значения:
60 = (1/2)*AB*15*sin30˚ = (1/2)*15*(1/2)*AB=(15/4)*AB.
Отсюда выражаем длину стороны AB: AB = (60*4)/15 = 16.
Если в задаче даны длины двух сторон треугольника и угол между ними, то можно применить формулу площади треугольника через синус.
Пример расчета площади треугольника через синус. Даны стороны a = 3, b = 4, и угол γ= 30°. По синус угла в 30° равен 0.5
Площадь треугольника будет равна 3 кв. см.
Также могут быть и другие условия. Если дана длина одной стороны и углы, то для начала нужно вычислить недостающий угол. Т.к. сумма всех углов треугольника равняется 180°, то:
Площадь будет равна половине квадрата стороны, умноженной на дробь. В ее числителе находится произведение синусов прилегающих углов, а в знаменателе синус противолежащего угла. Теперь рассчитываем площадь по следующим формулам:
Теперь рассчитываем площадь по следующим формулам:
Например, дан треугольник со стороной a=3 и углами γ=60°, β=60°. Вычисляем третий угол:
Подставляем данные в формулу
Получаем, что площадь треугольника равняется 3,87 кв. см.
II. Площадь треугольника через косинус
Чтобы найти площадь треугольника, нужно знать длины всех сторон. По теореме косинусов можно найти не известные стороны, а уже потом использовать .
По теореме косинусов квадрат неизвестной стороны треугольника равняется сумме квадратов остальных сторон минус удвоенное произведение этих сторон на косинус угла, находящегося между ними.
Из теоремы выводим формулы для поиска длины неизвестной стороны:
Зная как найти недостающую сторону, имея две стороны и угол между ними можно легко посчитать площадь. Формула площади треугольника через косинус помогает легко и быстро найти решение различных задач.
Пример расчета формулы площади треугольника через косинус
Дан треугольник с известными сторонами a = 3, b = 4, и углом γ= 45°. Для начала найдем недостающую сторону с . По косинус 45°=0,7. Для этого подставим данные в уравнение, выведенное из теоремы косинусов.
Для начала найдем недостающую сторону с . По косинус 45°=0,7. Для этого подставим данные в уравнение, выведенное из теоремы косинусов.
Сторону треугольника дозволено обнаружить не только по периметру и площади, но и по заданной стороне и углам. Для этого применяются тригонометрические функции – синус и косинус . Задачи с их применением встречаются в школьном курсе геометрии, а также в вузовском курсе аналитической геометрии и линейной алгебры.
Инструкция
1. Если знаменита одна из сторон треугольника и угол между ней и иной его стороной, воспользуйтесь тригонометрическими функциями – синус ом и косинус ом. Представьте себе прямоугольный треугольник НBC , у которого угол? равен 60 градусам. Треугольник НBC показан на рисунке. От того что синус , как знаменито, представляет собой отношение противолежащего катета к гипотенузе, а косинус – отношение прилежащего катета к гипотенузе, для решения поставленной задачи воспользуйтесь дальнейшим соотношением между этими параметрами:sin ?=НB/BCСоответственно, если вы хотите узнать катет прямоугольного треугольника, выразите его через гипотенузу дальнейшим образом:НB=BC*sin ?
2. Если в условии задачи, напротив, дан катет треугольника, обнаружьте его гипотенузу, руководствуясь дальнейшим соотношением между заданными величинами:BC=НB/sin ?По аналогии обнаружьте стороны треугольника и с применением косинус а, изменив предыдущее выражение дальнейшим образом:cos ?=НC/BC
Если в условии задачи, напротив, дан катет треугольника, обнаружьте его гипотенузу, руководствуясь дальнейшим соотношением между заданными величинами:BC=НB/sin ?По аналогии обнаружьте стороны треугольника и с применением косинус а, изменив предыдущее выражение дальнейшим образом:cos ?=НC/BC
3. В элементарной математике существует представление теоремы синус ов. Руководствуясь фактами, которые описывает данная теорема, также дозволено обнаружить стороны треугольника. Помимо этого, она разрешает обнаружить стороны треугольника, вписанного в окружность, если знаменит вестим радиус последней. Для этого воспользуйтесь соотношением, указанным ниже:a/sin ?=b/sin b=c/sin y=2RЭта теорема применима в том случае, когда знамениты две стороны и угол треугольника, либо дан один из углов треугольника и радиус описанной вокруг него окружности.
4. Помимо теоремы синус ов, существует и аналогичная ей по сути теорема косинус ов, которая, как и предыдущая, также применима к треугольникам всех 3 разновидностей: прямоугольному, остроугольному и тупоугольному. 2-2ab*cos ?
2-2ab*cos ?
Геометрическая фигура, состоящая из трёх точек, не принадлежащих одной прямой называемых вершинами, и трёх попарно соединяющих их отрезков, называемых сторонами, именуется треугольником. Существует уйма задач на нахождение сторон и углов треугольника по ограниченному числу начальных данных, одна из таких задач – нахождение стороны треугольника по одной из его сторон и двум углам .
Инструкция
1. Пускай построен треугольник?ABC и знамениты – сторона BC и углы?? и??.Знаменито, что сумма углов всякого треугольника равна 180?, следственно в треугольнике?ABC угол?? будет равен?? = 180? – (?? + ??).Обнаружить стороны AC и AB дозволено применяя теорему синусов, которая гласитAB/sin?? = BC/sin?? = AC/sin?? = 2 * R, где R – радиус описанной около треугольника?ABC окружности,тогда получаемR = BC/sin??,AB = 2 * R * sin??,AC = 2 * R * sin??.Теорему синусов дозволено использовать при всяких данных 2-х углах и стороне.
2. Стороны заданно треугольника дозволено обнаружить, вычислив его площадь по формулеS = 2 * R? * sin?? * sin?? * sin??,где R вычисляется по формулеR = BC/sin??, R – радиус описанной около треугольника?ABC отсюдаТогда сторону AB дозволено обнаружить, вычислив высоту, опущенную на неёh = BC * sin??,отсель по формуле S = 1/2 * h * AB имеемAB = 2 * S/hАналогичным образом дозволено вычислить сторону AC.
3. Если в качестве углов даны внешние углы треугольника?? и??, то обнаружить внутренние углы дозволено с поддержкой соответствующих соотношений?? = 180? – ??,?? = 180? – ??,?? = 180? – (?? + ??).Дальше действуем подобно первым двум пунктам.
Постижение треугольников ведется математиками на протяжении нескольких тысячелетий. Наука о треугольниках – тригонометрия – использует особые величины: синус и косинус.
Прямоугольный треугольник
Изначально синус и косинус появились из-за необходимости рассчитывать величины в прямоугольных треугольниках. Было подмечено, что если значение градусной меры углов в прямоугольном треугольнике не менять, то соотношение сторон, насколько бы эти стороны ни изменялись в длине, остается неизменно идентичным.Именно так и были введены представления синуса и косинуса. Синус острого угла в прямоугольном треугольнике – это отношение противолежащего катета к гипотенузе, а косинус – прилежащего к гипотенузе.
Теоремы косинусов и синусов
Но косинусы и синусы могут использоваться не только в прямоугольных треугольниках. Дабы обнаружить значение тупого либо острого угла, стороны всякого треугольника, довольно применить теорему косинусов и синусов.Теорема косинусов достаточно примитивна: «Квадрат стороны треугольника равен сумме квадратов 2-х других сторон за вычетом удвоенного произведения этих сторон на косинус угла между ними». Существует две трактовки теоремы синусов: малая и расширенная. Согласно малой: «В треугольнике углы пропорциональны противолежащим сторонам». Данную теорему зачастую расширяют за счет свойства описанной около треугольника окружности: «В треугольнике углы пропорциональны противолежащим сторонам, а их отношение равно диаметру описанной окружности».
Дабы обнаружить значение тупого либо острого угла, стороны всякого треугольника, довольно применить теорему косинусов и синусов.Теорема косинусов достаточно примитивна: «Квадрат стороны треугольника равен сумме квадратов 2-х других сторон за вычетом удвоенного произведения этих сторон на косинус угла между ними». Существует две трактовки теоремы синусов: малая и расширенная. Согласно малой: «В треугольнике углы пропорциональны противолежащим сторонам». Данную теорему зачастую расширяют за счет свойства описанной около треугольника окружности: «В треугольнике углы пропорциональны противолежащим сторонам, а их отношение равно диаметру описанной окружности».
Производные
Производная – математический инструмент, показывающий, как стремительно меняется функция касательно метаморфозы ее довода. Производные применяются в алгебре, геометрии, экономике и физике, ряде технических дисциплин. При решении задач требуется знать табличные значения производных тригонометрических функций: синуса и косинуса. Производной синуса является косинус, а косинуса – синус, но со знаком «минус».
Производной синуса является косинус, а косинуса – синус, но со знаком «минус».
Применение в математике
Особенно зачастую синусы и косинусы применяются при решении прямоугольных треугольников и задач, связанных с ними. Удобство синусов и косинусов обнаружило свое отражение и в технике. Углы и стороны было примитивно оценивать по теоремам косинусов и синусов, разбивая трудные фигуры и объекты на «примитивные» треугольники. Инженеры и архитекторы, зачастую имеющие дело с расчетами соотношения сторон и градусных мер, тратили много времени и усилий для вычисления косинусов и синусов не табличных углов. Тогда «на подмогу» пришли таблицы Брадиса, содержащие тысячи значений синусов, косинусов, тангенсов и котангенсов различных углов. В советское время некоторые преподаватели принуждали своих подопечных учить страницы таблиц Брадиса назубок.
{2},}a2+b2=c2, используется для нахождения длины любой стороны прямоугольного треугольника.
ccc
, а длины других сторон помечены какaaa
иbbb
, теорема Пифагора утверждает, что 9\circ90∘). Прямоугольный треугольник – это треугольник, в котором один угол прямой. Соотношение между сторонами и углами прямоугольного треугольника является основой тригонометрии.
Сторона, противолежащая прямому углу, называется гипотенузой (на рисунке сторона
ccc
). Стороны, примыкающие к прямому углу, называются катетами (стороны
aaa
и
bbb
). Сторона
aaa
может быть идентифицирована как сторона, прилегающая к углу
BBB
и напротив (или напротив) угла
AAA
. Сторона
Сторона
bbb
— это сторона, примыкающая к углу
AAA
и противолежащая углу
BBB
.
Прямоугольный треугольник: Теорему Пифагора можно использовать, чтобы найти значение длины недостающей стороны в прямоугольном треугольнике.
Если длины всех трех сторон прямоугольного треугольника являются целыми числами, такой треугольник называется пифагорейским треугольником, а длины его сторон в совокупности называются пифагорейской тройкой.
Теорема Пифагора
Теорема Пифагора, также известная как теорема Пифагора, является фундаментальным соотношением в евклидовой геометрии. Он определяет отношение между тремя сторонами прямоугольного треугольника. В нем говорится, что квадрат гипотенузы (сторона, противоположная прямому углу) равен сумме квадратов двух других сторон.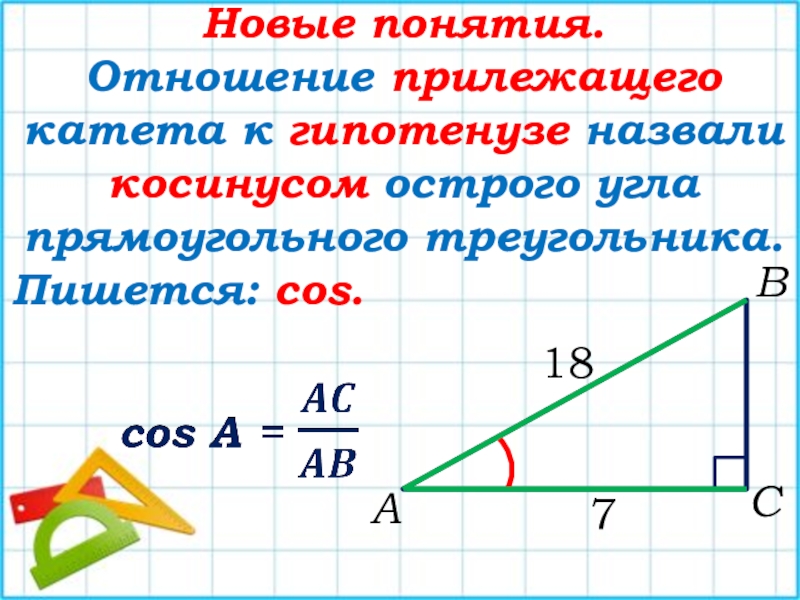 Теорему можно записать в виде уравнения, связывающего длины сторон
Теорему можно записать в виде уравнения, связывающего длины сторон
aaa
,
bbb
9{2}}a2+b2=c2В этом уравнении
ccc
представляют длину гипотенузы, а
aaa
и
bbb
длины гипотенузы две другие стороны треугольника.
Хотя часто говорят, что знание теоремы предшествовало ему, [2] теорема названа в честь древнегреческого математика Пифагора (ок. 570 – ок. 495 до н.э.). Ему приписывают первое зарегистрированное доказательство.
Теорема Пифагора: 92a2+b2=c2
.
Поиск недостающей длины стороны
Пример 1. Прямоугольный треугольник имеет длину стороны
101010
футов и длину гипотенузы
202020
футов. Найдите длину другой стороны. (округлить до десятых долей фута)
Найдите длину другой стороны. (округлить до десятых долей фута)
Подставить
a=10a=10a=10
и
c=20c=20c=20
в теорему Пифагора и найти
ббб
.
92} &=\sqrt{300} \\ б &=17,3 ~\mathrm{футов} \end{выравнивание} }a2+b2(10)2+b2100+b2b2b2b=c2=(20)2=400=300=300
=17,3 фута
Пример 2. Длина сторон прямоугольного треугольника равна
333
см и
444
см. Найдите длину гипотенузы.
Подставить
a=3a=3a=3
и
b=4b=4b=4
в теорему Пифагора и найти
ccc
900 08 . 92} &=\sqrt{25} \\ с &=5~\mathrm{см} \end{выравнивание} }a2+b232+429+1625c2c2c=c2=c2=c2=c2=25=25
=5 см
Как работают тригонометрические функции
Тригонометрические функции можно использовать для нахождения отсутствующих длин сторон в прямоугольных треугольниках.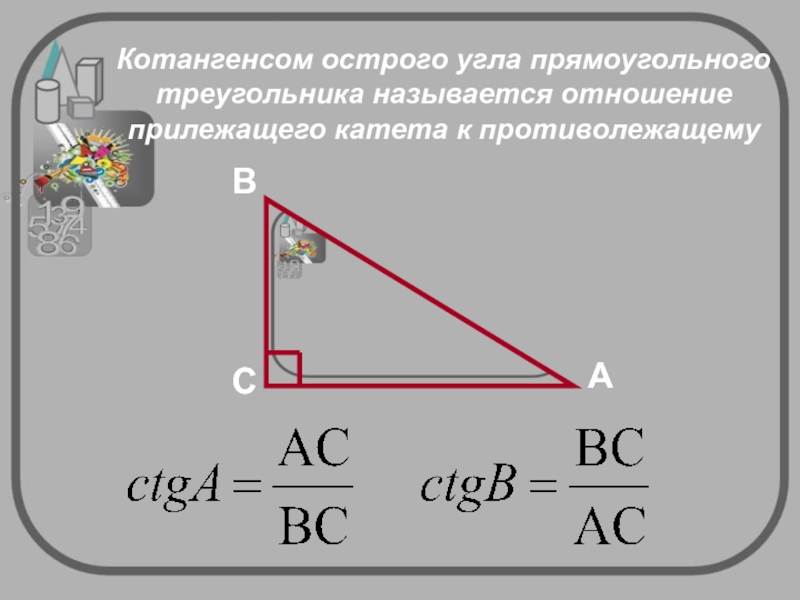
Цели обучения
Узнайте, как тригонометрические функции используются для решения задач о прямоугольных треугольниках, и определите их входы и выходы
Основные выводы
Ключевые моменты 9{\ circ} 90 ∘
) Три тригонометрические функции, наиболее часто используемые для определения недостающей стороны прямоугольного треугольника: }sint=hypotenuseopposite ,cost=adjacenthypotenuse\displaystyle{\cos{t} = \frac {adjacent}{hypotenuse}}cost=hypotenuseadjacent
, иtant=oppositeadjacent\displaystyle{\tan{ t} = \frac {противоположный} {смежный}} tant=соседний напротив
Тригонометрические функции
Мы можем определить тригонометрические функции через угол
ttt
и длины сторон треугольника. Прилегающая сторона – это сторона, ближайшая к углу. (Смежный означает «рядом с».) Противоположная сторона – это сторона, расположенная напротив угла.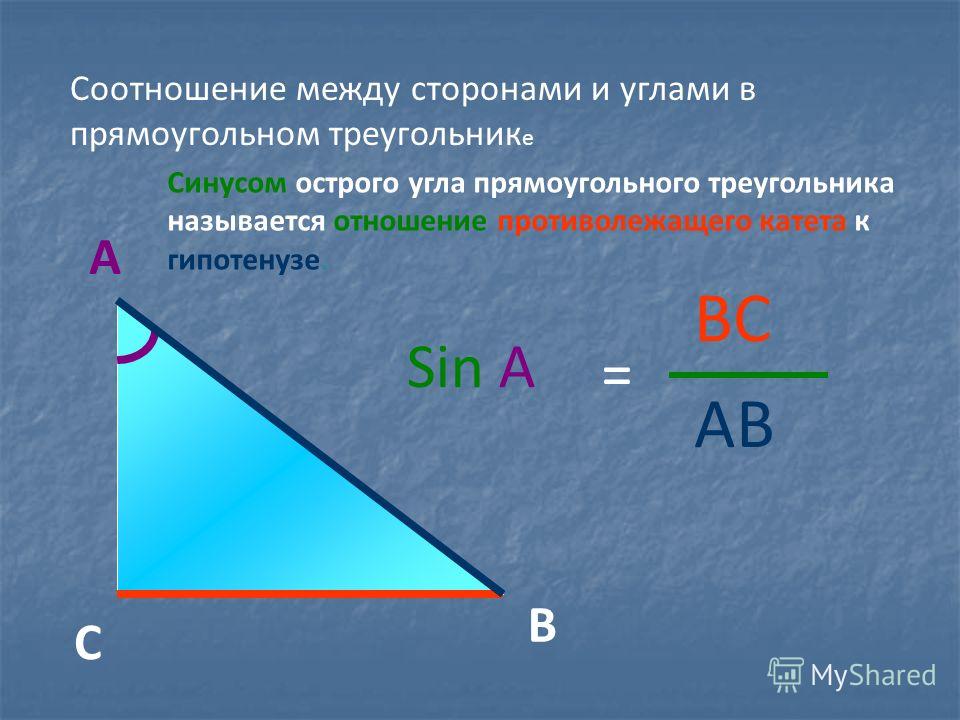 Гипотенуза — это сторона треугольника, противоположная прямому углу, и она самая длинная.
Гипотенуза — это сторона треугольника, противоположная прямому углу, и она самая длинная.
Прямоугольный треугольник: Стороны прямоугольного треугольника относительно угла
ttt
.
При поиске отсутствующей стороны прямоугольного треугольника, но единственной полученной информацией является измерение острого угла и длина стороны, используйте тригонометрические функции, перечисленные ниже:
- Синус {t} = \frac {напротив} {гипотенуза}}sint=гипотенузанапротив
- Косинус
cost=adjacenthypotenuse\displaystyle{\cos{t} = \frac {adjacent}{hypotenuse}}cost=hypotenuseadjacent
- Касательная
tant=противоположныйсмежный\displaystyle{\tan{t} = \frac {напротив}{смежный}}tant=adjacentopposite
Тригонометрические функции равны отношениям, которые связывают определенные длины сторон прямоугольного треугольника. При поиске отсутствующей стороны первым шагом является определение того, какие стороны и какой угол даны, а затем выбор подходящей функции для решения проблемы.
При поиске отсутствующей стороны первым шагом является определение того, какие стороны и какой угол даны, а затем выбор подходящей функции для решения проблемы.
Вычисление тригонометрической функции прямоугольного треугольника
Иногда вы знаете длину одной стороны треугольника и угла, и вам нужно найти другие измерения. Используйте одну из тригонометрических функций ( 9{\circ}34∘
и длину гипотенузы
252525
футов, найдите длину стороны, противоположной острому углу (округлите до десятых):
Прямоугольный треугольник: Дан прямоугольный треугольник с острого угла
343434
градусов и длины гипотенузы
252525
футов, найдите длину противоположной стороны.
Глядя на рисунок, найдите сторону, противоположную острому углу
343434 9{\circ}83∘
и длину гипотенузы
300300300
футов, найдите длину гипотенузы (округлив до десятых):
Прямоугольный треугольник: Дан прямоугольный треугольник с острым углом
838383
градусов и длину гипотенузы
300300300
футов, найдите длину гипотенузы.
Глядя на рисунок, найдите гипотенузу острого угла
838383
градусов. Отношение сторон равно 9{\circ}\right)}} \\ x &= \frac{300}{\left(0,1218\dots\right)} \\ х &=2461,7~\mathrm{футы} \end{выравнивание} }costcos(83∘)x⋅cos(83∘)xxx=hypotenuseadjacent=x300=300=cos(83∘)300=(0,1218…)300=2461,7 футов
Синус, косинус и Тангенс
Мнемоника
SohCahToa может быть использована для определения длины стороны прямоугольного треугольника.
Цели обучения
Используйте аббревиатуру SohCahToa для определения синуса, косинуса и тангенса в терминах прямоугольных треугольников
Key Takeaways
Key Points
- Общая мнемоника для запоминания отношений между функциями синуса, косинуса и тангенса — SohCahToa.
- SohCahToa образован из первых букв « S ine is o pposite over h ypotenuse ( Soh ), C osine is 903 19 a djacent over h ypotenuse ( Cah ), Тангенс противоположен соседнему ( Тоа ).

Определения тригонометрических функций
Для прямоугольного треугольника с острым углом
ttt
первые три тригонометрические функции таковы:
- сайт}{гипотенуза} } sint=hypotenuseopposite
- Косинус
cost=adjacenthypotenuse\displaystyle{ \cos{t} = \frac {adjacent}{hypotenuse} }cost=hypotenuseadjacent
- Касательная
tant=oppositeadjacent\displaystyle{ \tan{t} = \frac {напротив}{adjacent} }tant=adjacentopposite
Общая мнемоника для запоминания этих взаимосвязей — SohCahToa , образованная из первых букв « S ine is o pposite over h ypotenuse ( Soh ), 9 0319 C озин — это a djacent более ч ypotenuse ( Cah ), Тангенс противоположен соседнему ( 9{\ circ} 62∘
и смежная сторона
454545
футов, найдите длину противоположной стороны.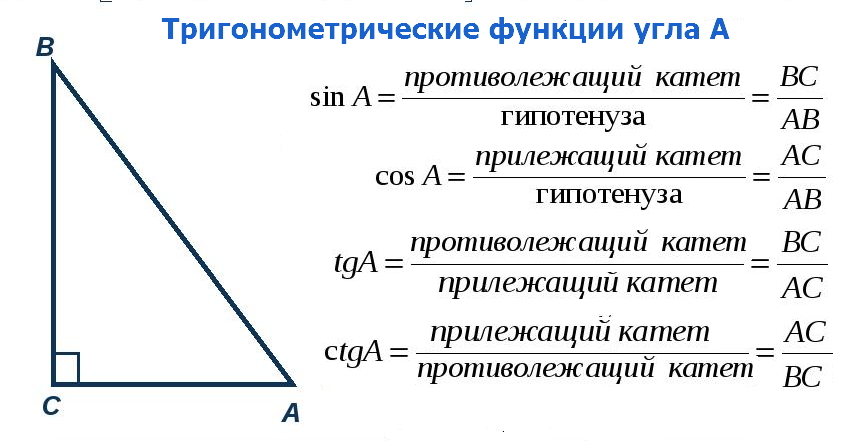 (округлить до десятых)
(округлить до десятых)
Прямоугольный треугольник: Дан прямоугольный треугольник с острым углом
626262
градусов и смежной стороной
454545
футов, найти противоположную сторону длина.
Сначала определите, какую тригонометрическую функцию использовать, если дана смежная сторона, и вам нужно решить для противоположной стороны. Всегда определяйте, какая сторона дана, а какая неизвестна по острому углу ( 9\circ32∘
, гипотенуза равна 30 футам, а недостающая длина стороны равна противоположному катету,
xxx
футов.
Определите, какую тригонометрическую функцию использовать, если задана гипотенуза, и вам нужно решить для противоположной стороны. Вспоминая мнемонику « S ohCahToa», указанные стороны представляют собой гипотенузу и противолежащие стороны или «h» и «o», которые использовали бы «S» или синусоидальную тригонометрическую функцию.
sint=противоположная гипотенуза in(32∘)=x3030⋅sin(32∘)=xx=30⋅sin(32∘)x=30⋅(0,529{\ круг} \ справа)} \\ x &= 30\cdot\left( 0.5299\dots\right) \\ х &= 15,9 ~\mathrm{футов} \end{выравнивание} }sintsin(32∘)30⋅sin(32∘)xxx=hypotenuseopposite=30x=x=30⋅sin(32∘)=30⋅(0,5299…)=15,9 футов
Нахождение углов из отношений : Обратные тригонометрические функции
Обратные тригонометрические функции можно использовать для нахождения измерения острого угла прямоугольного треугольника.
Цели обучения
Использование обратных тригонометрических функций при решении задач на прямоугольные треугольники 9{-1}tan−1
. Использование тригонометрических функций для определения отсутствующей стороны при заданном остром угле так же просто, как определение сторон относительно острого угла, выбор правильной функции, составление уравнения и решение. Найти недостающий острый угол по двум сторонам прямоугольного треугольника так же просто.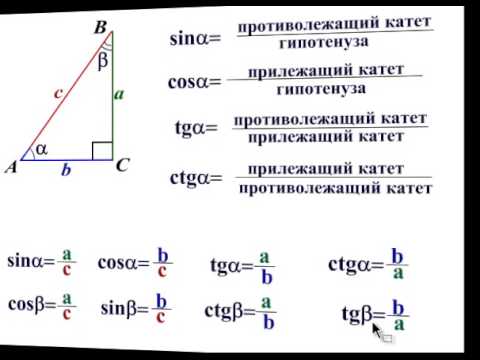
Обратные тригонометрические функции
Чтобы найти недостающий острый угол, используйте те же три тригонометрические функции, но используйте обратный ключ ( 9\circA∘
с длиной противоположной стороны
12 футов12~\mathrm{feet}12 футов
, найдите острый угол с точностью до ближайшего градуса:
Прямоугольный треугольник: Найдите величину угла
9000 2 ААА, если даны противолежащий катет и гипотенуза.
Из угла
AAA
даны стороны напротив и гипотенуза . Поэтому используйте тригонометрическую функцию синуса. ( Soh от SohCahToa) Напишите уравнение и решите его, используя обратный ключ для синуса.
9{\ круг}
\end{выравнивание}
}sinA∘sinA∘A∘A∘A=hypotenuseopposite=2512=sin-1(2512)=sin-1(0.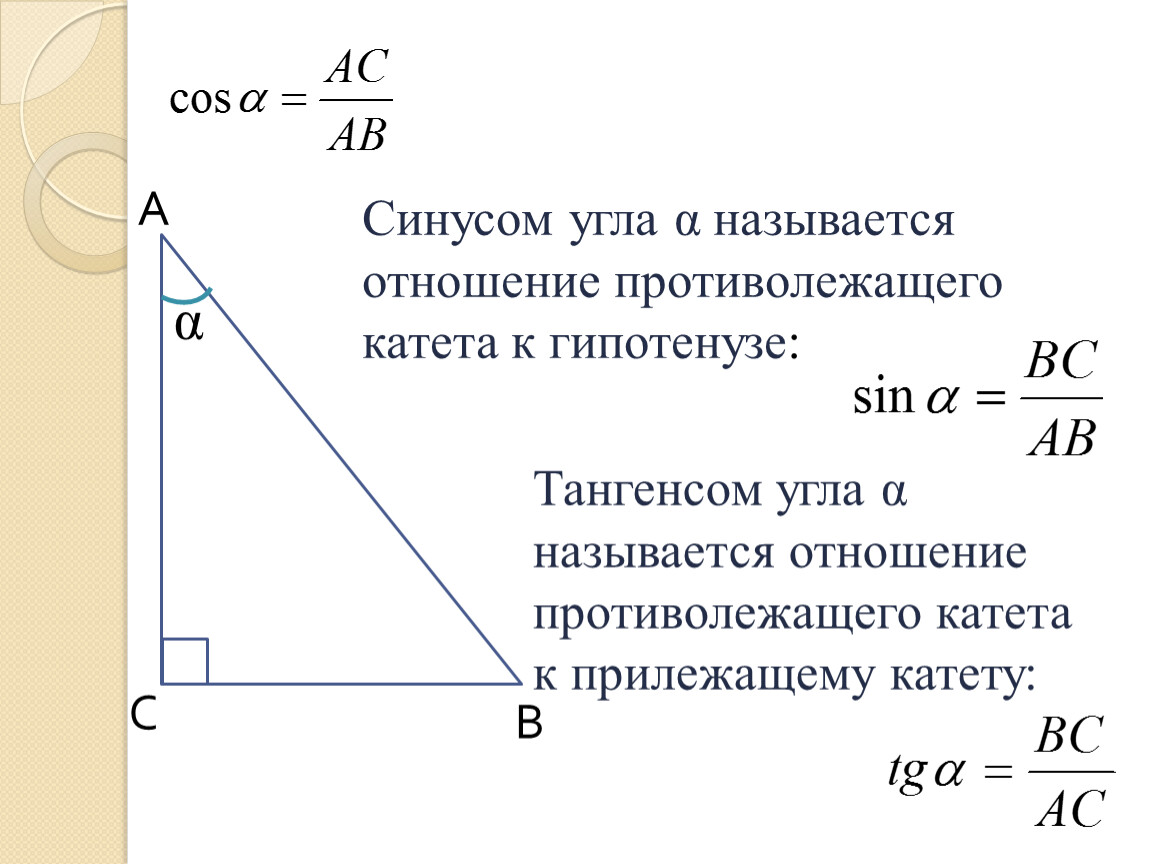 48)=29∘
48)=29∘
Лицензии и атрибуты
Лицензионный контент CC, опубликованный ранее
- Курирование и доработка. Автор : Boundless.com. Лицензия : Общественное достояние: Неизвестно Авторские права
Лицензионный контент CC, конкретное указание авторства
- Прямоугольный треугольник. Предоставлено : Википедия. Лицензия : CC BY-SA: Attribution-ShareAlike
- Теорема Пифагора. Предоставлено : Википедия. Лицензия : CC BY-SA: Attribution-ShareAlike
- 346px-Rtriangle.svg.jpg. Предоставлено : Википедия. Лицензия : CC BY-SA: Attribution-ShareAlike
- 265px-Pythagorean.svg.jpg. Предоставлено : Википедия. Лицензия : CC BY-SA: Attribution-ShareAlike
- Тригонометрия прямоугольного треугольника.
 Предоставлено : OpenStax. Расположен по адресу : https://openstax.org/books/алгебра-и-тригонометрия/pages/7-2-right-triangle-trigonometry. Лицензия : CC BY-SA: Attribution-ShareAlike
Предоставлено : OpenStax. Расположен по адресу : https://openstax.org/books/алгебра-и-тригонометрия/pages/7-2-right-triangle-trigonometry. Лицензия : CC BY-SA: Attribution-ShareAlike - Тригонометрические функции. Предоставлено : Википедия. Лицензия : CC BY-SA: Attribution-ShareAlike
- 346px-Rtriangle.svg.jpg. Предоставлено : Википедия. Лицензия : CC BY-SA: Attribution-ShareAlike
- 265px-Pythagorean.svg.jpg. Предоставлено : Википедия. Лицензия : CC BY-SA: Attribution-ShareAlike
- Оригинальная фигура Джанет Хеймбах. Лицензия CC BY-SA 4.0. Предоставлено : Джанет Хеймбах. Лицензия : CC BY-SA: Attribution-ShareAlike
- Оригинальная фигура Джанет Хеймбах. Лицензия CC BY-SA 4.0. Предоставлено : Джанет Хеймбах.
 Лицензия : CC BY-SA: Attribution-ShareAlike
Лицензия : CC BY-SA: Attribution-ShareAlike - CNX_Precalc_Figure_05_04_002.jpg. Предоставлено : OpenStax. Расположен по адресу : https://openstax.org/books/алгебра-и-тригонометрия/pages/7-2-right-triangle-trigonometry. Лицензия : CC BY-SA: Attribution-ShareAlike
- Тригонометрические функции. Предоставлено : Википедия. Расположен по адресу : https://en.wikipedia.org/wiki/Trigonometric_functions. Лицензия : CC BY-SA: Attribution-ShareAlike
- Тригонометрия прямоугольного треугольника. Предоставлено : OpenStax. Расположен по адресу : https://openstax.org/books/алгебра-и-тригонометрия/pages/7-2-right-triangle-trigonometry. Лицензия : CC BY-SA: Attribution-ShareAlike
- 346px-Rtriangle.svg.jpg. Предоставлено : Википедия.
 Лицензия : CC BY-SA: Attribution-ShareAlike
Лицензия : CC BY-SA: Attribution-ShareAlike - 265px-Pythagorean.svg.jpg. Предоставлено : Википедия. Лицензия : CC BY-SA: Attribution-ShareAlike
- Оригинальная фигура Джанет Хаймбах. Лицензия CC BY-SA 4.0. Предоставлено : Джанет Хеймбах. Лицензия : CC BY-SA: Attribution-ShareAlike
- Оригинальная фигура Джанет Хеймбах. Лицензия CC BY-SA 4.0. Предоставлено : Джанет Хеймбах. Лицензия : CC BY-SA: Attribution-ShareAlike
- CNX_Precalc_Figure_05_04_002.jpg. Предоставлено : OpenStax. Расположен по адресу : https://openstax.org/books/алгебра-и-тригонометрия/pages/7-2-right-triangle-trigonometry. Лицензия : CC BY-SA: Attribution-ShareAlike
- Оригинальная фигура Джанет Хеймбах. Лицензия CC BY-SA 4.0. Предоставлено : Джанет Хеймбах.
 Лицензия : CC BY-SA: Attribution-ShareAlike
Лицензия : CC BY-SA: Attribution-ShareAlike - CNX_Precalc_Figure_05_04_002.jpg. Предоставлено : OpenStax. Лицензия : CC BY-SA: Attribution-ShareAlike
- Оригинальная фигура Джанет Хаймбах. Лицензия CC BY-SA 4.0. Предоставлено : Джанет Хеймбах. Лицензия : CC BY-SA: Attribution-ShareAlike
- Тригонометрия прямоугольного треугольника. Предоставлено : openstax. Расположен по адресу : https://openstax.org/books/алгебра-и-тригонометрия/pages/7-2-right-triangle-trigonometry. Лицензия : CC BY-SA: Attribution-ShareAlike
- Тригонометрические функции. Предоставлено : Википедия. Лицензия : CC BY-SA: Attribution-ShareAlike
- 346px-Rtriangle.svg.jpg. Предоставлено : Википедия. Лицензия : CC BY-SA: Attribution-ShareAlike
- 265px-Pythagorean.
 svg.jpg. Предоставлено : Википедия. Лицензия : CC BY-SA: Attribution-ShareAlike
svg.jpg. Предоставлено : Википедия. Лицензия : CC BY-SA: Attribution-ShareAlike - Оригинальная фигура Джанет Хеймбах. Лицензия CC BY-SA 4.0. Предоставлено : Джанет Хеймбах. Лицензия : CC BY-SA: Attribution-ShareAlike
- Оригинальная фигура Джанет Хеймбах. Лицензия CC BY-SA 4.0. Предоставлено : Джанет Хеймбах. Лицензия : CC BY-SA: Attribution-ShareAlike
- CNX_Precalc_Figure_05_04_002.jpg. Предоставлено : OpenStax. Расположен по адресу : https://openstax.org/books/алгебра-и-тригонометрия/pages/7-2-right-triangle-trigonometry. Лицензия : CC BY-SA: Attribution-ShareAlike
- Оригинальная фигура Джанет Хаймбах. Лицензия CC BY-SA 4.0. Предоставлено : Джанет Хеймбах. Лицензия : CC BY-SA: Attribution-ShareAlike
- CNX_Precalc_Figure_05_04_002.
 jpg. Предоставлено : OpenStax. Лицензия : CC BY-SA: Attribution-ShareAlike
jpg. Предоставлено : OpenStax. Лицензия : CC BY-SA: Attribution-ShareAlike - Оригинальная фигура Джанет Хеймбах. Лицензия CC BY-SA 4.0. Предоставлено : Джанет Хеймбах. Лицензия : CC BY-SA: Attribution-ShareAlike
- Оригинальная фигура Джанет Хаймбах. Лицензия CC BY-SA 4.0. Предоставлено : Джанет Хеймбах. Лицензия : CC BY-SA: Attribution-ShareAlike
Предыдущая
Следующая
Смежные и противоположные углы в прямоугольных треугольниках (тригонометрия)
Задавать вопрос
спросил
Изменено 1 год, 8 месяцев назад
Просмотрено 3к раз
$\begingroup$
Итак, я первокурсник средней школы и хочу знать, как синус, косинус и тангенс помогают найти длины сторон. (Это не вопрос для домашнего задания)
(Это не вопрос для домашнего задания)
Я знаю, что в прямоугольном треугольнике 30-60-90 градусов соотношение равно 1, корень квадратный из 3, а гипотенуза равна 2.
Я также понимаю следующее:
- Синус противоположен гипотенузе
- Косинус примыкает к гипотенузе
- Касательная противоположна соседней
Главное, с чем у меня проблема, это определить, какие стороны какие; какой из них напротив, а какой рядом.
Например, какой угол вы бы использовали для sin30 (где угол c — прямой угол, a — верхний угол, а b — угол вправо) и какой угол вы бы использовали для sin60?
- тригонометрия
$\endgroup$
3
$\begingroup$
Допустим, у вас есть треугольник, как показано ниже. $A, B, C$ — его вершины, $a, b, c$ — его стороны, $\alpha, \beta, \gamma$ — углы (я не отметил $\beta$ и $\gamma$ , поэтому опишем все, что нам нужно для $\alpha$).
$\alpha$ — острый угол прямоугольного треугольника $ABC$. Сторона $BC$ (или $a$, как ей присвоено другое обозначение) является противоположным ему катетом, а $AC$ (или $b$) — примыкающим к нему катетом. $AB$ (или $c$) — гипотенуза.
Учитывая это, например, $\sin \alpha = \frac{\text{напротив}}{\text{гипотенуза}} = \frac{BC}{AB} = \frac ac$. Это очень похоже на другие функции, надеюсь, вы сможете с ними справиться.
Как правильно заметил @abel, тригонометрические функции определены не для треугольника, а для угла, поэтому вам нужно проверить, что треугольник прямоугольный, найти в нем заданный острый угол, и тогда у вас будут две стороны, прилегающие к этому углу ( гипотенуза и прилежащий катет) и одна сторона, противоположная ей. 9\circ.$
давайте сконцентрируемся на $\угол A.$ противоположная сторона $BC$ и смежная сторона $AC.$
если вы переключитесь на $\угол B,$ то противоположное сторона равна $AC$, а соседняя сторона равна $BC.$
имеет ли это смысл?
$\endgroup$
8
$\begingroup$
Гипотенуза — самая длинная сторона, обычно обозначаемая H. Он находится напротив прямого угла.
Он находится напротив прямого угла.
Другие стороны зависят от того, какой ракурс вас интересует. Таким образом, угол, по отношению к которому вы отмечаете стороны, будет между гипотенузой и соседним. Он находится рядом с углом. Обычно называется A
. Последний угол — это угол, противоположный углу, который вы выбрали для обозначения сторон. Обычно он называется О.
Интересующий вас ракурс будет варьироваться от задачи к задаче.
$\endgroup$
$\begingroup$
Google сказал мне это.
Гипотенуза — это сторона прямоугольного треугольника, противолежащая угол 90 градусов. Это термин, относящийся к математике, особенно к геометрии. Гипотенуза происходит от греческого слова гипотенуза, что означает «растягивание под». Гипотенуза «вытягивается» под прямым углом треугольника, угол которого равен 90 градусов.
Вы сами решаете, какой угол вы хотите исследовать.

 Предоставлено : OpenStax. Расположен по адресу : https://openstax.org/books/алгебра-и-тригонометрия/pages/7-2-right-triangle-trigonometry. Лицензия : CC BY-SA: Attribution-ShareAlike
Предоставлено : OpenStax. Расположен по адресу : https://openstax.org/books/алгебра-и-тригонометрия/pages/7-2-right-triangle-trigonometry. Лицензия : CC BY-SA: Attribution-ShareAlike  Лицензия : CC BY-SA: Attribution-ShareAlike
Лицензия : CC BY-SA: Attribution-ShareAlike 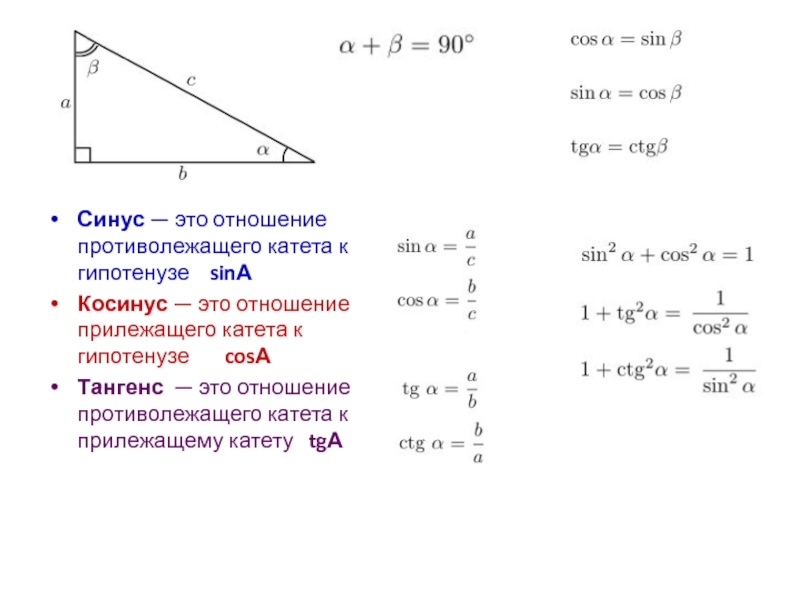 Лицензия : CC BY-SA: Attribution-ShareAlike
Лицензия : CC BY-SA: Attribution-ShareAlike  Лицензия : CC BY-SA: Attribution-ShareAlike
Лицензия : CC BY-SA: Attribution-ShareAlike  svg.jpg. Предоставлено : Википедия. Лицензия : CC BY-SA: Attribution-ShareAlike
svg.jpg. Предоставлено : Википедия. Лицензия : CC BY-SA: Attribution-ShareAlike 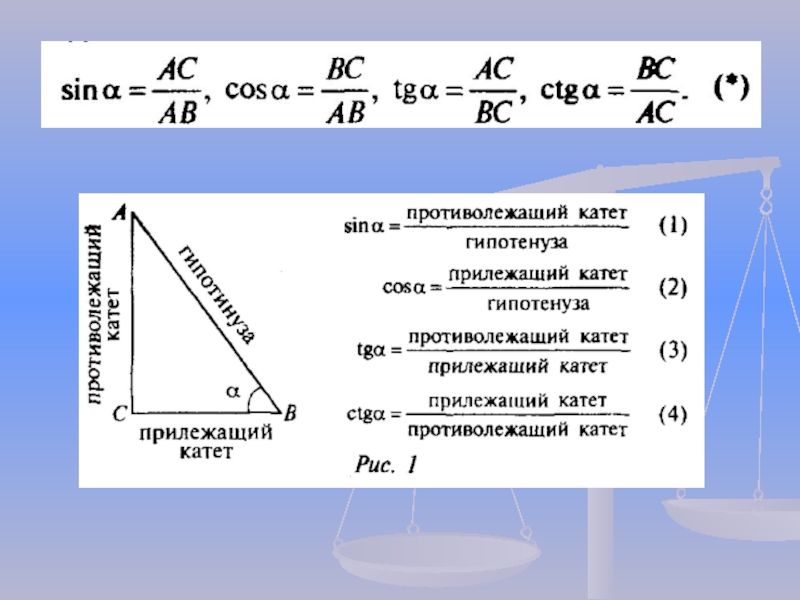 jpg. Предоставлено : OpenStax. Лицензия : CC BY-SA: Attribution-ShareAlike
jpg. Предоставлено : OpenStax. Лицензия : CC BY-SA: Attribution-ShareAlike