Синус удвоенного угла: Формулы двойного аргумента (базовый уровень) — урок. Алгебра, 10 класс.

Содержание

Урок по алгебре в 9-м классе «Синус и косинус двойного угла» (с применением элементов образовательных технологий А.С. Границкой, В.Ф. Шаталина, компьютерных технологий)

Цели:

Образовательные

Развивающие

Воспитательные

Задачи:

Образовательные

Развивающие —

Воспитательные

Методы обучения

Элементы адаптивной системы обучения А. С. Границкой: обучение учащихся приемам самостоятельной работы, умениям добывать знания, обобщать и делать выводы, самоконтроль и взаимоконтроль. Элементы технологии В.Ф. Шаталина. Элементы проблемного метода обучения. Элементы компьютерных технологий.

Формы организации урока: индивидуальная, парная, фронтальная.

Оборудование и источники информации:

компьютер, мультимедийный проектор, экран;
презентация для сопровождения урока;
схема с формулами синуса и косинуса двойного угла, листы самоконтроля, самостоятельные уровневые работы (2 типа).

Ход урока

Презентация

Организационный момент (2 мин).

Цель: сообщение темы урока, целей, формирование мотива желания работать на уроке, мобилизация внимания.

— Сообщение темы урока, целей, эпиграфа. Слайды 1-2.

Когда-то Блез Паскаль сказал, что «математика — наука настолько серьёзная, что нельзя упускать случая, сделать её немного занимательной». Поэтому я предлагаю наш урок начать с занимательной странички

(

тригонометрия

Актуализация знаний (1мин.) Слайд 4. Найдите ошибку!

Изучение нового материала (2-3 мин).

Цель: получение формул синуса и косинуса двойного угла, развитие логического мышления, внимания, умения говорить и слушать.

Учащимся предлагается упростить выражения:

ctg² x (1— cos² x ) =

ctg² x (1— cos² x ) — соs 2 x =

Какие затруднения возникли? (незнание формулы соs 2x)

А как можно её получить? (соs (x +x))

Какие формулы можно ещё получить?

Получите sin 2x, tg2x и ctg2x (работа в парах постоянного и сменного состава)

Итак, cos 2x = cos²x — sin²x

sin 2x = 2 sinx cosx

Совместная работа учителя с классом (5-7 мин).

Цель: показать применение формул синуса и косинуса двойного угла для преобразования тригонометрических выражений; развитие логического мышления, внимания, умения говорить и слушать.

Учащимся предъявляется 5 заданий (слайд 5). При фронтальной работе с классом проговаривается решение всех заданий, подробно записывается решение 3 заданий, выбранных учащимися.

Упростите выражения:

2) 3) 4)

2. cos 2x — 2 sin²x

1) cos ²x — 2 sin²x 2) 1 3) 1+ 2 sin²x 4) 1+ sin²x

1) ctgx 2) tgx 3) 4)

1) 2) 3) 4)

1) -cos2x 2) cos2x 3) sin2x 4) — sin2x

Закрепление изученного материала (10 мин).

Обучающая самостоятельная работа учащихся. Индивидуальная работа учителя. Цель: создание условий для логического мышления, умения делать выводы. Формирование тестовой культуры учащихся, развитие учебно — познавательной компетенции. Проверка первичного усвоения знаний, самокоррекция.

Работа проходит индивидуально (включенный контроль учителя) по карточкам с тестовыми заданиями(приложение 1). Карточки выбирают ученики с учетом их уровня. После решения каждый себя проверяет себя по ключам к самостоятельной работе и листам самоконтроля.(приложение 2)

Физминутка (1 мин.)— приёмы релаксации [3].
Примите удобную позу сидя на стуле. Начните с расслабления мышц. Плечи висят (лежат) свободно. Двигается предплечье. Согните предплечье под прямым углом к плечу (к туловищу). Опустите свободно, как плеть, так, чтобы оно падало лишь под действием собственной тяжести. Уловите контраст между напряжением при сгибании и расслаблением при опускании. Попеременно справа и слева. Вместе. В комбинации с расслаблением кистей и пальцев. Попробуйте добиться с помощью вышеописанных упражнений полного расслабления тела.

В положении сидя, ноги согнуты в коленях под углом приблизительно 100 градусов. Согните стопу, опираясь на пятку и приведя к голени, свободно отпустите. Вместе и попеременно. Вытянув слегка расставленные ноги, опора на пятки: раскачивайте стопы влево — вправо, свободно, как на шарнирах, попеременно и вместе.
Пофантазируйте. Закройте глаза и вообразите, что вы отправляетесь в своей фантазии в какое-нибудь место — знакомое и нравящееся вам или то, которое вы себе таким представляете. Сейчас вы вернётесь в класс и всё сможете решить.

Этап информации учащихся о домашнем задании (1-2 мин.).
25 (знать формулы)
Дифференцированное задание по уровням сложности:
1) №308(2,4), №310
2) №311, №314(2)
3) выписать и решить 5 заданий по данной теме из следующих заданий:
№352 — № 356

Этап всесторонней проверки знаний (10-16 мин.).
Проверочная самостоятельная работа учащихся. Цель: Всесторонне проверить знания учащихся при преобразовании тригонометрических выражений с применением формул синуса и косинуса двойного угла, развитие компетенций личностного совершенствования и ценностно — смысловой.

Учащимся предлагается самостоятельная работа по уровням. Приложение 3.
По истечении времени учащиеся меняются работами и проверяют в вариационных парах решения (по готовым ответам — слайд 12) — 1мин.
Решение проверяется карандашом, ставится оценка, фамилия проверяющего ученика.

Итог урока (2-3 мин).
Проходит в виде фронтальной работы с классом по вопросам (для учащихся 1 и 2 уровней) и индивидуальной работы с заданием №5 (для учащихся 3 уровня) — слайд 13.
4) Докажите тождество
5)
— Назовите ответ в заданиях 1 и 3.
— Какие формулы нужны для решения задания №2?
— Назовите самый рациональный способ решения задания №4.
— Урок окончен. До свидания! Слайд 14.

Литература
Алгебра: Учебник для 9 класса общеобразовательных учреждений/ Ш.А. Алимов, Ю.М. Колягин и др., 6-е изд.: — М: «Просвещение», 2005.

Сычёва Е.И., Сычёв А.В. Тестовые задания по математике: алгебра 9 класс.- М.: «Школьная пресса», 2006.

http://www.2mm.ru/psihologia/657

Приложение 1, приложение 2, приложение 3.
Mathway | Популярные задачи

1 Найти точное значение sin(30)
2 Найти точное значение sin(45)
3 Найти точное значение sin(30 град. )
4 Найти точное значение sin(60 град. )
5
Найти точное значение tan(30 град. )
6 Найти точное значение arcsin(-1)
7 Найти точное значение sin(pi/6)
8 Найти точное значение cos(pi/4)
9 Найти точное значение sin(45 град. )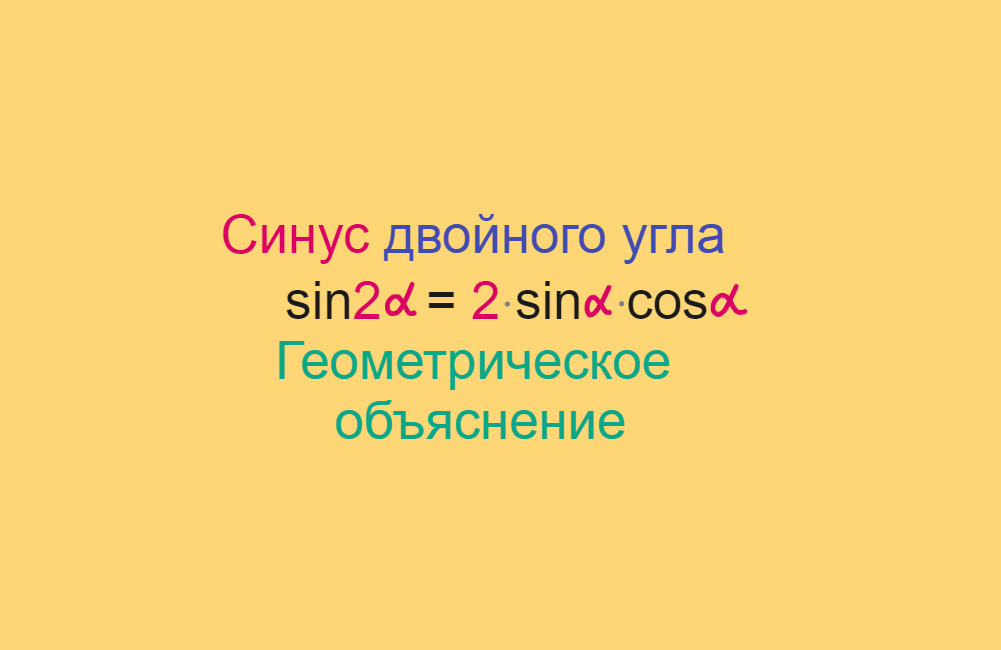
10 Найти точное значение sin(pi/3)
11 Найти точное значение arctan(-1)
12 Найти точное значение cos(45 град. )
13 Найти точное значение cos(30 град. )
14 Найти точное значение tan(60)
15 Найти точное значение csc(45 град. )
16 Найти точное значение tan(60 град. )
17 Найти точное значение sec(30 град. )
18 Найти точное значение cos(60 град. )
19 Найти точное значение cos(150)
20 Найти точное значение sin(60)
21 Найти точное значение cos(pi/2)
22 Найти точное значение tan(45 град. )
23 Найти точное значение arctan(- квадратный корень из 3)
24 Найти точное значение csc(60 град. )
25 Найти точное значение sec(45 град. )
26 Найти точное значение csc(30 град. )
27 Найти точное значение sin(0)
28 Найти точное значение sin(120)
29 Найти точное значение cos(90)
30 Преобразовать из радианов в градусы pi/3
31 Найти точное значение tan(30)
32 Преобразовать из градусов в радианы 45
33 Найти точное значение cos(45)
34 Упростить sin(theta)^2+cos(theta)^2
35 Преобразовать из радианов в градусы pi/6
36 Найти точное значение cot(30 град. )
37 Найти точное значение arccos(-1)
38 Найти точное значение arctan(0)
39 Найти точное значение cot(60 град. )
40 Преобразовать из градусов в радианы 30
41 Преобразовать из радианов в градусы (2pi)/3
42 Найти точное значение sin((5pi)/3)
43 Найти точное значение sin((3pi)/4)
44 Найти точное значение tan(pi/2)
45 Найти точное значение sin(300)
46 Найти точное значение cos(30)
47 Найти точное значение cos(60)
48 Найти точное значение cos(0)
49 Найти точное значение cos(135)
50 Найти точное значение cos((5pi)/3)
51 Найти точное значение cos(210)
52 Найти точное значение sec(60 град. )
53 Найти точное значение sin(300 град. )
54 Преобразовать из градусов в радианы 135
55 Преобразовать из градусов в радианы 150
56 Преобразовать из радианов в градусы (5pi)/6
57 Преобразовать из радианов в градусы (5pi)/3
58 Преобразовать из градусов в радианы 89 град.
59 Преобразовать из градусов в радианы 60
60 Найти точное значение sin(135 град. )
61 Найти точное значение sin(150)
62 Найти точное значение sin(240 град. )
63 Найти точное значение cot(45 град. )
64 Преобразовать из радианов в градусы (5pi)/4
65 Найти точное значение sin(225)
66 Найти точное значение sin(240)
67 Найти точное значение cos(150 град. )
68 Найти точное значение tan(45)
69 Вычислить sin(30 град. )
70 Найти точное значение sec(0)
71 Найти точное значение cos((5pi)/6)
72 Найти точное значение csc(30)
73 Найти точное значение arcsin(( квадратный корень из 2)/2)
74 Найти точное значение tan((5pi)/3)
75 Найти точное значение tan(0)
76 Вычислить sin(60 град. )
77 Найти точное значение arctan(-( квадратный корень из 3)/3)
78 Преобразовать из радианов в градусы (3pi)/4
79 Найти точное значение sin((7pi)/4)
80 Найти точное значение arcsin(-1/2)
81 Найти точное значение sin((4pi)/3)
82 Найти точное значение csc(45)
83 Упростить arctan( квадратный корень из 3)
84 Найти точное значение sin(135)
85 Найти точное значение sin(105)
86 Найти точное значение sin(150 град. )
87 Найти точное значение sin((2pi)/3)
88 Найти точное значение tan((2pi)/3)
89 Преобразовать из радианов в градусы pi/4
90 Найти точное значение sin(pi/2)
91 Найти точное значение sec(45)
92 Найти точное значение cos((5pi)/4)
93 Найти точное значение cos((7pi)/6)
94 Найти точное значение arcsin(0)
95 Найти точное значение sin(120 град. )
96 Найти точное значение tan((7pi)/6)
97 Найти точное значение cos(270)
98 Найти точное значение sin((7pi)/6)
99 Найти точное значение arcsin(-( квадратный корень из 2)/2)
100 Преобразовать из градусов в радианы 88 град.
2\text{(u)}}{2\text{tan(u)}}
Если задана одна тригонометрическая функция, ее значение и ее квадрант, вы можете найти точное значение каждого тождества двойного угла. Например, если нужно найти точное значение sin2u по $\text{sec(u)}=\frac{9}{2}$ для $0\leq\text{u}\leq\frac{\pi} {2}$ (и находится в квадранте 1). Вы можете начать решение задачи с изучения уравнения для sin2u. По формуле для sin2u значения sinu и cosu должен быть известен. Вторая часть задачи заключается в нахождении точных значений sinu и cosu, используя заданное значение, секу. Мы знаем, что sec = $\frac{\text{гипотенуза}}{\text{adjacent}}$, единственное неизвестное значение — длина противоположной стороны. Это можно рассчитать с помощью теоремы Пифагора, которая гласит: 92}
\text{opposite}=\sqrt{77}
\text{(в простейшей форме)}
Теперь, когда известна длина противоположной стороны, мы можем найти значения sinu и cosu:
\ text{sin}=\frac{\text{напротив}}{\text{гипотенуза}}
\text{sin}=\frac{(\sqrt{77})}{(9)}
\text{ (в простейшей форме)}
\text{cos}=\frac{\text{adjacent}}{\text{гипотенуза}}
\text{cos}=\frac{(2)}{(9)}
\text{cos}=\frac{2}{9}
\text{(в простейшей форме)}
Заключительной частью процесса вычисления двойного угла является подстановка найденных значений sin и cos в формулу для sin2u следующим образом:
\text{sin2u}=2\cdot \text{sinu}\cdot \text{cosu}
\text{sin2u}=2\cdot (\frac{\sqrt{77}}{9})\cdot (\frac{2}{9})
\text{sin2u}=\frac{4\sqrt{ 77}}{81}
\text{(в простейшей форме)}
Окончательное значение sin2u равно $\frac{4\sqrt{77}}{81}$.
Учебное пособие по калькулятору двойного угла С данным
Вы должны начать с выбора идентификатора, который вы хотите вычислить, из выпадающего списка. После того, как личность была выбрана, вы должны выбрать заданную функцию и соотношение. например: $\tan=\frac{5}{8}$. Как только функция и отношение известны, вы можете выбрать квадрант центрального угла. Центральный угол должен быть допустимым, иначе расчет не будет работать. При использовании sin или cos абсолютное значение этих Отношения должны быть больше 0 и меньше 1. При использовании tan или cot абсолютное значение отношения может быть любым. При использовании любой другой функции абсолютное значение коэффициента должно быть больше 1,
Без заданного
Использование тождества двойного угла без заданного значения является менее сложным процессом. Вы просто выбираете идентификатор из раскрывающегося списка и выберите значение U, которое может быть любым значением. например: $\csc2\cdot8=0,2756373558169992$.
Идентичности с двойным углом | Великолепная математика и естественные науки Wiki
Тригонометрические формулы двойного угла дают связь между основными тригонометрическими функциями, примененными к удвоенному углу, в терминах тригонометрических функций самого угла.
Советы по запоминанию следующих формул:
Мы можем подставить значения (2x)(2x)(2x) в формулы сумм для sin⁡\sinsin и cos⁡.\cos.cos. Используя треугольники 45-45-90 и 30-60-90 градусов, мы можем легко увидеть отношения между sin⁡x\sin xsinx и cos⁡x\cos xcosx по длинам, которые они представляют. Несколько определений cos⁡2x\cos 2xcos2x можно получить, используя теорему Пифагора и tan⁡x=sin⁡xcos⁡x. \tan x = \frac{\sin x}{\cos x}.tanx=cosxsinx. 92=\frac{3}{4}-\frac{1}{4}=\frac{1}{2}. \ _\squarecos2α=cos2α−sin2α=(23)2–(21)2=43−41=21. □
Используйте тождество двойного угла для решения следующих задач:
Предположим,
cos⁡θ=35,sin⁡2θ=ab,\cos\theta = \frac{3}{5},\quad \sin2\ theta = \frac{a}{b},cosθ=53,sin2θ=ba,
, где 0<θ<π20<\theta <\frac{\pi}{2}0<θ<2π с aaa и bbb взаимно простые положительные целые числа.
Каково значение a+b?a+b?a+b?
Если sin⁡θ=513\sin\theta=\frac{5}{13}sinθ=135 и 0
<θ<π2,0<\theta<\frac{\pi}{2},0<θ< 2π, каково значение sin⁡2θ?\sin2\theta?sin2θ? 92}=\frac{12}{13}.cosθ=1−sin2θ=1−(135)2=1312. Отсюда следует, что sin⁡2θ=2sin⁡θcos⁡θ=2⋅513⋅1213=120169. □\sin2\theta=2\sin\theta\cos\theta =2\cdot \frac{5}{13} \cdot \frac{12}{13}=\frac{120}{169}. \ _\squaresin2θ=2sinθcosθ=2⋅135⋅1312=169120. □
Если sin⁡α=35\sin\alpha=\frac{3}{5}sinα=53 и π2
<α<π,\frac{\pi}{2}<\alpha<\pi,2π< α<π, каково значение tan⁡2α?\tan2\alpha?tan2α?
Учитывая sin⁡α=35\sin\alpha=\frac{3}{5}sinα=53 и π2<α<π,\frac{\pi}{2}<\alpha<\pi,2π <α<π, имеем cos⁡α=−1−sin⁡2α=−1−(35)2=−45. 2\theta}\\\\ &=\frac{\sin\theta(\cos\theta+\sin\theta)}{\cos\theta(\sin\theta+\cos\theta)}\\\\ &=\тангенс\тета=-1. \end{выровнено}tan2θ+sec2θ+1tan2θ+sec2θ−1=cos2θsin2θ+cos2θ1+1cos2θsin2θ+cos2θ1−1=sin2θ+1+cos2θsin2θ+1−cos2θ=2sinθcosθ+2cos2θ2sin2scos cosθ(sinθ+cosθ)sinθ(cosθ+sinθ)=tanθ=−1.
Тогда, поскольку 0<θ<π,0<\theta<\pi,0<θ<π, θ=3π4.\theta=\frac{3\pi}{4}. θ=43π. □_\квадрат□
Если csc⁡α=233\csc\alpha=\frac{2\sqrt{3}}{3}cscα=323 для 0<α<π2,0<\alpha<\frac{\pi}{2} ,0<α<2π, что такое sin⁡2α+cos⁡2α?\sin2\alpha+\cos2\alpha?sin2α+cos2α?
Поскольку sin⁡α=1csc⁡α=323=32\sin\alpha=\frac{1}{\csc\alpha}=\frac{3}{2\sqrt{3}}=\frac{\sqrt {3}}{2}sinα=cscα1=233=23 и 0<α<π2,0<\alpha<\frac{\pi}{2},0<α<2π, α =π3\alpha=\frac{\pi}{3}α=3π и cos⁡α=12.\cos\alpha=\frac{1}{2}.cosα=21. Следовательно, 92\theta.X=(sinθsin2θ)2=(sinθ2sinθcosθ)2=4cos2θ.
Следовательно, ответ (b).(b).(b). □_\квадрат□
Используйте формулы двойного угла, чтобы доказать тождество
csc⁡2θ−cot⁡2θ=tan⁡θ.
No related posts.