Синус угла в обычном треугольнике — Dudom
Синус (sin) – это одна из прямых тригонометрических функций. Подробнее о ней можно узнать из нашей статьи Что такое синус.
Синус угла в прямоугольном треугольнике
Прежде чем выяснять, как найти синус угла, необходимо определиться с условными обозначениями. Пусть в прямоугольном треугольнике:
- α – острый угол, синус которого нужно найти;
- с – гипотенуза;
- b – прилежащий катет;
- a – противолежащий катет.
Тогда чтобы найти синус острого угла прямоугольного треугольника, достаточно посчитать соотношение длины противолежащего катета к длине гипотенузы: sin(α) = a/c. При этом стоит запомнить, что sin 90° всегда равен 1.
Синус угла в произвольном треугольнике
Находить синус угла в произвольном треугольнике проще всего с использованием теоремы косинусов (cos): квадрат длины любой стороны равен сумме квадратов длин двух других сторон за минусом их удвоенного произведения на косинус угла между ними.
a² = b² + c² — 2*b*c*cos(α)
Из данной формулы можно найти косинус: cos(α) = (b² + c² — a²)/(2*b*c)
А поскольку для одного и того же угла sin(α)² + cos(α)² = 1 и это константа, то можно вывести формулу для определения синуса:
Более детально нахождение синуса угла с использованием косинуса рассмотрено в нашей статье Как найти синус, если известен косинус.
Что такое синус в треугольнике? Как найти синус острого угла в прямоугольном треугольнике?
Синусом острого угла прямоугольного треугольника называется отношение противолежащего катета к гипотенузе.
для угла A треугольника ABC
противолежащий катет — это BC.
Соответственно, синус угла A в треугольнике ABC — это
Для угла B треугольника ABC
противолежащим является катет AC.
Соответственно, синус угла B в треугольнике ABC
равен отношению AC к AB:
Таким образом, синус острого угла в прямоугольном треугольнике — это некоторое число, получаемое в результате деления длины противолежащего катета на длину гипотенузы.
Поскольку длина катета всегда меньше длины гипотенузы, то синус острого угла прямоугольного треугольника — число, меньшее единицы.
Синус любого острого угла прямоугольного треугольника больше нуля, но меньше единицы:
Синус угла треугольника зависит не от длин сторон треугольника, а от отношения этих длин.
1) В треугольнике ABC катет BC=3 см, а гипотенуза AB=5 см.
2) В треугольнике ABC катет BC=21 дм, гипотенуза AB=35 дм.
Длины сторон треугольника изменилось, но отношения длин остались прежними, поэтому и значение синуса угла A не изменилось.
2
Для нахождения синусов углов в произвольном треугольнике, как это ни странно, проще использовать не теорему синусов, а теорему косинусов. Она гласит, что возведенная в квадрат длина любой стороны равна сумме квадратов длин двух других сторон без удвоенного произведения этих длин на косинус угла между ними: А²=В²+С2-2*В*С*cos(α).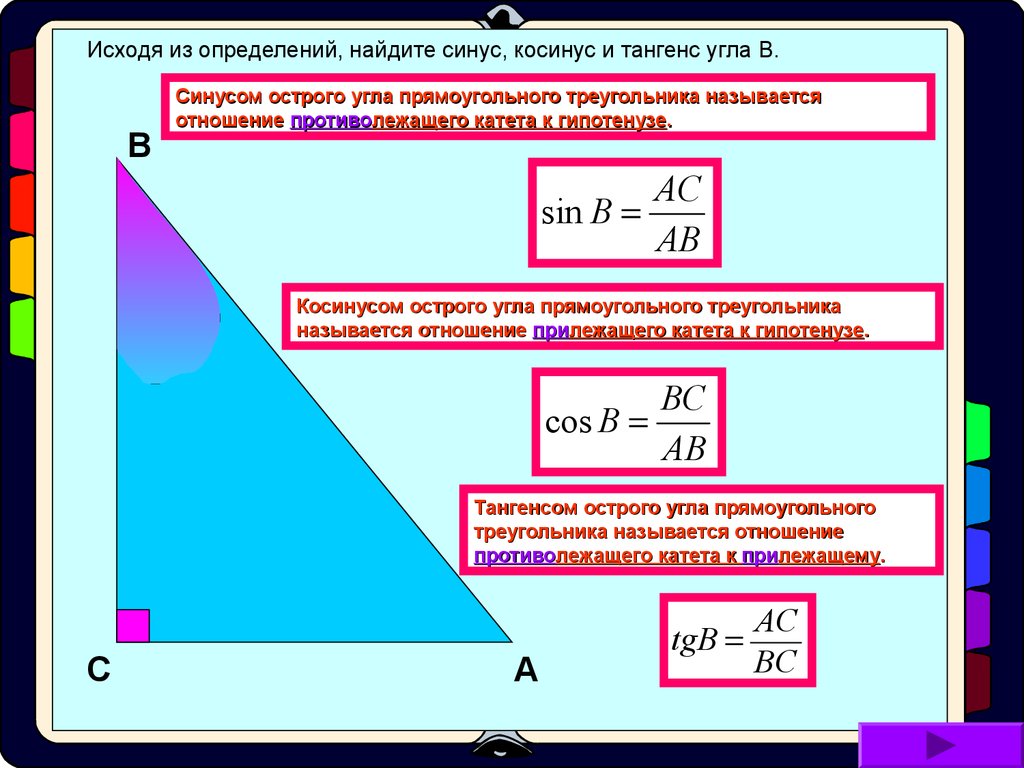
Площадь треугольника через синус и косинус
I. Площадь треугольника через синус
Если в задаче даны длины двух сторон треугольника и угол между ними, то можно применить формулу площади треугольника через синус.
Пример расчета площади треугольника через синус. Даны стороны a = 3, b = 4, и угол γ= 30°. По таблице синусов синус угла в 30° равен 0.5
Площадь треугольника будет равна 3 кв. см.
| Сторона a= | Сторона b= | Угол γ ° | |
Ответ: Площадь треугольника = 3. 000 000 |
|||
Также могут быть и другие условия. Если дана длина одной стороны и углы, то для начала нужно вычислить недостающий угол. Т.к. сумма всех углов треугольника равняется 180°, то:
Площадь будет равна половине квадрата стороны, умноженной на дробь. В ее числителе находится произведение синусов прилегающих углов, а в знаменателе синус противолежащего угла. Теперь рассчитываем площадь по следующим формулам:
Например, дан треугольник со стороной a=3 и углами γ=60°, β=60°. Вычисляем третий угол:
Получаем, что площадь треугольника равняется 3,87 кв. см.
II. Площадь треугольника через косинус
Чтобы найти площадь треугольника, нужно знать длины всех сторон. По теореме косинусов можно найти не известные стороны, а уже потом использовать формулу Герона.
По теореме косинусов квадрат неизвестной стороны треугольника равняется сумме квадратов остальных сторон минус удвоенное произведение этих сторон на косинус угла, находящегося между ними.
Из теоремы выводим формулы для поиска длины неизвестной стороны:
Зная как найти недостающую сторону, имея две стороны и угол между ними можно легко посчитать площадь. Формула площади треугольника через косинус помогает легко и быстро найти решение различных задач.
Пример расчета формулы площади треугольника через косинус
Теперь используя формулу, найдем площадь треугольника по трем сторонам:
| Сторона a= | Сторона b= | Угол γ ° | |
Ответ: Площадь треугольника = 4.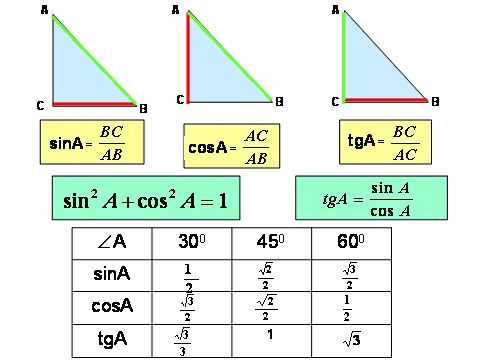 243 243 |
|||
косинусов
косинусовОпределение косинуса
Косинус угла определяется как синус дополнительного угла. Дополнительный угол равен данному углу, вычтенному из прямого угла, 90°. Например, если угол равен 30°, то его дополнение равно 60°. Вообще для любого углаЗаписанное в терминах радианного измерения, это тождество становится
Прямоугольные треугольники и косинусы
Рассмотрим прямоугольный треугольник ABC с прямым углом C. Как упоминалось ранее, обычно мы будем использовать букву a для обозначения стороны, противоположной углу A, букву b для обозначения стороны, противоположной углу B, и букву c для обозначения стороны.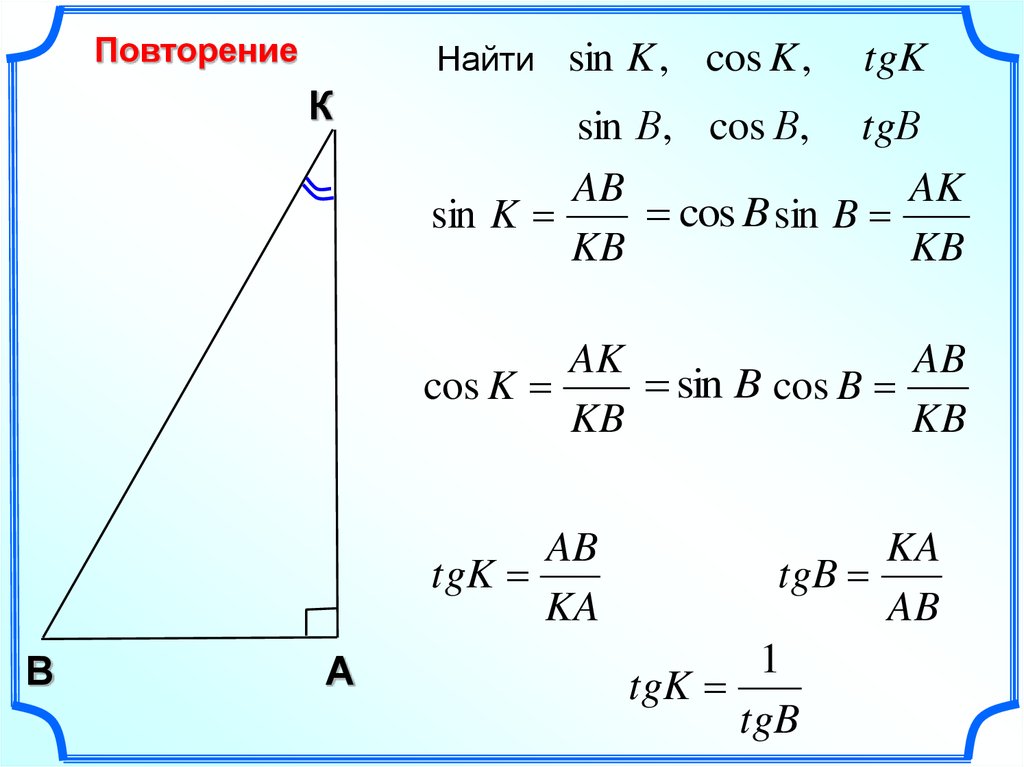 противоположный угол С. Так как сумма углов в треугольнике равна 180°, а угол С равен 90°, то углы А
противоположный угол С. Так как сумма углов в треугольнике равна 180°, а угол С равен 90°, то углы А
| соз = | прил гип |
Кроме того, cos A = sin B = b/c.
Тождество Пифагора для синусов и косинусов
Вспомним теорему Пифагора для прямоугольных треугольников. Он говорит, что где c — гипотенуза. Это очень легко переводится в пифагорейское тождество синусов и косинусов. Разделите обе части на
Это очень легко переводится в пифагорейское тождество синусов и косинусов. Разделите обе части на
Но A 2 / C 2 = (SIN A ) 2 и B 2 / C 2 = (COS A ) 9 2 2 = (COS A ) 9. Чтобы уменьшить количество круглых скобок, которые должны быть написаны, принято соглашение, что обозначение sin 2 A — это сокращение от (sin A ) 2 , и аналогично для степеней других триггерных функций. Таким образом, мы доказали, что
когда А острый угол. Мы еще не видели, какими должны быть синусы и косинусы других углов, но когда мы это увидим, мы будем иметь для любого угла t одно из важнейших тригонометрических тождеств, тождество Пифагора для синусов и косинусов:

Синусы и косинусы для особых общих углов
Мы можем легко вычислить синусы и косинусы для некоторых общих углов. Рассмотрим сначала угол 45°. Он находится в равнобедренном прямоугольном треугольнике, то есть в треугольнике 45°-45°-90°. В любом прямоугольном треугольнике c 2 = a 2 + b 2 , но в этом a = b, , поэтому c 2 = 2 a 2 . Следовательно, c = a 2. Следовательно, и синус, и косинус угла 45° равны 1/2, что также можно записать как 2 / 2.Далее рассмотрим углы 30° и 60°. В прямоугольном треугольнике 30°-60°-90° отношения сторон равны 1 : 3 : 2. Отсюда следует, что sin 30° = cos 60° = 1/2, а sin 60° = cos 30° = 3 / 2.
Эти данные заносятся в эту таблицу.
| Angle | Degrees | Radians | cosine | sine |
|---|---|---|---|---|
| 90° | /2 | 0 | 1 | |
| 60° | /3 | 1/2 | 3 / 2 | |
| 45° | /4 | 2 / 2 | 2 / 2 | |
| 30° | /6 | 3 / 2 | 1 /2 | |
| 0° | 0 | 1 | 0 |
Упражнения
Все эти упражнения относятся к прямоугольным треугольникам со стандартной маркировкой.
30. b = 2,25 метра и cos A = 0,15. Найдите a и c.
33. b = 12 футов и cos B = 1/3. Найдите c и a.
35. б = 6,4, в = 7,8. Найти А и А.
36. А = 23° 15′, c = 12,15. Найдите a и b.
Советы
30. Косинус A связывает b с гипотенузой c, , так что вы можете сначала вычислить c. Как только вы узнаете b и c, , вы сможете найти a по теореме Пифагора.
33. Вы знаете b и cos B. К сожалению, cos B — это отношение двух неизвестных вам сторон, а именно a/c. Тем не менее, это дает вам уравнение для работы: 1/3 = a/c. Тогда c = 3 a. Из теоремы Пифагора следует, что а 2 + 144 = 9 а 2 . Вы можете решить это последнее уравнение для и , а затем найдите c.
35. b и c дают A по косинусам и a по теореме Пифагора.
36. A и c дают a по синусам и b по косинусам.
Ответы
30. в = b /cos А = 2,25/0,15 = 15 метров; a = 14,83 метра.
33. 8 a 2 = 144, поэтому a 2 = 18. Следовательно, a равно 4,24 фута или 4 фута 3 дюйма.
c = 3 a , что равно 12,73 фута или 12 футов 9 дюймов.
35. cos A = b/c = 6,4/7,8 = 0,82. Следовательно, A = 34,86° = 34°52′, или около 35°.
a 2 = 7,8 2 6,4 2 = 19,9, поэтому a равно примерно 4,5.
36. a = c sin A = 12,15 sin 23°15′ = 4,796.
b = c cos A = 12,15 cos 23°15′ = 11,17.
Оглавление. | Вернемся к синусам. | К касательным и наклонам.
| Вернемся к синусам. | К касательным и наклонам.
© 1996, 1997, 1999.
Дэвид Э. Джойс
Кафедра математики и информатики
Университет Кларка
Вустер, Массачусетс 01610
Электронная почта: [email protected]
Краткий триггерный курс Дейва находится по адресу http://aleph0.clarku.edu/~djoyce/java/trig.
Как найти угол тета в тригонометрии
Обновлено 13 марта 2018 г.
Брайан Граббс
В математике изучение треугольников называется тригонометрией. Любые неизвестные значения углов и сторон могут быть обнаружены с помощью общих тригонометрических тождеств синуса, косинуса и тангенса. Эти тождества представляют собой простые вычисления, используемые для преобразования отношений сторон в градусы угла. Неизвестные углы обозначаются как угол тета и может быть рассчитан различными способами, исходя из известных сторон и углов.
Прямоугольные треугольники
Когда треугольник содержит угол 90 градусов, он известен как прямоугольный треугольник , а угол тета можно определить с помощью аббревиатуры SOHCAHTOA .
В разбивке это означает, что Синус (S) равен длине стороны, противоположной углу тета (O), деленной на длину гипотенузы (H), так что Sin(X) = Opp/Hyp. Точно так же косинус (C) равен длине прилежащей стороны (A), деленной на гипотенузу. (H) Cos(X) = Adj/Hyp. Тангенс (Т) равен противоположному (О), деленному на прилежащее (А). Tan(X) = Opp/Adj. 9-1(4/5)
Это должно вывести значение примерно 53,13 градуса. Если нет, убедитесь, что калькулятор находится в режиме DEGREE, а затем повторите попытку.
Закон синусов
Если в треугольнике нет 90-градусных углов, SOHCATOA не имеет смысла при вычислении углов. Однако, если угол и длина его противоположной стороны известны, закон синусов можно использовать в сочетании с другой известной длиной стороны для нахождения недостающих углов. Закон гласит, что sin A/a = sin B/b = sin C/c.
В разбивке это означает, что синус угла, деленный на длину его противоположной стороны, прямо пропорционален синусу другого угла, деленному на длину его противоположной стороны.
