Произведение синусов и косинусов: формулы, примеры
Формула произведения косинуса, синуса используется в школьной алгебре для обучения школьников, а также в математическом анализе в расчетах.
В этой статье разберем важные формулы для понятия тригонометрии: умножение косинусов и синусов, другие формулы, связанные с произведением двух алгебраических функций.
Важно
Теоремы умножения синусов и косинусов для α и β помогают превратиться из произведения в разность, сумму других углов.
Появилась необходимость, чтобы найти произведение косинусов, синусов углов α и , поэтому стоит изучить данную статью.
Данные формулы помогают преобразовать выражение от произведения к разности, сумме синусов и косинусов α−β и α+β.
Рассмотрим и выведем формулы синуса на синус, произведение синусов и косинусов. Также ниже разберем примерные задания с использованием формул.
Тригонометрические формулы произведения
Рассмотрим формулировки, формулы произведений.
В независимости какими значениями обладают углы α и β или какие греческие буквы используются вместо обозначений α и β, применяются данные формулы и вычисляют с помощью них.
Произведение синусов формула
Произведение sin угла α и sin угла β будет равно половине разности косинуса угла (α−β) и (α+β).
\[\sin \alpha \cdot \sin \beta=\frac{1}{2}(\cos (\alpha-\beta)-\cos (\alpha+\beta))\]
Произведение косинусов формула
Произведение cos угла α и cos угла β равно половине сумме косинуса угла (α-β) и (α+β).
\[\cos \alpha \cdot \cos \beta=\frac{1}{2}(\cos (\alpha-\beta)+\cos (\alpha+\beta))\]
Произведение синусов и косинусов формулы
Произведение синуса угла α на косинус угла β равно половине сумме синуса угла (α-β) и синуса угла (α+β).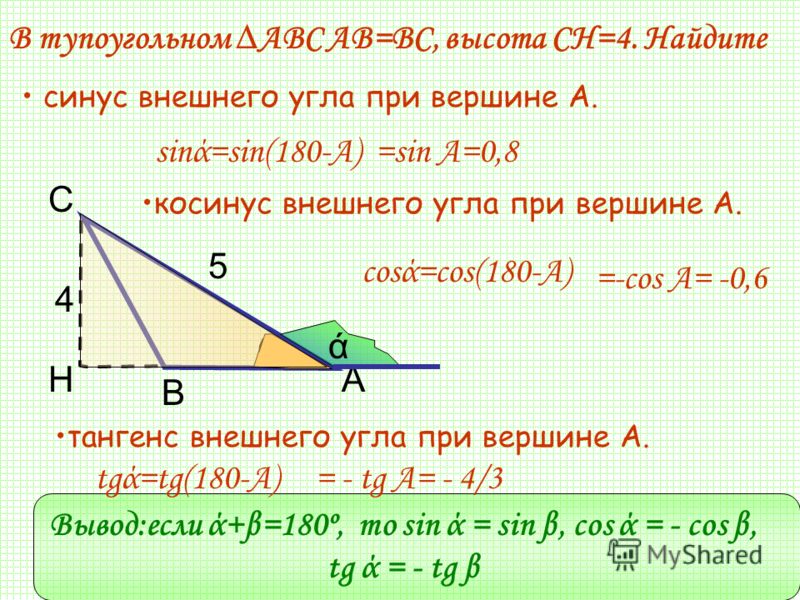
\[\sin \alpha \cdot \cos \beta=\frac{1}{2}(\sin (\alpha-\beta)+\sin (\alpha+\beta))\]
Выведение тригонометрических формул
Для выведения формул, которые расположены выше, используется формулы сложения функций cos и sin, а также свойства равенства. В свойстве подразумевается, что если просуммировать правую и левую часть правильного равенства с другим таким же верным равенством, образуется новое правильное равенство.
Произведение косинусов
Приведем подробный вывод изучаемых формул
Для этого возьмем формулы косинуса разности и суммы:
\[\cos (\alpha+\beta)=\cos \alpha \cdot \cos \beta-\sin \alpha \cdot \sin \beta\]
\[\cos (\alpha-\beta)=\cos \alpha \cdot \cos \beta+\sin \alpha \cdot \sin \beta\]
Далее, с каждой стороны проведем сложение двух формул. Получается следующее:
\[\cos (\alpha+\beta)+\cos (\alpha-\beta)=\cos \alpha \cdot \cos \beta-\sin \alpha \cdot \sin \beta+\cos \alpha \cdot \cos \beta+\sin \alpha \cdot \sin \beta\]
Одинаковые слагаемые складываем: \[\cos \alpha \cdot \cos \beta+\cos \alpha \cdot \cos \beta=2 \cdot \cos \alpha \cdot \cos \beta\]
Разноименные слагаемые отнимаем: \[-\sin \alpha \cdot \sin \beta+\sin \alpha \cdot \sin \beta=0\]
Следовательно, \[\cos (\alpha+\beta)+\cos (\alpha-\beta)=2 \cdot \cos \alpha \cdot \cos \beta\]
В данном равенстве делим правую, левую часть на 2 , меняем местами слагаемые.
Получается следующее выражение \[\cos \alpha \cdot \cos \beta=\frac{1}{2}(\cos (\alpha+\beta)+\cos (\alpha-\beta))\]
Мы доказали формулу умножения cos одного угла на cos другого угла.
Произведение синусов
Теперь докажем следующую. Распишем формулу суммы косинусов так:
\[-\cos (\alpha+\beta)=-\cos \alpha \cdot \cos \beta+\sin \alpha \cdot \sin \beta\]
Прибавим к данному равенству \[\cos (\alpha-\beta)=\cos \alpha \cdot \cos \beta+\sin \alpha \cdot \sin \beta\]
Слагаемые одноименными знаками и функциями сложим, разноименные — вычтем, преобразуем выражение:
\[-\cos (\alpha+\beta)+\cos (\alpha-\beta)=-\cos \alpha \cdot \cos \beta+\sin \alpha \cdot \sin \beta+\cos \alpha \cdot \cos \beta+\sin \alpha \cdot \sin \beta-\cos (\alpha+\beta)+\cos (\alpha-\beta)=2 \cdot \sin \alpha \cdot \sin \beta\]
В данном равенстве делим правую, левую часть на 2, меняем местами слагаемые.
\[\sin \alpha \cdot \sin \beta=\frac{1}{2}(\cos (\alpha-\beta)-\cos (\alpha+\beta))\]
Мы вывели формулу умножения синуса одного аргумента на синус другого аргумента.
Произведение синуса на косинус
Сделаем вывод формулы произведения синуса и косинуса разных аргументов. Теперь воспользуемся формулой суммы и разности функций sin. Складываем и правую, и левую часть выражений:
\[\sin (\alpha+\beta)=\sin \alpha \cdot \cos \beta+\cos \alpha \cdot \sin \beta\]
\[\sin (\alpha-\beta)=\sin \alpha \cdot \cos \beta-\cos \alpha \cdot \sin \beta\]
\[\sin (\alpha+\beta)+\sin (\alpha-\beta)=\sin \alpha \cdot \cos \beta+\cos \alpha \cdot \sin \beta+\sin \alpha \cdot \cos \beta-\cos \alpha \cdot \sin \beta\]
Слагаемые одноименными знаками и функциями сложим, разноименные — вычтем, преобразуем выражение:
\[\sin (\alpha+\beta)+\sin (\alpha-\beta)=2 \cdot \sin \alpha \cdot \cos \beta\]
В данном равенстве делим правую, левую часть на 2 , меняем местами слагаемые.
\[\sin \alpha \cdot \cos \beta=\frac{1}{2}(\sin (\alpha+\beta)+\sin (\alpha-\beta))\]
Мы вывели формулу произведения синуса на косинус.
Примеры задач
Рассмотрим и решим задания с применением формул произведения косинусов (cos), синусов (sin), синусов на косинусы (cos и sin).
{\circ}=\frac{1}{2}\left(\frac{\sqrt{3}}{2}+1\right)=\frac{\sqrt{3}}{4}+\frac{1}{2}\]
Ответ: \[\frac{\sqrt{3}}{4}+\frac{1}{2}\]
Пример 3
Пусть углы обладают значениями: \[\alpha=\frac{\Pi}{2}, \beta=\frac{\Pi}{6}\]. Найти значение произведение sin этих углов.
Решение:
Воспользуемся произведение синусов формулой:
\[\sin \alpha \cdot \sin \beta=\frac{1}{2}(\cos (\alpha-\beta)-\cos (\alpha+\beta))\]
Подставим данные и получим:
\[\sin \frac{\pi}{2} \cdot \sin \frac{\pi}{6}=\frac{1}{2}\left(\cos \left(\frac{\pi}{2}-\frac{\pi}{6}\right)-\cos \left(\frac{\pi}{2}+\frac{\pi}{6}\right)\right)\]
Найдем знаменатель для двух дробей:
\[\sin \frac{\pi}{2} \cdot \sin \frac{\pi}{6}=\frac{1}{2}\left(\cos \left(\frac{\pi}{3}\right)-\cos \left(\frac{2 \pi}{3}\right)\right)\]
Для этого нам понадобится таблица со значениями функций косинуса и синуса, трансформируем произведение синусов в сумму чисел:
\[\sin \frac{\pi}{2} \cdot \sin \frac{\pi}{6}=\frac{1}{2} \cdot\left(\frac{1}{2}-\left(-\frac{1}{2}\right)\right)\]
Вычислим и запишем ответ:
\[\sin \frac{\pi}{2} \cdot \sin \frac{\pi}{6}=\frac{1}{2}\]
Ответ: \[\frac{1}{2}\]
Пример 4
Дано следующее значение: \[\cos \cos \alpha=0,3\].
{2}-1=0,18-1=-0,82\]
Воспользуемся значениями в наше выражение, получим и запишем ответ:
\[\frac{1}{2} \cdot\left(\frac{1}{2}+\sin \sin \left(2 \alpha-\frac{\pi}{12}\right)\right) \cdot \frac{1}{2} \cdot\left(\frac{1}{2}-1\right)=-\frac{1}{4}\]
Ответ: \[-\frac{1}{4}\]
Замечание. Данные формулы произведения применяются, чтобы преобразовать сложные тригонометрические выражения в наиболее простые.
Угловая математика — Плутедев
Иногда вы хотите двигаться под углом или делаете бобышку с шарнирным соединением. спрайты и нужно крутить конечность, или вам нужен враг, который преследует плеер под произвольным углом и т.д. Для всего этого добра нужно научиться как сделать основные математические с углами. Эта страница покажет вам, как сделать некоторые общие вещи.
Эта страница , а не предполагает, что вы хорошо разбираетесь в
тригонометрия и объяснит все необходимые концепции.
Эти концепции хороши для игр в целом, но некоторые замечания
специфично для 68000 (или других старых процессоров).
- Различные единицы измерения угла
- Преобразование единиц измерения угла
- Синусы и косинусы
- Таблица синусов
- Движение под углом
- Вычисление углов 90°
- Вращение вокруг точки
- Получить угол между двумя точками
- Справочная таблица углов
- Подвести угол к другому
Различные угловые единицы
Угол показывает, в каком направлении что-то вращается. Углы идут от 0 до «полного круга», а любые значения за этим просто повторяют направления (например, один и четверть круга такие же, как четверть круга).
Углы можно измерять в разных единицах:
- Наиболее распространенной единицей измерения являются градусы (полный круг равен 360°).
- Другой распространенной единицей измерения являются радианы (полный круг равен 2×π)
Но нет причин, почему вы должны придерживаться их! Общий способ измерять углы в старых играх, выбирая степень двойки как полный круг например 256, 1024 или 65536. Это имеет то преимущество, что вы можете использовать И операция «нормализации» угла в диапазоне от 0 до полного круга (важно когда вы собираетесь использовать угол, например. со столом).
Мы рекомендуем использовать степень двойки в качестве полного круга в играх Mega Drive.
Преобразование между угловыми единицами
Преобразование из одних единиц в другие осуществляется просто:
угол ÷ круг в старом блоке × круг в новом блоке
Например. чтобы преобразовать из градусов в единицу, где круг равен 256:
угол ÷ 360 × 256
Синусы и косинусы
Прежде всего, вам абсолютно необходимо знать два понятия: синусы и косинусы.
Не волнуйтесь, мы не будем показывать трудные для понимания вещи с треугольниками из
класс тригонометрии, а лучше просто запомнить это:
-
sin(угол)сколько вы двигаетесь вверх -
cos(угол)сколько вы двигаетесь вправо
Другими словами:
х = cos(угол) у = -sin(угол)
Вышеприведенное предполагает, что углы отсчитываются против часовой стрелки и что 0° указывает Направо. Нам нужно перевернуть знак Y, потому что в наших играх Y уменьшается. вместо вверх (если вы этого не сделаете, вместо этого углы будут по часовой стрелке, Вам решать!).
Справочная таблица синусов
68000 не может работать с плавающей запятой с разумной скоростью, не говоря уже о
вычисление синусов на лету. Вместо этого мы используем «поиск синусов».
table», которая представляет собой таблицу, содержащую значения синуса для всех возможных
угол (или, если это сделает стол слишком большим, по крайней мере достаточно углов, чтобы
сделать его гладким).
Соберите какую-нибудь быструю программу или скрипт и запустите ее на своем компьютере, а затем
используйте полученную таблицу в своей игре. Создать таблицу просто,
просто посчитай sin(angle) для каждого угла (используя любой
стандартная библиотека предоставляет):
для угла = от 0 до MAX_ANGLE таблица [угол] = грех (угол) конец
Однако, как мы только что сказали, 68000 не может работать с плавающей запятой, и вы скорее всего, вместо этого работает с фиксированной точкой. Как таким образом, вы захотите «предварительно умножить» все значения на любую сумму вы чувствуете себя комфортно (например, игры Sonic предварительно умножаются на 256):
для угла = от 0 до MAX_ANGLE таблица[угол] = грех(угол) * предварительное умножение конец
Вам не нужна отдельная таблица для косинусов: cos(угол)
sin(angle+90°) , поэтому вы можете использовать то же самое
стол на двоих.
Если вы все еще хотите иметь отдельную таблицу косинусов или нет
зависит от тебя.Движение под углом
Теперь давайте изучим наиболее распространенную вещь, которую мы хотим сделать с этим: перемещение на определенное расстояние под углом. Мы уже видели этот синус и косинус такие же, как движение по каждой оси: это дает нам количество двигаться на 1 единицу. Поэтому умножьте их на расстояние, которое вы хотите переместить, и вы настроены:
new_x = x + (cos(угол) * расстояние) new_y = y - (sin(угол) * расстояние)
В идеале вы должны выбрать степень двойки, чтобы вместо этого можно было использовать битовые сдвиги. (которые намного быстрее, чем умножить). Кроме того, поскольку 68000 не может сделать с плавающей запятой, вы, вероятно, используете значения с предварительным умножением (например, на 256), поэтому, когда вам нужен результат в виде целого числа, не забудьте разделить его на это количество!
Например.
если ваши таблицы предварительно умножены на 256 и вы хотите продвинуться
на 16px:
new_x = x + (cos(угол) >> 4) new_y = y - (sin(угол) >> 4)
Это потому, что мы умножаем на 16 (<< 4) и делим на 256 (>> 8) и мы объединили результат обоих сдвигов в один сдвиг (при этом также избегая риска переполнения). Или вы могли бы думать об этом как вместо этого умножение на 16/256. Либо работает.
Вычисление углов 90°
Во многих случаях вам нужно несколько углов с шагом 90°. В этой ситуации, вы можете повторно использовать одни и те же значения синуса и косинуса, поэтому вам нужно только получить их один раз. Переворот обоих знаков аналогичен перевороту на 180°. Поменять их местами и перевернуть один знак так же, как 90° флип.
В следующей таблице показаны все повороты с шагом 90°:
| Вращение | X | Y |
|---|---|---|
| 0° | x = cos(угол) | y = -sin(угол) |
| 90° | x = -sin(угол) | y = -cos(угол) |
| 180° | x = -cos(угол) | y = sin(угол) |
| 270° | x = sin(угол) | y = cos(угол) |
Вращение вокруг точки
Еще одна вещь, которую нам может понадобиться сделать, это повернуть точку вокруг определенной точки.
(подумайте о таких вещах, как спецучасток Sonic 1). Это выглядит более сложным для
делать, но, в конце концов, все, что мы делаем, это продвигаем точку дважды (сначала в
угол, который мы хотим, затем снова 270 ° от него).
Сначала нам нужно узнать расстояние между точкой, которую мы собираемся переместить. и точка, вокруг которой он вращается (т.е. начало координат):
Distance_x = x - origin_x расстояние_у = у - происхождение_у
Затем продвигаемся дважды. Первые две строки задают начальную точку (которая является началом), следующие две строки продвигаются по «оси X» исходная точка и две последние на «оси Y»:
новый_x = исходный_x новый_у = исходный_у new_x += cos(угол) * Distance_x new_y -= sin(угол) * Distance_x new_x += sin(угол) * Distance_y new_y += cos(угол) * Distance_y
Или, если мы сложим их вместе:
new_x = origin_x + (cos(угол)*расстояние_x) + (sin(угол)*расстояние_y) new_y = origin_y - (sin(угол)*distance_x) + (cos(угол)*distance_y)
Получить угол между двумя точками
дх = х2 - х1 dy = y2 - y1
В любом случае, чтобы определить угол, вам нужно вычислить арктангенс
dy разделить на dx (т.
е. atan(dy/dx) ), а затем не забудьте
настроить квадрант на основе их знаков… Это боль, поэтому большинство
библиотеки программирования вместо этого предоставляют функцию atan2 который принимает значения отдельно и делает все это за вас:
угол = atan2(dy,dx)
Это возвращает значение в радианах, поэтому преобразуйте его во что угодно. используя вместо этого. И обратите внимание, что вместо этого они обычно возвращают от -180° до 180°. от 0° до 360° (т.е. обратите внимание на знак). Также не забудьте справиться с делом где dx и dy оба равны 0 (что не имеет допустимого угла).
Справочная таблица углов
Проблема с вышеизложенным в том, что и 68000 недостаточно хороши для
это , так же, как и синусы, нам нужно будет прибегнуть к поиску
столы.
Предлагаемый здесь метод может быть не идеальным, но его легко
понимать. На практике вам не нужна 100% точность, достаточно «закрыть
достаточно», а в худшем случае можно корректировать курс каждые несколько шагов.
Идея здесь такова:
- Определите, какой диапазон мы хотим хранить (например, 32 или 64 единицы). на ось)
- Вычислите все углы для всех возможных значений X/Y в этом диапазоне.
- При вычислении углов на больших расстояниях мы делим их на 2, пока оба подходят (всегда делите оба, даже если только один из диапазон)
Приведенное выше будет терять точность по мере увеличения расстояний, поэтому убедитесь, что найти разумный компромисс между диапазоном и размером стола (и для случаях, когда важна точность на большом расстоянии, для пересчета угла каждые несколько единиц).
И рассматриваемая таблица (не забудьте преобразовать из радианов во что угодно единица, которую вы используете для углов):
для x = от MIN_X до MAX_X и y = от MIN_Y до MAX_Y
если х == 0 и у == 0
table[x][y] = 0 или другое безопасное значение
еще
таблица[x][y] = atan2(y,x)
конец
конец Подвести угол к другому
Когда вы делаете что-то, что преследует цель, вы обычно не
хотят указать на его угол прямо, но скорее хотят, чтобы он поворачивался
вокруг к нему.
Проблема в том, чтобы убедиться, что это занимает кратчайшее
направление.
Если вы используете степень двойки в качестве полного круга, есть ловкий трюк здесь: вычтите текущий угол из целевого угла, затем И его (удалить лишние биты). Если результат ниже 180°, вам необходимо увеличьте угол, а если он выше, вам нужно уменьшить угол.
temp = (целевой_угол - угол) & ANGLE_MASK если темп = 0° ничего не делать иначе, если температура < 180° угол приращения еще угол уменьшения конец
В то время как та же концепция работает с обесточиванием двух блоков, нормализация более сложный процесс на тех, что является основной причиной, почему это предпочтительнее использовать единицы, основанные на степени двойки.
Важным математическим понятием является идея функция - значение одной переменной в задаче зависит
однозначно по значению другой переменной в задаче. Некоторые проблемы и отношения встречаются в математике и естественных науках так часто, что мы присваиваем функции специальные имена. Экспоненциальная функция связывает переменную с числом раз в качестве множителя используется другая переменная, даже если количество раз не является целым числом. Логарифмическая функция является обратной экспоненциальной; это дает количество раз, которое вы должны умножить переменную сам по себе, чтобы получить заданное число. Тригонометрические функции синус, косинус и тангенс соотнести различные стороны и углы треугольника. Мы можем узнать о функциях, рассмотрев несколько примеров.
Тригонометрические функции определяются в терминах отношения длины сторон прямоугольного треугольника и
утверждается, что это соотношение зависит только от величины
угол , образованный двумя сторонами треугольника, а не на
длина любой стороны. В этом примере мы будем использовать косинус угла, но
аналогичный пример можно сделать, используя синус или тангенс.
Рассмотрим большой желтый треугольник на рисунке. Он содержит несколько
другие подобные треугольники, которые мы будем использовать. Все треугольники
прямоугольные треугольники и все имеют один и тот же угол б внизу слева
угол.
Черный треугольник является самым маленьким треугольником и имеет гипотенузу «h» длины «y».
и смежная сторона «а» равна «х». Длина «x» произвольна, но
значение "y" не является произвольным, поскольку
отношение x к y (x/y) определяется как косинус «b», и это значение
фиксируется буквой «б».
Для черного треугольника косинус «b» равен x/y.
Теперь давайте рассмотрим красный треугольник.
Он был образован путем удвоения размера сторон
черный треугольник. Для красного треугольника длина гипотенузы «h» равна 2y,
в два раза больше гипотенузы черного треугольника. |
Изменение значения одной переменной приводит к изменению
значение другой переменной, которое каждый раз точно такое же
вы меняете первую переменную.
На этой странице мы показываем простой пример, который демонстрирует это
факт.
Аналогично, смежная сторона «а»
равно 2х
относительно черного треугольника. Оба красные
треугольник и черный треугольник имеют одинаковый угол «b», выделенный синим цветом. Для красного
треугольника, косинус "b" равен 2x/2y. Разделение «2» дает
x / y, то же значение, что и черный треугольник.
Наконец, давайте рассмотрим синий треугольник.
Он был образован путем утроения размеров сторон
черный треугольник. Для синего треугольника длина гипотенузы «h» равна 3y,
а смежная сторона «а» равна 3x.
Для синего
треугольника, косинус "b" равен 3x/3y. Разделение «3» дает
x / y, то же значение, что и у черного треугольника и у красного треугольника.
Если мы учетверим или увеличим размер сторон на любой множитель,
отношение прилежащего катета к гипотенузе остается прежним x/y.
Значение косинуса «b» зависит только от значения «b», а не от длины
сторон, образующих «b». Ученые называют этот тип зависимости функция . Отношение прилежащего катета к гипотенузе зависит от
угол «б».