Уравнения sinx=a и cosx=a. | Материал:
Опубликовано 06.04.2020 — 23:06 — Мунина Александра Анатольевна
Цель: ввести понятие арксинуса и арккосинуса числа а; выработать навык вычисления арксинуса и арккосинуса числа а.
Документ необходимо скачать и открыть в Word, а не присылать мне скрины, что в предварительном просмотре не открывается!!!
Скачать:
Предварительный просмотр:
Тема: Уравнения sinx=a и cosx=a.
Цель: ввести понятие арксинуса и арккосинуса числа а; выработать навык вычисления арксинуса и арккосинуса числа а.
Лекционный материал.
Изучив лекционный материал, прошу ответить на вопросы теста:
- Решением уравнения sinx=1 является:
А) x=+2πk,k∈Z;
Б) x=πk,k∈Z;
В) x=+2πk,k∈Z;
Г) нет решения.
- Найдите корни уравнения cosx=−8.
А) x=π+2πk,k∈Z;
Б) x=+2πk,k∈Z;
В) нет корней;
Г) x=2πk,k∈Z.
- Вычислите arcsin0:
А) ;
Б) 0;
В) ;
Г) .
- Найдите значение выражения arccos:
А) ;
Б) 2π;
В) ;
Г) π.
- Найдите корни уравнения sint=0,1 (вместо знака вопроса запишите необходимое значение):
t=(−1)k arcsin+πk,k∈Z.
- Найдите решения уравнения cosx= (вместо знака вопроса запишите необходимое значение):
x=±arccos+2πk,k∈Z.
- Вычислите: 6⋅arcsin(−1)+7⋅arcsin (Ответ округлите до десятых).
- Найдите значение выражения в радианах
7⋅arccos −10⋅arccos.
- Найдите значение выражения: arcsin(sin)+arcsin(sin)+6,75 (Ответ округли до десятых).
- Найдите значение выражения: arccos(cos)+)+arccos(cosπ)−5 (Ответ округли до десятых).
Требования к отчетности:
- Ознакомиться с материалом, оформить лекцию в рабочую тетрадь, ответить на вопросы теста;
- Фотоотчет присылать на почту: vismyt89@mail. ru своевременно (подписывайте ФИО и номер группы), можно в ВКонтакте в личные сообщения.
ru своевременно (подписывайте ФИО и номер группы), можно в ВКонтакте в личные сообщения.По теме: методические разработки, презентации и конспекты
Виды однородных уравнений. Системы однородных уравнений.
ВведениеВ своей работе я рассмотрела различные методы решения однородных уравнений и систем однородных уравнений, которые чаще всего встречаются при изучении. Представленные методы м…
Методическая разработка занятия по предмету Элементы высшей математики по теме: «Определение обыкновенных дифференциальных уравнений. Общее и частное решение. Уравнения с разделенными переменными».
Определение обыкновенных дифференциальных уравнений. Общее и частное решение. Уравнения с разделенными переменными.Тип занятия: комбинированный, с элементами игры.Формы занятия: индивидуальная, группо…
Задачи, приводящие к дифференциальным уравнениям. Дифференциальные уравнения первого порядка.
Презентация к занятию по дисциплине ЕН.02 Математика по теме «Задачи, приводящие к дифференциальным уравнениям.
Дифференциальные уравнения первого порядка»….
график функции sinx и ее свойства
Презентация со стихами, в шуточной форме. Описывает функцию sinx и ее свойства….
Свойства функций y=sinx и y=cosx, и их графики
Цель:детально рассмотреть функции y=sinx и y=cosx, выделить их основные свойства; построить в прямоугольной системе координат графики функции y=sinx и y=cosx на осно…
Решение уравнения sinx=a
Решение уравнения sinx=a…
Практическое занятие «Линейные уравнения и системы линейных уравнений»
Линейные уравнения и системы линейных уравнений…
Поделиться:
тригонометрия — Показать в виде $A\sin(x+c)=\sin x — \cos x$?
спросил
Изменено 10 лет, 3 месяца назад
Просмотрено 3к раз
$\begingroup$
Не уверен, какое удостоверение мне следует здесь использовать: моя интуиция подсказывает мне использовать формулу суммы Sin: $\sin(x+y) = \sin(x)\cos(y) + \cos(x)\sin (y)$, но не могу понять, как это сделать.
92=2$$
$$A=\pm\sqrt{2}$$
Возьмем $A=\sqrt{2}$. Помещая это в наши первые два уравнения, получаем, что:
$$\sqrt{2}\cos y=1$$ $$\cos y=\frac 1 {\sqrt 2}$$
И аналогично $$\sin y=\frac{-1}{\sqrt 2}$$
$y=-\pi/4$ решает обе эти задачи. Итак, наш ответ:
$$\sin x — \cos x = A\sin(x+c)=\sqrt{2}\sin(x-\frac{\pi}4)$$
Обратите внимание, что есть и другие решения, которые будут работать, но это, вероятно, самое простое.
$\endgroup$
0
$\begingroup$
Мы всегда можем выразить $a\sin x+b\cos x$ в виде $R\sin(x+\theta)$, где $R \ge 0$
Если $a\sin x+b\cos x =R\sin(x+\theta)$
Или если $a\sin x+b\cos x=R\sin x\cos\theta + R\cos x\sin\theta$
Сравнение коэффициентов $ \sin x$ и $\cos x$,
$a=R\cos\theta$ и $b=R\sin\theta$.
Возводя в квадрат и складывая, получаем $R^2=a^2+b^2=>R=\sqrt{a^2+b^2}$ as $R\ge 0$ 9{-1}(-1)=n\pi-\frac{\pi}{4}$
=> $\theta$ может лежать во 2-м или 4-м квадранте.
Заметим, что здесь $\cos\theta=\frac{1}{\sqrt2}$ и $\sin\theta=-\frac{1}{\sqrt2}$
Итак, $\theta$ лежит в 4-й квадрант.
Итак, $\theta=2m\pi-\frac{\pi}{4}$, где m — любое целое число.
$\endgroup$
1
Зарегистрируйтесь или войдите в систему
Зарегистрируйтесь с помощью Google
Зарегистрироваться через Facebook
Зарегистрируйтесь, используя электронную почту и пароль
Опубликовать как гость
Электронная почта
Требуется, но никогда не отображается
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie
.
Что такое домен и диапазон \\[\\sin x+\\cos x\\]?
Ответ
Проверено
172,8 тыс.+ просмотров
Подсказка: Этот тип вопросов зависит от базовой концепции тригонометрии. Мы знаем, что \[\sin x\] и \[\cos x\] определены для всех действительных значений \[x\]. Также абсолютное значение обеих функций никогда не может быть больше 1, поскольку \[-1\le \sin x\le 1\And -1\le \cos x\le 1\]. Наряду с этим в этом вопросе мы используем \[\sin \left( A+B \right)=\sin A\cos B+\cos A\sin B\] и \[\sin \left( \dfrac{\pi } {4} \right)=\cos \left( \dfrac{\pi }{4} \right)=\dfrac{1}{\sqrt{2}}\].
Полное пошаговое решение:
Теперь нам нужно найти домен и диапазон \[\sin x+\cos x\]
Для этого рассмотрим,
\[\Стрелка вправо \sin x+\cos x\]
Теперь умножаем и делим на \[\sqrt{2}\], получаем
\[\Стрелка вправо \sin x+\cos x=\sqrt{2}\left( \dfrac{\sin x+\cos x}{\ sqrt{2}} \right)\]
Разделив знаменатель, мы можем написать:
\[\Стрелка вправо \sin x+\cos x=\sqrt{2}\left( \dfrac{1}{\sqrt{2} }\sin x+\dfrac{1}{\sqrt{2}}\cos x \right)\]
Мы знаем, что \[\sin \left( \dfrac{\pi }{4} \right)=\ cos \left( \dfrac{\pi }{4} \right)=\dfrac{1}{\sqrt{2}}\] следовательно,
Кроме того, мы знаем, что \[\sin \left( A+B \right)=\sin A\cos B+\cos A\sin B\]
\[\Rightarrow \sin x+\cos x =\sqrt{2}\sin \left( x+\dfrac{\pi }{4} \right)\]
Следовательно, мы перепишем данную функцию \[\sin x+\cos x\] как \[\sqrt{ 2}\sin\left(x+\dfrac{\pi}{4}\right)\].
Поскольку мы знаем, что функция \[\sin x\] определена для всех действительных значений \[x\]. Таким образом, домен \[\sin x\] равен:
\[\Rightarrow x\in \left( -\infty ,\infty \right)\]
Аналогично можно сказать, что функция \[\sin x+\cos x=\sqrt{2}\sin \left ( x+\dfrac{\pi }{4} \right)\] также определяется для всех значений \[\left( x+\dfrac{\pi }{4} \right)\] и, следовательно, для всех значений \ [Икс\]. Таким образом, мы можем сказать, что область определения функции \[\sin x+\cos x=\sqrt{2}\sin \left( x+\dfrac{\pi }{4} \right)\] равна:
\[\ Стрелка вправо \ влево ( x + \ dfrac {\ pi } {4} \ right) \ in \ left ( — \ infty , \ infty \ right) \ to x \ in \ left ( — \ infty , \ infty \ right) \]
Также мы знаем, что абсолютное значение \[\sin x\] никогда не может быть больше 1. Итак, мы имеем:
\[\begin{align}
& \Rightarrow \left| \sin x \right|\le 1 \\
& \Rightarrow -1\le \sin x\le 1 \\
& \Rightarrow -1\le \sin \left( x+\dfrac{\pi }{4} \right)\le 1 \\
& \Rightarrow \sqrt{2}\times \left( -1 \right)\le \sqrt{2}\sin \left( x+\dfrac{\pi }{4} \ right)\le \sqrt{2}\times 1 \\
& \Rightarrow -\sqrt{2}\le \sqrt{2}\sin \left( x+\dfrac{\pi }{4} \right)\ ле \sqrt{2} \\
\end{align}\]
Таким образом, значение функции \[\sin x+\cos x=\sqrt{2}\sin \left( x+\dfrac{\pi }{4} \right)\] лежит от \[-\sqrt{2}\] до \[\sqrt{2}\].
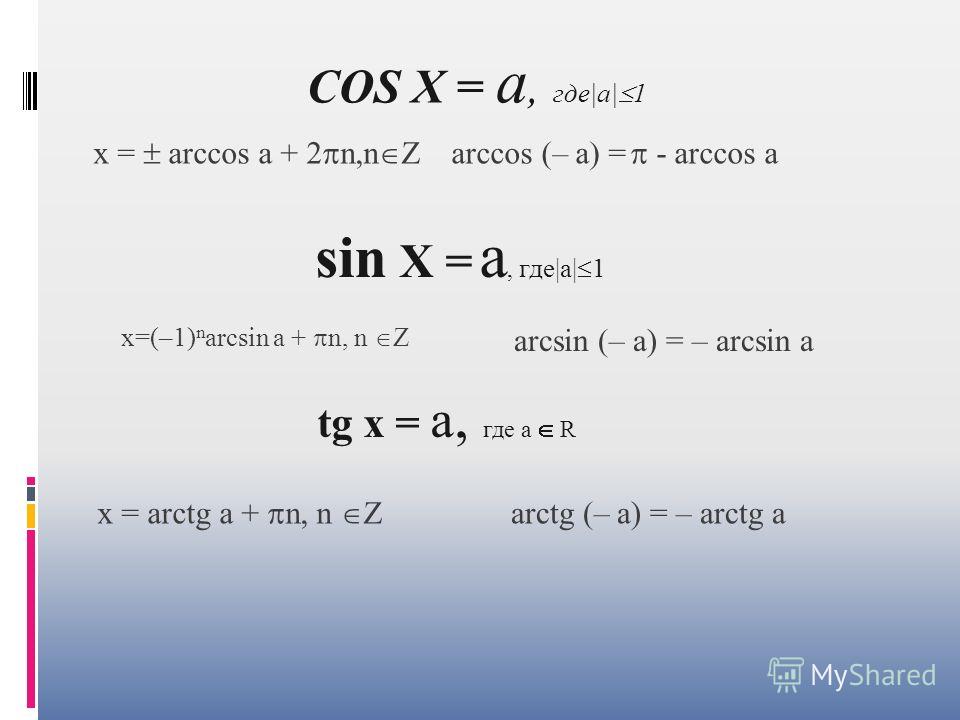
Следовательно, диапазон \[\sin x+\cos x=\sqrt{2}\sin \left( x+\dfrac{\pi }{4} \right)\] равен:
\[\Rightarrow \sqrt{ 2}\sin \left( x+\dfrac{\pi }{4} \right)\in \left[ -\sqrt{2},\sqrt{2} \right]\]
\[\Стрелка вправо \sin x+ \cos x\in \left[ -\sqrt{2},\sqrt{2} \right]\]
Следовательно, домен и диапазон \[\sin x+\cos x\]
\[\begin{align }
& \Домен со стрелкой вправо:\влево( x+\dfrac{\pi }{4} \right)\in \left( -\infty ,\infty \right)\to x\in \left( -\infty ,\infty \right) \\
& \Rightarrow Диапазон:\left[ -\sqrt{2},\sqrt{2} \right] \\
\end{align}\]
Примечание: В этом типе вопросов учащиеся могут преобразовать \[\sin x+\cos x\] в \[\sqrt{2}\sin \left( x+\dfrac{\pi }{4} \right)\]. Учащиеся могут рассмотреть функцию как она есть и попытаться определить домен и диапазон, или можно напрямую разделить на \[\sqrt{2}\]. Студенты должны быть осторожны при умножении и делении на \[\sqrt{2}\], а также при преобразовании.
Недавно обновленные страницы
Рассчитать изменение энтропии, связанное с конверсией Химия класса 11 JEE_Main
Закон, сформулированный доктором Нернстом, является первым законом термодинамики Химия класса 11 JEE_Main
Для реакции при rm0rm0rmC и нормальном давлении A класс 11 химия JEE_Main
Двигатель, работающий между rm15rm0rm0rmC и rm2rm5rm0rmC класс 11 химия JEE_Main
Для реакции rm2Cg в rmCrmlrm2rmg признаки химии 11 класса JEE_Main
Изменение энтальпии перехода жидкой воды в химический класс 11 JEE_Main
Рассчитайте изменение энтропии при переходе в химический класс 11 JEE_Main
Закон, сформулированный доктором Нернстом, является первым законом термодинамики.