Вершина треугольника – определение
4.2
Средняя оценка: 4.2
Всего получено оценок: 206.
4.2
Средняя оценка: 4.2
Всего получено оценок: 206.
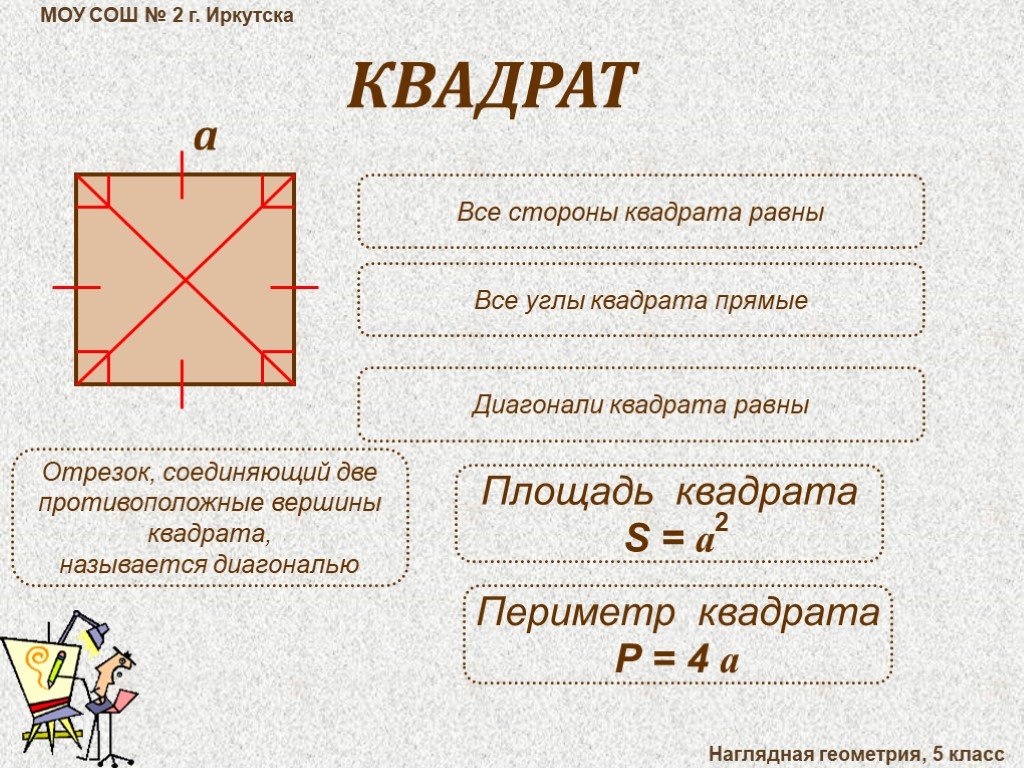
В геометрии нередко рассматривают такое понятие, как «вершина треугольника». Это точка пересечения двух сторон данной фигуры. Практически в каждой задаче встречается это понятие, поэтому имеет смысл рассмотреть его более подробно.
Определение вершины треугольника
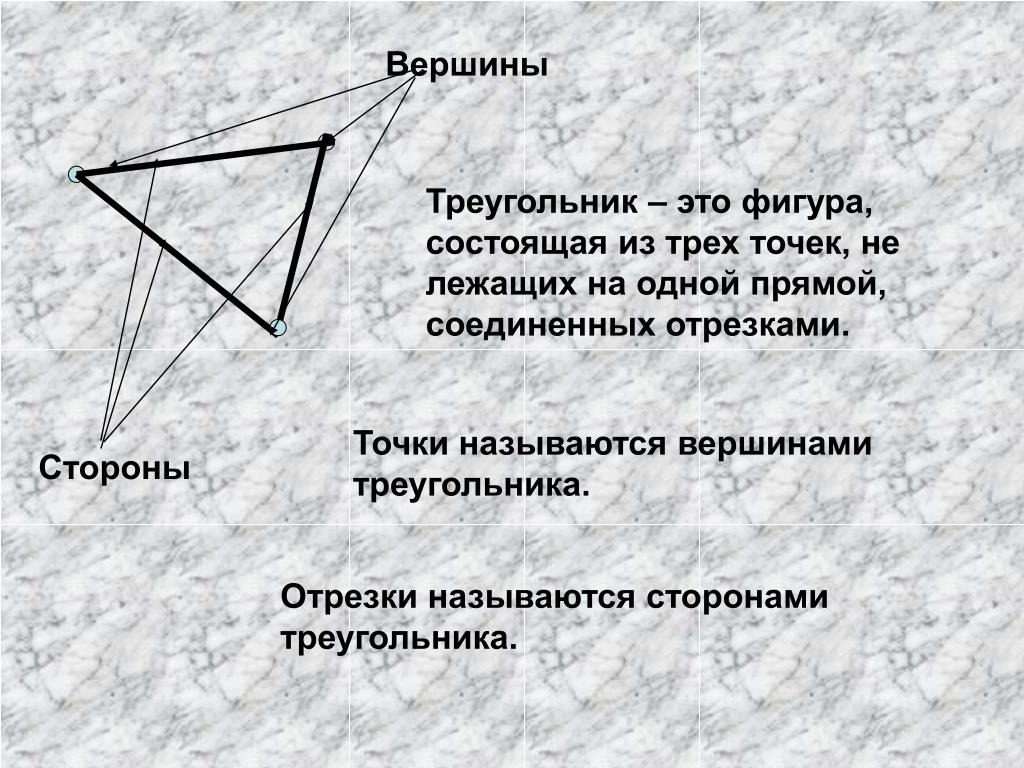
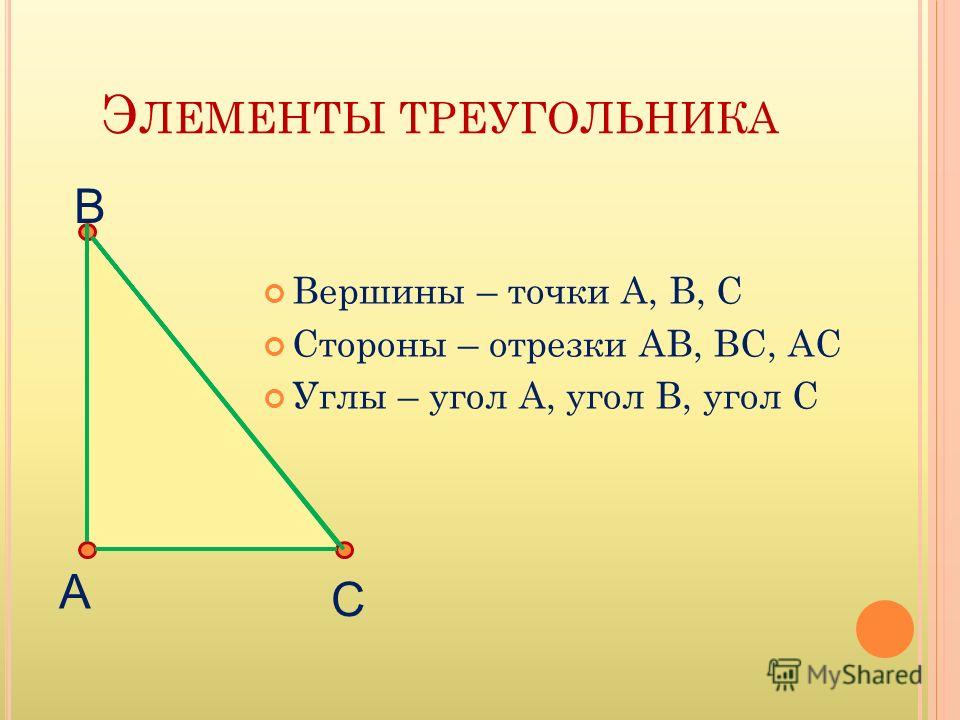
В треугольнике есть три точки пересечения сторон, образующие три угла. Их называют вершинами, а стороны, на которые они опираются – сторонами треугольника.
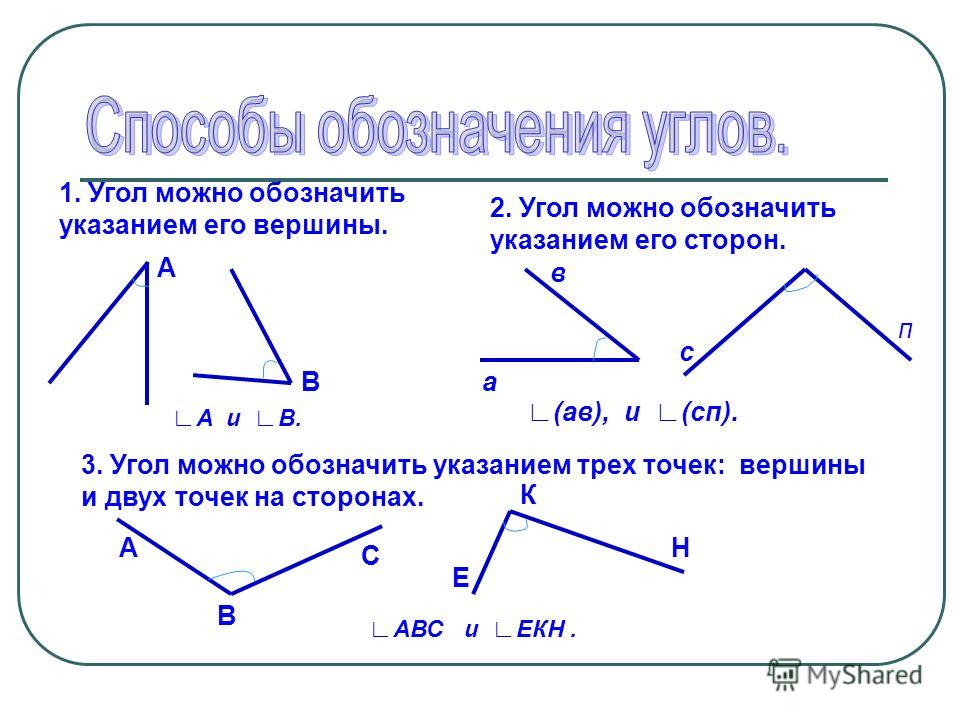
Рис. 1. Вершина в треугольнике.Вершины в треугольниках обозначают большими латинскими буквами. Поэтому чаще всего в математике стороны обозначают двумя заглавными латинскими буквами, по названию вершин, которые входят в стороны. Например стороной АВ называют сторону треугольника, соединяющую вершины А и В.
Рис. 2. Обозначение вершин в треугольнике.
Характеристики понятия
Если взять произвольно ориентированный в плоскости треугольник, то на практике очень удобно выразить его геометрические характеристики через координаты вершин этой фигуры. Так, вершину А треугольника можно выразить точкой с определенными числовыми параметрами А(х; y).
Зная координаты вершин треугольника можно найти точки пересечения медиан, длину высоты, опущенную на одну из сторон фигуры, и площадь треугольника.
Для этого используются свойства векторов, изображаемых в системе декартовой системе координат, ведь длина стороны треугольника определятся через длину вектора с точками, в которых находятся соответствующие вершины этой фигуры.
Использование вершины треугольника
При любой вершине треугольника можно найти угол, который будет смежным внутреннему углу рассматриваемой фигуры. Для этого придется продлить одну из сторон треугольника. Поскольку сторон при каждой вершин две, то и внешних углов при каждой вершине два. Внешний угол равен сумме двух внутренних углов треугольника, несмежных с ним.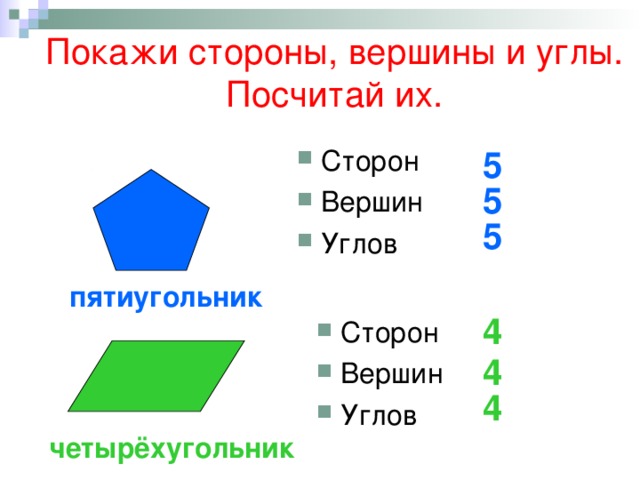
Если построить при одной вершине два внешних угла, то они будут равны, как вертикальные.
Что мы узнали?
Одним из важных понятий геометрии при рассмотрении различных типов треугольников является вершина. Это точка, где пересекаются две стороны угла данной геометрической фигуры. Ее обозначают одной из больших букв латинского алфавита. Вершину треугольника можно выразить через координаты x и y, это помогает определять длину стороны треугольника как длину вектора.
Тест по теме
Доска почёта
Чтобы попасть сюда — пройдите тест.
Лёня Кондратьев
5/5
Али Юсупов
3/5
Оценка статьи
4.2
Средняя оценка: 4.2
Всего получено оценок: 206.
А какая ваша оценка?
Терминология теории графов — iRunner Wiki
Содержание
- 1 Графы
- 2 Деревья
- 3 Подграфы
- 4 Цепи, циклы, пути
- 4.
 2[/math] обозначается множество всех упорядоченных пар (2-размещений), состоящих из двух различных элементов [math]V[/math].
2[/math] обозначается множество всех упорядоченных пар (2-размещений), состоящих из двух различных элементов [math]V[/math].Множество дуг орграфа [math]G[/math] обозначается через [math]A(G)[/math] или [math]AG[/math]. Аналогично определяются ориентированный мультиграф, с той лишь разницей, что совпадающие дуги ориентированного мультиграфа называются параллельными.
Основание орграфа [math]G[/math] — неориентированный мультиграф, получающийся в результате снятия ориентации с дуг орграфа [math]G[/math].
Смешанный граф — граф, в котором могут быть как дуги, так и неориентированные рёбра.
Термин граф может использоваться вместо любого из обобщений этого понятия, если из контекста ясно, о каком определении идёт речь. Поэтому чтобы отличать граф в исходном определении от других, используется понятие простого графа — неориентированного графа без петель и кратных рёбер.
Деревья
Дерево — связный граф, не содержащий циклов.
 [1]
[1]Ориентированный граф [math]D = (V, A)[/math] называется ориентированным деревом с корнем [math]r \in V[/math], если каждая его вершина достижима из [math]r[/math] и основание [math]D_b[/math] графа [math]D[/math] является деревом.
Лес (или ациклический граф) — граф без циклов. Каждая компонента леса является деревом. Заметим, что речь здесь идёт только о неориентированном простом графе.
Ациклический орграф — орграф без циклов. Стоит отметить, что основание ациклического орграфа может не являться ациклическим графом (лесом).
Подграфы
Граф [math]H[/math] называется подграфом (или частью) графа [math]G[/math], если [math]V(H) \subseteq V(G)[/math] и [math]E(H) \subseteq E(G)[/math].
Остовный подграф (или фактор) — подграф, содержащий все вершины исходного графа.
Остов (или каркас) графа [math]G[/math] — максимальный по включению лес, являющийся подграфом графа [math]G[/math].
 Другими словами, остов — это подграф графа [math]G[/math], состоящий из одного остовного дерева для каждой компоненты связности графа [math]G[/math]. Стоит отметить, что не всякий остовный лес является остовом, поскольку, к примеру, пустой остовный подграф является лесом, но не является остовом, если граф содержит хотя бы одно ребро.
Другими словами, остов — это подграф графа [math]G[/math], состоящий из одного остовного дерева для каждой компоненты связности графа [math]G[/math]. Стоит отметить, что не всякий остовный лес является остовом, поскольку, к примеру, пустой остовный подграф является лесом, но не является остовом, если граф содержит хотя бы одно ребро.Если множество вершин подграфа [math]H[/math] графа [math]G[/math] есть [math]S[/math], а сам подграф [math]H[/math] максимальный (по включению) среди всех таких подграфов, то подграфа [math]H[/math] называется подграфом, порождённым множеством [math]S[/math]
, или просто порождённым подграфом. Другими словами, подграф [math]H[/math] графа [math]G[/math] называется порождённым, если он содержит все возможные (для своего множества вершин) рёбра графа [math]G[/math].Цепи, циклы, пути
В неориентированном графе
Маршрут — чередующаяся последовательность [math]v_0, e_1, v_1, e_2, \ldots, e_{\ell}, v_{\ell} \tag{1}[/math] вершин и рёбер, в которой [math]e_i = \{\,v_{i-1}, v_i\,\}\label{route}[/math] ([math]i = \overline{1, \ell}[/math]).
 Вершины [math]v_0[/math] и [math]v_{\ell}[/math] называются крайними, а все остальные — промежуточными (или внутренними).
Маршрут, содержащий вершины [math]v_0[/math] и [math]v_{\ell}[/math] в качестве крайних, называется [math](v_0, v_{\ell})[/math]-маршрутом.
Вершины [math]v_0[/math] и [math]v_{\ell}[/math] называются крайними, а все остальные — промежуточными (или внутренними).
Маршрут, содержащий вершины [math]v_0[/math] и [math]v_{\ell}[/math] в качестве крайних, называется [math](v_0, v_{\ell})[/math]-маршрутом.Если в графе нет кратных рёбер, то маршрут можно однозначно задать последовательностью вершин.
Цепь — маршрут, все рёбра которого попарно различны.
Простая цепь — цепь, все вершины которой, кроме, возможно, крайних, попарно различны.
Цепь в графе также можно рассматривать как подграф этого графа. Тем не менее подграф, соответствующий цепи, однозначно (с точностью до направления) задаёт эту цепь, если и только если она является простой.
Циклический маршрут — маршрут, крайние вершины которого совпадают.
Цикл (или циклическая цепь) — циклический маршрут, являющийся цепью.
Простой цикл — простая циклическая цепь.
Гамильтонов цикл — простой цикл, содержащий все вершины графа.

Эйлеров цикл — цикл, содержащий все рёбра графа.
В ориентированном графе
Ориентированный маршрут (или просто маршрут) — последовательность вида (1) для ориентированного графа, в которой [math]e_i = (v_{i — 1}, v_i)[/math]. Понятия цепи, циклического маршрута и цикла переносятся на случай ориентированного графа без изменений.
Путь — ориентированный маршрут, все вершины которого, кроме, возможно, крайних, различны.
Контур — циклический путь.
Полумаршрут — последовательность вида (1), в которой [math]e_i = (v_{i-1}, v_i)[/math] или [math]e_i = (v_i, v_{i-1})[/math]. Аналогично определяются полуцепь, полупуть и полуконтур.
Если в орграфе существует [math](u, v)[/math]-маршрут, то говорят, что вершина [math]v[/math] достижима из вершины [math]u[/math]. Любая вершина считается достижимой из самой себя.
Связность
В неориентированном графе
Связный граф — граф, любые две несовпадающие вершины которого соединены маршрутом.

Связная компонента (или компонента связности, или просто
Область связности графа — множество всех вершин одной компоненты связности этого графа.
Точкой сочленения называется вершина, при удалении которой число компонент графа увеличивается.
Связный граф, не содержащий точек сочленения, называется двусвязным или вершинно двусвязным.
Мостом называется ребро, при удалении которого число компонент графа увеличивается.
Связный граф, не содержащий мостов, называется рёберно двусвязным.
В ориентированном графе
Орграф называется сильным (или сильносвязным), если любые две его вершины достижимы друг из друга.
Орграф называется односторонним (или односторонне связным), если для любой пары его вершин по меньшей мере одна достижима из другой.
Орграф называется слабым (или слабосвязным, или просто связным), если любые две его вершины соединены полупутём.

Сильная и слабая компоненты определяются аналогично компоненте в неориентированном графе.
Замечания
- ↑ Существуют альтернативные эквивалентные определения.
алгоритмов — Как я могу пометить вершины графа, чтобы они были такими же, как на другом помеченном графе?
спросил
Изменено 1 год, 4 месяца назад
Просмотрено 233 раза
$\begingroup$
Существует ли какой-нибудь алгоритм для пометки эквивалентных вершин неразмеченного графа?
Например, предположим, что у меня есть два различных графа $G_1$ и $G_2$, и они изоморфны. Однако в $G_1$ помечены вершины и ребра, тогда как в $G_2$ помечены только ребра (метки ребер в $G_1$ и $G_2$ могут быть разными).

Итак, если $G_1$ и $G_2$ выглядят примерно так. Мне нужно, чтобы $G_2$ был как там.
- теория графов
- алгоритмы
- граф-изоморфизм
$\endgroup$
2
$\begingroup$
Эту задачу можно решить с помощью канонических маркировок : вычислить каноническую маркировку как $G_1$, так и $G_2$; если в результате получается один и тот же (помеченный) граф, то $G_1$ и $G_2$ изоморфны. Тогда вершины с одинаковыми метками (в канонической маркировке) эквивалентны. Но обратите внимание, что и изоморфизмы, и канонические маркировки уникальны только с точностью до автоморфизма. (например: в вашем примере вершины 1 и 3 нельзя различить.)
Теоретическая сложность проблемы изоморфизма графов до сих пор неизвестна, но на практике существуют быстрые программы, такие как nauty, которые справятся даже с большими графами.

$\endgroup$
Зарегистрируйтесь или войдите в систему
Зарегистрируйтесь с помощью Google
Зарегистрироваться через Facebook
Зарегистрируйтесь, используя адрес электронной почты и пароль
Опубликовать как гость
Электронная почта
Требуется, но никогда не отображается
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie
Сколько помеченных связных графов на $4$ или $5$ вершинах?
спросил
Изменено 7 лет, 4 месяца назад
Просмотрено 2к раз
$\begingroup$
Четыре вершины помечены $1,2,3,4$.

а)Сколькими способами можно провести ребра между некоторыми парами этих вершин, чтобы в результате получился связный граф?
б) Пять вершин помечены $1,2,3,4,5$. Сколькими способами можно провести ребра между некоторыми парами этих вершин, чтобы в результате получился связный граф?
Я нарисовал схемы, но не знаю, как продолжить.
- теория графов
$\endgroup$ 9{\binom{n-k}{2}}$$ и $C_1=1$.
В небольших корпусах у нас есть \начать{выравнивать*} 2 &= С_1 + С_2 \\ 8 &= 2 С_1 + 2 С_2 + С_3 \\ 64 &= 8 С_1 + 6 С_2 + 3 С_3 + С_4 \\ 1024 &= 64 С_1 + 32 С_2 + 12 С_3 + 4 С_4 + С_5 \\ \конец{выравнивание*} который можно использовать для определения $C_2,\ldots,C_5$.
Между прочим, теоретически возможно сосчитать их, рисуя от руки, но это будет утомительно. Для $4$-вершинных графов ниже перечислены неизоморфные связные графы вместе с количеством помеченных графов, изоморфных ему:
Это дает $38$ связных помеченных графов на $4$ вершинах; по-видимому, $728$ на вершинах $5$ (см.

- 4.

 2[/math] обозначается множество всех упорядоченных пар (2-размещений), состоящих из двух различных элементов [math]V[/math].
2[/math] обозначается множество всех упорядоченных пар (2-размещений), состоящих из двух различных элементов [math]V[/math].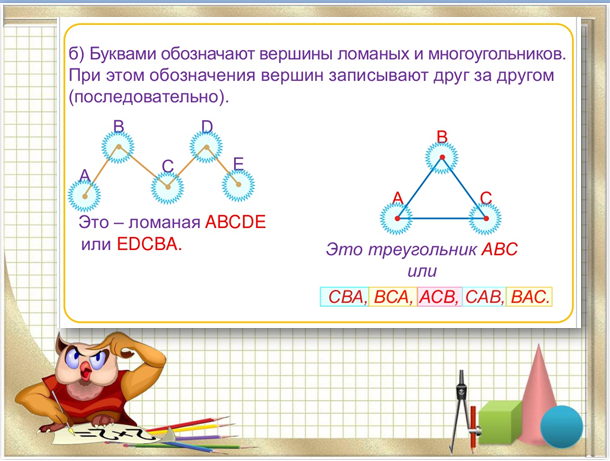 [1]
[1] Другими словами, остов — это подграф графа [math]G[/math], состоящий из одного остовного дерева для каждой компоненты связности графа [math]G[/math]. Стоит отметить, что не всякий остовный лес является остовом, поскольку, к примеру, пустой остовный подграф является лесом, но не является остовом, если граф содержит хотя бы одно ребро.
Другими словами, остов — это подграф графа [math]G[/math], состоящий из одного остовного дерева для каждой компоненты связности графа [math]G[/math]. Стоит отметить, что не всякий остовный лес является остовом, поскольку, к примеру, пустой остовный подграф является лесом, но не является остовом, если граф содержит хотя бы одно ребро. Вершины [math]v_0[/math] и [math]v_{\ell}[/math] называются крайними, а все остальные — промежуточными (или внутренними).
Маршрут, содержащий вершины [math]v_0[/math] и [math]v_{\ell}[/math] в качестве крайних, называется [math](v_0, v_{\ell})[/math]-маршрутом.
Вершины [math]v_0[/math] и [math]v_{\ell}[/math] называются крайними, а все остальные — промежуточными (или внутренними).
Маршрут, содержащий вершины [math]v_0[/math] и [math]v_{\ell}[/math] в качестве крайних, называется [math](v_0, v_{\ell})[/math]-маршрутом.