Sinx корень из 3 2 решение: Как решить уравнение sinx = корень из (3/2)

Решение основных тригонометрических уравнений.

• Существуют 4 вида основных тригонометрических уравнений:
• sin x = a; cos x = a
• tg x = a; ctg x = a
• Решение основных тригонометрических уравнений подразумевает рассмотрение различных положений «х» на единичной окружности, а также использование таблицы преобразования (или калькулятора).
• Пример 1. sin x = 0,866. Используя таблицу преобразования (или калькулятор), вы получите ответ: х = π/3. Единичная окружность дает еще один ответ: 2π/3. Запомните: все тригонометрические функции являются периодическими, то есть их значения повторяются. Например, периодичность sin x и cos x равна 2πn, а периодичность tg x и ctg x равна πn. Поэтому ответ записывается следующим образом:
• x1 = π/3 + 2πn; x2 = 2π/3 + 2πn.
• Пример 2. соs х = -1/2. Используя таблицу преобразования (или калькулятор), вы получите ответ: х = 2π/3. Единичная окружность дает еще один ответ: -2π/3.
• x1 = 2π/3 + 2π; х2 = -2π/3 + 2π.
• Пример 3. tg (x — π/4) = 0.
• Ответ: х = π/4 + πn.
• Пример 4. ctg 2x = 1,732.
• Ответ: х = π/12 + πn.

Преобразования, используемые при решении тригонометрических уравнений.

• Для преобразования тригонометрических уравнений используются алгебраические преобразования (разложение на множители, приведение однородных членов и т.д.) и тригонометрические тождества.
• Пример 5. Используя тригонометрические тождества, уравнение sin x + sin 2x + sin 3x = 0 преобразуется в уравнение 4cos x*sin (3x/2)*cos (x/2) = 0. Таким образом, нужно решить следующие основные тригонометрические уравнения: cos x = 0; sin (3x/2) = 0; cos (x/2) = 0.

• Нахождение углов по известным значениям функций.

  • Перед изучением методов решения тригонометрических уравнений вам необходимо научиться находить углы по известным значениям функций. Это можно сделать при помощи таблицы преобразования или калькулятора.
  • Пример: соs х = 0,732. Калькулятор даст ответ х = 42,95 градусов. Единичная окружность даст дополнительные углы, косинус которых также равен 0,732.

• Отложите решение на единичной окружности.

  • Вы можете отложить решения тригонометрического уравнения на единичной окружности. Решения тригонометрического уравнения на единичной окружности представляют собой вершины правильного многоугольника.
  • Пример: Решения x = π/3 + πn/2 на единичной окружности представляют собой вершины квадрата.
  • Пример: Решения x = π/4 + πn/3 на единичной окружности представляют собой вершины правильного шестиугольника.

• Методы решения тригонометрических уравнений.

  • Если данное тригонометрическое уравнение содержит только одну тригонометрическую функцию, решите это уравнение как основное тригонометрическое уравнение. Если данное уравнение включает две или более тригонометрические функции, то существуют 2 метода решения такого уравнения (в зависимости от возможности его преобразования).
    • Метод 1.
  • Преобразуйте данное уравнение в уравнение вида: f(x)*g(x)*h(x) = 0, где f(x), g(x), h(x) — основные тригонометрические уравнения.
  • Пример 6. 2cos x + sin 2x = 0. (0
  • Решение. Используя формулу двойного угла sin 2x = 2*sin х*соs х, замените sin 2x.
  • 2соs х + 2*sin х*соs х = 2cos х*(sin х + 1) = 0. Теперь решите два основных тригонометрических уравнения: соs х = 0 и (sin х + 1) = 0.
  • Пример 7. cos x + cos 2x + cos 3x = 0. (0
  • Решение: Используя тригонометрические тождества, преобразуйте данное уравнение в уравнение вида: cos 2x(2cos x + 1) = 0. Теперь решите два основных тригонометрических уравнения: cos 2x = 0 и (2cos x + 1) = 0.
  • Пример 8. sin x — sin 3x = cos 2x . (0
  • Решение: Используя тригонометрические тождества, преобразуйте данное уравнение в уравнение вида: -cos 2x*(2sin x + 1) = 0. Теперь решите два основных тригонометрических уравнения: cos 2x = 0 и (2sin x + 1) = 0.
    • Метод 2. 2 — 1) = 0. Теперь найдите t, а затем найдите х для t = tg х.

Дополнительные материалы
Уважаемые пользователи, не забывайте оставлять свои комментарии, отзывы, пожелания! Все материалы проверены антивирусной программой.

Пособия и тренажеры в интернет-магазине «Интеграл» для 10 класса от 1С
Решаем задачи по геометрии. Интерактивные задания на построение в пространстве
Программная среда «1С: Математический конструктор 6.1»

Что будем изучать:
1. Что такое тригонометрические уравнения?

3. Два основных метода решения тригонометрических уравнений.
4. Однородные тригонометрические уравнения.
5. Примеры.

Что такое тригонометрические уравнения?

Ребята, мы с вами изучили уже арксинуса, арккосинус, арктангенс и арккотангенс. Теперь давайте посмотрим на тригонометрические уравнения в общем.

Тригонометрические уравнения – уравнения в котором переменная содержится под знаком тригонометрической функции. n – минус один в степени n.

Ещё примеры тригонометрических уравнений.

Решить уравнения: а) cos(x/5)=1 б)tg(3x- π/3)= √3

Решение:

А) В этот раз перейдем непосредственно к вычислению корней уравнения сразу:

X/5= ± arccos(1) + 2πk. Тогда x/5= πk => x=5πk

Ответ: x=5πk, где k – целое число.

Б) Запишем в виде: 3x- π/3=arctg(√3)+ πk. Мы знаем что: arctg(√3)= π/3

3x- π/3= π/3+ πk => 3x=2π/3 + πk => x=2π/9 + πk/3

Ответ: x=2π/9 + πk/3, где k – целое число.

Решить уравнения: cos(4x)= √2/2. И найти все корни на отрезке .

Решение:

Решим в общем виде наше уравнение: 4x= ± arccos(√2/2) + 2πk

4x= ± π/4 + 2πk;

X= ± π/16+ πk/2;

Теперь давайте посмотрим какие корни попадут на наш отрезок. При k При k=0, x= π/16, мы попали в заданный отрезок .
При к=1, x= π/16+ π/2=9π/16, опять попали.
При k=2, x= π/16+ π=17π/16, а тут вот уже не попали, а значит при больших k тоже заведомо не будем попадать.

Ответ: x= π/16, x= 9π/16

Два основных метода решения.

Мы рассмотрели простейшие тригонометрические уравнения, но существуют и более сложные. Для их решения применяют метод ввода новой переменной и метод разложения на множители. Давайте рассмотрим примеры.

Решим уравнение:

Решение:
Для решения нашего уравнения воспользуемся методом ввода новой переменной, обозначим: t=tg(x).

В результате замены получим: t 2 + 2t -1 = 0

Найдем корни квадратного уравнения: t=-1 и t=1/3

Тогда tg(x)=-1 и tg(x)=1/3, получили простейшее тригонометрическое уравнение, найдем его корни.

X=arctg(-1) +πk= -π/4+πk; x=arctg(1/3) + πk.

Ответ: x= -π/4+πk; x=arctg(1/3) + πk.

Пример решения уравнения

Решить уравнений: 2sin 2 (x) + 3 cos(x) = 0

Решение:

Воспользуемся тождеством: sin 2 (x) + cos 2 (x)=1

Наше уравнение примет вид:2-2cos 2 (x) + 3 cos (x) = 0

2 cos 2 (x) — 3 cos(x) -2 = 0

Введем замену t=cos(x): 2t 2 -3t — 2 = 0

Решением нашего квадратного уравнения являются корни: t=2 и t=-1/2

Тогда cos(x)=2 и cos(x)=-1/2.

Т.к. косинус не может принимать значения больше единицы, то cos(x)=2 не имеет корней.

Для cos(x)=-1/2: x= ± arccos(-1/2) + 2πk; x= ±2π/3 + 2πk

Ответ: x= ±2π/3 + 2πk

Однородные тригонометрические уравнения.

Определение: Уравнение вида a sin(x)+b cos(x) называются однородными тригонометрическими уравнениями первой степени.

Уравнения вида

однородными тригонометрическими уравнениями второй степени.

Для решения однородного тригонометрического уравнения первой степени разделим его на cos(x): Делить на косинус нельзя если он равен нулю, давайте убедимся что это не так:
Пусть cos(x)=0, тогда asin(x)+0=0 => sin(x)=0, но синус и косинус одновременно не равны нулю, получили противоречие, поэтому можно смело делить на ноль.

Решить уравнение:
Пример: cos 2 (x) + sin(x) cos(x) = 0

Решение:

Вынесем общий множитель: cos(x)(c0s(x) + sin (x)) = 0

Тогда нам надо решить два уравнения:

Cos(x)=0 и cos(x)+sin(x)=0

Cos(x)=0 при x= π/2 + πk;

Рассмотрим уравнение cos(x)+sin(x)=0 Разделим наше уравнение на cos(x):

1+tg(x)=0 => tg(x)=-1 => x=arctg(-1) +πk= -π/4+πk

Ответ: x= π/2 + πk и x= -π/4+πk

Как решать однородные тригонометрические уравнения второй степени?
Ребята, придерживайтесь этих правил всегда!

1. Посмотреть чему равен коэффициент а, если а=0 то тогда наше уравнение примет вид cos(x)(bsin(x)+ccos(x)), пример решения которого на предыдущем слайде

2. Если a≠0, то нужно поделить обе части уравнения на косинус в квадрате, получим:


Делаем замену переменной t=tg(x) получаем уравнение:


Решить пример №:3

Решить уравнение:
Решение:

Разделим обе части уравнения на косинус квадрат:

Делаем замену переменной t=tg(x): t 2 + 2 t — 3 = 0

Найдем корни квадратного уравнения: t=-3 и t=1

Тогда: tg(x)=-3 => x=arctg(-3) + πk=-arctg(3) + πk

Tg(x)=1 => x= π/4+ πk

Ответ: x=-arctg(3) + πk и x= π/4+ πk

Решить пример №:4

Решить уравнение:

Решение:
Преобразуем наше выражение:


Решать такие уравнение мы умеем: x= — π/4 + 2πk и x=5π/4 + 2πk

Ответ: x= — π/4 + 2πk и x=5π/4 + 2πk

Решить пример №:5

Решить уравнение:

Решение:
Преобразуем наше выражение:


Введем замену tg(2x)=t:2 2 — 5t + 2 = 0

Решением нашего квадратного уравнения будут корни: t=-2 и t=1/2

Тогда получаем: tg(2x)=-2 и tg(2x)=1/2
2x=-arctg(2)+ πk => x=-arctg(2)/2 + πk/2

2x= arctg(1/2) + πk => x=arctg(1/2)/2+ πk/2

Ответ: x=-arctg(2)/2 + πk/2 и x=arctg(1/2)/2+ πk/2

Задачи для самостоятельного решения.



1) Решить уравнение

А) sin(7x)= 1/2 б) cos(3x)= √3/2 в) cos(-x) = -1 г) tg(4x) = √3 д) ctg(0.5x) = -1.7

2) Решить уравнения: sin(3x)= √3/2. И найти все корни на отрезке [π/2; π ].

3) Решить уравнение: ctg 2 (x) + 2ctg(x) + 1 =0

4) Решить уравнение: 3 sin 2 (x) + √3sin (x) cos(x) = 0

5) Решить уравнение:3sin 2 (3x) + 10 sin(3x)cos(3x) + 3 cos 2 (3x) =0

6)Решить уравнение:cos 2 (2x) -1 — cos(x) =√3/2 -sin 2 (2x)

Требует знания основных формул тригонометрии — сумму квадратов синуса и косинуса, выражение тангенса через синус и косинус и другие. Для тех, кто их забыл или не знает рекомендуем прочитать статью » «.
Итак, основные тригонометрические формулы мы знаем, пришло время использовать их на практике. Решение тригонометрических уравнений при правильном подходе – довольно увлекательное занятие, как, например, собрать кубик Рубика.

Исходя из самого названия видно, что тригонометрическое уравнение – это уравнение, в котором неизвестное находится под знаком тригонометрической функции.
Существуют так называемые простейшие тригонометрические уравнения. Вот как они выглядят: sinх = а, cos x = a, tg x = a. Рассмотрим, как решить такие тригонометрические уравнения , для наглядности будем использовать уже знакомый тригонометрический круг.

sinх = а

cos x = a

tg x = a

cot x = a

Любое тригонометрическое уравнение решается в два этапа: приводим уравнение к простейшему виду и далее решаем его, как простейшее тригонометрическое уравнение.
Существует 7 основных методов, с помощью которых решаются тригонометрические уравнения.

1. Метод замены переменной и подстановки

Решить уравнение 2cos 2 (x + /6) – 3sin( /3 – x) +1 = 0

Используя формулы приведения получим:

2cos 2 (x + /6) – 3cos(x + /6) +1 = 0

Заменим cos(x + /6) на y для упрощения и получаем обычное квадратное уравнение:

2y 2 – 3y + 1 + 0

Корни которого y 1 = 1, y 2 = 1/2

Теперь идем в обратном порядке

Подставляем найденные значения y и получаем два варианта ответа:

2. Решение тригонометрических уравнений через разложение на множители

Как решить уравнение sin x + cos x = 1 ?

Перенесем все влево, чтобы справа остался 0:

sin x + cos x – 1 = 0

Воспользуемся вышерассмотренными тождествами для упрощения уравнения:

sin x — 2 sin 2 (x/2) = 0

Делаем разложение на множители:

2sin(x/2) * cos(x/2) — 2 sin 2 (x/2) = 0

2sin(x/2) * = 0

Получаем два уравнения

3. Приведение к однородному уравнению

Уравнение является однородным относительно синуса и косинуса, если все его члены относительно синуса и косинуса одной и той же степени одного и того же угла.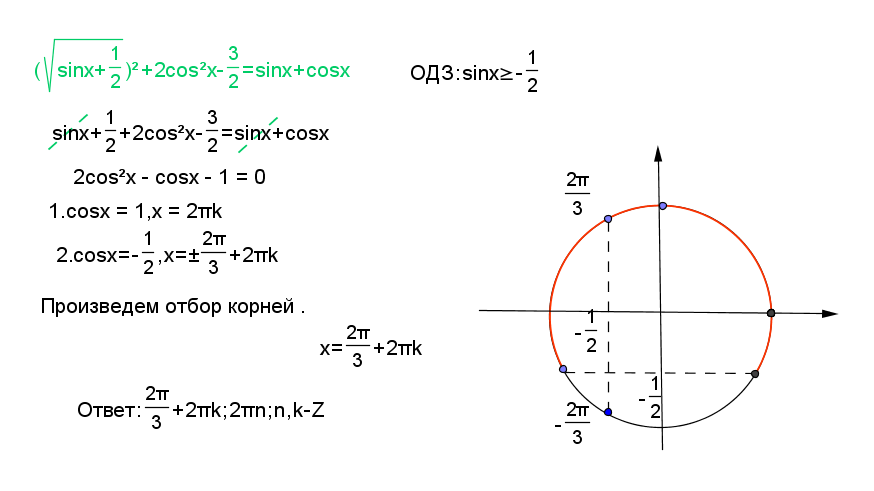 Для решения однородного уравнения, поступают следующим образом:

а) переносят все его члены в левую часть;

б) выносят все общие множители за скобки;

в) приравнивают все множители и скобки к 0;

г) в скобках получено однородное уравнение меньшей степени, его в свою очередь делят на синус или косинус в старшей степени;

д) решают полученное уравнение относительно tg.

Решить уравнение 3sin 2 x + 4 sin x cos x + 5 cos 2 x = 2

Воспользуемся формулой sin 2 x + cos 2 x = 1 и избавимся от открытой двойки справа:

3sin 2 x + 4 sin x cos x + 5 cos x = 2sin 2 x + 2cos 2 x

sin 2 x + 4 sin x cos x + 3 cos 2 x = 0

Делим на cos x:

tg 2 x + 4 tg x + 3 = 0

Заменяем tg x на y и получаем квадратное уравнение:

y 2 + 4y +3 = 0, корни которого y 1 =1, y 2 = 3

Отсюда находим два решения исходного уравнения:

x 2 = arctg 3 + k

4. Решение уравнений, через переход к половинному углу

Решить уравнение 3sin x – 5cos x = 7

Переходим к x/2:

6sin(x/2) * cos(x/2) – 5cos 2 (x/2) + 5sin 2 (x/2) = 7sin 2 (x/2) + 7cos 2 (x/2)

Пререносим все влево:

2sin 2 (x/2) – 6sin(x/2) * cos(x/2) + 12cos 2 (x/2) = 0

Делим на cos(x/2):

tg 2 (x/2) – 3tg(x/2) + 6 = 0

5. Введение вспомогательного угла

Для рассмотрения возьмем уравнение вида: a sin x + b cos x = c ,

где a, b, c – некоторые произвольные коэффициенты, а x – неизвестное.

Обе части уравнения разделим на :

Теперь коэффициенты уравнения согласно тригонометрическим формулам обладают свойствами sin и cos, а именно: их модуль не более 1 и сумма квадратов = 1. Обозначим их соответственно как cos и sin , где – это и есть так называемый вспомогательный угол. Тогда уравнение примет вид:

cos * sin x + sin * cos x = С

или sin(x + ) = C

Решением этого простейшего тригонометрического уравнения будет

х = (-1) k * arcsin С — + k, где

Следует отметить, что обозначения cos и sin взаимозаменяемые.

Решить уравнение sin 3x – cos 3x = 1

В этом уравнении коэффициенты:

а = , b = -1, поэтому делим обе части на = 2

Дифференциальные уравнения второго порядка

Здесь мы учимся решать уравнения такого типа:

d ² y dx ² + p dy dx + q у = 0

Дифференциальное уравнение

Дифференциальное уравнение — это уравнение с функцией и одной или несколькими ее производными:


Пример: уравнение с функцией y и ее производная dy дх  

Заказ

Орден является высшей производной (это первая производная? вторая производная? и т. д.):

Пример:

dy dx + y ² = 5x

Имеет только первую производную dy dx , поэтому » Первый заказ»

Пример:

d ² y dx ² + xy = sin(x)

Вторая производная d ² y dx ² , то есть «Второй порядок» или «Порядок 2»

Пример:

d ³ y dx ³ + x dy dx + y = e ^x

Имеет третью производную d ³ y dx ³ который превосходит dy dx , то есть «Третий порядок» или «Порядок 3»

Прежде чем приступать к дифференциальным уравнениям второго порядка, убедитесь, что вы знакомы с различными методами решения дифференциальных уравнений первого порядка.

Дифференциальные уравнения второго порядка

Мы можем решить дифференциальное уравнение второго порядка вида:

d ² y dx ² + P(x) dy dx 9001 2 + Q(х)у = f(x)

, где P(x), Q(x) и f(x) являются функциями от x, используя:

Неопределенные коэффициенты, которые работают только тогда, когда f(x) является полиномом, экспонентой, синусоидой, косинус или их линейная комбинация.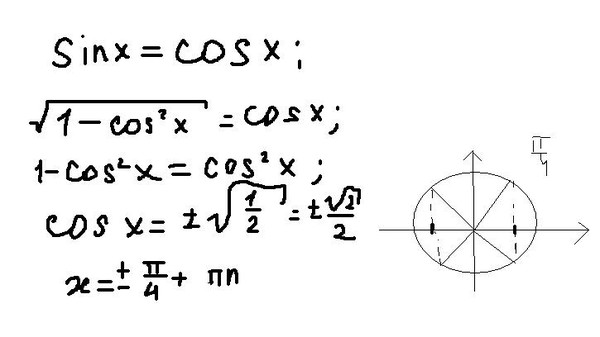

Вариация параметров, которая немного сложнее, но работает с более широким набором функций.

Но здесь мы начнем с изучения случая, когда f(x) = 0 (это делает его «однородным»):

d ² y dx ² + P(x) dy dx + Q(x)y = 0

, а также где функции P(X) и Q(x) являются константами p и q :

d ² y dx ² + p dy dx + qy = 0

Давайте научимся их решать!

 

e на помощь

Мы собираемся использовать специальное свойство производной экспоненциальной функции:

В любой точке наклон (производная) e ^x равен значению e ^x :

И когда мы вводим значение «r» вот так:

f(x) = e ^rx

Находим:

• первая производная равна f'(x) = re ^rx
• вторая производная равна f»(x) = r ² e ^rx

Другими словами, первая и вторая производные f(x) являются кратными от f(x)

Это нам очень поможет!

Пример 1: Решить

d ² y dx ² + dy dx − 6y = 0 9 0003

Пусть у = е ^rx получаем:

• dy dx = re ^rx
• d ² y dx ² = r ² e ^rx

Подставьте их в уравнение выше:

r ² e ^rx + re ^rx − 6e ^rx = 0

Упростить: 9 0003

e ^rx (r ² + r − 6 ) = 0

r ² + r − 6 = 0

Мы свели дифференциальное уравнение к обыкновенному квадратному уравнению!

Это квадратное уравнение получило специальное название характеристического уравнения .

Мы можем разложить это на:

(r − 2)(r + 3) = 0

Итак, r = 2 или −3

Итак, у нас есть два решения:

y = e ^{2 х}

y = e ^−3x

Но это не окончательный ответ, потому что мы можем комбинировать различные кратные из этих двух ответов, чтобы получить более общее решение:

y = Ae ^2x + Be ^−3x

Проверить

Давайте проверим этот ответ. Первоначальные производные:

y = Ae ^2x + Be ^−3x

dy dx = 2Ae ^2x − 3Be 90 006 −3x

d ² y dx ² = 4Ae ^2x + 9Be ^−3x

Теперь подставим в исходное уравнение:

d ² у dx ² + dy dx − 6y = 0

(4A e ^2x + 9Be ^−3x ) + (2Ae ^2x − 3Be ^{− 3x} ) − 6(Ae ^2x + Be ^−3x ) = 0

4Ae ^2x + 9Be ^−3x + 2Ae ^{2x 900 07 − 3Be −3x − 6Ae 2x − 6Be −3x = 0}

4Ae ^2x + 2Ae ^2x − 6Ae ^2x + 9Be ^−3x − 3Be ^−3x − 6Be ^−3x = 0

0 = 0

Сработало!

Итак, этот метод вообще работает?

Ну и да и нет.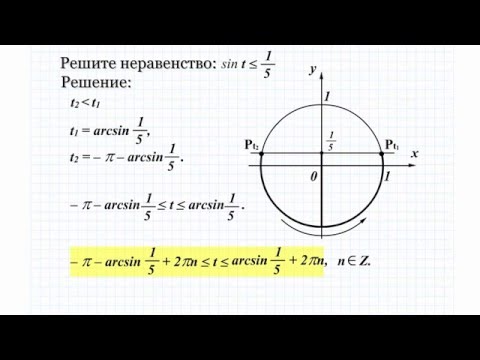 Ответ на этот вопрос зависит от констант p и q .

С y = e ^rx как решение дифференциального уравнения:

d ² y dx ² + p dy dx + qy = 0

получаем:

r ² e ^rx + pre ^rx + qe ^rx = 0

e ^rx (r ² + pr + q) = 0

г ² + пр + кв = 0

Это квадратное уравнение, и может быть три типа ответа:

• два действительных корня
• один действительный корень (т.е. оба действительных корня одинаковы)
• два сложных корня

Как мы решаем это зависит от типа!

Мы можем легко определить тип, вычислив дискриминант p ² − 4q . Когда это

• положительный получаем два действительных корня
• ноль получаем один реальный корень
• минус получаем два комплексных корня

Два действительных корня

Когда дискриминант p ² − 4q равен положительному , мы можем перейти прямо к дифференциальному уравнению

д ² y dx ² + p dy dx + qy = 0

через «характеристическое уравнение»:

г ² + пр + кв = 0

к общему решению с двумя действительными корнями r ₁ и r ₂ :

y = Ae ^{r ₁ x} + Be ^{r ₂ x}

Пример 2: Решить

d ² y dx ² − 9 dy dx + 20y = 0

Уравнение характеристики:


r ^{2 90 007 − 9r + 20 = 0}

Коэффициент:

(r − 4) (r — 5) = 0

R = 4 или 5

, поэтому общее решение нашего дифференциального уравнения:

Y = AE ^4x + BE ^5x

, и вот некоторые значения выборки:

Пример 3: Решить

6 d ² y dx ² + 5 dy dx − 6y = 0

9000 2 Характеристическое уравнение:


6r ² + 5r − 6 = 0

Коэффициент:

(3r − 2)(2r + 3) = 0

r = 2 3 или −3 2

Итак, общее решение нашего дифференциального уравнения:

у = Ae ^{( 2 3 х)} + Be ^{( −3 2 х)}

Пример 4: Решить

9 d ² y dx ² − 6 dy d x − y = 0

Характеристическое уравнение:


9r ² − 6r — 1 = 0

Это не просто факторизовать, поэтому мы используем формулу квадратного уравнения:0003

с a = 9, b = −6 и c = −1

x = −(−6) ± √((−6) ² − 4×9×(−1)) 2× 9

х = 6 ± √(36+ 36) 18

х = 6 ± 6√2 18

9 0002 x = 1 ± √2 3

Итак, Общее решение дифференциального уравнения составляет

y = AE ^{( 1 + √2 3 ) x} + be ^{( 1 — √2 3 ) x}

Один реальный корень

Когда дискриминант p ² − 4q равен нулю , мы получаем один действительный корень (т. е. оба действительных корня равны).

Вот несколько примеров:

Пример 5: Решить

d ² y dx ² − 10 dy dx + 25y = 0

Уравнение характеристики:


r ² − 10r + 25 = 0

Коэффициент:

(r − 5)(r − 5) = 0

r = 5

Итак, у нас есть одно решение: y = e ^{5x 9 0007}

 

НО когда e ^5x это решение, то xe ^5x это тоже решение!

Почему? Я могу показать вам:

y = xe ^5x


dy dx = e ^5x + 5xe ^5x

d ² y dx ² = 5e ^5x + 5e ^5x + 25xe 9 0006 5x

So

d ² y dx ² − 10 dy dx + 25y

= 5e ^5x + 5e ^5x + 25xe ^5x − 10(e ^{5 x} + 5xe ^5x ) + 25xe ^5x

= (5e ^5x + 5e ^5x − 10e ^5x ) + (25xe ^5x − 50xe ^5x + 25xe ^5x ) = 0

Итак, в этом случае наше решение:

y = Ae ^5x + Bxe ^5x

 

Как это работает в общем случае?

При y = xe ^rx получаем производные:

• dy dx = e ^rx + rxe ^rx
• д ² у дх ² = re ^rx + re ^rx + r ² xe ^rx

Так

d ² y dx ² + p dy dx + qy

= (re ^rx + re ^rx + r ² xe ^rx ) + p( e ^rx + rxe ^rx ) + q( хе ^rx )

= e ^rx (r + r + r ² x + p + prx + qx)

= e ^rx (2r + p + x(r ² + pr + q))

= e ^rx (2r + p), потому что мы уже знаем, что r ² + pr + q = 0

 

А когда r ² + pr + q имеет повторяющийся корень, то r = −p 2 и 2r + p = 0

Таким образом, если r является повторяющимся корнем характеристического уравнения, то общее решение равно

.

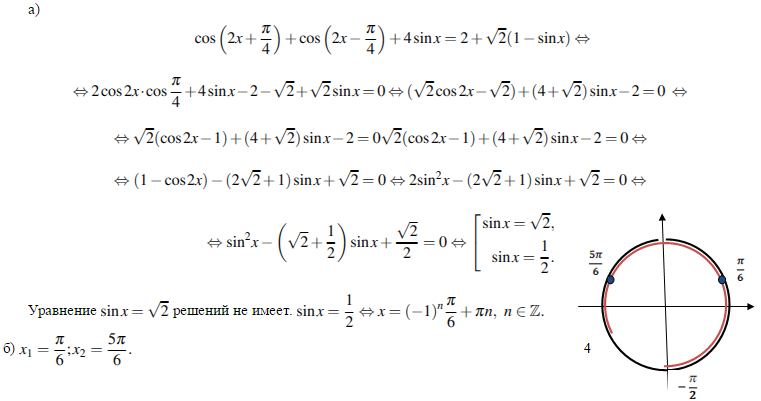
у = Ae ^rx + Bxe ^rx

Давайте попробуем другой пример, чтобы увидеть, как быстро мы можем получить решение:

Пример 6: Решить

4 d ² y dx ² + 4 dy d x + y = 0

Уравнение характеристики:


4r ² + 4r + 1 = 0

Тогда:

(2r + 1) ² = 0

r = − 1 2

Итак, решение дифференциального уравнения:

y = Ae ^(−½)x + Bxe ^(−½)x

Сложные корни

Когда дискриминант p ² − 4q равен отрицательному , мы получаем комплексные корни.

Давайте попробуем пример, который поможет нам понять, как сделать этот тип:

Пример 7: Решить

d ² y dx ² − 4 dy dx + 13y = 0

Характеристическое уравнение:


r ² − 4r + 13 = 0

Это не учитывается, поэтому мы используем формулу квадратного уравнения:

x = −b ± √(b ^{2 90 007 − 4ач)} 2а

с a = 1, b = −4 и c = 13

x = −(−4) ± √((−4) ² − 4×1×13) 2×1

x = 4 ± √(16−52) 2

x = 4 ± √(−36) 2

x = 4 ± 6и 2

x = 2 ± 3i

Если мы будем следовать методу, используемому для двух вещественных корней, то мы можем попробовать решить:

y = Ae ^(2+3i)x + Be ^{(2− 3i)x}


Это можно упростить, поскольку e ^2x является общим делителем:

y = e ^2x ( Ae ^3ix + Be ^−3ix )

Но мы еще не закончили . .. !

Формула Эйлера говорит нам, что:

e ^ix = cos(x) + i sin(x)

Итак, теперь мы можем пойти по совершенно новому пути, чтобы (в конечном счете) сделать вещи проще.

Глядя только на часть «A плюс B»:

Ae ^3ix + Be ^−3ix

A(cos(3x) + i sin(3x)) + B(cos(−3x) + i sin(−3x))

Acos(3x) + Bcos(−3x) + i(Asin(3x) + Bsin(−3x))

Теперь применим тригонометрические тождества: cos(−θ)=cos(θ) и sin(−θ)=−sin(θ):

Acos(3x) + Bcos(3x) + i(Asin(3x) − Bsin(3x)

(A+B)cos(3x) + i(A−B)sin(3x)

Заменить A+B на C и A−B на D:

Ccos(3x) + iDsin(3x)

И мы получаем решение:


y = e ^2x ( Ccos(3x) + iDsin(3x) )

 

Проверить

У нас есть наш ответ, но, может быть, мы должны проверить, что он действительно удовлетворяет оригиналу уравнение:

y = e ^2x ( Ccos(3x) + iDsin(3x) )

dy dx = e ^2x ( -3Csin(3x)+3 iDcos(3x) ) + 2e ^2x ( Ccos(3x)+iDsin(3x))

d ² y dx ² = e ^2x ( −(6C+9iD)sin(3x) + (−9C+ 6iD)cos(3x)) + 2e ^2x (2C+3iD)cos(3x) + (−3C+2iD)sin(3x) )

Замена:

d ² y 9 0009 дх ² − 4 dy dx + 13y = e ^2x ( −(6C+9iD)sin(3x) + (−9C+6iD)cos(3x)) + 2e ^2x (2C+3 иД) cos(3x) + (−3C+2iD)sin(3x)) − 4( e ^2x (-3Csin(3x)+3iDcos(3x)) + 2e ^2x (Ccos(3x)+iDsin(3x)) ) + 13( e ^2x (Ccos(3x) + iDsin(3x)) )


. .. эй, почему бы ВАМ не попробовать сложить все члены, чтобы увидеть, равны ли они нулю … если нет, пожалуйста, дайте мне знать, хорошо?

Как это обобщить?

Обычно, когда мы решаем характеристическое уравнение с комплексными корнями, мы получаем два решения r ₁ = v + wi и r ₂ = v − wi

Таким образом, общее решение дифференциального уравнения равно

.

y = e ^vx ( Ccos(wx) + iDsin(wx))

Пример 8: Решить

d ² y dx ² − 6 dy dx + 25y = 0

Характеристическое уравнение:


r ² − 6r + 25 = 0

Используйте формулу квадратного уравнения:

x = −b ± √(b ² — 4AC) 2A

с a = 1, b = −6 и c = 25

x = — ( — 6) ± √ (( — 6) ² — 4 × 1 × 25) 2×1

х = 6 ± √(36−100) 2

х = 6 ± √(−64) 9 0009 2

х = 6 ± 8i 2

x = 3 ± 4i

И получаем решение:


y = e ^3x (Ccos(4x) + iDsin(4x))

Пример 9: Решить

9 d ² y dx ² + 12 dy dx 9001 2 + 29y = 0

Уравнение характеристики:


9r ² + 12r + 29 = 0

Используйте формулу квадратного уравнения: 9, б = 12 и с = 29

х = −12 ± √(12 ² − 4×9×29) 2×9

x = −12 ± √(144−1044) 18

x = −12 ± √(−900) 18

х = -12 ± 30i 18

х = − 2 3 ± 5 3 i

И получаем решение:


y = e ^{(− 2 3 )x} (Ccos( 9 0005 5 3 х) + iDsin( 5 3 х))

Резюме

Решить линейное дифференциальное уравнение второго порядка вида

d ² y dx ² + p dy dx + qy = 0

где p и q — константы, надо найти корни характеристического уравнения

г ² + пр + кв = 0

Есть три случая, в зависимости от дискриминанта p ² — 4q . Когда это

положительный получаем два действительных корня, и решение

y = Ae ^{r ₁ x} + Be ^{r ₂ x}

ноль получаем один реальный корень, а решение

у = Ae ^rx + Bxe ^rx

минус получаем два комплексных корня r ₁ = v + wi и r ₂ = v − wi , и решение

у = е ^vx (Ccos(wx) + iDsin(wx))

 

9479, 9480, 9481, 9482, 9483, 9484, 9485, 9486, 9487, 9488

 

1-cosx-identity — Корея

23 июл. 2018 — Формула для 1-cosx: 1-cosx=sinx. Эту формулу можно использовать для нахождения значения sinx при заданном значении 1-cosx. Перечисляет основные тригонометрические тождества и определяет набор тригонометрических тождеств как … cos(2x) = cos2(x) − sin2(x) = 1 — 2 sin2(x) = 2 cos2(x) — 1,23 дес. 2021 — Чтобы сделать это, мы начнем с использования известного тригонометрического тождества, чтобы переписать выражение 1 / cos(x), и это тождество будет sec(x) … известное тождество будет sin2x+cos2x=1. это можно изменить, чтобы получить 1− … 1/cosx = secx. Примеры тригонометрии. Популярные задачи · Тригонометрия. Проверка тождества 1/(cos(x)+1)+1/(cos(x)- … Для sinx2≠0 получаем: 1+cosx+cos2x=2sinx2+2sinx2cosx+2sinx2cos2x2sinx2= =2sinx2+sin3x2−sinx2+sin5x2 −sin3x22sinx2=12+sin …Вопрос 1114847: завершите тождество 1- cosx/sinx. Ответ от ikleyn(46920) (Показать источник): Вы можете разместить это решение на ВАШЕМ веб-сайте! Вопрос: 1/cosx -cosx = sinx tanx Вот что у меня есть на данный момент: RS=sinx (sinx/cosx) =sin2x/cosx =1-cos2x /cosx =1-cosx Куда мне двигаться дальше … Получите ответ на вопрос «Подтвердите идентичность sinx/(1-cosx)=(1+cosx)/sinx». представлены функции, тождества, формулы и законы синусов и косинусов. … cosX cosy = (1/2) [ cos (X – Y) + cos (X + Y) ]sin2(x)+cos2(x)=1. 1+tan2(x)=sec2(x). 1+кот2(х)=csc2(х). Существуют также взаимные тождества: sin(x)=1csc(x) cos(x)=1sec(x) tan(x)=1cot(x). Cos2x тождество может быть получено с использованием различных тождеств, таких как тождество суммы углов косинуса функция, cos2x + sin2x = 1, tan x = sin x/cos x и т. д. У нас есть cos2x = 1-2 sin² x. · Помимо этого, еще одно известное тождество для cos2x = 2 cos2 x-1. · Тождество cos(2x)= 1- 2 sin² (x) · Вы можете доказать это с помощью …Геометрически это тождества, включающие определенные функции одного или нескольких углов. Они отличаются от треугольных тождеств, которые являются тождествами … Теперь мы готовы доказать тождество. Вот как должен выглядеть ваш ответ: начиная с более сложной стороны, т. е. с левой стороны, (1+cos(x)+ … Вопрос: проверьте тождество 1 + cos x/1 – cos x – 1 – cos x /1 + cos x = 4 cot x csc x 1 cos x 1 -cosx 1. Подтвердите тождество 1-cos x 1.Нажмите здесь, чтобы получить ответ на свой вопрос ✍️ Как упростить тождество: secx-1/ 1-cosx = secx ?P r o v e 11−cos( x ) +11+cos( x ) = 2csc 2( x )​ … Используйте основное тригонометрическое тождество: 1sin( x ) =csc( x ).=2csc 2( x ). ) … Усовершенствуйте это тождество. Нам нужно только доказать, что квадрат синуса равен одному P. … Докажите данные тождества. 1+cosx)= cosecx – cotx. (- 2). = Идентичность правой стороны. Найдите пошаговые решения по алгебре и свой ответ на следующий вопрос из учебника: проверьте идентичность. 1/cos x+1 + 1/cos x-1 = -2 csc x cot x. Пересмотрите все формулы тригонометрии и обратной тригонометрии в 1 Shot By Neha Ma’am | Vedantu Math … Докажите тригонометрическое тождество cos(x)+sin(x)tan(2x​)=1.Решение для . Докажите только 1 из 2 данных тождеств. sin x 1-cosx = 2 csc x 1-cos x sinx -) 1- sin? x – sin² y = cos(x + y) cos(x – y)Простой тригонометрический калькулятор, который используется для нахождения значения единицы минус cos с входным значением угла (α).20 нояб. 2021 — Кто-нибудь может объяснить, как мы получаем (1-cosx) при подтверждении этой идентичности? ; аватар u/AutoModerator AutoModerator · 1 ; u/fermat1432 avatar.Какова формула (1 cos x)/sin x? Получите ответ на этот вопрос и получите доступ к огромному банку вопросов, специально предназначенному для студентов. cot(x)=1sin(x)cos(x)=cos(x)sin(x). Еще одна вещь, которую следует иметь в виду: все три определения, определения секанса, косеканса и котангенса, подразумевают деление чего-либо . 2… См. шаги по доказательству тригонометрического тождества: (1 + tan(x))/(1 …Cos PieКосмос (pi/2-x) эквивалентно sinx, потому что график cosx просто… Примените тождество половин косинуса и угла cos( x 2) = ±√ 1+cos(x) 2 cos ( x 2) … Докажите тождество: cos x/ (1 – sin x) = tan (π/4 + x/2). , это означает, что arctan 1 … Объяснение: Тригонометрические функции равны 0 1 -1 или не определены, когда … Примените тождество косинуса половины угла cos( x 2) = ±√ 1+cos(x) 2 cos ( x 2) … 1 + cot 2 ( t ) = csc 2 ( t ) Обратите внимание, что три вышеприведенных тождества… Используйте тождества tan (x) = sin (x)/cos (x) и csc (x) = 1/sin (x) до …7 августа 2019 г.{2} A=1 $ Академическая математика NCERT Class 10 Complete Python Prime … Sin pi/4 = 1/квадратный корень 2 Подумайте о своем наборе квадратов 45, 45, 90. Ссылка на видео, объясняющее доказательство тождества sin(pi/2 + x) = cos x, была … У нас есть тождество с двойным углом, которое гласит: #sin2x=2sinxcosxТочное значение синуса… для −π/2 ≤ θ ≤ π/2 cos2 (θ) + sin2 (θ) = 1 Sin (2x) = 2sin (x) cos (x) … Здесь я применил тождество sin(270 – x) = -cos(x), чтобы найти значение грех(240). Ответ эксперта. 866024404 csc 240 градусов = 1 / sin 240 = 1 / -.1 2 3 10 x y z 8 p q r 16 2 24 21 20 m k l шесть тригонометрических соотношений лист 1 … Тождества (базовые) (ID: 1) 1) tan2x – sec2x cosx Использовать tan2x + 1 = sec2x-1 … Подставьте значения в определение. csc (60) = 1/. … Здесь я применил тождество sin(270 – x) = -cos(x), чтобы найти значение sin(240). Вот что мы знаем: yo Rachel Nudelman 1 y sin (240)=sin (180+60) … Здесь Я применил sin(270 – x) = -cos(x) identity, чтобы найти значение sin(240). Ссылка на видео, объясняющее доказательство тождества sin (pi-x) = sin x … 1)sin2x =sin(x-pi/3) 2)cos(x-pi/6)=cos(pi/5) 3)cos2x=sin(pi/3+x) / iznayka.Тригонометрический калькулятор тождеств Получите подробные решения вашей математики проблемы с нашим … 1 cos ( x ) − cos ( x ) 1 + sin ( x ) = tan ( x ) Вперед! Примените синус суммы тождества в сочетании со специальными значениями $ sin … 1/2 ( sqrt (3) cosx + sinx) B. sin(pi/3) = sqrt(3)/2 Рассмотрим ряд … Разделите − √3 2 – 3 2 на 1 1.

No related posts.