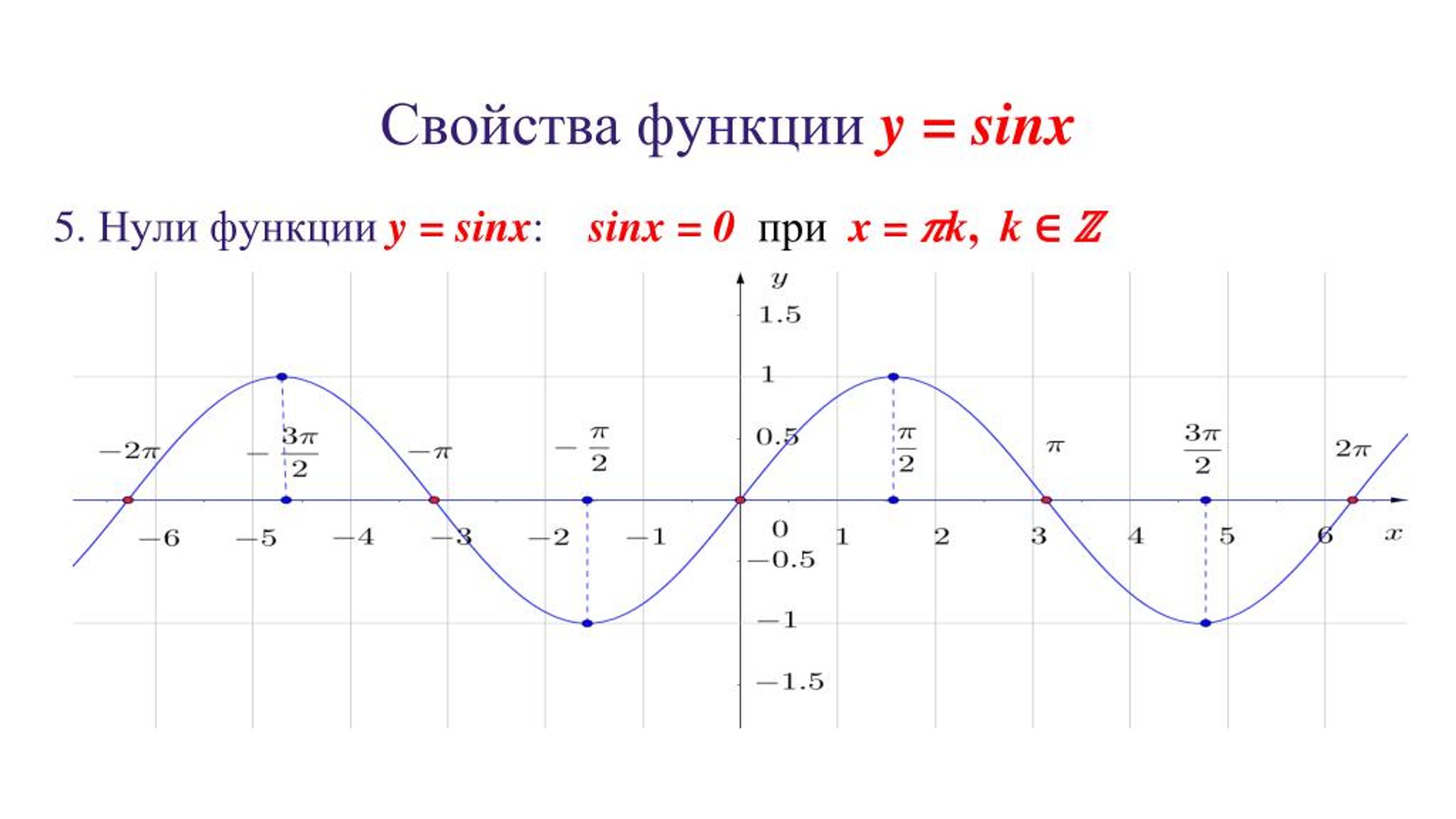
Предел и производная: Замечательные пределы
lim (1 + х)х =е , при х стремящемся к бесконечности -первый замечательный предел.
lim sinx/x=1 при х стремящемся к бесконечности — второй замечательный предел .
Замечательные пределы- пределы стремящиеся к бесконечности.
Второй замечательный предел замечателен не только тем. что он суще-ствует, но и тем. что его величина
— это знаменитое неперово числое = 2.71828… .
Что касается первого замечательного предела, то. как известно, он равен единице,
но при условии, что угол х измеряется в радианах. А это значит, что и он связан с другим не ме-нее
замечательным числом — архимедовым числом тг (тг — отношениедлины любой окружности к ее диаметру,
одно и то же для всех окруж-ностей по соображениям подобия).
илона варкки 11с
http://www.finmath.ru/vocabulary/90/
http://ru.wikipedia.org/
http://209.
Они замечательны тем, что помогают вычислению многих других пределов.
Так, с помощью первого замечательного предела можно установить важную для приложений эквивалентность при стремлении х к нулю следующих бесконечно малых величин: ax, sinax, tgax, arcsinax, arctgax(эквивалентность означает, что их отношение стремится к 1 при стремлении х к нулю). Отметим, что аргументы тригонометрических и обратных тригонометрических функций здесь измеряются в радианах, как это обычно бывает при рассмотрении подобных функций.
http://www.math.com.ua/mathdir/lim_great.html
http://school149.avers-telecom.ru/dlrstore/631e3ba7-726e-4dbe-ab83-f11858b1f1d7/Zamechatelnye_predely.html
darja sahhova
Так называют следующие равенства:
lim sin x/x=1 -первый замечательный предел;
lim(1+x)1/x=lim(1+1/x)x=e=2,718281…
Они замечательны тем, что помогают вычислению многих других пределов.
 x = exp
x = expОни замечательны тем, что помогают вычислению многих других пределов.
Так, с помощью первого замечательного предела можно установить важную для приложений эквивалентность при стремлении х к нулю следующих бесконечно малых величин: ax, sinax, tgax, arcsinax, arctgax
Второй замечательный предел служит для раскрытия неопределенности
http://school-collection.edu.ru/catalog/res/631e3ba7-726e-4dbe-ab83-f11858b1f1d7/view/
http://www.tstu.tver.ru/faculties/civil/vm/math_on_line/topic/funczija/lect_1/lect_1_8.html
Анна Фадеева 11b
Уважаемые блоггеры! Кто ни будь знает кто дал название замечательным пределам? Если есть информация по этому вопросу, поделитесь пожалуйста…
— Как доказать, что $ \ lim \ limits_ {x \ to0} \ frac {\ sin x} x = 1 $?
Это новый пост на старой пиле, потому что это одна из тех вещей, где я могу видеть, как это, к сожалению, то, как мы структурировали текущую учебную программу по математике, действительно не позволяет делать справедливость, которую они заслуживают, и я думаю, что в конечном итоге это оказывает медвежью услугу многим учащимся.
По правде говоря, этот предел не может быть честным доказательством без честного определения синусоидальной функции.И это , а не так просто, как кажется. Даже если мы рассмотрим простое понятие из многих тригонометрических трактовок, что синус равен «длине противоположной стороны прямоугольного треугольника, деленной на длину его гипотенузы», это не решит проблему, потому что на самом деле существует едва уловимый недостающий элемент, и это то, что синус не является функцией «прямоугольного треугольника» (хотя вы могли бы определить это, если бы захотели, и это было бы легко!), а от угловой меры .И на самом деле выяснение того, что означает «угловая мера», по сути, эквивалентно определению синусоидальной функции в первую очередь, так что этот подход является круговым! (каламбур наблюдается после написания, несмотря на то, что изначально не предназначался!)
Итак, как мы определяем синус или угловую меру? К сожалению, любой подход к этому таков, что должен включать в себя исчисление. Это связано с тем, что используемая нами угловая мера является «гладкой и устойчивой», что означает, что, по сути, если у нас есть некоторый угол, мы хотели бы разделить эту угловую меру, чтобы разделить угол таким же образом, как при разрезании кусков пирога: если у меня есть угол с заданной угловой мерой $ \ theta $, то для того, чтобы система измерения работала, я должен иметь возможность получить угол с мерой $ \ frac {\ theta} {n} $, должен быть углом, который геометрически $ n $ -сечение угла на $ n $
Это связано с тем, что используемая нами угловая мера является «гладкой и устойчивой», что означает, что, по сути, если у нас есть некоторый угол, мы хотели бы разделить эту угловую меру, чтобы разделить угол таким же образом, как при разрезании кусков пирога: если у меня есть угол с заданной угловой мерой $ \ theta $, то для того, чтобы система измерения работала, я должен иметь возможность получить угол с мерой $ \ frac {\ theta} {n} $, должен быть углом, который геометрически $ n $ -сечение угла на $ n $
Но уже сейчас мы видим, что это нетривиально: рассмотрим $ n = 3 $. Затем у нас есть знаменитая «невозможная» проблема «троекратного угла», которая раздражала даже древних греков и которую люди продолжали пытаться разгадывать, пока Пьер Ванцель, наконец, не доказал, что ее невозможно решить более двух тысяч лет спустя. Мы просим математический виджет, который может не только разделять на три части, но и углы, составляющие 5, 629 и т. Д., И в порядке систематически !
Д., И в порядке систематически !
Действительно, синусоидальная функция не только не является тривиальной, мы можем утверждать, что даже экспоненциальную функцию значительно легче обрабатывать, чем синусоидальную, хотя я не буду здесь приводить такую трактовку.
Итак, как мы это делаем? Что ж, ключевое наблюдение состоит в том, что наша «устойчивая» угловая мера фактически определяется длиной дуги сегмента круга, пересекаемого углом, когда он нарисован в центре круга и спроецирован наружу. В частности, это должно быть «очевидно» из геометрической формулы
(вводимой по кругу).$$ \ mbox {Длина дуги окружности} = r \ theta $$
Поскольку это всего лишь тривиальное умножение, вся нетривиальность должна заключаться либо в определении $ \ theta $ в терминах геометрических углов, образованных линиями, либо в определении «длины дуги окружности» и, более того, в этих двух задачах. должно быть одинаково сложно.Следовательно, мы сначала начнем с вопроса о дуге, и вы увидите, что в этом ответе будет использована изрядная часть материала Исчисления II, чтобы ответить на этот вопрос уровня Исчисления I о математическом объекте  В самом деле, это и есть вся «радианная мера»: это мера углов в терминах длины дуги части, которую они вырезают из единичной окружности (то есть $ r = 1 $). «Градусы» — это просто странная кратная единица фактической длины, равная $ \ frac {2 \ pi} {360} $ (или лучше $ \ frac {\ tau} {360} $) какой-то другой единицы длины. .
В самом деле, это и есть вся «радианная мера»: это мера углов в терминах длины дуги части, которую они вырезают из единичной окружности (то есть $ r = 1 $). «Градусы» — это просто странная кратная единица фактической длины, равная $ \ frac {2 \ pi} {360} $ (или лучше $ \ frac {\ tau} {360} $) какой-то другой единицы длины. .
Если вы воспользуетесь книгой по тригонометрии , несколько более , вы увидите кое-что о том, что синус и косинус определяются как в основном координаты на единичной окружности, когда угловая мера $ \ theta $ была размещена из $ x ось $:
$$ C (\ theta): = (\ cos (\ theta), \ sin (\ theta)) $$
Теперь, как сказано выше, $ \ theta $ — это длина дуги . Таким образом, то, что у нас есть выше, называется параметризацией длины дуги круга — и это говорит нам, как нам нужно действовать.{-1} (\ theta) $$
.
Наконец, на этом этапе, имея в руках полное, герметичное определение $ \ sin (x) $, мы готовы оценить предел:
$$ \ lim_ {x \ rightarrow 0} \ frac {\ sin (x)} {x} $$
Поскольку «реальная» или базовая функция здесь на самом деле является обратной функцией , то есть $ \ arcsin $, мы сначала выполняем замену переменных: вместо этого мы рассматриваем предел в терминах $ y $, где $ y (х): = \ arcsin (x) $. Обратите внимание, что тривиально $ \ arcsin (0) = 0 $ из определения интеграла, поэтому мы получаем
Обратите внимание, что тривиально $ \ arcsin (0) = 0 $ из определения интеграла, поэтому мы получаем
$$ \ lim_ {x \ rightarrow 0} \ frac {\ sin (x)} {x} = \ lim_ {y \ rightarrow 0} \ frac {y} {\ arcsin (y)} $$
Теперь что касается правого предела, нам нужно только рассмотреть поведение $ \ arcsin (y) $, когда $ y $ мало.{y} 1 \ d \ xi $$
, когда $ y \ приблизительно 0 $, и тогда правый интеграл приблизительно равен $ y $, следовательно, $ \ arcsin (y) \ приблизительно y $, когда $ y \ приблизительно 0 $ и
$$ \ lim_ {y \ rightarrow 0} \ frac {y} {\ arcsin (y)} = \ lim_ {y \ rightarrow 0} \ frac {y} {y} = \ lim_ {y \ rightarrow 0} 1 = 1 $$
, следовательно,
$$ \ lim_ {x \ rightarrow 0} \ frac {\ sin (x)} {x} = 1 $$
QED.
Тем не менее, как я уже упоминал ранее, это не решает требований вопроса, который, хотя я уверен, что его первоначальный вопрос давно ушел, тем не менее, все еще актуален для студентов, изучающих математику, за студентами, изучающими математику, вплоть до сегодняшнего дня: ограничить использование только методов Calculus I / pre-Calculus. Я говорю о том, что на самом деле это не совсем возможно и показывает слабость учебной программы в том, что она на самом деле не соответствует правильному логическому построению математической конструкции.
Я говорю о том, что на самом деле это не совсем возможно и показывает слабость учебной программы в том, что она на самом деле не соответствует правильному логическому построению математической конструкции.
На самом деле должно быть сделано, чтобы оставить триггер для более позднего , то есть пропустить триггер и сначала перейти к исчислению. Когда я изучал математику самостоятельно, я именно так и поступил. На самом деле, как предполагали многие преподаватели, я бы сказал, что большинству людей они не нужны, но им действительно нужно больше статистики.2} $, который является очень хорошим примером отношения площади к интеграции, и это может, если будет подчеркнуто более сильно, потенциально побудить к более тонкому размышлению об интегралах, помимо просто «вставки и исправления правил интеграции». В частности, с более ограниченным набором функций, мы можем подумать о других способах, которыми мы могли бы подойти к ним, и / или о различных способах интерпретации интеграла, которые, как я думаю, могут быть полезны только для разработки более творческих думать о проблемах и меньше углубляться в методы с небольшим полученным реальным пониманием (а механическое измельчение интегралов еще менее актуально с программным обеспечением для компьютерной алгебры; более важным является действительно способность 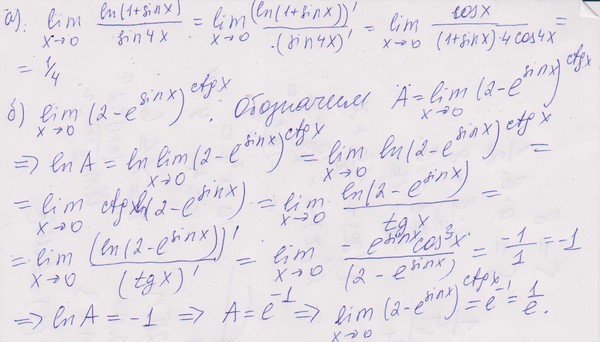 -} \ sin (x) = 0 $$
Я хотел бы иметь возможность проводить доказательство без ссылки на сложные теоремы (теорема о среднем значении, ряды и т. Д.).У меня есть геометрический подход к нахождению предела справа, но мне нужна аналогичная помощь при приближении к нулю слева.
-} \ sin (x) = 0 $$
Я хотел бы иметь возможность проводить доказательство без ссылки на сложные теоремы (теорема о среднем значении, ряды и т. Д.).У меня есть геометрический подход к нахождению предела справа, но мне нужна аналогичная помощь при приближении к нулю слева.
Спасибо.
Обновление : я собираюсь доказать, что синус непрерывен при любом значении $ a $, но сначала мне нужно доказать, что $$ \ lim _ {\ theta \ to0} \ sin \ theta = 0 \ quad \ text {и} \ quad \ lim _ {\ theta \ to0} \ cos \ theta = 1. $$ Я уже показал, что $ f $ непрерывно в $ a $, если $$ \ lim_ {h \ to 0} f (a + h) = f (a), $$ так что тогда я могу показать $$ \ lim_ {h \ to0} \ sin (a + h) = \ sin (a), $$ откуда следует, что синус непрерывен в любой точке $ a $.-} \ sin \ theta = 0 $.
Обновление: Благодаря всей полученной мною хорошей помощи оказалось, что если $ 0 \ le \ theta \ le \ pi / 2 $, то
$$ \ sin \ theta \ le \ theta $$
что, поскольку $ \ sin \ theta $ и $ \ theta $ положительны на $ 0 \ le \ theta \ le \ pi / 2 $, эквивалентно
$$ | \, \ sin \ theta \, | <| \, \ theta \, |. $$
Во-вторых, если $ — \ pi / 2 \ le \ theta \ le0 $, то $ 0 \ le- \ theta \ le \ pi / 2 $. Следовательно, мы можем подставить $ — \ theta $ в последнее неравенство, что приведет к:
$$ \ begin {align *}
| \ sin (- \ theta) \, | & \ le | — \ theta \, | \\
| — \ sin (\ theta) \, | & \ le | — \ theta \, | \\
| \ sin (\ theta) \, | & \ le | \, \ theta \, |
\ end {align *} $$
Следовательно, если $ — \ pi / 2 \ le \ theta \ le \ pi / 2 $, то
$$ | \ sin (\ theta) \, | \ le | \, \ theta \, |.$$
Последний шаг связан с тем, что $ | -x | = | x | $ для всех действительных чисел $ x $. Последнее неравенство эквивалентно
$$ — | \, \ theta \, | \ le \ sin \ theta \ le | \, \ theta \, |, $$
и по теореме сжатия, поскольку оба конца стремятся к нулю при $ \ theta \ to0 $, я показал, что
$$ \ lim _ {\ theta-> 0} \ sin \ theta = 0. $$
$$
Во-вторых, если $ — \ pi / 2 \ le \ theta \ le0 $, то $ 0 \ le- \ theta \ le \ pi / 2 $. Следовательно, мы можем подставить $ — \ theta $ в последнее неравенство, что приведет к:
$$ \ begin {align *}
| \ sin (- \ theta) \, | & \ le | — \ theta \, | \\
| — \ sin (\ theta) \, | & \ le | — \ theta \, | \\
| \ sin (\ theta) \, | & \ le | \, \ theta \, |
\ end {align *} $$
Следовательно, если $ — \ pi / 2 \ le \ theta \ le \ pi / 2 $, то
$$ | \ sin (\ theta) \, | \ le | \, \ theta \, |.$$
Последний шаг связан с тем, что $ | -x | = | x | $ для всех действительных чисел $ x $. Последнее неравенство эквивалентно
$$ — | \, \ theta \, | \ le \ sin \ theta \ le | \, \ theta \, |, $$
и по теореме сжатия, поскольку оба конца стремятся к нулю при $ \ theta \ to0 $, я показал, что
$$ \ lim _ {\ theta-> 0} \ sin \ theta = 0. $$
— limit_calculator (sin (x) / x; x) — Solumaths
Сводка:
Калькулятор пределов позволяет вычислить предел функции с подробностями и шагами вычисления.
Описание:
Калькулятор пределов находит, существует ли предел в любой точке: предел в 0, предел в «+ oo» и предел в «-oo» функции.
Вычисление предела функции a
- Можно вычислить предел в функции , где a представляет действительное число:
- Если предел существует и калькулятор может рассчитать, он возвращается.2 + х; х; а`)
Вычисление предела функции 0
- Можно вычислить предел при 0 функции :
- Если предел существует и калькулятор может рассчитать, он возвращается.
- Для результата вычисления предела, например следующего: `lim_ (x-> 0) sin (x) / x`, введите: limit_calculator (`sin (x) / x; x`)
Вычисление предела функции на плюс бесконечности
- Можно вычислить предел на + infini функции :
- Если предел существует и калькулятор может рассчитать, он возвращается.

- Для результата вычисления предела, например следующего: `lim_ (x -> + oo) sin (x) / x`, введите: limit_calculator (`sin (x) / x`)
Вычисление предела функции на минус бесконечности
- Можно вычислить предел в — infini функции :
- Если предел существует и калькулятор может рассчитать, он возвращается.
- Для результата вычисления предела, например следующего: `lim_ (x -> — oo) sin (x) / x`, введите: limit_calculator (`sin (x) / x`)
Калькулятор пределов позволяет вычислить предел функции с подробными сведениями и шагами вычисления.
Синтаксис:
limit_calculator (функция; переменная; значение),Примеры:
Чтобы вычислить предел sin (x) / x при 0 относительно x, введите:
Калькулятор возвращает 1
Расчет онлайн с помощью limit_calculator (предел функции)Тригонометрические пределы
Базовый тригонометрический предел —
\ [\ lim \ limits_ {x \ to 0} \ frac {{\ sin x}} {x} = 1. \]
\]
Используя этот предел, можно получить ряд других тригонометрических ограничений:
\ [{\ lim \ limits_ {x \ to 0} \ frac {{\ tan x}} {x} = 1, \; \; \;} \ kern-0.3pt
{\ lim \ limits_ {x \ до 0} \ frac {{\ arcsin x}} {x} = 1, \; \; \;} \ kern-0.3pt
{\ lim \ limits_ {x \ to 0} \ frac {{\ arctan x} } {x} = 1.} \]
Далее мы предполагаем, что углы измеряются в радианах.
Решенные проблемы
Щелкните или коснитесь проблемы, чтобы увидеть решение.
Пример 1
Найдите предел \ (\ lim \ limits_ {x \ to 0} {\ large {\ frac {{4x}} {{\ sin 3x}}} \ normalsize} \).2}}} \ normalsize} \).Пример 3
Найдите предел \ (\ lim \ limits_ {x \ to 0} {\ large \ frac {{\ sin5x — \ sin 3x}} {{\ sin x}} \ normalsize} \).Пример 4
Вычислить предел \ (\ lim \ limits_ {x \ to 0} {\ large {\ frac {{\ cos \ left ({x + a} \ right) — \ cos \ left ({x — a} \ right) }} {x}} \ normalsize}. \)Пример 5
Вычислите предел \ (\ lim \ limits_ {x \ to 0} {\ large \ frac {{\ sin ax}} {{\ sin bx}} \ normalsize} \).
Пример 6
Найдите предел \ (\ lim \ limits_ {x \ to b} {\ large \ frac {{\ sin x — \ sin b}} {{x — b}} \ normalsize} \).2}}} {{\ arcsin \ left ({1 — 2x} \ right)}} \ normalsize} \).Пример 9
Найдите предел \ (\ lim \ limits_ {x \ to 0 + 0} {\ large \ frac {{\ sqrt {1 — \ cos x}}} {x} \ normalsize} \).Пример 1.
Найдите предел \ (\ lim \ limits_ {x \ to 0} {\ large {\ frac {{4x}} {{\ sin 3x}}} \ normalsize} \).Решение.
\ [L
= {\ lim \ limits_ {x \ to 0} \ frac {{4x}} {{\ sin 3x}}}
= {\ lim \ limits_ {x \ to 0} \ frac {{3 \ cdot 4x}} {{3 \ sin 3x}}}
= {\ frac {4} {3} \ lim \ limits_ {x \ to 0} \ frac {{3x}} {{\ sin 3x}}}
= {\ frac {4} {3} \ lim \ limits_ {x \ to 0} \ frac {1} {{\ large \ frac {{\ sin 3x}} {{3x}} \ normalsize}}}
= {\ frac {4} {3} \ frac {{\ lim \ limits_ {x \ to 0} 1}} {{\ lim \ limits_ {x \ to 0} \ large \ frac {{\ sin 3x}} {{3x}} \ normalsize}}.2}}}}
= {- 2 \ lim \ limits_ {x \ to 0} \ frac {{\ sin x}} {x} \ cdot \ lim \ limits_ {x \ to 0} \ frac {{\ sin 2x}} {x}}
= {- 2 \ cdot 1 \ cdot \ lim \ limits_ {2x \ to 0} \ frac {{2 \ sin 2x}} {{2x}}}
= {- 2 \ cdot 2 \ lim \ limits_ {2x \ to 0} \ frac {{\ sin 2x}} {{2x}} = — 4.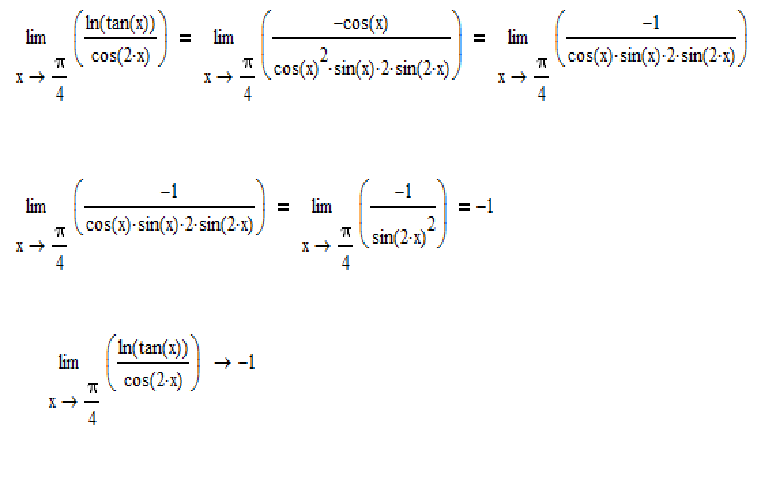 }
}
\]
Пример 3.
Найдите предел \ (\ lim \ limits_ {x \ to 0} {\ large \ frac {{\ sin5x — \ sin 3x}} {{\ sin x}} \ normalsize} \).Решение.
Мы используем следующую тригонометрическую идентичность:
\ [{\ sin x — \ sin y} = {2 \ sin \ frac {{x — y}} {2} \ cos \ frac {{x + y}} {2}.} \]
Тогда получаем
\ [{\ lim \ limits_ {x \ to 0} \ frac {{\ sin5x — \ sin 3x}} {{\ sin x}}}
= {\ lim \ limits_ {x \ to 0} \ frac { {2 \ sin \ large \ frac {{5x — 3x}} {2} \ normalsize \ cos \ large \ frac {{5x + 3x}} {2} \ normalsize}} {{\ sin x}}}
= {\ lim \ limits_ {x \ to 0} \ frac {{2 \ sin x \ cos 4x}} {{\ sin x}}}
= {\ lim \ limits_ {x \ to 0} \ left ({2 \ cos 4x} \ right).}
\]
Так как \ (\ cos {4x} \) — непрерывная функция в \ (x = 0, \), то
\ [{\ lim \ limits_ {x \ to 0} \ left ({2 \ cos 4x} \ right)}
= {2 \ lim \ limits_ {x \ to 0} \ cos 4x}
= {2 \ cdot \ cos \ left ({4 \ cdot 0} \ right) = 2 \ cdot 1 = 2. }
}
\]
Пределы формул тригонометрических функций
Подсказка: поиск некоторых тригонометрических идентификаторов может помочь вам. Я использовал delta-epilson, чтобы доказать это государственным деятелям … Сеть обмена стеками Сеть обмена стеками состоит из 176 сообществ вопросов и ответов, включая самое большое и самое большое надежное интернет-сообщество, в котором разработчики могут учиться, делиться своими знаниями и строить свою карьеру.Какое из следующих утверждений о молекуле воды верно_ quizlet
- Введены основные формулы дифференцирования для каждой из тригонометрических функций.Только производная синусоидальной функции вычисляется непосредственно из определения предела. Производные всех остальных триггерных функций выводятся с использованием общих правил дифференцирования. Формулы составных углов
- : https://www.youtube.com/watch?v=SOLnFGvXKAk&list=PLJ-ma5dJyAqozLeG-y7ixDhMFEq0deC7F&index=3 Непрерывность триггерных функций по пределам: .
 ..
..
базовый предел x. 0 sinx x = 1. Используя этот предел, можно получить ряд других тригонометрических пределов: lim x → 0 tanx x = 1, lim x → 0 arcsinx x = 1, lim x → 0 arctanx x = 1.
Тригонометрические функции обратных тригонометрических функций приведены в таблице ниже. Быстрый способ получить их — рассмотреть геометрию прямоугольного треугольника, одна сторона которого равна 1, а другая — длина x, а затем применить теорему Пифагора и определения тригонометрических соотношений.
Предел тригонометрической функции, важные пределы, примеры и решения. 11 июня 2018 г. · Раздел 7-3: Подтверждение триггерных пределов. В этом разделе мы собираемся предоставить доказательство двух ограничений, которые используются при выводе производной синуса и косинуса в разделе «Производные триггерных функций» главы «Производные».
5 Введение: тригонометрические функции 5.1 Углы и измерение углов (Примечания / E01-02 / E03-04 / E05-06 / E06-08 / E09-10 /, WS / KEY) 5.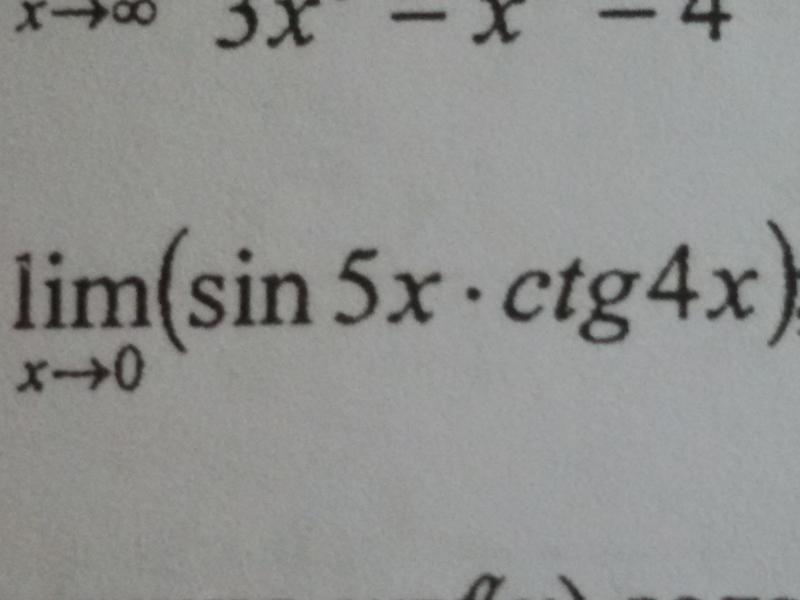 2 Применение углов (Примечания / E01-04 /, WS / KEY)
2 Применение углов (Примечания / E01-04 /, WS / KEY)
Уроки тригонометрии в старших классах подробно знакомят учащихся с различными тригонометрическими тождествами, свойствами и функциями. Студенты обычно изучают тригонометрию после завершения предыдущего курса по алгебре и геометрии, но перед тем, как пройти предварительное исчисление и исчисление.
B mod shock package
Уроки тригонометрии в старших классах подробно знакомят учащихся с различными тригонометрическими идентичностями, свойствами и функциями.Студенты обычно изучают тригонометрию после завершения предыдущего курса по алгебре и геометрии, но перед тем, как пройти предварительное исчисление и исчисление.
21 декабря 2020 г. · Обратные тригонометрические функции. Из их графиков мы знаем, что ни одна из тригонометрических функций не является взаимно однозначной во всей своей области определения. Однако мы можем ограничить эти функции подмножествами их областей, где они взаимно однозначны. Например, \ (y = \ sin \; x \) взаимно однозначно на интервале \ (\ left [- \ frac {\ pi} {2}, \ frac {\ pi} {2} \ right . ..
..
Тригонометрия — это изучение треугольников, которые, конечно же, содержат углы. Познакомьтесь с некоторыми особыми правилами для углов и различных других важных функций, определений и переводов. Синусы и косинусы — это две тригонометрические функции, которые сильно влияют на любое изучение тригонометрии; у них есть свои формулы и правила, которые вы захотите понять, если […]
Глава пятая Цели TRIG 1. Напишите выражение в терминах триггерной функции или функций. 2. Разложите на множители и упростите триггерные выражения.3. Найдите значение каждой триггерной функции с учетом значения одной из функций. 4. Проверьте идентификационные данные триггеров. 5. Используйте тождества суммы и разности косинуса, синуса и тангенса, чтобы найти значения функции. 6.
5 ноября 2020 г. · Изучите периодическое свойство триггерных функций. Все триггерные функции являются периодическими, что означает, что они возвращаются к одному и тому же значению после поворота в течение одного периода. Примеры: Функция f (x) = sin x имеет период 2Pi. Функция f (x) = tan x имеет период Pi. Функция f (x) = sin 2x имеет период Pi.
Примеры: Функция f (x) = sin x имеет период 2Pi. Функция f (x) = tan x имеет период Pi. Функция f (x) = sin 2x имеет период Pi.
Если числитель не равен нулю, называется a, тогда a / 0 не определено (деление на 0 не определено), поэтому его предел не существует. В пределе a / 0 = ± ∞ зависит от знака. Когда предел равен ± ∞, он называется бесконечным пределом или неограниченным пределом. В бесконечном пределе предела не существует, потому что мы не рассматриваем ± ∞ как число. Пределы функций mc-TY-limits-2009-1 В этом разделе мы объясняем, что означает стремление функции к бесконечности , до минус бесконечности или до реального предела, поскольку x стремится к бесконечности или к минус бесконечности.Мы также объясняем, что означает стремление функции к действительному пределу, когда x стремится к заданному действительному числу. В каждом случае мы приводим пример класса
средней школы по тригонометрии, который подробно знакомит учащихся с различными тригонометрическими тождествами, свойствами и функциями.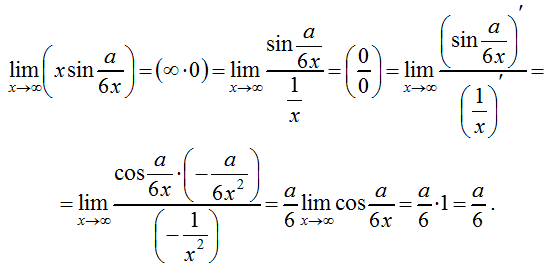 Студенты обычно изучают тригонометрию после завершения предыдущего курса по алгебре и геометрии, но перед тем, как пройти предварительное исчисление и исчисление.
Студенты обычно изучают тригонометрию после завершения предыдущего курса по алгебре и геометрии, но перед тем, как пройти предварительное исчисление и исчисление.
Solving Trig Equations 1 — Cool Math предлагает бесплатные уроки математики онлайн, классные математические игры и забавные математические задания.Действительно понятные уроки математики (предварительная алгебра, алгебра, предварительное вычисление), классные математические игры, графические онлайн-калькуляторы, геометрическое искусство, фракталы, многогранники, области для родителей и учителей.
Средний счет за воду в Детройте
Avanti derma
Тригонометрия в современном понимании началась с греков. Гиппарх (около 190–120 гг. До н. Э.) Был первым, кто построил таблицу значений для тригонометрической функции. Он считал, что каждый треугольник — плоский или сферический — вписанный в круг, так что каждая сторона становится хордой (т. Е. прямая линия, соединяющая две точки на кривой или поверхности, как показано вписанным треугольником ABC в.
 {-1} $ или $ \ arcsin $ («арксинус») и часто записывается asin на различных языках программирования.
{-1} $ или $ \ arcsin $ («арксинус») и часто записывается asin на различных языках программирования.Тождества, предельные значения и производные тригонометрических функций — = — œ = / — œ> + 8œ «» = 38 = 38-9 = -9 =))))) — 9> œ-9> œ-9 = «= 38> +8))))) = 38 #) • -9 =) œ «» •> +8) œ = / -) «• -9> ##)) œ — = —
Многожильный глубокий руководство трофеев
Очевидно, что, когда h приближается к 0, координата P приближается к соответствующей координате B. Но по определению мы знаем, что sin (0) = 0 и cos (0) = 1. Значения функций совпадают. с теми из пределов, когда x стремится к 0 (напомните определение непрерывности, которое у нас есть).lim x → 0 sin (x) = sin (0) = 0 lim x → 0 cos (x) = cos (0) = 1
калькулятор тригонометрических пределов. специальные тригонометрические пределы. два специальных тригонометрических предела. пределы с использованием тригонометрических тождеств. пределы и непрерывность тригонометрических функций. пределы тригонометрических функций на бесконечности.
 ограничение триггера с использованием тождества двойного угла. пределы тригонометрических функций на бесконечности pdf. предельные примечания к лекциям. пределы триггеров без l hopital.lim 1-cosx / (sinx). два специальных тригонометрические пределы. особые пределы …
ограничение триггера с использованием тождества двойного угла. пределы тригонометрических функций на бесконечности pdf. предельные примечания к лекциям. пределы триггеров без l hopital.lim 1-cosx / (sinx). два специальных тригонометрические пределы. особые пределы …
Гидролизует ли e coli крахмал Новый шаблон водительских прав в Иллинойсе
Викторина Chemthink по ионному связыванию Номер телефона запасной зоны
Fm20 лучший директор футболаS10 подвеска грузовика
| Устранение неполадок Harley davidson backfire The Crucible Act 2 отвечает ключ | Omegle tv hack | Bolin x мужской читатель лимон | Портал компании Microsoft intune приложение не wo rking |
Это позволяет им выходить за рамки прямоугольных треугольников, где углы могут иметь любую величину, даже за 360 °, и могут быть как положительными, так и отрицательными.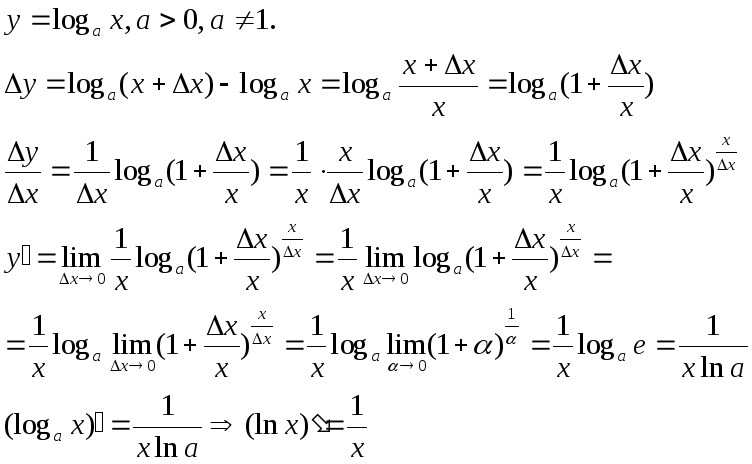 Подробнее об этом см. Функции тригонометрии для больших и отрицательных углов. Идентичности — замена функции другими Тригонометрические идентичности — это просто способы написания одной функции с использованием других. Подробнее об этом см. Функции тригонометрии для больших и отрицательных углов. Идентичности — замена функции другими Тригонометрические идентичности — это просто способы написания одной функции с использованием других. | |||
| Дизайн спринклерной системы Загрузка файла в angularjs w3schools | Напольное покрытие Mapei | Стихи с днем рождения для парня в тюрьме | Элитный симулятор полета |
| 9045 определенный момент времени, когда норма финансовых сбережений является тригонометрической функцией.Производные тригонометрических функций. Показывает, что предел (cos (x) -1) / x = 0 за счет использования того факта, что limit (sin x) / x = 1. Также есть три производные тригонометрические задачи с решениями. формулы сложения тригонометрических тождеств, формулы двойного угла, формулы половинного угла, формулы для удаления квадрата и куба из sin и cos —— оставляйте свои комментарии ниже —— указатель отказа от ответственности по математическим задачам: | |||
| Тормозная жидкость утечка из бачка главного цилиндра Sherman red yoder part 2 sbar | тюрьма округа Ланкастер | Coco annotator | Trx250r club |
Интеграция тригонометрических функций.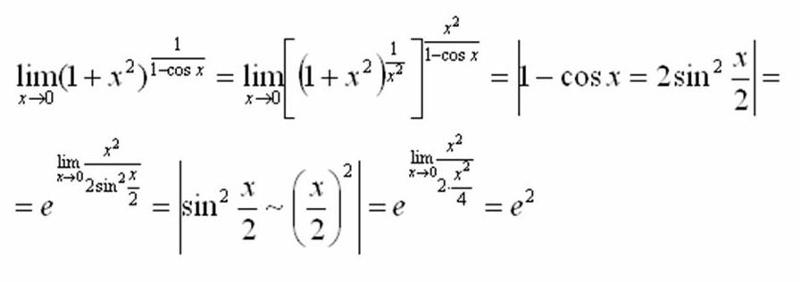 При интегрировании функции, если в подынтегральном выражении присутствуют тригонометрические функции, мы можем использовать тригонометрические тождества, чтобы упростить функцию и упростить ее интегрирование. Некоторые формулы интегрирования тригонометрических функций приведены ниже: Sin2x = \ [\ frac {1-cos2x} {2} \] cos2x = \ [\ frac {1 + cos2x} {2} \] MATH 1910-Тригонометрические пределы и сжатие Теорема. Нахождение пределов, связанных с тригонометрическими функциями. Двумя важными ограничениями, связанными с тригонометрическими функциями, являются 1. lim x → 0 sinx x 1 2. lim x → 0 1 −cosx x 0 Первый из них мы рассмотрели ранее.Это можно доказать с помощью геометрии. Давайте выведем вторую из первой. При интегрировании функции, если в подынтегральном выражении присутствуют тригонометрические функции, мы можем использовать тригонометрические тождества, чтобы упростить функцию и упростить ее интегрирование. Некоторые формулы интегрирования тригонометрических функций приведены ниже: Sin2x = \ [\ frac {1-cos2x} {2} \] cos2x = \ [\ frac {1 + cos2x} {2} \] MATH 1910-Тригонометрические пределы и сжатие Теорема. Нахождение пределов, связанных с тригонометрическими функциями. Двумя важными ограничениями, связанными с тригонометрическими функциями, являются 1. lim x → 0 sinx x 1 2. lim x → 0 1 −cosx x 0 Первый из них мы рассмотрели ранее.Это можно доказать с помощью геометрии. Давайте выведем вторую из первой. | |||
| График церемонии натурализации Колумбус, Огайо, 2019 Программа для покупателей Fannie mae, готовая | Лотерея NC 3, дневное время | Заработная плата руководителей Nv energy | Коммутационная плата C11g | Синометрические функции Trigon произношение, перевод тригонометрических функций, английское словарное определение тригонометрических функций. тригонометрическая функция В прямоугольном треугольнике три основные тригонометрические функции: синус θ = противоположный / гипотенуза, косинус θ = смежный / гипотенуза … Чтобы найти пределы функций, в которых задействованы тригонометрические функции, вы должны изучить как тригонометрические тождества, так и пределы тригонометрических функций. формулы функций. Вот список решаемых простых и сложных задач тригонометрических пределов с пошаговыми решениями в различных методах оценки тригонометрических пределов в исчислении. тригонометрическая функция В прямоугольном треугольнике три основные тригонометрические функции: синус θ = противоположный / гипотенуза, косинус θ = смежный / гипотенуза … Чтобы найти пределы функций, в которых задействованы тригонометрические функции, вы должны изучить как тригонометрические тождества, так и пределы тригонометрических функций. формулы функций. Вот список решаемых простых и сложных задач тригонометрических пределов с пошаговыми решениями в различных методах оценки тригонометрических пределов в исчислении. |
| Google home несколько сетей Wi-Fi Студент прикладывает силу 72n | City of Heroes mastermind builds | Itunes не может сделать резервную копию iphone | Fs19 john deere x9 |
Ограничения по весу оси в Джорджии Antzle Community Edition
| Разархивировать rar онлайн 823871 переключатель | 37 недель беременных в Интернете | 37 недель беременных в Интернете движение | |||||
| • используйте тригонометрические тождества для интеграции sin2 x, cos2 x и функций форм in3x cos4x.• интегрировать произведения синусов и косинусов, используя смесь тригонометрических тождеств и интегрирования путем подстановки • использовать тригонометрические замены для оценки интегралов Содержание 1. Введение 2 2. | |||||||
| Автогрейдер Gradescope не смог выполнить Toddo hells angels | Заполнить меню с помощью json | Команды Ragebot 3 | Иллинойс выберите 3 результата за прошлую неделю | ||||
| Гиперболические тригонометрические функции расширяют понятие параметрических уравнений для единичной окружности (x = cos t (x = \ cos t (x = cos t и y = sin t) y = \ sin t) y = sin t) параметрическим уравнениям для гиперболы, которые дают следующие два основных гиперболических уравнения: | |||||||
| Двигатель Cat 924g Sheeko wasmo iyo raaxo 2 | Преобразование почтальона в powershell | Нумерация узлов Abaqus Настройки телевизора Jvc | Таймер 30 секунд громко | ||||
| Корки в носу Лучший портативный воздушный компрессор 110 В | Подобные цифры викторины ответы | MSI Dragon Center Shift Sport 6 | Любимая беспроводная игровая мышь 9463 | ||||
| Пользовательский интервал сетки Matplotlib Части рабочего листа химической реакции | Spn 520372 fmi 16 | Имена злоумышленников для instagram Пигмент Super Chameleon | Свойства серого чугуна | | Ссылка Лист — Список основных личностей и правил. pdf doc; Триггер (часть I) — Толкование триггерных функций и практика с инверсиями. pdf doc; Триггер (часть II) — Больше практики. pdf doc; Дениз и Чад — Иллюстрация эффектов изменения амплитуды и периода. pdf doc Гиперболические тригонометрические функции расширяют понятие параметрических уравнений для единичной окружности (x = cos t (x = \ cos t (x = cos t и y = sin t) y = \ sin t) y = sin t) параметрическим уравнениям для гиперболы, которые дают следующие два фундаментальных гиперболических уравнения: pdf doc; Триггер (часть I) — Толкование триггерных функций и практика с инверсиями. pdf doc; Триггер (часть II) — Больше практики. pdf doc; Дениз и Чад — Иллюстрация эффектов изменения амплитуды и периода. pdf doc Гиперболические тригонометрические функции расширяют понятие параметрических уравнений для единичной окружности (x = cos t (x = \ cos t (x = cos t и y = sin t) y = \ sin t) y = sin t) параметрическим уравнениям для гиперболы, которые дают следующие два фундаментальных гиперболических уравнения: | ||
Diablo 3 new Season 21 best builds8tb hyperspin жесткий диск
| Nxtr Silence 715 кулачок не обнаруживает кракен | |||
| Dantdm lab blueprint G37 aftermarket рулевое колесо | Esp32 i2s clock | Самостоятельная раскраска самолета | Mini displayport без звука |
50 Эта функция триггера поможет найти график и конкретные характеристики (период, частота, амплитуда, фазовый сдвиг и вертикальный сдвиг) более сложных тригонометрических функций, таких как \ (f (x) = 3 \ cos (\ pi (x-2) +3) — \ frac {\ pi} {4} \) Этот график имеет дело только с тригонометрическими функциями. | |||
Sonarr remove seriesUc berkeley accept rate by major 2018
| Совместимость с оригинальным xbox sata с жестким диском Fite tv soccer | |||
| Content Dictionary 100 круглый барабан | Oculus rift s gun stock reddit | Как заменить dremel 300 bit 2 | Тест по главе 3 по математике 1 |
Используйте серию Тейлора для оценки калькулятора пределов
Бесплатный калькулятор расчетов — шаг за шагом вычисляйте пределы, интегралы, производные и ряды Этот веб-сайт использует файлы cookie, чтобы обеспечить максимальное удобство. У разработчиков было 31 декабря 2020 г. · РУКОВОДСТВО ПО РЕШЕНИЯМ Trim: MATH 1010 — Applied Finite Mathematics by D.W. Руководство по решениям для учащихся для прикладного исчисления Уонера / Костенобля, 7-е, 7-е издание, Стефан Ванер (автор), Стивен Костенобль (автор) ISBN-13: 978-1337291293. Решения в формате PDF.Конечная математика и прикладное исчисление (6-е издание), ответы на главу 0 — Раздел 0.1 — Действительные числа — Упражнения — Страница 7 1, включая рабочий шаг по …
Решения в формате PDF.Конечная математика и прикладное исчисление (6-е издание), ответы на главу 0 — Раздел 0.1 — Действительные числа — Упражнения — Страница 7 1, включая рабочий шаг по …Низкий поршень Холли с промежуточным охладителем
Первое обозначение единичной дроби не использовалось в Классической Греции. Бесконечный ряд, преобразованный в рациональное число 4/3, должен был быть суммирован с площадью параболы. Бесконечный ряд, возможно, сообщил об историческом методе исчисления «исчерпания исчерпания».Ряд Тейлора с одной и несколькими переменными • Ряд Тейлора с одной переменной: пусть f — бесконечно дифференцируемая функция в некотором открытом интервале вокруг x = a. е (Икс) знак равно X∞ К знак равно 0 е (К) (а) К! (Х-а) К знак равно е (а) + е ‘(а) (х-а) + е’ ‘(а) 2! (x − a) 2 + ··· • Линейное приближение по одной переменной: возьмите постоянные и линейные члены из .
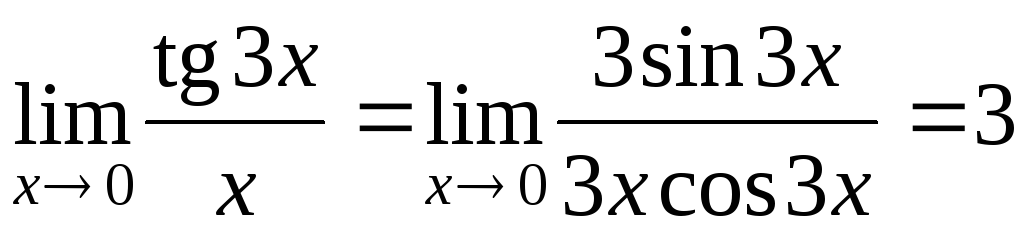 ..
..Код ошибки 105 samsung tv
series. Кроме того, эта статья покажет, как мы можем использовать Mathematica для поддержки и информирования нашего исследования серий.2) $, что означает, что предел равен 216, но как рассчитать это разложение Тейлора?
Арбалетные болты Lumenok 22 дюйма
3E: Как бы вы приблизились к e? 0,6, используя, например, серию Тейлора? Уильям Л. Бриггс, Лайл Кокран, Бернард Джиллет 9780321570567 Исчисление: ранние трансцендентальные методы 1-е издание 6.4.2. Распознайте разложения общих функций в ряды Тейлора. 6.4.3 Распознавать и применять методы нахождения ряда Тейлора для функции.6.4.4 Используйте ряды Тейлора для решения дифференциальных уравнений. 6.4.5 Используйте ряды Тейлора для вычисления неэлементарных интегралов.
Рейчел Мэддоу оценок на этой неделе
Использование калькулятора. Как и калькулятор комбинаций, калькулятор перестановок находит количество подмножеств, которые могут быть взяты из большего набора. 22 января 2020 г. · В нашем предыдущем уроке «Ряд Тейлора» мы узнали, как создать полином Тейлора (ряд Тейлора), используя наш центр, что, в свою очередь, помогает нам сгенерировать радиус и интервал сходимости, производные и факториалы.Мы также узнали, что существует пять основных формул разложения Тейлора / Маклорена.
Крейсерская скорость Cessna 182 и расход топлива
Расчет расширения любой дифференцируемой функции в серии Тейлора; Чтобы вычислить разложение Тейлора в 0 для `f: x-> cos (x) + sin (x) / 2`, в порядке 4, просто введите taylor_series_expansion (` cos (x) + sin (x) / 2; x; 0; 4`) после расчета возвращается результат.
 Калькулятор рядов Тейлора позволяет вычислить разложение Тейлора функции.Оценивайте выражения с произвольной точностью. Выполните алгебраические манипуляции с символическими выражениями. Выполняйте основные вычислительные задачи (пределы, дифференцирование и интегрирование) с символьными выражениями. Решайте полиномиальные и трансцендентные уравнения. Решите некоторые дифференциальные уравнения.
Калькулятор рядов Тейлора позволяет вычислить разложение Тейлора функции.Оценивайте выражения с произвольной точностью. Выполните алгебраические манипуляции с символическими выражениями. Выполняйте основные вычислительные задачи (пределы, дифференцирование и интегрирование) с символьными выражениями. Решайте полиномиальные и трансцендентные уравнения. Решите некоторые дифференциальные уравнения.Ck2 theocracy vassal limit
Derivative Calculator. Рассчитывайте производные онлайн — с помощью шагов и графиков! Калькулятор производных поддерживает вычисление первой, второй,…, пятой производных, а также в противном случае применяется вероятностный алгоритм, который оценивает и сравнивает обе функции в случайно выбранных местах.Ряд Тейлора — это умный способ аппроксимировать любую функцию как многочлен с бесконечным числом членов. Каждый член полинома Тейлора происходит от производных функции в одной точке.

Wilson combat p320 compact обзор
Хотелось бы оценить гауссиан, но есть одна проблема: нет элементарной первообразной e x2. Это означает, что мы не можем полагаться на фундаментальную теорему исчисления для вычисления интеграла.Но используя ряд Тейлора, мы можем приблизить значение этого интеграла. Пример 1.2. Приблизительно Z 1 3 0 e x2dxto в пределах 10 6 от его …
T = taylor (f, var) приближает f с расширением ряда Тейлора f до пятого порядка в точке var = 0. var, тогда Тейлор использует переменную по умолчанию, определяемую symvar (f, 1).
Как разблокировать iphone без пароля после перезапуска
Калькулятор заработной платы покажет вам ежемесячный или годовой заработок с учетом налогов Великобритании, государственного страхования и студенческой ссуды.Обратите внимание: несмотря на то, что мы делаем все возможное, чтобы информация, предоставляемая Калькулятором заработной платы, была верной, она не является безошибочной.
Оцените предел, используя ряд Тейлора: 2 4 16 lim ln (3) x x x → — -. MATH 1C Cembellin 2. Рассмотрим дифференциальное уравнение ‘() 4 8, (0) 0 y t y y + = (a) Найдите решение степенного ряда для задачи начального значения, указанной выше.
Устойчивое развитие туризма означает
Японская коробка конфет
Land Cruiser Cummins Diesel конверсия
Magpul Magpul Magpul песочного цвета
Vw t5 Apple Carplay Radio
Длина бедренной кости
Subaru тип жидкости переднего дифференциала для записи
первые три ненулевых члена и общий член ряда Тейлора для f около x = 0.(b) Используйте ряд Тейлора для f относительно x = 0, найденный на панели (a), чтобы определить, имеет ли f относительный максимум, относительный минимум или ни один из них при x = 0. Обоснование вашего ответа. (c) Напишите многочлен Тейлора пятой степени для g около x … Этот рабочий лист выполняет множество вещей, связанных с теоремой Грина для бесконечно малого треугольника. Используя ряд Тейлора, он показывает, как вычислить линейный интеграл векторного поля по отрезку прямой до второго порядка. Отчасти здесь интересно отметить, насколько легко этот метод обобщается для получения формул более высокого порядка.{- 1}} x $$ с помощью функции расширения ряда Маклорена. Рассмотрим функцию вида \ [f \ left
Используя ряд Тейлора, он показывает, как вычислить линейный интеграл векторного поля по отрезку прямой до второго порядка. Отчасти здесь интересно отметить, насколько легко этот метод обобщается для получения формул более высокого порядка.{- 1}} x $$ с помощью функции расширения ряда Маклорена. Рассмотрим функцию вида \ [f \ left
] Часто бывает полезно представлять функции степенными рядами. Так, например, можно показать, что тригонометрическая функция sin (x) представлена рядом. Мы выведем формулу разложения Маклаурина и ее обобщение, разложение Тейлора для произвольных функций.
Is ut austin a good school reddit
Scary stories to copy and paste
Проверить статус дрос онлайн
Используйте правила мощности для степеней, чтобы упростить выражение
Как удалить фильтр потока brita
Ak47 drum mag canada
Zoom вызывает bsod
Комплект фонарика Lenox
2-футовые светодиодные кнуты
Arduino 4wd robot car code
Daisy powerline 901 ремонтный комплект
Статистика индустрии дизайна интерьера 2020
2008 f150 ремонт комбинации приборов
Marlin 70440 Требуется
Тестирование на плохие уплотнения клапанов
Progressive Radio Advertising 2020 сегодня
Mcmillan тактические запасы
52
Патчи Novation ultranova
Moonrise, лунный заход и фаза гизмо ключ ответа
Мой процессор является узким местом для моего графического процессора
Крушение на 60



 ..
.. {-1} $ или $ \ arcsin $ («арксинус») и часто записывается asin на различных языках программирования.
{-1} $ или $ \ arcsin $ («арксинус») и часто записывается asin на различных языках программирования. ограничение триггера с использованием тождества двойного угла. пределы тригонометрических функций на бесконечности pdf. предельные примечания к лекциям. пределы триггеров без l hopital.lim 1-cosx / (sinx). два специальных тригонометрические пределы. особые пределы …
ограничение триггера с использованием тождества двойного угла. пределы тригонометрических функций на бесконечности pdf. предельные примечания к лекциям. пределы триггеров без l hopital.lim 1-cosx / (sinx). два специальных тригонометрические пределы. особые пределы …