Показательные уравнения неравенства. Системы показательных уравнений и неравенств
Разделы: Математика
Цели урока:
Образовательная: научить решать системы показательны уравнений; закрепить навыки решения уравнений входящих в эти системы
Воспитательная: воспитать аккуратность.
Развивающая: развить культуру письменной и устной речи.
Оборудование: компьютер; мультимедийный проектор.
Ход урока
Организационный момент
Учитель. Сегодня мы продолжим изучение главы “Показательная функция”. Тему урока сформулируем чуть позже. В течение урока вы будите заполнять бланки ответов, которые лежат у вас на столах (см. приложение №1 ). Ответы будут суммироваться.
Актуализация знаний.
Учащиеся отвечают на вопросы:
- Какой вид имеет показательная функция?
Устная работа.
Работа по слайдам с 1 по
5.
- Какое уравнение называется показательным?
- Какие методы решения вам известны?
Устная работа по слайдам с 6 по 10.
- Какое свойство показательной функции используют при решении показательного неравенства?
Устная работа по слайдам с 11 по 15.
Задание. Записать ответы на эти вопросы в бланке ответов №1. (см. приложение №1 ). (слайды с 16 по 31)
Проверка домашнего задания
.
Домашнюю работу проверяем следующим образом.
Замените корни уравнений на соответствующую букву и отгадайте слово.
Учащиеся смотрят в бланк ответов №2 (приложение 1 ) . Учитель демонстрирует слайд №33
(Учащиеся называют слово (слайд №34)).
- Какие явления протекают по законам этой функции?
Учащимся предлагается решить задания
из ЕГЭ В12 (слайд 35) и записать решение в бланк
ответа №3 (приложение 1 ).
В ходе проверки домашней работы и решая задание В12, мы повторим методы решения показательных уравниваний.
Учащиеся приходят к выводу, что для решения уравнения с двумя переменными требуется еще одно уравнение.
Затем формулируется тема урока (слайд № 37).
В тетрадях записывается система (слайд № 38).
Что бы решить эту систему, повторяем метод подстановки (слайд № 39).
Метод сложения повторяется в ходе решения системы (слайд с 38 по 39).
Первичное закрепление изученного
материала
:
Учащиеся самостоятельно решают системы уравнений в бланках ответа № 4 (приложение 1 ), получая индивидуальные консультации учителя.
Подведение итогов. Рефлексия.
Продолжите фразы.
- Сегодня на уроке я повторил…
- Сегодня на уроке я закрепил…
- Сегодня на уроке я научился…
- Сегодня на уроке я узнал…
В конце урока учащиеся записывают домашнее задание, сдают бланки ответов
Задание на дом:
№ 59 (четные) и № 62 (четные).
Литература
- Все задания группы ЕГЭ 3000 задач – Издательство “Экзамен” Москва, 2011. Под редакцией А.Л. Семенова, И.В. Ященко.
- С.А. Шестаков, П.И. Захаров ЕГЭ 2010 математика задача С1 под редакцией А.Л. Семенова, И.В. Ященко Москва издательство “МЦНМО”.
- Учебное пособие Алгебра и начала математического анализа,10 класс Ю.М.Колягин Москва “Просвещение”, 2008.
На данном уроке мы рассмотрим решение более сложных показательных уравнений, вспомним основные теоретические положения касательно показательной функции.
1. Определение и свойства показательной функции, методика решения простейших показательных уравненийНапомним определение и основные свойства показательной функции. Именно на свойствах базируется решение всех показательных уравнений и неравенств.
Показательная функция — это функция вида , где основание степени и Здесь х — независимая переменная, аргумент; у — зависимая переменная, функция.
Рис.
1. График показательной функции
На графике показаны возрастающая и убывающая экспоненты, иллюстрирующие показательную функцию при основании большем единицы и меньшем единицы, но большим нуля соответственно.
Обе кривые проходят через точку (0;1)
Свойства показательной функции :
Область определения: ;
Область значений: ;
Функция монотонна, при возрастает, при убывает.
Монотонная функция принимает каждое свое значение при единственном значении аргумента.
При когда аргумент возрастает от минус до плюс бесконечности, функция возрастает от нуля не включительно до плюс бесконечности. При наоборот, когда аргумент возрастает от минус до плюс бесконечности, функция убывает от бесконечности до нуля не включительно.
2. Решение типовых показательных уравненийНапомним, как решать простейшие показательные уравнения. Их решение основано на монотонности показательной функции. К таким уравнениям сводятся практически все сложные показательные уравнения.
Равенство показателей степени при равных основаниях обусловлено свойством показательной функции, а именно ее монотонностью.
Методика решения:
Уравнять основания степеней;
Приравнять показатели степеней.
Перейдем к рассмотрению более сложных показательных уравнений, наша цель — свести каждое из них к простейшему.
Освободимся от корня в левой части и приведем степени к одинаковому основанию:
Для того чтобы свести сложное показательное уравнение к простейшим, часто используется замена переменных.
Воспользуемся свойством степени:
Вводим замену. Пусть , тогда
Умножим полученное уравнение на два и перенесем все слагаемые в левую часть:
Первый корень не удовлетворяет промежутку значений у, отбрасываем его. Получаем:
Приведем степени к одинаковому показателю:
Вводим замену:
Пусть , тогда . При такой замене очевидно, что у принимает строго положительные значения.
Получаем:
Решать подобные квадратные уравнения мы умеем, выпишем ответ:
Чтобы удостовериться в правильности нахождения корней, можно выполнить проверку по теореме Виета, т. е. найти сумму корней и их произведение и сверить с соответствующими коэффициентами уравнения.
Получаем:
Изучим следующий важный тип показательных уравнений:
Уравнения такого типа называют однородными второй степени относительно функций f и g. В левой его части стоит квадратный трехчлен относительно f с параметром g или квадратный трехчлен относительно g с параметром f.
Методика решения:
Данное уравнение можно решать как квадратное, но легче поступить по-другому. Следует рассмотреть два случая:
В первом случае получаем
Во втором случае имеем право разделить на старшую степень и получаем:
Следует ввести замену переменных , получим квадратное уравнение относительно у:
Обратим внимание, что функции f и g могут быть любыми, но нас интересует тот случай, когда это показательные функции.
Перенесем все слагаемые в левую часть уравнения:
Поскольку показательные функции приобретают строго положительные значения, имеем право сразу делить уравнение на , не рассматривая случай, когда :
Получаем:
Вводим замену: (согласно свойствам показательной функции)
Получили квадратное уравнение:
Определяем корни по теореме Виета:
Первый корень не удовлетворяет промежутку значений у, отбрасываем его, получаем:
Воспользуемся свойствами степени и приведем все степени к простым основаниям:
Несложно заметить функции f и g:
Показательными уравнениями и неравенствами считают такие уравнения и неравенства, в которых неизвестное содержится в показателе степени.
Решение показательных уравнений часто сводится к решению уравнения а х = а b , где а > 0, а ≠ 1, х – неизвестное. Это уравнение имеет единственный корень х = b, так как справедлива следующая теорема:
Теорема.
Если а > 0, а ≠ 1 и а х 1 = а х 2 , то х 1 = х 2 .
Обоснуем рассмотренное утверждение.
Предположим, что равенство х 1 = х 2 не выполняется, т.е. х 1 1, то показательная функция у = а х возрастает и поэтому должно выполняться неравенство а х 1 а х 2 . В обоих случаях мы получили противоречие условию а х 1 = а х 2 .
Рассмотрим несколько задач.
Решить уравнение 4 ∙ 2 х = 1.
Решение.
Запишем уравнение в виде 2 2 ∙ 2 х = 2 0 – 2 х+2 = 2 0 , откуда получаем х + 2 = 0, т.е. х = -2.
Ответ. х = -2.
Решить уравнение 2 3х ∙ 3 х = 576.
Решение.
Так как 2 3х = (2 3) х = 8 х, 576 = 24 2 , то уравнение можно записать в виде 8 х ∙ 3 х = 24 2 или в виде 24 х = 24 2 .
Отсюда получаем х = 2.
Ответ. х = 2.
Решить уравнение 3 х+1 – 2∙3 х — 2 = 25.
Решение.
Вынося в левой части за скобки общий множитель 3 х — 2 , получаем 3 х — 2 ∙ (3 3 – 2) = 25 – 3 х — 2 ∙ 25 = 25,
откуда 3 х — 2 = 1, т.
е. х – 2 = 0, х = 2.
Ответ. х = 2.
Решить уравнение 3 х = 7 х.
Решение.
Так как 7 х ≠ 0, то уравнение можно записать в виде 3 х /7 х = 1, откуда (3/7) х = 1, х = 0.
Ответ. х = 0.
Решить уравнение 9 х – 4 ∙ 3 х – 45 = 0.
Решение.
Заменой 3 х = а данное уравнение сводится к квадратному уравнению а 2 – 4а – 45 = 0.
Решая это уравнение, находим его корни: а 1 = 9, а 2 = -5, откуда 3 х = 9, 3 х = -5.
Уравнение 3 х = 9 имеет корень 2, а уравнение 3 х = -5 не имеет корней, так как показательная функция не может принимать отрицательные значения.
Ответ. х = 2.
Решение показательных неравенств часто сводится к решению неравенств а х > а b или а х
Рассмотрим некоторые задачи.
Решить неравенство 3 х
Решение.
Запишем неравенство в виде 3 х 1, то функция у = 3 х является возрастающей.
Следовательно, при х
Таким образом, при х 3 х
Ответ.
х
Решить неравенство 16 х +4 х – 2 > 0.
Решение.
Обозначим 4 х = t, тогда получим квадратное неравенство t2 + t – 2 > 0.
Это неравенство выполняется при t 1.
Так как t = 4 х, то получим два неравенства 4 х 1.
Первое неравенство не имеет решений, так как 4 х > 0 при всех х € R.
Второе неравенство запишем в виде 4 х > 4 0 , откуда х > 0.
Ответ. х > 0.
Графически решить уравнение (1/3) х = х – 2/3.
Решение.
1) Построим графики функций у = (1/3) х и у = х – 2/3.
2) Опираясь на наш рисунок, можно сделать вывод, что графики рассмотренных функций пересекаются в точке с абсциссой х ≈ 1. Проверка доказывает, что
х = 1 – корень данного уравнения:
(1/3) 1 = 1/3 и 1 – 2/3 = 1/3.
Иными словами, мы нашли один из корней уравнения.
3) Найдем другие корни или докажем, что таковых нет. Функция (1/3) х убывающая, а функция у = х – 2/3 возрастающая. Следовательно, при х > 1 значения первой функции меньше 1/3, а второй – больше 1/3; при х 1 и х
Ответ.
х = 1.
Заметим, что из решения этой задачи, в частности, следует, что неравенство (1/3) х > х – 2/3 выполняется при х 1.
сайт, при полном или частичном копировании материала ссылка на первоисточник обязательна.
Способы решения систем уравнений
Для начала кратко вспомним, какие вообще существуют способы решения систем уравнений.
Существуют четыре основных способа решения систем уравнений:
Как решить текстовую задачу с помощью системы неравенств?
Математика может подкрасться в самых разных местах, поэтому важно быть готовым! Следуйте этому руководству, чтобы увидеть реальную математическую задачу, включающую систему неравенств!
Как решить систему уравнений с помощью подстановки, если одно уравнение является квадратным?
Подстановка — отличный способ решить систему уравнений! В этом уроке вы увидите, как метод подстановки используется для решения системы уравнений, включающей как линейное, так и квадратное уравнение!
Что такое решение системы линейных неравенств?
Что является решением системы неравенств? Может ли такая система иметь более одного решения? Следуйте этому руководству, чтобы узнать ответы на эти и другие вопросы!
Как решить систему уравнений с помощью графика?
Существует множество различных способов решения системы линейных уравнений.
В этом уроке вы увидите, как решить систему линейных уравнений, построив обе линии и найдя их пересечение. Взглянем!Как вы используете систему линейных уравнений для поиска координат на карте?
Нравятся загадки? Словесная задача похожа на загадку! В этой текстовой задаче вам нужно найти решение системы линейных уравнений, решить загадку и найти место на карте. Проверьте это!
Какой пример текстовой задачи имеет систему линейных уравнений с бесконечными решениями?
Нравятся загадки? Словесная задача похожа на загадку! В этой текстовой задаче вам нужно найти решение системы линейных уравнений, решить загадку и найти место на карте. Проверьте это!
Как решить систему уравнений методом подстановки?
Существует множество различных способов решения системы линейных уравнений. В этом уроке вы увидите, как решить систему линейных уравнений, подставив одно уравнение в другое и найдя переменную.
Затем посмотрите, как использовать это значение переменной, чтобы найти значение другой переменной. Проверьте это!Как решить систему уравнений методом исключения путем сложения?
Существует множество различных способов решения системы линейных уравнений. В этом уроке вы увидите, как решить систему линейных уравнений, объединив уравнения вместе, чтобы исключить одну из переменных. Затем посмотрите, как найти значение этой переменной и использовать его для поиска значения другой переменной. Взглянем!
Как решить систему уравнений методом исключения методом вычитания?
Существует множество различных способов решения системы линейных уравнений. В этом уроке вы увидите, как решить такую систему, объединив уравнения таким образом, чтобы исключить одну из переменных. Затем посмотрите, как найти значение этой переменной и использовать его для поиска значения другой переменной. Взглянем!
Как показать, что система уравнений не имеет решения?
Существует множество различных способов решения системы линейных уравнений.
В этом уроке вы увидите, как решить систему линейных уравнений, построив обе линии и найдя их пересечение. Взглянем!Как решить систему уравнений методом исключения методом умножения?
Существует множество различных способов решения системы линейных уравнений. В этом уроке вы увидите, как решить такую систему, объединив уравнения таким образом, чтобы исключить одну из переменных. Затем посмотрите, как найти значение этой переменной и использовать его для поиска значения другой переменной. Взглянем!
Какой другой способ решения системы уравнений методом исключения методом умножения?
Существует множество различных способов решения системы линейных уравнений. В этом уроке вы увидите, как решить систему линейных уравнений, объединив уравнения вместе, чтобы исключить одну из переменных. Затем посмотрите, как найти значение этой переменной и использовать его для поиска значения другой переменной.
Взглянем!Как решить систему неравенств с помощью графика?
Существует много разных способов решения системы неравенств. В этом уроке вы увидите, как решить такую систему, построив график обоих неравенств и найдя их пересечение. Проверьте это!
Как решить текстовую задачу методом исключения методом вычитания?
Словесные задачи — отличный способ увидеть математику в действии! В этом уроке вы увидите, как написать систему линейных уравнений на основе информации, представленной в текстовой задаче. Затем вы увидите, как решить эту систему методом исключения. Посмотрите весь этот процесс, посмотрев этот урок!
Что такое система линейных уравнений?
Система уравнений представляет собой набор уравнений с одинаковыми переменными. Если все уравнения линейные, то у вас есть система линейных уравнений! Чтобы решить систему уравнений, вам нужно выяснить значения переменных, которые решают все задействованные уравнения.
Этот учебник познакомит вас с этими системами.Что такое система линейных неравенств?
Система уравнений представляет собой набор уравнений с одинаковыми переменными. Система неравенств почти такая же, за исключением того, что вы работаете с неравенствами вместо уравнений! Чтобы решить такую систему, нужно найти такие значения переменных, при которых каждое неравенство будет верным одновременно. Этот учебник познакомит вас с системами неравенств.
Какими способами можно решить систему линейных уравнений?
Знать определение системы уравнений — это здорово, но вы также должны знать, как их решать! В этом учебном пособии вы познакомитесь с графическим методом, методом замены и методом исключения для решения системы уравнений. Посмотрите и изучите их все!
Что такое решение системы линейных уравнений?
Если у вас есть система уравнений, содержащая два уравнения с двумя одинаковыми неизвестными переменными, то решением этой системы является упорядоченная пара, которая делает оба уравнения верными одновременно.
Следуйте инструкциям, поскольку в этом руководстве используется пример для объяснения решения системы уравнений!Что такое непротиворечивая независимая система уравнений?
Глядя на систему уравнений только с одним решением? Это означает, что эти уравнения пересекаются только в этой одной точке. Такое решение называется последовательным и независимым! В этом руководстве объясняются системы с одним решением и даже приводится пример!
Как решить текстовую задачу с помощью двух уравнений?
Иногда текстовые задачи описывают систему уравнений, состоящую из двух уравнений с двумя неизвестными в каждом. Решение словесных задач, подобных этой, не так уж плохо, если вы знаете, что делать. Проверьте это с помощью этого урока!
Как решить два уравнения с двумя переменными?
Пытаетесь решить два уравнения с одними и теми же двумя неизвестными переменными? Возьмите одно из уравнений и решите его для одной из переменных.
Способ подстановки: берется любое из данных уравнений и выражается $y$ через $x$, затем $y$ подставляется в уравнение системы, откуда и находится переменная $x.$ После этого мы легко можем вычислить переменную $y.$
Способ сложения: в данном способе необходимо умножать одно или оба уравнения на такие числа, чтобы при сложении вместе обоих одна из переменных «исчезла».
Графический способ: оба уравнения системы изображается на координатной плоскости и находится точка их пересечения.
Способ введения новых переменных: в этом способе мы делаем замену каких-либо выражений для упрощения системы, а потом применяем один из выше указанных способов.
{\varphi (x)} $, где $a >0,a\ne 1$ равносильна совокупности двух систем
\}
Показательные системы. Решение систем показательных уравнений
Рубрика: Наука
На этапе подготовки к заключительному тестированию учащимся старших классов необходимо подтянуть знания по теме «Показательные уравнения». Опыт прошлых лет свидетельствует о том, что подобные задания вызывают у школьников определенные затруднения. Поэтому старшеклассникам, независимо от уровня их подготовки, необходимо тщательно усвоить теорию, запомнить формулы и понять принцип решения таких уравнений. Научившись справляться с данным видом задач, выпускники смогут рассчитывать на высокие баллы при сдаче ЕГЭ по математике.
Готовьтесь к экзаменационному тестированию вместе со «Школково»!
При повторении пройденных материалов многие учащиеся сталкиваются с проблемой поиска нужных для решения уравнений формул.
Школьный учебник не всегда находится под рукой, а отбор необходимой информации по теме в Интернете занимает долгое время.
Образовательный портал «Школково» предлагает ученикам воспользоваться нашей базой знаний. Мы реализуем совершенно новый метод подготовки к итоговому тестированию. Занимаясь на нашем сайте, вы сможете выявить пробелы в знаниях и уделить внимание именно тем заданиям, которые вызывают наибольшие затруднения.
Преподаватели «Школково» собрали, систематизировали и изложили весь необходимый для успешной сдачи ЕГЭ материал в максимально простой и доступной форме.
Основные определения и формулы представлены в разделе «Теоретическая справка».
Для лучшего усвоения материала рекомендуем попрактиковаться в выполнении заданий. Внимательно просмотрите представленные на данной странице примеры показательных уравнений с решением, чтобы понять алгоритм вычисления. После этого приступайте к выполнению задач в разделе «Каталоги». Вы можете начать с самых легких заданий или сразу перейти к решению сложных показательных уравнений с несколькими неизвестными или .
База упражнений на нашем сайте постоянно дополняется и обновляется.
Те примеры с показателями, которые вызвали у вас затруднения, можно добавить в «Избранное». Так вы можете быстро найти их и обсудить решение с преподавателем.
Чтобы успешно сдать ЕГЭ, занимайтесь на портале «Школково» каждый день!
Способы решения систем уравнений
Для начала кратко вспомним, какие вообще существуют способы решения систем уравнений.
Существуют четыре основных способа решения систем уравнений:
Способ подстановки: берется любое из данных уравнений и выражается $y$ через $x$, затем $y$ подставляется в уравнение системы, откуда и находится переменная $x.$ После этого мы легко можем вычислить переменную $y.$
Способ сложения: в данном способе необходимо умножать одно или оба уравнения на такие числа, чтобы при сложении вместе обоих одна из переменных «исчезла».
Графический способ: оба уравнения системы изображается на координатной плоскости и находится точка их пересечения.
{\varphi (x)} $, где $a >0,a\ne 1$ равносильна совокупности двух систем
\}
Обзор экспоненциальных и логарифмических неравенств
Экспоненциальные неравенства — это неравенства с переменным показателем степени на одной (или обеих) сторонах. Они удобны в обстоятельствах, требующих многократного умножения, особенно по сравнению с постоянной суммой, такой как проценты. Например, экспоненциальное неравенство можно использовать для расчета того, сколько времени потребуется, чтобы удвоить свои деньги при определенной процентной ставке; например, при постоянной процентной ставке 6% деньги удвоятся примерно через 12 лет.
Определение
Давайте начнем с основных определений, чтобы различать экспоненциальное и логарифмическое неравенство. Экспоненты используются в экспоненциальных неравенствах, а логарифмы используются в логарифмических неравенствах. Оба используют одно из четырех неравенств. Используемые слова больше, больше или равно, меньше и меньше или равно.
Давайте решим аналогичную математическую задачу, начав с ответа, прежде чем предлагать метод решения. Звучит интригующе, правда? Что такое 2 5 ? Ответ: 2(2)(2)(2)(2) равно 32. Ответ положительный, но в чем вопрос?
Задача состоит в том, чтобы найти x такой, что 2 x > 32.
Поскольку 2 5 равно 32, подойдет любой x больше 5.
Теперь о способе решения:
Шаг 1: Подставим в неравенстве знак равенства.
Шаг 2: Используйте логарифмы с показателями степени.
Шаг 3: Решить.
Шаг 4: Оценить.
Шаг 5: Выберите доменное имя.
Шаг 6: График (это необязательный шаг).
Логарифмические неравенства
Обратные операции включают логарифмы и экспоненты.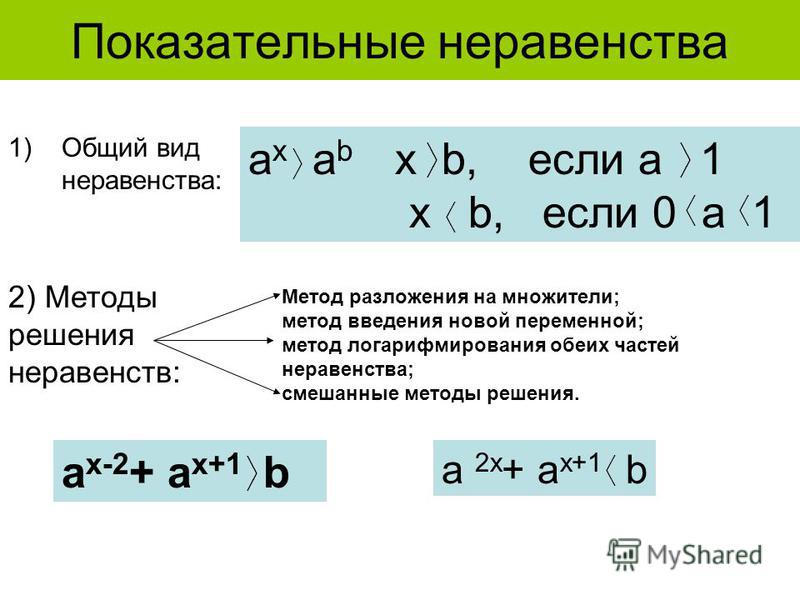
Иными словами, один процесс реверсирует другой. Например, log 100 = 2 и 10 2 = 100. Кроме того, 10 logx равно x. Журнал находится в базе 10.
Вычислите значения x для журнала x 2 .
Шаг 1: Замените неравенство знаком равенства.
Шаг 2: Возведение в степень основания с использованием логарифма.
Шаг 3: Решите проблему.
Шаг 4: Оценка.
Шаг 5: Выберите имя для своего веб-сайта.
Шаг 6: График.
Система неравенств
Набор из двух или более неравенств по одной или нескольким переменным называется системой неравенств. Когда проблема требует различных решений и существует несколько ограничений на эти ответы, используются системы неравенств.
Системы неравенств, подобные приведенному выше примеру, часто используются для задания ограничений на решение.
Когда проблема требует выбора оптимального решения, требуется линейное программирование или другие подходы к оптимизации (комбинаторная оптимизация или оптимизация с исчислением).
Графики систем линейных неравенств
Чтобы построить график линейного неравенства с двумя переменными (скажем, x и y), начните с y с одной стороны. Рассмотрим уравнение, которое получается при замене знака неравенства знаком равенства. График этого уравнения представляет собой линию.
Нарисуйте пунктирную линию, если неравенство строгое (или >). Начертите сплошной линией, если неравенство не является строгим (или).
Наконец, выберите точку, которая не находится ни на одной из прямых ((0,0) обычно проще всего) и определите, удовлетворяют ли координаты неравенству. Заштрихуйте полуплоскость, содержащую эту точку, если это так. Затените другую полуплоскость, если они этого не делают.
Таким же образом начертите все неравенства системы.
Область пересечения всех решений системы является решением системы неравенств.
Системы линейных неравенств
Прежде чем решать системы линейных неравенств, определим неравенство. Термин «неравенство» относится к математическому уравнению, стороны которого не равны.
Обычно пять символов неравенства используются для обозначения уравнений неравенства.
Меньше (<), больше (>), меньше или равно (≤), больше или равно (≥) и не равно (≠) — используемые символы. Неравенства используются для сравнения чисел и поиска диапазона или диапазонов значений, удовлетворяющих критериям переменной.
Что такое системы линейных неравенств
Система линейных неравенств с одинаковыми переменными называется системой линейных неравенств.
Система линейных неравенств решается с помощью нескольких методов решения систем линейных уравнений. Однако вычисление системы линейных неравенств отличается от решения линейных уравнений тем, что знаки неравенства делают невозможными методы замены и исключения.
Графические неравенства могут быть лучшим способом решения систем линейных неравенств.
Примеры экспоненциальных неравенств
Пример 1: Решите 27 / (3 -x ) = 3 6 .
Решение: знайте, что 27 равно 3 3 . Мы можем использовать это, чтобы сделать основания идентичными с обеих сторон.
3 3 / (3 -x ) = 3 6
Am/an = am – n, используя факторное свойство показателей степени. Используя этот метод, основания с обеих сторон теперь идентичны. В результате мы можем сделать показатели равными.
3 3-(-x) = 3 6
3 3 + x = 3 6
3 + x = 6
, вычитая три с обеих сторон,
x = 3.
В результате полученное решение экспоненциального уравнения равно x = 3.
Пример 2: Решите экспоненциальную задачу 7 3x+7 = 490.
Решение: Число 490 нельзя представить в виде степени семи. В результате базы не могут быть здесь одинаковыми. Поэтому мы используем логарифмы для решения этой экспоненциальной задачи.
Log 7 3x+7 = log 490
Используя свойство логарифмов, log am = m log an применяется к обеим частям данного уравнения. При этом
(3x + 7) log 7 = log 490 … (1)
Здесь 490 = 49 × 10 = 7 2 × 10.
Таким образом, log 490 = log (7 2 × 10)
= log 7 2 + log 10 (поскольку log (mn) = log m + log n)
= 2 log 7 + 1 (поскольку log a m = m log a и log 10 = 1 )
Вместо (1),
(3x + 7) log 7 = 2 log 7 + 1
Log 7 используется для разделения обеих сторон.
3x + 7 = (2 log 7 + 1) / (log 7)
3x + 7 = 2 + (1 / log 7)
7 с обеих сторон
3x = -5 + (1 / log 7) )
Разделив обе части на 3,
X = -5/3 + (1/(3 log 7)).
Пример 3: 20 000 долларов ежегодно начисляются по ставке 8% годовых. Сколько времени потребуется, чтобы они удвоились? Ваш ответ следует округлить до ближайшего целого числа.
Решение: P = $20000 – основная сумма.
Процентная ставка равна r = 8%, что равно 8/100 = 0,08.
A = 20 000 x 2 = 40 000 долларов — это окончательная цифра.
Предположим, что необходимое количество времени составляет t лет.
При ежегодном начислении сложных процентов с использованием расчета сложных процентов
A = P (1 + r) t
40000 = 20000 (1 + 0,08)t
Разделив обе части на 20000,
2 = (1,08)t
Взятие бревна с обеих сторон,
Log 2 = log (1,08)t
Log 2 = t log (1,08)
T = (log 2) / (log 1,08)
T = 9
Окончательный ответ округляется до ближайшего целого числа.
Example 4: Solve the following equation:
10 x = 175
Possible Answers:
X ≈ 22.4
X ≈ 2.24
X ≈ 4.48
X ≈ 0.224
X = 2,24
Решение: Чтобы решить это уравнение, вспомните следующее свойство:
Журнал b y = x Можно переписать как b x = y.
10 x = 175
Log 10 175 = x
Evaluate with your calculator to get
X ≈ 2.24
Example 5: Solve
10 3x = 100
Possible Ответы:
X = 10
X = 2
X = 3
X = 2/3
X = 3/2
0273 10 , по соглашению) решить.
Log(10 3x ) = log(100)
Log(10 3x ) = log(10 2 )
3x = 2
. X = 2 .Заключение
Показательные неравенства — это неравенства с переменным показателем степени с одной (или обеих) сторон. Они удобны в обстоятельствах, требующих многократного умножения, особенно по сравнению с постоянной суммой, такой как проценты.
В этом уроке вы увидите, как решить систему линейных уравнений, построив обе линии и найдя их пересечение. Взглянем!
Затем посмотрите, как использовать это значение переменной, чтобы найти значение другой переменной. Проверьте это!
В этом уроке вы увидите, как решить систему линейных уравнений, построив обе линии и найдя их пересечение. Взглянем!
Взглянем!
Этот учебник познакомит вас с этими системами.
Следуйте инструкциям, поскольку в этом руководстве используется пример для объяснения решения системы уравнений!