Системы линейных уравнений решить: Решение систем линейных уравнений — как решать СЛАУ методами Гаусса, Крамера, подстановки и почленного сложения

Решение СЛАУ методами подстановки и сложения

• Понятие системы линейных уравнений
• Решение систем линейных уравнений методом подстановки
• Решение систем линейных уравнений методом сложения

Уравнение называется линейным, если оно содержит переменные только в первой степени и не содержит произведений переменных.

Например, уравнение

—

линейное, а уравнения и не являются линейными.

В общем виде система m линейных уравнений с n переменными записывается так:

. (1)

Числа
 
называются коэффициентами при переменных, а
 —
свободными членами.

Совокупность чисел

называется решением системы (1) линейных уравнений, если при подстановке их вместо переменных во все уравнения они обращаются в верные равенства.

Изучение систем линейных уравнений начинается в средней школе. В школьном курсе рассматриваются в основном системы двух линейных уравнений с двумя переменными и два метода их решения — метод подстановки и метод сложения. Эти методы являются основой изучаемого в курсе высшей математике метода Гаусса. (Принципиально иной метод — метод Крамера — основан на использовании определителей).

Чтобы последовательно двигаться от простому к ещё более простому (сложному), повторим два школьных метода.

Решение. При решении системы линейный уравнений методом подстановки сначала из какого-нибудь уравнения выражают одну переменную через другую (другие, если неизвестных больше двух). Полученное выражение подставляют в другие уравнения, в результате чего приходят к уравнению с одной переменной. Затем находят соответствующее значение второй (и третьей, если она есть) переменной.

Начнём со вполне школьного примера системы двух линейных уравнений с двумя переменными.

Пример 1. Решить систему линейных уравнений методом подстановки:

Выразим из первого уравнения данной системы y через x (можно и наоборот) и получим:

Подставив во второе уравнение данной системы вместо y выражение , получим систему

Данная и полученная системы равносильны. В последней системе второе уравнение содержит только одну переменную. Решим это уравнение:

Соответствующее значение y найдём, подставив вместо x число -5 в выражение , откуда

Пара (-5; 2) является решением системы линейных уравнений.

Методом подстановки можно решать и системы трёх линейных уравнений с тремя переменными.

Пример 2. Решить систему линейных уравнений методом подстановки:

Из третьего уравнения системы выразим :

.

Подставим это выражение во второе уравнение данной системы:

.

Произведём преобразования и выразим из этого уравнения :

Полученные выражения для и подставим в первое уравнение системы и получим

.

Вместо можно вновь подставить его выражение, тогда получим уравнение с одним неизвестным:

откуда

.

Теперь из ранее полученных выражений для остальных переменных найдём и эти переменные:

Итак, решение данной системы линейных уравнений:

.

Пример 3. Решить систему линейных уравнений методом подстановки:

Из первого уравнения системы выразим :

.

Подставим это выражение во второе уравнение данной системы, после чего выполним преобразования и получим:

Из третьего уравнения выразим :

Полученное выражение для подставим в преобразованное второе уравнение системы и получим уравнение с одним неизвестным:

.

Произведём преобразования и найдём :

Теперь из ранее полученных выражений для остальных переменных найдём и эти переменные:

Итак, решение данной системы линейных уравнений:

.

Нет времени вникать в решение? Можно заказать работу!

К началу страницы

Пройти тест по теме Системы линейных уравнений

При решении систем линейных уравнений методом сложения уравнения системы почленно складывают, причём одно или оба (несколько) уравнений могут быть умножены на различные числа. В результате приходят к эквивалентной (равносильной) системе линейных уравнений, в которой одно из уравнений содержит только одну переменную.

Пример 4. Решить систему линейных уравнений методом сложения:

Решение. В уравнениях данной системы в этом примере системы коэффициенты при y — противоположные числа. Сложив почленно левые и правые части уравнений, получим уравнение с одной переменной:

, или , .

Заменим одно из уравнений исходной системы, например, первое, уравнением . Получим систему

Решим полученную систему. Подставив значение в уравнение , получим уравнение с одной переменной y:

Пара (2; 1) является решением полученной системы линейных уравнений. Она является также решением исходной системы, так как эти две системы линейных уравнений равносильны.

Пример 5. Решить систему линейных уравнений методом сложения

Почленное сложение уравнений системы не приводит к исключению одной из переменных. Но если умножить все члены первого уравнения на -3, а второго уравнения на 2, то коэффициенты при x в полученных уравнениях будут противоположными числами:

Почленное сложение уравнений полученной в результате преобразований системы приводит к уравнению с одной переменной: .

Из этого уравнения находим, что . Получили

Решением полученной системы, а следовательно и исходной системы линейных уравнений является пара чисел (-3; 0).

Пример 6. Решить систему линейных уравнений методом сложения:

Решение. Для упрощения решения произведём замену переменных:

, .

Приходим к системе линейных уравнений:

или

Умножим второе уравнение полученной системы на -2 и сложим с первым уравнением, получим , . Тогда .

Следовательно, имеем систему уравнений

или

Умножим второе уравнение полученной системы на 3 и сложим с первым уравнением. Получим

.

Решив задачи из примеров на решение систем линейных уравнений методом подстановки и методом сложения, мы научились производить элементарные преобразования, необходимые для решениях систем линейных уравнений в курсе высшей математики.

Назад

Листать

Вперёд>>>

Нет времени вникать в решение? Можно заказать работу!

К началу страницы

Пройти тест по теме Системы линейных уравнений

Продолжение темы «Системы уравнений и неравенств»

Решение систем линейных уравнений методом Крамера

Решение систем линейных уравнений методом Гаусса

Условие совместности системы линейных уравнений. Теорема Кронекера-Капелли

Решение систем линейных уравнений матричным методом (обратной матрицы)

Системы линейных неравенств и выпуклые множества точек

Начало темы «Линейная алгебра»

Определители

Матрицы

Поделиться с друзьями

Элементы высшей математики: Решение систем линейных уравнений

7.

Решение систем линейных уравнений

7.1.

Системы линейных алгебраических уравнений

Сегодня вы изучите вопросы

1. Методы решения систем линейных алгебраических уравнений (СЛАУ)

2. Метод обратной матрицы

3. Метод Крамера

4. Метод Гаусса

5. Условия разрешимости данных систем

6. Критерий совместности

Изучив тему занятия, вы сможете

• решать СЛАУ методом обратной матрицы, по формулам Крамера, методом Гаусса;

• решать произвольные системы линейных уравнений и системы однородных уравнений.

Основные понятия

7.1.1.

Системы линейных алгебраических уравнений

Системой линейных алгебраических уравнений (СЛАУ) называется система вида

(4.1)

Решением системы (4.1) называется такая совокупность n чисел

, при подстановке которых каждое уравнение системы обращается в верное равенство.

Решить систему означает найти все ее решения или доказать, что ни одного решения нет.

СЛАУ называется совместной, если она имеет хотя бы одно решение, и несовместной, если она решений не имеет.

Если совместная система имеет только одно решение, то она называется определенной, и неопределенной, если она имеет более чем одно решение.

Например, система уравнений совместная и определенная, так как имеет единственное решение ; система

несовместная, а система совместная и неопределенная, так как имеет более одного решения .

Две системы уравнений называются равносильными или эквивалентными, если они имеют одно и то же множество решений. В частности, две несовместные системы считаются эквивалентными.

Основной матрицей СЛАУ (4.1) называется матрица А размера , элементами которой являются коэффициенты при неизвестных данной системы, то есть

.

Матрицей неизвестных СЛАУ (4.1) называется матрица-столбец Х, элементами которой являются неизвестные системы (4.1):

.

Матрицей свободных членов СЛАУ (4.1) называется матрица-столбец В, элементами которой являются свободные члены данной СЛАУ:

.

С учетом введенных понятий СЛАУ (4.1) можно записать в матричном виде или

. (4.2)

7.1.2.

Решение систем линейных уравнений. Метод обратной матрицы

Перейдем к изучению СЛАУ (4.1), которой соответствует матричное уравнение (4.2). Сначала рассмотрим частный случай, когда число неизвестных равно числу уравнений данной системы () и , то есть основная матрица системы A невырождена. В этом случае, согласно предыдущему пункту, для матрицы существует единственная обратная матрица A^-1. Ясно, что она согласована с матрицами и . Покажем это. Для этого умножим слева обе части матричного уравнения (4.2) на матрицу :

Следовательно, с учетом свойств умножения матриц получаем

Так как , а , тогда

. (4.3)

Убедимся, что найденное значение является решением исходной системы. Подставив (4.3) в уравнение (4.2), получим , откуда имеем .

Покажем, что это решение единственное. Пусть матричное уравнение (4.2) имеет другое решение , которое удовлетворяет равенству

.

Покажем, что матрица равна матрице

С этой целью умножим предыдущее равенство слева на матрицу A^-1.

В результате получим

Такое решение системы уравнений с неизвестными называется решением системы (4.1) методом обратной матрицы.

Пример. Найти решение системы

.

Выпишем матрицу системы:

,

Для этой матрицы ранее мы уже нашли обратную:

или

Здесь мы вынесли общий множитель , так как нам в дальнейшем нужно будет произведение .

Ищем решение по формуле: .

Найденные значения переменных подставляем в уравнения системы и убеждаемся, что они являются ее решением.

Упражнение. Проверку этого факта сделайте самостоятельно.

7.1.3.

Правило и формулы Крамера

Рассмотрим систему линейных уравнений с неизвестными

От матричной формы (4.3) перейдем к более удобным и в ряде случаев более простым при решении прикладных задач формулам для нахождения решений системы линейных алгебраических уравнений.

Учитывая равенство , или в развернутом виде

.

Таким образом, после перемножения матриц получаем:

или

.

Заметим, что сумма есть разложение определителя

по элементам первого столбца, который получается из определителя путем замены первого столбца коэффициентов столбцом из свободных членов.

Таким образом, можно сделать вывод, что

Аналогично: , где получен из путем замены второго столбца коэффициентов столбцом из свободных членов, .

Следовательно, нами найдено решение заданной системы по равенствам

, , ,

известным и как формулы Крамера.

Для нахождения решения СЛАУ, последние равенства можно записать в общем виде следующим образом:

. (4.4)

Согласно этим формулам, имеем правило Крамера для решения СЛАУ:

• по матрице системы вычисляется определитель системы ;

• если , то в матрице системы каждый столбец последовательно заменяется столбцом свободных членов и вычисляются определители получаемых при этом матриц;

• решение системы находится по формулам Крамера (4.4).

Пример. С помощью формул Крамера решить систему уравнений

Решение. Определитель данной системы

.

Так как , то формулы Крамера имеют смысл, то есть система имеет единственное решение. Находим определители:

, , .

Следовательно, по формулам (4.4) получаем:

, , .

Найденные значения переменных подставляем в уравнения системы и убеждаемся, что они являются ее решением.

Упражнение. Проверку этого факта сделайте самостоятельно.

Критерий совместности СЛАУ (теорема Кронекера-Капелли)

Расширенной матрицей системы (4.1) называется матрица, получаемая добавлением к основной матрице А справа столбца свободных членов с отделением его вертикальной чертой, то есть матрица

.

Заметим, что при появлении у матрицы новых столбцов ранг может увеличиться, следовательно . Расширенная матрица играет очень важную роль в вопросе совместности (разрешимости) системы уравнений. Исчерпывающий ответ на этот вопрос дает теорема Кронекера-Капелли.

Сформулируем теорему Кронекера-Капелли (без доказательства).

Система линейных алгебраических уравнений (4.1) совместна тогда и только тогда, когда ранг матрицы системы равен рангу расширенной матрицы . Если   — число неизвестных системы, то система имеет единственное решение, а если , то система имеет бесчисленное множество решений.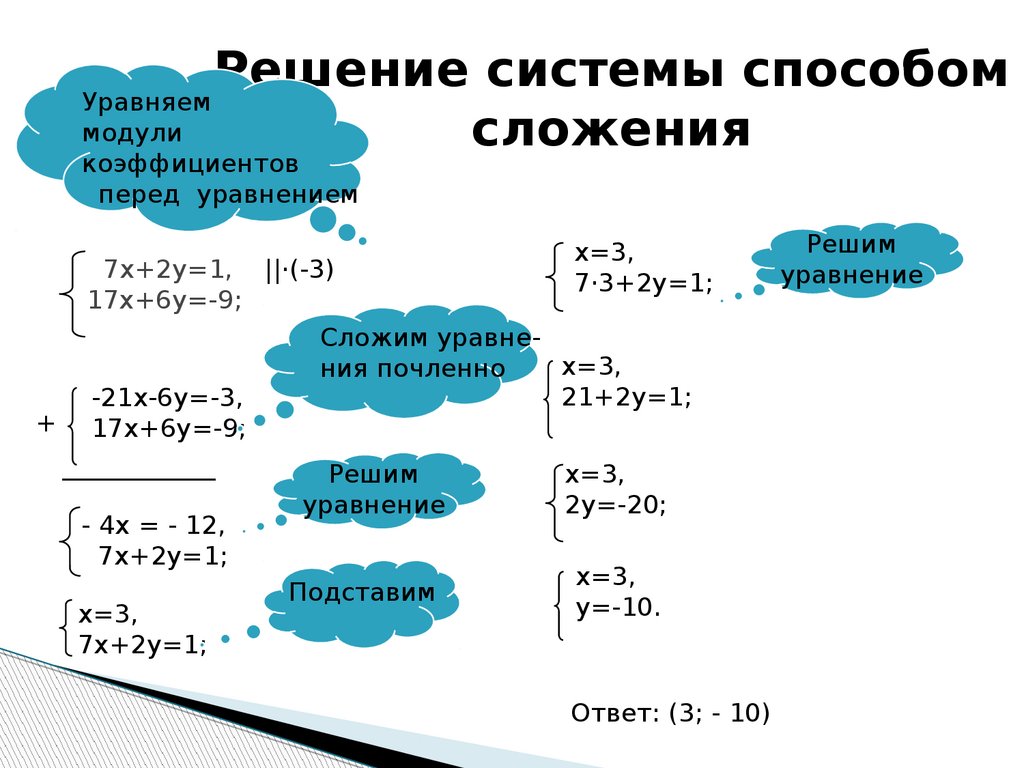

Опираясь на теорему Кронекера-Капелли, сформулируем алгоритм решения произвольной системы линейных уравнений.

1. Вычисляют ранги основной и расширенной матриц СЛАУ. Если , то система не имеет решений (несовместна).

2. Если , система совместна. В этом случае берут любой отличный от нуля минор основной матрицы порядка и рассматривают уравнений, коэффициенты которых входят в этот базисный минор, а остальные уравнения отбрасывают. Неизвестные коэффициенты, которые входят в этот базисный минор, объявляют главными или базисными, а остальные свободными (неосновными). Новую систему переписывают, оставляя в левых частях уравнений только члены, содержащие базисных неизвестных, а все остальные члены уравнений, содержащих неизвестных, переносят в правые части уравнений.

3. Находят выражения базисных неизвестных через свободные. Полученные решения новой системы с базисными неизвестными называются общим решением СЛАУ (4. 1).

4. Придавая свободным неизвестным некоторые числовые значения, находят так называемые частные решения.

Проиллюстрируем применение теоремы Кронекера-Капелли и вышеприведенного алгоритма на конкретных примерах.

Пример. Определить совместность системы уравнений

Решение. Запишем матрицу системы и определим ее ранг.

Имеем:

Так как матрица имеет порядок , то наивысший порядок миноров равен 3. Число различных миноров третьего порядка Нетрудно убедиться, что все они равны нулю (проверьте самостоятельно). Значит, . Ранг основной матрицы равен двум, так как существует отличный от нуля минор второго порядка этой матрицы, например,

Ранг расширенной матрицы этой системы равен трем, так как существует отличный минор третьего порядка этой матрицы, например,

Таким образом, согласно критерию Кронекера-Капелли, система несовместна, то есть не имеет решений.

Пример. Исследовать совместность системы уравнений

Решение. Ранг основной матрицы этой системы равен двум, так как, например, минор второго порядка равен

а все миноры третьего порядка основной матрицы равны нулю. Ранг расширенной матрицы также равен двум, например,

а все миноры третьего порядка расширенной матрицы равны нулю (убедиться самостоятельно). Следовательно, система совместна.

Возьмем за базисный минор, например . В этот базисный минор не входят элементы третьего уравнения, поэтому ее отбрасываем.

Неизвестные и объявляем базисными, так как их коэффициенты входят в базисный минор, неизвестную объявляем свободной.

В первых двух уравнениях члены, содержащие переменную , перенесем в правые части. Тогда получим систему

Решаем эту систему с помощью формул Крамера.

,

.

Таким образом, общим решением исходной системы является бесконечное множество наборов вида ,

где  — любое действительное число.

Частным решением данного уравнения будет, например, набор , получающийся при .

7.1.4.

Решение систем линейных алгебраических уравнений методом Гаусса

Одним из наиболее эффективных и универсальных методов решений СЛАУ является метод Гаусса. Метод Гаусса состоит из однотипных циклов, позволяющих последовательно исключать неизвестные СЛАУ. Первый цикл направлен на то, чтобы во всех уравнениях, начиная со второго, обнулить все коэффициенты при . Опишем первый цикл. Полагая, что в системе коэффициент (если это не так, то следует на первое место поставить уравнение с отличным от нуля коэффициентом при x₁ и переобозначить коэффициенты), преобразуем систему (4.1) следующим образом: первое уравнение оставляем без изменения, а из всех остальных уравнений исключаем неизвестную x₁ с помощью элементарных преобразований. Для этого умножим обе части первого уравнения на и сложим почленно со вторым уравнением системы. Затем умножим обе части первого уравнения на и сложим с третьим уравнением системы. Продолжая этот процесс, на последнем шаге цикла умножим обе части первого уравнения на и сложим с последним уравнением системы. Первый цикл завершен, в результате получим эквивалентную систему

(4.5)

Замечание. Для удобства записи обычно используют расширенную матрицу системы. После первого цикла данная матрица принимает следующий вид:

(4.6)

Второй цикл является повторением первого цикла. Предположим, что коэффициент . Если это не так, то перестановкой уравнений местами добьемся того, что . Первое и второе уравнение системы (4.5) перепишем в новую систему (в дальнейшем будем оперировать только расширенной матрицей).

Умножим второе уравнение (4.5) или вторую строку матрицы (4.6) на , сложим с третьим уравнением системы (4.5) или третьей строкой матрицы (4.6). Аналогично поступаем с остальными уравнениями системы. В результате получим эквивалентную систему:

(4.7)

Продолжая процесс последовательного исключения неизвестных, после k — 1-го шага, получим расширенную матрицу

(4.8)

Последние m — k уравнений для совместной системы (4.1) являются тождествами . Если хотя бы одно из чисел не равно нулю, то соответствующее равенство противоречиво, следовательно, система (4. 1) несовместна. В совместной системе при ее решении последние m — k уравнений можно не рассматривать. Тогда полученная эквивалентная система (4.9) и соответствующая расширенная матрица (4.10) имеют вид

(4.9)

(4.10)

После отбрасывания уравнений, являющихся тождествами, число оставшихся уравнений может быть либо равно числу переменных , либо быть меньше числа переменных. В первом случае матрица имеет треугольный вид, а во втором — ступенчатый. Переход от системы (4.1) к равносильной ей системе (4.9) называется прямым ходом метода Гаусса, а нахождение неизвестных из системы (4.9) — обратным ходом.

Пример. Решить систему методом Гаусса:

.

Решение. Расширенная матрица этой системы имеет вид

.

Проведем следующие преобразования расширенной матрицы системы: умножим первую строку на и сложим со второй строкой, а также умножим первую строку на и сложим с третьей строкой. Результатом будет расширенная матрица первого цикла (в дальнейшем все преобразования будем изображать в виде схемы)

.

Полученная расширенная матрица соответствует системе уравнений

которая эквивалентна исходной системе. Далее последовательно находим:

, , .

Пример. Решить систему методом Гаусса:

.

Преобразуем расширенную матрицу системы по методу Гаусса:

Последняя строка последней матрицы соответствует не имеющему решения уравнению .

Следовательно, исходная система несовместна.

Системы однородных уравнений

Система линейных алгебраических уравнений называется однородной, если она тождественными преобразованиями приводится к виду:

(4.11)

Ясно, что однородная система всегда совместна, хотя бы потому, что она всегда имеет тривиальное решение x₁ = x₂ = … = x_n = 0.

Сплошь нулевое решение часто называют тривиальным решением системы.

Содержательным вопросом, очевидно, является следующий: при каких условиях однородная система имеет и ненулевые решения? Ответом служит следующая теорема.

Теорема. Для того чтобы система однородных уравнений имела ненулевые решения, необходимо и достаточно, чтобы ранг r ее основной матрицы был меньше числа n неизвестных, .

Необходимость.

Так как ранг не может превосходить размера матрицы, то, очевидно, . Пусть . Тогда один из миноров размера отличен от нуля. Поэтому соответствующая система линейных уравнений имеет единственное решение:

. Значит, других, кроме тривиальных, решений нет. Итак, если есть нетривиальное решение, то .

Достаточность.

Пусть r < n. Тогда однородная система, будучи совместной, является неопределенной. Значит, она имеет бесчисленное множество решений, т.е. имеет и ненулевые решения.

В заключении выделим частный случай последней теоремы.

Пусть дана однородная система n линейных уравнений с n неизвестными (4.11).

Теорема. Для того чтобы однородная система n линейных уравнений с n неизвестными имела ненулевые решения, необходимо и достаточно, чтобы ее определитель ∆ был равен нулю, т. е. ∆ = 0.

Если система имеет ненулевые решения, то ∆ = 0, так как при ∆ ≠ 0 система имеет единственное, нулевое решение. Если же ∆ = 0, то ранг r основной матрицы системы меньше числа неизвестных, то есть r < n. Это означает, что система имеет бесконечное множество ненулевых решений.

Пример. Решить систему

Решение. 

Так как r < n, то система имеет бесчисленное множество решений. Найдем их.

 

Стало быть,  — общее решение.

Положив х₃ = 0, получаем одно частное решение: х₁ = 0, х₂ = 0, х₃ = 0. Положив х₃ = 1, получаем второе частное решение: х₁ = 2, х₂ = 3, х₃ = 1, и т.д.

Контрольные вопросы

1. Что понимается под системой линейных алгебраических уравнений?

2. Запишите в общем виде СЛАУ. Каков смысл величин, входящих в уравнения системы?

3. Дайте определение решения системы, определения совместной, несовместной системы.

4. При каких условиях СЛАУ имеет единственное решение?

5. К какой СЛАУ применим метод обратной матрицы?

6. К какой СЛАУ применимо правило Крамера?

7. Сформулируйте теорему Кронекера-Капелли.

8. Сформулируйте алгоритм решения произвольной системы линейных уравнений.

9. Какая система линейных алгебраических уравнений называется однородной?

10. При каких условиях система однородных уравнений имеет ненулевое решение?

Задания для самостоятельной работы

Задание 1. Примеры для самоподготовки

(решение систем линейных уравнений)

1. Решить следующие системы уравнений по формулам Крамера

   1.1.

   Ответ.

   1.2.

   Ответ. Нет решений.

   1.3.

   Ответ. x = α, y = 3,5 —0,5α, где α — произвольное действительное число.

   1.4.

   Ответ. .

2. Решить систему уравнений с применением теории матриц:

   2.1.

   Ответ. x = 2; y = 0; z = 3.

   2.2.

   Ответ. x₁ = 2; x₂ = -1; x₃ = 0; x₄ = -2.

   2.3.

   Ответ. x₁ = -17α + 29β + 5; x₂ = 10α — 17β — 2; x₃ = α; x₄ = β

Задание 2. Примеры для самопроверки

(отметьте правильный вариант ответа)

1. Решить следующую систему уравнений

   1) ;

   2) ;

   3) ;

   4) ;

   5) .

2. Решить следующую систему уравнений

   1) ;

   2) ;

   3) нет решений;

   4) ;

   5) .

3. Решить следующую систему уравнений

   1) ;

   2) ;

   3) ;

   4) ;

   5) .

4. Решить следующую систему уравнений

   1) ;

   2) ;

   3) ;

   4) ;

   5) .

5. Решить следующую систему уравнений

   1) ;

   2) ;

   3) ;

   4) ;

   5) .

6. Решить следующую систему уравнений

   1) ;

   2) ;

   3) ;

   4) ;

   5) .

Решения систем линейных уравнений

Результаты обучения

• Поиск решений систем уравнений
• Решение систем уравнений с помощью графика

Система линейных уравнений состоит из двух или более линейных уравнений, состоящих из двух или более переменных, так что все уравнения в системе рассматриваются одновременно. Чтобы найти единственное решение системы линейных уравнений, мы должны найти числовое значение для каждой переменной в системе, которое будет удовлетворять всем уравнениям в системе одновременно. Некоторые линейные системы могут не иметь решения, а другие могут иметь бесконечное число решений. Чтобы линейная система имела единственное решение, в ней должно быть не меньше уравнений, чем переменных. Тем не менее, это не гарантирует уникальности решения.

В этом разделе мы рассмотрим системы линейных уравнений с двумя переменными, которые состоят из двух уравнений, каждое из которых содержит две разные переменные. Например, рассмотрим следующую систему линейных уравнений с двумя переменными.

[латекс]\begin{array}{l}2x+y=\text{ }15\\3x-y=\text{ }5\end{array}[/latex]

Решение для Система линейных уравнений с двумя переменными — это любая упорядоченная пара, удовлетворяющая каждому уравнению независимо. В этом примере упорядоченная пара [латекс](4, 7)[/латекс] является решением системы линейных уравнений.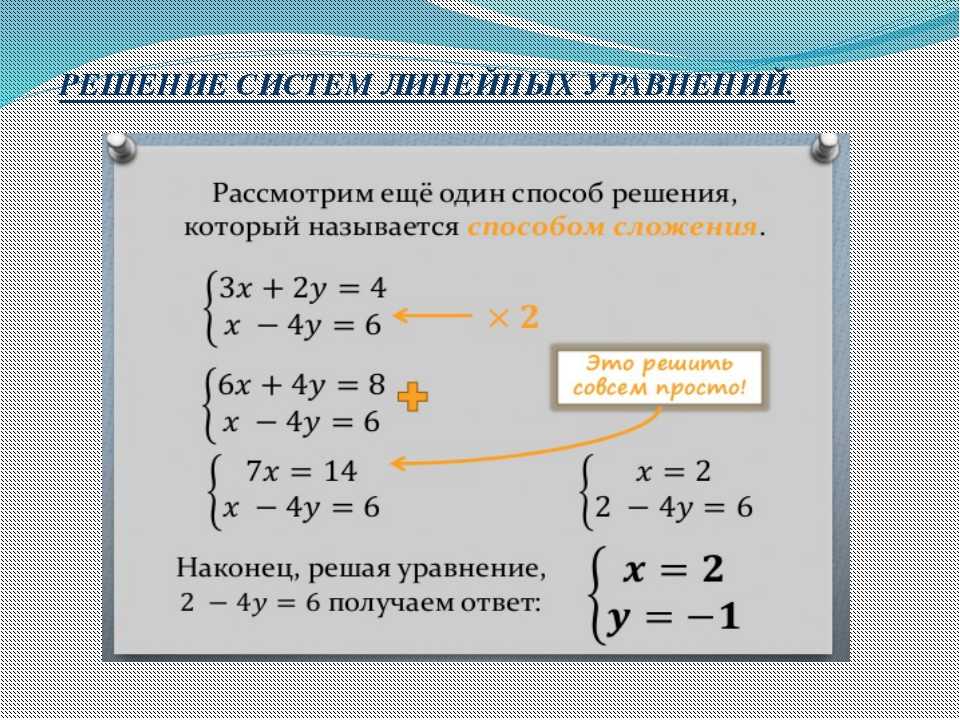 Мы можем проверить решение, подставив значения в каждое уравнение, чтобы увидеть, удовлетворяет ли упорядоченная пара обоим уравнениям. Вскоре мы исследуем методы нахождения такого решения, если оно существует.

[латекс]\begin{array}{l}2\left(4\right)+\left(7\right)=15\text{ }\text{True}\hfill \\ 3\left(4\ right)-\left(7\right)=5\text{ }\text{True}\hfill \end{array}[/latex]

Помимо учета количества уравнений и переменных, мы можем классифицировать системы линейные уравнения по количеству решений. непротиворечивая система уравнений имеет хотя бы одно решение. Непротиворечивая система считается независимой системой , если она имеет единственное решение, подобное только что рассмотренному нами примеру. Две линии имеют разные наклоны и пересекаются в одной точке плоскости. Непротиворечивая система считается зависимая система , если уравнения имеют одинаковый наклон и одинаковые и -перехваты. Другими словами, прямые совпадают, поэтому уравнения представляют одну и ту же прямую. Каждая точка на прямой представляет собой пару координат, удовлетворяющую системе. Таким образом, существует бесконечное множество решений.

Другой тип системы линейных уравнений — это противоречивая система , в которой уравнения представляют две параллельные линии. Линии имеют одинаковый наклон и разные г- перехватов. Нет общих точек для обеих прямых; следовательно, система не имеет решений.

 

A Общее примечание: Типы линейных систем

Существует три типа систем линейных уравнений с двумя переменными и три типа решений.

• Независимая система имеет ровно одну пару решений [латекс]\лево(х,у\право)[/латекс]. Точка пересечения двух прямых является единственным решением.
• Несовместимая система не имеет решения. Две прямые параллельны и никогда не пересекутся.
• зависимая система имеет бесконечно много решений. Линии совпадают. Это одна и та же линия, поэтому каждая пара координат на линии является решением обоих уравнений.

Ниже приведены графические изображения каждого типа системы.

Независимая и зависимая системы также непротиворечивы, поскольку обе они имеют хотя бы одно решение.

Как: Имея систему линейных уравнений и упорядоченную пару, определить, является ли упорядоченная пара решением

1. Подставьте упорядоченную пару в каждое уравнение в системе.
2. Определить, верны ли утверждения в результате замены в обоих уравнениях; если да, то упорядоченная пара является решением.

Пример

Определить, является ли упорядоченная пара [латекс]\влево(5,1\вправо)[/латекс] решением заданной системы уравнений.

[латекс]\begin{array}{l}x+3y=8\hfill \\ 2x — 9=y\hfill \end{array}[/latex]

Показать решение

В следующем видео мы покажем еще один пример того, как проверить, является ли упорядоченная пара решением системы уравнений.

Существует несколько методов решения систем линейных уравнений. Для системы линейных уравнений с двумя переменными мы можем определить как тип системы, так и решение, построив график системы уравнений на одном и том же наборе осей.

Пример

Решите следующую систему уравнений с помощью графика. Определите тип системы.

[латекс]\begin{array}{c}2x+y=-8\x-y=-1\end{массив}[/latex]

Показать решение

Графики можно использовать, если система непоследовательна или зависима. В обоих случаях мы все еще можем построить систему, чтобы определить тип системы и решения. Если две прямые параллельны, то система не имеет решений и несовместна. Если две линии идентичны, система имеет бесконечные решения и является зависимой системой.

В следующем видео мы покажем еще один пример того, как определить, имеет ли графическая система решение, и определить, какой тип решения представлен.

В нашем последнем видео мы покажем, как решить систему уравнений, сначала нарисовав линии, а затем найдя решение системы.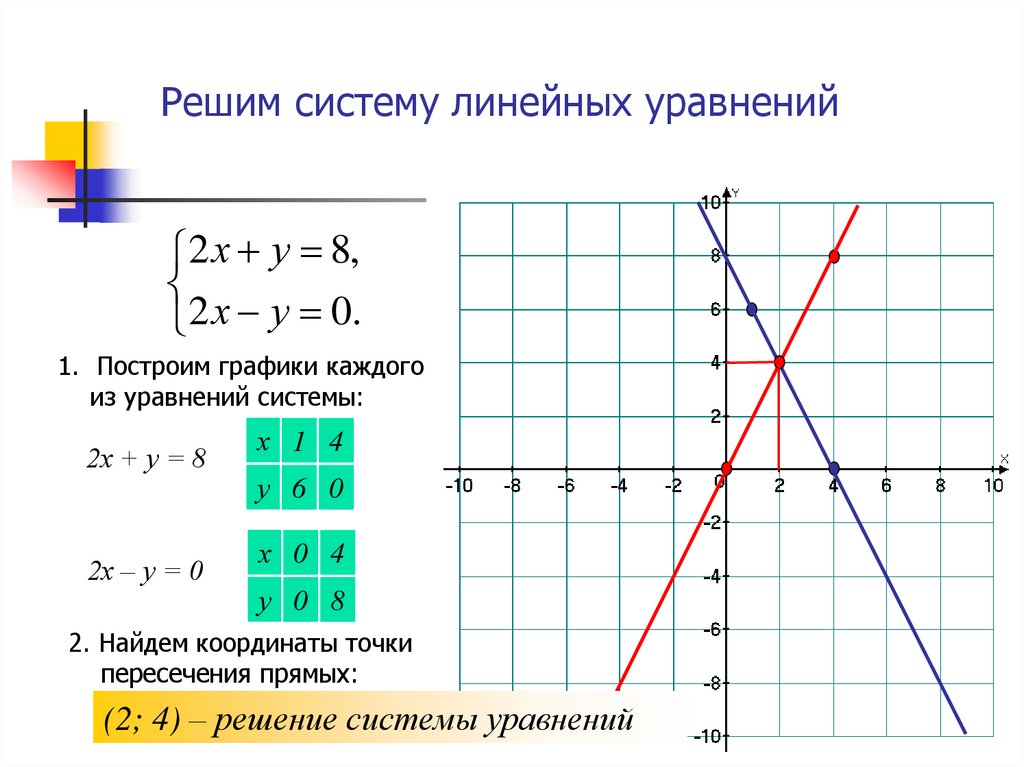

Системы линейных уравнений

Система линейных уравнений с двумя переменными представляет собой два линейных уравнения с одной или двумя переменными, рассматриваемые вместе.

Решение системы линейных уравнений с двумя переменными представляет собой упорядоченную пару (значение x и y), которая делает каждое уравнение верным. Решение системы примера (2,3) .

 

	Нажмите на колоду карт, чтобы просмотреть карту. Перетащите карточку снизу в нужную категорию.
Для этого содержимого требуется Flash Player 10 или выше.

 

Решение систем линейных уравнений с двумя переменными методом сложения/исключения:

 

 

 

 

	Посмотреть видео: Алгебра: решение системы уравнений Пэта МакКега
	Смотреть видео: Решение систем уравнений методом исключения путем сложения, автор: PatrickJMT

 

Решение систем линейных уравнений с двумя переменными методом подстановки:

Посмотрите видео: Решение линейных систем уравнений с помощью подстановки от Патрика ДжМТ

 

Системы с бесконечным числом решений и без решения

Абсолютные значения

Решение уравнения, включающего абсолютное значение:

Посмотрите видео: Решение уравнений абсолютного значения — пример 1 от PatrickJMT
	Посмотрите видео: «Абсолютное значение и оценка чисел» Патрика ДжМТ

 

График уравнений абсолютного значения с двумя переменными

  Нанесите на график точки, удовлетворяющие уравнению (как описано ранее). График имеет V-образную форму, поэтому вы должны использовать достаточно упорядоченных пар, чтобы найти самую низкую точку V . График будет

симметричен относительно вертикальной линии, проходящей через эту точку.

 

Смотреть видео: Решение линейных уравнений и неравенств с абсолютными значениями от PatrickJMT

 

 

Quadratic Equations

 

 

 

Решение нелинейных систем уравнений с двумя переменными с помощью графика

Постройте график каждого уравнения (как описано ранее) на одном наборе осей. Точки пересечения графиков имеют координаты, удовлетворяющие системе уравнений.

 

 

 

Решение нелинейных систем уравнений с двумя переменными с помощью замены

Используйте описанный ранее метод подстановки для решения систем линейных уравнений с двумя переменными.