Системы уравнений с тремя переменными как решать – —

Решение систем линейных уравнений с тремя неизвестными

Решение системы трех линейных уравнений с тремя неизвестными

Калькулятор для решения систем линейных уравнений 2×2 и 3×3.

Решение системы трех линейных уравнений методом Крамера

Решение систем линейных уравнений (правило Крамера)

Рассмотрим систему трех линейных уравнений с тремя неизвестными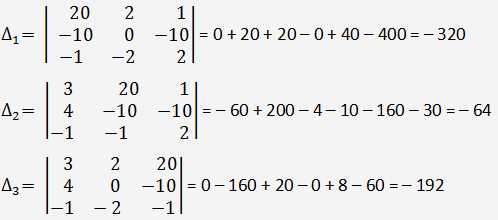

По формулам Крамера получаем

Решение системы трех линейных уравнений методом Гаусса

Разделим первое уравнение системы на 3

Умножим уравнение (**) на 4 и вычтем из второго уравнения, затем умножим уравнение (**) на (-1) и вычтем из третьего уравнения. Получим систему уравнений

Разделим второе уравнений на и получим
Умножим уравнений (***) на и вычтем из третьего уравнения. В результате получаем следующую систему уравнений
Из последнего уравнения находим z=3. Подстaвляя найденное значение во второе уравнение, получаем:
=> y=1.
Подставляя найденные значения y и z в первое уравнение, найдем x => x=5.
Ответ: x=5, y=1, z=3

Решение систем двух линейных уравнений с двумя неизвестными методом Крамера.

ru.intemodino.com

Уравнение с тремя неизвестными | Математика

62. Одно уравнение с тремя неизвестными. Пусть имеем уравнение

3x + 4y – 2z = 11.

На это уравнение можно смотреть, как на запись задачи: найти числовые значения для x, y и z, чтобы трехчлен 3x + 4y – 2z оказался равен числу 11. Таким образом это уравнение является уравнением с тремя неизвестными. Так как мы можем решить одно уравнение с одним неизвестным, то уже с первого взгляда возникает мысль, что 2 неизвестных здесь являются как бы лишними, и им можно давать произвольные значения. И действительно, если, например, взять для y число 3 и для z число 5, то получим уравнение с одним неизвестным:

3x + 12 – 10 = 11,

откуда

3x = 9 и x = 3.

Возьмем другие числа для y и z. Например, пусть

y = –1 и z = 0.

Тогда получим уравнение:

3x – 4 = 11,

откуда

3x = 15 и x = 5.

Продолжая эту работу дальше, мы придем к заключению:

Одно уравнение с тремя неизвестными имеет бесконечно много решений, и для получения их надо двум неизвестным давать произвольные значения.

Результаты этой работы можно записать в таблице (мы, кроме двух уже найденных решений, записали в ней еще одно, которое получится, если положить y = –1 и z = –2):

Так как для y и для z мы берем произвольные значения, то они являются независимыми переменными, а x является зависимым (от них) переменным. Другими словами: x является функциею от y и z.

Чтобы удобнее получать решения этого уравнения, можно определить из него x через y и z. Получим:

3x + 4y – 2z = 11; 3x = 11 – 4y + 2z;
x = (11 – 4y + 2z) / 3.

Дадим, напр., значения: y = 5 и z = 1; получим: x = (11 – 20 + 2) / 3 = –2(1/3) и т. д.

Возьмем еще уравнение

3x – 5y – 2z = 7.

Примем x и y за независимые переменные, а z — за зависимое и определим z через x и y

–2z = 7 – 3x + 5y; 2z = 3x – 5y – 7; z = (3x – 5y – 7) / 2

Теперь легко составить таблицу решений:

 

maths-public.ru

Как решить систему из трёх уравнений

2 сентября 2011

Автор КакПросто!

Все системы из трех уравнений с тремя неизвестными решаются одним способом – путем последовательной замены неизвестного выражением, содержащим в себе другие два неизвестных, сокращая таким образом их число.

Статьи по теме:

Инструкция

Чтобы разобраться, как работает алгоритм замены неизвестных, качестве примера возьмем следующую систему уравнений с тремя неизвестными x, y и z:2x+2y-4z=-12
4x-2y+6z=36
6x-4y-2z=-16 В первом уравнении перенесите все слагаемые кроме х, умноженное на 2, в правую часть и разделите на множитель, стоящий перед x. Таким образом вы получите значение х, выраженное через две другие неизвестные z и y.х=-6-y+2z. Теперь работайте со вторым и третьим уравнениями. Замените все х на полученное выражение, содержащее только неизвестные z и y.4*(-6-y+2z)-2y+6z=36
6*(-6-y+2z)-4y-2z=-16 Раскройте скобки, учитывая знаки перед множителями, выполните действия сложения и вычитания в уравнениях. Перенесите слагаемые без неизвестных (числа) в правую часть уравнения. Вы получите систему из двух линейных уравнений с двумя неизвестными.-6y+14z=60
-10y+10z=20.

Теперь выделите неизвестное y, чтобы его можно было выразить через z. Не обязательно делать это в первом уравнении. На примере видно, что множители у y и z совпали за исключением знака, поэтому работайте с этим уравнением, так будет удобнее. Перенесите z со множителем в правую часть уравнения и разделите обе части на множитель y -10.y=-2+z.

Подставьте полученное выражение y в уравнение, которое не было задействовано, раскройте скобки, учитывая знак множителя, совершите действия сложения и вычитания, и вы получите:-6*(-2+z)+14z=60
12-6z+14z=60
8z=48
z=6.

Теперь вернитесь к уравнению, где y определен с помощью z, и поставьте значение z в уравнение. У вас получится:y=-2+z=-2+6=4

Вспомните самое первое уравнение, в котором x выражен через z y. Подставьте в него их числовые значения. У вас получится:x=-6-y+2z=-6-4+12=2Таким образом, все неизвестные найдены. Точно таким способом решаются нелинейные уравнения, где множителями выступают математические функции.

Источники:

• Решение и исследование системы трёх уравнений первой

Совет полезен?

Статьи по теме:

Не получили ответ на свой вопрос?
Спросите нашего эксперта:

www.kakprosto.ru

Как решить систему уравнений с тремя переменными

Точка О – центр окружности, ?AOB=72° (см. рисунок). Найдите величину угла ACB(в градусах). Точка О – центр окружности, ?ACB=24° (см. рисунок). Найдите величину угла AOB(в градусах).

Примеры систем линейных уравнений: метод решения

Системы уравнений получили широкое применение в экономической отрасли при математическом моделировании различных процессов. Например, при решении задач управления и планирования производства, логистических маршрутов (транспортная задача) или размещения оборудования.

Системы уравнения используются не только в области математики, но и физики, химии и биологии, при решении задач по нахождению численности популяции.

Системой линейных уравнений называют два и более уравнения с несколькими переменными, для которых необходимо найти общее решение. Такую последовательность чисел, при которых все уравнения станут верными равенствами или доказать, что последовательности не существует.

Линейное уравнение

Уравнения вида ax+by=c называют линейными. Обозначения x, y — это неизвестные, значение которых надо найти, b, a — коэффициенты при переменных, c — свободный член уравнения.

Решение уравнение путем построение его графика будет иметь вид прямой, все точки которой являются решением многочлена.

Виды систем линейных уравнений

Наиболее простыми считаются примеры систем линейных уравнений с двумя переменными X и Y.

F1(x, y) = 0 и F2(x, y) = 0, где F1,2 — функции, а (x, y) — переменные функций.

Решить систему уравнений — это значит найти такие значения (x, y), при которых система превращается в верное равенство или установить, что подходящих значений x и y не существует.

Пара значений (x, y), записанная в виде координат точки, называется решением системы линейных уравнений.

Если системы имеют одно общее решение или решения не существует их называют равносильными.

Однородными системами линейных уравнений являются системы правая часть которых равна нулю. Если правая после знака «равенство» часть имеет значение или выражена функцией, такая система неоднородна.

Количество переменных может быть гораздо больше двух, тогда следует говорить о примере системы линейных уравнений с тремя переменными или более.

Сталкиваясь с системами школьники предполагают, что количество уравнений обязательно должно совпадать с количеством неизвестных, но это не так. Количество уравнений в системе не зависит от переменных, их может быть сколь угодно много.

Простые и сложные методы решения систем уравнений

Не существует общего аналитического способа решения подобных систем, все методы основаны на численных решениях. В школьном курсе математики подробно описаны такие методы как перестановка, алгебраическое сложение, подстановка, а так же графический и матричный способ, решение методом Гаусса.

Основная задача при обучении способам решения — это научить правильно анализировать систему и находить оптимальный алгоритм решения для каждого примера. Главное не вызубрить систему правил и действий для каждого способа, а понять принципы применения того или иного метода

Решение примеров систем линейных уравнений 7 класса программы общеобразовательной школы довольно простое и объяснено очень подробно. В любом учебнике математике этому разделу отводится достаточно внимания. Решение примеров систем линейных уравнений методом Гаусса и Крамера более подробно изучают на первых курсах высших учебных заведений.

Решение систем методом подстановки

Действия метода подстановки направлены на выражение значения одной переменной через вторую. Выражение подставляется в оставшееся уравнение, затем его приводят к виду с одной переменной. Действие повторяется в зависимости от количества неизвестных в системе

Приведем решение примера системы линейных уравнений 7 класса методом подстановки:

Как видно из примера, переменная x была выражена через F(X) = 7 + Y. Полученное выражение, подставленное во 2-е уравнение системы на место X, помогло получить одну переменную Y во 2-е уравнении. Решение данного примера не вызывает трудностей и позволяет получить значение Y. Последний шаг это проверка полученных значений.

Решить пример системы линейных уравнений подстановкой не всегда возможно. Уравнения могут быть сложными и выражение переменной через вторую неизвестную окажется слишком громоздким для дальнейших вычислений. Когда неизвестных в системе больше 3-х решение подстановкой также нецелесообразно.

Решение примера системы линейных неоднородных уравнений:

Решение с помощью алгебраического сложения

При поиске решении систем методом сложения производят почленное сложение и умножение уравнений на различные числа. Конечной целью математических действий является уравнение с одной переменной.

Для применений данного метода необходима практика и наблюдательность. Решить систему линейных уравнений методом сложения при количестве переменных 3 и более непросто. Алгебраическое сложение удобно применять когда в уравнениях присутствуют дроби и десятичные числа.

Алгоритм действий решения:

Умножить обе части уравнения на некое число. В результате арифметического действия один из коэффициентов при переменной должен стать равным 1. Почленно сложить полученное выражение и найти одно из неизвестных. Подставить полученное значение во 2-е уравнение системы для поиска оставшейся переменной.

Способ решения введением новой переменной

Новую переменную можно вводить, если в системе требуется найти решение не более чем для двух уравнений, количество неизвестных тоже должно быть не больше двух.

Способ используется, чтобы упростить одно из уравнений, вводом новой переменной. Новое уравнение решается относительно введенной неиз

poiskvstavropole.ru

Как решить систему с тремя неизвестными

Линейная система с тремя неизвестными имеет несколько способов решения. Найти решение системы можно с помощью правила Кремера через определители, методом Гаусса или используя простой способ подстановки. Метод подстановки является основным для решения систем линейных уравнений небольшого порядка. Он заключается в поочередном выражении из каждого уравнения системы одной неизвестной переменной, подстановки ее в следующее уравнение и упрощение получаемых выражений.

Инструкция

• Запишите исходную
  систему уравнений третьего порядка. Из первого уравнения системы выразите первую неизвестную переменную х. Для этого перенесите члены, содержащие другие переменные за знак равенства. Перенесенным членам поменяйте знак на противоположный.
• Если при множителе с выражаемой переменной присутствует коэффициент отличный от единицы, поделите на его значение все уравнение. Таким образом, вы получите переменную х, выраженную через остальные члены уравнения.
• Подставьте во второе уравнение вместо х то выражение, которое вы получили из первого уравнения. Упростите полученную запись, произведя сложение или вычитание подобных членов. Аналогично предыдущему шагу выразите из второго уравнения следующую неизвестную переменную у. Также перенесите все другие члены за знак равенства и поделите все уравнение на коэффициент при у.
• В последнее третье уравнение подставьте вместо двух неизвестных переменных х и у выраженные значения из первого и второго уравнений системы. Причем в выражении х также замените переменную у. Упростите полученное уравнение. В нем в качестве неизвестной величины останется лишь третья переменная z. Выразите ее из уравнения, как описано выше, и высчитайте ее значение.
• В выражение у из второго уравнения подставьте известное значение переменной z. Подсчитайте значение переменной у. Далее в выражение переменной х подставьте значения переменных у и z. Вычислите х. Запишите полученные значения х, у и z – это и есть решение системы с тремя неизвестными.

completerepair.ru

Как решать линейные уравнения с несколькими переменными Как? Так!

Содержимое:

3 метода:

Линейное уравнение с несколькими переменными – это уравнение, содержащее две или более переменные (как правило, «х» и «у»). Есть несколько способов решить эти уравнения, включая метод исключения и метод подстановки.

Шаги

Метод 1 Линейные уравнения

1. 1 Два (или более) объединенных линейных уравнения называются системой линейных уравнений. Например:
   • 8x — 3y = -3
   • 5x — 2y = -1
   • Это система линейных уравнений. Оба уравнения включаются в процесс нахождения «х» и «у».
2. 2 Решение системы уравнений – это некоторые числа, при подстановке которых вместо переменных каждое из уравнений обращается в верное равенство.
   • Нужно найти «х» и «у». В нашем примере х = -3 и у = -7. Подставьте эти значения в уравнения системы: 8(-3) — 3(-7) = -3; -3 = -3 – равенство соблюдено. 5(-3) — 2(-7) = -1; -1 = -1 — равенство соблюдено.
3. 3 Коэффициент – это множитель (число) при переменной.Вы будете использовать коэффициенты в методе исключения. В нашем примере коэффициентами являются:
   • 8 и 3 в первом уравнении; 5 и 2 во втором уравнении.
4. 4 Метод исключения заключается в избавлении от одной из переменных (например, от «х») и нахождении другой переменной («у»). Найдя «у», вы подставляете эту переменную в любое из уравнений и находите «х».
   • Метод подстановки заключается в обособлении одной из переменных в одном из уравнений и ее подстановки в другое уравнение. Найдя одну из переменных, вы подставляете ее в любое из уравнений и находите вторую переменную.
5. 5 Уравнения с тремя переменными решаются аналогично уравнениям с двумя переменными (теми же методами).

Метод 2 Исключение

1. 1 Рассмотрим пример:
   • 8x — 3y = -3
   • 5x — 2y = -1
2. 2 Для исключения переменной ее коэффициент в обоих уравнениях должен быть равным (при этом знаки у коэффициента могут быть противоположными, например, 5 и -5). Цель – сложить/вычесть два уравнения и при этом избавиться от одной из переменных (например, 5 + (-5) = 0). Например:
   • Умножьте уравнение 8x — 3y = -3 на 2 и получите 16x — 6у = -6.
   • Умножьте уравнение 5x — 2y = -1 на 3 и получите 15x – 6у = -3
   • Таким образом, вы получили -6у в обоих уравнениях.
3. 3 Сложите или вычтите оба уравнения. Если знаки у коэффициента одинаковые – вычитайте, если противоположные – складывайте. В нашем примере необходимо вычесть уравнения (так как -6 = -6).
   • (16x – 6у = -6) — (15x – 6у = -3) = 1x = -3. Поэтому х = -3.
   • Если коэффициент при «х» не равен 1, разделите обе стороны равенства на этот коэффициент, чтобы найти «х».
4. 4 Подставьте найденное значение переменной в любое уравнение системы, чтобы найти вторую переменную (в нашем примере подставьте х = -3 во второе уравнение и найдите «у»).
   • 5(-3) — 2y = -1; -15 — 2y = -1; -2у = 14. Разделите обе стороны равенства на -2 и получите у = -7.
   • Ответ: х = -3 и у = -7.
5. 5 Проверьте ответ, подставив найденные значения переменных в оба уравнения. Если одно из уравнений не обращается в равенство, то проверьте ваши вычисления.
   • 8(-3) — 3(-7) = -3; -3 = -3 — верно.
   • 5(-3) — 2(-7) = -1; -1 = -1 — верно.
   • Таким образом, вы получили правильный ответ.

Метод 3 Подстановка

1. 1 В любом уравнении обособьте любую переменную на одной стороне уравнения (для упрощения вычислений выберите то уравнение, с которым легче работать). Например, если в одном из уравнений коэффициент при переменной равен 1 (например, х — 3у = 7), выберите это уравнение. Рассмотрим пример:
   • х — 2y = 10
   • -3x -4y = 10
   • В этом случае выберите уравнение х — 2у = 10, потому что в нем коэффициент при «х» равен 1.
   • Обособьте «х», перенеся 2у на другую сторону уравнения: х = 10 + 2y.
2. 2 Подставьте найденное «х» в другое уравнение и найдите «у».
   • Подставьте х = 10 + 2y в уравнение -3x -4y = 10: -3 (10 + 2y) -4y = 10.
3. 3 Найдите вторую переменную (в нашем случае «у»).
   • -3(10 + 2y) — 4y = 10; -30 — 6у — 4y = 10.
   • -30 — 10у = 10.
   • Перенесите -30 на другую сторону уравнения и получите: -10y = 40.
   • у = -4.
4. 4 Найдите первую переменную (в нашем случае «х»). Для этого подставьте найденное значение «у» в любое уравнение системы.
   • Подставьте у = -4 в уравнения х — 2y = 10: х — 2(-4) = 10.
   • х + 8 = 10.
   • х = 2.
5. 5 Проверьте ответ, подставив найденные значения переменных в оба уравнения. Если одно из уравнений не обращается в равенство, то проверьте ваши вычисления.
   • 2 — 2(-4) = 10; 10 = 10 – верно.
   • -3(2) — 4(-4) = 10; 10 = 10 – верно.

Советы

• Один неправильный знак может привести к ошибочному ответу. Внимательно следите за знаками!
• Проверяйте ответ, подставив найденные значения переменных в оба уравнения. Если оба уравнения обращаются в равенство, то вы нашли правильный ответ.

Прислал: Макарова Анна . 2017-11-11 19:08:39

kak-otvet.imysite.ru