Скалярное произведение векторов: теория и решения задач
- Определения и смысл скалярного произведения векторов
- Нахождение скалярного произведения через координаты перемножаемых векторов
- Свойства скалярного произведения векторов
- Матричное представление скалярного произведения векторов и произведение n-мерных векторов
- Угол между двумя векторами
- Применения скалярного произведения векторов
- Скалярное произведение векторов Калькулятор онлайн
Будут и задачи для самостоятельного решения, к которым можно посмотреть ответы.
Найти скалярное произведение векторов можно несколькими различными способами. Способ зависит от того, какие условия даны в задаче. Поэтому существуют несколько определений скалярного произведения.
В задаче могут в явном или неявном виде присутствовать длины перемножаемых векторов
и косинус угла между ними. В этом случае действует следующее определение.
Определение 1. Скалярным произведением векторов называется число (скаляр), равное произведению длин (модулей) этих векторов на косинус угла между ними. Формула скалярного произведения векторов согласно определению 1: (1)
Можно встретить и другое название этой операции: внутреннее произведение.
Скалярное произведение вектора на себя называется скалярным квадратом.
Справедливо и другое определение, полностью равносильное определению 1.
Определение 2. Скалярным произведением векторов называется число (скаляр), равное произведению длины одного их этих векторов на проекцию другого вектора на ось, определяемую первым из указанных векторов. Формула согласно определению 2:
(2)
или
(3)
Но в задаче могут в явном или неявном виде присутствовать координаты перемножаемых
векторов.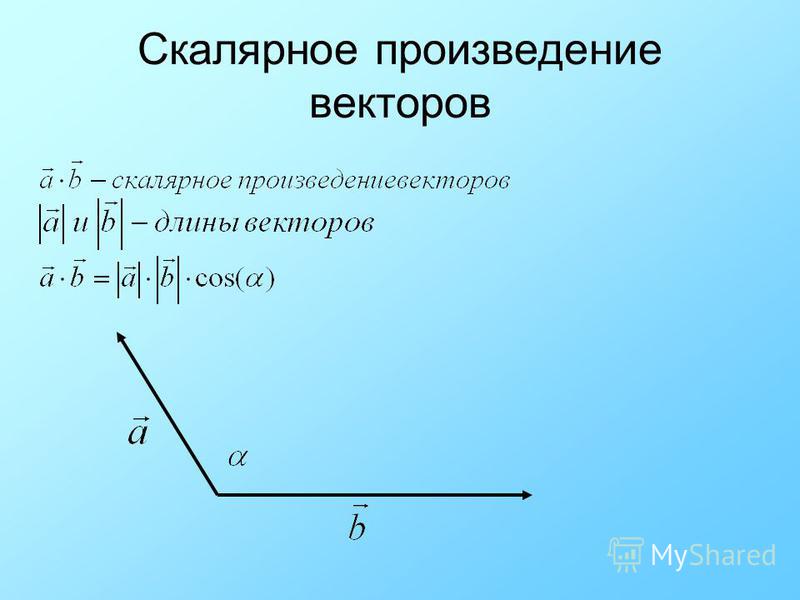
Определение 3. Скалярное произведение векторов — это число, равное сумме попарных произведений их соответствующих координат.
Два перемножаемых вектора могут быть представлены также в виде матриц: первый вектор — в виде матрицы-строки, а второй — в виде матрицы-столбца:
.
В этом случае верно следующее определение.
Определение 4. Скалярное произведение векторов, представленных в виде матрицы-строки и матрицы-столбца представляет собой произведение этих матриц.
Почему скалярное произведение векторов называется именно скалярным и что представляет собой?
Чем оно отличается от результатов других операций над векторами? Что такое скаляр?  Этим оно и отличается от уже рассмотренной суммы векторов, и от векторного произведения векторов, которое ещё предстоит рассмотреть. В отличие от
скалярного произведения, сумма векторов — это вектор, и векторное произведение — тоже вектор.
Этим оно и отличается от уже рассмотренной суммы векторов, и от векторного произведения векторов, которое ещё предстоит рассмотреть. В отличие от
скалярного произведения, сумма векторов — это вектор, и векторное произведение — тоже вектор.
На этом уроке будем решать распространённые задачи не только на непосредственное вычисление скалярного произведения, но и на выяснение ортогональности (перпендикулярности) векторов, вида угла (тупой, острый, прямой) между векторами, вычисление скалярного произведения векторов, которые даны в координатах, вычисление длин диагоналей параллелограма, построенного на вектора. Но все по порядку. Перед каждым видом задач будем обращать внимание на то, что на этот счёт гласит теория. По ходу урока вам пригодится онлайн-калькулятор для проверки решения задач на скалярное произведение векторов.
- Пригодится: тригонометрическая таблица (синусы, косинусы, тангенсы и котангенсы распространенных углов)
Если в задаче и длины векторов, и угол между ними преподнесены «на блюдечке с голубой каёмочкой», то условие задачи и её решение выглядят так:
Пример 1. Даны векторы .
Найти скалярное произведение векторов
, если их длины и угол между ними представлены
следующими значениями:
Даны векторы .
Найти скалярное произведение векторов
, если их длины и угол между ними представлены
следующими значениями:
Решение:
Задачу с применением этой формулы решим после следующего важного теоретического пункта.
То же самое число можно получить, если перемножаемые векторы заданы своими координатами. Повторим определение для этого случая.
Определение 3. Скалярное произведение векторов — это число, равное сумме попарных произведений их соответствующих координат.
На плоскости
Если два вектора и на плоскости определены своими двумя декартовыми прямоугольными координатами
и
,
то скалярное произведение этих векторов равно сумме попарных произведений их соответствующих координат:
.
Пример 2. Найти численную величину проекции вектора на ось, параллельную вектору .
Решение. Находим скалярное произведение векторов, складывая попарные произведения их координат:
.
Теперь нам требуется приравнять полученное скалярное произведение произведению длины вектора на проекцию вектора на ось, параллельную вектору (в соответствии с формулой ).
Находим длину вектора как квадратный корень из суммы квадратов его координат:
.
Составляем уравнение и решаем его:
Ответ. Искомая численная величина равна минус 8.
Для самопроверки можно использовать онлайн калькулятор Скалярное произведение векторов и косинус угла между ними.
В пространстве
Если два вектора и в пространстве определены своими тремя декартовыми прямоугольными координатами
и
,
то скалярное произведение этих векторов также равно сумме попарных произведений их соответствующих координат, только координат уже три:
.
Задача на нахождение скалярного произведения рассмотренным способом — после разбора свойств скалярного произведения. Потому что в задаче потребуется определить, какой угол образуют перемножаемые векторы.
Алгебраические свойства
1. (переместительное свойство: от перемены местами перемножаемых векторов величина их скалярного произведения не меняется).
2. (сочетательное относительно числового множителя свойство: скалярное произведение вектора, умноженного на некоторый множитель, и другого вектора, равно скалярному произведению этих векторов, умноженному на тот же множитель).
3. (распределительное относительно суммы векторов свойство: скалярное произведение суммы двух векторов на третий вектор равно сумме скалярных произведений первого вектора на третий вектор и второго вектора на третий вектор).
4. (скалярный квадрат вектора больше нуля),
если — ненулевой вектор, и ,
если — нулевой вектор.
Геометрические свойства
В определениях изучаемой операции мы уже касались понятия угла между двумя векторами. Пора уточнить это понятие.
На рисунке выше видны два вектора, которые приведены к общему началу. И первое, на что нужно
обратить внимание: между этими векторами существуют два угла — φ1
и φ2. Какой из этих углов фигурирует в определениях и свойствах
скалярного произведения векторов? Сумма рассмотренных углов равна 2π и поэтому
косинусы этих углов равны. В определение скалярного произведения входит только косинус угла, а не значение его выражения.
Но в свойствах рассматривается только один угол. И это тот из двух углов, который не превосходит π,
то есть 180 градусов. На рисунке этот угол обозначен как
1. Два вектора называют ортогональными и угол между этими векторами — прямой (90 градусов или π/2), если скалярное произведение этих векторов равно нулю:
.
Ортогональностью в векторной алгебре называется перпендикулярность двух векторов.
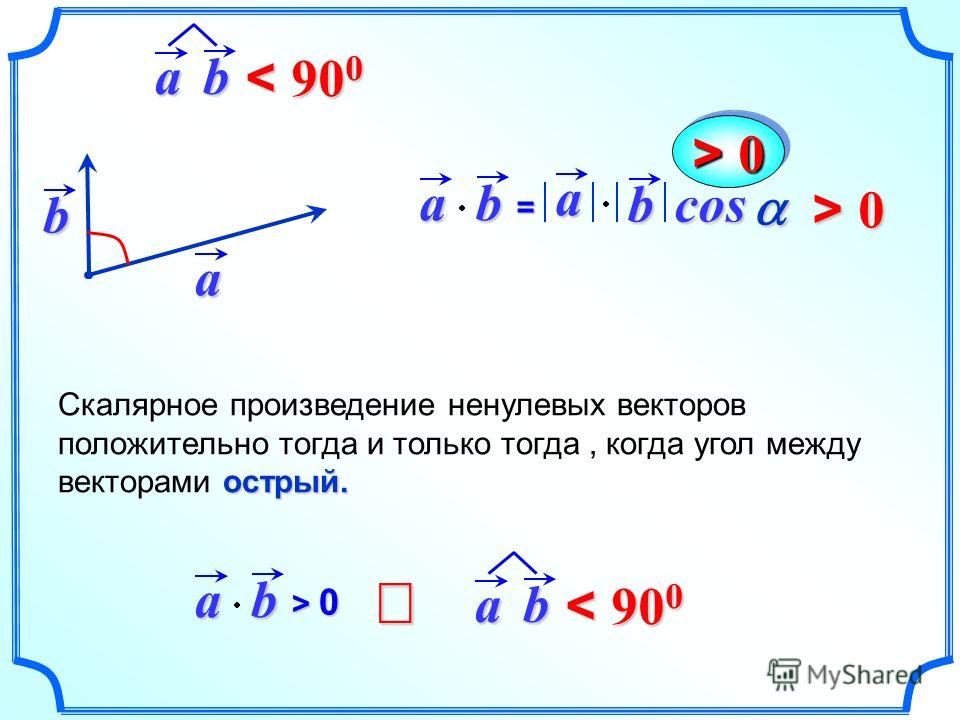
2. Два ненулевых вектора составляют острый угол (от 0 до 90 градусов, или, что тоже самое — меньше π/2) тогда и только тогда, когда их скалярное произведение положительно.
3. Два ненулевых вектора составляют тупой угол (от 90 до 180 градусов, или, что то же самое — больше π
/2) тогда и только тогда, когда их скалярное произведение отрицательно.- Пригодится: тригонометрическая таблица (синусы, косинусы, тангенсы и котангенсы распространенных углов)
Пример 3. В координатах даны векторы:
.
Вычислить скалярные произведения всех пар данных векторов. Какой угол (острый, прямой, тупой) образуют эти пары векторов?
Решение. Вычислять будем путём сложения произведений соответствующих координат.
Вычислять будем путём сложения произведений соответствующих координат.
.
Получили отрицательное число, поэтому векторы образуют тупой угол.
.
Получили положительное число, поэтому векторы образуют острый угол.
.
Получили положительное число, поэтому векторы образуют острый угол.
.
Получили нуль, поэтому векторы образуют прямой угол.
.
Получили положительное число, поэтому векторы образуют острый угол.
.
Получили положительное число, поэтому векторы образуют острый угол.
Для самопроверки можно использовать онлайн калькулятор Скалярное произведение векторов и косинус угла между ними.
Пример 4. Даны длины двух векторов и угол между ними:
.
Определить, при каком значении числа векторы и ортогональны (перпендикулярны).
Решение. Перемножим векторы по правилу умножения многочленов:
.
Теперь вычислим каждое слагаемое:
.
Составим уравнение (равенство произведения нулю), приведём подобные члены и решим уравнение:
Ответ: мы получили значение λ = 1,8, при котором векторы ортогональны.
- Пригодится: тригонометрическая таблица (синусы, косинусы, тангенсы и котангенсы распространенных углов)
Пример 5. Доказать, что вектор ортогонален (перпендикулярен) вектору
Решение. Чтобы проверить ортогональность, перемножим векторы и как многочлены, подставляя вместо его выражение, данное в условии задачи:
.
Для этого нужно каждый член (слагаемое) первого многочлена умножить на каждый член второго и полученные произведения сложить:
.
В полученном результате дробь за счёт сокращается. Получается следующий результат:
.
Вывод: в результате умножения получили нуль, следовательно, ортогональность (перпендикулярность) векторов доказана.
Решить задачу самостоятельно, а затем посмотреть решение
Пример 6. Даны длины векторов и , a угол между этими векторами равен π/4. Определить, при каком значении μ векторы и взаимно перпендикулярны.
Посмотреть правильное решение и ответ.
Для самопроверки можно использовать онлайн калькулятор Скалярное произведение векторов и косинус угла между ними.
Иногда выигрышным для наглядности является представление двух перемножаемых векторов
в виде матриц. Тогда первый вектор представлен в виде матрицы-строки, а второй — в виде матрицы-столбца:
Тогда первый вектор представлен в виде матрицы-строки, а второй — в виде матрицы-столбца:
Тогда скалярное произведение векторов будет произведением этих матриц:
Результат тот же, что и полученный способом, который мы уже рассмотрели. Получили одно единственное число, и произведение матрицы-строки на матрицу-столбец также является одним единственным числом.
В матричной форме удобно представлять произведение абстрактных n-мерных векторов. Так, произведение двух четырёхмерных векторов будет произведением матрицы-строки с четырьмя элементами на матрицу-столбец также с четырьмя элементами, произведение двух пятимерных векторов — произведением матрицы-строки с пятью элементами на матрицу-столбец также с пятью элементами и так далее.
Пример 7. Найти скалярные произведения пар векторов
и
,
используя матричное представление.
Решение. Первая пара векторов. Представляем первый вектор в виде матрицы-строки, а второй — в виде матрицы-столбца. Находим скалярное произведение этих векторов как произведение матрицы-строки на матрицу-столбец:
Аналогично представляем вторую пару и находим:
Как видим, результаты получились те же, что и у тех же пар из примера 2.
Вывод формулы косинуса угла между двумя векторами очень красив и краток.
Чтобы выразить скалярное произведение векторов
(1)
в координатной форме, предварительно найдём скалярные произведение ортов. Скалярное произведение вектора на само себя по определению:
То, что записано в формуле выше, означает: скалярное произведение вектора на самого себя равно квадрату его длины. Косинус нуля равен единице, поэтому квадрат каждого орта будет равен единице:
Так как векторы
попарно перпендикулярны, то попарные произведения ортов будут равны нулю:
Теперь выполним умножение векторных многочленов:
Подставляем в правую часть равенства значения соответствующих скалярных произведений ортов:
Получаем формулу косинуса угла между двумя векторами:
- Пригодится: тригонометрическая таблица (синусы, косинусы, тангенсы и котангенсы распространенных углов)
Пример 8. Даны три точки A(1;1;1), B(2;2;1), C(2;1;2).
Даны три точки A(1;1;1), B(2;2;1), C(2;1;2).
Найти угол .
Решение. Находим координаты векторов:
,
.
По формуле косинуса угла получаем:
Следовательно, .
Для самопроверки можно использовать онлайн калькулятор Скалярное произведение векторов и косинус угла между ними.
Пример 9. Даны два вектора
и
Найти сумму, разность, длину, скалярное произведение и угол между ними.
Решение.
1.Сумма
2.Разность
3.Длина
4.Скалярное произведение
5.Угол между и :
Решить задачи самостоятельно, а затем посмотреть решения
Пример 10. Определить, какой угол (острый, тупой или прямой) образуют
и
.
Определить, какой угол (острый, тупой или прямой) образуют
и
.
Посмотреть правильное решение и ответ.
Для самопроверки можно использовать онлайн калькулятор Скалярное произведение векторов и косинус угла между ними.
Пример 11. Определить угол треугольника ABC при вершине A, если , , .
Посмотреть правильное решение и ответ.
Пример 12. На векторах и построен параллелограмм. Вычислить длины диагоналей параллелограмма, если , , угол .
Посмотреть правильное решение и ответ.
- Пригодится: тригонометрическая таблица (синусы, косинусы, тангенсы и котангенсы распространенных углов)
Пример 13. Среди векторов
Найти а) коллинеарные; б) ортогональные.
Решение.
а) проверим пропорциональность соответствующих координат векторов — условие коллинеарности (повторение материала предыдущей части темы «Векторы»).
Для векторов и :
Равенство не выполняется.
Для векторов и :
Равенство выполняется.
Для векторов и :
Равенство не выполняется.
Наше исследование показало, что коллинеарны векторы и .
б) найдём скалярные произведения векторов.
Наше исследование показало, что ортогональны векторы и и и .
Расчёт работы постоянной силы
Посмотрите ещё раз на рисунок в начале статьи. Пусть материальная
точка перемещается прямолинейно из начала координат в конец вектора B под
действием постоянной силы F = A, образующей угол
с перемещением S = A. Из физики известно, что работа силы F при перемещении S равна
.
Таким образом, работа постоянной силы при прямолинейном перемещении её точки
приложения равна скалярному произведению вектора силы F = B на
вектор перемещения S = A.
Из физики известно, что работа силы F при перемещении S равна
.
Таким образом, работа постоянной силы при прямолинейном перемещении её точки
приложения равна скалярному произведению вектора силы F = B на
вектор перемещения S = A.
Скалярное произведение векторов позволяет находить угол между двумя векторами. Поэтому оно часто встречается в последующих разделах математики, особенно, аналитической геометрии. Стоит ли говорить о том, что нахождение скалярного произведения векторов — фундаментальный навык для любого будущего инженера, проектирующего всё что угодно, от гладильных досок и лестниц-стремянок до зданий, или для программиста, собирающегося разрабатывать игры?
Экономический смысл скалярного произведения векторов
В экономических задачах можно рассматривать скалярное произведение вектора цен p
на вектор объёма проданных товаров x . Скалярное произведение px в этом случае даёт суммарную стоимость проданных товаров x при ценах p . Например, если объём всех товаров, проданных предприятием, выражается вектором x = (400; 750; 200; 300), элементы которого означают соответственно количество товаров различных групп, а цены в одних и тех же денежных единицах заданы в соответствующем порядке вектором p = (3; 2,1; 1,2; 0,5), то скалярное произведение
Например, если объём всех товаров, проданных предприятием, выражается вектором x = (400; 750; 200; 300), элементы которого означают соответственно количество товаров различных групп, а цены в одних и тех же денежных единицах заданы в соответствующем порядке вектором p = (3; 2,1; 1,2; 0,5), то скалярное произведение
выражает суммарную стоимость всех товаров x.
| Назад | Листать | Вперёд>>> |
Нет времени вникать в решение? Можно заказать работу!
К началу страницы
Пройти тест по теме Векторы
Поделиться с друзьями
Начало темы «Векторы»
Векторы: определения и действия над векторами
Сложение векторов: длина суммы векторов и теорема косинусов
Продолжение темы «Векторы»
Линейная зависимость векторов
Базис системы векторов. Аффинные координаты
Векторное и смешанное произведение векторов
Скалярное произведение векторов
Навигация по странице:
- Геометрическая интерпретация скалярного произведения векторов
- Алгебраическая интерпретация скалярного произведения векторов
- Формулы скалярного произведения векторов заданных координатами
- для плоских задач
- для пространственных задач
- для n -мерных векторов
- Свойства скалярного произведения векторов
- Примеры задач на скалярное произведение векторов
- плоские задачи
- пространственные задачи
- задачи в n -мерном пространстве
Онлайн калькулятор. Скалярное произведение векторов.
Скалярное произведение векторов.
Онлайн упражнения на тему скалярное произведение двух векторов на плоскости.
Онлайн упражнения на тему скалярное произведение двух векторов в пространстве.
Геометрическая интерпретация. Скалярным произведением двух векторов a и b будет скалярная величина, равная произведению модулей этих векторов умноженного на косинус угла между ними:
a · b = |a| · |b| cos α
Алгебраическая интерпретация. Скалярным произведением двух векторов a и b будет скалярная величина, равная сумме попарного произведения координат векторов a и b.
Формулы скалярного произведения векторов заданных координатами
Формула скалярного произведения векторов для плоских задач
В случае плоской задачи скалярное произведение векторов a = {ax ; ay} и b = {bx ; by} можно найти воспользовавшись следующей формулой:
a · b = ax · bx + ay · by
Формула скалярного произведения векторов для пространственных задач
В случае пространственной задачи скалярное произведение векторов a = {ax ; ay ; az} и b = {bx ; by ; bz} можно найти воспользовавшись следующей формулой:
a · b = ax · bx + ay · by + az · bz
Формула скалярного произведения n -мерных векторов
В случае n-мерного пространства скалярное произведение векторов a = {a1 ; a2 ; . .. ; an} и b = {b1 ; b2 ; … ; bn} можно найти воспользовавшись следующей формулой:
.. ; an} и b = {b1 ; b2 ; … ; bn} можно найти воспользовавшись следующей формулой:
a · b = a1 · b1 + a2 · b2 + … + an · bn
Свойства скалярного произведения векторов
Скалярное произведение вектора самого на себя всегда больше или равно нуля:
a · a ≥ 0
Скалярное произведение вектора самого на себя равно нулю тогда и только тогда, когда вектор равен нулевому вектору:
a · a = 0 <=> a = 0
Скалярное произведение вектора самого на себя равно квадрату его модуля:
a · a = |a|2
Операция скалярного умножения коммуникативна:
a · b = b · a
Если скалярное произведение двух не нулевых векторов равно нулю, то эти вектора ортогональны:
a ≠ 0, b ≠ 0, a · b = 0 <=> a ┴ b
(αa) · b = α(a · b)
Операция скалярного умножения дистрибутивна:
(a + b) · c = a · c + b · c
Примеры задач на вычисление скалярного произведения векторов
Примеры вычисления скалярного произведения векторов для плоских задач
Пример 1. Найти скалярное произведение векторов a = {1; 2} и b = {4; 8}.
Найти скалярное произведение векторов a = {1; 2} и b = {4; 8}.
Решение: a · b = 1 · 4 + 2 · 8 = 4 + 16 = 20.
Пример 2. Найти скалярное произведение векторов a и b, если их длины |a| = 3, |b| = 6, а угол между векторами равен 60˚.
Решение: a · b = |a| · |b| cos α = 3 · 6 · cos 60˚ = 9.
Пример 3. Найти скалярное произведение векторов p = a + 3b и q = 5a — 3 b, если их длины |a| = 3, |b| = 2, а угол между векторами a и b равен 60˚.
Решение:
p · q = (a + 3b) · (5a — 3b) = 5 a · a — 3 a · b + 15 b · a — 9 b · b =
= 5 |a|2 + 12 a · b — 9 |b|2 = 5 · 32 + 12 · 3 · 2 · cos 60˚ — 9 · 22 = 45 +36 -36 = 45.
Пример 4. Найти скалярное произведение векторов (a + 2i)·(b — 2j),если a = {1; 2} и b = {4; -8}.
Решение: Запишем вектора a и b через ортонормированные базисные вектора i и j:
a = i + 2j
b = 4i — 8j
Тогда используя свойства ортов (i2 = 1, j2 = 1, i·j = 0)
(a + 2i)·(b — 2j) = (i + 2j + 2i)·(4i — 8j — 2j) = (3i + 2j)·(4i — 10j) = 12i2 — 30i·j + 12j·i — 20j2 = 12 — 0 + 0 — 20 = -8
Пример вычисления скалярного произведения векторов для пространственных задач
Пример 5. Найти скалярное произведение векторов a = {1; 2; -5} и b = {4; 8; 1}.
Найти скалярное произведение векторов a = {1; 2; -5} и b = {4; 8; 1}.
Решение: a · b = 1 · 4 + 2 · 8 + (-5) · 1 = 4 + 16 — 5 = 15.
Пример вычисления скалярного произведения для n -мерных векторов
Пример 6. Найти скалярное произведение векторов a = {1; 2; -5; 2} и b = {4; 8; 1; -2}.
Решение: a · b = 1 · 4 + 2 · 8 + (-5) · 1 + 2 · (-2) = 4 + 16 — 5 -4 = 11.
Вектора Вектор: определение и основные понятия Определение координат вектора заданного координатами его начальной и конечной точки Модуль вектора. Длина вектора Направляющие косинусы вектора Равенство векторов Ортогональность векторов Коллинеарность векторов Компланарность векторов Угол между векторами Проекция вектора Сложение и вычитание векторов Умножение вектора на число Скалярное произведение векторов Векторное произведение векторов Смешанное произведение векторов Линейно зависимые и линейно независимые вектора Разложение вектора по базису
Онлайн калькуляторы с векторами
Онлайн упражнения с векторами на плоскости
Онлайн упражнения с векторами в пространстве
Геометрия данных 3.
 Скалярное произведение пар / Хабр
Скалярное произведение пар / ХабрИнвариант дистанции (квадрат расстояния) между элементами можно обобщить, если умножать разность элементов не на саму себя, а на другую разность элементов. Полученное значение будет отражать скалярное произведение упорядоченных пар.
Оглавление
1. Симплексы и графы
2. Определение ди- и би-координат
3. Скалярное произведение пар
4. Пространство графа
5. Преобразование базиса
6. Граф-звезда
Упорядоченная пара
Координаты вектора могут быть получены на как разность координат элементов, но обратное неверное — по координатам вектора невозможно восстановить координаты образовавших его элементов. Координаты двух элементов несут в себе больше информации, чем координаты вектора. Поэтому из элементов можно образовать пару — улучшенный аналог вектора. Такой набор из двух элементов называют упорядоченной парой.
Каждой упорядоченной паре можно сопоставить вектор — разность элементов, образующих пару. Для двух векторов можно определить скалярное произведение, которое можно также рассматривать как характеристику четырех элементов пространства.
Скалярное произведение
Для уменьшения громоздкости в данной части будем обозначать элементы строчными символами. Пара — это совокупность двух элементов: . Вектор, соответствующий паре, — это разность элементов пары:
Норма элемента — это его скалярное произведение с самим собой:
Это же определение можно использовать для вектора пары, которая, как известно, отражает квадрат расстояния между элементами пары:
Если заданы две разных пары и , то можно определить скалярное произведение между соответствующими векторами:
Индексы задают одну пару, а индексы — другую.
Выражение (3.4) определяет скаляр, зависящий от взаимного положения 4-х элементов. Важно, что данный скаляр может быть выражен через расстояния между элементами .
Как известно, расстояние между элементами связано со скалярным произведением между ними:
.
Раскрывая произведение (3.4) с учетом (3.5), получаем:
Это общая формула скалярного произведения пар. Порядок индексов важен — задает пары и направление соответствующих им векторов.
Выражения, подобные (3.6), часто возникают в разных местах математики. Связано это с общностью вывода данной формулы. Отметим, что мы использовали только самые общие свойства алгебраического выражения. Поэтому в качестве элементов могут использоваться любые объекты, для которых определена операция произведения. Тождество будет справедливо и для них, в общей форме оно выглядит так:
Пары с общей вершиной — смежные пары
Если пары имеют общую вершину , то формула (3.6) упрощается:
Формула (3.7) — это теорема косинусов для треугольника. Здесь пары, между которыми определена взаимная норма, имеют общий элемент k — смежные пары.
На 3-х вершинах можно определить три скалярных произведения. Их сумма выражается через сумму дистанций между вершинами:
Квадрат скалярного произведения на 3-х вершинах связан с площадью образуемого ими треугольника (формула Герона):
Независимые пары — четыре разных вершины
В общем случае вершины пар могут не лежать в одной плоскости, поэтому данному определению скалярного произведения не всегда можно сопоставить косинус угла между направлениями.
Перечислим свойства скалярного произведения (3.6).
1) Не зависит от перестановки пар:
2) Антисимметрично относительно перестановки элементов в паре или :
3) Для 4-х элементов существует только два независимых скалярных произведения пар ввиду тождества:
Математики увидят в формуле (3.9.3) первое тождество Бьянки. Из чего можно сделать вывод, что структуры тензора кривизны (Римана) и скалярного произведения пар — подобны.
4) Норма независимых пар может быть выражена через разность норм смежных пар:
Этим тождеством воспользуемся в следующей статье.
5) Дистанция между элементами и может быть выражена через значения скалярных произведений смежных и независимых пар:
Пары на элементах базиса
В качестве элементов, образующих пару, могут быть выбраны вершины базиса. Тогда скалярное произведение пар становится тензором — набором скалярных произведений между всеми возможными парами элементов данного базиса. Чтобы отличать тензоры от скаляров будем использовать для первых заглавные буквы. То есть вместо скаляра для элементов базиса получаем тензор .
Скалярное произведение и кофакторы лапласиана
Скалярное произведение пар, образованных элементами базиса, может быть выражено через свойства лапласиана базиса.
Если заданы две пары вершин и , то значение их скалярного произведения можно получить делением кофактора 2-го порядка на скалярный потенциал лапласиана :
Кофактором называется определитель минора квадратной матрицы (с учетом знака). Скалярный потенциал — это кофактор 1-го порядка от лапласиана (см. (1.12) из первой статьи).
Скалярный потенциал — это кофактор 1-го порядка от лапласиана (см. (1.12) из первой статьи).
Таким образом необходимо из матрицы лапласиана удалить столбцы, соответствующие одному вектору (в формуле это -й столбцы), и строки, соответствующие другому (), после чего разделить определитель получившегося минора на скалярный потенциал . Если удаляемые столбцы и строки лапласиана — одни и те же, то получим значение дистанции между узлами.
Скалярное произведение пар на графе
Между любыми парами вершин графа можно определить их взаимную норму — скалярное произведение. Поскольку граф обычно задан лапласианом, то для расчета можно использовать формулу (3.10.1).
Пусть, например, в качестве образующих вершин двух пар выбраны — и . Тогда скалярное произведение между данными парами дается формулой (3.6):
Для графа, представляющего собой электрическую цепь, значение скалярного произведения отражает понятие обобщенного сопротивления в электрической цепи. Для измерения такого («кажущегося») сопротивления источник тока (напряжение) прикладывается к одним узлам (A и B), а разность потенциалов измеряется между другими (M и N). Взаимная норма (скалярное произведение) пар равна нулю, если внешняя разность потенциалов не приводит к разности потенциалов на измеряемой паре.
Для измерения такого («кажущегося») сопротивления источник тока (напряжение) прикладывается к одним узлам (A и B), а разность потенциалов измеряется между другими (M и N). Взаимная норма (скалярное произведение) пар равна нулю, если внешняя разность потенциалов не приводит к разности потенциалов на измеряемой паре.
Граф не обязательно должен быть дискретным,- грунт является примером сплошного (непрерывного) графа, на котором можно проводить измерения скалярного произведения между выбранными элементами.
Схема установки для исследования методом сопротивления: A и B – питающие заземления; M и N – измерительные заземления; 1 – измерительный прибор (из книги «Электроразведка», Якубовский Ю. B., M., 1980).
На рисунке показана схема измерения скалярного произведения пар и на грунте.
В следующей статье разберем подробнее, почему отношение заданной и измеряемой разностей потенциалов узлов оказалось связанным со скалярным произведением пар.
Обращение минора лапласиана
Подматрицу значений взаимных норм (скалярных произведений) пар можно получить обращением минора лапласиана. Обозначим лапласиан, из которого удалены -я строка и -й столбец, как . Тогда имеет место тождество:
Отметим, что в матрице отсутствуют -я строка и -й столбец.
Если известна матрица скалярных произведений пар , то можно восстановить дистанционную матрицу на основании преобразования дистанции. Вначале расширяем подматрицу отсутствующей строкой и столбцом с нулевыми значениями. К полученной матрице применяем преобразование дистанции:
которое в нашем случае принимает вид тождества (3.9.5):
Совокупность формул (3.10.2) и (3.10.3) — один из способов получить дистанционную матрицу по заданному лапласиану. Удаляем из лапласиана какой-либо из узлов (пусть будет ) и обращаем. Получаем матрицу скалярных произведений пар (ее другое название — фундаментальная матрица, см. следующую часть). Значение индекса фиксировано — базовая вершина. В матрице первая вершина пар находится в базовом узле , а вторая пробегает по остальным вершинам базиса.
следующую часть). Значение индекса фиксировано — базовая вершина. В матрице первая вершина пар находится в базовом узле , а вторая пробегает по остальным вершинам базиса.
Далее применяем к матрице преобразование дистанции (3.10.3).
Квадрат скалярного произведения, матрица Якоби
Если в графе изменить значение проводимости ребра (элемент лапласиана), то очевидно, что изменятся и все дистанции между вершинами (нормы векторов) . При увеличении проводимости дистанции должны сократиться (уменьшиться). Подарок богов в том, что можно оценить изменение дистанций не только качественно, но и количественно. Обозначим производную матрицы дистанций по лапласиану как
Тензор — это матрица Якоби, то есть выражение изменений значений дистанционной матрицы при изменении значений лапласиана . Оказывается, что данный тензор выражается через квадрат скалярного произведения пар:
То есть изменение величины связи узлов приводит к изменению дистанции между узлами пропорционально величине скалярного произведения пар и .
Тензор квадросвязности вершин
Тензор квадратов скалярного произведения обратим. Представим выражение (3.11) в следующем эквивалентном виде:
Данную формулу можно трактовать как отклик на воздействие . Тензор играет роль передаточной функции (реакции на воздействие).
Возможна и обратная ситуация, при которой воздействие и отклик меняются местами. Прямая и обратная передаточные функции связаны соотношением:
Снова удача — тензор можно выразить через лапласиан:
Значения тензора назовем квадросвязностью.
Свойства тензора квадросвязности
Значения тензора определены через значения лапласиана для 4-х вершин. Будем считать данные вершины вершинами графа. Допустим, что все 4 вершины различны:
Здесь векторами обозначены пары вершин, между которыми считается квадросвязность. Пары имеют отличную от нуля квадросвязность только тогда, когда их вершины попарно связаны (необходимые связи показаны на рисунке одинаковым цветом).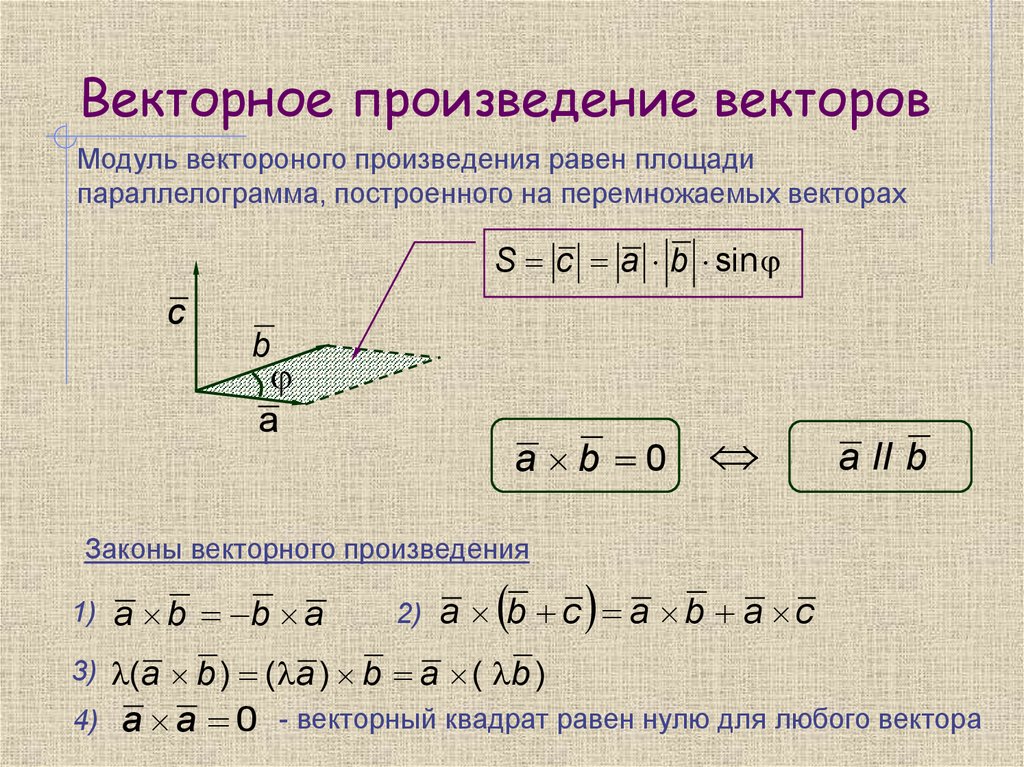 Если все связи в графе положительны, то квадросвязность между разными вершинами также всегда больше или равна нулю.
Если все связи в графе положительны, то квадросвязность между разными вершинами также всегда больше или равна нулю.
Если пары имеют общую вершину, то смысл квадросвязности меняется. Это связано с тем, что диагональные элементы лапласиана не равны нулю (как в дистанционной матрице), а отражают общую связность (проводимость) узла.
Пары вершин могут совпадать — диагональные элементы тензора квадросвязности.
Здесь характеризует связь двух узлов i и j. Считается как сумма произведения их суммарной проводимости (степени вершины) и квадрата связи между узлами .
Несмотря на то, что формально для тензора могут вычисляться элементы вида (одна из пар вырождена), данные (вырожденные) элементы являются линейно-зависимыми от остальных. Могут быть вычислены через сумму тензора по одному из индексов пары:
___
Подведем итоги. Рассмотрено полезное во всех отношениях понятие скалярного произведения пар элементов. В следующей статье поработаем с подпространством графа — что это такое, и каковы его свойства.
Векторы для чайников. Часть 2. Скалярное и векторное произведение. — Блог
Векторы для чайников. Часть 2. Скалярное и векторное произведение.
18 июня 2021 0 Marina Pashnina
Логическое продолжение статьи «Векторы для чайников. Часть 1». В первой части рассказывается о том, что такое вектор и о простейших операциях с векторами (сложение и разность векторов, умножении вектора на число).
На этом котики кончаются и начинается злая математика.
Скалярное произведение векторов
Сложение векторов, умножение вектора на число…. Было бы наивным думать, что математикам было это достаточно и они не придумали что-то еще.
Скалярное произведение векторов ā и b̅ — это ЧИСЛО, которое равно произведению длин векторов ā и b̅ и косинуса угла между ними:
С математической точки зрения скалярное произведение безразмерно — это просто число и все. Скалярное произведение векторов часто применяется в физике и размерность скалярного произведения будет уже зависеть от конкретной задачи.
Типовая задача при которой используется скалярное произведение — это работа постоянной силы, где в качестве векторов принимаются постоянная сила F, применяемая к какому-то объекту и вектор перемещения s. В этом случае скалярное произведение векторов — это конкретное число — работа силы. Так как работа измеряется в Джоулях и каждый вектор имеет свой физический смысл, то и результат скалярного произведения в данном случае будет измеряться в Джоулях.
Так иногда бывает, что для полного счастья математикам нужно что-то еще, и если скалярное произведение еще может быть знакомо со школы, то векторное произведение чаще всего изучают в ВУЗе на курсах вышмата.
Обрадую всех вас — если все, что происходило до этого работало и в двухмерном и в трехмерном пространстве, то векторное произведение векторов подразумевает работу ТОЛЬКО с трехмерным пространством. (Стало проще, да ведь?)
В данном произведении участвуют также 2 вектора. Отличие от скалярного произведения тех же двух векторов будет в том, что в результате векторного произведения получается ВЕКТОР, а не число.
Формальное определение:
Векторным произведением ā x b̅ неколлинеарных векторов ā и b̅, взятых в определенном порядке, называется ВЕКТОР ā x b̅ , длина которого численно равна площади параллелограмма, построенного на данных векторах; вектор ā x b̅ ортогонален векторам ā и b̅, и направлен так, что базис (ā; b̅;ā x b̅) имеет правую ориентацию.
Это определение сложное и требует некоторых комментариев:
1.
Векторы ā и b̅ по определению должны быть неколлинеарны. Два вектора называются коллинеарными, если они лежат на одной прямой или на параллельных прямых. Таким образом такие векторы могут называться параллельными, но так называть вектора просто не принято — их называют коллинеарными. Касаемо ситуации с векторным произведением — векторы должны быть, наоборот, непараллельными.
2.
Важен порядок векторов. От этого зависит направление результата.
3.
Длина результирующего вектора равна площади заштрихованного параллелограмма.
4.
Результирующий вектор ортогонален векторам ā и b̅, т.е. ā ┴ [ā x b̅] и b ┴ [ā x b̅]
5.
Результирующий вектор направлен так, что базис (ā; b̅;ā x b̅) имеет правую ориентацию.
Мысленно совместите указательный палец с вектором ā и средний палец с вектором b̅. Безымянный палец и мизинец прижмите к ладони. В результате большой палец – результирующий вектор [ā x b̅] будет смотреть вверх. Это правоориентированный базис.
В результате большой палец – результирующий вектор [ā x b̅] будет смотреть вверх. Это правоориентированный базис.
Указательный палец левой руки с тем же вектором ā, а средний – с вектором b̅. При этом большой палец будет неизбежно смотреть вниз – по направлению вектора . Это левый или левоориентированный базис.
Эти базисы не являются чем-то абстрактным. Примером может служить изображение и его отражение в зеркале. Самое обычное зеркало меняет ориентацию пространства, а изображение и зеркальное отражение этого отображения невозможно просто наложить друг на друга (попробуйте совместить «базисы» левой и правой руки, после чего станет понятно, что указательные и средние пальцы не совмещаются).
Что же будет, если вектора ā и b̅ будут коллинеарны (т.е. параллельны, говоря на простом языке) — все просто, параллелаграм, который образуется этими векторами “складывается” в плоскую прямую, а площадь такой прямой равна нулю, из-за чего и результирующий вектор равен нулевому.
Скалярное произведение векторов. Он-лайн калькуляторы скалярного произведения и угла между векторами по координатам.
Раздел недели: Плоские фигуры. Свойства, стороны, углы, признаки, периметры, равенства, подобия, хорды, секторы, площади и т.д. | ||||||||||||||||||||||||
| Поиск на сайте DPVA Поставщики оборудования Полезные ссылки О проекте Обратная связь Ответы на вопросы. Оглавление Таблицы DPVA.ru — Инженерный Справочник | Адрес этой страницы (вложенность) в справочнике dpva.ru: главная страница / / Техническая информация/ / Математический справочник / / Линейная алгебра. Вектора, матрицы, определители, миноры, детерминанты. Поделиться:
| |||||||||||||||||||||||
Если Вы не обнаружили себя в списке поставщиков, заметили ошибку, или у Вас есть дополнительные численные данные для коллег по теме, сообщите , пожалуйста. | ||||||||||||||||||||||||
Коды баннеров проекта DPVA. Сформулируем определение произведения для двух векторов: Скалярное произведение двух векторов a→ на b→ называют произведение длины вектора a→ на проекцию b→ на направление a→ или произведение длины b→ на проекцию a→ соответственно. Скалярное произведение в координатахВычисление скалярного произведения можно производить через координаты векторов в заданной плоскости или в пространстве. Скаларное произведение двух векторов на плоскости, в трехмерном простарнстве называют сумму координат заданных векторов a→ и b→. При вычислении на плоскости скаларного произведения заданных векторов a→=(ax,ay), b→=(bx,by) в декартовой системе используют: a→,b→=ax·bx+ay·by, для трехмерного пространства применимо выражение: a→,b→=ax·bx+ay·by+az·bz. Фактически это является третьим определением скалярного произведения. Докажем это. – соответственно для векторов трехмерного пространства. Скалярное произведение векторов с координатами говорит о том, что скалярный квадрат вектора равен сумме квадратов его координат в пространстве и на плоскости соответственно. a→=(ax,ay,az), b→=(bx,by,bz) и (a→,a→)=ax2+ay2. Скалярное произведение и его свойстваСуществуют свойства скалярного произведения, которые применимы для a→,b→ и c→:
Свойства объяснимы благодаря определению скалярного произведения на плоскости и свойствам при сложении и умножении действительных чисел. Доказать свойство коммутативности (a→,b→)=(b→,a→). Из определения имеем, что (a→,b→)=ay·by+ay·by и (b→,a→)=bx·ax+by·ay. Ответ:(a→,b→)=212. Пример 3Заданны векторы a→=(1,-1,2-3), b→=(0,2,2+3). Чему равно скалярной произведение. Решение В данном примере рассматривается формула вычисления по координатам, так как они заданы в условии задачи: (a→,b→)=ax·bx+ay·by+az·bz==1·0+(-1)·2+(2+3)·(2+3)==0-2+(2-9)=-9 Ответ: (a→,b→)=-9 Пример 4Найти скалярное произведение AB→ и AC→. На координатной плоскости заданы точки A(1,-3), B(5,4), C(1,1). Решение Для начала вычисляются координаты векторов, так как по условию даны координаты точек: AB→=(5-1,4-(-3))=(4,7)AC→=(1-1,1-(-3))=(0,4) Подставив в формулу с использованием координат, получим: (AB→,AC→)=4·0+7·4=0+28=28. Ответ: (AB→,AC→)=28. Пример 5Заданы векторы a→=7·m→+3·n→ и b→=5·m→+8·n→, найти их произведение.m→ равен 3 и n→ равен 2 единицам, они перпендикулярные. Решение (a→,b→)=(7·m→+3·n→, 5·m→+8·n→). Применив свойство дистрибутивности, получим: (7·m→+3·n→, 5·m→+8·n→)==(7·m→, 5·m→)+(7·m→, 8·n→)+(3·n→, 5·m→)+(3·n→, 8·n→) Выносим коэффициент за знак произведения и получим: (7·m→, 5·m→)+(7·m→, 8·n→)+(3·n→, 5·m→)+(3·n→, 8·n→)==7·5·(m→,m→)+7·8·(m→,n→)+3·5·(n→,m→)+3·8·(n→,n→)==35·(m→,m→)+56·(m→,n→)+15·(n→,m→)+24·(n→,n→) По свойству коммутативности преобразуем: 35·(m→,m→)+56·(m→,n→)+15·(n→,m→)+24·(n→,n→)==35·(m→,m→)+56·(m→,n→)+15·(m→,n→)+24·(n→,n→)==35·(m→,m→)+71·(m→,n→)+24·(n→,n→) В итоге получим: (a→,b→)=35·(m→,m→)+71·(m→,n→)+24·(n→,n→). Ответ: (a→,b→)=411 Если имеется числовая проекция. Пример 6Найти скалярное произведение a→и b→. Вектор a→ имеет координаты a→=(9,3,-3), проекция b→ с координатами (-3,-1,1). Решение По условию векторы a→ и проекция b→ противоположно направленные, потому что a→=-13·npa→b→→, значит проекция b→ соответствует длине npa→b→→, при чем со знаком «-»: npa→b→→=-npa→b→→=-(-3)2+(-1)2+12=-11, Подставив в формулу, получим выражение: (a→,b→)=a→·npa→b→→=92+32+(-3)2·(-11)=-33. Ответ: (a→,b→)=-33. Задачи при известном скалярном произведении, где необходимо отыскать длину вектора или числовую проекцию. Пример 7Какое значение должна принять λ при заданном скалярном произведении a→=(1,0,λ+1) и b→=(λ,1,λ) будет равным -1. Решение Из формулы видно, что необходимо найти сумму произведений координат: (a→,b→)=1·λ+0·1+(λ+1)·λ=λ2+2·λ. В дано имеем (a→,b→)=-1. Ответ: A=1522. Пример 9Материальная точка, перемещаясь из M(2,-1,-3) в N(5,3λ-2,4) под силой F→=(3,1,2), совершила работа равную 13 Дж. Вычислить длину перемещения. Решение При заданных координатах вектора MN→ имеем MN→=(5-2, 3λ-2-(-1), 4-(-3))=(3, 3λ-1,7). По формуле нахождения работы с векторами F→=(3,1,2) и MN→=(3, 3λ-1,7) получим A=(F⇒, MN→)=3·3+1·(3λ-1)+2·7=22+3λ. По условию дано, что A=13Дж, значит 22+3λ=13. Отсюда следует λ=-3, значит и MN→=(3,3λ-1,7)=(3,-10,7). Чтобы найти длину перемещения MN→ , применим формулу и подставим значения: MN→=32+(-10)2+72=158. Ответ: 158. Решение задач
от 1 дня / от 150 р.
Курсовая работа
от 5 дней / от 1800 р. Автор: Ирина Мальцевская Преподаватель математики и информатики. Кафедра бизнес-информатики Российского университета транспорта Скалярное произведение — формула, примеры Скалярное произведение — это один из способов умножения двух или более векторов.
Что такое скалярный продукт?Скалярное произведение векторов равно произведению величин двух векторов и косинуса угла между двумя векторами. Результат скалярного произведения двух векторов лежит в одной плоскости двух векторов. Скалярный продукт может быть положительным действительным числом, отрицательным действительным числом или нулем. 9{n} a_i b_i\) Формула скалярного произведения для векторовПусть a и b — два ненулевых вектора, а θ — угол между векторами. Тогда скалярное произведение или скалярное произведение обозначается как \(\overrightarrow a. \overrightarrow b\), который определяется как: \(\overrightarrow a. \overrightarrow b\) = \(|\overrightarrow a||\ b|\) cos θ. Здесь
Примечание: θ не определено, если либо \(\overrightarrow a\) = 0, либо \(\overrightarrow b\) = 0. Геометрический смысл скалярного произведенияСкалярное произведение двух векторов строится путем взятия компонента одного вектора в направлении другого и умножения его на величину другого вектора. Чтобы понять векторное скалярное произведение, нам сначала нужно узнать, как найти величину двух векторов и угол между двумя векторами, чтобы найти проекцию одного вектора на другой вектор. 92}\) Проекция вектораСкалярное произведение полезно для нахождения компонента одного вектора в направлении другого. Проекция вектора одного вектора на другой вектор — это длина тени данного вектора на другой вектор. Он получается путем умножения величины данных векторов на косинус угла между двумя векторами. Результатом формулы векторной проекции является скалярное значение. Пусть OA = \(\overrightarrow a\), OB = \(\overrightarrow b\), два вектора и θ угол между \(\overrightarrow a\) и \(\overrightarrow b\) . Из прямоугольного треугольника OAL , cos θ = OL/OA OL = OA cos θ = \(|\overrightarrow a|\) cos θ OL — векторная проекция a на b. \(\overrightarrow a. \overrightarrow b\) = \(|\overrightarrow a||\overrightarrow b|\) cos θ = \(|\overrightarrow b|\) OL = \(|\overrightarrow b |\) (проекция \(\overrightarrow a\) на \(\overrightarrow b\)) Таким образом, проекция \(\overrightarrow a\) на \(\overrightarrow b = \dfrac{\overrightarrow a. \ overrightarrow b}{|\overrightarrow b|}\) Аналогично, векторная проекция \(\overrightarrow b\) на \(\overrightarrow a = \dfrac{\overrightarrow a. \overrightarrow b}{|\overrightarrow a|}\) Угол между двумя векторами с помощью точки Продукт Угол между двумя векторами рассчитывается как косинус угла между двумя векторами. Косинус угла между двумя векторами равен сумме произведений отдельных составляющих двух векторов, деленной на произведение величины двух векторов. Рабочее правило для нахождения скалярного произведения двух векторовЕсли два вектора выражены через единичные векторы i, j, k вдоль осей x, y, z, то скалярное произведение получается следующим образом: Если \(\overrightarrow a = a_1\hat i + a_2 \hat j + a_3 \hat k\) и \(\overrightarrow b = b_1 \hat i + b_2 \hat j + b_3\hat k\), тогда \(\overrightarrow a. \overrightarrow b\) = \((a_1 \hat i + a_2 \hat j + a_3 \hat k)(b_1 \hat i + b_2 \hat j + b_3 \ шапка к)\) = \((a_1b_1) (\hat i. \hat i) + (a_1b_2) (\hat i.\hat j)+ (a_1b_3) (\hat i. \hat k) + \\(a_2b_1) ( \hat j. \hat i) + (a_2b_2)(\hat j. \hat j) + (a_2b_3 (\hat j. \hat k) + \\(a_3b_1)(\hat k. \hat i) + ( a_3b_2)(\hat k. \hat j) + (a_3b_3)(\hat k. \hat k)\) = \(a_1b_1\) + \(a_2b_2\)+ \(a_3b_3\) Матричное представление скалярного произведения Скалярное произведение векторов легко вычислить, если векторы представлены в виде матриц строк или столбцов. Свойства скалярного произведенияНиже приведены свойства скалярного произведения векторов.
Коммутативное свойство скалярного произведения:При обычном определении \(\overrightarrow a\). \(\overrightarrow b\) = \(\overrightarrow b\) . \(\overrightarrow a\) , поскольку мы имеем \(|\overrightarrow a||\overrightarrow b|\) cos θ = \(|\overrightarrow b||\overrightarrow a|\) cos θ Распределение скалярного произведения Пусть a, b и c — любые три вектора, тогда скалярное произведение является дистрибутивным относительно сложения и вычитания.
Природа скалярного произведения
Другие свойства скалярного произведения
Идентичности векторов
Скалярное произведение единичных векторов Скалярное произведение единичных векторов изучается путем взятия единичных векторов \(\hat i\) вдоль оси x, \(\hat j\) вдоль оси y и \(\hat k\) по оси Z соответственно. \(\шляпа i.\шляпа i\) = \(\шляпа j.\шляпа j\) = \(\шляпа k.\шляпа k\)= 1 \(\шляпа i.\шляпа j \) = \(\шляпа j.\шляпа k\) = \(\шляпа k.\шляпа i\)= 0 Применение скалярного произведения Применение скалярного произведения для расчета работы. Произведение приложенной силы на перемещение называется работой. Если сила приложена под углом θ к смещению, проделанная работа определяется как скалярное произведение силы и смещения как W = f d cos θ. Скалярное произведение также используется для проверки того, являются ли два вектора ортогональными или нет. \(\overrightarrow a. \overrightarrow b\) = \(|\overrightarrow a||\overrightarrow b|\) cos 90º ⇒ \(\overrightarrow a. Важные замечания о скалярном произведении:
☛ Связанные темы:
Часто задаваемые вопросы о Dot ProductЧто такое скалярное произведение двух векторов? Скалярное произведение двух векторов имеет два определения. Что такое скалярное произведение двух параллельных векторов?Скалярное произведение двух параллельных векторов равно произведению модуля двух векторов. Для двух параллельных векторов угол между векторами равен 0°, а Cos0°= 1. Следовательно, для двух параллельных векторов a и b имеем \(\overrightarrow a. \overrightarrow b\) = \(|\overrightarrow a|| \overrightarrow b|\) cos 0° = \(|\overrightarrow a|.|\overrightarrow b|\).1 = \(|\overrightarrow a|.|\overrightarrow b|\). В чем разница между скалярным произведением и перекрестным произведением? Скалярное произведение — это скалярное произведение, а перекрестное произведение — векторное произведение. Что такое формула скалярного произведения? Формула скалярного произведения представляет скалярное произведение двух векторов как произведение двух векторов и косинуса угла между ними. Формула скалярного произведения заданных векторов может быть выражена следующим образом. Здесь a и b — два вектора, \(|\overrightarrow a|\) и \(|\overrightarrow b|\) — их соответствующие величины, а θ — угол между двумя векторами a . b = \(|\overrightarrow a||\overrightarrow b|\) cosθ. Включает ли формула скалярного произведения умножение?Умножение двух векторов — это не то же самое, что скалярное умножение. Есть два типа умножения с участием двух векторов. Скалярный продукт — это «точечный продукт», а векторный продукт — «перекрестный продукт». Формула скалярного произведения представляет собой скалярное произведение двух векторов как произведение двух векторов и косинуса угла, образованного между ними. Какова цель формулы скалярного произведения?Скалярное произведение предназначено для того, чтобы сообщить нам величину вектора силы, приложенного в направлении вектора движения. Скалярное произведение также позволяет нам измерить угол, образованный парой векторов, и относительное положение вектора относительно осей координат. Что происходит, когда скалярное произведение после использования формулы скалярного произведения равно 0? Формула скалярного произведения представляет скалярное произведение двух векторов как произведение двух векторов и косинуса угла между ними. Где мы используем скалярный продукт?Концепция скалярного произведения широко используется в физике и технике. Для двух величин, расположенных под углом друг к другу, скалярное произведение дает результат этих двух векторов. Возьмем пример силы, приложенной к телу F, и перемещение тела равно d. Если угол между вектором силы F и вектором смещения d равен θ, то выполненная работа является произведением силы на перемещение. W = FdCosθ. Как рассчитать скалярный продукт? Скалярный продукт можно рассчитать в три простых шага. Сначала найдите величину двух векторов a и b, то есть \(|\overrightarrow a|\) и \(|\overrightarrow b|\). Во-вторых, найдите косинус угла θ между двумя векторами. Наконец, возьмите произведение величины двух векторов и косинуса угла между двумя векторами, чтобы получить скалярное произведение двух векторов. Почему скалярное произведение называется скалярным?Скалярное произведение является скалярным, поскольку все отдельные составляющие ответа являются скалярными значениями. В \(\overrightarrow a. \overrightarrow b\) = \(|\overrightarrow a|.|\overrightarrow b|\).Cosθ, \(|\overrightarrow a|, |\overrightarrow b|\) и Cosθ равны все скалярные значения. Следовательно, скалярное произведение также называют скалярным произведением. Почему мы используем косинус в скалярном произведении? Для нахождения скалярного произведения нам нужно, чтобы два вектора a, b были направлены в одном направлении. Поскольку векторы a и b расположены под углом друг к другу, значение acosθ является компонентом вектора a в направлении вектора b. Следовательно, мы можем найти cosθ в скалярном произведении двух векторов. Почему скалярное произведение ортогональных векторов равно 0?Два ортогональных вектора перпендикулярны друг другу, а угол между двумя векторами равен 90°. Поскольку Cos90° = 0, скалярное произведение двух ортогональных векторов равно 0. \(\overrightarrow a. \overrightarrow b\) = \(|\overrightarrow a|.|\overrightarrow b|\).cos90° = \ (|\overrightarrow a|.|\overrightarrow b|\).0 = 0. Почему скалярное произведение коммутативно?Скалярное произведение двух векторов равно произведению величины двух векторов и косинуса угла между двумя векторами. И все отдельные компоненты величины и угла являются скалярными величинами. Следовательно, \(\overrightarrow a. \overrightarrow b\) = \(\overrightarrow b. \overrightarrow a\), и скалярное произведение векторов следует коммутативному свойству. Может ли скалярный продукт быть равен нулю? Скалярное произведение двух векторов может быть равно нулю, если любой из двух векторов равен нулю или если два вектора перпендикулярны друг другу. Является ли скалярное произведение двух коллинеарных векторов равным 0?Нет. Это потому, что угол между двумя коллинеарными векторами равен 0, поэтому скалярное произведение двух коллинеарных векторов есть просто произведение их величин (так как cos 0 = 1). Фактически, векторное произведение двух коллинеарных векторов является нулевым вектором. Точечный продуктВектор имеет величину (длину) и направление : Вот два вектора: Они могут быть умножены на с использованием « Скалярного произведения » (см. также Перекрестное произведение). РасчетСкалярный продукт записывается с использованием центральной точки: a · b Мы можем вычислить скалярное произведение двух векторов следующим образом: а · б = | и | × | б | × cos(θ) Где: Итак, мы умножаем длину на a умножить на длину b , затем умножить на косинус угла между a и b
ИЛИ мы можем рассчитать это так: а · б = а х х б х + а у х б у Итак, мы умножаем x, умножаем y, а затем складываем. Оба метода работают! И результат номер (называемый «скаляром», чтобы показать, что это не вектор). Пример: вычислить скалярное произведение векторовa и b :a · b = | и | × | б | × cos(θ) a · b = 10 × 13 × cos(59,5°) a · b = 10 × 13 × 0,5075… a · b 90,389 = 65,389 = 66 (округлено) ИЛИ мы можем вычислить это так: a · b = а х х б х + а у х б у а · б = -6 х 5 + 8 х 12 2 + 8 х 122 + 9 -380a · b = 66 Оба метода дали один и тот же результат (после округления) Также обратите внимание, что мы использовали минус 6 для x (оно направлено в отрицательном направлении x) Примечание: вы можете использовать векторный калькулятор чтобы помочь вам. Почему cos(θ) ? Хорошо, чтобы умножить два вектора, имеет смысл перемножить их длины вместе , но только тогда, когда они указывают в одном направлении . Итак, мы делаем одну «точку в том же направлении», что и другая, умножая на cos(θ):
ТОГДА умножаем!
ПрямоугольныеКогда два вектора расположены под прямым углом друг к другу, скалярное произведение равно нулю . Пример: рассчитать скалярный продукт для:a · b = | и | × | б | × cos(θ) а · б = | и | × | б | × cos(90°) а · б = | и | × | б | × 0 a · b = 0 или мы можем вычислить это так: a · b = a x × b x + a y × b y a · b = -12 × 12 + 16 × 9 a · b = -144 + 144 а · б = 0 Это может быть удобным способом узнать, находятся ли два вектора под прямым углом. Три или более измеренийВсе это прекрасно работает и в 3-х (или более) измерениях. И действительно может быть очень полезным! Пример: Сэм измерил концы двух шестов и хочет узнатьугол между ними. Y + A Z × B ZA · B = 9 × 4 + 2 × 8 + 7 × 10 0003 A · B = 36 + 410 3 A · B = 36 + 70 A · B = 36 + 70 0003 A · B = 36 + 700003 A · B = 36 + 700003 A. b = 122
Теперь другая формула: a · b = | и | × | б | × cos(θ) Но что такое | и | ? Это величина или длина вектора a . Мы можем использовать Пифагор:
Аналогично для | б |:
И мы знаем из вычислений выше, что a · b = 122, поэтому: a · b = | и | × | б | × cos(θ) 122 = √180 × √134 × cos(θ) cos(θ) = 122 / (√180 × √134) cos(θ) = 0,7855. θ cos -1 (0,7855…) = 38,2…° Готово! Я когда-то пробовал такое вычисление, но работал все в углах и расстояниях… это было очень тяжело, включало много тригонометрии, и у меня болел мозг. Способ выше намного проще. Перекрестное произведениеСкалярное произведение дает скалярный ответ (обычное число) и иногда называется скалярным произведением . Но есть также перекрестное произведение, которое дает вектор в качестве ответа, и иногда его называют векторный продукт .
3036, 3037, 3030, 3031, 3032, 3033, 3034, 3035, 3903, 3904 Понимание скалярного произведения – BetterExplainedЯ думаю о скалярном произведении как о направленном умножении. Умножение выходит за рамки повторного подсчета: это применение сущности одного элемента к другому. (Например, сложное умножение — это вращение, а не повторный счет.) При работе с простыми темпами роста умножение масштабирует одну скорость на другую:
При работе с векторами («направленный рост») мы можем выполнить несколько операций:
Сегодня мы построим наше интуитивное представление о том, как работает скалярное произведение. Избавьтесь от формулыВы везде видели уравнение скалярного произведения: А также обоснование: «Ну, Билли, закон косинусов (ты ведь помнишь это, не так ли? ) говорит, что следующие вычисления одинаковы, так что они есть». Недостаточно хорошо — это не щелкает! Помимо вычислений, что это значит? Цель состоит в том, чтобы применить один вектор к другому. Уравнение выше показывает два способа сделать это:
Уравнение «тот материал = тот материал» просто означает «Вот два эквивалентных способа ‘направленного умножения’ векторов». Восприятие чисел как векторовДавайте начнем с простого и рассмотрим 3 x 4 как скалярное произведение: Число 3 означает «направленный рост» в одном измерении (скажем, по оси X), а 4 является «направленным ростом» в том же направлении. 3 x 4 = 12 означает, что мы получаем 12-кратный рост в одном измерении. Ok. Теперь предположим, что 3 и 4 относятся к разным измерениям. Допустим, 3 означает «втрое больше бананов» (ось X), а 4 означает «вчетверо больше апельсинов» (ось Y). Теперь они не одного и того же типа чисел: что произойдет, если применить рост (использовать скалярное произведение) в нашей вселенной «бананы, апельсины»?
Применение (0,4) к (3,0) означает «Уничтожьте рост бананов, увеличьте рост апельсинов в четыре раза». Но у (3, 0) изначально не было оранжевого роста, поэтому конечный результат равен 0 («Уничтожь все свои фрукты, приятель»). Видите, как мы «применяем», а не просто добавляем? При регулярном сложении мы смешаем векторы вместе: (3,0) + (0, 4) = (3, 4) [вектор, который утроит ваши апельсинов, а увеличит ваши бананы в четыре раза]. «Приложение» другое. Мы мутируем исходный вектор на основе правил второго. И правила (0, 4) таковы: «Уничтожьте рост бананов и увеличьте рост апельсинов в четыре раза». Применительно к чему-то, состоящему только из бананов, например (3, 0), мы остаемся ни с чем. Конечным результатом процесса скалярного произведения может быть:
Понимание расчета«Применение векторов» все еще немного абстрактно. Я думаю: «Сколько энергии/толчка отдает один вектор другому?». Вот как я себе это представляю: Прямоугольные координаты: перекрытие компонентов Подобно умножению комплексных чисел, посмотрите, как взаимодействует каждая компонента x и y: х с у, у с у). Полярные координаты: Проекция Слово «проекция» настолько бесплодно: я предпочитаю «по пути». Сколько энергии на самом деле идет в нашем первоначальном направлении? Вот как это можно увидеть: Возьмем два вектора a и b. Поверните наши координаты так, чтобы b стала горизонтальной: она становится (|b|, 0), и все находится на этой новой оси x. Что такое точечный продукт сейчас? (Это не должно измениться только потому, что мы наклонили голову). Итак, вектор a имеет новые координаты (a1, a2), и мы получаем: a1 на самом деле «Какова координата x точки a, если предположить, что b является осью x?». Это |a|cos(θ), также известная как «проекция»: Аналогии скалярного произведения Общепринятая интерпретация — «геометрическая проекция», но она такая пресная. Поглощение энергии Один вектор — солнечные лучи, другой — куда указывает солнечная панель (да-да, нормальный вектор). Большие числа означают более сильные лучи или большую панель. Сколько энергии поглощается?
Если вы держите панель боком к солнцу, лучи не попадают (cos(θ) = 0). Фото предоставлено Но… но… солнечные лучи уходят от солнца, и панель обращена к солнцу, и скалярное произведение отрицательно, когда векторы противоположны! Сделайте глубокий вдох и помните, что цель состоит в том, чтобы принять аналогию (кроме того, физики все время теряют из виду отрицательные знаки). Mario-Kart Speed Boost В Mario Kart на земле есть «ускорители», которые увеличивают вашу скорость (Никогда не играл? Извините.) Источник фото Представьте, что красный вектор — это ваша скорость (направление x и y), а синий вектор — это ориентация площадки усиления (направление x и y). Сколько буста вы получите? Для аналогии представьте, что пэд дает бонус к скорости, подобный этому:
Аккуратно, да? Другой способ увидеть это: ваша входящая скорость равна $|a|$, а максимальное ускорение равно $|b|$. Процент повышения, который вы фактически получаете (в зависимости от того, как вы выстроились в очередь), составляет $\cos(\theta)$, для общего повышения $|a||b|\cos(\theta)$, что является скалярное произведение. Физика Физика Физика Скалярное произведение появляется во всей физике: какое-то поле (электрическое, гравитационное) притягивает какую-то частицу. Это полезное обобщение: интегралы — это «умножение с учетом изменений», а скалярное произведение — «умножение с учетом направления». А что, если ваше направление изменится? Да взять, конечно, интеграл скалярного произведения! Вперед и вверхНе соглашайтесь на «Скалярное произведение — это геометрическая проекция, оправдываемая законом косинусов». Найдите аналогии, которые подходят именно вам! Счастливая математика. Другие сообщения из этой серии
Скалярное произведение двух векторов Векторы можно умножать двумя способами, а именно скалярным произведением или скалярным произведением, в котором результатом является скаляр, и векторным произведением или перекрестным произведением, в котором результатом является вектор. Определение скалярного произведенияСкалярное произведение двух различных ненулевых векторов обозначается буквой a.b и определяется как: 0 ≤ θ ≤ π (Изображение будет загружено в ближайшее время) Если a = 0 или b = 0, θ не будет определено, и в этом случае a.b= 0 Формула скалярного произведения Вы можете определить скалярное произведение двух векторов двумя разными способами: геометрическим и алгебраическим. Определение геометрии скалярного произведенияГеометрический смысл скалярного произведения гласит, что скалярное произведение двух заданных векторов a и b обозначается следующим образом: a.b = |a||b| cos θ Здесь |a| и |б| называются величинами векторов a и b, а θ — угол между векторами a и b. Если два вектора ортогональны, то есть угол между ними равен 90, то a.b = 0, так как cos 90 = 0. Если два вектора параллельны друг другу, то a.b =|a||b| так как cos 0 = 1, Алгебра скалярного произведения ОпределениеАлгебра скалярного произведения говорит, что скалярное произведение данных двух произведений – a = (a1, a2, a3) и b= (b1, b2, b3) определяется как: a.b= (a1b1 + a2b2 + a3b3) Свойства скалярного произведения двух векторовНиже приведены свойства векторов:
b|cos θ a.
A. (B + C) = A.B + A.C
A. (RB + C) = R. (A.B) + (A.C)
(xa) . (yb) = xy (a.b)
Поскольку скалярное произведение между скаляром и вектором не допускается.
Два вектора ортогональны только тогда, когда a.b = 0 Скалярное произведение векторнозначных функций Скалярное произведение векторнозначных функций, т. Решенные примерыПример 1: Найдите скалярное произведение a= (1, 2, 3) и b= (4, −5, 6). Какой угол образуют векторы? Решение: Используя формулу скалярных произведений, a.b = (a1b1 + a2b2 + a3b3) Скалярное произведение можно рассчитать следующим образом: = 1(4) + 2(−5) + 3(6) = 4 − 10 + 18 12 Поскольку a.b — положительное число, можно сделать вывод, что векторы образуют острый угол. Пример 2: Два вектора A и B задаются формулой: A = 2i − 3j + 7k и B= −4i + 2j −4k Найдите скалярное произведение данных двух векторов. Решение: A.B = (2i − 3j +7k) . (−4i + 2j − 4k) = 2 (-4) + (-3)2 + 7 (-4) = -8 — 6 — 28 = -42 продукты, выходной сигнал представляет собой вектор, ортогональный двум заданным векторам. Правило большого пальца правой руки определяет направление векторного произведения двух векторов, а величина определяется площадью параллелограмма, созданного исходными двумя векторами. Нулевой вектор представляет собой перекрестное произведение двух линейных векторов или параллельных векторов. Заключение Вектор – это величина, которая имеет как величину, так и направление. К векторам можно применить несколько математических операций, таких как сложение и умножение. Умножение векторов можно выполнить двумя способами: точечным произведением и перекрестным произведением. Скалярное произведение двух векторов представляет собой сумму произведений их соответствующих компонентов. Это произведение их величин на косинус угла между ними. Скалярное произведение вектора на самого себя равно квадрату его величины. 12.3: Скалярный продукт — Mathematics LibreTexts
Цели обучения
Если мы прикладываем силу к объекту, чтобы объект двигался, мы говорим, что сила совершает работу. В этом разделе мы разработаем операцию, называемую скалярным произведением, которая позволяет вычислить работу в случае, когда вектор силы и вектор движения имеют разные направления. Скалярное произведение, по сути, говорит нам, какая часть вектора силы приложена в направлении вектора движения. Скалярное произведение также может помочь нам измерить угол, образованный парой векторов, и положение вектора относительно осей координат. Он даже обеспечивает простой тест, чтобы определить, пересекаются ли два вектора под прямым углом. Скалярный продукт и его свойства Мы уже научились складывать и вычитать векторы. В этой главе мы исследуем два типа умножения векторов. Определение: скалярное произведениескалярное произведение векторов \(\vecs{ u}=⟨u_1,u_2,u_3⟩\) и \(\vecs{ v}=⟨v_1,v_2,v_3⟩\) задается суммой произведений компонент \[\vecs{ u}⋅\vecs{ v}=u_1v_1+u_2v_2+u_3v_3. \nonumber \] Обратите внимание, что если \(u\) и \(v\) являются двумерными векторами, скалярное произведение вычисляется аналогичным образом. Таким образом, если \(\vecs{ u}=⟨u_1,u_2⟩\) и \(\vecs{ v}=⟨v_1,v_2⟩,\), то \[\vecs{ u}⋅\vecs{ v }=u_1v_1+u_2v_2. \nonumber \] Когда два вектора объединяются при сложении или вычитании, результатом является вектор. Когда два вектора объединяются с помощью скалярного произведения, результатом является скаляр. По этой причине скалярное произведение часто называют числом 9.0899 скалярное произведение. Его также можно назвать внутренним продуктом . Пример \(\PageIndex{1}\): вычисление скалярных произведений
Раствор : а. Подставляем компоненты вектора в формулу скалярного произведения: \[ \begin{align*} \vecs{ u}⋅\vecs{ v} &=u_1v_1+u_2v_2+u_3v_3 \\[4pt] &=3(−1)+5(3)+2(0) \\[4pt] &=−3+15+0 \\[4pt] &=12. \end{выравнивание*}\] б. Расчет такой же, если векторы записываются с использованием стандартных единичных векторов. У нас все еще есть три компонента для каждого вектора, которые нужно подставить в формулу скалярного произведения: \[ \begin{align*} \vecs{ p}⋅\vecs{ q} &=p_1q_1+p_2q_2+p_3q_3 \\[4pt ] &=10(−2)+(−4)(1)+(7)(6) \\[4pt] &=−20−4+42 \\[4pt] &=18. Упражнение \(\PageIndex{1}\)Найти \(\vecs{ u}⋅\vecs{ v}\), где \(\vecs{ u}=⟨2,9,−1⟩\) и \(\vecs{v}=⟨−3,1,−4⟩.\)
Подобно сложению и вычитанию векторов, скалярное произведение имеет несколько алгебраических свойств. Мы докажем три из этих свойств, а остальные оставим в качестве упражнений. Свойства скалярного произведенияПусть \(\vecs{ u}\), \(\vecs{ v}\) и \(\vecs{ w}\) — векторы, и пусть \(c\) быть скаляром.
Доказательство Пусть \(\vecs{ u}=⟨u_1,u_2,u_3⟩\) и \(\vecs{ v}=⟨v_1,v_2,v_3⟩. \[ \begin{ выровнять*} \vecs{ u}⋅\vecs{ v} &=⟨u_1,u_2,u_3⟩⋅⟨v_1,v_2,v_3⟩ \\[4pt] &=u_1v_1+u_2v_2+u_3v_3 \\[4pt] &= v_1u_1+v_2u_2+v_3u_3 \\[4pt] &= ⟨v_1,v_2,v_3⟩⋅⟨u_1,u_2,u_3⟩ \\[4pt] &=\vecs{ v}⋅\vecs{ u}.\end{align *}\] Ассоциативное свойство похоже на ассоциативное свойство для умножения действительных чисел, но обратите особое внимание на разницу между скалярными и векторными объектами: \[ \begin{align*} c(\vecs{ u}⋅\vecs{ v}) &=c(u_1v_1+u_2v_2+u_3v_3) \\[4pt] &=c(u_1v_1)+c(u_2v_2) +c(u_3v_3) \\[4pt] &=(cu_1)v_1+(cu_2)v_2+(cu_3)v_3 \\[4pt] &=⟨cu_1,cu_2,cu_3⟩⋅⟨v_1,v_2,v_3⟩ \\[4pt ] &=c⟨u_1,u_2,u_3⟩⋅⟨v_1,v_2,v_3⟩ \\[4pt] &=(c\vecs{ u})⋅\vecs{ v}.\end{align*}\] Доказательство того, что \(c(\vecs{ u}⋅\vecs{ v})=\vecs{ u}⋅(c\vecs{ v})\), аналогично. Четвертое свойство показывает связь между величиной вектора и его скалярным произведением на самого себя: 92.\end{align*}\] □ Обратите внимание, что определение скалярного произведения дает \(\vecs{ 0}⋅\vecs{ v}=0. Пример \(\PageIndex{2}\): Использование Свойства скалярного произведенияПусть \(\vecs{ a}=⟨1,2,−3⟩\), \(\vecs{ b}=⟨0,2,4⟩\) и \(\vecs { c} =⟨5,−1,3⟩\). Найдите каждый из следующих продуктов.
Раствор а. Обратите внимание, что это выражение запрашивает скалярное число, кратное \(\vecs{ c}\) на \(\vecs{ a}⋅\vecs{ b}\): \[ \begin{align*} (\vecs{ a}⋅\vecs{ b})\vecs{ c} &=(⟨1,2,−3⟩⋅⟨0,2,4⟩)⟨5,−1,3⟩ \\[4pt] &=( 1(0)+2(2)+(−3)(4))⟨5,−1,3⟩ \\[4pt] &=−8⟨5,−1,3⟩ \\[4pt] &= ⟨−40,8,−24⟩.\end{align*}\] б. Это выражение представляет собой скалярное произведение вектора \(\vecs{ a}\) и скалярного числа, кратного 2\(\vecs{ c}\): \[ \begin{align*} \vecs{ a}⋅(2\ vecs{ c}) &=2(\vecs{a}⋅\vecs{c}) \\[4pt] &=2(⟨1,2,−3⟩⋅⟨5,−1,3⟩) \\ [4pt] &=2(1(5)+2(-1)+(-3)(3)) \\[4pt] &=2(-6)=-12. Использование скалярного произведения для нахождения угла между двумя векторамиКогда два ненулевых вектора помещаются в стандартное положение в двух или трех измерениях, они образуют между собой угол (рис. \(\PageIndex{1}\) ). Скалярное произведение позволяет найти меру этого угла. Это свойство является результатом того факта, что мы можем выразить скалярное произведение через косинус угла, образованного двумя векторами. Рисунок \(\PageIndex{1}\): Пусть \(θ\) — угол между двумя ненулевыми векторами \(\vecs{ u}\) и \(\vecs{ v}\), такой, что \(0≤θ≤π\).Оценка скалярного произведенияСкалярное произведение двух векторов представляет собой произведение величины каждого вектора на косинус угла между ними: \[\vecs{ u}⋅\vecs{ v}=‖\ vecs{ u}‖‖\vecs{ v}‖\cos θ. \label{evaldot} \] Доказательство Поместите векторы \(\vecs{ u}\) и \(\vecs{ v}\) в стандартное положение и рассмотрим вектор \(\vecs{ v}−\vecs { u}\) (Рисунок \(\PageIndex{2}\)). □ Мы можем использовать форму скалярного произведения в уравнении \ref{evaldot}, чтобы найти меру угла между двумя ненулевыми векторами, перестроив уравнение \ref{evaldot} для решения для косинуса угла: \[\cos θ=\dfrac{\vecs{u}⋅\vecs{v}}{‖\vecs{u}‖‖\vecs{v}‖}. \метка{точка2} \] Используя это уравнение, мы можем найти косинус угла между двумя ненулевыми векторами. Поскольку мы рассматриваем наименьший угол между векторами, мы предполагаем \(0°≤θ≤180°\) (или \(0≤θ≤π\), если мы работаем в радианах). Арккосинус уникален в этом диапазоне, поэтому мы можем определить меру угла \(θ\). Пример \(\PageIndex{3}\): нахождение угла между двумя векторами Найдите меру угла между каждой парой векторов. Теперь \(\cos θ=0\ ) и \(0≤θ≤π\), поэтому \(θ=π/2\). Упражнение \(\PageIndex{3}\)Найдите меру угла в радианах, образованного векторами \(\vecs{ a}=⟨1,2,0⟩\) и \(\vecs{ б}=⟨2,4,1⟩\). Округлить до сотых.
Угол между двумя векторами может быть острым \((0<\cos θ<1),\), тупым \((−1<\cos θ<0)\) или прямым \((\cos θ=− 1)\). Если \(\cos θ=1\), то оба вектора имеют одинаковое направление. Если \(\cos θ=0\), то векторы в стандартном положении образуют прямой угол (рисунок \(\PageIndex{3}\)). Мы можем формализовать этот результат в виде теоремы об ортогональных (перпендикулярных) векторах. Рисунок \(\PageIndex{3}\): (a) Острый угол имеет \(0<\cos θ<1\). (b) Тупой угол имеет \(−1<\cos θ<0.\) (c) Прямая линия имеет \(\cos θ=−1\). (d) Если векторы имеют одинаковое направление, \(\cos θ=1\). (e) Если векторы ортогональны (перпендикулярны), \(\cos θ=0.\) (b) Тупой угол имеет \(−1<\cos θ<0.\) (c) Прямая линия имеет \(\cos θ=−1\). (d) Если векторы имеют одинаковое направление, \(\cos θ=1\). (e) Если векторы ортогональны (перпендикулярны), \(\cos θ=0.\)Ортогональные векторыНенулевые векторы \(\vecs{u}\) и \(\vecs{v}\) являются ортогональными векторами тогда и только тогда, когда \(\vecs{u}⋅\vecs{v}= 0.\) ДоказательствоПусть \(\vecs{u}\) и \(\vecs{v}\) ненулевые векторы, и пусть \(θ\) обозначает угол между ними. Сначала предположим \(\vecs{u}⋅\vecs{v}=0.\)Затем \[‖\vecs{u}‖‖\vecs{v}‖\cos θ=0. \nonumber \] Однако \(‖\vecs{u}‖≠0\) и \(‖\vecs{v}‖≠0,\), поэтому мы должны иметь \(\cos θ=0\). Следовательно, \(θ=90°\) и векторы ортогональны. Теперь предположим, что \(\vecs{u}\) и \(\vecs{v}\) ортогональны. Тогда \(θ=90°\) и мы имеем \[ \begin{align*} \vecs{u}⋅\vecs{v} &=‖\vecs{ u}‖‖\vecs{ v}‖\ cos θ \\[4pt] &=‖\vecs{ u}‖‖\vecs{ v}‖\cos 90° \\[4pt] &=‖\vecs{ u}‖‖\vecs{ v}‖(0 ) \\[4pt] &=0. □ Термины ортогональный, перпендикулярный, и нормальный каждый указывает на то, что математические объекты пересекаются под прямым углом. Использование каждого термина определяется главным образом его контекстом. Мы говорим, что векторы ортогональны, а прямые перпендикулярны. Срок норма используется чаще всего при измерении угла, выполненного с плоскостью или другой поверхностью. Пример \(\PageIndex{4}\): определение ортогональных векторов ,−2⟩\) — ортогональные векторы.Решение Используя определение, нам нужно только проверить скалярное произведение векторов: \[ \vecs{ p}⋅\vecs{ q}=1(10)+(0)(3)+ (5)(-2)=10+0-10=0. \nonumber \] Поскольку \(\vecs{p}⋅\vecs{q}=0,\) векторы ортогональны (рис. \(\PageIndex{4}\)). Рисунок \(\PageIndex{4}\): Векторы \(\vecs{ p}\) и \(\vecs{ q}\) образуют прямой угол, когда их начальные точки совпадают.Упражнение \(\PageIndex{4}\)Для какого значения \(x\) \(\vecs{ p}=⟨2,8,−1⟩\) ортогонально \(\vecs{ q} =⟨x,−1,2⟩\)?
Пример \(\PageIndex{5}\): измерение угла, образованного двумя векторамиПусть \(\vecs{ v}=⟨2,3,3⟩.\) Найдите меры углов, образованных двумя векторами следующие векторы.
Решение а. Пусть α будет углом, образованным \(\vecs{ v}\) и \(\mathbf{\hat i}\): 92}\sqrt{1}}=\dfrac{3}{\sqrt{22}} \\[4pt]γ &=\arccos\dfrac{3}{\sqrt{22}}≈0,877\,\text{ рад.} \end{align*}\] Упражнение \(\PageIndex{5}\)Пусть \(\vecs{ v}=⟨3,−5,1⟩.\) Найдите меру углы, образованные каждой парой векторов.
Угол, который вектор образует с каждой из осей координат, называемый углом направления, очень важен в практических вычислениях, особенно в таких областях, как инженерия. Например, в космонавтике угол запуска ракеты должен определяться очень точно. Очень маленькая ошибка в угле может привести к тому, что ракета отклонится от курса на сотни миль. Углы направления часто рассчитываются с помощью скалярного произведения и косинусов углов, называемых направляющими косинусами. Поэтому мы определяем как эти углы, так и их косинусы. Определение: углы направленияУглы, образованные ненулевым вектором и осями координат, называются углами направления для вектора (рисунок \(\PageIndex{5}\)). Косинусы этих углов называются косинусами направления . Рисунок \(\PageIndex{5}\): Угол \(α\) образован вектором \(\vecs{ v}\) и единичным вектором \(\mathbf{\hat i}\). Угол β образован вектором \(\vecs{v}\) и единичным вектором \(\mathbf{\hat j}\). Угол γ образован вектором \(\vecs{v}\) и единичным вектором \(\mathbf{\hat k}\). Угол γ образован вектором \(\vecs{v}\) и единичным вектором \(\mathbf{\hat k}\).В примере \(\PageIndex{5}\) направляющие косинусы \(\vecs{ v}=⟨2,3,3⟩\) равны \(\cos α=\dfrac{2}{\sqrt{ 22}}, \cos β=\dfrac{3}{\sqrt{22}},\) и \(\cos γ=\dfrac{3}{\sqrt{22}}\). Углы направления \(\vecs{v}\) равны \(α=1,130\) рад, \(β=0,877\) рад и \(γ=0,877\) рад. До сих пор мы в основном фокусировались на векторах, связанных с силой, движением и положением в трехмерном физическом пространстве. Однако векторы часто используются более абстрактно. Например, предположим, что продавец фруктов продает яблоки, бананы и апельсины. В данный день он продает 30 яблок, 12 бананов и 18 апельсинов. Он может использовать количественный вектор \(\vecs{ q}=⟨30,12,18⟩,\) для представления количества фруктов, которое он продал в тот день. Точно так же он может захотеть использовать ценовой вектор \(\vecs{ p}=⟨0,50,0,25,1⟩,\), чтобы указать, что он продает свои яблоки по 50 центов за штуку, бананы по 25 центов за штуку и апельсины по 1 доллар за штуку. Эта идея может показаться немного странной, но если мы будем рассматривать векторы просто как способ упорядочивания и хранения данных, мы обнаружим, что они могут быть весьма мощным инструментом. Возвращаясь к продавцу фруктов, давайте подумаем о скалярном произведении \(\vecs{ q}⋅\vecs{ p}\). Мы вычисляем его, умножая количество проданных яблок (30) на цену одного яблока (50 центов), количество проданных бананов на цену одного банана и количество проданных апельсинов на цену одного апельсина. Затем мы складываем все эти значения вместе. Итак, в этом примере скалярный продукт говорит нам, сколько денег было у продавца фруктов в продажах в этот конкретный день. Когда мы используем векторы более общим образом, нет причин ограничивать число компонентов тремя. Пример \(\PageIndex{6}\): Использование векторов в экономическом контексте Магазин товаров для вечеринок AAA продает приглашения, подарки для вечеринок, украшения и предметы общественного питания, такие как бумажные тарелки и салфетки. Когда AAA покупает свой инвентарь, она платит 25 центов за упаковку за приглашения и сувениры для вечеринок. Украшения стоят 50 центов AAA за штуку, а предметы общественного питания — 20 центов за упаковку. AAA продает приглашения по 2,50 доллара за упаковку и сувениры для вечеринок по 1,50 доллара за упаковку. В течение мая в магазине товаров для вечеринок AAA было продано 1258 приглашений, 342 сувенира для вечеринок, 2426 украшений и 1354 предмета общественного питания. Используйте векторы и скалярные произведения, чтобы рассчитать, сколько денег AAA заработала на продажах в мае месяце. Какую прибыль получил магазин? Решение Векторы стоимости, цены и количества: p} &=⟨2.50,1.50,4.50,1.25⟩ \\[4pt] \vecs{q} &=⟨1258,342,2426,1354⟩. \end{выравнивание*}\] Продажи AAA в мае можно рассчитать с помощью скалярного произведения \(\vecs{ p}⋅\vecs{ q}\). У нас есть \[ \begin{align*} \vecs{ p}⋅\vecs{ q} &=⟨2.50,1.50,4.50,1.25⟩⋅⟨1258,342,2426,1354⟩ \\[4pt] & =3145+513+10917+1692,5 \\[4pt] &= 16267,5. \end{align*}\] Итак, в мае ААА заработала 16 267,50 долларов. Чтобы рассчитать прибыль, мы должны сначала подсчитать, сколько ААА заплатила за проданные товары. \[ \begin{align*} \vecs{ c}⋅\vecs{ q} &=⟨0,25,0,25,0,50,0,20⟩⋅⟨1258,342,2426,1354⟩ \\[4pt] &=314,5+ 85,5+1213+270,8 \\[4pt] &=1883,8. \end{align*}\] Итак, AAA заплатила 1 883,80 долларов за проданные товары. Таким образом, их прибыль равна \[\vecs{ p}⋅\vecs{ q}−\vecs{ c}⋅\vecs{ q}=16267,5−1883,8 =14383,7. \nonumber \] Таким образом, в мае магазин товаров для вечеринок AAA заработал 14 383,70 долларов США. Упражнение \(\PageIndex{6}\) 1 июня магазин товаров для вечеринок AAA решил повысить цену на сувениры для вечеринок до 2 долларов за упаковку. Они также сменили поставщиков своих приглашений и теперь могут покупать приглашения всего за 10 центов за упаковку. Все остальные их расходы и цены остаются прежними. Если ААА продаст 1408 приглашений, 147 подарков для вечеринок, 2112 украшений и 1894 пункта общественного питания в июне месяце, используйте векторы и точечные произведения, чтобы рассчитать их общий объем продаж и прибыль за июнь.
ПроекцииКак мы видели, сложение объединяет два вектора для создания результирующего вектора. Но что, если нам дан вектор и нужно найти его составные части? Мы используем векторные проекции для выполнения противоположного процесса; они могут разбить вектор на его компоненты. Величина векторной проекции является скалярной проекцией. Например, если ребенок тянет ручку тележки под углом 55°, мы можем использовать проекции, чтобы определить, какая сила на ручке фактически двигает тележку вперед (\(\PageIndex{6}\)) . Мы вернемся к этому примеру и научимся его решать после того, как увидим, как вычислять проекции. Рисунок \(\PageIndex{6}\): Когда ребенок тянет тележку, только горизонтальная составляющая силы толкает тележку вперед. Определение: вектор и проекцияПроекция вектора из \(\vecs{ v}\) на \(\vecs{ u}\) — это вектор с меткой \(\text{proj}_\vecs{ u} \vecs{ v}\) на рисунке \(\PageIndex{7}\). Он имеет ту же начальную точку, что и \(\vecs{ u}\) и \(\vecs{ v}\), и то же направление, что и \(\vecs{ u}\), и представляет компонент \(\vecs { v}\), который действует в направлении \(\vecs{ u}\). Если \(θ\) представляет собой угол между \(\vecs{ u}\) и \(\vecs{ v}\), то по свойствам треугольников мы знаем длину \(\text{proj}_ \vecs{ u}\vecs{ v}\) равно \(\|\text{proj}_\vecs{ u}\vecs{ v}\|=‖\vecs{ v}‖\cos θ.\) Когда выражая \(\cos θ\) через скалярное произведение, это становится 92}\vecs{у}. \nonumber \] Длина этого вектора также известна как скалярная проекция из \(\vecs{ v}\) на \(\vecs{ u}\) и обозначается как \[\| \text{proj}_\vecs{u}\vecs{v}\|=\text{comp}_\vecs{u}\vecs{v}=\dfrac{\vecs{u}⋅\vecs{v} }{‖\vecs{ u}‖.} \nonumber \] Рисунок \(\PageIndex{7}\): проекция \(\vecs{ v}\) на \(\vecs{ u}\) показывает компонента вектора \(\vecs{ v}\) в направлении \(\vecs{ u}\).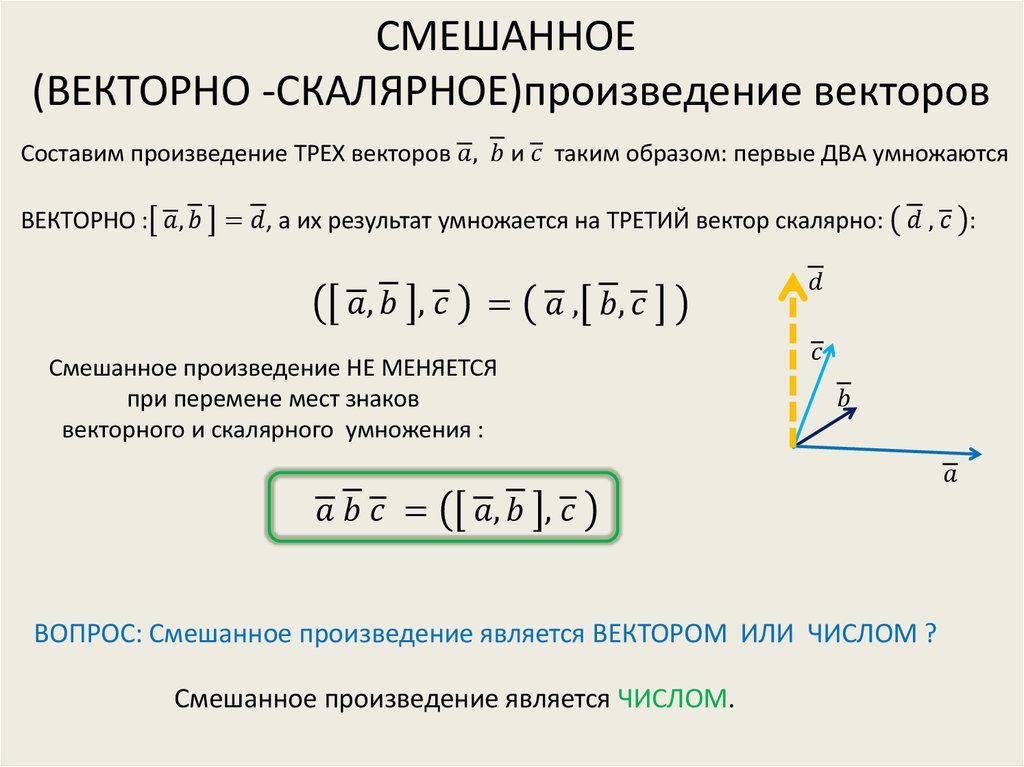 2}⟨−1,4,3⟩ \\[4pt] &=\dfrac{20}{26}⟨−1,4, 3⟩ \\[4pt] &=⟨−\dfrac{10}{13},\dfrac{40}{13},\dfrac{30}{13}⟩. \end{выравнивание*}\] 92}(\mathbf{\шляпа i}+6\mathbf{\шляпа j}) \\[4pt] &= -\dfrac{9}{37}(\mathbf{\шляпа i}+6\mathbf{\ шляпа j}) \\[4pt] &= -\dfrac{9}{37}\mathbf{\hat i}-\dfrac{54}{37}\mathbf{\hat j}.\end{align*} \] 2}⟨−1,4,3⟩ \\[4pt] &=\dfrac{20}{26}⟨−1,4, 3⟩ \\[4pt] &=⟨−\dfrac{10}{13},\dfrac{40}{13},\dfrac{30}{13}⟩. \end{выравнивание*}\] 92}(\mathbf{\шляпа i}+6\mathbf{\шляпа j}) \\[4pt] &= -\dfrac{9}{37}(\mathbf{\шляпа i}+6\mathbf{\ шляпа j}) \\[4pt] &= -\dfrac{9}{37}\mathbf{\hat i}-\dfrac{54}{37}\mathbf{\hat j}.\end{align*} \]Иногда бывает полезно разложить векторы, то есть разбить вектор на части в виде суммы. Этот процесс называется разложением вектора на компоненты. Проекции позволяют нам идентифицировать два ортогональных вектора, имеющих желаемую сумму. Например, пусть \(\vecs{ v}=⟨6,−4⟩\) и пусть \(\vecs{ u}=⟨3,1⟩.\) Мы хотим разложить вектор \(\vecs{ v }\) на ортогональные компоненты, так что один из векторов компонентов имеет то же направление, что и \(\vecs{ u}\). 92}\vecs{ u} \\[4pt] = \dfrac{18−4}{9+1}\vecs{ u} \\[4pt] = \dfrac{7}{5}\vecs{ u}= \dfrac{7}{5}⟨3,1⟩=⟨\dfrac{21}{5},\dfrac{7}{5}⟩. \end{align*}\] Теперь рассмотрим вектор \(\vecs{ q}=\vecs{ v}−\vecs{ p}. \[\begin{align*} \vecs { q} =\vecs{ v}−\vecs{ p} \\[4pt] = ⟨6,−4⟩−⟨\dfrac{21}{5},\dfrac{7}{5}⟩ \\[ 4pt] = ⟨\dfrac{9}{5},−\dfrac{27}{5}⟩. \end{align*}\] Очевидно, по тому, как мы определили \(\vecs{ q}\), имеем \(\vecs{ v}=\vecs{ q}+\vecs{ p},\ ) и \[\begin{align*}\vecs{ q}⋅\vecs{ p} =⟨\dfrac{9}{5},−\dfrac{27}{5}⟩⋅⟨\dfrac{21}{5 },\dfrac{7}{5}⟩ \\[4pt] = \dfrac{9(21)}{25}+−\dfrac{27(7)}{25} \\[4pt] = \dfrac{ 189}{25}−\dfrac{189}{25}=0. \end{align*}\] Следовательно, \(\vecs{ q}\) и \(\vecs{ p}\) ортогональны. Пример \(\PageIndex{8}\): преобразование векторов в компонентыВыразите \(\vecs{ v}=⟨8,−3,−3⟩\) в виде суммы ортогональных вектора имеют то же направление, что и \(\vecs{ u}=⟨2,3,2⟩.\) 92}⟨2,3,2⟩ \\[4pt] &=\dfrac{1}{17}⟨2,3,2⟩ \\[4pt] &=⟨\dfrac{2}{17},\dfrac {3}{17},\dfrac{2}{17}⟩. \end{align*} \nonumber \] Затем \[ \begin{align*} \vecs{q} &=\vecs{v}-\vecs{p}=⟨8,-3,- 3⟩−⟨\dfrac{2}{17},\dfrac{3}{17},\dfrac{2}{17}⟩\\[4pt] &=⟨\dfrac{134}{17},−\ dfrac{54}{17},−\dfrac{53}{17}⟩. Чтобы проверить нашу работу, мы можем использовать скалярное произведение, чтобы убедиться, что векторы \(\vecs{ p}\) и \(\vecs{ q}\) являются ортогональными векторами: \[ \begin{align*}\vecs{ p}⋅\vecs{ q}&=⟨\dfrac{2}{17},\dfrac{3}{17},\dfrac{2}{17}⟩ ⋅⟨\dfrac{134}{17},−\dfrac{54}{17},−\dfrac{53}{17}⟩\\[4pt] &=\dfrac{268}{289}-\dfrac{162}{289}-\dfrac{106}{289}=0. \end{align*} \nonumber \] Затем \[\vecs{ v}=\vecs{ p}+\vecs{ q}=⟨\dfrac{2}{17},\dfrac{3 }{17},\dfrac{2}{17}⟩+⟨\dfrac{134}{17},-\dfrac{54}{17},-\dfrac{53}{17}⟩. \nonumber \] Упражнение \(\PageIndex{7}\)Выразите \(\vecs{ v}=5\mathbf{\hat i}−\mathbf{\hat j}\) в виде суммы ортогональных такие, что один из векторов имеет то же направление, что и \(\vecs{u}=4\mathbf{\hat i}+2\mathbf{\hat j}\).
Пример \(\PageIndex{9}\): Скалярная проекция скорости Контейнеровоз выходит из порта и движется \(15°\) к северу от востока. Решение Пусть \(\vecs{ v}\) будет вектором скорости, создаваемой двигателем, и пусть \(\vecs{w}\) будет вектором скорости течения. Мы уже знаем \(‖\vecs{ v}‖=20\) вдоль нужного маршрута. Нам просто нужно добавить скалярную проекцию \(\vecs{w}\) на \(\vecs{v}\). Получаем \[ \begin{align*} \text{comp}_\vecs{ v}\vecs{w}=\dfrac{\vecs{ v}⋅\vecs{w}}{‖\vecs{ v }‖} \\[4pt] =\dfrac{‖\vecs{ v}‖‖\vecs{ w}‖\cos(30°)}{‖\vecs{ v}‖} =‖\vecs{ w}‖ \cos(30°) =2\dfrac{\sqrt{3}}{2}=\sqrt{3}≈1,73\,\text{узлы.}\end{align*}\] Судно движется со скоростью 21,73 узла в направлении \(15°\) к северо-востоку. Упражнение \(\PageIndex{8}\) Повторите предыдущий пример, но предположите, что океанское течение движется на юго-восток, а не на северо-восток, как показано на следующем рисунке.
РаботаТеперь, когда мы понимаем точечные произведения, мы можем увидеть, как применять их в реальных ситуациях. Чаще всего скалярное произведение двух векторов применяется для расчета работы. Из физики мы знаем, что работа совершается, когда объект перемещается под действием силы. Когда сила постоянна и приложена в том же направлении, в котором движется объект, тогда мы определяем проделанную работу как произведение силы на расстояние, которое проходит объект: \(W=Fd\). Мы видели несколько примеров этого типа в предыдущих главах. Теперь представьте, что направление силы отличается от направления движения, как в примере с ребенком, тянущим тележку. Чтобы найти совершенную работу, нужно умножить составляющую силы, действующей в направлении движения, на величину перемещения. Определение: постоянная силаКогда к объекту приложена постоянная сила, так что объект движется по прямой из точки \(P\) в точку \(Q\), работа \(W\), выполненная сила \(\vecs{ F}\), действующая под углом θ от линии движения, равна \[W=\vecs{ F}⋅\vecd{PQ}=∥\vecs{ F }∥∥\vecd{PQ}∥\cos θ. \nonumber \] Давайте вернемся к проблеме детской тележки, представленной ранее. Предположим, ребенок тянет тележку с силой 8 фунтов на ручке под углом 55° . Если ребенок протащит тележку на 50 футов, найдите работу силы (рисунок \(\PageIndex{8}\)). Рисунок \(\PageIndex{8}\): Горизонтальная составляющая силы представляет собой проекцию \(\vecs{ F}\) на положительную ось \(x\).Имеем \[W=∥\vecs{ F}∥∥\vecd{PQ}∥\cos θ=8(50)(\cos(55°))≈229\,\text{ft⋅lb. В стандартных единицах США мы измеряем величину силы \(∥\vecs{ F}∥\) в фунтах. Величина вектора смещения \(∥\vecd{PQ}∥\) говорит нам, как далеко переместился объект, и измеряется в футах. Таким образом, общепринятой единицей измерения труда является футо-фунт. Один футо-фунт — это количество работы, необходимой для перемещения объекта весом 1 фунт на расстояние 1 фут по прямой. В метрической системе единицей измерения силы является ньютон (Н), а единицей измерения величины работы — ньютон-метр (Н·м) или джоуль (Дж). Пример \(\PageIndex{10}\): Расчет работыКонвейерная лента создает силу \(\vecs{ F}=5\mathbf{\hat i}−3\mathbf{\hat j}+\ mathbf{\hat k}\), который перемещает чемодан из точки \((1,1,1)\) в точку \((9,4,7)\) по прямой. Найдите работу, совершенную конвейерной лентой. Расстояние измеряется в метрах, а сила измеряется в ньютонах. Решение Вектор смещения \(\vecd{PQ}\) имеет начальную точку \((1,1,1)\) и конечную точку \((9,4,7)\): \[\vecd{PQ}=⟨9−1,4−1,7−1⟩=⟨8,3,6⟩=8\mathbf{\шляпа i}+3 \mathbf{\шляпа j}+6\mathbf{\шляпа k}. Работа есть точечный продукт силы и перемещения: \[\begin{align*} W &=\vecs{ F}⋅\vecd{PQ} \\[4pt] &= (5\ mathbf {\ шляпа i} −3 \ mathbf {\ шляпа j} + \ mathbf {\ шляпа k}) ⋅ (8 \ mathbf {\ шляпа i} +3 \ mathbf {\ шляпа j} +6 \ mathbf {\ шляпа k}) \\[4pt] = 5(8)+(−3)(3)+1(6) \\[4pt] &=37\,\text{N⋅m} \\[4pt] &= 37\,\text{J} \end{align*}\] Упражнение \(\PageIndex{9}\)Постоянная сила 30 фунтов приложена под углом 60°, чтобы протащить ручную тележку на 10 футов по земле. Какую работу совершает эта сила?
Ключевые понятия
 \) \)Ключевые уравнения
\(\vecs{ u}⋅\vecs{ v}=u_1v_1+u_2v_2+u_3v_3=‖\vecs{ u}‖‖\vecs{ v}‖\cos θ\)
\(\cos θ=\dfrac{\vecs{ u}⋅\vecs{v}}{‖\vecs{ u}‖‖\vecs{v}‖}\)
| ||||||||||||||||||||||||

 .. / / Скалярное произведение векторов. Он-лайн калькуляторы скалярного произведения и угла между векторами по координатам.
.. / / Скалярное произведение векторов. Он-лайн калькуляторы скалярного произведения и угла между векторами по координатам. 




 =a→·npa→b→=b→·npb→a→ показывает, что npb→a→ — это числовая проекция a→ на b→, npa→a→- проекция b→ на a→ соостветсвенно.
=a→·npa→b→=b→·npb→a→ показывает, что npb→a→ — это числовая проекция a→ на b→, npa→a→- проекция b→ на a→ соостветсвенно. )==ax·bx+ay·by+az·bz
)==ax·bx+ay·by+az·bz )=3·7·cos60°=3·7·12=212
)=3·7·cos60°=3·7·12=212 )+24·n→2==35·32+71·3·2·cosπ2+24·22=411.
)+24·n→2==35·32+71·3·2·cosπ2+24·22=411. )=5·3·cos(45°)=1522.
)=5·3·cos(45°)=1522. Реферат
от 1 дня / от 700 р.
Реферат
от 1 дня / от 700 р. Результат скалярного произведения векторов является скалярной величиной. Таким образом, скалярное произведение также известно как скалярное произведение. Алгебраически это сумма произведений соответствующих записей двух последовательностей чисел. Геометрически это произведение евклидовой величины двух векторов и косинуса угла между ними. Скалярное произведение векторов находит различные применения в геометрии, механике, технике и астрономии. Давайте подробно обсудим скалярный продукт в следующих разделах.
Результат скалярного произведения векторов является скалярной величиной. Таким образом, скалярное произведение также известно как скалярное произведение. Алгебраически это сумма произведений соответствующих записей двух последовательностей чисел. Геометрически это произведение евклидовой величины двух векторов и косинуса угла между ними. Скалярное произведение векторов находит различные применения в геометрии, механике, технике и астрономии. Давайте подробно обсудим скалярный продукт в следующих разделах.

 Проведите AL перпендикулярно OB.
Проведите AL перпендикулярно OB. Формула для угла между двумя векторами выглядит следующим образом. 92}}\)
Формула для угла между двумя векторами выглядит следующим образом. 92}}\) Матрица транспонирования первого вектора получается как матрица-строка. Производится умножение матриц. Матрица-строка и матрица-столбец перемножаются, чтобы получить сумму произведения соответствующих компонентов двух векторов.
Матрица транспонирования первого вектора получается как матрица-строка. Производится умножение матриц. Матрица-строка и матрица-столбец перемножаются, чтобы получить сумму произведения соответствующих компонентов двух векторов. Это свойство можно распространить на любое количество векторов.
Это свойство можно распространить на любое количество векторов. ].
]. \overrightarrow a\) = \(|\overrightarrow a\)| 2 (или) можно записать как 2
\overrightarrow a\) = \(|\overrightarrow a\)| 2 (или) можно записать как 2  Скалярное произведение единичных векторов \(\hat i\), \(\hat j\), \(\hat k\) подчиняется тем же правилам, что и скалярное произведение векторов. Угол между одинаковыми векторами равен 0º, а значит, их скалярное произведение равно 1. А угол между двумя перпендикулярными векторами равен 90º, а их скалярное произведение равно 0,9.0003
Скалярное произведение единичных векторов \(\hat i\), \(\hat j\), \(\hat k\) подчиняется тем же правилам, что и скалярное произведение векторов. Угол между одинаковыми векторами равен 0º, а значит, их скалярное произведение равно 1. А угол между двумя перпендикулярными векторами равен 90º, а их скалярное произведение равно 0,9.0003 \overrightarrow b\) = 0
\overrightarrow b\) = 0 Алгебраически скалярное произведение двух векторов равно сумме произведений отдельных компонентов двух векторов. \(\overrightarrow a. \overrightarrow b\) = \(a_1b_1\) + \(a_2b_2\)+ \(a_3b_3\). Геометрически скалярное произведение двух векторов есть произведение величины векторов и косинуса угла между двумя векторами. ( \(\overrightarrow a. \overrightarrow b\) = \(|\overrightarrow a||\overrightarrow b|\) cos θ). Результат скалярного произведения векторов является скалярным значением.
Алгебраически скалярное произведение двух векторов равно сумме произведений отдельных компонентов двух векторов. \(\overrightarrow a. \overrightarrow b\) = \(a_1b_1\) + \(a_2b_2\)+ \(a_3b_3\). Геометрически скалярное произведение двух векторов есть произведение величины векторов и косинуса угла между двумя векторами. ( \(\overrightarrow a. \overrightarrow b\) = \(|\overrightarrow a||\overrightarrow b|\) cos θ). Результат скалярного произведения векторов является скалярным значением. Скалярное произведение двух векторов равно \(\overrightarrow a. \overrightarrow b\) = \(|\overrightarrow a|.|\overrightarrow b|\)Cosθ, а перекрестное произведение двух векторов равно \(\overrightarrow a \) × \(\overrightarrow b\) = \(|\overrightarrow a|.|\overrightarrow b|\) Sinθ.\(\hat{n}\). Результат скалярного произведения двух векторов лежит в той же плоскости, что и два вектора, тогда как результат перекрестного произведения лежит в плоскости, перпендикулярной плоскости, охватывающей два вектора.
Скалярное произведение двух векторов равно \(\overrightarrow a. \overrightarrow b\) = \(|\overrightarrow a|.|\overrightarrow b|\)Cosθ, а перекрестное произведение двух векторов равно \(\overrightarrow a \) × \(\overrightarrow b\) = \(|\overrightarrow a|.|\overrightarrow b|\) Sinθ.\(\hat{n}\). Результат скалярного произведения двух векторов лежит в той же плоскости, что и два вектора, тогда как результат перекрестного произведения лежит в плоскости, перпендикулярной плоскости, охватывающей два вектора.
 Если скалярное произведение равно 0, то мы можем заключить, что либо длина одного или обоих векторов равна 0, либо угол между ними равен 90 градусов.
Если скалярное произведение равно 0, то мы можем заключить, что либо длина одного или обоих векторов равна 0, либо угол между ними равен 90 градусов. (\(\overrightarrow a. \overrightarrow b\) = \(|\overrightarrow a|.|\overrightarrow b|\).Cosθ. Также проверьте калькулятор скалярного произведения, чтобы легко найти векторное скалярное произведение.
(\(\overrightarrow a. \overrightarrow b\) = \(|\overrightarrow a|.|\overrightarrow b|\).Cosθ. Также проверьте калькулятор скалярного произведения, чтобы легко найти векторное скалярное произведение.
 Для двух ненулевых векторов скалярное произведение равно нулю, если угол между двумя векторами равен 90º, потому что Cos90º = 0.
Для двух ненулевых векторов скалярное произведение равно нулю, если угол между двумя векторами равен 90º, потому что Cos90º = 0.


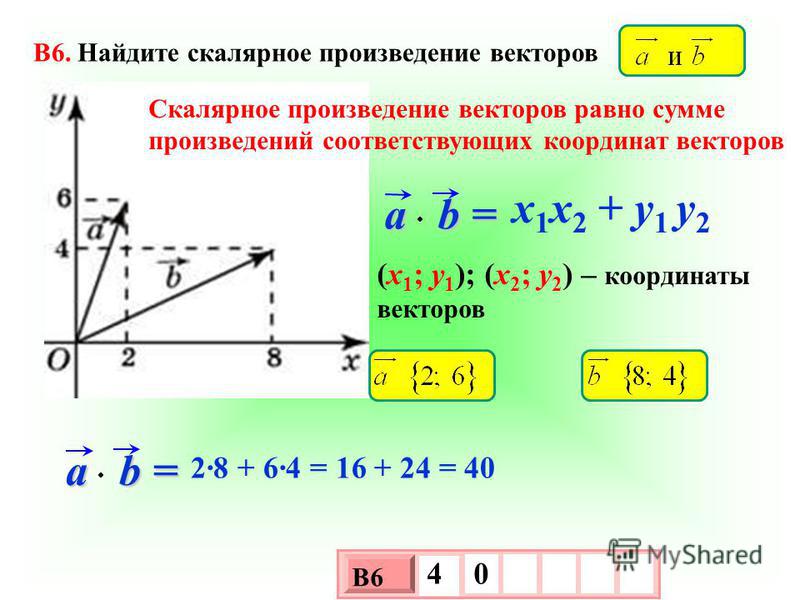 ..
..


 Поскольку координаты x и y не влияют друг на друга (как держать ведро боком под водопадом — ничего не падает), полное поглощение энергии равно поглощению (x) + поглощению (y):
Поскольку координаты x и y не влияют друг на друга (как держать ведро боком под водопадом — ничего не падает), полное поглощение энергии равно поглощению (x) + поглощению (y): Вот некоторые аналогии, которые меня зацепили:
Вот некоторые аналогии, которые меня зацепили: Чем больше число, тем больше сила.
Чем больше число, тем больше сила. Мы хотели бы размножаться, и мы могли бы, если бы все было выстроено в ряд. Но это не так, поэтому мы берем скалярное произведение для учета возможных различий в направлении.
Мы хотели бы размножаться, и мы могли бы, если бы все было выстроено в ряд. Но это не так, поэтому мы берем скалярное произведение для учета возможных различий в направлении. Скалярное произведение двух векторов означает скалярное произведение двух заданных векторов. Это скалярное число, которое получается путем выполнения определенной операции над различными компонентами вектора. Скалярное произведение применимо только для пар векторов с одинаковым числом измерений. Символ, используемый для скалярного произведения, — толстая точка. Это скалярное произведение широко используется в математике и физике. В этой статье мы подробно обсудим скалярное произведение векторов, определение скалярного произведения, формулу скалярного произведения и пример скалярного произведения.
Скалярное произведение двух векторов означает скалярное произведение двух заданных векторов. Это скалярное число, которое получается путем выполнения определенной операции над различными компонентами вектора. Скалярное произведение применимо только для пар векторов с одинаковым числом измерений. Символ, используемый для скалярного произведения, — толстая точка. Это скалярное произведение широко используется в математике и физике. В этой статье мы подробно обсудим скалярное произведение векторов, определение скалярного произведения, формулу скалярного произведения и пример скалярного произведения.
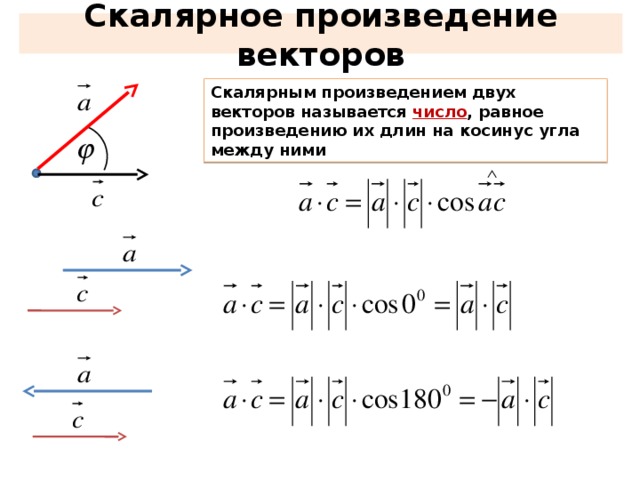 b =|b||a|cos θ
b =|b||a|cos θ время t, и, следовательно, функция r(t)⋅u(t) называется скалярной функцией.
время t, и, следовательно, функция r(t)⋅u(t) называется скалярной функцией.

 Раньше мы рассматривали постоянную силу и предполагали, что сила приложена в направлении движения объекта. В этих условиях работу можно выразить как произведение силы, действующей на объект, и расстояния, которое этот объект перемещает. Однако в этой главе мы увидели, что и сила, и движение объекта могут быть представлены векторами.
Раньше мы рассматривали постоянную силу и предполагали, что сила приложена в направлении движения объекта. В этих условиях работу можно выразить как произведение силы, действующей на объект, и расстояния, которое этот объект перемещает. Однако в этой главе мы увидели, что и сила, и движение объекта могут быть представлены векторами. Первый тип векторного умножения называется скалярным произведением, основанным на обозначениях, которые мы используем для него, и определяется следующим образом:
Первый тип векторного умножения называется скалярным произведением, основанным на обозначениях, которые мы используем для него, и определяется следующим образом:
 \end{align* }\]
\end{align* }\] \) Тогда
\) Тогда \) По свойству iv. если \(\vecs{ v}⋅\vecs{ v}=0,\), то \(\vecs{ v}=\vecs{ 0}.\)
\) По свойству iv. если \(\vecs{ v}⋅\vecs{ v}=0,\), то \(\vecs{ v}=\vecs{ 0}.\) \end{align*}\] 92=53\)
\end{align*}\] 92=53\) Эти три вектора образуют треугольник с длинами сторон \(‖\vecs{ u}‖,‖\vecs{ v}‖\) и \(‖\vecs{ v}−\vecs{ u}‖\). 92−2‖\vecs{ u}‖‖\vecs{ v}‖\cos θ \\[4pt] −2\vecs{ u}⋅\vecs{ v} &=−2‖\vecs{ u}‖‖ \vecs{ v}‖\cos θ \\[4pt] \vecs{ u}⋅\vecs{ v} &=‖\vecs{ u}‖‖\vecs{ v}‖\cos θ. \end{align*}\]
Эти три вектора образуют треугольник с длинами сторон \(‖\vecs{ u}‖,‖\vecs{ v}‖\) и \(‖\vecs{ v}−\vecs{ u}‖\). 92−2‖\vecs{ u}‖‖\vecs{ v}‖\cos θ \\[4pt] −2\vecs{ u}⋅\vecs{ v} &=−2‖\vecs{ u}‖‖ \vecs{ v}‖\cos θ \\[4pt] \vecs{ u}⋅\vecs{ v} &=‖\vecs{ u}‖‖\vecs{ v}‖\cos θ. \end{align*}\] 2}} \\[4pt] &=\dfrac{-2}{\sqrt{3}\sqrt{14}} =\ dfrac{−2}{\sqrt{42}}. \end{выравнивание*}\] 92}} \\[4pt] &=\dfrac{0}{\sqrt{65}\sqrt{36}}=0.\end{align*}\]
2}} \\[4pt] &=\dfrac{-2}{\sqrt{3}\sqrt{14}} =\ dfrac{−2}{\sqrt{42}}. \end{выравнивание*}\] 92}} \\[4pt] &=\dfrac{0}{\sqrt{65}\sqrt{36}}=0.\end{align*}\] \end{align*}\]
\end{align*}\]
 α≈1,04\) рад; б. \(β≈2,58\) рад; в. \(γ≈1,40\) рад
α≈1,04\) рад; б. \(β≈2,58\) рад; в. \(γ≈1,40\) рад В этом примере, хотя мы все еще можем изобразить эти векторы, мы не интерпретируем их как буквальное представление положения в физическом мире. Мы просто используем векторы для отслеживания отдельных фрагментов информации о яблоках, бананах и апельсинах.
В этом примере, хотя мы все еще можем изобразить эти векторы, мы не интерпретируем их как буквальное представление положения в физическом мире. Мы просто используем векторы для отслеживания отдельных фрагментов информации о яблоках, бананах и апельсинах. Что, если продавец фруктов решит начать продавать грейпфруты? В этом случае он хотел бы использовать четырехмерные векторы количества и цены для представления количества проданных яблок, бананов, апельсинов и грейпфрутов и их цены за единицу. Как и следовало ожидать, чтобы вычислить скалярное произведение четырехмерных векторов, мы просто складываем произведения компонентов, как и раньше, но сумма состоит из четырех членов вместо трех.
Что, если продавец фруктов решит начать продавать грейпфруты? В этом случае он хотел бы использовать четырехмерные векторы количества и цены для представления количества проданных яблок, бананов, апельсинов и грейпфрутов и их цены за единицу. Как и следовало ожидать, чтобы вычислить скалярное произведение четырехмерных векторов, мы просто складываем произведения компонентов, как и раньше, но сумма состоит из четырех членов вместо трех. Украшения продаются по 4,50 доллара за штуку, а предметы общественного питания по 1,25 доллара за упаковку.
Украшения продаются по 4,50 доллара за штуку, а предметы общественного питания по 1,25 доллара за упаковку. Мы используем скалярное произведение \(\vecs{c}⋅\vecs{q}\), чтобы получить
Мы используем скалярное произведение \(\vecs{c}⋅\vecs{q}\), чтобы получить
 \) У нас есть
\) У нас есть \end{align*} \nonumber \]
\end{align*} \nonumber \] Его двигатель развивает на этом пути скорость 20 узлов (см. следующий рисунок). Кроме того, океанское течение перемещает корабль на северо-восток со скоростью 2 узла. Учитывая и двигатель, и течение, с какой скоростью корабль движется в направлении \(15°\) к северу от востока? Округлите ответ до двух знаков после запятой.
Его двигатель развивает на этом пути скорость 20 узлов (см. следующий рисунок). Кроме того, океанское течение перемещает корабль на северо-восток со скоростью 2 узла. Учитывая и двигатель, и течение, с какой скоростью корабль движется в направлении \(15°\) к северу от востока? Округлите ответ до двух знаков после запятой.
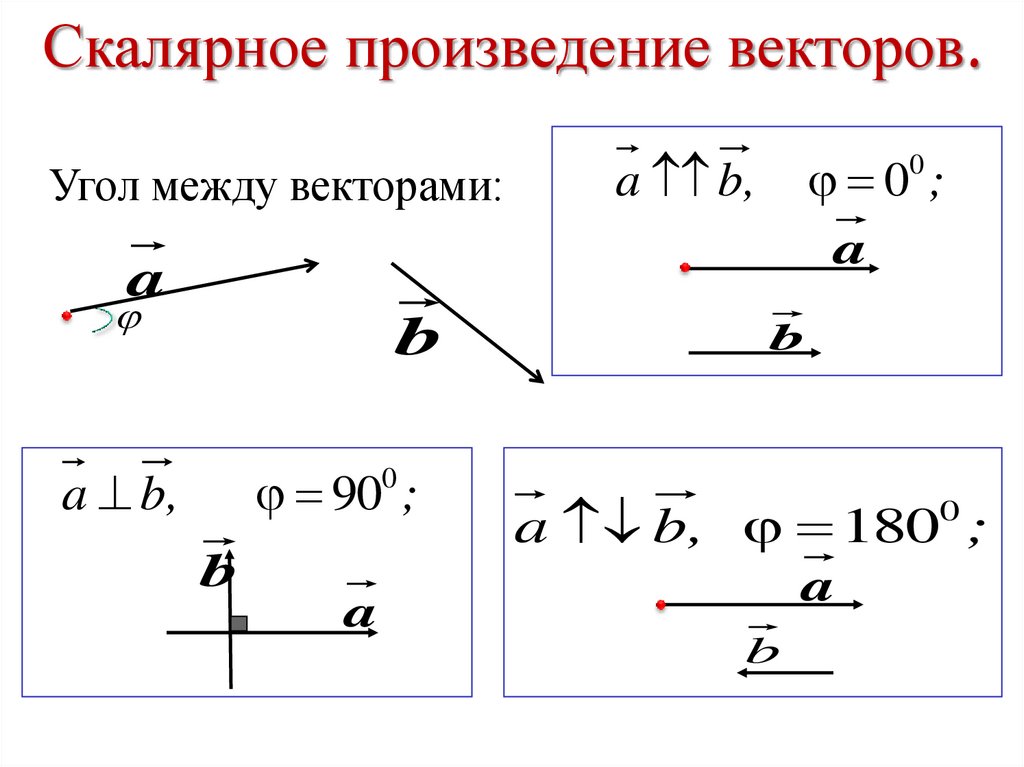 Скалярный продукт позволяет нам сделать именно это. Если представить приложенную силу вектором \(\vecs{ F}\), а перемещение объекта вектором \(\vecs{ s}\), то работа, выполненная силой , является скалярным произведением \(\vecs{F}\) и \(\vecs{s}\).
Скалярный продукт позволяет нам сделать именно это. Если представить приложенную силу вектором \(\vecs{ F}\), а перемещение объекта вектором \(\vecs{ s}\), то работа, выполненная силой , является скалярным произведением \(\vecs{F}\) и \(\vecs{s}\). } \nonumber \]
} \nonumber \] \nonumber \]
\nonumber \] 92\)
92\)
 org/details/books/calculus-volume-1
org/details/books/calculus-volume-1 14). Доказательство третьего свойства заключается в расширении правой части уравнения с использованием CVN и свойств, объясненных ниже.
14). Доказательство третьего свойства заключается в расширении правой части уравнения с использованием CVN и свойств, объясненных ниже. Уравнение 2.15 показывает, что для вычисления скалярного произведения (уравнение 2.14) не нужны величины двух векторов и угол между ними, если векторы выражены в CVN.
Уравнение 2.15 показывает, что для вычисления скалярного произведения (уравнение 2.14) не нужны величины двух векторов и угол между ними, если векторы выражены в CVN. Точнее, нужно найти составляющую вектора вдоль определенного направления или оси. Разложение вектора по декартовым осям уже продемонстрировано. В этом разделе мы объясняем разложение вектора на общую прямую в пространстве с помощью скалярного произведения. Использование скалярного произведения упрощает вычисления, особенно в трех измерениях.
Точнее, нужно найти составляющую вектора вдоль определенного направления или оси. Разложение вектора по декартовым осям уже продемонстрировано. В этом разделе мы объясняем разложение вектора на общую прямую в пространстве с помощью скалярного произведения. Использование скалярного произведения упрощает вычисления, особенно в трех измерениях.
