Пракикум «Решение задач по комбинаторике»
Комбинаторика – это раздел математики, посвящённый решению задач выбора и расположения элементов некоторого множества в соответствии с заданными правилами. Комбинаторика изучает комбинации и перестановки предметов, расположение элементов, обладающее заданными свойствами. Обычный вопрос в комбинаторных задачах: сколькими способами….
К комбинаторным задачам относятся также задачи построения магических квадратов, задачи расшифровки и кодирования.
Рождение комбинаторики как раздела математики связано с трудами великих французских математиков 17 века Блеза Паскаля (1623–1662) и Пьера Ферма (1601–1665) по теории азартных игр. Эти труды содержали принципы определения числа комбинаций элементов конечного множества. С 50-х годов 20 века интерес к комбинаторике возрождается в связи с бурным развитием кибернетики.
Основные правила комбинаторики – это правило суммы и правило произведения

- Правило суммы
Если некоторый элемент А можно выбрать n способами, а элемент В можно выбрать m способами, то выбор «либо А, либо В» можно сделать n + m способами.
Например, Если на тарелке лежат 5 яблок и 6 груш, то один плод можно выбрать 5 + 6 = 11 способами.
- Правило произведения
Если элемент А можно выбрать n способами, а элемент В можно выбрать m способами, то пару А и В можно выбрать n • m способами.
Например, если есть 2 разных конверта и 3 разные марки, то выбрать конверт и марку можно 6 способами (2 • 3 = 6).
Правило произведения верно и в том случае, когда рассматривают элементы нескольких множеств.
Например, если есть 2 разных конверта, 3 разные марки и 4 разные открытки, то выбрать конверт, марку и открытку можно 24 способами (2 • 3 • 4 = 24).
Произведение всех натуральных чисел от 1 до n включительно называется n – факториалом и обозначается символом n!
n! = 1 • 2 • 3 • 4 •…• n.
Например, 5! = 1 • 2 • 3 • 4 • 5 = 120.
Принято считать 0! равным 1.
Число перестановок из n равна n!
Например, если есть 3 шарика – красный, синий и зелёный, то выложить их в ряд можно 6 способами (3 • 2 • 1 = 3! = 6).
Иногда комбинаторная задача решается с помощью построения дерева возможных вариантов.
Например, решим предыдущую задачу о 3-х шарах построением дерева.
Практикум по решению задач по комбинаторике.
ЗАДАЧИ и решения
1. В вазе 6 яблок, 5 груш и 4 сливы. Сколько вариантов выбора одного плода?
6 + 5 + 4 = 15
Ответ: 15 вариантов.
2. Сколько существует вариантов покупки одной розы, если продают 3 алые, 2 алые и 4 жёлтые розы?
3 + 2 + 4 = 9
Ответ: 9 вариантов.
3. Из города А в город В ведут пять дорог, а из города В в город С ведут три дороги. Сколько путей, проходящих через В, ведут из А в С?
5 • 3 = 15
Ответ: 15 путей.
4. Сколькими способами можно составить пару из одной гласной и одной согласной букв слова «платок»?
гласные: а, о – 2 шт.
согласные: п, л, т, к – 4 шт.2 • 4 = 8
Ответ: 8 способами.
5. Сколько танцевальных пар можно составить из 8 юношей и 6 девушек?
6 • 8 = 48
Ответ: 48 пар.
6. В столовой есть 4 первых блюда и 7 вторых. Сколько различных вариантов обеда из двух блюд можно заказать?
4 • 8 = 28
Ответ: 28 вариантов.
7. Сколько различных двузначных чисел можно составить, используя цифры 1, 4 и 7, если цифры могут повторяться?
1 цифра – 3 способа
2 цифра – 3 способа
3 цифра – 3 способа3 • 3 = 9
Ответ: 9 различных двузначных чисел.
8. Сколько различных трёхзначных чисел можно составить, используя цифры 3 и 5, если цифры могут повторяться?
1 цифра – 2 способа
2 цифра – 2 способа
3 цифра – 2 способа2 • 2 • 2 = 8
Ответ: 8 различных чисел.
9. Сколько различных двузначных чисел можно составить из цифр 0, 1, 2, 3, если цифры могут повторяться?
1 цифра – 3 способа
2 цифра – 4 способа3 • 4 = 12
Ответ: 12 различных чисел.
10. Сколько существует трёхзначных чисел, у которых все цифры чётные?
Чётные цифры – 0, 2, 4, 6, 8.
1 цифра – 4 способа
2 цифра – 5 способов
3 цифра – 5 способов4 • 5 • 5 = 100
Ответ: существует 100 чисел.
11. Сколько существует четных трёхзначных чисел?
1 цифра – 9 способов (1, 2, 3, 4, 5, 6, 7, 8, 9)
3 цифра – 5 способов (0, 2, 4, 6, 8)
2 цифра – 10 способов (0, 1, 2, 3, 4, 5, 6, 7, 8, 9)9 • 10 • 5 = 450
Ответ: существует 450 чисел.
12.Сколько различных трёхзначных чисел можно составить из трёх различных цифр 4, 5, 6?
1 цифра – 3 способа
2 цифра – 2 способа
3 цифра – 1 способ3 • 2 • 1 = 6
Ответ: 6 различных чисел.
13. Сколькими способами можно обозначить вершины треугольника, используя буквы А, В, С, D?
1 вершина – 4 способа
2 вершина – 3 способа
3 вершина – 2 способа4 • 3 • 2 = 24
Ответ: 24 способа.
14. Сколько различных трёхзначных чисел можно составить из цифр 1, 2, 3, 4, 5,при условии, что ни одна цифра не повторяется?
1 цифра – 5 способов
2 цифра – 4 способа
3 цифра – 3 способа5 • 4 • 3 = 60
Ответ: 60 различных чисел.
15. Сколько различных трёхзначных чисел, меньших 400, можно составить из цифр 1, 3, 5, 7, 9, если любая из этих цифр может быть использована только один раз?
1 цифра – 2 способа
2 цифра – 4 способа
3 цифра – 3 способа2 • 4 • 3 = 24
Ответ: 24 различных числа.
16. Сколькими способами можно составить флаг, состоящий из трёх горизонтальных полос различных цветов, если имеется материал шести цветов?
1 полоса – 6 способов
2 полоса – 5 способов
3 полоса – 4 способа6 • 5 • 4 = 120
Ответ: 120 способов.
17. Из класса выбирают 8 человек, имеющих лучшие результаты по бегу. Сколькими способами можно составить из них команду из трёх человек для участия в эстафете?
1 человек – 8 способов
2 человек – 7 способов
3 человек – 6 способов8 • 7 • 6 = 336
Ответ: 336 способов.
18. В четверг в первом классе должно быть четыре урока: письмо, чтение, математика и физкультура. Сколько различных вариантов расписания можно составить на этот день?
1 урок – 4 способа
2 урок – 3 способа
3 урок – 2 способа
4 урок – 1 способ4 • 3 • 2 • 1 = 24
Ответ: 24 варианта.
19. В пятом классе изучаются 8 предметов. Сколько различных вариантов расписания можно составить на понедельник, если в этот день должно быть 5 уроков и все уроки разные?
1 урок – 8 вариантов
2 урок – 7 вариантов
3 урок – 6 вариантов
4 урок – 5 вариантов
5 урок – 4 варианта8 • 7 • 6 • 5 • 4 = 6720
Ответ: 6720 вариантов.
20. Шифр для сейфа составляется из пяти различных цифр. Сколько различных вариантов составления шифра?
1 цифра – 5 способов
2 цифра – 4 способа
3 цифра – 3 способа
4 цифра – 2 способа
5 цифра – 1 способ5 • 4 • 3 • 2 • 1 = 120
Ответ: 120 вариантов.
21. Сколькими способами можно разместить 6 человек за столом, на котором поставлено 6 приборов?
6 • 5 • 4 • 3 • 2 • 1 = 720Ответ: 720 способов.
22. Сколько вариантов семизначных телефонных номеров можно составить, если исключить из них номера, начинающиеся с нуля и 9?
1 цифра – 8 способов
2 цифра – 10 способов
3 цифра – 10 способов
4 цифра – 10 способов
5 цифра – 10 способов
6 цифра – 10 способов
7 цифра – 10 способов8 • 10 • 10 • 10 • 10 • 10 • 10 = 8.000.000
Ответ: 8.000.000 вариантов.
23. Телефонная станция обслуживает абонентов, у которых номера телефонов состоят из 7 цифр и начинаются с 394. На сколько абонентов рассчитана эта станция?
№ телефона 394
10 • 10 • 10 • 10 = 10.000
Ответ: 10.000 абонентов.
24. Имеется 6 пар перчаток различных размеров. Сколькими способами можно выбрать из них одну перчатку на левую руку и одну перчатку на правую руку так, чтобы эти перчатки были различных размеров?
Левые перчатки – 6 способов
Правые перчатки – 5 способов (6 перчатка того же размера, что и левая)6 • 5 = 30
Ответ: 30 способов.
25 . Из цифр 1, 2, 3, 4, 5 составляют пятизначные числа, в которых все цифры разные. Сколько таких чётных чисел?
5 цифра – 2 способа (две чётные цифры)
4 цифра – 4 способа
3 цифра – 3 способа
2 цифра – 2 способа
1 цифра – 1 способ2 • 4 • 3 • 2 • 1 = 48
Ответ: 48 чётных чисел.
26. Сколько существует четырёхзначных чисел, составленных из нечётных цифр и делящихся на 5?
Нечётные цифр – 1, 3, 5, 7, 9.
Из них делятся на 5 – 5.
4 цифра – 1 способ (цифра 5)
3 цифра – 4 способа
2 цифра – 3 способа
1 цифра – 2 способа1 • 4 • 3 • 2 = 24
Ответ: 24 числа.
27. Сколько существует пятизначных чисел, у которых третья цифра – 7, последняя цифра – чётная?
1 цифра – 9 способов (все, кроме 0)
2 цифра – 10 способов
3 цифра – 1 способ (цифра 7)
4 цифра – 10 способов
5 цифра – 5 способов (0, 2, 4, 6, 8)9 • 10 • 1 • 10 • 5 = 4500
Ответ: 4500 чисел.
28. Сколько существует шестизначных чисел, у которых вторая цифра – 2, четвёртая – 4, шестая – 6, а все остальные – нечётные?
1 цифра – 5 вариантов (из 1, 3, 5, 7, 9)
2 цифра – 1 вариант (цифра 2)
3 цифра – 5 вариантов
4 цифра – 1 вариант (цифра 4)
5 цифра – 5 вариантов
6 цифра – 1 вариант (цифра 6)5 • 1 • 5 • 1 • 5 • 1 = 125
Ответ: 125 чисел.
29.Сколько различных чисел, меньших миллиона, можно записать с помощью цифр 8 и 9?
Однозначных – 2
Двузначных – 2 • 2 = 4
Трёхзначных – 2 • 2 • 2 = 8
Четырёхзначных – 2 • 2 • 2 • 2 =16
Пятизначных – 2 • 2 • 2 • 2 • 2 = 32
Шестизначных – 2 • 2 • 2 • 2 2 • 2 = 64Всего: 2 + 4 + 8 + 16 + 32 + 64 = 126
Ответ: 126 чисел.
30. В футбольной команде 11 человек. Нужно выбрать капитана и его
заместителя. Сколькими способами это можно сделать?
В футбольной команде 11 человек. Нужно выбрать капитана и его
заместителя. Сколькими способами это можно сделать?
Капитан – 11 способов
Заместитель – 10 способов11 • 10 = 110
Ответ: 110 способов.
31.В классе учатся 30 человек. Сколькими способами из них можно выбрать старосту и ответственного за проездные билеты?
Староста – 30 способов
Ответ. за билеты – 29 способов30 • 29 = 870
Ответ: 870 способов.
32. В походе участвуют 12 мальчиков, 10 девочек и 2 учителя. Сколько вариантов групп дежурных из трёх человек (1 мальчик, 1 девочка, 1 учитель) можно составить?
12 • 10 • 2 = 240
Ответ: 240 способов.
33. Сколько комбинаций из четырёх букв русского алфавита (в алфавите всего 33 буквы) можно составить при условии, что 2 соседние буквы будут разными?
1 буква – 33 способа
2 буква – 32 способа
3 буква – 32 способа
4 буква – 32 способа33 • 32 • 32 • 32 = 1.
081.344
Ответ: 1.081.344 комбинаций.
Подборка по базе: Биология в моей жизни – это все живое вокруг меня. Но разве мож, Как можно объяснить значение слова.pptx, В мире чисел 2 кл.docx, Урок математики.4 класс. Деловая игра. Многозначные числа. Умнож, 11.11. но-22с. мкш. составить глоссарий. срок выполнения 12 нояб, Где можно работать тренером или инструктором.docx, Деление отрицательных чисел карантин.ppt, Самостоятельная работа по теме «Сложение и вычитание смешанных ч, Отсканированный документ перевести в формат Word можно применив , Лекция 5. Закон больших чисел.pdf Комбинаторика 1 вариант Сколько четырехзначных чисел можно составить из цифр 1,2,3,0,5? Сколькими способами можно распределить 9 апельсинов, 5 банана, 1 яблоко, 2 груши на 2 обезьяны и 1 человека, так, чтобы каждому достался хотя бы один фрукт? Сколькими способами можно оформить витрину, если она заполняется 15 видами шоколада, расставленными в три ряда с одинаковым количеством плиток? Из колоды, содержащей 36 карт, вынули 10 карт.  Во скольких случаях среди этих карт окажется ровно три туза? Во скольких случаях среди этих карт окажется ровно три туза?Сколько различных слов можно получить, переставляя буквы в слове «программирование»? Комбинаторика 2 вариант 1.Сколько четных трехзначных чисел можно составить из цифр 4,2,3,0,1? 2.Сколькими способами можно распределить 18 одинаковых конфет по четырем различным карманам так, чтобы не было пустых карманов? 3.На железнодорожной станции имеется 10 светофоров. Сколько может быть дано различных сигналов, если каждый светофор имеет три состояния: красный, желтый и зеленый? 4. Из колоды, содержащей 36 карт, вынули 10 карт. Во скольких случаях среди этих карт окажется ровно две карты крести? 5.Сколькими способами можно выбрать12 человек из 17, если данные двое не могут быть выбраны вместе? 3 вариант 1. Сколько четырехзначных чисел можно составить из цифр 1,2,3,5? 2. Сколькими способами можно распределить 8 апельсинов, 3 банана, 1 яблоко, 1 грушу и 1 ананас на 4 человек, так, чтобы каждому достался хотя бы один фрукт? 3. 4.Из колоды, содержащей 52 карты, вынули 10 карт. Во скольких случаях среди этих карт окажется пиковая дама? 5.Сколько различных слов можно получить, переставляя буквы в слове «кибернетика»? Комбинаторика4 вариант Сколькими способами можно переставить буквы слова “каракули” так, чтобы никакие две гласные не стояли рядом? Сколько можно построить различных прямоугольных параллелепипедов, длина каждого ребра которых является целым числом от 1 до 10? У одного человека есть 7 книг, а у другого – 9 книг. Сколькими способами они могут обменять три книги одного на три книги другого? Сколькими способами можно разложить 9 книг на 4 бандероли по 2 книги и 1 бандероль в 1 книгу (порядок бандеролей не принимается во внимание)? Сколькими способами можно распределить купюру 50 р., 4 купюры по 100 р.  , 3 купюры по 500 р. и 4 купюры по 1000 р. на 3 человек, так, чтобы каждому досталась хотя бы одна купюра? , 3 купюры по 500 р. и 4 купюры по 1000 р. на 3 человек, так, чтобы каждому досталась хотя бы одна купюра? 5 вариант 1. Сколькими способами можно распределить купюру 50 р., 3 купюры по 100 р., 3 купюры по 500 р. и 4 купюры по 1000 р. на 5 человек, так, чтобы каждому досталась хотя бы одна купюра? Сколько чисел, меньше 1000, можно написать с помощью цифр 2,3 и 0? В автобус сели 9 человек. Сколькими способами они могут выйти на 6-х остановках? Скольким способами можно разделить колоду карт (36) на три равных части так, чтобы в каждой пачке было хотя бы по одному тузу? Сколько существует прямоугольников, длины сторон которых принимают одно из значений 4, 5,6,7? 6 вариант 1. Сколькими способами можно распределить купюру 50 р., 3 купюры по 100 р., 3 купюры по 500 р. и 4 купюры по 1000 р. на 5 человек? 2. 3. В лифт сели 9 человек. Сколькими способами они могут выйти на 4-х этажах, так, чтобы на каждом этаже вышел хотя бы один человек? 4. Скольким способами можно разделить колоду карт (36) пополам так, чтобы в каждой пачке было по два туза? 5. Сколько существует треугольников, длины сторон которых принимают одно из значений 4, 5,6,7? Комбинаторика7 вариант 1. Сколькими способами можно закодировать сейф с 5 дисками, содержащими по 10 различных цифр и 2 диска, содержащих по 30 различных букв? Сколькими способами можно распределить купюру 50 р., 4 купюры по 100 р., 3 купюры по 500 р., 2 купюры по 1000 р. на 6 человек, так, чтобы каждому досталась хотя бы одна купюра? Для премии на математической олимпиаде выделено 3 экземпляра одной книги, два экземпляра другой и один экземпляр третьей книги. Сколькими способами могут быть вручены премии, если в олимпиаде участвовало 20 человек, и никому не дают двух экземпляров одной и той же книги, но могут быть вручены две или три различные книги? Из колоды, содержащей 36 карт, вынули 10 карт.  Во скольких случаях среди этих карт окажется хотя бы один туз? Во скольких случаях среди этих карт окажется хотя бы один туз?Сколько существует кодов из пяти 0, четырех 1 и семи 2? 8 вариант Сколько различных слов можно получить, переставляя буквы в слове «публицистика»? Сколько 4-х значных чисел можно составить из цифр 0,1,2,3,4,5,6, если каждая из них, кроме 1, может повторяться несколько раз? Сколькими способами из группы студентов (5 девушек и 7 юношей) можно выбрать 4 человека так, чтобы в ней был хотя бы один юноша? Студент сдает 5 экзаменов. Какой набор оценок он может получить? Во сколько чисел от 0 до 9999 входит цифра 8? 9 вариант 1.Сколькими способами можно составить 6 слов из 32 букв, если в совокупности этих 6 слов каждая буква используется один и только один раз? 2.Из группы, состоящей из 8 мужчин и 9 женщин, надо выбрать 6 человек так, чтобы среди них было 4 мужчин. 3.Четверо студентов сдают экзамен. Сколькими способами могут быть поставлены им отметки, если известно, что все сдали экзамен? 4.Сколько существует целых чисел от 1 до 1000, которые не делятся ни на 3, ни на 7? 5.Сколько четырехзначных чисел оканчиваются цифрой 8? Комбинаторика10 вариант 1.Сколькими способами можно разложить 16 одинаковых купюр по шести различным карманам так, чтобы ни один из карманов не был пустым? 2.Из группы, состоящей из 9 мужчин и 5 женщин, надо выбрать 7 человек так, чтобы среди них было 2 женщины. Сколькими способами это можно сделать? 3.Четверо студентов сдают экзамен. Сколькими способами могут быть поставлены им отметки? 4.Сколько существует целых чисел от 1 до 1000, которые делятся на 4 или, на 6 или, на 9? 5.В селении проживает 2000 жителей. Доказать, что по крайней мере двое из них имеют одинаковые инициалы? Комбинаторика11 вариант Семь девушек и пятеро юношей играют в волейбол.  Сколькими способами они могут разбиться на две команды по 6 человек в каждой команде, если в каждой команде должно быть хотя бы по два юноше? Сколькими способами они могут разбиться на две команды по 6 человек в каждой команде, если в каждой команде должно быть хотя бы по два юноше?Сколько существует целых чисел от 1 до 1000, которые не делятся ни на 2, ни на 7, ни на 9? Сколькими способами 12 одинаковых монет можно разложить по пяти различным карманам, если ни один из карманов не должен быть пустым? Сколько чётных чисел можно составить из цифр числа 2378, если каждую цифру можно использовать не более одного раза? Сколькими способами можно распределить 9 студентов на 5 разных мест прохождения практики? 12 вариант 1. Сколькими способами можно из пяти одинаковых изумрудов, шести одинаковых рубинов и семи одинаковых сапфиров выбрать три камня для кольца? Сколькими способами можно распределить по трем пакетам (пакеты не различать) 8 различных книг? Сколько различных слов можно получить, переставляя буквы в слове “пересечение”? Сколькими способами можно расставить 12 белых и 12 черных шашек на черных полях шахматной доски? Сколькими способами можно послать 8 различных фотографий, используя 5 различных конвертов? 13 вариант 1. 2. Переплетчик должен переплести 12 различных книг в красный, зеленый, синий переплеты. Сколькими способами он может это сделать? 3.Сколькими способами можно расставить 20 книг в книжном шкафу с 5 полками, если каждая полка может вместить все 20 книг? 4. В сессии 6 экзаменов. Сколько существует вариантов сдачи сессии для одного студента? 5.Сколькими способами из полной колоды карт можно выбрать по три карты каждой масти? Комбинаторика14 вариант 1.Сколькими способами можно раздать 10 одинаковых конфет пятерым детям так, чтобы ни один ребенок не остался без конфет? 2.Из группы, состоящей из 7 мужчин и 4 женщин и 5 детей, надо выбрать 6 человек так, чтобы среди них было 2 женщины и 3 детей. Сколькими способами это можно сделать? 3.Пятеро студентов сдают экзамен одному из трех преподавателей комиссии. Сколькими способами может быть осуществлен выбор преподавателей этими студентами? 4. 5.Сколькими способами можно выбрать из полной колоды (52 карты) 6 карт так, чтобы среди них были все четыре масти. Комбинаторика15 вариант 1.В сессии 6 экзаменов. Сколько существует вариантов сдачи сессии в смысле оценок для одного студента? 2.Сколько существует целых чисел от 1 до 1000, которые не делятся ни на 2, ни на 3, ни на 5? 3. Сколькими способами можно разделить колоду из 36 карт пополам так, чтобы в каждой пачке было по два туза? 4. Сколькими способами можно выбрать из 15 человек группу для работы? В группу могут входить 1, 2, 3,…, 15 человек. 5.В лифт зашли 11 человек. Сколькими способами они могут распределиться на 6 этажах? Комбинаторика16 вариант 1. Сколькими способами можно переставить буквы в слове «перешеек» так, чтобы буквы «е» не шли подряд? 2.Сколько натуральных чисел, меньше 1 000 000, содержат хотя бы одну из цифр 1,2,3,4? 3. 4.Сколькими способами можно разложить в два кармана девять монет различного достоинства? 5. Сколькими способами можно рассортировать 10 файлов в каталоге? 17вариант 1. Сколько четырехзначных чисел, кратных 5, можно составить из карточек, на которых написаны цифры 1,2,3,0,5? 2. Сколькими способами можно распределить 9 апельсинов, 5 банана, 1 яблоко, 2 груши на 5 человек, так, чтобы каждому достался хотя бы один фрукт? 3. 25 человек обмениваются фотографиями друг с другом. Сколько было передано фотографий? 4. Из колоды, содержащей 36 карт, вынули 8 карт. Во скольких случаях среди этих карт окажется ровно два туза? 5.Сколько различных слов можно получить, переставляя буквы в слове «юриспруденция»? Комбинаторика 18 вариант 1.Сколько нечетных трехзначных чисел можно составить из карточек, на которых написаны цифры 4,2,3,0,1? 2. 3.На железнодорожной станции имеется 10 светофоров. Сколько может быть дано различных сигналов, если каждый светофор имеет два состояния: красный и зеленый? 4. Из колоды, содержащей 36 карт, вынули 8 карт. Во скольких случаях среди этих карт окажется ровно три карты крести? 5.Сколькими способами можно написать список группы, состоящей из 12 человек? 19 вариант 1. Сколько существует четырехзначных чисел, делящихся на 7, или на3, или на 2? 2. Сколько существует телефонных номеров, состоящих из 6 цифр, у которых 3 цифры одинаковые, остальные различны? 3. Сколькими способами можно отправить 9 различных открыток по 9 адресам (по одной открытке по каждому адресу)? 4.Сколькими способами из 5 левых и 7 правых перчаток можно составить пару? 5.Сколько различных слов можно получить, переставляя буквы в слове «сессия»? Комбинаторика20 вариант 1. 2. Сколько можно построить различных прямоугольников, длина каждой стороны которых является целым числом от 1 до 10? 3. У одного человека есть 7 дисков, а у другого – 10 . Сколькими способами они могут обменять три диска одного на три диска другого? 4. Сколькими способами можно разложить 8 книг на 4 бандероли по 2 книги в каждую (порядок бандеролей не принимается во внимание)? 5.Сколькими способами можно расставить в один ряд 7 книг в синем переплете, 5 – в красном, 8 — в зеленом, учитывая различие книг только по цвету? 21 вариант 1. Сколькими способами можно распределить 10 файлов по 5 каталогам? 2. Сколько существует вариантов расписания 6 экзаменов в сессии? 3. В автобус сели 8 человек. Сколькими способами они могут выйти на 10 остановках, если все вышли на разных остановках? 4. Скольким способами можно разделить колоду карт (36) на 4 равных части так, чтобы в каждой пачке было по тузу? 5. 22 вариант 1. Сколькими способами можно распределить купюру 50 р., 2 купюры по 100 р., 3 купюры по 500 р. и 5 купюры по 1000 р. на 6 человек, так, чтобы каждому досталась хотя бы одна купюра? 2. Сколько чисел, меньше 100000, можно написать с помощью цифр 7 и 3? 3. В лифт сели 9 человек. Сколькими способами они могут выйти на 3-х различных этажах? 4. Скольким способами можно разделить колоду карт (36) пополам так, чтобы все тузы были в одной пачке? 5.Сколько существует шестизначных телефонных номеров, в которых нет цифр 0,7,5? Комбинаторика23 вариант 1. Сколькими способами можно распределить 15 апельсинов на 5 детей так, чтобы единственному младшему среди них достался хотя бы один фрукт? 2. Сколькими способами можно закодировать дверь пятизначным кодом? 3. Сколькими способами можно рассортировать в базе данных 12 фамилий? 4. 5. 15 человек обменялись адресами. Сколько адресов было передано? Комбинаторика24 вариант 1.Сколько различных слов можно получить, переставляя буквы в слове «университет»? 2.Сколько 4-х значных чисел можно составить из цифр 0,1,2,3,4,5,6, если каждая из них, кроме 0, может повторяться несколько раз? 3.Ребёнок рисует три геометрические фигуры: круг, квадрат, треугольник. Сколькими способами он может их раскрасить, имея 7 карандашей различных цветов? 4.Сколько существует целых чисел от 1 до 1000, которые делятся на 2, или на 5, или на 9 ? 5.Во сколько чисел от 0 до 10000 входит цифра 6? Комбинаторика25 вариант 1.Сколькими способами можно составить 5 слов из 20 букв, если в совокупности этих 5 слов каждая буква используется один и только один раз? 2.Из группы, состоящей из 10 мужчин и 6 женщин, надо выбрать 8 человек так, чтобы среди них было менее 4 женщин. 3.Четверо студентов сдают экзамен. Сколькими способами могут быть поставлены им отметки, если известно, что только 1 не сдал экзамен? 4.Сколько существует целых чисел от 1 до 1000, которые не делятся ни на 3, ни на5, ни на 7? 5.Сколько четырехзначных чисел начинаются цифрой 8? Комбинаторика26 вариант 1.Сколькими способами можно разложить 10 одинаковых купюр по 5 различным карманам так, чтобы первый из них не был пустым? 2.Из группы, состоящей из 10 мужчин и 4 женщин, надо выбрать 6 человек так, чтобы среди них было 2 мужчины. Сколькими способами это можно сделать? 3.Пятеро студентов сдают экзамен. Сколькими способами могут быть поставлены им отметки, если известно, что только 2 имеют одинаковые отметки? 4.Сколько существует целых чисел от 1 до 1000, которые делятся на 3, или на 5, или на 11 ? 5. Сколько инициалов существует (Ф.И.О.)? Комбинаторика27 вариант 1. 2.Сколько существует двоичных чисел, длина которых не превосходит 5? 3.Сколькими способами 12 разных монет можно разложить по пяти различным карманам? 4.Сколько чётных чисел можно составить из цифр числа 2478, если каждую цифру можно использовать не более одного раза? 5.Сколькими способами можно сформировать покупку из 4 сортов шоколада и 7 сортов пирожных, содержащую 3 шоколадки и 5 пирожных? Комбинаторика28 вариант 1. Тест состоит из 30 вопросов и 4 вариантов ответа на каждый. Сколько вариантов ответить на тест существует при условии выбора одного варианта ответа на каждый вопрос? 2.Сколькими способами можно разложит в три пакета 9 различных дисков? 3.Сколько различных слов можно получить, переставляя буквы в слове “перекрёсток”? 4. 5.Сколькими способами можно обменять одну из 8 различных фотографий на две из 12 различных открыток? Комбинаторика29 вариант 1.Сколькими способами можно купить 2 сорта чая из имеющихся 15 сортов зеленого и 7 сортов черного? 2. Сколько пятизначных чисел можно образовать из цифр 1,2,3, если допускается повторение этих цифр? 3.Сколькими способами можно расставить 30 книг в книжном шкафу с 5 полками, если каждая полка может вместить 30 книг? 4. В сессии 6 экзаменов. Сколько существует вариантов получения оценок для одного студента? 5.Сколькими способами из полной колоды карт можно выбрать по две карты каждой масти? Комбинаторика30 вариант 1. У мамы 2 яблока, 3 груши, 4 апельсина. Каждый день в течение 9 дней подряд она выдает по одному фрукту. Сколькими способами это можно сделать? 2.Надо послать 8 писем. 3.Шестеро студентов сдают экзамен одному из четырех преподавателей комиссии. Сколькими способами может быть осуществлен выбор преподавателей этими студентами? 4. Сколько различных слов можно получить из слова “объединение”? 5.Сколькими способами можно выбрать из полной колоды (36 карты) 8 карт так, чтобы среди них были все четыре масти. Комбинаторика31 вариант 1.Между 4 игроками в домино поровну распределяются 28 костей. Сколькими способами могут распределиться кости домино? 2.В тесте 24 вопроса с двумя вариантами ответа на каждый (один верный, другой — нет). Считается, что студент сдал экзамен успешно, если он правильно ответил на 75 % вопросов. Сколько вариантов результата тестирования может получиться у успешно сдавших экзамен? 3.Сколькими способами 13 одинаковых монет можно разложить по пяти различным копилкам? 4. 5.В аудиторию вошли 12 студентов. Сколькими способами они могут распределиться на 30 местах? Комбинаторика32 вариант 1. В классе 15 двухместных парт. Сколькими способами можно рассадить на них 30 школьников? 2.В забеге участвуют 5 спортсменов. Сколькими способами могут распределиться 2 первых места? 3.Сколько имеется шестизначных чисел, у которых 2 цифры четные, а 4 — нечетные? 4.Сколькими способами можно расставить на полке 8 книг, если две определенные книги должны стоять рядом? 5.Сколькими способами можно сдать по порядку из колоды в 52 карты одному игроку 5 пик, 4 червы, 6 треф, 3 бубны? Комбинаторика33 вариант 1. Тест состоит из 30 вопросов и 3 вариантов ответа на каждый. Кроме того, известно, что на первые 15 существует возможность множественного выбора, на оставшиеся вопросы возможен единственный вариант ответа. 2.Сколькими способами можно скомпоновать компьютер из 10 различных мониторов, 7 различных системных блоков, 6 разных клавиатур и 12 мышек? 3.Сколькими способами можно разделить поровну на 4 человек 12 различных призов? 4.Сколькими способами можно расставить 12 белых и 12 черных шашек на белых полях шахматной доски? 5.Сколькими способами Ваня может поменять одну из 7 кукол своей сестры на два из 10 футбольных мячей брата своей подруги? Комбинаторика34 вариант 1. Сколькими способами на три разные флэшки можно разместить поровну 15 разных файлов? 2. Сколько чисел меньше 100000 можно образовать из цифр 1,2,3, 9 если допускается повторение этих цифр? 3.У преступника есть 8 ключей, которые, по полученной информации, подходят к 3 сейфам. Сколько вариантов он перебрать, чтобы убедиться, что информация полностью ложна? 4. В сессии 6 экзаменов. Сколько существует вариантов получения оценок для двоих друзей? 5. 35 вариант 1Сколькими способами на три разные флэшки можно разместить 21 файл, объем которых в совокупности не больше вместимости меньшей флэшки? 2. Сколькими способами можно послать 8 различных писем на один из 3 адресов друга, используя 5 своих электронных адресов? 3.Пятеро студентов сдают экзамен одному из троих преподавателей комиссии. Сколькими способами может быть осуществлен выбор преподавателей этими студентами? 4. Сколько различных списков фамилий 20 студентов группы можно составить, если известно, что в ней 3 брата «Умниковых»? 5.Сколькими способами можно выбрать из полной колоды (36 карты) 6 карт так, чтобы среди них были карты одной масти? |
|
Навигация: Главная Случайная страница Обратная связь ТОП Интересно знать Избранные Топ: Характеристика АТП и сварочно-жестяницкого участка: Транспорт в настоящее время является одной из важнейших отраслей народного. Выпускная квалификационная работа: Основная часть ВКР, как правило, состоит из двух-трех глав, каждая из которых, в свою очередь… Комплексной системы оценки состояния охраны труда на производственном объекте (КСОТ-П): Цели и задачи Комплексной системы оценки состояния охраны труда и определению факторов рисков по охране труда… Интересное: Искусственное повышение поверхности территории: Варианты искусственного повышения поверхности территории необходимо выбирать на основе анализа следующих характеристик защищаемой территории… Влияние предпринимательской среды на эффективное функционирование предприятия: Предпринимательская среда – это совокупность внешних и внутренних факторов, оказывающих влияние на функционирование фирмы… Аура как энергетическое поле: многослойную ауру человека можно представить себе подобным… Дисциплины: Автоматизация Антропология Археология Архитектура Аудит Биология Бухгалтерия Военная наука Генетика География Геология Демография Журналистика Зоология Иностранные языки Информатика Искусство История Кинематография Компьютеризация Кораблестроение Кулинария Культура Лексикология Лингвистика Литература Логика Маркетинг Математика Машиностроение Медицина Менеджмент Металлургия Метрология Механика Музыкология Науковедение Образование Охрана Труда Педагогика Политология Правоотношение Предпринимательство Приборостроение Программирование Производство Промышленность Психология Радиосвязь Религия Риторика Социология Спорт Стандартизация Статистика Строительство Теология Технологии Торговля Транспорт Фармакология Физика Физиология Философия Финансы Химия Хозяйство Черчение Экология Экономика Электроника Энергетика Юриспруденция |
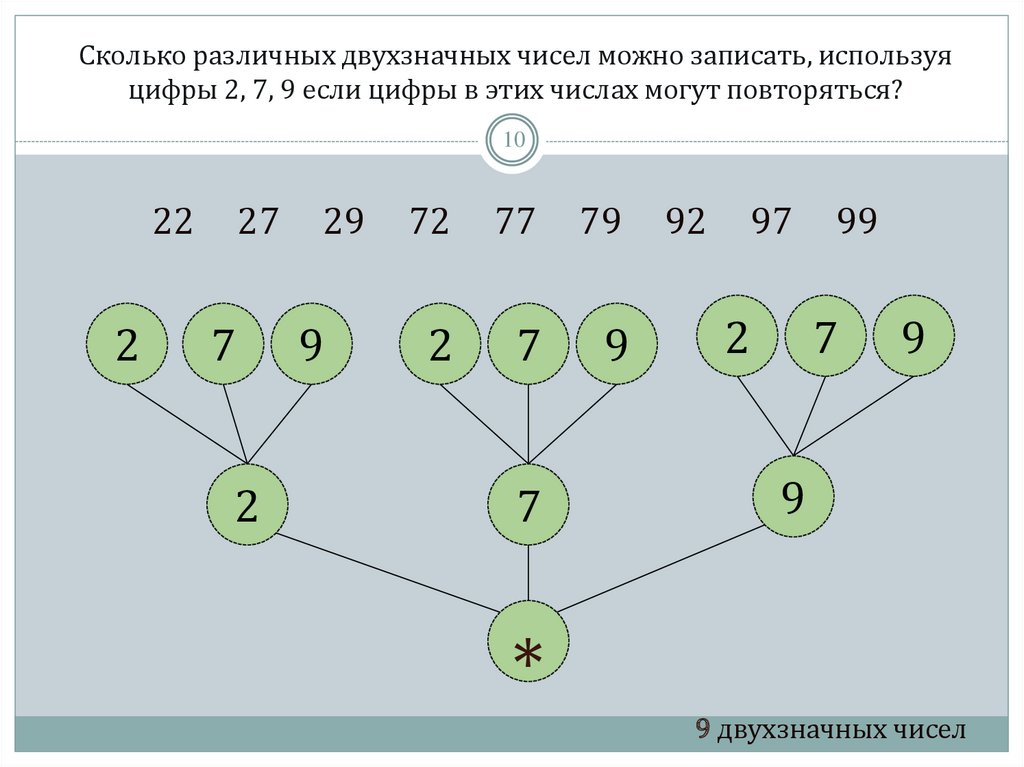
⇐ ПредыдущаяСтр 2 из 6Следующая ⇒ Если из множества, содержащего m элементов, требуется выбрать какие-то k элементов, то возникает вопрос: сколькими способами это можно сделать и какие подмножества при этом получаются. Все формулы для подсчета числа решений в комбинаторных задачах опираются на правило произведения: если элемент X можно выбрать k способами, а элемент Y можно выбрать n способами, то пару XY можно составить kn способами.
Размещение с повторением. Из множества, содержащего m элементов, нужно выбрать k элементов, причем выбранный элемент, после того, как его взяли, вновь возвращается в исходное множество (то есть элементы в выбранном множестве могут повторяться). Пользуясь правилом произведения, получим, что каждый из k элементов может быть выбран m способами. Таким образом, общее число комбинаций равно . Пример. Имеются цифры 2, 3, 5, 7. Сколько различных четырехзначных чисел можно составить из этих цифр? Решение. Первой цифрой в числе может быть любая из четырех имеющихся. То же самое можно сказать и о последующих цифрах числа, поэтому общее число комбинаций:
Размещение без повторений. Пример. Сколько различных четырехзначных чисел можно составить из цифр 1, 2, 3, 4, 5, 6, при условии. Что цифры в числе не повторяются? Решение. Общее число комбинаций равно числу размещений из 6 элементов по 4: Перестановки. Пример. Сколько различных четырехзначных чисел можно составить из цифр 2, 3, 5. 7, если цифры в числе не повторяются? Решение. Количество чисел равно числу перестановок из четырех элементов:
Сочетания. Пусть из множества, содержащего m различных элементов, требуется выбрать подмножество, содержащее k различных элементов (k £ m). Получаемые при этом подмножества не упорядочены. Такие неупорядоченные подмножества называются сочетаниями. Число сочетаний из m элементов по k элементов вычисляется по формуле: Пример. В группе 10 студентов. Решение. Число способов равно числу сочетаний из 10 элементов по 3 элемента: .
Теоретические вопросы к разделу 1.
1. Сформулировать правило произведения. 2. Указать формулы для подсчета числа размещений при выборке с повторениями и без повторений. 3. Записать формулы для подсчета числа сочетаний.
Задание к разделу 1.
1. В группе 20 студентов. Сколькими способами можно выбрать троих студентов для участия в конференции? 2. В группе 24 студентов. Требуется выбрать старосту и профорга. Сколькими способам можно это сделать? 3. Сколько различных пятизначных чисел можно составить из цифр 1, 2, 3, 4, 5? 4. Сколько можно составить трехзначных чисел из цифр 1, 2, 3, 4, 5, 6, 7, 8. 9, если все цифры, входящие в одно и то же число, различные? 5. Сколькими способами четыре человека могут разместиться за круглым столом? 6. 7. Электрическая цепь имеет 6 переключателей. Каждый переключатель может быть включен или выключен. Сколько существует различных положений, в которых могут оказаться все переключатели? 8. Сколько четырехзначных чисел можно образовать из нечетных цифр, если каждая из этих цифр в числе может повторяться? 9. В бригаде 8 человек. Для проведения работ требуется группа из четырех человек. Сколькими способами можно составить такую группу работников? 10. Имеется 6 билетов в театр, 4 из которых на места из первого ряда. Сколькими способами можно выбрать из шести имеющихся билетов три так, чтобы два билета оказались на места первого ряда, а один билет – на место в другом ряду?
⇐ Предыдущая123456Следующая ⇒ Организация стока поверхностных вод: Наибольшее количество влаги на земном шаре испаряется с поверхности морей и океанов (88‰). Поперечные профили набережных и береговой полосы: На городских территориях берегоукрепление проектируют с учетом технических и экономических требований, но особое значение придают эстетическим… Общие условия выбора системы дренажа: Система дренажа выбирается в зависимости от характера защищаемого… Кормораздатчик мобильный электрифицированный: схема и процесс работы устройства… |
Решение комбинаторных задач — презентация онлайн
1. элементы КомбинаторикИ
Выполнила Арсибекова Ольга Ивановнаучитель математики
2. Правило умножение
Задача № 1. Из цифр 2, 4, 7 следует составитьтрехзначное число, в котором ни одна цифра не
может повторяться более двух раз. Сколько всего
таких чисел можно составить?
Решение.
1 способ. Найдем количество всех трехзначных чисел, которые
начинаются с цифры 2: 224, 227, 242, 272, 244, 277, 247, 274 – 8
чисел.
Найдем количество всех трехзначных чисел, которые
начинаются с цифры 4: 442, 447, 424, 474, 422, 477, 427, 472 – 8
чисел.

Найдем количество всех трехзначных чисел, которые
начинаются с цифры 7: 772, 774, 727, 747, 722, 744, 724, 742
– 8 чисел.
Ответ. 24 числа.
3. 2 способ
2 СПОСОБ2
4
2
22
4
224
7
27
24
7
227
2
242
4
244
7
247
2
272
4
7
274
277
Всего 8чисел
Мы составили дерево возможных вариантов трехзначных
чисел, где на первом месте стоит цифра 2. Составим дерево
возможных вариантов для трехзначных чисел, где на первом
месте стоит цифра 4, получим 8 чисел и для трехзначных
чисел, где на первом месте стоит цифра 7, тоже 8 чисел. Всего
24 числа.
Задача № 2. «Этот вечер свободный можно так провести…»:
пойти погулять к реке, на площадь или в парк и потом пойти
в гости к Вити или к Вике. А можно остаться дома, сначала
посмотреть телевизор или почитать книжку, а потом
поиграть с братом или разобраться у себя на письменном
столе. Сколько всего вариантов существует для проведения
данного вечера.

Решение.
вечер
прогулка
река
Витя
парк
площадь
Витя
Вика
дом
Витя
Вика
брат
Вика
книга
ТВ
брат
стол
стол
Всего 10 вариантов
Задача № 3 На завтрак Вова может выбрать
плюшку, бутерброд, пряник или кекс, а запить их
он может кофе, соком или кефиром. Из скольких
вариантов завтрака Вова может выбирать?
Решение
Плюшка
Бутерброд
Пряник
Кекс
Кофе
Кофе,
плюшка
Кофе,
бутерброд
Кофе,
пряник
Сок
Сок,
плюшка
Сок,
бутерброд
Сок, пряник Сок,
кекс
Кефир Кефир,
плюшка
Кефир,
бутерброд
Кефир,
пряник
12 вариантов завтрака
Кофе,
кекс
Кефир,
кекс
7. Задача № 4. Сколько различных танцевальных пар (юноша, девушка) можно составить из пяти юношей и восьми девушек.
ЗАДАЧА № 4. СКОЛЬКО РАЗЛИЧНЫХ ТАНЦЕВАЛЬНЫХ ПАР(ЮНОША, ДЕВУШКА) МОЖНО СОСТАВИТЬ ИЗ ПЯТИ
ЮНОШЕЙ И ВОСЬМИ ДЕВУШЕК.
Решение.

Каждый из пяти юношей может пригласить любую из
восьми девушек.
Поэтому различных танцевальных пар можно
составить 5 ∙ 8 = 40.
Ответ. 40 танцевальных пар.
Выполненные при решении этих
задач рассуждения опираются на
следующее утверждение.
8. Правило умножения.
ПРАВИЛО УМНОЖЕНИЯ.Для того чтобы найти число всех возможных
исходов независимого проведения двух испытаний
А и В, следует перемножить число всех исходов
испытания А и число всех исходов испытания В.
9. Задача. Сколько среди четырёхзначных чисел, составленных из цифр 3, 4, 6, 8 (без повторений), таких, которые начинаются с цифры 3? А. 24 Б. 18 В. 6 Г. 12
ЗАДАЧА. СКОЛЬКО СРЕДИ ЧЕТЫРЁХЗНАЧНЫХ ЧИСЕЛ,СОСТАВЛЕННЫХ ИЗ ЦИФР 3, 4, 6, 8 (БЕЗ ПОВТОРЕНИЙ),
ТАКИХ, КОТОРЫЕ НАЧИНАЮТСЯ С ЦИФРЫ 3?
А. 24
Б. 18
В. 6
Г. 12
Решение
На первое место можно поставить только одну цифру – 3
На второе место можно поставить любую из трёх: 4, 6 или 8
На третье место можно поставить любую из двух оставшихся
цифр
На четвертое место можно поставить одну оставшуюся
цифру
Используя правило умножения получаем 1∙3∙2∙1=6
Ответ.
 В
В10. Задача. Найдите сумму цифр всех четырехзначных чисел, которые можно составить из цифр 2, 4, 6, 8(без повторения). А. 360 Б. 480 В. 240 Г. 400
ЗАДАЧА. НАЙДИТЕ СУММУ ЦИФР ВСЕХЧЕТЫРЕХЗНАЧНЫХ ЧИСЕЛ, КОТОРЫЕ МОЖНО
СОСТАВИТЬ ИЗ ЦИФР 2, 4, 6, 8(БЕЗ ПОВТОРЕНИЯ).
А. 360
Б. 480 В. 240 Г. 400
Решение
Все числа состоят из одних и тех же цифр, значит сумма
цифр каждого числа одинаковая и равна 2+4+6+8= 20.
Выясним сколько таких четырехзначных чисел существует.
На первое место можно поставить любую из четырех данных
цифр.
На второе место любую из трёх оставшихся цифр.
На третье место любую из двух оставшихся цифр.
На четвёртое место одну оставшуюся цифру.
По правилу умножения получаем 4∙3∙2∙1=24 числа.
Сумма цифр 24 чисел составляет 24∙20=480.
Ответ Б.
11. Задача. Из класса, в котором учится 15 девочек и 10 мальчиков, нужно выбрать одну девочку и одного мальчика для ведения школьного вечера. Скол
ЗАДАЧА. ИЗ КЛАССА, В КОТОРОМ УЧИТСЯ 15 ДЕВОЧЕК И10 МАЛЬЧИКОВ, НУЖНО ВЫБРАТЬ ОДНУ ДЕВОЧКУ И
ОДНОГО МАЛЬЧИКА ДЛЯ ВЕДЕНИЯ ШКОЛЬНОГО ВЕЧЕРА.

СКОЛЬКИМИ СПОСОБАМИ ЭТО МОЖНО СДЕЛАТЬ?
Решение
Применим правило умножения: девочку можно выбрать 15
способами,
мальчика – 10 способами,
пару мальчик – девочка – 15 ∙ 10 = 150 способами.
Ответ. 150
12. Задача. В чемпионате города по футболу играет десять команд. Сколькими способами могут распределиться три призовых места?
ЗАДАЧА. В ЧЕМПИОНАТЕ ГОРОДА ПО ФУТБОЛУ ИГРАЕТДЕСЯТЬ КОМАНД. СКОЛЬКИМИ СПОСОБАМИ МОГУТ
РАСПРЕДЕЛИТЬСЯ ТРИ ПРИЗОВЫХ МЕСТА?
Решение
На первое место можно поставить любую из 10 команд,
на второе – любую из 9 оставшихся,
на третье – любую из 8 оставшихся.
По правилу умножения общее число способов, которыми
можно распределить три места, равно 10 ∙ 9 ∙ 8 = 720.
Ответ. 720.
13. Задача. В расписании уроков на среду для первого класса должно быть четыре урока: два урока математики, урок чтения и урок физкультуры. Скол
ЗАДАЧА. В РАСПИСАНИИ УРОКОВ НА СРЕДУ ДЛЯПЕРВОГО КЛАССА ДОЛЖНО БЫТЬ ЧЕТЫРЕ УРОКА: ДВА
УРОКА МАТЕМАТИКИ, УРОК ЧТЕНИЯ И УРОК
ФИЗКУЛЬТУРЫ.
 СКОЛЬКИМИ СПОСОБАМИ МОЖНО
СКОЛЬКИМИ СПОСОБАМИ МОЖНОСОСТАВИТЬ РАСПИСАНИЕ НА ЭТОТ ДЕНЬ?
Решение
Урок чтения можно поставить на любой из четырёх
уроков,
Урок физкультуры – на любой из трёх оставшихся.
После этого для двух уроков математики останется
единственный вариант поставить их в расписание.
По правилу умножения общее число способов
составить расписание на среду равно 4 ∙ 3 = 12.
Ответ. 12.
14. Задача. В конференции участвовало 30 человек. Каждый участник с каждым обменялся визитной карточкой. Сколько всего понадобилась карточек?
ЗАДАЧА. В КОНФЕРЕНЦИИ УЧАСТВОВАЛО 30 ЧЕЛОВЕК.КАЖДЫЙ УЧАСТНИК С КАЖДЫМ ОБМЕНЯЛСЯ ВИЗИТНОЙ
КАРТОЧКОЙ. СКОЛЬКО ВСЕГО ПОНАДОБИЛАСЬ
КАРТОЧЕК?
Решение.
Каждый из 30 участников конференции раздал 29
карточек.
Значит, всего было роздано 30 ∙ 29 = 870 карточек.
Ответ. 870.
15. Задача. Сколько трёхзначных чисел можно записать, используя только цифры 0, 2, 4, 6?
ЗАДАЧА. СКОЛЬКО ТРЁХЗНАЧНЫХ ЧИСЕЛ МОЖНОЗАПИСАТЬ, ИСПОЛЬЗУЯ ТОЛЬКО ЦИФРЫ 0, 2, 4, 6?
Решение
На первое место можно поставить любую из цифр,
кроме нуля, — это 3 варианта ;
на второе место – любую из 4 цифр и
на третье – тоже любую из 4 цифр.

По правилу умножения общее количество вариантов
равно 3 ∙ 4 ∙ 4 = 48.
Ответ. 48.
16. Задача. В меню школьной столовой 2 различных супа, 4 вторых блюда и 3 вида сока. Сколько можно составить вариантов обеда из трех блюд?
ЗАДАЧА. В МЕНЮ ШКОЛЬНОЙ СТОЛОВОЙ 2 РАЗЛИЧНЫХСУПА, 4 ВТОРЫХ БЛЮДА И 3 ВИДА СОКА. СКОЛЬКО
МОЖНО СОСТАВИТЬ ВАРИАНТОВ ОБЕДА ИЗ ТРЕХ БЛЮД?
Решение
Первое блюдо можно выбрать 2 способами,
второе блюдо – 4 способами и
третье блюдо – 3 способами.
По правилу умножения общее количество
вариантов равно 2 ∙ 4 ∙ 3 = 24.
Ответ. 24.
17. Перестановки
Задача № 1. В семье шесть человек, а за столом в кухнешесть стульев. Было решено каждый вечер перед ужином
рассаживаться на эти шесть стульев по-новому. Сколько
дней члены семьи смогут делать это без повторений?
Решение
Предположим, что первой садится бабушка. У нее имеется 6
вариантов выбора стула.
Вторым садится дедушка и независимо выбирает стул из 5
оставшихся
Мама делает свой выбор третьей, и выбор у нее будет из 4
стульев
У папы будет уже 3 варианта, у дочки – 2, ну а у сын сядет на
единственно незанятый стул.

По правилу умножения имеем 6 ∙ 5 ∙ 4 ∙ 3 ∙ 2 ∙ 1 = 720 .
Ответ. 720 дней.
Определение. Произведение подряд идущих первых n
натуральных чисел обозначают n! и называют «эн
факториал»: n! = 1 ∙ 2 ∙ 3 ∙…∙ (n-1) ∙ n.
Задача № 2. В 9 «А» классе в среду семь уроков: алгебра,
геометрия, литература, русский язык, английский язык,
биология и физкультура. Сколько вариантов расписания
можно составить на среду?
Решение
Для алгебры – 7 вариантов. Для геометрии – 6 вариантов.
Для литературы – 5 вариантов и т. д.
По правилу умножения получаем:
7 ∙ 6 ∙ 5 ∙ 4 ∙ 3 ∙ 2 ∙ 1 = 7! = 5040.
Ответ. 5040.
Определение.
Перестановкой
множество из n элементов,
определённом порядке.
называется
записанных в
Теорема о перестановках элементов конечного
множества:
n различных элементов можно расставить
по одному на n различных мест ровно
n! способами.
Рn=n!
20. Задача. Четыре друга купили билеты в кино: на 1-е и 2-е места в первом ряду и на 1-е и 2-е места во втором ряду.
 Сколькими способами друзья могут зЗадача. Четыре друга купили билеты в кино: на 1-е и
Сколькими способами друзья могут зЗадача. Четыре друга купили билеты в кино: на 1-е и2-е места в первом ряду и на 1-е и 2-е места во
втором ряду. Сколькими способами друзья могут
занять эти 4 места в кинотеатре?
Решение
Используя теорему о перестановках имеем:4-е друга
могут занять по одному 4-е различных места ровно
4! способами.
Pn = 4! = 4 ∙ 3 ∙ 2 ∙ 1 = 24
Ответ. 24 способа
21. Задача. Сколькими способами можно с помощью букв K, L, M, N обозначить вершины четырехугольника?
ЗАДАЧА. СКОЛЬКИМИ СПОСОБАМИ МОЖНО С ПОМОЩЬЮБУКВ K, L, M, N ОБОЗНАЧИТЬ ВЕРШИНЫ
ЧЕТЫРЕХУГОЛЬНИКА?
Решение
Используя теорему о перестановках имеем:4-е различные
буквы можно записать по одной около 4-ех различных вершин
многоугольника ровно 4! способами.
Pn = 4! = 4 ∙ 3 ∙ 2 ∙ 1 = 24
Ответ. 24 способа
22. Задача. Сколько различных нечетных пятизначных чисел, в которых нет одинаковых цифр, можно записать с помощью цифр 1, 2, 4, 6, 8?
ЗАДАЧА. СКОЛЬКО РАЗЛИЧНЫХ НЕЧЕТНЫХ ПЯТИЗНАЧНЫХ
СКОЛЬКО РАЗЛИЧНЫХ НЕЧЕТНЫХ ПЯТИЗНАЧНЫХЧИСЕЛ, В КОТОРЫХ НЕТ ОДИНАКОВЫХ ЦИФР, МОЖНО
ЗАПИСАТЬ С ПОМОЩЬЮ ЦИФР 1, 2, 4, 6, 8?
Решение
Т.к. числа должны быть нечётными, то на последнем
пятом месте может быть только нечётная цифра – это 1.
Осталось 4-е цифры(2, 4, 6, 8) и 4-е разряда.
Используя теорему о перестановках имеем: Pn = 4! = 24
Ответ. 24 числа.
23. Задача. Сколько различных чётных пятизначных чисел, все цифры которых различны, можно записать с помощью цифр 1, 2, 3, 4, 5?
ЗАДАЧА. СКОЛЬКО РАЗЛИЧНЫХ ЧЁТНЫХ ПЯТИЗНАЧНЫХЧИСЕЛ, ВСЕ ЦИФРЫ КОТОРЫХ РАЗЛИЧНЫ, МОЖНО
ЗАПИСАТЬ С ПОМОЩЬЮ ЦИФР 1, 2, 3, 4, 5?
Решение
Т. к. числа должны быть чётными, значит на последнем
пятом месте должна стоять чётная цифра – это 2 или 4.
Найдем сколько пятизначных чётных чисел, которые
оканчиваются цифрой 2.
Осталось 4-е цифры(1, 3, 4, 5) и 4-е разряда. Применяя
теорему о перестановках имеем: Pn = 4! = 24 числа.
Рассуждая аналогично, получим, что пятизначных
чётных чисел, оканчивающихся цифрой 4, тоже 24.

Получаем: 24 + 24 = 48.
Ответ. 48 чисел.
24. Размещения
Задача. Сколькими способами можно записатьдвузначных чисел с помощью цифр 1, 2, 3, 4 при
условии, что в каждой записи нет одинаковых
цифр?
Решение
Решим эту задачу, используя правило умножения.
В записи двузначного числа на первом месте может
стоять любая из данных четырёх цифр, а на втором –
любая из трёх оставшихся.
По правилу умножения таких двузначных чисел: 4 ∙ 3 = 12
Ответ. 12 чисел.
При решении задач из 4-ёх данных элементов (цифр 1,
2, 3, 4) были образованы всевозможные соединения
по 2 элемента в каждом, причём любые два
соединения отличались либо составом элементов
(например, 12 и 24), либо порядком их
расположения (например, 12 и 21).
Такие соединения называются размещениями.
Определение. Размещениями из m элементов по n
элементов (n ≤ m) называются такие соединения,
каждое из которых содержит n элементов, взятых из
данных m разных элементов, и которые отличаются
друг от друга либо самими элементами, либо порядком
их расположения.

Число всевозможных размещений из m элементов по n
элементов обозначают
m!
= (m-n)!
Формула для вычисления:
26. Задача. Сколькими способами 3 ученика могут занять места в классе, в котором стоят 20 одноместных столов
ЗАДАЧА. СКОЛЬКИМИСПОСОБАМИ
ЗАНЯТЬ МЕСТА В КЛАССЕ,
ОДНОМЕСТНЫХ СТОЛОВ
В
3
УЧЕНИКА МОГУТ
КОТОРОМ
СТОЯТ
20
Решение
Задача сводится к нахождению числа размещений из 20
элементов по 3 элемента в каждом.
Используя формулу для вычисления числа размещений
имеем
20!
20!
3
A20
18 19 20 6840
(20 3)! 17!
Ответ. 6840
27. Задача. В классе изучают 9 предметов. Сколькими способами можно составить расписание на понедельник, если в этот день должно быть 6 разных у
ЗАДАЧА. ВСКОЛЬКИМИ
КЛАССЕ
ИЗУЧАЮТ
9
ПРЕДМЕТОВ.
СПОСОБАМИ
МОЖНО
СОСТАВИТЬ
РАСПИСАНИЕ НА ПОНЕДЕЛЬНИК, ЕСЛИ В ЭТОТ ДЕНЬ
ДОЛЖНО БЫТЬ
6 РАЗНЫХ УРОКОВ?
Решение
Найдем число размещений из 9 элементов по 6
элементов в каждом.

9!
9!
6
A
4 5 6 7 8 9
Применяя формулу получаем: 9
(9 6)! 3!
60480
Ответ. 60480
28. Задача. Сколько существует способов для обозначения вершин данного четырёхугольника с помощью букв A, B, C, D, E, F?
ЗАДАЧА.СКОЛЬКО
СУЩЕСТВУЕТ
СПОСОБОВ
ДЛЯ
ОБОЗНАЧЕНИЯ ВЕРШИН ДАННОГО ЧЕТЫРЁХУГОЛЬНИКА
С ПОМОЩЬЮ БУКВ A, B, C, D, E, F?
Решение
Задача опять сводится к нахождению
размещений из 6 элементов по 4 элемента.
Получаем:
A64
6!
6!
3 4 5 6 360
(6 4)! 2!
Ответ. 360
числа
29. Задача. В классе 30 человек. Сколькими способами могут быть выбраны из их состава староста и казначей?
ЗАДАЧА.В
КЛАССЕ
30
ЧЕЛОВЕК.
СКОЛЬКИМИ
СПОСОБАМИ МОГУТ БЫТЬ ВЫБРАНЫ ИЗ ИХ СОСТАВА
СТАРОСТА И КАЗНАЧЕЙ?
Решение
Для того, чтобы ответить на вопрос задачи найдем
число размещений из 30 элементов по 2 элемента в
каждом.
2
A30
30!
30!
29 30 870
(30 2)! 28!
Ответ.
 870
87030. Задача. В чемпионате по футболу участвуют 10 команд. Сколько существует различных возможностей занять командам первые три места?
ЗАДАЧА. ВКОМАНД.
ЧЕМПИОНАТЕ ПО ФУТБОЛУ УЧАСТВУЮТ
СКОЛЬКО
ВОЗМОЖНОСТЕЙ
МЕСТА?
СУЩЕСТВУЕТ
ЗАНЯТЬ КОМАНДАМ
10
РАЗЛИЧНЫХ
ПЕРВЫЕ ТРИ
Решение
Найдем размещения из 10 элементов по 3 элемента в
каждом.
3
A10
10!
10!
8 9 10 720
(10 3)! 7!
Ответ. 720
31. Сочетания
Задача. Из пяти шахматистов для участия втурнире нужно послать двух. Сколькими
способами это можно сделать?
Решение
Из пяти шахматистов можно составить A52 пар.
Но из этих пар надо выбрать те, которые отличаются
составом участников, но не их порядком.
Таких пар в 2 раза меньше, т.е.
A52 5 4
10
2
2
Ответ. 10 способов.
При решении задач из пяти человек были образованы
соединения по 2, которые отличаются только
составом пар.
Такие соединения называются сочетаниями.

Определение. Сочетаниями из m элементов по n
элементов (n ≤ m) называются такие соединения,
каждое из которых содержит n элементов,
взятых из данных m разных элементов, и которые
отличаются друг от друга по крайней мере одним
элементом.
Число всевозможных сочетаний из m элементов по n
элементов обозначают
Формула для вычисления:
m!
= (m-n)! n!
33. Задача. Сколькими способами можно делегировать троих студентов на межвузовскую конференцию из 9 членов научного общества.
ЗАДАЧА.СКОЛЬКИМИ
СПОСОБАМИ
МОЖНО
ДЕЛЕГИРОВАТЬ ТРОИХ СТУДЕНТОВ НА МЕЖВУЗОВСКУЮ
КОНФЕРЕНЦИЮ ИЗ 9 ЧЛЕНОВ НАУЧНОГО ОБЩЕСТВА.
Решение
Создание групп из трех человек без учета их порядка
расположения является сочетанием.
Используя формулу находим C93
9!
7 8 9
7 4 3 84
6! 3!
2 3
Ответ. 84 способа.
34. Задача. В школьном хоре 6 девочек и 4 мальчика. Сколькими способами можно выбрать из состава хора двух девочек и одного мальчика для участия
ЗАДАЧА.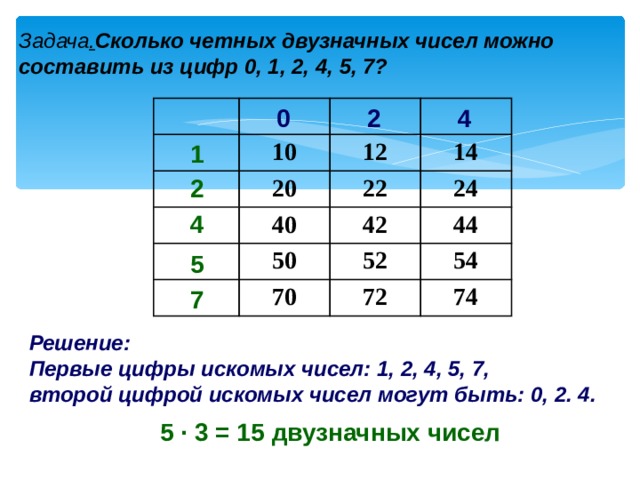 В ШКОЛЬНОМ ХОРЕ 6 ДЕВОЧЕК И 4 МАЛЬЧИКА.
В ШКОЛЬНОМ ХОРЕ 6 ДЕВОЧЕК И 4 МАЛЬЧИКА.СКОЛЬКИМИ СПОСОБАМИ МОЖНО ВЫБРАТЬ ИЗ СОСТАВА
ХОРА ДВУХ ДЕВОЧЕК И ОДНОГО МАЛЬЧИКА ДЛЯ УЧАСТИЯ
В ВЫСТУПЛЕНИИ ОКРУЖНОГО ХОРА?
Решение
Составление пар из числа девочек без учета их порядка
расположения – есть сочетание.
C62
6!
5 6
5 3 15
4! 2!
2
Мальчика можно выбрать 4 способами.
Используя правило умножения, получаем
4 ∙ 15 = 60
Ответ. 60 вариантов.
35. Задача. В вазе лежат 5 разных яблок и 6 различных апельсинов. Сколькими способами из них можно выбрать 2 яблока и 2 апельсина.
ЗАДАЧА. В ВАЗЕ ЛЕЖАТ 5 РАЗНЫХ ЯБЛОК И 6 РАЗЛИЧНЫХАПЕЛЬСИНОВ. СКОЛЬКИМИ СПОСОБАМИ ИЗ НИХ МОЖНО
ВЫБРАТЬ 2 ЯБЛОКА И 2 АПЕЛЬСИНА.
Решение
Выбор 2 яблок из 5(порядок не важен) – сочетания.
C52
5!
4 5
2 5 10
3! 2!
2
Выбор 2 апельсинов из 6(порядок не важен) – сочетания.
C62
6!
5 6
5 3 15
4! 2!
2
По правилу умножения – 10 ∙ 15=150.
Ответ.
 150 способов.
150 способов.36. Задача. Имеется 3 разноцветных мяча, 5 разноцветных кубиков и 4 разноцветных скакалки. Сколькими способами можно получить набор из двух мяче
ЗАДАЧА.ИМЕЕТСЯ
3
РАЗНОЦВЕТНЫХ КУБИКОВ И
РАЗНОЦВЕТНЫХ
4
РАЗНОЦВЕТНЫХ
МЯЧА,
5
СКАКАЛКИ.
СКОЛЬКИМИ СПОСОБАМИ МОЖНО ПОЛУЧИТЬ НАБОР ИЗ ДВУХ
МЯЧЕЙ,
ДВУХ
КУБИКОВ
И
ДВУХ
СКАКАЛОК?
А. 180
Б. 60
В. 23
Г. 12
Решение
Найдем сколько различных вариантов выбора мячей.
3!
3
2
C3
3
1! 2!
1
Найдем сколько различных вариантов выбора кубиков.
5! 4 5 2 5 10
2
C5
2
3! 2!
Найдем сколько различных вариантов выбора скакалок.
4!
3 4
2
C4
3 2 6
2! 2!
2
3 ∙10 ∙ 6 = 180.
Ответ. А
Р(А+В)=Р(А)+Р(В)
Тема урока: «Элементы комбинаторики» (2 часа).
Произведение всех натуральных чисел от 1 до n включительно называется факториалом числа n и записывается n! (читается как «эн факториал»).
n! =1⋅ 2⋅ 3⋅… ⋅ (n− 2)⋅ (n− 1)⋅ n.
Принято, что 0! =1.
1! =1;
2! =2⋅ 1=2;
3! =3⋅ 2⋅ 1=6;
4! =4⋅ 3⋅ 2⋅ 1=24;
5! =5⋅ 4⋅ 3⋅ 2⋅ 1=120;
6! =6⋅ 5⋅ 4⋅ 3⋅ 2⋅ 1=720.
Пример:
Вычисли значение выражения.
а) 5! +4! =5⋅ 4⋅ 3⋅ 2⋅ 1+4⋅ 3⋅ 2⋅ 1=120+24=144.
б) = = = 5⋅ 41 = 205 (4! выносится за скобки. В дроби равные факториалы можно сокращать).
в) + = + = 80+59 = 139.
Каждый больший факториал можно выразить меньшим факториалом, т. е.
n! = n(n− 1)! = n(n− 1)(n− 2)! = n(n− 1)(n− 2)(n− 3)! и т. д.
Комбинаторика — раздел математики о вычислении количества различных комбинаций каких-либо элементов.
Основные элементы комбинаторики:
1) Размещение:
а) с повторениями б) без повторений
2) Перестановка
3) Сочетание
Всякий упорядоченный набор, имеющий k элементов, взятых из наперед заданных n элементов, будем называть размещением с повторениями из n по k.
Размещение с повторениями: m = nk
Например:
Сколько всех четырехзначных чисел можно составить из цифр 1, 5, 6, 7, 8?
Решение. Всего цифр 5, то есть n = 5, из них надо составить четырехзначные числа, то есть k = 4. Для каждого разряда четырехзначного числа имеется пять возможностей, значит m = 5*5*5*5 = nk = 54 = 625.
Цифры в числе могут повторяться, например, 1122, 1223, 4444 …
Ответ: 625
Всякий упорядоченный набор, имеющий k элементов, взятых из наперед заданных n элементов без повторений, будем называть размещением из n по k (без повторений).
Размещение без повторений: Аkn = .
Например:
Сколько существует двузначных чисел, в которых цифра десятков и цифра единиц различные и нечетные?
Решение: т. к. нечетных цифр пять, а именно 1, 3, 5, 7, 9 (n = 5), то эта задача сводится к выбору и размещению на две разные позиции (k= 2) двух из пяти различных цифр, т. е. указанных чисел будет: А25 = = = = 4 ꞏ 5 = 20.
е. указанных чисел будет: А25 = = = = 4 ꞏ 5 = 20.
Цифры в числе не могут повторяться, то есть 13, 51, 73… Но нельзя 33, 11, 77…
Ответ: 20
Всякий упорядоченный набор имеющий n элементов, взятых из наперед заданных n элементов без повторений, будем называть перестановкой из n.
Перестановка из n элементов: Рn = n!
Например:
Сколькими различными способами можно составить список учеников (не по алфавиту, любым способом), если в нём должно быть 25 различных учеников?
Решение: Р25 = 25! = 1⋅ 2⋅ 3⋅… ⋅ 24⋅ 25=25!
Ответ: список можно составить 25! различными способами.
Всякий неупорядоченный набор имеющий k элементов, взятых из наперед заданных n элементов без повторений, будем называть сочетанием из n по k.
Сочетание из n элементов по k: Ckn =
Например:
Сколькими способами читатель может выбрать две книжки из шести имеющихся?
Решение: Число способов равно числу сочетаний из шести книжек по две, т. е. равно:
е. равно:
C26 = = = = = 15
Заметьте, книги, естественно, не повторяются и какую из двух мы взяли первой или второй роли не играет.
Ответ: 15.
Различные способы решения задач:
В заданиях по комбинаторике обычно нужно выяснить, возможно ли составить комбинацию определённого вида, и сколько различных комбинаций можно составить.
Один из способов решения задач комбинаторики — это рассмотреть все возможные комбинации элементов, что называется полным перебором вариантов.
Древовидная диаграмма
Древовидная диаграмма — один из способов показать и систематизировать все размещения. С помощью древовидной диаграммы осуществляется полный перебор.
Пример 1: Сколько различных двузначных чисел можно составить из цифр 1, 2 и 3, если каждую использовать только один раз?
Решение:
составляется древовидная диаграмма.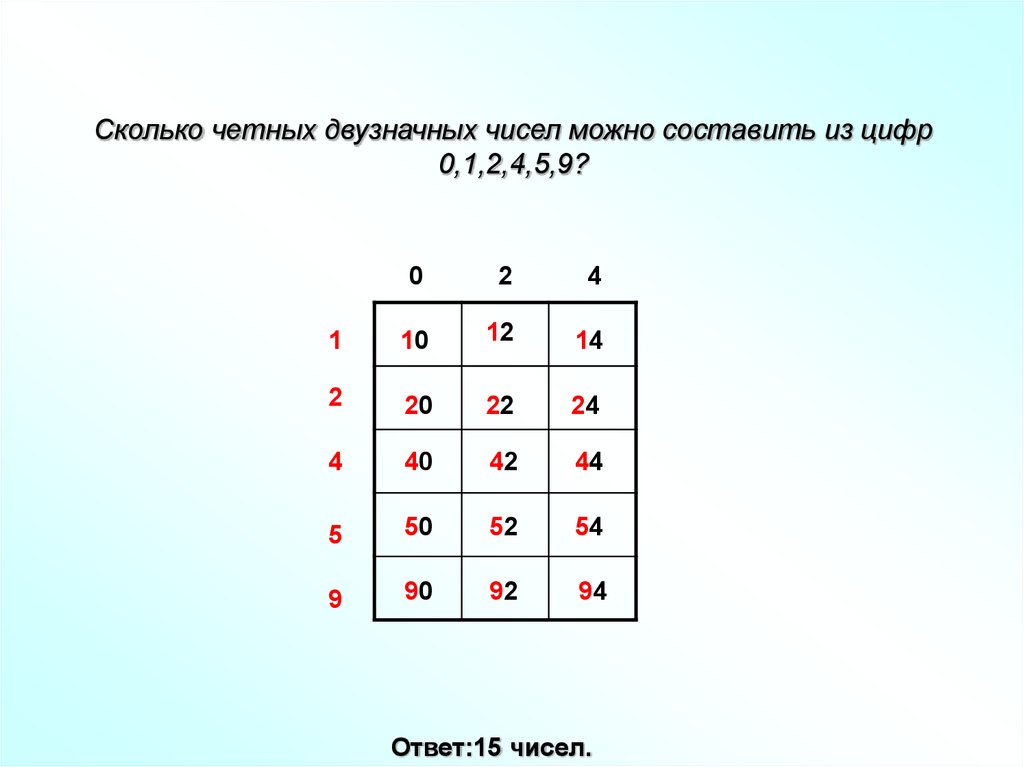
Ответ: можно составить 6 различных чисел.
Пример 2: Сколькими различными способами можно образовать пару дежурных, если в
классе остались Надя, Вика, Саша и Юра?
На древовидной диаграмме видно, что можно образовать только 6 пар дежурных (Надя и Вика, Надя и Саша, Надя и Юра, Вика и Саша, Саша и Юра, Вика и Юра), т. к. каждая пара повторяется 2 раза.
Эту задачу можно решить с помощью сочетания: C24 = = = = 6
Ответ: 6
Пример 3:
Сколькими различными способами можно выбрать двух учеников (одного — чистить доску, второго — подметать пол), если в классе остались Надя, Вика, Саша и Юра?
Используется та же древовидная диаграмма, но в данном случае ответ будет — 12 пар, т. к. каждая пара из диаграммы отличается. Если детей поменять местами, они выполняют уже другие функции.
Эту задачу можно решить с помощью размещения без повторения: А24 = = = = 3· 4 = 12.
С помощью древовидной диаграммы были получены различные результаты, т. к. в 3 и 4 примере были рассмотрены различные виды комбинаций: сочетания и размещения.
Такого рода диаграммы в подробностях удобно рисовать только для сравнительно небольшого числа вариантов, а, например, для сотен комбинаций дерево вариантов целиком не нарисуешь. Тогда приходится действовать по-другому. Чаще всего при различных подсчётах используют правило умножения.
Правило умножения: для того чтобы найти число всех возможных исходов независимого проведения двух испытаний А и В, следует перемножить число всех исходов испытания А и число всех исходов испытания В.
Например:
Сколькими различными способами можно составить танцевальную пару, если в коллективе 3 мальчика и 4 девочки?
Решение: 3 · 4 = 12
Ответ: 12
Таблица
В отдельных случаях для систематизации данных составляются таблицы комбинаций.
Простой игровой кубик бросается 2 раза, и полученные пункты перемножаются (или суммируются, в зависимости от задачи). Сколько различных произведений можно получить?
Различные произведения — это 1; 2; 3; 4; 5; 6; 8; 9; 10; 12; 15; 16; 18; 20; 24; 25; 30; 36 — всего 18 различных результатов.
Тема урока: «Классическое определение вероятности» (2 часа).
Испытанием называется осуществление определенных действий.
Событие — факт, который может произойти в результате испытания.
Любой результат испытания называется исходом .
Достоверным называют событие, которое в результате испытания обязательно произойдёт.
Невозможным называют событие, которое заведомо не произойдёт в результате испытания.
Пространство элементарных событий — множество всех различных исходов произвольного испытания.
Если события не могут произойти одновременно в одном испытании, то события называются несовместными .
Противоположное событие происходит тогда, когда исходное событие А не происходит.
Событие, противоположное данному, обычно обозначается той же латинской буквой с чёрточкой сверху.
Например:
A – сдал экзамен по математике;
Ᾱ – не сдал экзамен по математике.
Суммой событий А и В называется событие А+В, которое состоит в том, что наступит или событие А, или событие В, или оба события одновременно.
Произведением событий А и В называется событие А•В, состоящее в совместном осуществлении событий А и В.
Например:
Пусть А — идет дождь, B — идет снег, тогда А + В – «идет снег или дождь»
При 3-х выстрелах по мишени события: А0 – «попаданий нет», А1 – «одно попадание», А2 – «два попадания», тогда А=А0+А1+А2 — «произошло не больше двух попаданий»
Пусть С — из урны вынули белый шар, D — из урны вынули белый шар, тогда C⋅ D — из урны вынули два белых шара
Пусть С — из урны вынули белый шар, D — из урны вынули белый шар, тогда C⋅ — из урны вынули два шара: белый и не белый.
Теорема сложения вероятностей несовместных событий: вероятность появления одного из двух несовместных событий А или В равна сумме вероятностей этих событий:
Р(А+В)=Р(А)+Р(В)
Классическое определение вероятности применяется для равновозможных событий.
К равновозможным (равновероятностным) относятся такие события, для которых нет никаких объективных оснований считать, что одно является более возможным, чем другие.
Например, при бросании игрального кубика события выпадения любого из очков равно возможны.
Рассмотрим произвольный эксперимент.
Пусть n − число всех исходов эксперимента, которые образуют полную группу попарно несовместных и равновозможных событий, m – число благоприятных событию А исходов.
Тогда вероятностью события А называется число:
P(A) =
Из классического определения вероятности вытекают следующие ее свойства:
1. Вероятность достоверного события А всегда равна единице, то есть P(А) = 1;
это объясняется тем, что достоверному событию благоприятствуют все элементарные события, то есть m = n;
2. Вероятность невозможного события В всегда равна нулю, то есть P(В) = 0;
Вероятность невозможного события В всегда равна нулю, то есть P(В) = 0;
это объясняется тем, что невозможному событию не благоприятствует ни одно из элементарных, то есть m = 0;
3. Вероятность любого случайного события A всегда удовлетворяет условию 0 ≤ P(A) ≤ 1.
Если в процентах, то 0 ≤ P(A) ≤ 100
Задача: Из колоды в 36 карт вынимается одна карта. Какова вероятность появления карты червовой масти?
Решение. Количество элементарных исходов (количество карт) n=36. Событие A — появление карты червовой масти. Число случаев, благоприятствующих появлению события A, m=9. Следовательно, P(A)= = =0, 25.
Если в процентах, то 0, 25 · 100 = 25%.
Теорема
Для нахождения вероятности противоположного события следует из единицы вычесть вероятность самого события: P(A) = 1 − P( ).
Задача: В коробке находятся 4 мячика белого цвета и 13 мячиков красного цвета.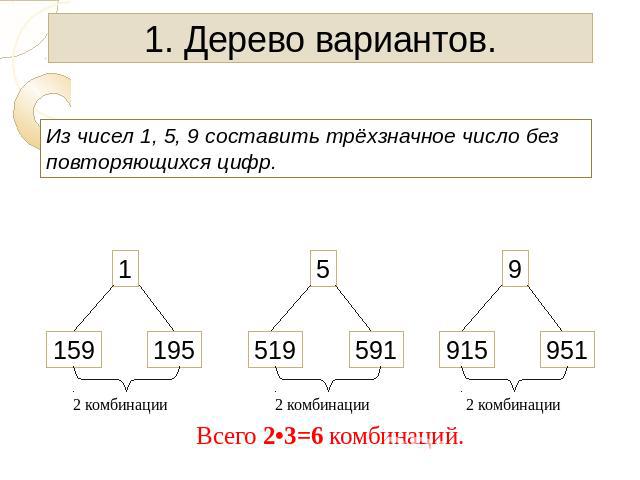
Вытаскивают три мячика. Какова вероятность, что хотя бы один будет белого цвета?
Решение: Благоприятные исходы, когда из трех мячей один белого цвета, два или три (так как в задаче сказано: хотя бы один).
Нас не устраивает только исход, в котором вытащим три красных мяча. Это и есть противоположное событие. Найдем его вероятность и вычтем из 1.
m = C313 = = = = 286
n = C317 = = = = 680
Р( ) = = =
P(A) = 1 − = ≈ 0, 579 (57, 9%)
Ответ: 0, 579
Есть второй способ решения: Р( ) = · · = …
Затем, P(A) = 1 − Р( ) =…
Решите вероятностную задачу с помощью таблицы.
Подбрасываются две игральные кости. Какова вероятность события А, заключающегося в том, что сумма выпавших очков нечетная?
Решение:
Всего исходов (сумм) 36, n = 36.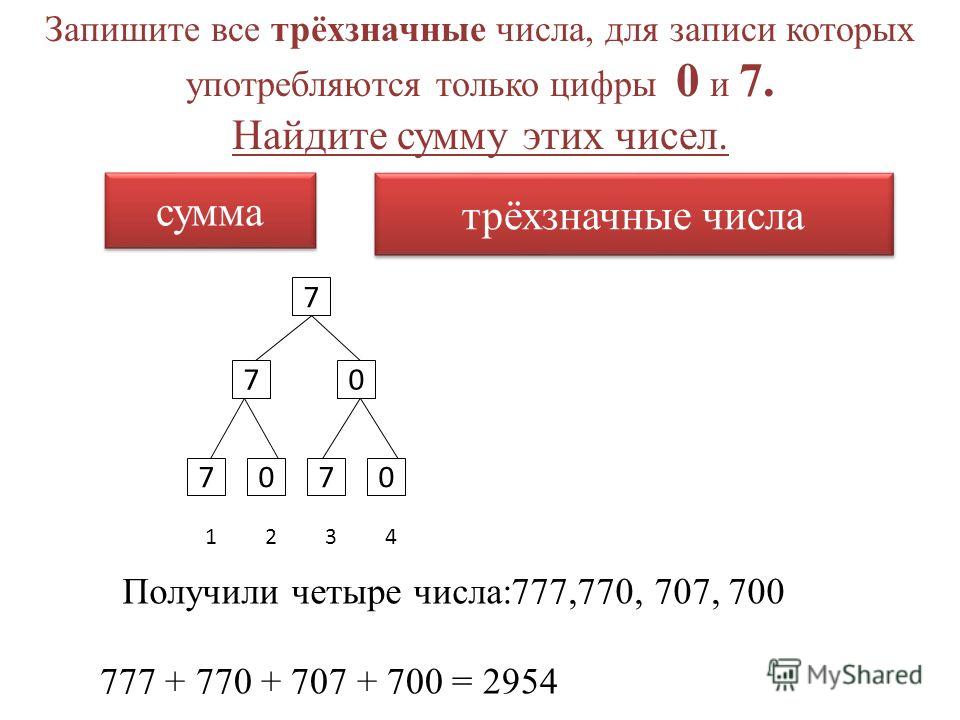 Нечетных сумм (выделенные зеленым) 18, m = 18.
Нечетных сумм (выделенные зеленым) 18, m = 18.
P(A) = = = = 0, 5 (50%)
Ответ: 0, 5
Задача: Найти вероятность того, что наудачу взятое двузначное число от 10 до 99 окажется кратным либо 3, либо 8, либо тому и другому одновременно.
Решение: Всего чисел 90 (можете посчитать и проверить).
Событие А: из них делятся на 3 – 30.
Событие В: из них делятся на 8 – 11.
В этих двух событиях есть повторяющиеся числа, а берут только один раз, поэтому повторение надо исключить. Таких чисел (те, которые делятся и на 3, и на 8, то есть на 24, событие С) – 4.
P(A) = P(В) = P(С) =
Р = P(A) + P(В) − P(С) = + − = ≈ 0, 41 (41%).
Ответ: 0, 41
| Главная Другое |
страница 1страница 2 .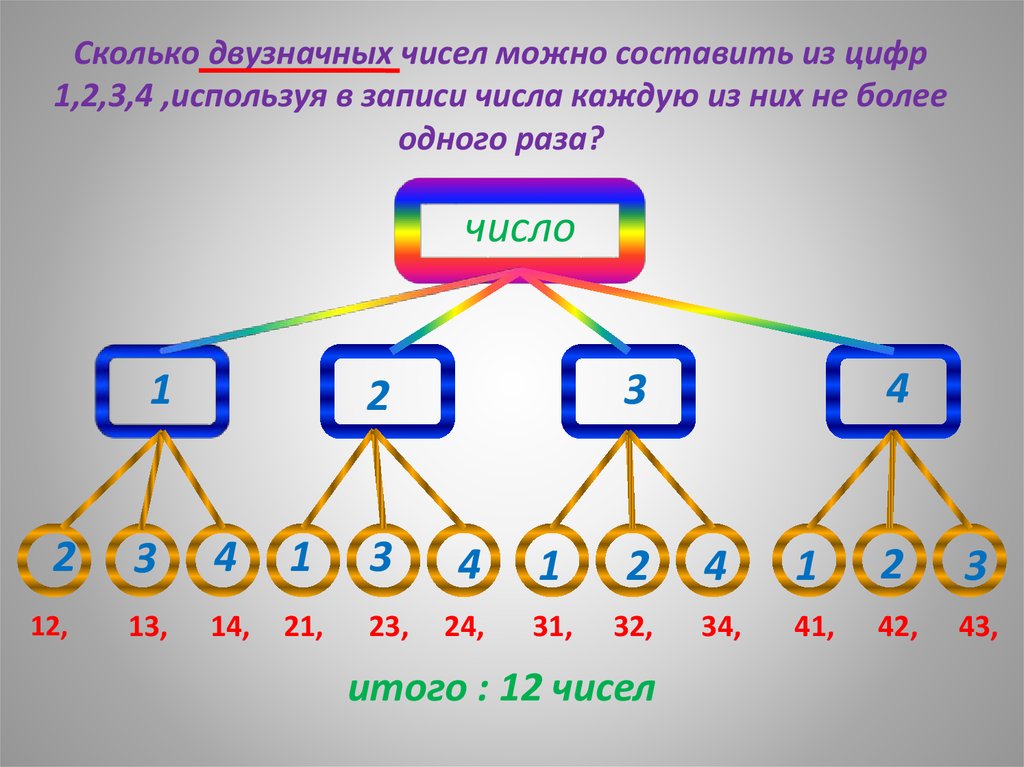 .. страница 18страница 19 .. страница 18страница 19Сборник задач по курсу “Программирование на языке Pascal” Оглавление Линейные программы 3 Линейные программы 6 Операторы выбора и условия 8 Операторы выбора и условия 11 Циклы 14 Вычисление последовательности 18 Типизированные файлы 20 Типизированные файлы 23 Процедуры и функции 26 Процедуры и функции 30 Процедуры и функции 32 Анимация 34 Поиск в массивах 35 Поиск и обработка в массивах 37 Сортировка массивов 40 Матрицы 42 Матрицы 44 Строки 47 Строки 49 Строки 51 Строки 54 Записи 57 Файлы и записи 60 Рекурсия 64 Рекурсия 65 Рекурсия 67 Модули 70
Смотрите также: Сборник задач по курсу » Программирование на языке Pascal» 1113. 19 стр. Программирование на языке Pascal 120.27kb. 1 стр. Сборник задач по курсу неорганической химии часть 3 Методическая разработка 413.64kb. 1 стр. Решение 50 типовых задач по программированию на языке Pascal Дата размещения сборника в сети: 31. 08. 2012 1668.96kb. 24 стр. Рабочая программа дисциплины программирование на языке C# Направление (специальность) подготовки 97.36kb. 1 стр. Курсовая работа по курсу «Программирование» Тема работы: «Разработка приложения с графическим интерфейсом на языке C++ с использованием библиотеки qt» 301.1kb. 1 стр. Курсовая работа по курсу «Программирование» Тема работы: «Разработка приложения с графическим интерфейсом на языке программирования С++ с использованием библиотеки qt» 108. 1 стр. Сборник задач по логическому программированию для студентов специальности «030100 информатика» 747.53kb. 8 стр. Задачник по программированию на языке Pascal 1079.61kb. 8 стр. Программа курса «Программирование на языке С++» 31.04kb. 1 стр. Программирование на Pascal 29.35kb. 1 стр. Элективный курс Программирование в среде delphi класс : 10 Количество часов: 68 Пояснительная записка Delphi 16.23kb. 1 стр. |
— Сколько четырехзначных нечетных чисел, все цифры которых различны, можно составить из цифр от 0 до 9, если в числе обязательно должна быть 5?
Спросил
Изменено 7 лет, 3 месяца назад
Просмотрено 7к раз
$\begingroup$
Сколько четырехзначных нечетных чисел, все цифры которых различны, можно составить из цифр от 0 до 9, если в числе должна быть 5?
Я знаю, что есть 4 разных случая, когда в числе 5:
5 _ _ _
_ 5 _ _
_ _ 5 _
_ _ _ 5
Первая цифра не может быть 0, так как это должно быть 4-значное число.
- комбинаторика
- перестановки
- комбинации
$\endgroup$
2
$\begingroup$
Я бы сначала ввел последнее число и рассмотрел два случая: последнее число равно $5$, а последнее число не равно $5$.
Случай 1: Последнее число — пять.
Это простой случай, остальные цифры могут быть любыми различными цифрами, кроме $5$ (и не начинаться с нуля). Это дает $8$ вариантов для первого числа (не 5 и не 0), $8$ вариантов для второго числа (не первого числа и не $5$) и $7$ вариантов для третьего числа (не первых двух, и не $5$ — последний). Это дает $8\cdot 8\cdot 7=448 вариантов.
Случай 2: Последнее число не пять.
Сначала мы убедимся, что число нечетное. Для этого последняя цифра должна быть $1, 3, 5, 7,$ или $9$. Поскольку это не $5$, у нас есть выбор $4$ для последней цифры. Теперь давайте заполним первую цифру (поскольку она не может быть нулем). Снова есть варианты $8$ для первой цифры (не последней цифры и не нуля). Опять же, есть варианты $8$ для второго числа и $7$ для третьего (точно по тем же причинам, которые упоминались ранее). Теперь у нас есть $4\cdot 8\cdot 8\cdot 7=1792$ номера. Однако некоторые из этих номеров не использовали $5$. Сколько не использовали $5$? Давайте посчитаем это и вычтем. Для последнего числа снова есть варианты $4$ (поскольку $5$ там не было). Теперь есть только $7$ вариантов для первого числа: не $5$, не $0$ и не последняя цифра. Точно так же есть варианты за 7 долларов для второй цифры и за 6 долларов для третьей цифры. Таким образом, есть $7\cdot 7\cdot 6\cdot 4=1176$ чисел, которые вообще не используют $5$. Таким образом, у нас есть $ 1792-1162=616$ хорошие цифры.
Теперь давайте заполним первую цифру (поскольку она не может быть нулем). Снова есть варианты $8$ для первой цифры (не последней цифры и не нуля). Опять же, есть варианты $8$ для второго числа и $7$ для третьего (точно по тем же причинам, которые упоминались ранее). Теперь у нас есть $4\cdot 8\cdot 8\cdot 7=1792$ номера. Однако некоторые из этих номеров не использовали $5$. Сколько не использовали $5$? Давайте посчитаем это и вычтем. Для последнего числа снова есть варианты $4$ (поскольку $5$ там не было). Теперь есть только $7$ вариантов для первого числа: не $5$, не $0$ и не последняя цифра. Точно так же есть варианты за 7 долларов для второй цифры и за 6 долларов для третьей цифры. Таким образом, есть $7\cdot 7\cdot 6\cdot 4=1176$ чисел, которые вообще не используют $5$. Таким образом, у нас есть $ 1792-1162=616$ хорошие цифры.
Объединение case 1 и case 2 дает нам $448+616=1064$ четырехзначные нечетные числа с различными цифрами и $5$ встречающиеся ровно один раз.
$\endgroup$
$\begingroup$
Существуют особые условия для символов $\color{red}{\text{first}}$ и $\color{blue}{\text{last}}$, поэтому сгруппируйте их в 3 случая:
- $5 Сначала $: затем для оставшихся мест (сначала выбирая последнюю цифру) $\color{blue}{4}\times 8\times 7 = 224$ вариантов
- $5$ секунда/третья: тогда для оставшихся мест есть $\color{blue}{4}\times \color{red}{7}\times 7 = 196$ вариантов для каждого, так что всего $2 \times 196 =392$ для этого случая.
- $5$ в последний раз: тогда для оставшихся мест есть $\color{red}{8}\times 8\times 7 = 448$ вариантов
Итого вариантов: $224+392+448=1064$.
$\endgroup$
0
$\begingroup$
Другой способ сделать это — подумать обо всех случаях в целом и вычесть все случаи без каких-либо $5$, потому что ваш вопрос, по сути, спрашивает: «Сколько 4-значных нечетных чисел, все цифры разные, мы можем составить, где одна из цифр $5$?»
Итак, количество 4-значных нечетных чисел в общем равно $8\cdot8\cdot7\cdot5$. Объяснение: $5$ возможных чисел в последнем слоте, чтобы сделать его нечетным, $8$ в первом слоте, потому что это не может быть то, что было в последнем слоте, и это не может быть $0$, $8$ во втором слоте (ни первый и последний, но вы можете использовать $0$), а затем $7$ в третьем слоте.
Объяснение: $5$ возможных чисел в последнем слоте, чтобы сделать его нечетным, $8$ в первом слоте, потому что это не может быть то, что было в последнем слоте, и это не может быть $0$, $8$ во втором слоте (ни первый и последний, но вы можете использовать $0$), а затем $7$ в третьем слоте.
Количество 4-значных нечетных чисел без каких-либо $5$s равно $7*7*5*4$. Объяснение: $4$ возможных чисел в последнем слоте, чтобы сделать его нечетным, без $5$. Следуйте тем же аргументам, что и выше.
Окончательный ответ: $8\cdot8\cdot7\cdot5 — 7\cdot7\cdot5\cdot4=1064$.
$\endgroup$
Твой ответ
Зарегистрируйтесь или войдите в систему
Зарегистрируйтесь с помощью Google
Зарегистрироваться через Facebook
Зарегистрируйтесь, используя электронную почту и пароль
Опубликовать как гость
Электронная почта
Требуется, но никогда не отображается
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie
.
алгебраическое предварительное исчисление — Сколько 4-значных нечетных чисел можно составить, используя цифры 0, 1, 2 и 3, только если повторение цифры не допускается?
Спросил
Изменено 1 год, 5 месяцев назад
Просмотрено 6к раз
$\begingroup$
Как указано в заголовке выше: сколько четырехзначных нечетных чисел можно составить, используя только цифры 0, 1, 2 и 3, если повторение цифры запрещено?
У меня уже есть ответ на это и это 8.
(2)(2)(1)(2) = 8
Однако я не понимаю, как так получилось. Любое понятное объяснение будет оценено!
- алгебра-предварительное исчисление
- перестановки
- комбинации
$\endgroup$
1
$\begingroup$
Подсказка #1 : Поскольку число нечетное, цифра единицы может быть только $1$ или $3$.
Подсказка #2 : Поскольку число состоит из $4$ цифр, цифра тысячи не может быть $0$.
Вы можете закончить?
$\endgroup$
$\begingroup$
Вот как бы я это сделал. Есть $4!=24$ перестановок цифр $4$. Половина из них оканчивается на $0$ или $2$, так что только $12$ из них нечетные. Поскольку четырехзначное число не может начинаться с $0$, мы должны исключить перестановки, начинающиеся с $0$.
После того, как мы исправим последнюю цифру, останется три цифры, и одна из них равна $0$, поэтому мы исключаем треть случаев $12$. Остается 12-4$=8$.
$\endgroup$
$\begingroup$
- Поместите цифру $0$, но не первой (без начального $0$) и не последней (не нечетной), с возможностью $2$
- Выберите нечетную цифру для последнего места с возможностью $2$
- Поместите цифру $2$ на оставшееся место с возможностью $2$
- Поместите другую нечетную цифру на оставшееся место с вероятностью $1$
- Умножить
$\endgroup$
$\begingroup$
Альтернативный подход.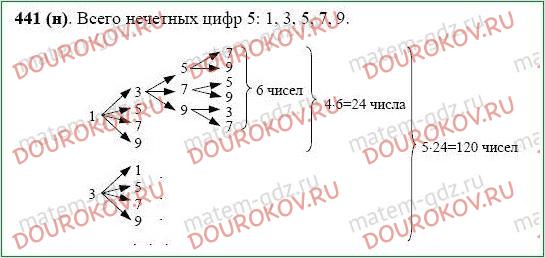
Для любого набора из $k$ цифр, включая $0$, которые не должны повторяться, перечисление того, сколько $k$ цифр можно составить, равно $$к! — (k-1)!.\tag1$$
Второй член выражает удаление $0$ как самой левой цифры.
В данной задаче самая правая цифра может быть либо $1$, либо $3$.
Предположим без ограничения общности, что это $3$, завершите перечисление в соответствии с этим предположением, а затем умножьте результат на $2$, чтобы отразить, что самая правая цифра также может быть $1$.
С $3$ в качестве самой правой цифры у вас останется $(4-1)$ цифр, включая $0$. Затем используйте приведенное выше уравнение (1) с $k=3$.
Следовательно, окончательное перечисление равно
$$2 \times [(3!) — (2!)].$$
$\endgroup$
$\begingroup$
Причина, по которой ответ (2)(2)(1)(2), заключается в том, что
Первая цифра: не может быть 0, поэтому есть три оставшихся числа 1,2,3.
 Но вы должны зарезервировать одно число (1 или 3) для последней цифры, поэтому на самом деле их 9.0045 два возможных числа для выбора первой цифры.
Но вы должны зарезервировать одно число (1 или 3) для последней цифры, поэтому на самом деле их 9.0045 два возможных числа для выбора первой цифры.Вторая цифра: после того, как вы выбрали число для первой цифры, теперь вы можете выбрать число 0 и какое-либо число, отличное от первой цифры, также имея в виду, что другое число (1 или 3) зарезервировано для последней цифры. Таким образом, в качестве второй цифры можно выбрать двух возможных чисел.
Третья цифра: Только один возможный номер для третьей цифры.
Четвертая цифра: Два возможных числа для четвертой цифры (1 или 3).
Использование правила произведения дает (2)(2)(1)(2).
Более простой способ: $4!-2(3!)-4=8$, где
- $4!$ — общее количество способов упорядочить $0123$
- $2(3!)$ — общее количество способов получить последнюю цифру числа как $0$ или $2$
- $3!-2=4$ — это общее количество способов, при которых первая цифра числа равна $0$, за исключением двух случаев, когда последняя цифра числа содержит $2$
$\endgroup$
Твой ответ
Зарегистрируйтесь или войдите в систему
Зарегистрируйтесь с помощью Google
Зарегистрироваться через Facebook
Зарегистрируйтесь, используя электронную почту и пароль
Опубликовать как гость
Электронная почта
Требуется, но никогда не отображается
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie
.
Чисел до 4-х цифр — Разложение, Советы и рекомендации
Четырехзначный номер серии начинается с числа 1000 и заканчивается числом 9999. 4-значные числа — это числа, имеющие 4 цифры, и мы можем сформировать 4-значные числа, используя любые цифры от 0 до 9, но число должно начинаться с цифры 1 или числа больше 1. Числа классифицируются в соответствии с числом цифр, которые они имеют, и значение разряда числа помогает понять значение каждой цифры.
| 1. | Что такое четырехзначные числа? |
| 2. | Как записывать числа до 4 цифр? |
| 3. | Как разложить числа до 4 цифр? |
| 4. | Советы и подсказки по номерам до 4 цифр |
| 5. | Часто задаваемые вопросы о номерах до 4 цифр |
Что такое четырехзначные числа?
4-значные числа — это числа, состоящие только из 4 цифр, в которых первая цифра должна быть 1 или больше 1, а остальные цифры могут быть любым числом от 0 до 9. Например, 5693, 1023 и 9825 — четырехзначные числа.
Например, 5693, 1023 и 9825 — четырехзначные числа.
Как записывать числа до 4 цифр?
Четырехзначные числа записываются или читаются в соответствии со значением разряда цифр. В четырехзначных числах четыре цифры соответствуют четырем разрядам — единицам, десяткам, сотням и тысячам. Когда число записывается в стандартной форме, каждая группа цифр отделяется запятой, образующей точку. Первый период, известный как «период единиц», состоит из первых трех цифр числа, если считать с правой стороны. Следует отметить, что расстановка запятых начинается с 4-значных чисел. Мы ставим запятую непосредственно перед разрядом сотен, потому что заканчивается первый период (единицы) и начинается второй период тысяч. Например, 3210 — это 4-значное число, и после запятой оно записывается как 3210.
Наименьшее четырехзначное число — 1000, а самое большое четырехзначное число — 9999, а всего существует 9000 чисел от 1000 до 9999. Мы можем составить много четырехзначных чисел, используя цифры от 0 до 9, но мы нужно помнить, что разряд тысяч в 4-значном числе не должен быть 0. Например, 0875 не является четырехзначным числом, число считается трехзначным, то есть 875.
Например, 0875 не является четырехзначным числом, число считается трехзначным, то есть 875.
4- числовые числа могут быть записаны в трех формах, т. е. в числовой форме, словами и в развернутой форме. Например, 2345 — это четырехзначное число. В числовой форме это записывается как 2345. Прописью это записывается так: Две тысячи триста сорок пять. В развернутом виде это записывается так: 2000 + 300 + 40 + 5, или 2 тысячи + 3 сотни + 4 десятка + 5 единиц.
Как разложить числа до 4 цифр?
Как уже говорилось выше, четырехзначное число имеет следующие разрядные значения — Тысячи, Сотни, Десятки и Единицы. Чтобы разложить 4-значные числа, мы умножаем каждую цифру 4-значного числа на его значение, то есть 1000, 100, 10 и 1 соответственно. Например, данное 4-значное число 5627 можно разложить следующим образом:
- 5 находится в тысячном разряде, а его разрядное значение равно 5 × 1000 = 5000 .
- 6 стоит на разряде сотен и его разрядное значение равно 6 × 100 = 600
- 2 стоит на разряде десятков и его разрядное значение равно 2 × 10 = 20
- 7 стоит на месте, и его разрядное значение равно 7 × 1 = 7
Итак, расширенная форма 5627 = 5000 + 600 + 20 + 7
Обратите внимание на следующий рисунок, на котором показано, как записать 4-значное число в соответствии с его разрядными значениями. В данном случае мы взяли пример с 4-значным числом: 4123. Здесь 4 пишется в разряде тысяч, 1 — в разряде сотен, 2 — в разряде десятков и 3 — в разряде единиц.
В данном случае мы взяли пример с 4-значным числом: 4123. Здесь 4 пишется в разряде тысяч, 1 — в разряде сотен, 2 — в разряде десятков и 3 — в разряде единиц.
Советы и рекомендации по номерам до 4 цифр
Ниже приведены некоторые советы и рекомендации по числам до 4 цифр, которые могут помочь при решении проблем, связанных с этими числами.
- При умножении любого однозначного числа (от 1 до 9) на 1000 получается четырехзначное число. Например, 5 × 1000 = 5000
- При умножении любого двузначного числа на 100 получается четырехзначное число. Например, 44 × 100 = 4400
- При умножении любого трехзначного числа на 10 получается четырехзначное число. Например, 678 × 10 = 6 780 .
- Когда любое четырехзначное число умножается на 1, в результате получается четырехзначное число. Например, 2345 × 1 = 2345
- Наименьшее четырехзначное число, состоящее из разных цифр, равно 1023.
- Наименьшее четырехзначное число, состоящее только из одной цифры, — 1111.

- Наименьшее четырехзначное число, состоящее из двух разных цифр, равно 1000. (1000 также является наименьшим четырехзначным числом).
- Наибольшее четырехзначное число, использующее только одну цифру, равно 9 999 (9 999 также является наибольшим четырехзначным числом).
- Наибольшее четырехзначное число, состоящее из двух разных цифр, равно 9998.
- Наибольшее четырехзначное число, состоящее из всех цифр, равно 9876.
Важные примечания
Ниже приведены некоторые важные примечания, относящиеся к числам до 4 цифр, которые мы изучали в этой статье.
- Есть 4 номера (любое число от 0 до 9) в виде 4-значного числа, а начальный номер должен быть 1 или больше 1.
- Разряд тысяч в 4-значном числе не может быть равен 0.
- Наименьшее четырехзначное число — 1000, а наибольшее четырехзначное число — 9999.
- Всего существует 9000 четырехзначных чисел.
Наименьшее 4-значное число
Наименьшее 4-значное число — 1000, поскольку предшествующее ему число — 999, является 3-значным числом. Четырехзначные числа начинаются с 1000 и заканчиваются на 9.999.
Четырехзначные числа начинаются с 1000 и заканчиваются на 9.999.
Наибольшее 4-значное число
Наибольшее 4-значное число — 9999, потому что за ним следует 10000, которое является 5-значным числом. 4-значные числа начинаются с 1000 и заканчиваются на 9999.
☛ Похожие статьи
- Номера до 2 цифр
- Номера до 3 цифр
- Номера до 5 цифр
- Номера до 6 цифр
- Номера до 7 цифр
- номеров до 8 цифр
- Номера до 9 цифр
- Номера до 10 цифр
Часто задаваемые вопросы о номерах до 4 цифр
Что такое четырехзначные числа?
Простыми словами, 4-значное число является 4-значным числом. Первая цифра 4-значного числа должна быть 1 или больше единицы, а остальные цифры могут быть любым числом от 0 до 9. Четырехзначные числа начинаются с 1000 и заканчиваются на 9999. Значения разрядов в 4-значном числе, начиная справа, это единицы, десятки, сотни и тысячи.
Какое самое большое четырехзначное число?
9999 — самое большое четырехзначное число. Мы можем прочитать это число словами как девять тысяч девятьсот девяносто девять. Число после 9 999 равно 10 000 и является пятизначным числом, поэтому наибольшее четырехзначное число равно 9 999.
Какое самое маленькое четырехзначное число?
1000 — наименьшее четырехзначное число. Мы можем прочитать число словами как тысяча. Число до 1000 равно 999 и является трехзначным числом, поэтому наименьшее четырехзначное число равно 1000.
Сколько существует четырехзначных чисел?
Есть 9000 четырехзначных чисел, и они начинаются с числа 1000 и заканчиваются числом 9999.
Как поставить запятую в четырехзначном числе?
В четырехзначных числах четвертая крайняя слева цифра представляет разряд тысяч. Запятая в 4-значном числе ставится между 4-й и 3-й цифрой справа, то есть между разрядом тысяч и разрядом сотен. Например, четырехзначное число 3674 записывается как 3674.
Каковы простые делители наибольшего четырехзначного числа?
Простые делители наибольшего четырехзначного числа 9999 равны 3, 11 и 101.
Какое наибольшее четырехзначное число является полным квадратом?
Наибольшее четырехзначное число, являющееся полным квадратом, равно 9801.
Сколько четырехзначных чисел можно составить из повторяющихся цифр 1, 2, 3, 4, 5?
В математике перестановка относится к функции упорядочивания всех членов группы в некоторый ряд или порядок. Другими словами, если группа уже направлена, то перенаправление ее компонентов называется процессом перестановки. Перестановки происходят более или менее важным образом почти в каждой области математики. Они часто появляются при соблюдении различных команд на определенных ограниченных местах.
Перестановка
Перестановка известна как процесс упорядочивания группы, тела или чисел по порядку, выбор или чисел из набора, известный как комбинации таким образом, что последовательность целых чисел не беспокоить.
Формула перестановки
При перестановке r элементов собираются из n элементов без какой-либо замены. В этой последовательности собираем материю.
п Р r = (n!)/(n – r)!
Здесь
n = размеры набора, общее количество объектов в наборе
r = размеры подмножества, количество объектов на выбор из набора
Комбинация
Комбинация является способом выбора объектов из группы, так что (в отличие от перестановок) последовательность выбора не имеет значения. В меньших случаях можно представить, суммируя, количество комбинаций. Комбинация относится к комбинации n объектов, взятых k одновременно без повторения. Говоря о комбинациях, в которых допускается повторение, часто используются выражения k-выбор или k-комбинация с повторением.
Формула комбинации
В комбинации r объектов выбираются из группы n объектов, причем последовательность выбора не имеет значения.
n C r = n!⁄((n – r)! r!)
Здесь
n = количество объектов, выбранных из группы
r = количество объектов, выбранных из группы
Сколько четырехзначных чисел можно составить из чисел 1, 2, 3, 4, 5 с повторяющимися цифрами?
Решение:
Аналогичные вопросыДопускается повторение цифры. Итак, для разряда единиц у нас есть 5 вариантов, т.е. 1,2,3,4,5, аналогично для разряда десятков у нас снова 5 вариантов, т.е. 1,2,3,4,5 для сотого места, у нас есть 5 вариантов, т.е. , 1,2,3,4,5 аналогично, для тысячного разряда имеем 5 вариантов т.е. 1,2,3,4,5.
Общее количество четырехзначного числа = 5 × 5 × 5 × 5
= 625
Вопрос 1: Сколько шестизначных чисел можно составить, используя цифры 0,1,2,3,4,5. Допускается ли повторение цифр?
Ответ:
Допускается повтор цифр.
Итак, для первого места у нас есть 6 вариантов, т.е. 0,1,2,3,4,5, аналогично для второго места у нас снова 6 вариантов, т.е. 0,1,2,3,4,5 для третьего места мы имеем 6 вариантов, т.е. 0,1,2,3,4,5, для четвертого места имеем 6 вариантов, т.е. 0,1,2,3,4,5, а для пятого тысячного места имеем 6 вариантов, т.е. 0 ,1,2,3,4,5, а для шестого места у нас есть 5 вариантов, то есть 1,2,3,4,5, мы не можем взять 0 на последнем месте, потому что если 0 будет заполнен на последнем месте, он будет не станет 6-значным числом, оно будет принято как 5-значное число.
Общее количество шестизначного числа = 4 × 5 × 5 × 5 × 5 × 5
= 12500
, Вопрос 2 1,0) если повтор цифр не допускается?
Ответ:
Для четного числа единиц целое число должно быть 0, Теперь целые числа выдерживают 5 т.е., 3,5,7,9,1 теперь для тысячного разряда у нас есть 5 вариантов для сотого разряда мы есть 4 варианта, а для разряда десятков у нас есть 3 варианта
Общее количество из 4 цифр можно найти равномерное число = 5 × 4 × 3
= 60
Вопрос 3: сколько 8 -значных чисел можно найти с помощью цифр 1, 2, 3,4,5,6 и 7 ( разрешены повторения) таким образом, чтобы число читалось одинаково слева направо или справа налево?
Решение:
Восьмизначное число, которое читается одинаково слева направо и справа налево, означает, что последние четыре цифры совпадают с первыми четырьмя цифрами, но в противоположном направлении.
Итак, это четырехзначное число.
Повторение цифры разрешено. Итак, для первого числа у нас есть 7 вариантов, аналогично для второго числа у нас снова 7 вариантов, для третьего числа у нас есть 7 вариантов, а для четвертого числа у нас есть 7 вариантов.
Таким образом, возможные числа = 7 × 7 × 7 × 7
и 7, чтобы цифры не повторялись, а последние цифры были четными, это
Решение:
Так как последние цифры четные.
Таким образом, 1-е место можно проникнуть 3 способами, а последнее место можно проникнуть 2 способами, а остальные места можно проникнуть
5 P 4 = 120 способами
Следовательно, число шесть число, так что последние цифры четные, равно 3 × 120 × 2 = 720.
без повторения цифр сколько четырехзначных чисел можно составить из 2 6 7 и 3
Мохаммед
Ребят, кто-нибудь знает ответ?
найдите без повторения цифр, сколько четырехзначных чисел можно составить из 2 6 7 и 3 с экрана.
Количество четырехзначных чисел без повторения, которые могут быть образованы из цифр 1,2,3,4,5,6,7, в которых каждое число имеет две нечетные цифры и две четные цифры
Число четырехзначное числа без повторений, которые можно составить из цифр 1, 2, 3, 4, 5, 6, 7, в которых каждое число состоит из двух нечетных и двух четных цифр, равно
Главная >
Количество четырехзначных чисел без повторений, которые можно составить из цифр 1, 2, 3, 4, 5, 6, 7, в которых каждое число состоит из двух нечетных и двух четных цифр, равно
.Вопрос Число 4
значных чисел без повторения, которые могут быть образованы из цифр
1 , 2 , 3 , 4 , 5 , 6 , 7
, в котором каждое число имеет две нечетные цифры и две четные цифры равно
A 450 B 432 C 454 D 436 Решение
Правильный вариант B
432 Нечетные цифры = 1 , 3 , 5 , 7 Четные цифры = 2 , 4 , 6
3 C 2 направления.
Опять же, эти 4 цифры можно составить как
4 ! способы.
∴
Число образованных цифр
= 4 C 2 × 3 C 2 × 4 ! = 432
MathematicsStandard XII
Предложить исправления 2
ПОХОЖИЕ ВОПРОСЫ
Q. Сколькими способами
4
-значные числа можно составить из цифр
1 , 2 , 3 , 7 , 8 , 9
без повторения? Сколько из них четных чисел?
Mathematicsstandard XII
Q. Количество
4
цифры ровные числа, которые могут быть сформированы с использованием
0, 1, 2, 3, 4, 6
без повторения —
Mathematicsdard Vi VI.
Посмотреть ещё
स्रोत : byjus.com
Сколько 4
Ответ (1 из 22): Просто перейдите к главе P&C по математике 😀 если какая-либо цифра не повторяется, то это всегда «n!» n — это число. как в вашем вопросе это n=4 , так что 4!=24 теперь вы можете ответить на любой вопрос этим методом.
Сколько четырехзначных чисел можно составить из цифр 2, 5, 6 и 9, не повторяя ни одной цифры?
Реклама Amazon Web Services (AWS)
AWS это как.
AWS упрощает создание, обучение и развертывание моделей машинного обучения в любом масштабе.
Sort Ellis Cave
Более 40 лет работы инженером-электрикомУ автора 5 тысяч ответов и 2,5 миллиона просмотров ответов за 4 года цифра?
Используя язык программирования J:
#a=.10#.2 5 6 9{~perm 4
24 Ответ 24 перечислите их: a
2569 2596 2659 2695 2956 2965 5269 5296 5629 5692 5926 5962 6259 6295 6529 6592 6925 6952 9256 9265 9526 9562 9625 9652
,> >> >> >> >> astemance Avidance Avidance Avidance Avidance Avidance Avidance Avidance Avidance Avidance Avidance Avidance 9565 9625 9652 9000
110, >> >> >> >>. может выполнять, не думая о них».
― Alfred North Whitehead
621 просмотр Вопросы по теме
Сколько четырехзначных чисел можно составить от 0 до 9 без повторения?
Сколько четырехзначных чисел можно составить из 1,2,4,5,7 и 8?
Какие четырехзначные числа можно записать, используя цифры 2,5,7,9?
Сколько четырехзначных чисел можно составить из 2, 4, 5 и 7, если нет двух одинаковых цифр?
Сколько четырехзначных чисел можно составить из цифр 1, 2, 3, 4, 5 и 6 без повторения цифр?
Сайед Атар
Изучал вычислительную технику У автора 120 ответов и 573,2 тыс.
просмотров ответов4y
Связанные
Сколько трехзначных чисел можно составить, используя 1,2 и 3 без повторения цифры?
Первоначальный ответ: сколько трехзначных чисел можно составить, используя 1,2 и 3 без повторения цифры?
Рассмотрим эту задачу как заполнение 3 пробелов 3 цифрами, где повторение цифр не допускается. Теперь давайте поговорим о трех пространствах поточечно.
Первое пустое место можно заполнить, используя 1, 2 или 3, что оставляет нам 3 способа выполнения этой задачи. Следовательно, первое место можно заполнить 3 способами.
Второе пустое пространство может быть заполнено только двумя способами, так как наш выбор уменьшается после заполнения первого пробела, поскольку повторения не допускаются. Например, если мы заполнили первое пространство цифрой 3, то второе пространство можно заполнить, используя только 1 или 2, как повторы не допускаются. Следовательно, второе пространство можно заполнить двумя способами.
Аналогично можно утверждать, что последнее место можно заполнить 1 способом.
Теперь, поскольку заполнение всех этих пространств является независимым заданием, Следовательно, у нас есть правило по продукту.
Общее количество путей= 3*2*1=6 путей.
Спасибо за прочтение 🙂 .
8K просмотровПроголосовать за
При поддержке USAFIS
Это лучшее время для подачи заявки на участие в лотерее Green Card DV!
Получите шанс выиграть и подайте заявку сегодня! Америка ждет вас с множеством удивительных возможностей.
Rising Raiser Engineer6y
Первоначальный ответ: Сколько четырехзначных чисел можно составить из 2,6,9,5 без повторения цифр?
_ _ _ _ ПОЗИЦИИ 1 2 3 4
В 1-й позиции мы можем выбрать либо 2, либо 6, либо 9, либо 5
, поэтому первую позицию можно выбрать 4 способами.
Во 2-й позиции мы можем выбрать цифру 3-мя способами, так как мы хотим 4-значное число без повторения, так как уже одна цифра выбрана в 1-й позиции. Итак, оставшиеся 3 числа 3-мя способами.
Аналогично, в 3-й позиции мы можем выбрать цифру двумя способами
В 4-й позиции мы можем выбрать цифру одним способом
Таким образом, наконец, 4*3*2*1=24 способа выбрать 4-значное число без повторения через (2,6,9,5) цифр.
8,6 тыс. просмотровПросмотреть отзывы
HsBadarinath
Инженер-строительУ автора 51 тыс. ответов и 32,3 млн просмотров ответов4y
Связанные
Сколько трехзначных чисел можно составить из 5, 3 и 2?
3-значные числа равны
235, 253, 325, 352, 523 и 532 — всего 6.
1K просмотровПроголосовать за
Вопросы по теме
Сколько двузначных чисел можно составить, используя цифры 1,2,5,7,8 и 9 без повторения?
Сколько трехзначных чисел можно составить из цифр 2, 3, 4, 5, 7, 9, если образуемое число четное и не повторяется?
Сколько четырехзначных чисел можно составить из цифр 0, 7, 1 и 9, не повторяя их?
Сколько четырехзначных чисел можно составить из цифр 1, 2, 4 и 5, если ни одна цифра не используется более одного раза? Сколько из этих чисел будет четным?
Сколько чисел можно составить из цифр 4, 5, 6 и 9, не повторяя ни одну из цифр? Сколько из них лежит между 4000 и 6000?
Tanmay Pandit
IITJ CSE ’22Автор имеет 573 ответа и 2,3 миллиона просмотров ответа6y
Исходный ответ: Сколько четырехзначных чисел можно составить из 2,6,9,5 без повторения каких-либо цифр?
Возьмем 2 в разряде тысяч.
Теперь из оставшихся 3 цифр можно составить 6 трехзначных чисел.
Мы можем перевести любую из этих 4 цифр в разряд тысяч.
Ответ. 4*6=24. Подсказка:
Если вам нужно составить n-значное число из заданных n цифр без повторения, то answer=n!
Исключение:
Когда любое из заданных чисел равно 0, мы не можем занять его последнее место.
Тогда Анс.= n! — (н-1)!
3,9 тыс. просмотровПросмотреть отзывыОтвет запрошен
Джой Пол
При поддержке Brand Push
Как получить сотни авторитетных ссылок на свой сайт?
Вы можете получить 200 безопасных обратных ссылок с авторитетных сайтов в течение 10 дней, используя службу публикации новостей.
Ричард Дарвин
Бывший (34+ лет) почтовый клерк (1977–2011). Автор имеет 168 ответов и 76,7K wives4y
Связанный
स्रोत: www.quora.com
Количество 4 цифр даже даже цифровых. Числа, которые можно составить из 0,1,2,3,4,5,6 без повторения, это
Нажмите здесь👆, чтобы получить ответ на свой вопрос ✍️ Количество четных 4-значных чисел, которые можно составить из 0,1 ,2,3,4,5,6 без повторения
Вопрос
Количество четырехзначных четных чисел, которые можно составить из 0,1,2,3,4,5,6 без повторения, равно
A
120
B
0091010 300 300
420
D
20
Средний разомкнутый в приложении.
Решение, подтвержденное Toppr
Правильный вариант C)
Для ровной цифры может быть последняя цифра
. Но первая цифра не может быть 0
Итак: I:6×5×4=120 II:5×5×4=100 III:5×5×4=100 IV:5×5×4=100
∴ Общее количество четных 4 цифр
№. =120+100+100+100
=420
Был ли этот ответ полезен?
31 8
स्रोत: www.toppr.com
Сколько четырехзначных нечетных чисел
Ваш ответ
1 Ответ
Они начинаются с 1001 и конец на 999. Так что есть 8999 4- числовые числа от 1001 до 9999, и примерно половина из них нечетные, то есть 4500 нечетных чисел.
ответил по Стержень Пользователь с самым высоким рейтингом (1,0 млн баллов)Похожие вопросы
1 ответ
Сколько различных комбинаций семизначных чисел, начинающихся с 555, возможно?
спросил 15 апреля 2013 г.
в Word ответы на задачи по Роуз42459 Пользователь 1-го уровня (120 баллов) | 382 просмотра
- Математика 8-го класса
- текстовые задачи
1 ответ
Сколько четных двузначных чисел имеют нечетные числа в виде суммы своих цифр?
спросил 29 сент. 2021 г. в Pre-алгебра ответы по Чан Туан Ань | 317 просмотров
1 ответ
Сколько нечетных пятизначных счетных чисел можно составить, выбирая цифры из набора 1, 2, 3, 4, 5, 6, 7, если цифры могут повторяться?
спросил 27 ноября 2015 г. в других математических темах по гуппи | 745 просмотров
- подсчет и вероятность
2 ответа
в ростерном методе, набор A — это набор двузначных нечетных чисел больше 39которые делятся на 5
спросил 5 февраля 2017 г. по алгебре 2 Ответы по канеша Пользователь 1-го уровня (140 баллов) | 5,0 тыс. просмотров
- математическая задача
1 ответ
Напишите пять трехзначных чисел, которые нечетны и делятся на 3.
спросил 5 февраля 2013 г. в Pre-алгебра ответы по анонимный | 376 просмотров
- математическая задачка
1 ответ
сколько четырех нечетных чисел, если их сложить, то получится 15 в сумме
спросил 6 августа 2014 г. в Pre-алгебра ответы по Теджусинг | 319 просмотров
2 ответа
сумма n и еще трех последовательных нечетных чисел равна 56. какие четыре числа
спросили 4 марта 2014 г. в порядке операций по Тайлор Робертсон | 594 просмотра
- предварительная алгебра
- последовательные числа
- решение уравнений
- задачи по алгебре
1 ответ
Сколько возможных трехзначных чисел можно составить из этих чисел
спросил 1 мая 2020 г. по анонимный | 123 просмотров
- подсчет и вероятность
- словесные задачи
- пожалуйста, покажите работу
- перестановки и комбинации
1 ответ
В числе больше десятков, чем единиц.
Значение цифры единиц равно 8. Каковы возможные числа?
спросил 4 сентября 2012 г. в Word ответы на задачи по анонимный | 1,8 тыс. просмотров
- словесных задач
1 ответ
Найдите разницу между суммой двухзначных нечетных чисел и суммой двузначных четных чисел?
спросил 27 февраля 2014 г. в Word ответы на задачи по ГБ Рана | 463 просмотра
- словесные задачи
1 ответ
Сколько различных четырехзначных чисел можно составить, используя цифры 2, 4 и 6? (неповторяющийся)
спросил 12 июня 2013 г. в ответы по геометрии по анонимный | 422 просмотра
- решение уравнений
0 ответов
сколько четырехзначных чисел от 1000 до 9999
задано 3 ноября 2011 г. в Word ответы на задачи по анонимный | 945 просмотров
1 ответ
Сколько различных 5-значных почтовых индексов возможно, если цифры могут повторяться?
спросил 21 апр.
2013 г. в Word ответы на задачи по анонимный | 867 просмотров
2 ответа
Сколько различных адресов возможно, если в каждом адресе есть цифры 0, 3, 4 и 8?
спросил 28 января 2013 г. по алгебре 1 ответы по анонимный | 334 просмотров
3 ответа
сколько различных произведений можно получить, если перемножить два однозначных положительных числа
вопрос 25 сентября 2012 г. по алгебре 1 ответы по анонимный | 1.3k просмотров
- Алгебра 8 класс
1 ответ
Какие два четырехзначных числа имеют сумму 7635 и разность 1127
спросил 4 декабря 2013 г. по алгебре 2 Ответы по анонимный | 2,9 тыс. просмотров
- задачи по алгебре
- текстовые задачи
1 ответ
Какие четыре четырехзначных числа делятся на 2,3,5 и 9
вопрос 9 января 2013 г. по алгебре 1 ответы по анонимный | 414 просмотров
- математическая задача
- задачи со словами
3 ответа
если бы у вас были числа 1 2 3 4 5 6 7 8 9 и 0 какие четырехзначные числа вы можете получить
9001 8 октября 2011 г.









 081.344
081.344 Сколькими способами можно распределить 21 человека на три равные по количеству группы?
Сколькими способами можно распределить 21 человека на три равные по количеству группы? Сколько чисел, меньше 100000, можно написать с помощью цифр 7 и 0?
Сколько чисел, меньше 100000, можно написать с помощью цифр 7 и 0? Сколькими способами это можно сделать?
Сколькими способами это можно сделать? Сколько чётных чисел можно составить из цифр числа 2567, если каждую цифру можно использовать не более одного раза?
Сколько чётных чисел можно составить из цифр числа 2567, если каждую цифру можно использовать не более одного раза?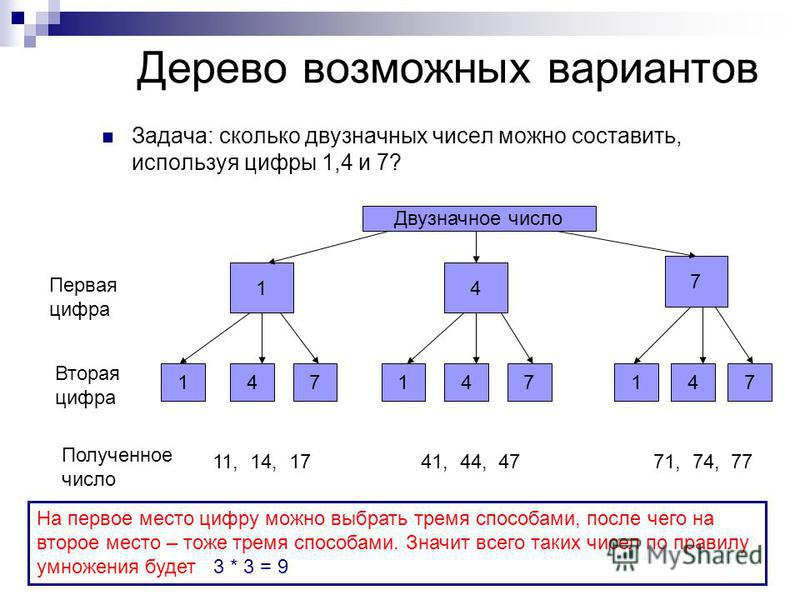 Сколько различных слов можно получить из слова “обороноспособность”?
Сколько различных слов можно получить из слова “обороноспособность”? Сколько имеется шестизначных чисел, у которых три цифры четные, а три — нечетные?
Сколько имеется шестизначных чисел, у которых три цифры четные, а три — нечетные? Сколькими способами можно распределить 10 одинаковых цветов по трем различным вазам так, чтобы не было пустых ваз?
Сколькими способами можно распределить 10 одинаковых цветов по трем различным вазам так, чтобы не было пустых ваз? Сколькими способами можно переставить буквы слова “парабола” так, чтобы никакие две гласные не стояли рядом?
Сколькими способами можно переставить буквы слова “парабола” так, чтобы никакие две гласные не стояли рядом? Сколько существует четырехзначных чисел, все цифры которых различны?
Сколько существует четырехзначных чисел, все цифры которых различны? Из колоды, содержащей 36 карт, вынули 12 карт. Во скольких случаях среди этих карт окажется хотя бы 3 туза?
Из колоды, содержащей 36 карт, вынули 12 карт. Во скольких случаях среди этих карт окажется хотя бы 3 туза? Сколькими способами это можно сделать?
Сколькими способами это можно сделать?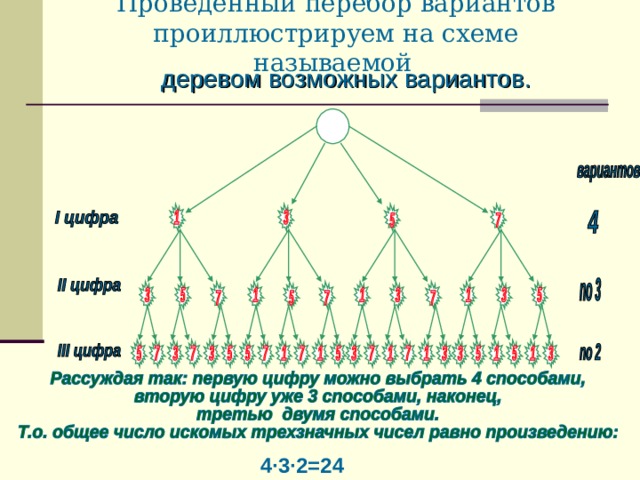 Семь девушек и пятеро юношей играют в волейбол. Сколькими способами они могут разбиться на две команды по 6 человек в каждой команде, если в каждой команде должно быть хотя бы по три девушки?
Семь девушек и пятеро юношей играют в волейбол. Сколькими способами они могут разбиться на две команды по 6 человек в каждой команде, если в каждой команде должно быть хотя бы по три девушки? Сколькими способами можно расставить 12 белых и 12 черных шашек на белых полях шахматной доски?
Сколькими способами можно расставить 12 белых и 12 черных шашек на белых полях шахматной доски? Сколькими способами это можно сделать, если для передачи писем можно послать трех курьеров и каждое письмо можно дать любому курьеру?
Сколькими способами это можно сделать, если для передачи писем можно послать трех курьеров и каждое письмо можно дать любому курьеру? Сколько нечётных чисел можно составить из цифр числа 2567, если каждую цифру можно использовать не более одного раза?
Сколько нечётных чисел можно составить из цифр числа 2567, если каждую цифру можно использовать не более одного раза? Сколько вариантов ответить на тест существует?
Сколько вариантов ответить на тест существует? Сколькими способами из полной колоды карт можно выбрать по 4 карты каждого цвета?
Сколькими способами из полной колоды карт можно выбрать по 4 карты каждого цвета? ..
.. Такие задачи называются комбинаторными, а соответствующий раздел математики – комбинаторикой.
Такие задачи называются комбинаторными, а соответствующий раздел математики – комбинаторикой. Из множества, содержащего m различных элементов, надо выбрать упорядоченное подмножество из k элементов (k£m), то есть такое подмножество, в котором элементы располагаются в определенном порядке, и изменение порядка элементов изменяет подмножество. Кроме этого, элементы в выбранном подмножестве не повторяются. Требуется выяснить, сколько таких комбинаций существует. По правилу произведения получаем, что первый элемент можно выбрать m способами, второй элемент – (m-1) способом, и так далее, а элемент с номером k можно выбрать (m – k + 1) способами. Следовательно, число упорядоченных k-элементных подмножеств, взятых из множества, содержащего m элементов равно m(m-1)(m-2)…(m-k+1). Такие подмножества называются размещениями из m элементов по k элементов, а их общее число можно выразить формулой .
Из множества, содержащего m различных элементов, надо выбрать упорядоченное подмножество из k элементов (k£m), то есть такое подмножество, в котором элементы располагаются в определенном порядке, и изменение порядка элементов изменяет подмножество. Кроме этого, элементы в выбранном подмножестве не повторяются. Требуется выяснить, сколько таких комбинаций существует. По правилу произведения получаем, что первый элемент можно выбрать m способами, второй элемент – (m-1) способом, и так далее, а элемент с номером k можно выбрать (m – k + 1) способами. Следовательно, число упорядоченных k-элементных подмножеств, взятых из множества, содержащего m элементов равно m(m-1)(m-2)…(m-k+1). Такие подмножества называются размещениями из m элементов по k элементов, а их общее число можно выразить формулой . Пусть множество содержит m различных элементов. Рассмотрим все возможные варианты перестановок элементов этого множества. Получаемые при этом упорядоченные множества отличаются друг от друга только порядком входящих в них элементов. Такие упорядоченные множества называются перестановками. Число перестановок из m элементов равно:
Пусть множество содержит m различных элементов. Рассмотрим все возможные варианты перестановок элементов этого множества. Получаемые при этом упорядоченные множества отличаются друг от друга только порядком входящих в них элементов. Такие упорядоченные множества называются перестановками. Число перестановок из m элементов равно: Сколькими способами можно выбрать из этой группы троих студентов для участия в конференции?
Сколькими способами можно выбрать из этой группы троих студентов для участия в конференции? Сколько различных слов, каждое из которых содержит 4 буквы, можно составить из букв слова ВЫБОРКА? (Под словом понимаем любой набор букв.)
Сколько различных слов, каждое из которых содержит 4 буквы, можно составить из букв слова ВЫБОРКА? (Под словом понимаем любой набор букв.) ..
.. Записать решение в виде линейного алгоритма.
Записать решение в виде линейного алгоритма. 


 Каждый квадратный сантиметр содержит 300 точек, любая точка описывается 4-мя битами. Каков общий информационный объем документа в Кбайтах?
Каждый квадратный сантиметр содержит 300 точек, любая точка описывается 4-мя битами. Каков общий информационный объем документа в Кбайтах?  Найти координаты самой низкой точки траектории и другой наивысшей точки подъема.
Найти координаты самой низкой точки траектории и другой наивысшей точки подъема.  19kb.
19kb. 12kb.
12kb. Но вы должны зарезервировать одно число (1 или 3) для последней цифры, поэтому на самом деле их 9.0045 два возможных числа для выбора первой цифры.
Но вы должны зарезервировать одно число (1 или 3) для последней цифры, поэтому на самом деле их 9.0045 два возможных числа для выбора первой цифры.
 Итак, это четырехзначное число.
Итак, это четырехзначное число.
 ∴
∴
 просмотров ответов4y
просмотров ответов4y


 Решение, подтвержденное Toppr
Решение, подтвержденное Toppr в Word ответы на задачи
по
Роуз42459
Пользователь 1-го уровня
(120 баллов)
| 382 просмотра
в Word ответы на задачи
по
Роуз42459
Пользователь 1-го уровня
(120 баллов)
| 382 просмотра
 Значение цифры единиц равно 8. Каковы возможные числа?
Значение цифры единиц равно 8. Каковы возможные числа? 2013 г.
в Word ответы на задачи
по
анонимный
| 867 просмотров
2013 г.
в Word ответы на задачи
по
анонимный
| 867 просмотров