Задание 9 из ЕГЭ по информатике
Все для самостоятельной подготовки к ЕГЭ
Зарегистрироваться
Русский язык Математика (профильная) Математика (базовая) Обществознание Физика История Биология Химия Английский язык Литература Информатика География
Задания Варианты Теория
Задание 1 Задание 2 Задание 3 Задание 4 Задание 5 Задание 6 Задание 7 Задание 8 Задание 9 Задание 10 Задание 11 Задание 12 Задание 13 Задание 14 Задание 15 Задание 16 Задание 17 Задание 18 Задание 19 Задание 20 Задание 21 Задание 22 Задание 23 Задание 24 Задание 25 Задание 26 Задание 27
За это задание вы можете получить 1 балл на ЕГЭ в 2023 году
Разбор сложных заданий в тг-канале:
Посмотреть
Задача 1
Откройте файл электронной таблицы, содержащей в каждой строке шесть натуральных чисел.
Определите, сколько существует строк, в которых выполняются сразу два условия:
1) в строке р…
Задача 2
Откройте файл электронной таблицы, содержащей в каждой строке шесть натуральных чисел. Определите, сколько существует строк, в которых выполняются сразу два условия:
1) в строке р…
Задача 3
Откройте файл электронной таблицы, содержащей в каждой строке шесть натуральных чисел. Определите, сколько существует строк, в которых выполняются сразу два условия:
1) в строке в…
Задача 4
Откройте файл электронной таблицы, содержащей в каждой строке шесть натуральных чисел. Определите, сколько существует строк, в которых выполняются сразу два условия:
1) в строке вс…
Задача 5
Откройте файл электронной таблицы, содержащей в каждой строке пять натуральных чисел. Определите сколько существует строк, в которых сумма утроенного квадратов максимального и удво…
Задача 6
Откройте файл электронной таблицы, содержащей в каждой строке пять натуральных чисел.
Задача 7
Откройте файл электронной таблицы, содержащей в каждой строке три натуральных числа. Определите сколько существует строк, в которых эти числа могут составлять арифметическую прогре…
Задача 8
Откройте файл электронной таблицы, содержащей в каждой строке три натуральных числа. Определит сколько существует строк, в которых эти числа могут составлять арифметическую прогрес…
Задача 9
Откройте файл электронной таблицы, содержащей в каждой строке шесть целых чисел (координаты трёх точек: x1, y1, x2, y2, x3, y3). Определит сколько существует треугольников с периме…
Задача 10
Откройте файл электронной таблицы, содержащей в каждой строке шесть натуральных чисел, координаты и радиус двух окружностей: x1, y1, r1, x2, y2, r2. Определите количество строк, в …
Задача 11
Откройте файл электронной таблицы, содержащей в каждой строке четыре натуральных числа, координаты двух точек, начала и конца отрезка: x1, y1, x2, y2.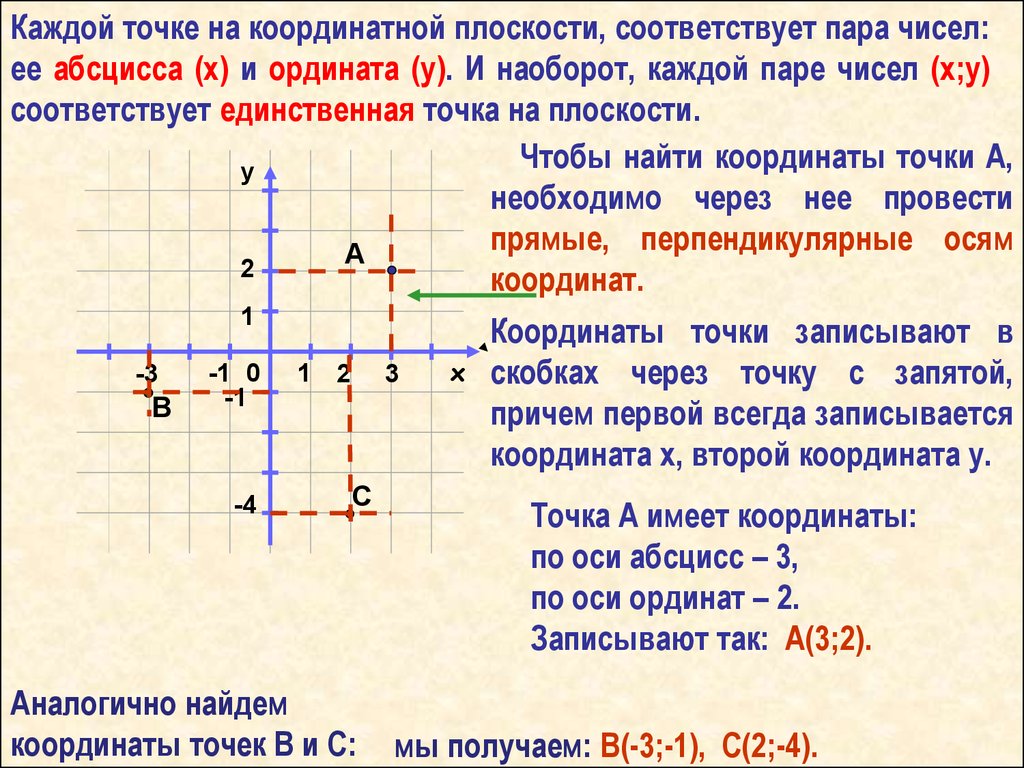
Найдите сумму длин отрезков …
Задача 12
Откройте файл электронной таблицы, содержащей в каждой строке четыре натуральных числа, координаты двух точек, начала и конца отрезка: x1, y1, x2, y2. Найдите минимальную длину ср…
Задача 13
Откройте файл электронной таблицы, содержащей в каждой строке три натуральных числа (длины трёх отрезков). Определит сколько существует треугольников с тупым углом. При решении дан…
Откройте файл электронной таблицы, содержащей в каждой строке три натуральных числа (длины трёх отрезков). Определит сколько существует треугольников с площадью больше 1000 и меньш…
Задача 15
Откройте файл электронной таблицы, содержащей в каждой строке четыре натуральных числа. Определите количество строк, в которых числа расположены в порядке возрастания: каждое следу…
Задача 16
Откройте файл электронной таблицы, содержащей в каждой строке четыре натуральных числа.
Определите количество строк, в которых числа расположены в порядке убывания: каждое следующе…
Задача 17
Откройте файл электронной таблицы, содержащей в каждой строке три натуральных числа. Назовём тройку «подходящей», если в ней самое большее число равно удвоенному среднему (по велич…
Задача 18
Откройте файл электронной таблицы, содержащей в каждой строке четыре натуральных числа. Определите количество строк, в которых числа расположены в порядке не возрастания: каждое сл…
Задача 19
Откройте файл электронной таблицы, содержащей в каждой строке четыре натуральных числа. Определите количество строк, в которых числа расположены в порядке не убывания: каждое следу…
Задача 20
Откройте файл электронной таблицы, содержащей в каждой строке четыре натуральных числа. Определите количество строк, в которых числа расположены в порядке возрастания: каждое следу…
1 2 3 4
Номер девять по информатике — это еще одно задание, для решения которого требуется воспользоваться программами для обработки таблиц.
Хоть оно и является легким, но определенные знания все же потребуются. Также будут производиться внутри таблицы расчеты, поэтому стоит выучить простые формулы в Excel, чтобы уменьшить время решения. За верный ответ дается один балл. Преподаватели считают, что тратить на решение стоит не больше 2-3 минут, поэтому подготовка должна больше отвечать за наработку навыков.
Формулировка 9 задания разнообразна, но смысл везде остается похожим — вам дана файл-таблица, внутри данные, к примеру, о температуре в определенный период. Вас просят рассчитать среднюю температуру или найти минимальное значение. Формулировок огромное количество, но они не представляют для выпускников особой сложности. Ее решить можно просто механически — разыскать, посчитать на калькуляторе — но займет такой способ большое количество времени.
Девятая задача по праву считается одной из самых легких, так как иногда ее можно решить даже не применяя формул, но все еще за очень короткий срок. Готовьтесь к экзамену структурировано, и тогда вы получите желанный результат!
Теория к заданию 9 по информатике: Обработка данных в электронных таблицах
<< Задание 8
Задание 10 >>
Популярные материалы
Составим твой персональный план подготовки к ЕГЭ
Что такое целое число? Примеры
Поможем понять и полюбить математику
Начать учиться
129.
2K
Среди множества разных чисел, чаще всего мы используем целые числа. Ими можно считать, как в положительную, так и в отрицательную сторону. В этом материале узнаем подвиды таких чисел, их свойства и как их использовать.
Определение целых чисел
Что такое целое число — это натуральное число, а также противоположное ему число и нуль. Примеры целых чисел: -7, 222, 0, 569321, -12345 и др.
Что важно знать о целых числах:
- Сумма, разность и произведение целых чисел в результате дают целые числа.
- Обыкновенные и десятичные дроби нельзя назвать целыми числами. Но иногда в задачах можно встретить целые числа, у которых дробная часть равна нулю и при этом нет долей.
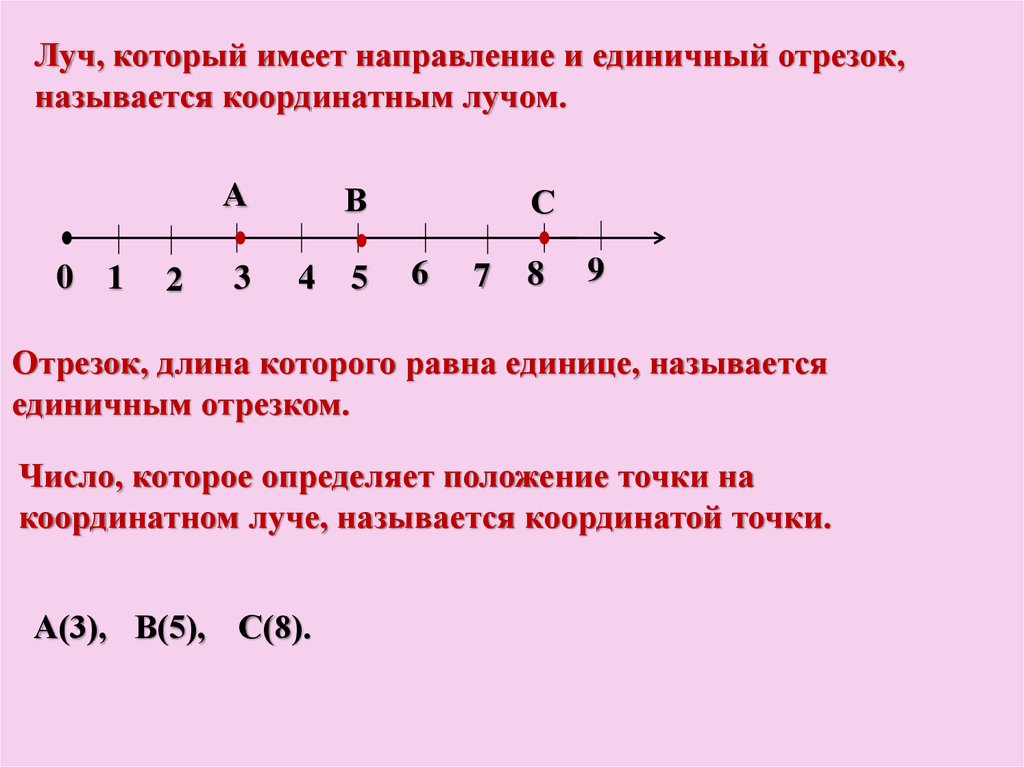
Целые числа на числовой оси выглядят так:
На координатной прямой начало отсчета всегда начинается с точки 0. Слева находятся все отрицательные целые числа, справа — положительные. Каждой точке соответствует единственное целое число.
В любую точку прямой, координатой которой является целое число, можно попасть, если отложить от начала координат данное количество единичных отрезков.
Натуральные числа — это целые, положительные числа, которые мы используем для подсчета. Вот они: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13 + ∞.
Целые числа — это расширенное множество натуральных чисел, которое можно получить, если добавить к ним нуль и противоположные натуральным отрицательные числа. Множество целых чисел обозначают Z.
Выглядит эти ребята вот так:
Последовательность целых чисел можно записать так:
∞ + .
.. -4, -3, -2, -1, 0, 1, 2, 3, 4 … + ∞
Курсы обучения математике помогут подтянуть оценки, подготовиться к контрольным, ВПР и экзаменам.
Реши домашку по математике на 5.
Подробные решения помогут разобраться в самой сложной теме.
Свойства целых чисел
Таблица содержит основные свойства сложения и умножения для любых целых
Свойство | Сложение | Умножение |
Замкнутость | a + b — целое | a × b — целое |
Ассоциативность | a + (b + c) = (a + b) + c | a * (b * c) = (a * b) * c |
Коммутативность | a + b = b + a | a * b = b * a |
Существование нейтрального элемента | a + 0 = a | a * 1 = a |
Существование противоположного элемента | a + (−a) = 0 | a ≠ ±1 ⇒ 1/a не является целым |
Дистрибутивность умножения относительно сложения | a * (b + c) = (a * b) + (a * c) | |
Пару слов о делении.
В стандартном виде невозможно разделить число на множестве целых чисел, но можно делить с остатком. Это правило можно сформулировать так:
- Для всяких целых a и b (b ≠ 0), есть один набор целых чисел q и r. При этом:
a = bq + r, где a — делимое, b — делитель, q — частное, r — остаток,
0 ≤ r < |b|, где |b| — абсолютная величина (модуль) числа b.
Положительные и отрицательные целые числа
Ряд целых чисел состоит из положительных и отрицательных чисел. Справа от нуля живут натуральные числа — их еще называют целыми положительными числами. А слева от нуля — целые отрицательные числа.
Отрицательные целые числа — это целые числа со знаком «минус». Они всегда меньше нуля. Примеры целых отрицательных чисел: -944, -1287, -1, -19.
Положительные целые числа — это целые числа со знаком «плюс».
Они всегда больше нуля. Примеры положительных целых чисел: 13, 401, 55, 29, 12345.
Бесконечное множество — это ряд целых чисел в положительную и в отрицательную сторону.
Если выбрать два любых целых числа, то те числа, которые находятся между заданными, можно называть конечным множеством.
Например, напишем целые числа от -4 до 3. Все числа, стоящие между этими числами, входят в конечное множество. Данное конечное множество чисел выглядит так:
- -3, -2, -1, 0, 1, 2
Пример 1. Сколько целых чисел расположено между числами -30 и 100?
Как рассуждаем:
- Можно построить прямую и посчитать сколько отрезков находится между заданными числам.
- Или можно посчитать в уме: у нас есть 29 отрицательных числа, нуль и 99 положительных чисел.
29 + 1 + 99 = 129
Ответ: 129.
Пример 2. Сколько нечетных целых чисел расположено между числами -4 и 5?
Как рассуждаем:
- Выпишем все целые числа, которые находятся между -4 и 5:
-3, -2, -1, 0, 1, 2, 3, 4 - Подчеркнем нечетные числа в данному ряду.
Ответ: -3, -1, 1, 3.
Неположительные и неотрицательные целые числа
Неотрицательные целые числа — это положительные целые числа и число нуль. Примеры неотрицательных целых чисел: 43, 878, 0.
Неположительные целые числа — это отрицательные целые числа и число нуль. Примеры неположительных целых чисел: -43, -878, 0.
Нуль — это граница между положительными и отрицательными числами.
То есть нуль это ни положительное и ни отрицательное число.
Эти два термина помогают формулировать мысли кратко. Например, вместо того, чтобы говорить, что число a — целое число, которое меньше или равно нулю, можно сказать: a — целое неположительное число.
Целые числа в описании изменения величины
Какие числа называют целыми мы уже знаем. Их удобно использовать, чтобы считать предметы или чтобы сказать, что чего-то стало больше или меньше. А теперь примерчик!
Вы участвуете в конкурсе в инстаграм: нужно написать 5 постов про свои самые заветные мечты. А пока вы это не сделали, можно сказать, что сейчас у вас -5 постов. То есть число 5 описывает сколько вы должны сделать постов, а знак «минус» говорит о том, что вы все еще не выполнили условия конкурса. Постов то нет🙄
А если помимо 5 постов, нужно опубликовать еще 5 сторис — общий долг можно вычислить по правилу сложения отрицательных чисел:
- -5 (постов, которых еще нет) + (-5 сториз, которых тоже еще нет) = -10 публикаций
Итого: чтобы участвовать в конкурсе, нужно сделать 10 публикаций в инстаграм.
Шпаргалки для родителей по математике
Все формулы по математике под рукой
Лидия Казанцева
Автор Skysmart
К предыдущей статье
Что такое квадратный корень
К следующей статье
Иррациональные числа
Получите план обучения, который поможет понять и полюбить математику
На вводном уроке с методистом
Выявим пробелы в знаниях и дадим советы по обучению
Расскажем, как проходят занятия
Подберём курс
10.7 Естественные координаты лучше горизонтальных координат.
10.7 Натуральные координаты лучше горизонтальных координат.
Понимание результатов баланса сил часто может быть проще, если мы выберем горизонтальную систему координат, которая естественным образом выровнена с воздушным потоком, а не просто задана в декартовых координатах x и y или сферических координатах λ и φ .
Мы можем выбрать одно направление — назовем его с для линии тока — так, чтобы она была выровнена с линией тока (и, таким образом, всегда была параллельна потоку) и увеличивалась в направлении потока (т. е. по ветру). Второе направление — назовем его n для нормального — увеличивается слева от потока. Интересной и примечательной особенностью естественных координат является то, что скорость ветра всегда положительна, потому что по определению естественных координат вектор скорости всегда направлен в положительном направлении.
Для уравнения горизонтального импульса без трения:
DV→Dt=−f k→×V→−∇→pΦ
, где V→=i→u+j→v и ∇→pMathType@MTEF@5@5 @+=faaagCart1ev2aaaKnaaaaWenf2ys9wBH5garuavP1wzZbItLDhis9wBH5garmWu51MyVXgaruWqVvNCPvMCG4uz3bqee0evGueE0jxyaibaieYlf9irVeeu0dXdh9vqqj=hHeeu0xXdbba9frFj0=OqF fea0dXdd9vqaq=JfrVkFHe9pgea0dXdar=Jb9hs0dXdbPYxe9vr0=vr0=vqpi0dc9GqpWqaaeaabiGaciaacaqabeaadaqaaqaaaOqaamaaFiaabaGaey4bIenacaGLxdcadaWgaaWcbaGaamiCaaqabaaaaa@3725 @ — это оператор горизонтального градиента на поверхности давления, а не на поверхности высоты.
Давайте посмотрим на каждый член уравнения и поместим его в натуральные координаты.
Ускорение воздушной посылки : DV→Dt
Существует два способа изменения V→. Он может измениться, изменив свою скорость (V=|V→|), DVDt, что происходит в направлении линии тока с, , или изменив направление, которое происходит в нормальном направлении, n . Напомним, что n указывает слева от вектора скорости.
Вспомните вашу физику, которая показала, что ускорение за счет вращения (центростремительное ускорение) равно квадрату скорости, деленному на радиус кривизны вращения. В этом случае вращение — это вращение воздушной посылки при ее горизонтальном движении над Землей (а не вращение самой Земли). Ускорение направлено перпендикулярно движению и направлено к центру кривизны. R — это радиус кривизны изменяющегося направления, и по соглашению R > 0, если кривизна направлена против часовой стрелки, и R < 0, если кривизна направлена по часовой стрелке.
Следовательно, знак всегда работает, если центростремительное ускорение равно В 2 / R .
Сила Кориолиса ruWqVvNCPvMCG4uz3bqee0evGueE0jxyaibaieYlf9irVeeu0dXdh9vqqj=hHeeu0xXdbba9frFj0=OqFfea0dXdd9vqaq=JfrVkFHe9pgea0dXdar=Jb9hs0dXdbPYxe9vr0=vr0=vqpi0dc9GqpWqaaeaabiGaciaacaqabeaadaqaaqaaaOqaaiabg kHiTiaadAgacaaMc8+aa8HaaeaacaWGRbaacaGLxdcacqGHxdaTdaWhcaqaaiaadAhaaiaawEniamaaBaaaleaacaWGibaabeaaaaa@3E90@
Компонент n равен −fV MathType@MTEF@5@5@ +=faaagCart1ev2aaaKnaaaaWenf2ys9wBH5garuavP1wzZbItLDhis9wBH5garmWu51MyVXgaruWqVvNCPvMCG4uz3bqee0evGueE0jxyaibaieYlf9irVeeu0dXdh9vqqj=hHeeu0xXdbba9frFj0=OqFfea 0dXdd9vqaq=JfrVkFHe9pgea0dXdar=Jb9hs0dXdbPYxe9vr0=vr0=vqpi0dc9GqpWqaaeaabiGaciaacaqabeaadaqaaqaaaOqaaiabgkHiTiaadAgacaaMc8UaamODamaaBaaaleaacaWGibaabeaaaaa@3821@ потому что когда f 900 06 > 0, сила находится справа от движения (т. е. по линии тока) и, таким образом, отрицательна, поскольку положительные n точек слева от движения .
Когда f < 0, сила будет направлена влево в положительном направлении n .
Сила градиента давления (PGF) :
−∇→pΦMathType@MTEF@5@5@+=faaagCart1ev2aaaKnaaaaWenf2ys9wBH5garuavP1wzZbItLDhis9wBH5garmWu51MyVXgaruWqVvNCPvMCG4uz3bqee0evGueE0jxyaibaieYlf9irVeeu0dXdh9 vqqj=hHeeu0xXdbba9frFj0=OqFfea0dXdd9vqaq=JfrVkFHe9pgea0dXdar=Jb9hs0dXdbPYxe9vr0=vr0=vqpi0dc9GqpWqaaeaabiGaciaacaqabeaadaqaaqaaaOqaaiabgkHiTmaaFiaabaGaey4 bIenacaGLxdcadaWgaaWcbaGaamiCaaqabaGccqqHMoGraaa@3996@
Компонент n −∇→pΦMathType@MTEF@5@5@+ =faaagCart1ev2aaaKnaaaaWenf2ys9wBH5garuavP1wzZbItLDhis9wBH5garmWu51MyVXgaruWqVvNCPvMCG4uz3bqee0evGueE0jxyaibaieYlf9irVeeu0dXdh9vqqj=hHeeu0xXdbba9frFj0=OqFfea0dXdd9vqaq=JfrVkFHe9pgea0dXdar=Jb9hs0dXdbPYxe9vr0=vr0=vqpi0dc9GqpWqaaeaabiGaciaacaqabeaadaqaaqaaaOqaaiabg kHiTmaaFiaabaGaey4bIenacaGLxdcadaWgaaWcbaGaamiCaaqabaGccqqHMoGraaa@3996@ — это просто −∂Φ∂nMathType@MTEF@5@5@+=faaagCart1ev2aqaKnaaaaWenf2ys9wBH5garuavP1wzZbItLDhis9wBH5garmWu 51MyVXgaruWqVvNCPvMCG4uz3bqee0evGueE0jxyaibaieYlf9irVeeu0dXdh9vqqj=hHeeu0xXdbba9frFj0=OqFfea0dXdd9vqaq=JfrVkFHe9pgea0dXdar=Jb9hs0dXdbPYxe9vr0=vr0=vqpi 0dc9GqpWqaaeaabiGaciaacaqabeaadaqaaqaaaOqaaiabgkHiTmaalaaabaGaeyOaIyRaeuOPdyeabaGaeyOaIyRaamOBaaaaaaa@3901@ .
Соединяя эти части вместе, мы получаем уравнение для компонента n уравнения горизонтального импульса: ZbItLDhis9wBH5garmWu51MyVXgaruWqVvNCPvMCG4uz3bqee0evGueE0jxyaibaieYlf9irVeeu0dXdh9vqqj=hHeeu0xXdbba9frFj0=OqFfea0dXdd9vqaq=JfrVkFHe9pgea0dXdar =Jb9hs0dXdbPYxe9vr0=vr0=vqpi0dc9GqpWqaaeaabiGaciaacaqabeaadaqaaqaaaOqaaabbaaaaaaaaIXwyJTgapeWaaSaaa8aabaWdbiaadAfapaWaaWbaaSqabeaapeGaaGOmaaaaaOWdaeaapeGaamOuaaa acqGH9aqpcqGHsislcaWGMbGaamOvaiabgkHiTmaalaaapaqaa8qacqGHciITcqqHMoGra8aabaWdbiabgkGi2kaad6gaaaaaaa@4228@
[10.34a]
Это уравнение называется уравнением градиента ветра . . Иногда бывает полезна форма уравнения в координатах z : XgaruWqVvNCPvMCG4uz3bqee0evGueE0jxyaibaieYlf9irVeeu0dXdh9vqqj=hHeeu0xXdbba9frFj0=OqFFea0dXdd9vqaq=JfrVkFHe9pgea0dXdar=Jb9hs0dXdbPYxe9vr0=vr0=vqpi0dc9GqpWqaaeaabiGaciaacaqabeaadaqaaqaaaOqaaabbaaaaaaaaIXwyJTgapeWaaSaaa8aabaWdbiaadAfapaWaaWbaaSqabeaapeGaaGOmaaaaaOWdaeaap eGaamOuaaaacqGH9aqpcqGHsislcaWGMbGaamOvaiaabgkHiTmaalaaabaGaaGymaaqaaiabeg8aYbaadaWcaaWdaeaapeGaeyOaIyRaamiCaaWdaeaapeGaeyOaIyRaamOBaaaaaaa@442E@
[10.
34b] 9001 9
Имейте в виду, что V всегда положителен в уравнениях [10.34], потому что они отлиты в естественных координатах.
Давайте немного изменим уравнение [10.34a], переместив центростремительное ускорение в правую часть, где оно представляет собой центробежную силу. Затем, рассмотрев, какие из терминов являются наиболее важными, мы можем применить это уравнение к различным ситуациям:
−V2R−fV−∂Φ∂n=0, градиентный баланс –fV–∂Φ∂n=0, геострофический баланс–V2R –∂Φ∂n=0, циклострофический баланс–V2 R−fV =0, инерционный балансMathType@ MTEF@5@5@+=faaahmart1ev3aaaKnaaaaWenf2ys9wBH5garuavP1wzZbItLDhis9wBH5garmWu51MyVXgaruWqVvNCPvMCaebbnrfifHhDYfgasaacH8srps0lbbf9q8WrFfeuY=ribbf9v8qqaqFr0xc9 pk0xbba9q8WqFfea0=yr0RYxir=Jbba9q8aq0=yq=He9q8qqQ8frFve9Fve9Ff0dc9Gqpi0dmeaabaqaciGacaGaaeqabaWaaeaaeaaakeaaafaWaaeabbaaaaeaaqqaaaaaaaaGySf2yRbWdbiabgkHiTmaalaa apaqaa8qacaWGwbWdamaaCaaaleqabaWdbiaaikdaaaaak8aabaWdbiaadkfaaaGaeyOeI0IaamOzaiaadAfacqGHsisldaWcaaWdaeaapeGaeyOaIyRaeuOPdyeapaqaa8qacqGHciITcaWGUbaaaiabg2da9iaaicdacaqGSaGaaeiaiaabccacaqGGaGaaeiaiaiaabccacaqGNbGaaeOCaiaabggacaqGKbGaaeyAaiaabwgacaqGUbGaaeiDaiaabccacaqGIbGaaeyyaiaabYgacaqGHbGaaeOBaiaabogacaqGLbaapaqaa8qacaaMf8UaaGzbVlaaykW7c qGHsislcaWGMbGaamOvaiabgkHiTmaalaaapaqaa8qacqGHciITcqqHMoGra8aabaWdbiabgkGi2kaad6gaaaGaeyypa0JaaGimaiaabYcacaqGGaGaaeiiaiaabccacaqGGaGaaeiaiaabEgacaqGLbGaae4BaiaabohacaqG0bGaaeOCaiaab+gaca qGWbGaaeiAaiaabMgacaqGJbGaaeiaiaabkgacaqGHbGaaeiBaiaabggacaqGUbGaae4yaiaabwgaa8aabaWdbiabgkHiTmaalaaapaqaa8qacaWGwbWdamaaCaaaleqabaWdbiaaikdaaaaak8aabaWdbiaadkfaaaGaaGzbVlaaywW7caaM c8UaaGPaVlabgkHiTmaalaaapaqaa8qacqGHciITcqqHMoGra8aabaWdbiabgkGi2kaad6gaaaGaeyypa0JaaGimaiaabYcacaqGGaGaaeiaiaiaabccacaqGGaGaaeiaiaabogacaqG5bGaae4yaiaabYgacaqGVbGaae4CaiaabshacaqGYbGa ae4BaiaabchacaqGObGaaeyAaiaabogacaqGGaGaaeOyaiaabggacaqGSbGaaeyyaiaab6gacaqGJbGaaeyzaaWdaeaapeGaeyOeI0YaaSaaa8aabaWdbiaadAfapaWaaWbaaSqabeaapeGaaGOmaaaaOWdaeaapeGaamOuaaaacqGHsislcaWGMbGaamO vaiaaywW7caaMf8UaaeiiaiaabccacaaMc8UaaGPaVlabg2da9iaaicdacaqGSaGaaeiaiaabccacaqGGaGaaeiaiaiaabccacaqGPbGaaeOBaiaabwgacaqGYbGaaeiDaiaabMgacaqGHbGaaeiBaiaabccacaqGIbGaaeyyaiaabYgacaqGHbGaaeOBaiaabogacaqGLbaaaaaa@C58C@
[10.
35]
Мы можем использовать число Россби , чтобы определить, какой из приведенных выше балансов доминирует. Число Россби определяется как величина ускорения, деленная на величину силы Кориолиса. Применительно к уравнению градиентного ветра число Россби определяется как
Ro=accelerationCoriolis force=V2/RfV=VfRMathType@MTEF@5@5@+=faaahmart1ev3aqaKnaaaaWenf2ys9wBH5garuavP1wzZbItLDhis9wBH5garmWu51MyVXgaruWqVvNCPvMCG4uz3bqee0evGueE0jxyaibaieYlf9irVeeu0dXdh9vqqj=hHeeu0xXdbba9frFj0=OqFfea0dXdd9vqaq=JfrVkFHe9pgea0dXdar =Jb9hs0dXdbPYxe9vr0=vr0=vqpi0dc9GqpWqaaeaabiGaciaacaqabeaadaqaaqaaaOqaaiaadkfadaWgaaWcbaGaam4BaaqabaGccqGH9aqpdaWcaaqaaiaabggacaqGJbGaae4yaiaabwgacaqGSbGaaeyzaiaabkhacaq GHbGaaeIDaiaabMgacaqGVbGaaeOBaaqaaiaaboeacaqGVbGaaeOCaiaabMgacaqGVbGaaeiBaiaabMgacaqGZbGaaeiaiaabAgacaqGVbGaaeOCaiaabogacaqGLbaaaiabg2da9maalaaabaWaaSGbaeaacaWGwbWaaWbaaSqabeaacaaIYaa aaaGcbaGaamOuaaaaaeaacaWGMbGaamOvaaaacqGH9aqpdaWcaaqaaiaadAfaaeaacaWGMbGaamOuaaaaaaa@56D5@
Если R o << 1, то центробежная сила намного меньше силы Кориолиса, а сила Кориолиса должна уравновешивать PGF (геострофический баланс).
Если R o >> 1, то сила Кориолиса намного меньше центробежной силы, а центробежная сила должна уравновешивать PGF (циклострофическое равновесие).
Если R o ~ 1, то сила Кориолиса и центробежная сила уравновешивают друг друга (инерционный баланс).
Тест 10-2: Координаты и масштабы.
- Найдите Практический тест 10-2 на холсте. Вы можете пройти этот практический тест столько раз, сколько захотите. Он не оценивается, но позволяет вам проверить свой уровень подготовки перед прохождением оцениваемого теста.
- Когда почувствуете, что готовы, пройдите тест 10-2 . Вам будет разрешено пройти этот тест только раз . Удачи!
Что такое географические системы координат? — ArcMap
Географическая система координат (ГСК) использует трехмерную сферическую поверхность для определения местоположения на Земле. ОСК часто неправильно называют датумом, но датум — это только одна часть ОСК.
GCS включает в себя угловую единицу измерения, нулевой меридиан и датум (на основе сфероида).
Точка определяется ее значениями долготы и широты. Долгота и широта — это углы, измеряемые от центра земли до точки на поверхности земли. Углы часто измеряются в градусах (или в градах). На следующем рисунке мир показан в виде глобуса со значениями долготы и широты.
В сферической системе горизонтальные линии, или линии восток-запад, являются линиями равной широты или параллелями. Вертикальные линии, или линии север-юг, — это линии равной долготы, или меридианы. Эти линии охватывают земной шар и образуют сеть с координатной сеткой, называемую координатной сеткой.
Линия широты на полпути между полюсами называется экватором. Он определяет линию нулевой широты. Линия нулевой долготы называется нулевым меридианом. Для большинства географических систем координат нулевой меридиан — это долгота, проходящая через Гринвич, Англия. Другие страны используют линии долготы, которые проходят через Берн, Боготу и Париж, в качестве нулевых меридианов.
Начало координатной сетки (0,0) определяется точкой пересечения экватора и нулевого меридиана. Затем земной шар делится на четыре географических квадранта, которые основаны на азимутах по компасу от начала координат. Север и юг находятся выше и ниже экватора, а запад и восток — слева и справа от нулевого меридиана.
На этом рисунке показаны параллели и меридианы, образующие координатную сетку.
Значения широты и долготы традиционно измеряются либо в десятичных градусах, либо в градусах, минутах и секундах (DMS). Значения широты измеряются относительно экватора и колеблются от -90° на Южном полюсе до +90° на Северном полюсе. Значения долготы измеряются относительно нулевого меридиана. Они варьируются от -180° при движении на запад до 180° при движении на восток. Если нулевой меридиан находится в Гринвиче, то Австралия, которая находится к югу от экватора и к востоку от Гринвича, имеет положительные значения долготы и отрицательные значения широты.
Может оказаться полезным приравнять значения долготы к X, а значения широты к Y.
Данные, определенные в географической системе координат, отображаются так, как если бы градус был линейной единицей измерения. Этот метод в основном такой же, как и проекция Пластины Карре.
Узнайте больше о проекции Платформы Карре
Хотя долгота и широта могут точно определять положение на поверхности земного шара, они не являются едиными единицами измерения. Только вдоль экватора расстояние, представленное одним градусом долготы, приблизительно соответствует расстоянию, представленному одним градусом широты. Это потому, что экватор является единственной параллелью размером с меридиан. (Круги того же радиуса, что и сферическая Земля, называются большими кругами. Экватор и все меридианы — большие круги.)
Выше и ниже экватора круги, определяющие параллели широты, постепенно уменьшаются, пока не становятся единой точкой на Северном и Южном полюсах, где сходятся меридианы. Когда меридианы сходятся к полюсам, расстояние, представленное одним градусом долготы, уменьшается до нуля.