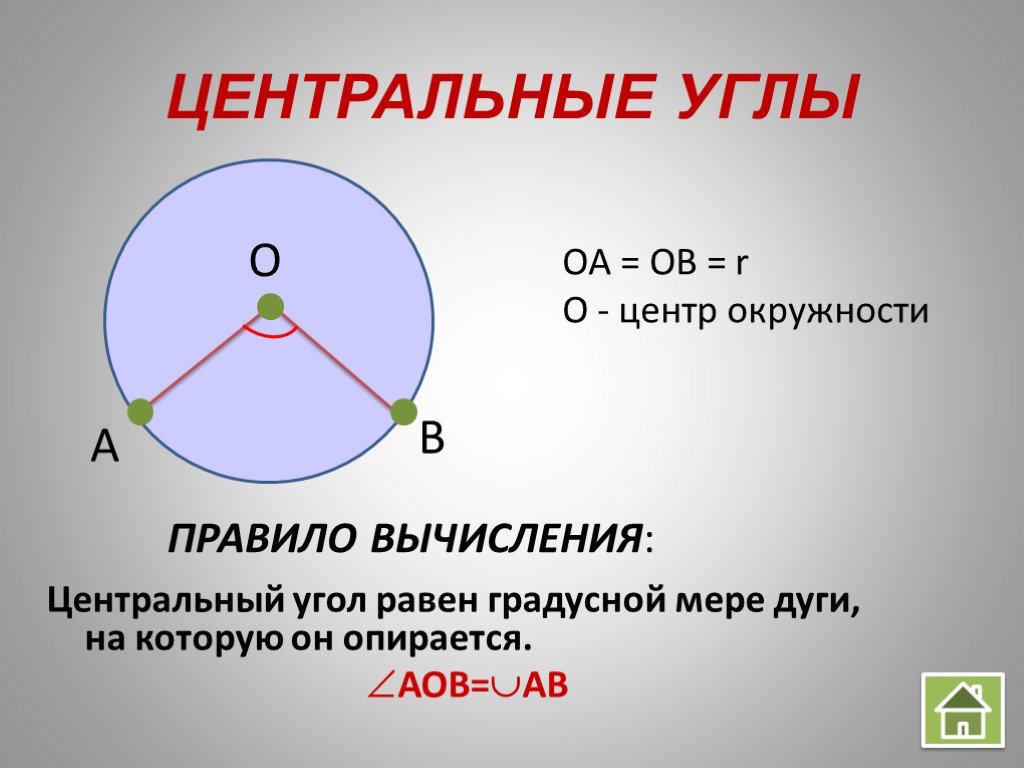
Идеального математического круга не существует / Хабр
ANIDEANIВремя на прочтение 2 мин
Количество просмотров19K
Математика *
Из песочницы
В точном компьютерном и физическом моделировании нуждается любой инженер, особенно если компания хочет создать самый износостойкий и прочный подшипник, его свойства окружность и параметры должны быть известны, чуть ли не до уровня атома.
Представьте, вы даёте задачу программисту найти точный процент и модель соприкосновения подшипника, и оказывается что это невозможно, так как и невозможно смоделировать точную окружность. Как и невозможно смоделировать точную площадь соприкосновения.
Понятие круга является одним из универсальных математических понятий, дословно обобщаемым на случай произвольных метрических пространств.
Так что такое круг? И почему его точная математическая модель невозможна.
В научном понимании круг это правильный 65537 угольник (шестьдеся̀тпятьты̀сячпятисо̀ттридцатисемиуго́льник) — правильный многоугольник с 65 537 углами и 65 537 сторонами.
Значит для программиста круг это многоугольник с 65 537 углами — и эти углы будут соприкасаться с плоской поверхностью или такой же окружностью, и меняя равновесие всего это математического круга с 65 537 углами. Согласитесь что модель уже устарела?
Гауссом в 1796 году было доказано, что правильный n-угольник можно построить циркулем и линейкой, если нечётные простые делители n являются различными числами Ферма. В 1836 году П. Ванцель доказал, что других правильных многоугольников, которые можно построить циркулем и линейкой, не существует. Ныне это утверждение известно как теорема Гаусса — Ванцеля.
Могу даже открыть секрет настолько узкий в отрасли подшипников, что большинство автомобильных, железнодорожных и авиа катастроф происходит именно по причине некачественных подшипников так как проверить качество и окружность порой невозможно так как наука работает в основном не с числами а «диапазонами» то и процент брака в подшипниковой индустрии из-за проблемы создания идеально ровного подшипника самый высокий.
Такую проблему мы наблюдаем и в играх
Точность
И эта точность очень низкая.
А 65 тысяч углов у круга это меньше миллиона.
Но даже и это не предел. Идеальный круг вообще бесконечен (имеет бесконечное количество углов). Как тогда его выразить в программировании, если любое число будет его неточной моделью? Или уже такая высокая точность будет ненужна? Ведь в любом массовом моделировании иза мельчайшей детали образуются каскадные лавинообразные эффекты которые дают разные результаты.
Спасибо за внимание.
Теги:
- математика и реальная жизнь
Хабы:
- Математика
Всего голосов 66: ↑12 и ↓54 -42
Комментарии 60
@ANIDEANI
Пользователь
ВКонтакте
Комментарии Комментарии 60
Углы в круге | Математика
132.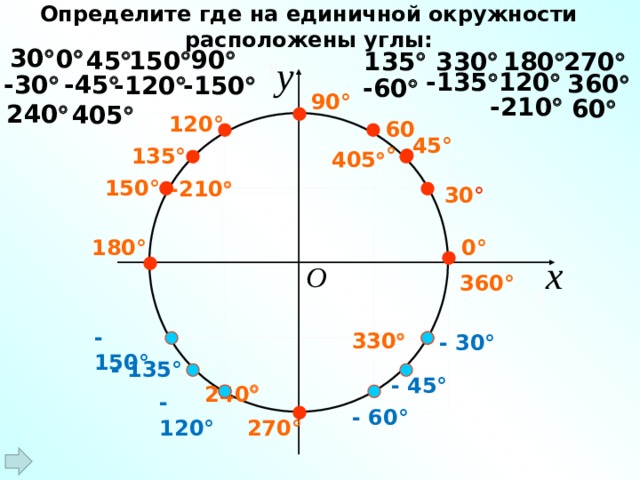 Мы уже знакомы с центральными углами. Построим теперь угол, вершина которого лежит на окружности и сторонами служат хорды. Такой угол называется вписанным в круг. Пусть построен ∠ABC (чер. 135, I или II), вписанный в круг O. Он опирается на дугу AC. Построим еще центральный ∠AOC, опирающийся на ту же дугу. Тогда между ∠ABC и ∠AOC существует простая зависимость. Для ее выяснения построим диаметр DB — мы будем сначала рассматривать случай, когда этот диаметр идет внутри ∠ABC, – получим два равнобедренных треугольника — ∆AOB и ∆BOC, у которых углы при основании равны: на чертеже равные углы обозначены одним и тем же нумером, – ∠A = ∠ABO = ∠1 и ∠C = ∠CBO = ∠2.
Мы уже знакомы с центральными углами. Построим теперь угол, вершина которого лежит на окружности и сторонами служат хорды. Такой угол называется вписанным в круг. Пусть построен ∠ABC (чер. 135, I или II), вписанный в круг O. Он опирается на дугу AC. Построим еще центральный ∠AOC, опирающийся на ту же дугу. Тогда между ∠ABC и ∠AOC существует простая зависимость. Для ее выяснения построим диаметр DB — мы будем сначала рассматривать случай, когда этот диаметр идет внутри ∠ABC, – получим два равнобедренных треугольника — ∆AOB и ∆BOC, у которых углы при основании равны: на чертеже равные углы обозначены одним и тем же нумером, – ∠A = ∠ABO = ∠1 и ∠C = ∠CBO = ∠2.
Тогда ∠AOD является внешним для ∆AOB, и он равен сумме внутренних с ним несмежных, т. е.
∠AOD = ∠1 + ∠1 = 2∠1.
Также ∠DOC есть внешний для ∆BOC и, следовательно,
∠DOC = ∠2 + ∠2 = 2∠2.
Отсюда сложением находим:
∠AOC = ∠AOD + ∠DOC = 2∠1 + 2∠2 = 2(∠1 + ∠2) = 2∠B, где под обозначением ∠B понимаем ∠ABC.
Итак,
∠AOC = 2∠ABC
или ∠ABC = ½ ∠AOC = ∠AOC / 2.
Если одна из сторон вписанного угла проходила бы чрез центр, то дело упрощалось бы и еще скорее получилась бы та же зависимость. Например, для вписанного угла ABD:
∠AOD = 2∠1 = 2∠ABD или ∠ABD = ½ ∠AOD = ∠AOD / 2.
Рассмотрим теперь случай, когда диаметр BD проходит вне угла ABC (чер. 136). Тогда, согласно предыдущему, имеем:
∠ABD = ½ ∠AOD,
∠CBD = ½ ∠COD,
так как одна сторона углов ABD и CBD служит диаметром.
Вычитанием находим:
∠ABC = ∠ABD – ∠CBD = ½ ∠AOD – ½ ∠COD =
= ½ (∠AOD – ∠COD) = (∠AOD – ∠COD) / 2.
Но разность ∠AOD – ∠COD равна ∠AOC, следовательно, ∠ABC = ∠AOC / 2.
Итак, найденная зависимость справедлива для всех возможных случаев. Поэтому имеем:
Вписанный угол равен половине центрального угла, опирающегося на ту же дугу.
133. Если хорду AB (чер. 136) вращать по направлению от BC вокруг точки B, то вписанный угол ABC станет увеличиваться, но все время будет сохраняться найденная выше зависимость между вписанным и центральным углом. Наконец, прямая AB может сделаться касательною к кругу (чер. 137) и тогда получим ∠ABC, составленный хордою и касательною; если касательную продолжить, то получим другой такой же ∠DBC. Уже из того процесса вращения, которым мы перешли от вписанного угла к этому новому углу, видно, что угол, составленных хордою и касательною, являясь предельным случаем вписанного угла, должен подчиниться той же зависимости, которая была найдена в предыдущем п. для вписанного угла. Но возможно то же самое увидать иначе. Рассмотрим, например, ∠CBD (чер. 137). Построим диаметр MN ⊥ BC и соединим точку касания B с O; тогда BO ⊥ AD. Так как ∆KBO прямоугольный, то ∠KBO + ∠KOB = d, но ∠ABO = d или ∠ABK + ∠KBO = d. Отсюда заключаем, что ∠KOB = ∠ABK, так как каждый из этих углов дополняет один и тот же ∠KBO до прямого.
Наконец, прямая AB может сделаться касательною к кругу (чер. 137) и тогда получим ∠ABC, составленный хордою и касательною; если касательную продолжить, то получим другой такой же ∠DBC. Уже из того процесса вращения, которым мы перешли от вписанного угла к этому новому углу, видно, что угол, составленных хордою и касательною, являясь предельным случаем вписанного угла, должен подчиниться той же зависимости, которая была найдена в предыдущем п. для вписанного угла. Но возможно то же самое увидать иначе. Рассмотрим, например, ∠CBD (чер. 137). Построим диаметр MN ⊥ BC и соединим точку касания B с O; тогда BO ⊥ AD. Так как ∆KBO прямоугольный, то ∠KBO + ∠KOB = d, но ∠ABO = d или ∠ABK + ∠KBO = d. Отсюда заключаем, что ∠KOB = ∠ABK, так как каждый из этих углов дополняет один и тот же ∠KBO до прямого.
Но ∠CBD = выпрямленному углу – ∠ABK и ∠BON = выпрямленному углу – ∠KOB. Следовательно, ∠CBD = ∠BON = ∠COB / 2, где под именем ∠COB надо понимать угол, больший выпрямленного и который опирается на дугу CNB, то и ∠CMB равен половине того же центрального угла COB.
Угол, составленный хордой и касательной, равен вписанному углу, опирающемуся на дугу, заключенную внутри первого угла.
134. Построим в круге O (чер. 138) диаметр AC и какой-либо вписанный ∠ABC, опирающийся на полуокружность ADC или, как часто говорят, опирающийся на диаметр AC.
Тогда ∠ABC = ½ ∠AOC, но ∠AOC выпрямленный; следовательно, ∠ABC = d, т. е.:
Вписанный угол, опирающийся на диаметр, – прямой.
135. Построим в круге какую-либо хорду AB (чер. 139) и ряд вписанных углов, опирающихся на ◡AB: ∠C, ∠C1 и т. д.
Тогда каждый из этих углов равен половине центрального угла, опирающегося на дугу AB, и следовательно ∠C = ∠C1 = …
Этот результат можно истолковать в следующей форме. Пусть в точке C помещен наш глаз, тогда лучи зрения, идущие из глаза к концам отрезка AB, составляют ∠ACB, – говорят, что из точки C отрезок AB виден под углом ACB.
Поместим теперь наш глаз в какую-либо точку M, находящуюся внутри круга; тогда из этой точки отрезок AB будет виден под углом AMB, который уже неравен прежнему; продолжив AM до пересечения с окружностью в точке D и соединив D с B, получим ∆MBD, для которого ∠AMB есть внешний, и, следовательно, ∠AMB > ∠ADB или ∠AMB > ∠C (ибо ∠ADB = ∠C).
Поместим теперь наш глаз в какую-либо точку N вне круга. Чтобы упростить чертеж, возьмем точку N на продолжении прямой AD; тогда из точки N отрезок AB виден под углом ANB. Рассматривая ∆BDN, найдем ∠ADB > ∠N (ибо ∠ADB внешний для ∆BDN) или ∠N < ∠ADB или ∠N < ∠C, т. е. из внешней точки отрезок AB виден под меньшим углом, чем из точек дуги ACDB.
Заметим, что мы здесь должны брать точки C, M и N только по одну сторону от прямой AB.
Общим результатом предыдущих изысканий является заключение:
Геометрическим местом точек, из которых какой-либо отрезок виден под одним и тем же углом, есть дуга круга, проходящего чрез концы этого отрезка.
Если бы мы захотели рассмотреть точки и по другую сторону прямой AB, то нашли бы и с другой ее стороны такую же дугу, так что полное геометрическое место указанных точек состоит из двух дуг (см. чер. 140).
136. Построить геометрическое место точек, из которых данный отрезок виден под данным углом.
Пусть дан отрезок AB и угол m (чер. 141). Построим геометрическое место точек, из которых AB виден под углом m. Постараемся сначала найти одну точку этого места. Чрез точку A построим произвольный луч AN и на нем выберем произвольную точку M, при которой построим ∠AMC = ∠m. Тогда замечаем, что из нашей точки M виден под углом m не весь отрезок AB, а лишь его часть AC. Но теперь не трудно на луче AM найти такую точку, из которой весь отрезок AB виден под углом m, для чего следует построить чрез точку B прямую BN || CM, – точка N пересечения луча AN и BN и явится искомою точкою.
Вот другой способ построения того же геометрического места. При точке A (чер. 142) отрезка AB построим ∠BAD = m, затем построим чрез середину отрезка AB перпендикуляр CO к этому отрезку AO ⊥ AD; точка пересечения O этих двух перпендикуляров служит центром искомого круга; так как O лежит на CO, то круг, описанный радиусом OA, принимая O за центр, пройдет и чрез точку B; ∠AOC = ∠BAD = ∠m, ибо ∠AOC И ∠BAD каждый в отдельности дополняет ∠OAB до прямого, но ∠AOC есть половина центрального угла AOB; поэтому всякий вписанный ∠AMB должен равняться ∠AOC и, следовательно, = ∠m.
137. Упражнения. 1. Найти точки, из которых два данных отрезка видны под прямыми углами.
2. Найти точки, из которых два данных отрезка видны каждый под данным углом.
3. Построить треугольник по основанию, противолежащему углу и по высоте.
Треугольников, имеющих данное основание и данный противолежащий угол, можно построить бесчисленное множество: их вершины расположены на том же геометрическом месте точек, из которых данное основание видно под данным углом.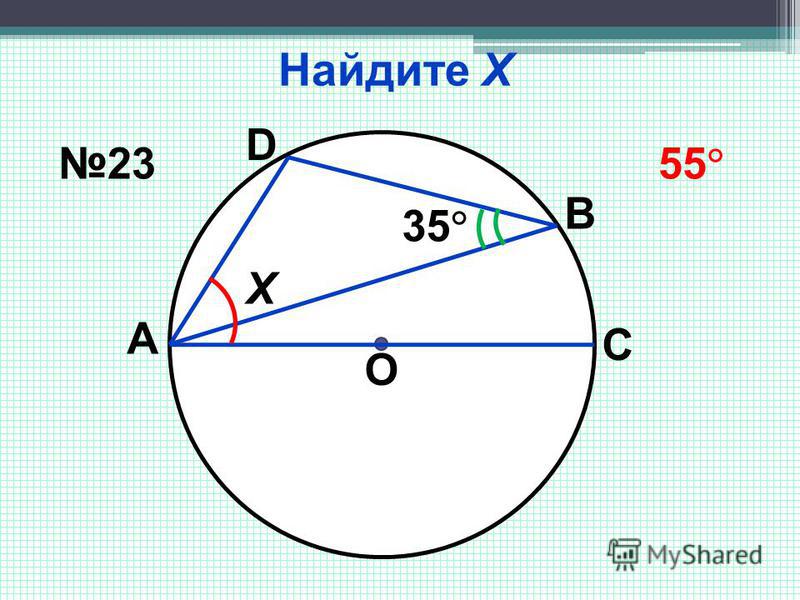 Остается среди этих вершин выбрать те, которые удалены от основания на расстояние, равное данной высоте, для чего строим прямую, параллельную основанию и отстоящую от него на расстояние, равное данной высоте.
Остается среди этих вершин выбрать те, которые удалены от основания на расстояние, равное данной высоте, для чего строим прямую, параллельную основанию и отстоящую от него на расстояние, равное данной высоте.
4. Построить треугольник по основанию, медиане и углу при вершине.
138. В круг O (чер. 143) впишем какой-либо четырехугольник (выпуклый), для чего возьмем 4 точки A, B, C и D круга и соединим их по порядку прямыми. Рассмотрим полученные вписанные углы. Построив радиусы OA и OC и называя 2 полученных центральных угла m и n, а именно ∠AOC, опирающийся на дугу ABC, обозначим m (он меньше выпрямленного) и ∠AOC, опирающийся на дугу ADC, обозначим n (он больше выпрямленного), найдем:
∠D = m/2 и ∠B = n/2.
Сложением отсюда получим:
∠D + ∠B = (m + n) / 2,
но углы m и n в сумме составляют два выпрямленных угла (что легко увидеть, продолжив, напр. сторону OC) или 4 прямых угла; поэтому (m + n) / 2 = выпрямленному углу = 2d и, следовательно, ∠D + ∠B = 2d.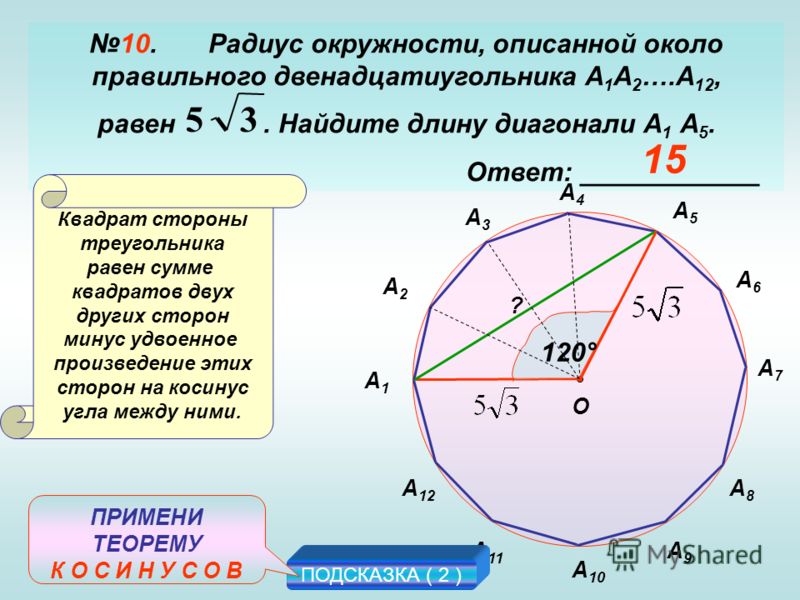
То же можно получить и для суммы углов A и C. Поэтому имеем:
Во всяком вписанном в круг выпуклом четырехугольнике сумма противоположных углов равна 2d.
Найденное свойство является необходимым признаком вписанного в круг четырехугольника, т. е., если 4-угольник вписан в круг, то необходимо, чтобы сумма двух противоположных углов = 2d. Посмотрим, достаточен ли этот признак для того, чтобы четырехугольник мог быть вписанным, или, другими словами, чтобы около него можно было бы описать круг (ведь, вообще говоря, через 4 произвольно взятых точки нельзя построить окружность, так как она определяется вполне тремя точками и может, следовательно, не пройти чрез четвертую точку).
Пусть имеем 4-угольник ABCD такой, что ∠B + ∠D = 2d (чер. 144). Прежде всего заметим, что тогда непременно сумма двух других углов, т. е. ∠A + ∠C, тоже равна 2d: в самом деле, мы имели (п. 81), что сумма всех четырех углов четырехугольника = 4d; так как ∠B + ∠D = 2d, то, следовательно, ∠A + ∠C = 2d.
Построим чрез три точки A, B и C круг, что делать умеем; возникает вопрос: пройдет ли он чрез точку D или нет? Допустим сначала, что точка D окажется вне круга и последний пересечет сторону AD в точке E. Соединив C и E, получим 4-угольник ABCE, вписанный в этот круг, и тогда имеем:
∠B +∠E = 2d.
Сравнивая это равенство с данным, что ∠B + ∠D = 2d, придем к заключению, что ∠E = ∠D (суммы равны и одно слагаемое одинаковое, следовательно, и другие слагаемые равны), но этого быть не может, так как ∠E (точнее ∠AEC) есть внешний для ∆ECD, а ∠D внутренний.
Допустим, что точка D окажется внутри круга и последний пересечет продолжение стороны AD в точке F. Тогда ∠B + ∠F = 2d, так как 4-угольник ABCF вписанный. Сравнивая с данным равенством ∠B + ∠D = 2d, получим, что ∠D = ∠F, чего быть не может, так как ∠D есть внешний, а ∠F внутренний угол для ∆DCF.
Остается, следовательно, принять, что круг пройдет чрез точку D и что, следовательно, около данного четырехугольника можно описать круг.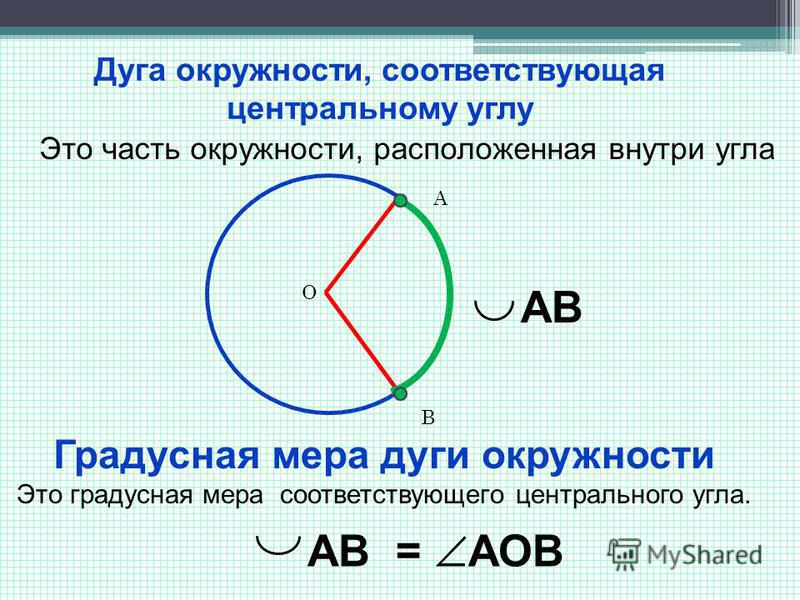 Итак:
Итак:
Если в выпуклом четырехугольнике сумма противоположных углов равна 2d, то около него можно описать круг.
Четырехугольник, около которого можно описать круг, называют часто вписываемым.
Прямое и обратное заключение этого п. можно выразить в иной форме:
Для того, чтобы выпуклый четырехугольник был вписываемым, необходимо и достаточно, чтобы сумма его двух противоположных углов равнялась 2d.
Упражнения. 1. В каком случае около параллелограмма можно описать круг?
2. В каком случае можно описать круг около трапеции?
139. Задача. Построить касательную к данному кругу чрез точку, данную вне круга.
Пусть дан круг O и точка A вне его (чер. 145). Требуется чрез A построить касательную к кругу.
Соединив центр круга O с данною точкою A, примем отрезок OA за диаметр нового круга. Построив этот второй круг (его центр есть середина отрезка OA), найдем его точки пересечения B и C с первым.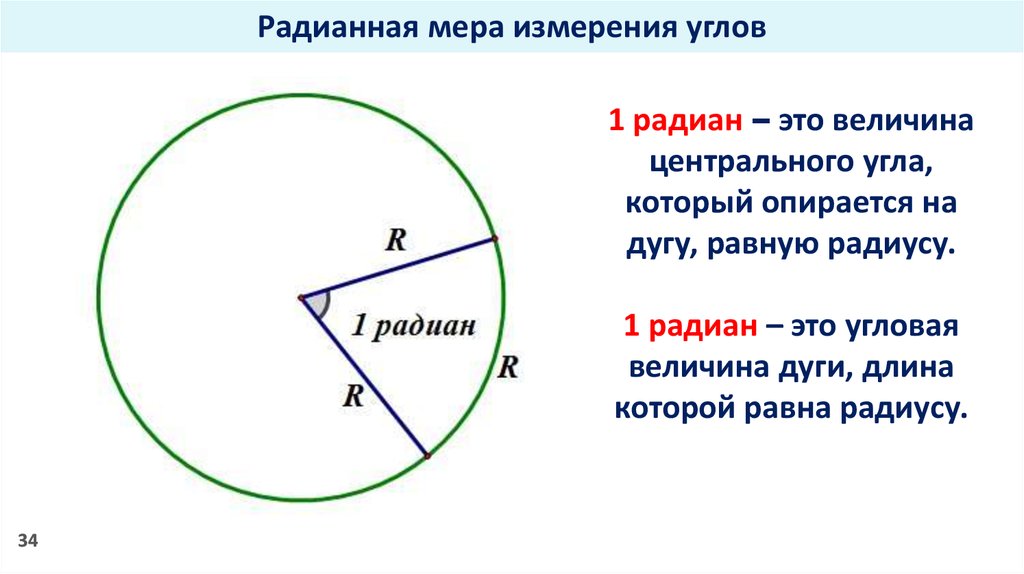 Тогда прямые AB и AC служат касательными из точки A к кругу O.
Тогда прямые AB и AC служат касательными из точки A к кругу O.
В самом деле, соединив B с O, получим ∠OBA, вписанный во второй круг и опирающийся на его диаметр OA; такой угол прямой (п. 134), следовательно, AB ⊥ OB, а этого достаточно для того, чтобы прямая AB была касательной к кругу (п. 118). Также выясним, что AC есть касательная к кругу O.
OA есть линия центров наших кругов, поэтому она является осью симметрии всей фигуры: перегибая фигуру по оси OA, найдем, что B совместится с C и AB с AC, т. е. AB = AC. Итак, имеем:
Чрез точку, взятую вне круга, можно построить две касательных к этому кругу, и отрезки их от данной точки до точек касания равны между собою.
140. Построим треугольник, описанный около круга; для этого возьмем 4 точки A, B, C и D данного круга (чер. 146) и построим чрез эти точки касательные к кругу, точки пересечения M, N, P и Q последовательных касательных служат вершинами этого четырехугольника.
Выбор 4 точек A, B, C и D несколько ограничен: две соседних точки не должны лежать на одном диаметре круга; напр. , если бы точки B и C были концами одного диаметра, то касательные в них были бы параллельны и вершины N нельзя было бы найти.
, если бы точки B и C были концами одного диаметра, то касательные в них были бы параллельны и вершины N нельзя было бы найти.
Применяя к полученному описанному 4-угольнику MNPQ свойство касательных предыдущего п., найдем:
MA = MB = a; NB = NC = b; PC = PD = C; QD = QA = d,
где мы ввели обозначения a, b, c и d для четырех пар отрезков, равных между собой.
Мы можем скомбинировать 8 полученных отрезков в две группы, по 4 в каждой, равных попарно отрезков. Такая комбинация напрашивается сама собою. Возьмем сумму двух противоположных сторон четырехугольника:
MN + PQ = MB + BN + PD + DQ = a + b + c + d.
Также для двух других сторон найдем:
QM + PN = QA + AM + NC + CP = d + a + b + c.
Отсюда заключаем:
MN + PQ = QM + PN
т. е. сумма двух противоположных сторон описанного четырехугольника равна сумме двух других сторон.
Найденное свойство является необходимым признаком описанного 4-угольника, т. е., если 4-угольник описан около круга, то необходимо должно иметь место найденное свойство.
Посмотрим, является ли это свойство достаточным признаком для того, чтобы при его наличности этот четырехугольник мог бы быть рассматриваем, как описанный около круга, т. е. достаточно ли этого свойства для того, чтобы в четырехугольник можно было вписать круг (вписать круг в 4-угольник значит построить такой круг, который касался бы всех четырех его сторон).
Пусть имеем 4-угольник MNPQ (чер. 147), у которого
MN + QP = MQ + NP.
Построим круг, касающийся прямых MQ, MN и NP, чтобы его центр лежал внутри полосы QMNP (п. 125 задача 4). Возникает вопрос, коснется ли этот круг стороны QP?
Допустим, что круг не коснется стороны QP и расположится внутри 4-угольника QMNP. Тогда, построив чрез Q вторую касательную QR к кругу, которая пересечет сторону NP в точке R, получим описанный 4-угольник QMNR, для которого имеем:
MN + QR = MQ + NR.
Вычитая это равенство по частям из данного, найдем:
QP – QR = NP – NR или QP – QR = RP.
Но это равенство противоречит свойству треугольника RPQ (п. 91), согласно которому должны иметь
91), согласно которому должны иметь
RP > QP – QR.
Допустим затем, что круг пересекает сторону QP. Тогда касательная к этому кругу чрез точку Q займет положение QS и пересечет сторону NP в точке S. Из описанного 4-угольника QMNS имеем:
MN + QS = MQ + NS.
Вычитая отсюда данное равенство MN + QP = MQ + NP по частям, получим:
QS – QP = NS – NP или QS – QP = PS,
что опять-таки невозможно, так как из треугольника SQP имеем:
PS > QS – QP.
Поэтому остается принять, что построенный нами круг касается и стороны QP, т. е. в наш 4-угольник удалось вписать круг. Итак:
Если сумма двух противоположных сторон выпуклого четырехугольника равна сумме двух других его противоположных сторон, то в такой четырехугольник можно вписать круг.
Четырехугольник, в который можно вписать круг, называют описываемым. Прямое и обратное заключение этого пункта можно выразить в такой форме:
Для того, чтобы четырехугольник был описываемым, необходимо и достаточно, чтобы сумма одной пары его противоположных сторон равнялась сумме другой пары.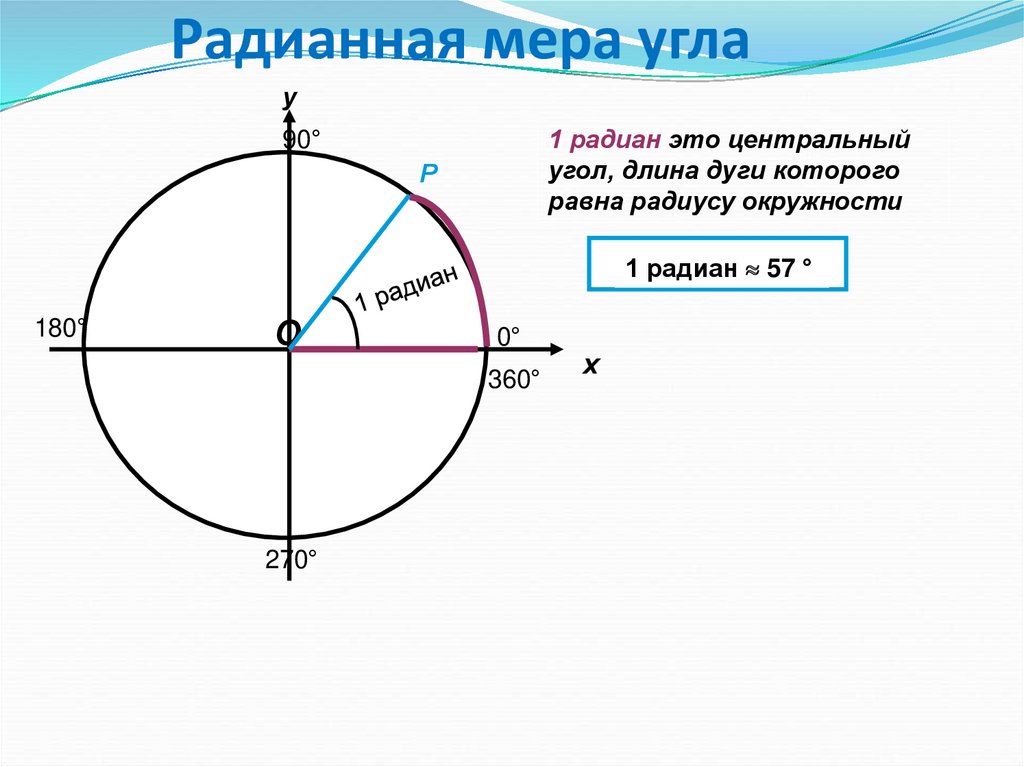
Упражнения. 1. Найти необходимый и достаточный признак того, чтобы параллелограмм был описываемым.
2. Пусть около данной трапеции можно описать круг и в нее можно вписать круг. Показать, что каждая из непараллельных сторон этой трапеции равна ее средней линии.
141. Упражнения на всю главу.
- Свойство углов вписанного в круг 4-угольника, найденное в п. 138, можно выяснить иным способом. Построим диагональ BD (чер. 143) четырехугольника и касательную MN к кругу в точке B. Тогда ∠ADC = ∠MBA + ∠NBC (на осн. п. 133). Отсюда можно увидать, что ∠B + ∠D = выпрямленному углу (на чер. 143 BD и MN не даны).
- Геометрическим местом середин хорд, проходящих чрез данную точку внутри данного круга, служит другой круг, диаметр которого есть прямолинейный отрезок между центром данного круга и данною точкою.
- Отрезки прямых, проходящих чрез точку пересечения двух кругов, ограниченные двумя другими точками пересечения с этими кругами, видны из другой точки пересечения кругов под одним и тем же углом.

Следует построить 2 таких отрезка и углы, под которыми они видны из другой точки; тогда можно заметить, что каждый из углов слагается из двух других углов: одно слагаемое общее и другие слагаемые равны между собою. - Найти точку, из которой стороны треугольника видны под равными углами.
(Надо суметь построить угол = 1(1/3)d.) - Около треугольника описан круг; из какой-либо точки этого круга опущены перпендикуляры на его стороны. Основания всех трех перпендикуляров расположены на одной прямой (прямая Симсона).
Надо найти четырехугольник, около которых можно описать круги, и рассмотреть полученные вписанные углы. - Биссекторы внутренних углов какого-либо четырехугольника образуют, пересекаясь, вписываемый 4-угольник.
Сколько сторон у круга?
Это домашнее задание начальной школы, которое вызывает разногласия среди опытных математиков. Чтобы найти правильный ответ, я обратился к самому строгому из научных инструментов — опросу в Твиттере:
.Сколько сторон у круга?
— Ричард Элвис (@RichardElwes) 4 августа 2019 г. В этом посте я собираюсь рассмотреть эти три ответа (и «Ни один из вышеперечисленных») и обсудить их плюсы и минусы, как я их вижу, прежде чем резко раскрыть правильный ответ.
Но сначала: почему мы не можем прямо дать правильный ответ? Слова в вопросе вряд ли можно назвать загадочными. Все мы знаем, что такое «окружность», что значит «считать, сколько» чего-то и что такое «сторона»… или не знаем? Вот (грубые) определения, которые я выделил из бесед с двумя учащимися начальной школы, которым задавали этот вопрос:
1. Линия, образующая часть границы плоской фигуры.
Цель высказывания плоскость цифра , а не «форма», заключается в том, что нам нужны формы, живущие в двух измерениях (например, квадраты или круги, но не сферы или кубы). Следующий вопрос — что такое «линия» в определении 1. Вот вариант, который уточняет это:
2. Прямая линия, образующая часть границы плоской фигуры.
Если вы наберете в Google «define: side» , наиболее подходящим определением будет:
3. часть или область рядом с краем и вдали от середины чего-либо.
“ микроавтобус стоял у обочины»синонимы: кромка, грань, грань, граница, кромка, бахрома, бахрома, бок, край, берег, край, обод, губа, периметр, окружность, оконечность, периферия, предел, внешний предел, пределы, граница, границы,…
антонимы: центр, сердце, конецкаждая из линий, образующих границу плоской прямолинейной фигуры.
«хозяйственные постройки образуют три стороны квадрата»A прямолинейный 9Фигура 0018 построена из прямых линий. Таким образом, это определение является дальнейшим уточнением определения 2 и позволяет нам утверждать, что квадрат имеет четыре стороны, но на первый взгляд ничего не говорит о непрямолинейных плоских фигурах, таких как круги.
Бесконечно много сторон?
Думаю, можно с уверенностью сказать, что респонденты моего опроса в Твиттере имеют более высокий уровень математического образования, чем в среднем по стране.
Тот факт, что они вообще разделились по этому вопросу и что незначительное большинство выбрало ответ, который в значительной степени недоступен для обычной аудитории этого вопроса (учеников начальной школы), безусловно, предполагает, что что-то где-то идет не так.
Итак, у круга бесконечно много сторон? Определенно полезно рассматривать круг как предел n – многоугольников, поскольку n становится все больше и больше. Это именно тот подход, который Архимед, Лю Хуэй и бесчисленное множество других использовали на протяжении веков для изучения круговой геометрии, в том числе для приближения числа π.
Издание XVI века династии Мин Цзючжан suanshu ( Девять глав о математическом искусстве)0062, третий век н.э.
Иногда совершенно разумно, в качестве удобного сокращения, думать о круге как о многоугольнике с бесконечным числом сторон.
Но, поскольку
невыносимый педантматематик, я хотел бы различать удобное сокращение и буквальную истину .Если мы твердо уверены в том, что круг на самом деле является многоугольником с бесконечным числом сторон, то возникает вопрос: каковы стороны? И уж точно единственный правдоподобный ответ [1] это: отдельные точки окружности. Какова длина этих так называемых сторон? Ноль сантиметров. И разделены ли эти стороны углами? Не видно, либо углов вообще нет, либо каждая точка есть и сторона, и угол.
Я бы сказал, что стороны нулевой длины — это… проблематичное понятие. Как узнать, есть ли они у вас? Например, предположим, что я изучаю систему, в которой квадрат возникает как предел восьмиугольников, подобных этому:
. имеют нулевую длину. Но если я буду настаивать на том, чтобы мой (совершенно обычный) квадрат действительно имеет восемь сторон , вы можете удивленно поднять бровь.
Таким образом, это — победивший в моем опросе ответ — единственный, который я собираюсь объявить безусловно неверным, и в то же время единственный, который предлагает хоть какое-то геометрическое понимание.
Парадокс? Не совсем. Рассуждения по аналогии — ценный навык в математике и в жизни; в то же время важно сохранять понимание того, что именно это мы и делаем.
Для бесконечного множества сторон: геометрически освещающий.
Против бесконечного множества сторон: восьмиугольных квадратов.Отклонение от касательной 1: апейрогоны
Даже если круг не один, существуют ли многоугольники с бесконечным числом сторон? Ну, есть такое слово, чтобы описать такую штуку, как apeirogon . Тогда правильный апейрогон будет иметь стороны равной (ненулевой) длины с равными углами между ними. Единственным вариантом здесь является этот удивительно неинтересный объект:
Если вы возражаете против того, чтобы это был «многоугольник» (либо из-за углов 180°, либо из-за цепочки ребер, не замыкающихся в петлю), как насчет чего-то вроде это: начните с нижней части круга и на каждом этапе перемещайтесь вокруг половины того, что осталось от круга, и замените дугу, которую вы только что прошли, прямым краем:
Это настоящий полигон? Опять же, это зависит от ваших условий.
Согласно одному распространенному определению «замкнутой многоугольной цепи», это не соответствует требованиям, поскольку начальный угол (нижний левый) соединяется только с одним ребром. Но это очень близко к промаху: эта точка является пределом последовательности ребер справа, что делает эту форму «несамопересекающейся кусочно-линейной замкнутой кривой» — еще одно определение многоугольника, которое используют люди.
Если выйти из нашего привычного евклидова мира и войти в гиперболическое пространство, то двусмысленности нет. Апейрогоны (даже обычные апейрогоны) просто существуют:
Замощение гиперболической плоскости правильными апейрогонами. (Автор Антон Шервуд — собственная работа, общественное достояние, https://commons.wikimedia.org/w/index.php?curid=13260274)
Вне тангенса 2: крайние точки
Возможно, было бы более оправданно сказать что у круга бесконечно много углов , чем бесконечно много сторон (хотя это не тот вопрос, который, кажется, задают очень часто).
Начнем с того, что если угол квадрата — это точка, в которой его граничная линия не является прямой, то каждая точка на окружности удовлетворяет этому. Более сложно, есть понятие крайняя точка фигуры: это любая точка, через которую можно провести отрезок прямой линии, касающийся фигуры только в этой точке. Для квадрата и многих знакомых фигур крайние точки точно совпадают с углами. Каждая точка на границе круга является крайней точкой, поэтому верно, что у круга их бесконечно много.
Нас может беспокоить, что некоторые формы, такие как этот шеврон, имеют углы, которые не являются крайними точками:
Здесь нижний центральный угол не является крайней точкой (остальные три угла являются). Что происходит неправильно, так это то, что эта форма не является выпуклой (грубо говоря, некоторые ее части торчат слишком далеко) . Окружность выпукла, так что, возможно, нам не о чем беспокоиться. В качестве альтернативы мы могли бы исправить ситуацию, определив «угол» как точку, которая является крайней точкой либо рассматриваемой формы, либо ее дополнения , то есть всей плоскости с вырезанной из нее формой.
Такой подход позволит обнаружить углы всех полигонов, включая шеврон. Для гладких кривых он идентифицировал бы все граничные точки как «углы», за исключением точек перегиба (что вполне разумно, поскольку мы могли бы утверждать, что здесь граница прямая).
Одна сторона?
В начальной школе кажется, что «один» — это ответ, который ставит галочку. И есть в меру приличное обоснование. Помните определение 1 выше:
1. Линия, образующая часть границы плоской фигуры.
Сразу же возникает вопрос, что считать «линии», особенно если мы не настаиваем на прямолинейности. Если мы будем слишком расслаблены в этом вопросе, то можно сказать, что любая плоская фигура имеет «одну сторону» в том же смысле, что у нее есть одна граница, периметр или окружность. Но это должно быть неправильно, так как мы, конечно же, хотим, чтобы в квадрате было четыре. Ну, у квадрата четыре точки там, где не 9.0017 гладкий, с четырьмя гладкими участками между ними. Возможно, это действительно были гладкие участки, которые мы считали все это время.
Таким образом, неявно мы имеем новое уточнение определения 1 (а также пользуемся случаем избавиться от неясного термина «фигура»):
4. Каждый гладкий участок кусочно-гладкой замкнутой кривой.
«Замкнутая кривая» — это кривая, которая закручивается, чтобы встретиться с самой собой, так что у нее нет свободных концов. «Кусочно-гладкий» означает, что он строится из гладких сечений, сходящихся в изолированных негладких точках. Совершенно законно хотеть подсчитать гладкие участки границы такой формы, и ни в коем случае не возмутительно использовать слово «сторона» при этом. Так что я, конечно, не говорю, что это определенно неверный ответ.
Вопрос в том, является ли эта интерпретация «стороны» не просто последовательной, но и достаточно естественной, чтобы ее можно было просто предположить, не формулируя явно (что бывает редко, если вообще когда-либо). Что происходит, когда гладкость и прямолинейность совпадают? Рассмотрим эту форму надгробия, созданную путем замены вершины квадрата полукругом такого же диаметра.
Имеет два гладких участка (нижняя линия и остальная часть), но три прямых края (плюс плавно изогнутый участок [2] присоединение к двум из них). Так сколько у него сторон? Я снова посоветовался со своими друзьями в Твиттере:
.Сколько сторон у надгробной плиты? (Фото в предыдущем твите.)
— Ричард Элвис (@RichardElwes) 20 августа 2019 г.
На этот раз я должен был включить «бесконечно много» в качестве опции, хотя это можно включить в «Ничего из вышеперечисленного». Любой, кто голосует за то, что у круга бесконечно много сторон, должен автоматически проголосовать здесь «Ни за одну из вышеперечисленных», если только — важная оговорка — природа этой формы не указывает читателю на другое понятие «стороны». Тот факт, что самые популярные варианты в этих двух опросах несовместимы, предполагает, что это может иметь место (или, по крайней мере, подтверждает, что вода мутная).
Хотя два вполне респектабельный ответ, совместимый с определением 4 выше и с односторонностью круга, я не удовлетворен тем, что это однозначно правильный один, или что три или четыре категорически неверны . Это зависит от того, что вы хотите считать: гладкие участки, прямые края или прямые края плюс все, что осталось, любой из которых может быть ответом, который вы хотите, в зависимости от контекста (подробнее об этом ниже). Соответственно, я не уверен, что подсчет количества гладких участков полностью соответствует моему интуитивному пониманию слова «сторона». Ведь две вертикальные части надгробия находятся, я думаю, справедливо сказать, «на противоположных сторонах». Действительно ли мы довольны тем, что они одновременно являются частью «одной и той же стороны»? [3]
Вы можете возразить, что я смешиваю два разных значения слова «сторона», что терминология иногда конфликтует, и нам просто приходится с этим жить. Хотя я не так уверен.
Смысл этого упражнения состоит в том, чтобы экстраполировать ситуацию (прямолинейные фигуры), где два понятия довольно хорошо сочетаются. Если бы существовала новая идея, которая охватила бы все, что нам нравилось в оригинале, но при этом применима к более широкой категории форм, то она бы претендовала на то, чтобы быть единственно правильным ответом. Но если все наши попытки обобщения связаны с принесением в жертву желательных аспектов оригинала, то, возможно, единственного правильного обобщения не существует. Есть разные варианты с разными компромиссами, которые могут быть подходящими в разных контекстах (и если мы находимся в ситуации, когда в игре участвует более одного, то им можно дать разные имена).
Вот еще вариант: надгробие Вейерштрасса, созданное заменой верхнего края квадрата участком функции Вейестресса, бесконечно волнистой линией, нигде не гладкой.
Вот (и обратите внимание на опечатку) то, что сделали из этого мои друзья в Твиттере, хотя меньше рискнули высказать свое мнение:
Сколько сторон у надгробия Вейштрасса? (Фото и объяснение в предыдущем твите.
) 2/3
— Ричард Элвис (@RichardElwes) 21 августа 2019 г.
Несмотря на скептицизм моих подписчиков в Твиттере, я объясню через минуту, почему я не думаю, что глупо видеть, что у этого есть четыре стороны (одна из которых не гладкая). С другой стороны, если вы предпочитаете, чтобы ваши стороны были гладкими, то у вас снова есть выбор между тем, что он имеет бесконечно много сторон (три из которых имеют длину 1, а остальные имеют длину 0), или имеет 3 стороны плюс участок определенно-не-сторонняя граница.
Для одной стороны : одна плавная кривая.
С одной стороны: С той же стороны с противоположных сторон.Отклонение от касательной 3: стороны против краев
Сколько сторон у квадрата? Четыре. Сколько у него ребер? Четыре. Значит, ребра и стороны — это одно и то же? Не обязательно. Вот две конфигурации, каждая из которых — по крайней мере предположительно — четырехсторонняя, но с 5 и 3 ребрами соответственно:
Обычно я бы сказал, что «ребро» — это топологический объект в том, что касается его функции, а не формы.
, вот что важно. Вспомните карту лондонского метро. Если вы спросите, сколько ребер в этой сети, нет смысла подсчитывать прямые или гладкие участки. Это связи между станциями (или вершин ), которые учитываются.
Как уже упоминалось, многоугольник принято представлять как очень простую сеть, называемую замкнутой полигональной цепочкой: цепочкой вершин (в данном случае углов многоугольника), соединенных ребрами в такой таким образом, что каждая вершина лежит ровно на двух ребрах, и все это образует единую петлю. В этой ситуации ребра и стороны совпадают, как и вершины и углы. Но в целом вы можете нарушить это совпадение, как в двух небольших сетях выше.
Если вы хотите думать о вещах с точки зрения теории сети, но вершины не отмечены четко, вам нужно угадать, где они находятся. С многоугольником это легко — вершины находятся в углах — поэтому переключение между геометрическим и топологическим подходами происходит так естественно. Но с другими формами, такими как любое из надгробий выше, это может быть не так очевидно.
Тем не менее, в каждом случае, если бы вам сказали, что где-то там есть вершины, и попросили найти их, я думаю, было бы разумно [4] , чтобы догадаться, что их четыре, а именно углы исходного квадрата, и что верхний край по какой-то причине представлен непрямой линией. И если мы действительно хотим думать о вещах таким образом, когда у каждого из надгробий есть 4 края, то может показаться неприятным (хотя и логически последовательным!) настаивать на том, что у них есть какое-то другое количество сторон (тем более, что верхняя сторона — несмотря на собственную геометрию – явно «с одной стороны» фигуры). На самом деле, вместо того, чтобы гадать, один из моих корреспондентов в Твиттере спросил меня: «Удалены ли обе верхние вершины?» — вопрос, который имеет смысл только с теоретико-сетевой точки зрения.
Где заканчивается круг? Беда в том, что ни одна точка окружности не может претендовать на звание вершины лучше, чем любая другая. Таким образом, хотя заманчиво (и опять-таки правильно) рассматривать окружность как сеть с одним ребром, если мы собираемся вставлять вершины, нет очевидной причины предпочесть одну из них любому другому числу.
Можем ли мы рассматривать это как сеть вообще без вершин, своего рода линию метро без станций? Обычная математическая концепция сети не позволяла бы этого, но это не должно нас слишком отпугивать. Это предполагает чисто топологический подход. Беда в том, что с этой точки зрения, хотя круг может быть своего рода сетью без вершин и с одним ребром, то же самое можно сказать и о квадрате (если именно так устроена линия Трубы). В топологии квадрат — это круг. (Это не парадокс, это просто говорит о том, что граница представляет собой одиночную петлю, форма которой не имеет значения.) Таким образом, хотя у такого рода сети есть «одно ребро», очевидно, что у квадрата нет «одной стороны». таким образом, отношения между сторонами (геометрическими) и ребрами (топологическими) снова нарушены, как это происходит в двух маленьких сетях, изображенных выше. Так что этот подход не уводит нас далеко вперед.
Нет сторон?
Может показаться парадоксальным утверждение, что у круга (или любой формы) «нет сторон».
Но аргумент защиты очевиден. Вернемся к определению 2:
2. Прямая линия, являющаяся частью границы плоской фигуры.
Это простая, легко понятная фраза, которая прекрасно описывает стороны квадрата. Нам не удалось найти удовлетворительного обобщения этого на изогнутые фигуры, поэтому лучше всего придерживаться оригинала. А у круга их нет.
Без сторон : верно, согласно разумному понятию «стороны».
Ни против кого: звучит как дзенский коан.Ничего из вышеперечисленного?
Напомним определение, предоставленное Google:
3. Каждая из линий, образующих границу плоской прямолинейной фигуры.
Попытка применить это к кругу — непрямолинейной фигуре — ничего не дает. Вопрос так же бессмыслен, как и «Сколько сторон у понедельника?»
Поскольку определение 3 является наиболее официальным (единственным в этом посте, не придуманным мной или моими детьми), разве это не делает «Ничего из вышеперечисленного» категорически правильным ответом? Может быть.
С другой стороны: когда кто-то задает нам вопрос, принцип милосердия, возможно, требует от нас допустить, что он имеет смысл, если мы не можем твердо установить обратное, и определения 1, 2, 4 и другие варианты делают это возможным. Кроме того, определение 3 является скорее лингвистическим, чем формально-математическим, и, следовательно, носит описательный, а не предписывающий характер, поэтому мы не должны ограничиваться им.
Ни для одного из вышеперечисленных: семантическая неисправность.
Против ничего из вышеперечисленного: диалогическая благотворительность.Правильный ответ
Что побудило меня написать этот пост? Как и бесчисленное множество учеников начальных классов, моим пятилетним сыновьям-близнецам — ученикам начальных классов, упомянутым в начале, — недавно задали этот вопрос в домашнем задании. Один набрал «1», а другой «0», и я попытался уловить и развить их рассуждения выше. Я думаю, что оба ответа вполне оправданы, и ни один из них не является окончательно правильным.
Итак, что делать, если вам задают вопрос: сколько сторон у круга? На мой взгляд, оптимальным ответом будет обратиться к математику в вашей жизни, чтобы написать трактат на 3000 слов по теме, который вы затем сможете распечатать и с триумфом вручить своему несчастному учителю. Но в противном случае лучший подход — последовать примеру Сократа и ответить на вопрос встречным вопросом: что вы подразумеваете под «стороной»?
Когда все сказано и сделано, счет до нуля или до единицы или отказ отвечать на вопрос практически ничего не говорит нам о геометрии окружностей. Но можно многого добиться, разбивая знакомые понятия, опуская или добавляя дополнительные условия, бросая вызов нашей интуиции, переходя от одного контекста к немного другому, и пытаясь записать точно то, что мы подразумеваем под конкретным термином в конкретной обстановке. Вот что такое настоящая математика.
Сноски
[1] Вы можете сделать что-то еще: например. выберите начальную точку P на окружности, от которой нужно измерить расстояние по окружности.
Затем объявите, что точки, находящиеся на рациональном расстоянии от P, являются углами, а остальные — сторонами. В результате получается счетно бесконечное число углов и несчетно бесконечное количество сторон. Или можно было бы оговорить обратное. Это может быть удобно для полигонального подхода к кругам, но я бы не согласился с тем, что это просто или достаточно очевидно, чтобы считаться «правильным ответом».
[2] Один из моих корреспондентов в Твиттере был обеспокоен тем, насколько гладкой является кривая. Это надгробие непрерывно дифференцируемо, но не дважды. Конечно, было бы интересно, если бы многие люди думали, что это критический вопрос, и это, вероятно, можно было бы проверить с бесконечно гладким надгробием, построенным из чего-то подобного, хотя я не продумывал детали.
[3] Мы могли бы попытаться формализовать это следующим образом: в квадрате (или любом многоугольнике) сторона обладает тем свойством, что, начиная с любой точки внутри, вы можете разрезать фигуру прямо через ваше местоположение, так что ваша выбранная сторона твердо находится на одной стороне разреза.
Это не работает для двустороннего надгробия: любой надрез всегда отрежет длинную сторону. Мы могли бы ослабить это, сказав, что для того, чтобы считаться стороной, должен быть хотя бы один способ разрезания фигуры так, чтобы сторона находилась на одной стороне разреза. Это позволило бы нам сказать, что надгробие имеет четыре стороны (даже если криволинейный участок находится не на одной стороне точек в верхней области). Однако для круга его предполагаемая сторона равна 9.0017 никогда не с одной стороны (это будет исключено), и только прямая часть полукруга будет считаться стороной.
[4] Нелегко придумать строгое обоснование, которое работает для обоих надгробий, но я думаю более неформально в терминах точек Шеллинга: то есть места, которые выделяются как особые по причинам, которые могут не быть легко предсказать заранее.
Благодарности
Спасибо всем, кто участвовал в моих опросах, ретвитил их или обсуждал это со мной в Твиттере.
Нравится:
Нравится Загрузка.
..
Сколько сторон у круга?(a) 10 сторон(b) 20 сторон(c) 300 сторон(d) бесконечные стороны
Дата последнего обновления : 02-й март 2023
•
Всего просмотров: 203,7K
•
Просмотры сегодня: 2,87K
Ответ
Проверено
203,7K+ View
HINT: A Circle-Dimes фигура, в которой все точки на поверхности круга равноудалены от центральной точки. Сторона – это линия, являющаяся частью плоской фигуры, состоящей из прямых линий. Окружность имеет бесконечно много точек.
Полное пошаговое решение:
Нам нужно найти количество сторон у окружности. Давайте сначала разберемся, что такое круг. Окружность представляет собой замкнутую двумерную кривую фигуру, все точки на поверхности которой равноудалены от центральной точки. Мы можем изобразить окружность с центром O геометрически, как показано ниже.Мы знаем, что сторона — это линия, являющаяся частью плоской фигуры, состоящей из прямых линий.
Или мы можем сказать, что все фигуры состоят из линий, называемых сторонами. Когда три линии соединены, мы назовем эту геометрическую фигуру треугольником. Точно так же при соединении четырех сторон мы получим квадрат (или прямоугольник, трапецию, ромб или параллелограмм). Давайте впишем квадрат, двенадцатиугольник (многоугольник с 12 сторонами) и пятиугольник (многоугольник с 50 сторонами) внутри круга, как показано ниже.
Из приведенного выше рисунка видно, что при вписании квадрата в круг остается много пробелов. Но когда вписан двенадцатиугольник, пробел уменьшается. Когда мы вписали пятиугольник, мы видим, что пустое пространство сильно уменьшилось.
Точно так же, когда мы соединим бесконечные стороны, мы получим круг.Итак, правильный ответ «Вариант г».
Примечание: Учащиеся могут ошибиться, приняв количество сторон круга за 0 из-за определения стороны. Сторона также определяется как отрезок линии, соединяющий две вершины формы или двумерной фигуры.

 Тот факт, что они вообще разделились по этому вопросу и что незначительное большинство выбрало ответ, который в значительной степени недоступен для обычной аудитории этого вопроса (учеников начальной школы), безусловно, предполагает, что что-то где-то идет не так.
Тот факт, что они вообще разделились по этому вопросу и что незначительное большинство выбрало ответ, который в значительной степени недоступен для обычной аудитории этого вопроса (учеников начальной школы), безусловно, предполагает, что что-то где-то идет не так. Если мы твердо уверены в том, что круг на самом деле является многоугольником с бесконечным числом сторон, то возникает вопрос: каковы стороны? И уж точно единственный правдоподобный ответ [1] это: отдельные точки окружности. Какова длина этих так называемых сторон? Ноль сантиметров. И разделены ли эти стороны углами? Не видно, либо углов вообще нет, либо каждая точка есть и сторона, и угол.
Если мы твердо уверены в том, что круг на самом деле является многоугольником с бесконечным числом сторон, то возникает вопрос: каковы стороны? И уж точно единственный правдоподобный ответ [1] это: отдельные точки окружности. Какова длина этих так называемых сторон? Ноль сантиметров. И разделены ли эти стороны углами? Не видно, либо углов вообще нет, либо каждая точка есть и сторона, и угол. Парадокс? Не совсем. Рассуждения по аналогии — ценный навык в математике и в жизни; в то же время важно сохранять понимание того, что именно это мы и делаем.
Парадокс? Не совсем. Рассуждения по аналогии — ценный навык в математике и в жизни; в то же время важно сохранять понимание того, что именно это мы и делаем. Согласно одному распространенному определению «замкнутой многоугольной цепи», это не соответствует требованиям, поскольку начальный угол (нижний левый) соединяется только с одним ребром. Но это очень близко к промаху: эта точка является пределом последовательности ребер справа, что делает эту форму «несамопересекающейся кусочно-линейной замкнутой кривой» — еще одно определение многоугольника, которое используют люди.
Согласно одному распространенному определению «замкнутой многоугольной цепи», это не соответствует требованиям, поскольку начальный угол (нижний левый) соединяется только с одним ребром. Но это очень близко к промаху: эта точка является пределом последовательности ребер справа, что делает эту форму «несамопересекающейся кусочно-линейной замкнутой кривой» — еще одно определение многоугольника, которое используют люди. Начнем с того, что если угол квадрата — это точка, в которой его граничная линия не является прямой, то каждая точка на окружности удовлетворяет этому. Более сложно, есть понятие крайняя точка фигуры: это любая точка, через которую можно провести отрезок прямой линии, касающийся фигуры только в этой точке. Для квадрата и многих знакомых фигур крайние точки точно совпадают с углами. Каждая точка на границе круга является крайней точкой, поэтому верно, что у круга их бесконечно много.
Начнем с того, что если угол квадрата — это точка, в которой его граничная линия не является прямой, то каждая точка на окружности удовлетворяет этому. Более сложно, есть понятие крайняя точка фигуры: это любая точка, через которую можно провести отрезок прямой линии, касающийся фигуры только в этой точке. Для квадрата и многих знакомых фигур крайние точки точно совпадают с углами. Каждая точка на границе круга является крайней точкой, поэтому верно, что у круга их бесконечно много. Такой подход позволит обнаружить углы всех полигонов, включая шеврон. Для гладких кривых он идентифицировал бы все граничные точки как «углы», за исключением точек перегиба (что вполне разумно, поскольку мы могли бы утверждать, что здесь граница прямая).
Такой подход позволит обнаружить углы всех полигонов, включая шеврон. Для гладких кривых он идентифицировал бы все граничные точки как «углы», за исключением точек перегиба (что вполне разумно, поскольку мы могли бы утверждать, что здесь граница прямая). Таким образом, неявно мы имеем новое уточнение определения 1 (а также пользуемся случаем избавиться от неясного термина «фигура»):
Таким образом, неявно мы имеем новое уточнение определения 1 (а также пользуемся случаем избавиться от неясного термина «фигура»):
 Смысл этого упражнения состоит в том, чтобы экстраполировать ситуацию (прямолинейные фигуры), где два понятия довольно хорошо сочетаются. Если бы существовала новая идея, которая охватила бы все, что нам нравилось в оригинале, но при этом применима к более широкой категории форм, то она бы претендовала на то, чтобы быть единственно правильным ответом. Но если все наши попытки обобщения связаны с принесением в жертву желательных аспектов оригинала, то, возможно, единственного правильного обобщения не существует. Есть разные варианты с разными компромиссами, которые могут быть подходящими в разных контекстах (и если мы находимся в ситуации, когда в игре участвует более одного, то им можно дать разные имена).
Смысл этого упражнения состоит в том, чтобы экстраполировать ситуацию (прямолинейные фигуры), где два понятия довольно хорошо сочетаются. Если бы существовала новая идея, которая охватила бы все, что нам нравилось в оригинале, но при этом применима к более широкой категории форм, то она бы претендовала на то, чтобы быть единственно правильным ответом. Но если все наши попытки обобщения связаны с принесением в жертву желательных аспектов оригинала, то, возможно, единственного правильного обобщения не существует. Есть разные варианты с разными компромиссами, которые могут быть подходящими в разных контекстах (и если мы находимся в ситуации, когда в игре участвует более одного, то им можно дать разные имена). ) 2/3
) 2/3 , вот что важно. Вспомните карту лондонского метро. Если вы спросите, сколько ребер в этой сети, нет смысла подсчитывать прямые или гладкие участки. Это связи между станциями (или вершин ), которые учитываются.
, вот что важно. Вспомните карту лондонского метро. Если вы спросите, сколько ребер в этой сети, нет смысла подсчитывать прямые или гладкие участки. Это связи между станциями (или вершин ), которые учитываются. Тем не менее, в каждом случае, если бы вам сказали, что где-то там есть вершины, и попросили найти их, я думаю, было бы разумно [4] , чтобы догадаться, что их четыре, а именно углы исходного квадрата, и что верхний край по какой-то причине представлен непрямой линией. И если мы действительно хотим думать о вещах таким образом, когда у каждого из надгробий есть 4 края, то может показаться неприятным (хотя и логически последовательным!) настаивать на том, что у них есть какое-то другое количество сторон (тем более, что верхняя сторона — несмотря на собственную геометрию – явно «с одной стороны» фигуры). На самом деле, вместо того, чтобы гадать, один из моих корреспондентов в Твиттере спросил меня: «Удалены ли обе верхние вершины?» — вопрос, который имеет смысл только с теоретико-сетевой точки зрения.
Тем не менее, в каждом случае, если бы вам сказали, что где-то там есть вершины, и попросили найти их, я думаю, было бы разумно [4] , чтобы догадаться, что их четыре, а именно углы исходного квадрата, и что верхний край по какой-то причине представлен непрямой линией. И если мы действительно хотим думать о вещах таким образом, когда у каждого из надгробий есть 4 края, то может показаться неприятным (хотя и логически последовательным!) настаивать на том, что у них есть какое-то другое количество сторон (тем более, что верхняя сторона — несмотря на собственную геометрию – явно «с одной стороны» фигуры). На самом деле, вместо того, чтобы гадать, один из моих корреспондентов в Твиттере спросил меня: «Удалены ли обе верхние вершины?» — вопрос, который имеет смысл только с теоретико-сетевой точки зрения.
 Но аргумент защиты очевиден. Вернемся к определению 2:
Но аргумент защиты очевиден. Вернемся к определению 2: С другой стороны: когда кто-то задает нам вопрос, принцип милосердия, возможно, требует от нас допустить, что он имеет смысл, если мы не можем твердо установить обратное, и определения 1, 2, 4 и другие варианты делают это возможным. Кроме того, определение 3 является скорее лингвистическим, чем формально-математическим, и, следовательно, носит описательный, а не предписывающий характер, поэтому мы не должны ограничиваться им.
С другой стороны: когда кто-то задает нам вопрос, принцип милосердия, возможно, требует от нас допустить, что он имеет смысл, если мы не можем твердо установить обратное, и определения 1, 2, 4 и другие варианты делают это возможным. Кроме того, определение 3 является скорее лингвистическим, чем формально-математическим, и, следовательно, носит описательный, а не предписывающий характер, поэтому мы не должны ограничиваться им.
 Затем объявите, что точки, находящиеся на рациональном расстоянии от P, являются углами, а остальные — сторонами. В результате получается счетно бесконечное число углов и несчетно бесконечное количество сторон. Или можно было бы оговорить обратное. Это может быть удобно для полигонального подхода к кругам, но я бы не согласился с тем, что это просто или достаточно очевидно, чтобы считаться «правильным ответом».
Затем объявите, что точки, находящиеся на рациональном расстоянии от P, являются углами, а остальные — сторонами. В результате получается счетно бесконечное число углов и несчетно бесконечное количество сторон. Или можно было бы оговорить обратное. Это может быть удобно для полигонального подхода к кругам, но я бы не согласился с тем, что это просто или достаточно очевидно, чтобы считаться «правильным ответом». Это не работает для двустороннего надгробия: любой надрез всегда отрежет длинную сторону. Мы могли бы ослабить это, сказав, что для того, чтобы считаться стороной, должен быть хотя бы один способ разрезания фигуры так, чтобы сторона находилась на одной стороне разреза. Это позволило бы нам сказать, что надгробие имеет четыре стороны (даже если криволинейный участок находится не на одной стороне точек в верхней области). Однако для круга его предполагаемая сторона равна 9.0017 никогда не с одной стороны (это будет исключено), и только прямая часть полукруга будет считаться стороной.
Это не работает для двустороннего надгробия: любой надрез всегда отрежет длинную сторону. Мы могли бы ослабить это, сказав, что для того, чтобы считаться стороной, должен быть хотя бы один способ разрезания фигуры так, чтобы сторона находилась на одной стороне разреза. Это позволило бы нам сказать, что надгробие имеет четыре стороны (даже если криволинейный участок находится не на одной стороне точек в верхней области). Однако для круга его предполагаемая сторона равна 9.0017 никогда не с одной стороны (это будет исключено), и только прямая часть полукруга будет считаться стороной.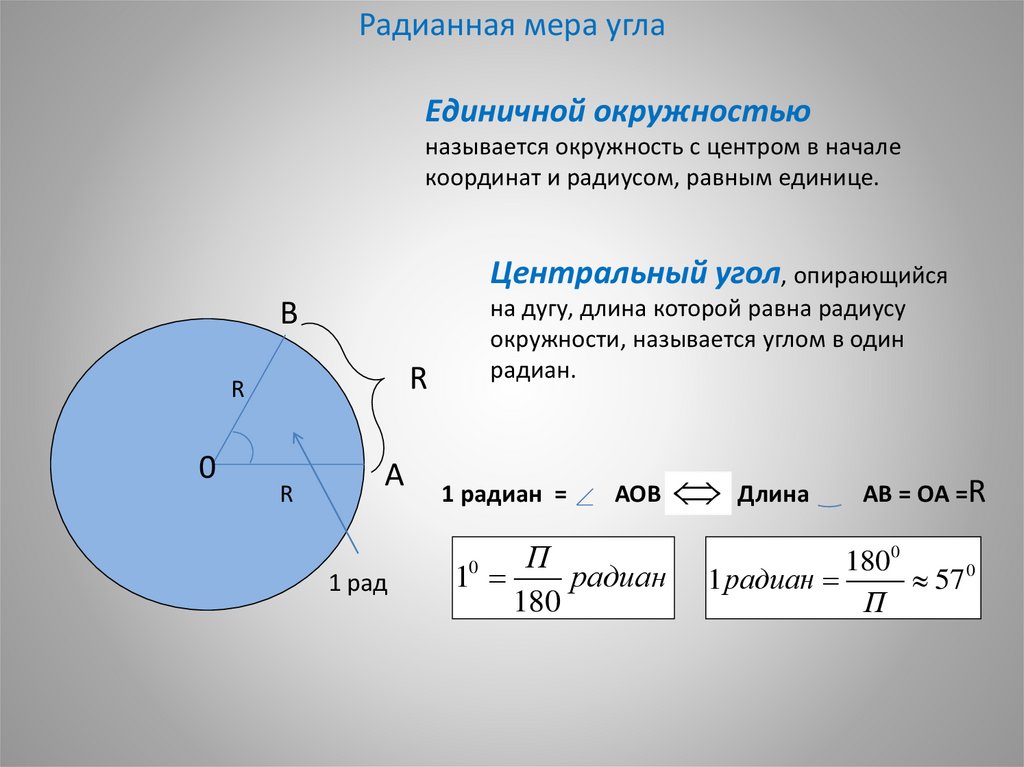 ..
.. Или мы можем сказать, что все фигуры состоят из линий, называемых сторонами. Когда три линии соединены, мы назовем эту геометрическую фигуру треугольником. Точно так же при соединении четырех сторон мы получим квадрат (или прямоугольник, трапецию, ромб или параллелограмм). Давайте впишем квадрат, двенадцатиугольник (многоугольник с 12 сторонами) и пятиугольник (многоугольник с 50 сторонами) внутри круга, как показано ниже.
Или мы можем сказать, что все фигуры состоят из линий, называемых сторонами. Когда три линии соединены, мы назовем эту геометрическую фигуру треугольником. Точно так же при соединении четырех сторон мы получим квадрат (или прямоугольник, трапецию, ромб или параллелограмм). Давайте впишем квадрат, двенадцатиугольник (многоугольник с 12 сторонами) и пятиугольник (многоугольник с 50 сторонами) внутри круга, как показано ниже.