Zero To Hero
Совершенно очевидно, что в круге 360 градусов, не так ли?
А вот и нет. Большинство из нас совершенно не понимают, почему в круге 360 градусов. Мы запоминаем это магическое число как «размер окружности», а затем, изучая физику или высшую математику, удивляемся всем этим «радианам».
«Радианы делают математику проще!» — так говорят математики; вот бы они еще научились конкретнее объяснять, в чем заключается простота (чтобы и мы чувствовали себя в дискуссиях на тему рядов Тейлора, как рыба в воде). Сегодня мы откроем, что на самом деле представляют собой радианы, и поймем, почему именно они делают математику проще.
Откуда берутся градусы?
До чисел и языка слов у нас были звезды. Древние цивилизации использовали астрономию для определения времен года, предсказания будущего и задабривания богов (если уж приносить в жертву богам людей, то лучше делать это в правильное время).
И как всё это относится к углам? Попробуйте разгадать: не странно ли то, что в окружности 360 градусов, а в году 365 дней? И с чего это вдруг созвездия в течение года совершают оборот на небосклоне?
Спорим, вы не сможете определить время года по картине ночного неба? Вот созвездие Большой Медведицы, видимое в 2008 году из Нью-Йорка:
Созвездия каждую ночь немного продвигаются по кругу. Если Вы будете смотреть на небо в одно и то же время (например, в полночь), то заметите, что созвездия совершают полный круг по небу в течение года. Вот теория о возникновении градусов:
Если Вы будете смотреть на небо в одно и то же время (например, в полночь), то заметите, что созвездия совершают полный круг по небу в течение года. Вот теория о возникновении градусов:
- Люди заметили, что за год созвездия совершали полный круг
- Каждый день они отодвигались совсем на немножно (это и есть «градус»)
- Поскольку в году около 360 дней, то и в круге было 360 градусов.
Но, есть одно но… Почему бы не сделать 365 градусов в окружности?
Простим древним эту погрешность: они пользовались солнечными часами, и не знали, что за год должно было набежать ровно 365.242199 градусов или дней, как вам теперь известно.
360 — достаточно точная цифра для тех времен. Она отлично согласуется с Вавилонской 60-ричной системой счисления, а также отлично делится (на 2, 3, 4, 6, 10, 12, 15, 30, 45, 90… ну вы поняли).
Математические расчеты по Солнцу выглядят вполне уместными
Земле везет: ~360 — отличное количество дней в году. Но эта цифра выглядит довольно субъективно: на Марсе у нас было бы ~680 градусов в окружности, так как марсианский год длится дольше (и сам марсианский день также длится дольше, как вы понимаете). В некоторых странах Европы люди пользуются градами, при которых круг приходится делить на 400 частей.
В некоторых странах Европы люди пользуются градами, при которых круг приходится делить на 400 частей.
Многие из объяснений сходятся к следующему: «Ну, градус — довольно субъективная мера, но нам нужно было выбрать какое-то число». Не сейчас: далее мы увидим, что же на самом деле скрывают градусы.
Радианы спорят с градусами
Градус — это то, насколько мне, стоя в центре стадиона, приходится повернуть голову, чтобы увидеть человека, бегущего по беговой дорожке.
Представьте, что вы заметили друга, бегущего по огромному кругу:
— Привет, как далеко ты добежал?
— Ну, пробежался я нехило, около 10 километров.
— Ты что, совсем? Как сильно я повернул свою голову, чтобы тебя увидеть?
— Что?
— Я поясню словами покороче для непонятливых. Я в центре круга. Ты бежал вокруг. Насколько… я… повернул… свою… голову?
— Придурок.
Эгоистично, не так ли? Вот как вся эта математика построена! Мы пишем уравнения по типу «Слушай, как сильно я повернул свою голову, чтобы увидеть движущуюся планету/маятник/колесо?» Я уверен, что вы никогда не думали о том, что чувствует, о чем мечтает и на что надеется маятник. Это эгоистичный подход. Не кажется ли вам, что уравнения должны быть простыми не только для зрителя, но и для самого бегуна?
Это эгоистичный подход. Не кажется ли вам, что уравнения должны быть простыми не только для зрителя, но и для самого бегуна?
Радианы: скажи эгоизму нет
Многие вещи из физики (да и из жизни!) заставляет нас вылезти из своей привычной системы координат и посмотреть на вещи с другой точки. Вместо того, чтобы вычислять поворот своей головы, задумайтесь, как далеко продвинулся бегун.
Градусы измеряют уголы по повороту головы. А радианы измеряют углы по пройденной дистанции.
Но само по себе расстояние не особо полезно, так как дистанция в 10 км может состоять из разного количества кругов, всё зависит от длины самого круга. Так что мы делим пройденную дистанцию на радиус круга, чтобы получить приведенный угол:
Вы часто будете встречать эту же формулу в таком виде:
угол в радианах (тета) — это длина дуги (s), поделенная на радиус (r).
Окружность описывает 360 градусов или 2π радиан — пройти весь круг будет 2*π* r / r. То есть, радиан — это примерно 360 /(2 * π) или 57. 3 градусов.
3 градусов.
Надеюсь, вы не будете думать, как я: «Ну вот, еще одна непонятная единица. 57.3 — такое странное число». Оно странное только потому, что вы всё еще думаете о себе!
Пройти 1 радиан (единицу) — вполне себе нормальная дистанция для путешествия.
Другими словами, наш «чистый, ровный угол в 90°» означает то же, что и непонятные π/2 единицы для пройденного бегуном пути. Подумайте об этом: «Эй, парень, а не пробежишь ли ты для меня еще 90°? Сколько это? А, ну да, для тебя это будет π/2 километра». Для бегуна дистанция в градусах выглядит также странно, как и поворот в радианах для зрителя.
Радианы в математике — это как бы поставить себя на место другого: передвинуть свою точку зрения с поворота головы на движение бегуна.
Что в имени тебе моем?
Радианы — это единица измерения движения по кругу, характеризуемого радиусом. Я думаю, слово «радиан» иллюстрирует как раз связь с радиусом движения.
По сути, радианы — это такие же числа, как 1.5 или 73, без каких либо единиц измерения (в формуле «радианы = пройденный путь / радиус» длина делится на длину, так что любые единицы измерения сокращаются).
Но, говоря практическим языком, мы не математические роботы, так что проще думать о радиане как о «пути», пройденному по единичной окружности.
Использование радиан
Я пока и сам привыкаю думать радианами. Но мы уже довольно близко подобрались к понятию «дистанции бегуна»:
- Мы используем «вращений в минуту», а не «градусов в секунду» при измерении определенных угловых скоростей. Это ближе к точке зрения бегуна («Как много кругов он уже намотал?»)
- Когда спутник движется вокруг Земли, мы понимаем его скорость как «километров в час», а не «градусов в час». Разделите эту скорость на расстояние от земли к спутнику, и вы получите орбитальную скорость в радианах в час.
- Синус, эта замечательная функция, определяется в радианах, как:
Эта формула работает, только если х представлен в радианах! Почему? Синус непосредственно связан с пройденным путем, а не с поворотом головы. Но мы отложим эту беседу до следующего раза.
Пример 1: Колеса автобуса
Давайте попробуем разобрать реальный пример: у вас есть автобус с колесами, радиус которых 2 метра (это автобус в стиле монстр-трак). Я скажу, как быстро вращаются колеса, а вы мне скажете, как быстро едет автобус. Готовы? «Колеса вращаются со скоростью 2000 градусов в секунду». Вы думаете:
Я скажу, как быстро вращаются колеса, а вы мне скажете, как быстро едет автобус. Готовы? «Колеса вращаются со скоростью 2000 градусов в секунду». Вы думаете:
- Хорошо, колеса вращаются на 2000 градусов в секунду. Это значит, они делают 2000/360 или 5 и 5/9 оборота в секунду. Длина окружности = 2*π*r, так что автобус движется со скоростью, эм, 2 * 3.14 * 5 и 5/9… где же мой калькулятор…
«Колеса проходят 6 радиан в секунду». Вы подумаете:
- Радианы — это длина единичной окружности, мы просто масштабируем эту величину согласно реальному радиусу, чтобы рассчитать, как далеко мы уедем. 6 * 2 = 12 метров в секунду. Следующий вопрос.
Вау! Никаких сумасшедших формул, никакого π — просто умножаем, чтобы конвертировать угловую скорость в линейную. А всё потому, что радианы говорят на языке движущегося тела.
Обратное действие также простое. Предположим, что мы несёмся 30 метров в секунду по автостраде (108 км/ч) на 24-дюймовых колесах (радиус которых равен 30 см). Как быстро вращаются колеса?
Как быстро вращаются колеса?
Ну, 30 метров в секунду / 0.3 м радиуса = 100 радианов в секунду.
Это было просто.
Пример 2: sin(x)
Пришло время для примера помощнее. Выберите число градусов (х) и вычислите значение sin(x) в калькуляторе:
Когда вы берете х очень маленьким, вроде 0.01, sin(x) тоже становится маленьким. И отношение sin(x)/x будет около 0.017 — что это означает? И еще страннее, что означает деление или умножение на градусы? Можно ли иметь квадратные или кубические градусы?
Радианы нас спасут. Зная, что они отвечают за пройденную дистанцию (это не просто пропорция!), мы можем интерпретировать уравнение таким образом:
- х — это то, как далеко вы прошли по кругу
- sin(x) — это то, как высоко вы взобрались по нему
- Так что sin(x)/x — это отношение того, как высоко вы находитесь, к тому, как далеко вы прошли: количество энергии, которое ушло в направлении «вверх». Если вы двигались вертикально, то это отношение будет равно 100%.
 Если вы двигались горизонтально, то равенство будет давать 0%.
Если вы двигались горизонтально, то равенство будет давать 0%.
Когда что-то пододвигается на крошечное расстояние, как 0 или 1 градус с прежнего места, оно движется практически вверх. Если вы шагнете еще на меньшее расстояние, например с 0 до 0.00001 градуса, то вы действительно пройдете прямо вверх. Пройденное расстояние (х) очень близко к высоте (sin(x)).
Чем меньше х, тем ближе отношение к 100% — больше движения происходит вверх.
Радианы помогают увидеть, интуитивно, почему sin(x)/x стремится к 1 по мере уменьшения х. Мы просто топчемся на крошечном отрезке пути вверх. Между прочим, это также поясняет, почему sin(x) ~ x для маленьких чисел.
Конечно, вы можете точно доказать это с помощью калькулятора, но мышление радианами помогает вам это понять.
Запомните, эти связи работают только при измерении углов радианами. С градусами вы сравниваете высоты на окружности (sin(x)) с тем, насколько какой-то зритель поверную свою голову (х градусов).
Так в чем же смысл?
Градусы занимают свое место в нашей жизни. Нам ведь важно знать, насколько надо повернуть телескоп, развернуть сноуборд или покрутить рулем? По законам природы мы наблюдаем за тем, как движутся другие. И радианы больше подходят тем, кто движется, чем тем, кто за ними наблюдает. У меня ушло много лет на то, чтобы понять:
Нам ведь важно знать, насколько надо повернуть телескоп, развернуть сноуборд или покрутить рулем? По законам природы мы наблюдаем за тем, как движутся другие. И радианы больше подходят тем, кто движется, чем тем, кто за ними наблюдает. У меня ушло много лет на то, чтобы понять:
- Градусы выбраны произвольно, так как они основываются на солнце (365 дней ~ 360 градусов), но они как бы идут от обратного, потому что описывают процессы с точки зрения наблюдателя.
- Радианы описывают движение с точки зрения самих его участников, и поэтому «всё стает на свои места». Конвертировать угловую скорость в линейную довольно просто, и идеи вроде sin(x)/x приобретают смысл.
Даже углы можно рассматривать с более, чем одной точки зрения. Понимание радиан делают математические и физические формулы более осмысленными.
Приятных вычислений!
Перевод статьи «Intuitive Guide to Angles, Degrees and Radians»
«Почему принято считать, что в окружности 360 градусов, а не 100 или 1000?» — Яндекс Кью
Популярное
Сообщества
Математика
Коринец Э.
·
82,3 K
ОтветитьУточнитьВиктор Брыксин
101
пенсионер · 24 июл 2021
Я уже высказывался, что число 360 возникает из попыток древних построить календарь. Но, как заметили многие авторы, число 360 удобно делимо на равные доли: и пополам, и на три, и на четыре, и на пять, и на шесть, и т.д. Количество вариантов деления большое, поэтому удовлетворялись разнообразные потребности практики. Число 360 не могло быть не популярным. Геометрическая особенность состоит в том, что окружность легко делится циркулем и пополам, и на три, и на четыре, и на шесть. Я, думаю, что древние умели это делать и сопоставляли числовые свойства и геометрические. Деление дуги окружности пополам простая процедура, способствовавшая дроблению этой шкалы. Так что возникновение 360 равномерных засечек по периметру диска, т.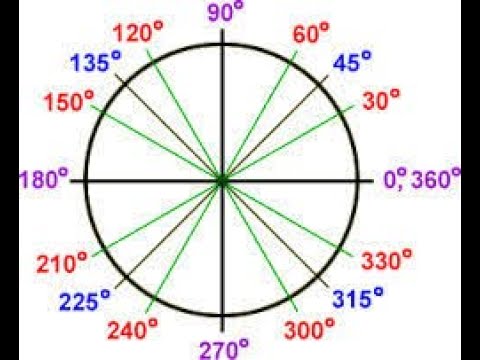
nosad_nobad
16 ноября 2022
По делению — не шибко. Если бы хотели получить число которое делится на любые равные доли, то взяли бы например… Читать дальше
Комментировать ответ…Комментировать…
Виктор Брыксин
101
пенсионер · 1 мар 2021
В древние времена на месте нынешних Сирии и Ирака, в междуречье Тигра и Евфрата существовало государство Месопотамия. Там возникла 60-ричная система исчисления, задолго до появления римских и арабских цифр. Пробег минутной стрелки в современных часах (60 минут за 1 час) это отголосок того времени. Я думаю, что 360 угловых единиц (градусов) возникли из временных… Читать далее
Комментировать ответ…Комментировать…
Александр Капри
5
Художник-график. Вероисповедание – православное. Политические взгляды – монархист. Хобби… · 5 февр 2020
Вероисповедание – православное. Политические взгляды – монархист. Хобби… · 5 февр 2020
Диаметр Солнца с Земли, укладывается на окружность эклиптики примерно 360 раз.
Проще всего поделить окружность, на 6, 12, 24… и так далее.
По этому и сложилась система счисления на этих числах.
Влад .
Угловой диаметр Солнца с Земли примерно полградуса (точнее 32″) и в окружности эклиптики он укладывается примерно… Читать дальше
Комментировать ответ…Комментировать…
Алферьевский Сергей
3
Механик, точные науки · 2 сент 2020
В древности, без компьютеров и графопостраителей сложно было поделить круг более, чем на 360 частей ручками и с примитивными чертежными приспособлениями. Вот и взяли по мах.
Сколько дней в году, так же, у разных народов по разному было, кто как придумал.
В мореходстве круг 32 румба.
Не хватает градусов, есть минута, а там еще секунда и тд.
Комментировать ответ…Комментировать…
Аркаим
5инженер-хитротехник, «специалист по мягкому металлу, по хлебу и по салу» (с) · 5 сент 2020
Одно время была попытка ввести «правильные» числа, и появились «грады». При этом прямой угол был равен ста градам, а окружность, соответственно, четырем сотням. Но, как показала практика, не прижилось.
А еще окружность меряется в радианах, и тогда она «два пи»
Комментировать ответ…Комментировать…
Иван Григорьевич Стрельников
4
5 авг 2020
Оборот Земли вокруг Солнца до известной катастрофы составлял 360 дней. Круг был разделён на 9 (девять) сроков или 40 (четырдцать) недель по 9 дней. Срок = сърок = сорок!!! 14 — это четырнадцать 4+10, 40 — это четырдцать 4 * 10.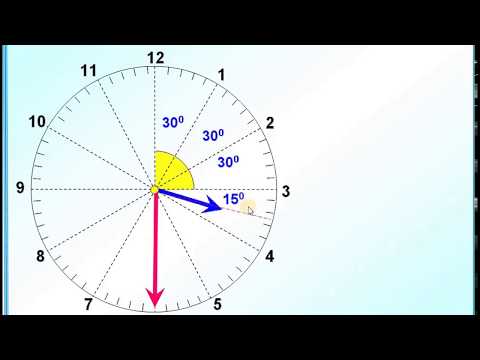 До сих пор мы поминаем покойника в неделю (9=девять дней) и в срок (40=четырдцать) дней.
Потом дней стало 365,25.
41+40+41+40+41+40+41+40+41=365… Читать далее
До сих пор мы поминаем покойника в неделю (9=девять дней) и в срок (40=четырдцать) дней.
Потом дней стало 365,25.
41+40+41+40+41+40+41+40+41=365… Читать далее
lavzariu
5 августа 2020
А есть еще административный календарь, вспомните 10 дней на рассмотрение челобитной царю, 100 дней восхождения на… Читать дальше
Комментировать ответ…Комментировать…
lavzariu
-2
хххххххххххххххххххххххххххххххххххххххххххххххххххххххххххххххххххххххххххххххххххххххххх… · 18 июл 2020
360 легко делить, но тяжело считать. В свою очередь, 1000 легко считать, но тяжело делить по-справедливости. В шумерские времена, справедливо разделить, был вопрос жизни и смерти. Сейчас все наоборот: точный расчет решает все!.
Отсюда вывод; надо переходить на новое летоисчисление, которое будет включать в себя и все старые (мертвые) календари!.
Комментировать ответ…Комментировать…
Владимир Брунбендер
3
28 мая 2020
У древних шумеров на каждой руке было по 6 пальцев, поэтому они применяли 12-ричную систему счисления. Сутки они разделили на 2 части (день — ночь), каждую часть по 12 часов. Окружность при помощи циркуля легко разделить на 3 равные части. Если каждую часть разделить на 120, то как раз и получится 360.
Комментировать ответ…Комментировать…
Первый
Анатолий Е.
5
7 мая 2020
Градус,это «Два шага», вот и получается что в » в горизонт суток» помещается 720 проекций солнечных дисков.720 разделить на 2 (два шага) получаем 360.
Комментировать ответ…Комментировать…
Владимир Сивохин
17
28 мар 2020
Диск Солнца с восхода до заката укладывается на небосклоне в определённое время года на определённой широте 180 раз. Ночью — тоже ( от заката до рассвета). Отсюда один угловой градус — это одна «денежка» Солнца; прямой угол — это Солнце в полдень = 90 градусов, всё остальное — от деления 180 (или 360 ) градусов.
Ночью — тоже ( от заката до рассвета). Отсюда один угловой градус — это одна «денежка» Солнца; прямой угол — это Солнце в полдень = 90 градусов, всё остальное — от деления 180 (или 360 ) градусов.
Александр Новиков
21 июля 2020
солнце в полночь?
Комментировать ответ…Комментировать…
Сколько градусов в окружности?
МАТЕМАТИКА — Геометрия
Задумывались ли вы когда-нибудь…
- Сколько градусов в окружности?
- Какая связь между радиусом и диаметром круга?
- Как называется расстояние вокруг края круга?
Теги:
См. все теги- 2πr,
- Вавилоняне,
- форма,
- πr2,
- Математика,
- Геометрия,
- Круг,
- Степень,
- Площадь,
- Треугольник,
- Пирог,
- Хулахуп,
- Самолет,
- Точка,
- Расстояние,
- Диаметр,
- Окружность,
- Район,
- Периметр,
- Пи,
- Экспонента,
- Земля,
- Вс,
- Орбита,
- Календарь
Сегодняшнее чудо дня было вдохновлено Анной Грейс из Зимнего Интервилля.
Любишь геометрию? Мы делаем! Мы хотели сделать Чудо дня об особой форме, но не могли решить, какую фигуру использовать. Однако чем больше мы думали об этом, тем больше мы возвращались к той же форме. Что это было? Круг, конечно!
Что вам больше всего нравится в кругах? Нам нравятся их идеально круглые формы. У них нет тех заостренных концов, которые вы найдете на квадратах и треугольниках.
Некоторые из наших любимых вещей имеют форму кругов. Например, наш любимый десерт — пирог — имеет форму круга. Как и наша любимая игрушка: хула-хуп. Какие еще предметы в форме круга вы видите или используете каждый день?
Учителя геометрии определяют окружность как набор точек на плоскости, находящихся на одинаковом расстоянии от центральной точки. Это означает, что круги плоские. Когда вы изучаете круги, вы узнаете, что у каждого круга есть радиус, диаметр, длина окружности и площадь.
Радиус круга — это расстояние от его центра до края. Диаметр круга — это расстояние поперек круга в его самом широком месте. Диаметр круга всегда ровно в два раза больше его радиуса.
Периметр круга — расстояние вокруг его края — называется его окружностью. Чтобы вычислить длину окружности, нужно знать ее радиус.
Формула длины окружности: 2πr, где r — радиус окружности, а π — число пи (приблизительно 3,141592). Поскольку диаметр круга в два раза больше радиуса, вы также можете представить формулу длины окружности как πd, где d — диаметр круга.
Площадь круга измеряется количеством квадратных единиц внутри круга. Еще раз, вам нужно знать радиус. Формула площади круга: πr 2 . 2 в формуле — это показатель степени, что означает, что вы умножаете радиус сам на себя. Таким образом, вместо формулы площади круга можно было бы написать πrr.
Одна замечательная вещь о кругах, которую знают все учителя геометрии, заключается в том, что если вы знаете один из этих фактов — радиус, диаметр, длину окружности или площадь — вы можете вычислить все остальные значения! Например, если вы знаете радиус круга, вы можете вычислить его диаметр, длину окружности и площадь.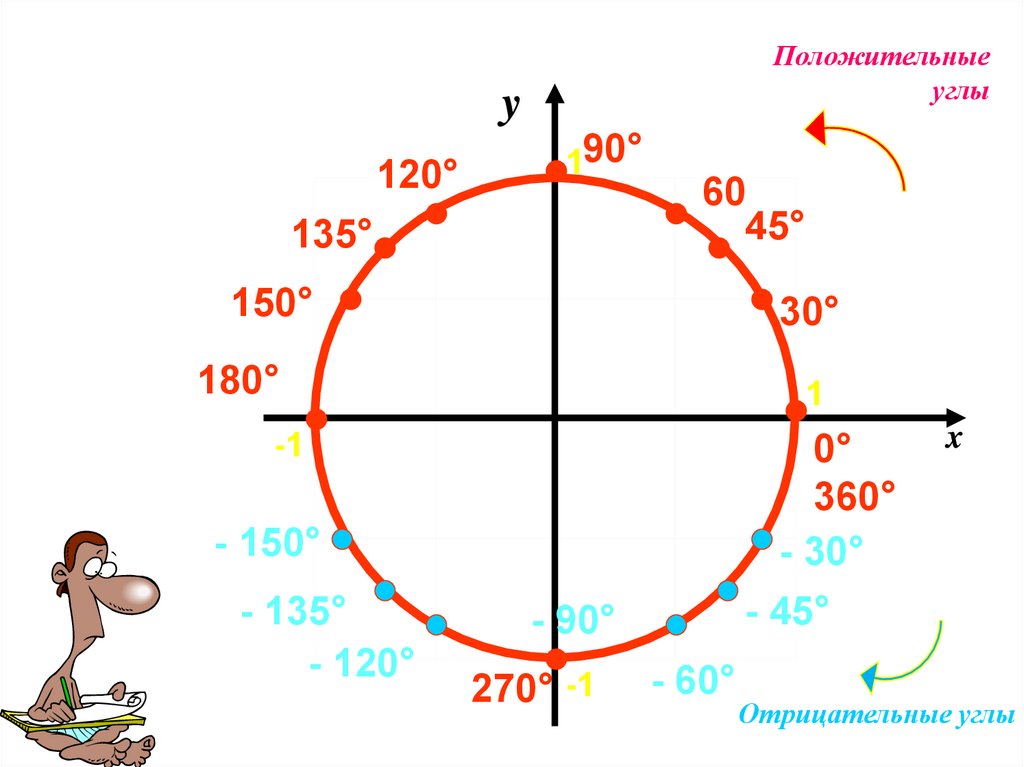
Еще один интересный аспект кругов заключается в том, что каждый круг можно разделить на 360 единиц, называемых градусами. Итак, если вы совершите полный круг, вы повернетесь на 360 градусов. Если вы просто повернетесь наполовину — полукругом — вы повернетесь на 180 градусов.
Так почему же 360 градусов вместо чего-то попроще, например, 100 градусов? Математики считают, что виноваты древние вавилоняне. Около 2400 г. до н.э. они заметили круговое движение Земли вокруг Солнца. Они также подсчитали, что для завершения этой круговой орбиты потребовалось около 360 дней.
Поэтому круговой путь решили разделить на 360 градусов. Таким образом, они могли легко отслеживать прохождение каждого дня по круговому календарю. Так что если вы запутались в геометрии с количеством градусов в окружности, виноваты вавилоняне!
Интересно, что дальше?
Завтрашнее чудо дня — это глоток свежего воздуха!
Попробуйте
Готовы повеселиться с геометрией? Обязательно проверьте следующие задания с другом или членом семьи:
- Если вы хотите узнать больше о градусах и углах, посмотрите это увлекательное онлайн-занятие «Углы».
 Сможете ли вы правильно угадать все углы, которые вам нужны, чтобы брызгать водой из шланга на различные предметы?
Сможете ли вы правильно угадать все углы, которые вам нужны, чтобы брызгать водой из шланга на различные предметы? - После того, как вы попрактикуетесь с углами, попробуйте онлайн-задание «Угадай случайный угол». Нажмите кнопку, чтобы сгенерировать случайный угол, введите свое предположение, а затем посмотрите, насколько близко вы были к метке!
- Вам трудно представить себе, как определяется число Пи? Зайдите в Интернет, чтобы посмотреть визуальное представление о том, как катящийся круг иллюстрирует число Пи. Попробуйте повторить то, что видите, с помощью круга и линейки дома.
Wonder Sources
- http://www.coolmath.com/reference/circles-geometry.html
- http://mathforum.org/library/drmath/view/59075.html
Получили?
Проверьте свои знанияWonder Contributors
Благодарим:
Braeden
за ответы на вопросы по сегодняшней теме Wonder!
Продолжайте удивляться вместе с нами!
Что вас интересует?
Wonder Words
- радиус
- диаметр
- окружность
- район
- геометрия
- самолет
- периметр
- формула
- заостренный
- аспект
- расстояние
- показатель степени
- решил
- запутался
- интересно
- рассчитано
- измерение
- математиков
Примите участие в конкурсе Wonder Word
Оцените это чудо
Поделись этим чудом
×ПОЛУЧАЙТЕ СВОЕ ЧУДО ЕЖЕДНЕВНО
Подпишитесь на Wonderopolis и получайте Чудо дня® по электронной почте или SMS
Присоединяйтесь к Buzz
Не пропустите наши специальные предложения, подарки и рекламные акции. Узнай первым!
Узнай первым!
Поделитесь со всем миром
Расскажите всем о Вандополисе и его чудесах.
Поделиться Wonderopolis
Wonderopolis Widget
Хотите делиться информацией о Wonderopolis® каждый день? Хотите добавить немного чуда на свой сайт? Помогите распространить чудо семейного обучения вместе.
Добавить виджет
Ты понял!
Продолжить
Не совсем!
Попробуйте еще раз
Как найти угол в процентах от окружности
Все ресурсы по промежуточной геометрии
8 Диагностические тесты 250 практических тестов Вопрос дня Карточки Learn by Concept
← Предыдущая 1 2 Следующая →
Промежуточная геометрия Помощь » Плоская геометрия » Круги » Сектора » Как найти угол в процентах от окружности
Сколько градусов в окружности?
Возможные ответы:
Правильный ответ:
Объяснение:
В круге есть градусы, поэтому уравнение, которое нужно решить, превращается в простую процентную задачу:
Сообщить об ошибке
Сектор содержит круг.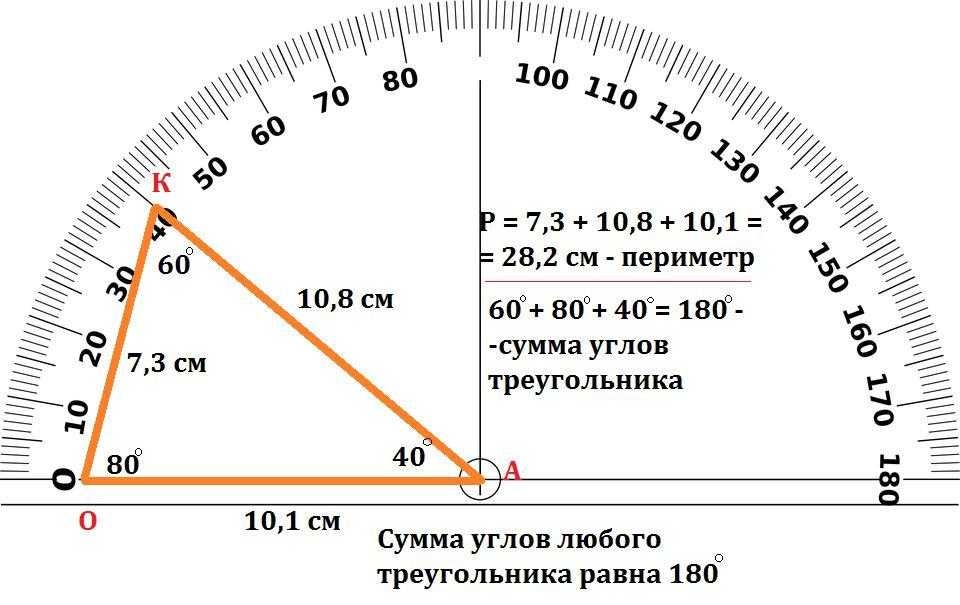 Чему равен центральный угол сектора?
Чему равен центральный угол сектора?
Возможные ответы:
Правильный ответ:
Объяснение:
Целый круг . Таким образом, сектор, принадлежащий кругу, имеет центральный угол, равный .
Следовательно, наш центральный угол равен
Сообщить об ошибке
Если у вас есть процент от круга, какой угол в градусах образует эту область?
Возможные ответы:
Правильный ответ:
Объяснение:
Полный круг имеет 360 градусов, что означает, что 100% круга составляют 360 градусов.
Теперь нужно преобразовать в десятичное число.
Если умножить 360 на 0,667, получится градусная мера, соответствующая проценту, который равен 240.
Сообщить об ошибке что создает этот регион?
Возможные ответы:
Правильный ответ:
Объяснение:
Полный круг имеет 360 градусов, что означает, что 100% круга составляет 360 градусов.
Сначала преобразуйте в десятичное число.
Если умножить 360 на 0,20, получится градусная мера, соответствующая проценту, который равен 72.
Сообщить об ошибке что создает этот регион?
Возможные ответы:
Правильный ответ:
Объяснение:
Полный круг имеет 360 градусов, что означает, что 100% круга составляет 360 градусов.
Чтобы начать эту задачу, нам нужно преобразовать проценты в десятичные числа.
Если умножить 360 на 0,30, получится градусная мера, соответствующая проценту, который равен 108.
Сообщить об ошибке что создает этот регион?
Возможные ответы:
Правильный ответ:
Объяснение:
Полный круг имеет 360 градусов, что означает, что 100% круга составляет 360 градусов.
Сначала преобразуйте проценты в десятичные числа.
Теперь, если вы умножите 360 на 0,35, вы получите градусную меру, соответствующую проценту, который равен 126.
Сообщить об ошибке , что создает этот регион?
Возможные ответы:
Правильный ответ:
Объяснение:
Полный круг имеет 360 градусов, что означает, что 100% круга составляет 360 градусов.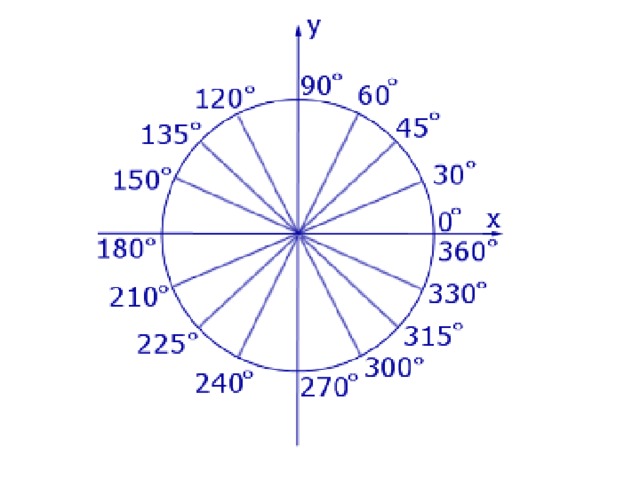
Сначала преобразуйте проценты в десятичные числа.
Если умножить 360 на 0,90, получится градусная мера, соответствующая проценту, который равен 324.
Сообщить об ошибке что создает этот регион?
Возможные ответы:
Правильный ответ:
Объяснение:
Полный круг имеет 360 градусов, что означает, что 100% круга составляет 360 градусов.
Сначала нам нужно преобразовать проценты в десятичные числа.
Если умножить 360 на 0,45, получится градусная мера, соответствующая проценту, который равен 162.
Сообщить об ошибке что создает этот регион?
Возможные ответы:
Правильный ответ:
Объяснение:
Полный круг имеет 360 градусов, что означает, что 100% круга составляет 360 градусов.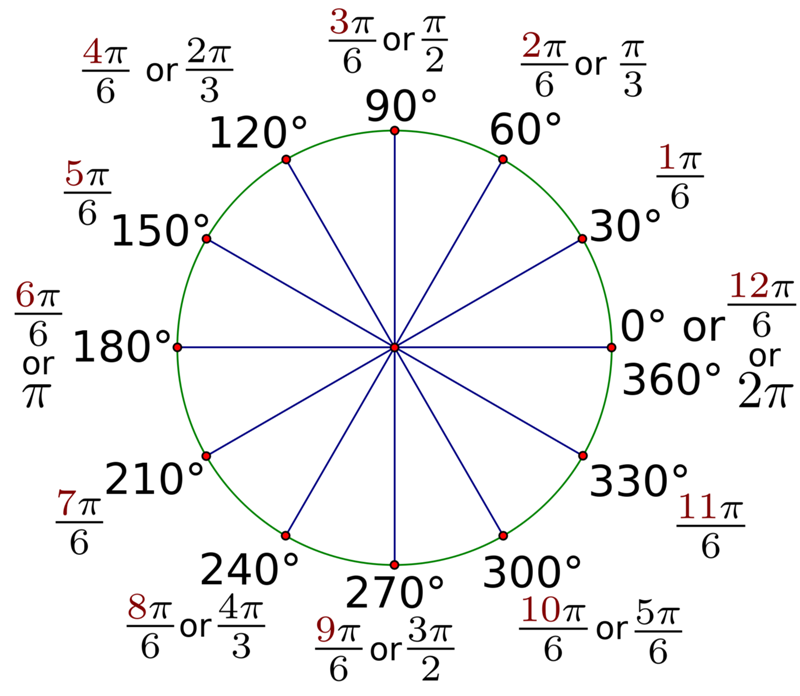

 Если вы двигались горизонтально, то равенство будет давать 0%.
Если вы двигались горизонтально, то равенство будет давать 0%. Сможете ли вы правильно угадать все углы, которые вам нужны, чтобы брызгать водой из шланга на различные предметы?
Сможете ли вы правильно угадать все углы, которые вам нужны, чтобы брызгать водой из шланга на различные предметы?