Замечательный предел это: Замечательные пределы, формулы и доказательства

Математический анализ. Начальный курс

Ильин В. А. и др. Математический анализ. Начальный курс/В. А. Ильин, В. А. Садовничий, Бл. Х. Сендов. Под ред. А. Н. Тихонова,— 2-е изд., перераб., — М.: Изд-во МГУ, 1985. — 662 с. Учебник представляет собой первую часть трехтомного курса математического анализа для высших учебных заведений СССР, Болгарии и Венгрии, написанного в соответствии с соглашением о сотрудничестве между Московским, Софийским и Будапештским университетами. Книга включает в себя теорию вещественных чисел, теорию пределов, теорию непрерывности функций, дифференциальное и интегральное исчисления функций одной переменной и их приложения, дифференциальное исчисление функций многих переменных и теорию неявных функций. Оглавление ПРЕДИСЛОВИЕ ТИТУЛЬНОГО РЕДАКТОРА ПРЕДИСЛОВИЕ КО ВТОРОМУ ИЗДАНИЮ ПРЕДИСЛОВИЕ К ПЕРВОМУ ИЗДАНИЮ Глава 1. ОСНОВНЫЕ ПОНЯТИЯ МАТЕМАТИЧЕСКОГО АНАЛИЗА Глава 2. ВЕЩЕСТВЕННЫЕ ЧИСЛА 2. Недостаточность рациональных чисел для измерения отрезков числовой оси. 3. Упорядочение множества бесконечных десятичных дробей. § 2. ОГРАНИЧЕННЫЕ СВЕРХУ (ИЛИ СНИЗУ) МНОЖЕСТВА ЧИСЕЛ, ПРЕДСТАВИМЫХ БЕСКОНЕЧНЫМИ ДЕСЯТИЧНЫМИ ДРОБЯМИ 2. Существование точных граней. § 3. ПРИБЛИЖЕНИЕ ЧИСЕЛ, ПРЕДСТАВИМЫХ БЕСКОНЕЧНЫМИ ДЕСЯТИЧНЫМИ ДРОБЯМИ, РАЦИОНАЛЬНЫМИ ЧИСЛАМИ § 4. ОПЕРАЦИИ СЛОЖЕНИЯ И УМНОЖЕНИЯ. ОПИСАНИЕ МНОЖЕСТВА ВЕЩЕСТВЕННЫХ ЧИСЕЛ 2. Существование и единственность суммы и произведения вещественных чисел. § 5. СВОЙСТВА ВЕЩЕСТВЕННЫХ ЧИСЕЛ 2. Некоторые часто употребляемые соотношения. 3. Некоторые конкретные множества вещественных чисел. § 6. ДОПОЛНИТЕЛЬНЫЕ ВОПРОСЫ ТЕОРИИ ВЕЩЕСТВЕННЫХ ЧИСЕЛ 2. Аксиоматическое введение множества вещественных чисел. § 7. ЭЛЕМЕНТЫ ТЕОРИИ МНОЖЕСТВ 2. Операции над множествами. 3. Счетные и несчетные множества. Несчетность сегмента [0, 1]. Мощность множества. 4. Свойства операций над множествами. Отображение множеств. Глава 3. ТЕОРИЯ ПРЕДЕЛОВ § 1. ПОСЛЕДОВАТЕЛЬНОСТЬ И ЕЕ ПРЕДЕЛ 2. Ограниченные, неограниченные, бесконечно малые и бесконечно большие последовательности. 3. Основные свойства бесконечно малых последовательностей. 4. Сходящиеся последовательности и их свойства. § 2. МОНОТОННЫЕ ПОСЛЕДОВАТЕЛЬНОСТИ 2. Теорема о сходимости монотонной ограниченной последовательности. 4. Примеры сходящихся монотонных последовательностей. § 3. ПРОИЗВОЛЬНЫЕ ПОСЛЕДОВАТЕЛЬНОСТИ 2. Расширение понятий предельной точки и верхнего и нижнего пределов. 3. Критерий Коши сходимости последовательности. § 4. ПРЕДЕЛ (ИЛИ ПРЕДЕЛЬНОЕ ЗНАЧЕНИЕ) ФУНКЦИИ 2. Предел функции по Гейне и по Коши. 3. Критерий Коши существования предела функции. 4. Арифметические операции над функциями, имеющими предел. 5. Бесконечно малые и бесконечно большие функции. § 5. ОБЩЕЕ ОПРЕДЕЛЕНИЕ ПРЕДЕЛА ФУНКЦИИ ПО БАЗЕ Глава 4. НЕПРЕРЫВНОСТЬ ФУНКЦИИ § 1. ПОНЯТИЕ НЕПРЕРЫВНОСТИ ФУНКЦИИ 2. Арифметические операции над непрерывными функциями. 3. Сложная функция и ее непрерывность. § 2. СВОЙСТВА МОНОТОННЫХ ФУНКЦИЙ 2. Понятие обратной функции. § 3. ПРОСТЕЙШИЕ ЭЛЕМЕНТАРНЫЕ ФУНКЦИИ 2. Логарифмическая функция. 3. Степенная функция. 4. Тригонометрические функции. 5. Обратные тригонометрические функции. 6. Гиперболические функции. § 4. ДВА ЗАМЕЧАТЕЛЬНЫХ ПРЕДЕЛА 2. Второй замечательный предел. § 5. ТОЧКИ РАЗРЫВА ФУНКЦИИ И ИХ КЛАССИФИКАЦИЯ 2. О точках разрыва монотонной функции. § 6. ЛОКАЛЬНЫЕ И ГЛОБАЛЬНЫЕ СВОЙСТВА НЕПРЕРЫВНЫХ ФУНКЦИЙ 2. Глобальные свойства непрерывных функций. 3. Понятие равномерной непрерывности функции. 4. Понятие модуля непрерывности функции. § 7. ПОНЯТИЕ КОМПАКТНОСТИ МНОЖЕСТВА 2. О покрытиях множества системой открытых множеств. 3. Понятие компактности множества. Глава 5. ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ § 1. ПОНЯТИЕ ПРОИЗВОДНОЙ 2. Определение производной. 3. Геометрический смысл производной. § 2. ПОНЯТИЕ ДИФФЕРЕНЦИРУЕМОСТИ ФУНКЦИИ 2. Дифференцируемость и непрерывность. 3. Понятие дифференциала функции. § 3. ДИФФЕРЕНЦИРОВАНИЕ СЛОЖНОЙ ФУНКЦИИ И ОБРАТНОЙ ФУНКЦИИ 2. Дифференцирование обратной функции. 3. Инвариантность формы первого дифференциала. 4. Применение дифференциала для установления приближенных формул. § 4. ДИФФЕРЕНЦИРОВАНИЕ СУММЫ, РАЗНОСТИ, ПРОИЗВЕДЕНИЯ И ЧАСТНОГО ФУНКЦИЙ § 5. ПРОИЗВОДНЫЕ ПРОСТЕЙШИХ ЭЛЕМЕНТАРНЫХ ФУНКЦИЙ 2. Производная логарифмической функции. 3. Производные показательной и обратных тригонометрических функций. 4. Производная степенной функции. 5. Таблица производных простейших элементарных функций. 6. Таблица дифференциалов простейших элементарных функций. 7. Логарифмическая производная. Производная степенно-показательной функции. § 6. ПРОИЗВОДНЫЕ И ДИФФЕРЕНЦИАЛЫ ВЫСШИХ ПОРЯДКОВ 2. n-ые производные некоторых функций. 3. Формула Лейбница для n-й производной произведения двух функций. 4. Дифференциалы высших порядков. § 7. ДИФФЕРЕНЦИРОВАНИЕ ФУНКЦИИ, ЗАДАННОЙ ПАРАМЕТРИЧЕСКИ § 8. ПРОИЗВОДНАЯ ВЕКТОРНОЙ ФУНКЦИИ Глава 6. ОСНОВНЫЕ ТЕОРЕМЫ О ДИФФЕРЕНЦИРУЕМЫХ ФУНКЦИЯХ § 1. ВОЗРАСТАНИЕ (УБЫВАНИЕ) ФУНКЦИИ В ТОЧКЕ. ЛОКАЛЬНЫЙ ЭКСТРЕМУМ § 2. ТЕОРЕМА О НУЛЕ ПРОИЗВОДНОЙ § 3. ФОРМУЛА КОНЕЧНЫХ ПРИРАЩЕНИЙ (ФОРМУЛА ЛАГРАНЖА) § 4. НЕКОТОРЫЕ СЛЕДСТВИЯ ИЗ ФОРМУЛЫ ЛАГРАНЖА 2. Условия монотонности функции на интервале. 3. Отсутствие разрывов первого рода и устранимых разрывов у производной. 4. Вывод некоторых неравенств. § 5. ОБОБЩЕННАЯ ФОРМУЛА КОНЕЧНЫХ ПРИРАЩЕНИЙ (ФОРМУЛА КОШИ) § 6. РАСКРЫТИЕ НЕОПРЕДЕЛЕННОСТЕЙ (ПРАВИЛО ЛОПИТАЛЯ) 2. Раскрытие неопределенности вида oo/oo 3. Раскрытие неопределенностей других видов. § 7. ФОРМУЛА ТЕЙЛОРА § 8. РАЗЛИЧНЫЕ ФОРМЫ ОСТАТОЧНОГО ЧЛЕНА. ФОРМУЛА МАКЛОРЕНА 2. Другая запись формулы Тейлора. 3. Формула Маклорена. § 9. ОЦЕНКА ОСТАТОЧНОГО ЧЛЕНА. РАЗЛОЖЕНИЕ НЕКОТОРЫХ ЭЛЕМЕНТАРНЫХ ФУНКЦИЙ 2. Разложение по формуле Маклорена некоторых элементарных функций. § 10. ПРИМЕРЫ ПРИЛОЖЕНИЙ ФОРМУЛЫ МАКЛОРЕНА 2. Доказательство иррациональности числа е. 3. Вычисление значений тригонометрических функций. 4. Асимптотическая оценка элементарных функций и вычисление пределов. Глава 7. ИССЛЕДОВАНИЕ ГРАФИКА ФУНКЦИИ И ОТЫСКАНИЕ ЭКСТРЕМАЛЬНЫХ ЗНАЧЕНИИ § 1. ОТЫСКАНИЕ СТАЦИОНАРНЫХ ТОЧЕК 2. Отыскание стационарных точек. 3. Первое достаточное условие экстремума. 4. Второе достаточное условие экстремума. 5. Третье достаточное условие, экстремума. 6. Экстремум функции, недифференцируемой в данной точке. 7. Общая схема отыскания экстремумов. § 2. ВЫПУКЛОСТЬ ГРАФИКА ФУНКЦИИ § 3. ТОЧКИ ПЕРЕГИБА 2. Первое достаточное условие перегиба. 3. Некоторые обобщения первого достаточного условия перегиба. 4. Второе достаточное условие перегиба. 5. Третье достаточное условие перегиба. § 4. АСИМПТОТЫ ГРАФИКА ФУНКЦИИ § 6. ГЛОБАЛЬНЫЕ МАКСИМУМ И МИНИМУМ ФУНКЦИИ НА СЕГМЕНТЕ. КРАЕВОЙ ЭКСТРЕМУМ 2. Краевой экстремум. 3. Теорема Дарбу. ДОПОЛНЕНИЕ Алгоритм отыскания экстремальных значений функции, использующий только значения этой функции Глава 8. ПЕРВООБРАЗНАЯ ФУНКЦИЯ И НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ § 1. ПОНЯТИЕ ПЕРВООБРАЗНОЙ ФУНКЦИИ И НЕОПРЕДЕЛЕННОГО ИНТЕГРАЛА 2. Неопределенный интеграл. 3. Основные свойства неопределенного интеграла. 4. Таблица основных неопределенных интегралов. § 2. ОСНОВНЫЕ МЕТОДЫ ИНТЕГРИРОВАНИЯ 2. Интегрирование по частям. § 3. КЛАССЫ ФУНКЦИЙ, ИНТЕГРИРУЕМЫХ в ЭЛЕМЕНТАРНЫХ ФУНКЦИЯХ 2. Краткие сведения о корнях алгебраических многочленов. 3. Разложение алгебраического многочлена с вещественными коэффициентами на произведение неприводимых множителей. 4. Разложение правильной рациональной дроби на сумму простейших дробей. 5. Интегрируемость рациональной дроби в элементарных функциях. 6. Интегрируемость в элементарных функциях некоторых тригонометрических и иррациональных выражений. § 4. ЭЛЛИПТИЧЕСКИЕ ИНТЕГРАЛЫ Глава 9. ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ РИМАНА ИНТЕГРАЛ РИМАНА: § 2. ВЕРХНИЕ И НИЖНИЕ СУММЫ И ИХ СВОЙСТВА 2. Основные свойства верхних и нижних сумм. § 3. ТЕОРЕМЫ О НЕОБХОДИМЫХ И ДОСТАТОЧНЫХ УСЛОВИЯХ ИНТЕГРИРУЕМОСТИ ФУНКЦИЙ. КЛАССЫ ИНТЕГРИРУЕМЫХ ФУНКЦИЙ 2. Классы интегрируемых функций. § 4. СВОЙСТВА ОПРЕДЕЛЕННОГО ИНТЕГРАЛА. ОЦЕНКИ ИНТЕГРАЛОВ. ТЕОРЕМЫ О СРЕДНЕМ ЗНАЧЕНИИ 2. Оценки интегралов. § 5. ПЕРВООБРАЗНАЯ НЕПРЕРЫВНОЙ ФУНКЦИИ. ПРАВИЛА ИНТЕГРИРОВАНИЯ ФУНКЦИЙ 2. Основная формула интегрального исчисления. 3. Важные правила, позволяющие вычислять определенные интегралы. 4. Остаточный член формулы Тейлора в интегральной форме. § 6. НЕРАВЕНСТВА ДЛЯ СУММ И ИНТЕГРАЛОВ 2. Неравенство Гёльдера для сумм. 3. Неравенство Минковского для сумм. 4. Неравенство Гёльдера для интегралов. 5. Неравенство Минковского для интегралов. § 7. ДОПОЛНИТЕЛЬНЫЕ СВЕДЕНИЯ ОБ ОПРЕДЕЛЕННОМ ИНТЕГРАЛЕ РИМАНА 2. Критерий интегрируемости Лебега. ДОПОЛНЕНИЕ 1. НЕСОБСТВЕННЫЕ ИНТЕГРАЛЫ 2. Критерий Коши сходимости несобственного интеграла первого рода. 3. Абсолютная и условная сходимость несобственных интегралов. 4. Замена переменных под знаком несобственного интеграла и формула интегрирования по частям. § 2. Несобственные интегралы второго рода § 3. Главное значение несобственного интеграла ДОПОЛНЕНИЕ 2. Интеграл Стилтьеса 2. Свойства интеграла Стилтьеса. Глава 10. ГЕОМЕТРИЧЕСКИЕ ПРИЛОЖЕНИЯ ОПРЕДЕЛЕННОГО ИНТЕГРАЛА § 1. ДЛИНА ДУГИ КРИВОЙ 2. Понятие параметризуемой кривой. 3. Длина дуги кривой. Понятие спрямляемой кривой. 4. Критерий спрямляемости кривой. Вычисление длины дуги кривой. 5. Дифференциал дуги. 6. Примеры. § 2. ПЛОЩАДЬ ПЛОСКОЙ ФИГУРЫ 2. Площадь плоской фигуры. 3. Площадь криволинейной трапеции и криволинейного сектора. 4. Примеры вычисления площадей. § 3. ОБЪЕМ ТЕЛА В ПРОСТРАНСТВЕ 2. Некоторые классы кубируемых тел. 3. Примеры. Глава 11. m. 3. Предел функции m переменных. 4. Бесконечно малые функции m переменных. 5. Повторные пределы. § 3. НЕПРЕРЫВНОСТЬ ФУНКЦИИ m ПЕРЕМЕННЫХ 2. Непрерывность функции m переменных по одной переменной. 3. Основные свойства непрерывных функций нескольких переменных. § 4. ПРОИЗВОДНЫЕ И ДИФФЕРЕНЦИАЛЫ ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ 2. Дифференцируемость функции нескольких переменных. 3. Геометрический смысл условия дифференцируемости функции двух переменных. 4. Достаточные условия дифференцируемости. 5. Дифференциал функции нескольких переменных. 6. Дифференцирование сложной функции. 7. Инвариантность формы первого дифференциала. 8. Производная по направлению. Градиент. § 5. ЧАСТНЫЕ ПРОИЗВОДНЫЕ И ДИФФЕРЕНЦИАЛЫ ВЫСШИХ ПОРЯДКОВ 2. Дифференциалы высших порядков. 3. Формула Тейлора с остаточным членом в форме Лагранжа и в интегральной форме. 4. Формула Тейлора с остаточным членом в форме Пеано. § 6. ЛОКАЛЬНЫЙ ЭКСТРЕМУМ ФУНКЦИИ m ПЕРЕМЕННЫХ 2. Достаточные условия локального экстремума функции m переменных. 3. Случай функции двух переменных. ДОПОЛНЕНИЕ 1. Градиентный метод поиска экстремума сильно выпуклой функции 1. Выпуклые множества и выпуклые функции. 2. Существование минимума у сильно выпуклой функции и единственность минимума у строго выпуклой функции. 3. Поиск минимума сильно выпуклой функции. ДОПОЛНЕНИЕ 2. Метрические, нормированные пространства 2. Открытые и замкнутые множества. 3. Прямое произведение метрических пространств. 4. Всюду плотные и совершенные множества. 5. Сходимость. Непрерывные отображения. 6. Компактность. 7. Базис пространства. Топологические пространства Линейные нормированные пространства, линейные операторы ДОПОЛНЕНИЕ 3. Дифференциальное исчисление в линейных нормированных пространствах 2. Формула Лагранжа конечных приращений. 3. Связь между слабой и сильной дифференцируемостью. 4. Дифференцируемость функционалов. 5. Интеграл от абстрактных функций. 6. Формула Ньютона — Лейбница для абстрактных функций. 7. Производные второго порядка. 8. Отображение m-мерного евклидова пространства в n-мерное. 9. Производные и дифференциалы высших порядков. 10. Формула Тейлора для отображений одного нормированного пространства в другое. Исследование на экстремум функционалов в нормированных пространствах 2. Достаточные условия экстремума. Глава 13. НЕЯВНЫЕ ФУНКЦИИ § 1. СУЩЕСТВОВАНИЕ И ДИФФЕРЕНЦИРУЕМОСТЬ НЕЯВНО ЗАДАННОЙ ФУНКЦИИ 2. Вычисление частных производных неявно заданной функции. 3. Особые точки поверхности и плоской кривой. 4. Условия, обеспечивающие существование для функции y=f(x) обратной функции. § 2. НЕЯВНЫЕ ФУНКЦИИ, ОПРЕДЕЛЯЕМЫЕ СИСТЕМОЙ ФУНКЦИОНАЛЬНЫХ УРАВНЕНИЙ 2. Вычисление частных производных функций, неявно определяемых посредством системы функциональных уравнений. 3. Взаимно однозначное отображение двух множеств m-мерного пространства. § 3. ЗАВИСИМОСТЬ ФУНКЦИЙ 2. Функциональные матрицы и их приложения. § 4. УСЛОВНЫЙ ЭКСТРЕМУМ 2. Метод неопределенных множителей Лагранжа. 3. Достаточные условия. 4. Пример. ДОПОЛНЕНИЕ Отображения банаховых пространств. Аналог теоремы о неявной функции 2. Случай конечномерных пространств. 3. Особые точки поверхности в пространстве n измерений. Обратное отображение. 4. Условный экстремум в случае отображений нормированных пространств.

Доказательство второго замечательного предела и следствий

Приводится доказательство второго замечательного предела и его следствий.

Второй замечательный предел и его следствия

Второй замечательный предел – это предел, на основе которого вычисляются производные показательной функции и логарифма.

Лемма. Второй замечательный предел
.
Здесь x – действительное число.
Доказательство ⇓

Следствия второго замечательного предела
1)   ;
2)   ;     ;
3)   ;     ;
4)   ;     ;     ;     .
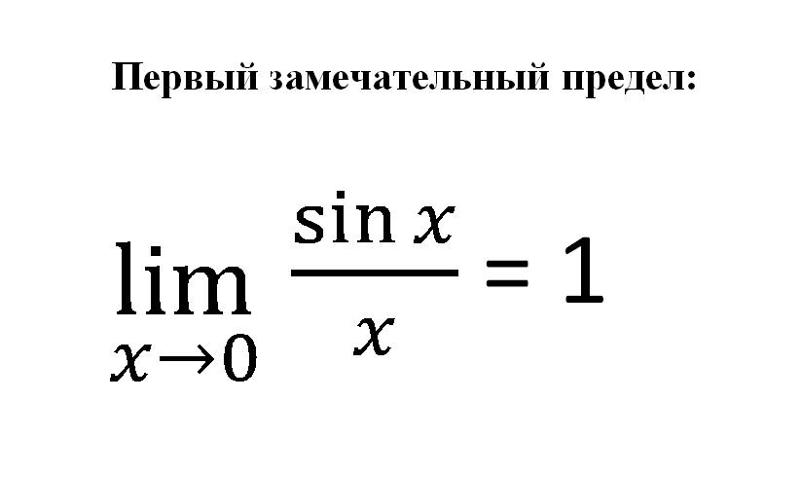
Доказательство ⇓

Доказательство второго замечательного предела

Формулировка ⇑

При доказательстве мы будем использовать тот факт, что последовательность строго возрастает и имеет конечный предел, равный числу e:   .
Доказательство приведено на странице «Число e – его смысл и доказательство сходимости последовательности».

Сначала рассмотрим правый предел
.
Для его существования должна существовать такая окрестность точки , на которой функция определена. В нашем случае, определена при . Но мы можем выбрать любую окрестность. Для удобства считаем, что .

Пусть – функция, которая означает, целую часть числа x. Например: . Она не убывает. Рассмотрим сложную функцию
.
Докажем, что она имеет предел при , равный числу e:   .

Поскольку последовательность строго возрастает, а функция не убывает, то сложная функция не убывает. Тогда по теореме о пределе монотонной функции, имеет конечный или бесконечный предел при :
.
Покажем, что . Для этого используем определение предела функции по Гейне, согласно которому, если функция имеет предел при :   , то для любой последовательности , сходящейся к , последовательность сходится к A:   . Возьмем последовательность . Она сходится к . Тогда . Но последовательность совпадает с :
.
Поэтому ее предел равен . Таким образом A = e:
(1)   .

Сделаем подстановку . Заметим, что . Заменив переменную t на x получим:
(2)   .

Теперь воспользуемся тем, что . Тогда

;
(3)   .
Далее замечаем, что
,   .
Применяем арифметические свойства предела функции и пределы (1) и (2):
;
.

Применяя к (3) теорему о промежуточной функции, получаем, что
.

Теперь рассмотрим левый предел
.
Считаем, что . Сделаем подстановку . Тогда . При .

.
Применяем арифметические свойства предела функции.

.

Поскольку существуют равные пределы справа и слева, то существует и двусторонний предел
.
Второй замечательный предел доказан.

Доказательство следствий второго замечательного предела

Формулировка ⇑

1) Докажем, что   .
Делаем замену переменной . Тогда   . При . Поэтому
.

Заметим, что фактически мы представили как сложную функцию   , где   . Далее мы применили теорему о пределе сложной функции.

Следствие 1) доказано.

2) Докажем, что   .
Выполняем преобразования, учитывая что показательная функция является обратной к логарифмической:
.

Делаем замену переменной   . В силу непрерывности показательной функции,
. Поскольку при , то

.
В предпоследнем равенстве мы воспользовались непрерывностью логарифмической функции и теоремой о пределе непрерывной функции от функции. В последнем равенстве мы применили следствие второго замечательного предела.

Также заметим, что применяя подстановку, мы представили функцию как сложную:
, где , и применили теорему о пределе сложной функции.

Применяем арифметические свойства предела функции:
.
Также здесь мы воспользовались свойством логарифма:   .

Полагая a = e, имеем:
.
Следствие 2) доказано.

3) Докажем, что .
Выполняем преобразования.
.
Функция определена при . Логарифм непрерывен на своей области определения. Применяем доказанное выше следствие 1 и теорему о пределе непрерывной функции от функции:
.
Также здесь мы воспользовались свойством логарифма:   .

Подставляя a = e, получаем:
.

4) Докажем, что .
Для этого воспользуемся определением гиперболического синуса и следствием 2) ⇑. Выполняем преобразования.

.

Докажем, что .
Для этого используем определения гиперболических функций и предыдущий предел.
;
.

Докажем, что .
Для этого сделаем замену переменной .
Тогда при ;   при ;
(см. «Обратные гиперболические функции, их графики и формулы»).
.

Докажем, что .
Сделаем замену переменной .
Тогда при ;   при ;
при (см. «Обратные гиперболические функции, их графики и формулы»).
.

Следствия доказаны.

Автор: Олег Одинцов.     Опубликовано: 30-03-2019   Изменено: 02-05-2019

Поиск пределов: определение, правила и функции

Подобно бусам на нитке, ведущей к подвеске, точки на графике могут привести вас к пределу функции. Как мы можем использовать точки на графике для оценки пределов? Хороший вопрос! Здесь мы рассмотрим некоторые из различных способов нахождения пределов функций!

Нахождение пределов в исчислении

Существует множество способов найти предел функции!

• Вы можете использовать определение предела \(\epsilon\), \(\delta\) и написать доказательство. См. Пределы функции для примеров этого метода.

• Вы можете посмотреть на график или таблицу значений, чтобы увидеть, каким может быть предел. См. Поиск пределов с помощью графика или таблицы для множества примеров нахождения пределов таким способом.

• Вы можете посмотреть на ограничение слева и справа функции и посмотреть, совпадают ли они. См. Односторонние ограничения для определений и примеров использования этого метода.

• Вы можете использовать законы пределов, которые являются уже доказанными теоремами для нахождения предела. Если ваша функция хороша, люди часто находят предел именно так. Для получения дополнительной информации о свойствах лимитов см. Законы лимитов 9.0003

• Вам может понадобиться использовать специальную теорему, чтобы найти предел, например, теорему сжатия или теорему о промежуточном значении. Оба они очень полезны, и теорема о промежуточном значении появится позже в таких темах, как нахождение максимального значения функции. См. «Теорему о сжатии» или см. «Теорему о промежуточном значении», чтобы узнать, как их использовать.

Здесь вы увидите пример способов нахождения предела функции.

Использование определения предела

Для просмотра определения предела функции см. Пределы функции.

Возьмем \(f(x)=k\), где \(a\) и \(k\) — постоянные действительные числа. Верно ли, что

\[lim_{x \rightarrow a} f(x)=k\]

Ответ:

Да. Используя определение, для любого \(\epsilon > 0\) вам дано

\[|f(x)-k|=|k-k|=0< \epsilon\]

независимо от того, что \(\delta \) ты используешь. Таким образом, константные функции имеют предел, которого вы от них ожидаете.

Возьмем \(f(x)=x\), и пусть \(a\) будет постоянным действительным числом. Откуда вы знаете, что

\[lim_{x \rightarrow a} f(x)=a\]

Ответ:

У вас может возникнуть соблазн сказать: «Конечно, предел равен \(a\) — функция — это просто строка». На самом деле этого почти достаточно. Вы не можете использовать какие-либо свойства пределов, но вы можете использовать определение и взять \(\delta = \epsilon\), чтобы показать, что предел равен \(a\).

Использование правил нахождения пределов 92+7\), а \(а\) — постоянное действительное число. Найдите

\[lim_{x \rightarrow a} f(x)\]

Ответ:

Обратите внимание, что функция представляет собой просто сумму и произведение степеней \(x\) вместе с константой \( 7\). Вы уже знаете, что

\(lim_{x \rightarrow a} x=a\) и \(lim_{x \rightarrow a} 7 =7\)

из двух приведенных выше примеров, что означает условия для применения Правило суммы, правило произведения и правило константы выполняются. Затем их применение дает 92+7\]

Нахождение пределов графически

Ниже приведен пример использования графика для нахождения предела функции. Дополнительные сведения о подобных проблемах см. в разделе Поиск пределов с помощью графика или таблицы.

Рассмотрим функцию

\[f(x)=\dfrac{1}{4}(x+1)(x-1)(x-5)\]

Найдите предел функции как \( х \стрелка вправо 3 \).

Ответ:

Сначала нарисуйте график функции и составьте таблицу значений рядом с \(x=3\). Хотя у функции больше корней, чем показано на графике, поскольку вас интересует только предел как \(x \стрелка вправо 3\), имеет смысл увеличить масштаб функции.

Использование графика с несколькими точками для нахождения предела функции, выделенной красным цветом.

3,0 504 1,0 09 2,0 377474 2,802

\(x\)	\(f(x)\)
2,5	-3,28
2,6	-3,46
2,65	-3,54
2,7	-3,62
2,75	-3,69
-3,76
2,85	-3,83
2,9	-3,89
2,95	4 — 9 0107
3,0	-4,0
3,05	-4,05
3,1	-4,09
3,15	-4,13
3,2	-4,16
-4,18
3,3	-4,20
3,35	-4,22
3,4	-4,22
3,45 4 — 90 0107

Таблица 1. Пример ограничения количества точек.

Точки на графике соответствуют точкам в таблице. Как на графике, так и в таблице видно, что по мере того, как \(x\) становится все ближе и ближе к \(x= 3\), значения функции все ближе и ближе к \(-4\). Это означает, что

\[ lim_{x \rightarrow 3} f(x)=-4\]

.

Обратите внимание, что при поиске предела значение функции в точке \(x=3\) на самом деле не интересует, потому что в определении говорится, что нужно смотреть близко к \(x=3\), но не к \(x=3 \).

Алгебраическое нахождение пределов

Другие примеры алгебраического нахождения пределов приведены в отдельной статье. См. раздел «Нахождение пределов конкретных функций».

На самом деле ограничения и непрерывность тоже идут рука об руку.

Если функция непрерывна в точке, то предел функции существует и равен значению функции в этой точке. 92-2x-8}{x-4}=\dfrac{(x-4)(x+2)}{x-4}=x+2\]

до тех пор, пока \(x \neq 4\) . Это означает, что график функции на самом деле представляет собой прямую линию \(y=x+2\) с отверстием в точке \((4, 6)\). Итак, \(lim_{x \rightarrow 4} f(x)=6\).

Нахождение производной с использованием определения предела

Использование определения производной требует ограничений. Это большая тема, и ей посвящена целая статья! См. нашу статью о производных, чтобы узнать больше о том, как найти производную с использованием предела.

Нахождение пределов — ключевые выводы

• Для любого многочлена \(f(x), lim_{x \rightarrow \infty} f(x)=f(a)\).
• Таблицу или график можно использовать для нахождения предела функции.
• Алгебраический поиск пределов может включать факторизацию числителя и знаменателя и проверку того, не сокращаются ли они. Это особенно полезно в тех случаях, когда в графике есть дыра.
• Свойства пределов также можно использовать для ограничения функций.

1: Пределы — Математика LibreTexts

1. Последнее обновление

2. Сохранить как PDF

Идентификатор страницы

4156

• Gregory Hartman et al.
• Военный институт Вирджинии

Исчисление означает «метод расчета или рассуждения». Когда кто-то вычисляет налог с продаж на покупку, он использует простое исчисление. Когда находят площадь многоугольника, разбивая его на набор треугольников, один использует другое исчисление Доказательство теоремы в геометрии использует еще одно исчисление Несмотря на замечательные успехи в математике, которые произошли в первой половине 17 ^-го века, математики и ученые хорошо знали, что 903:20 они не могли этого сделать. (Это верно и сегодня.) В частности, великие мыслители того времени ускользали от овладения двумя важными понятиями: площадь и скорость изменения.

• Район кажется достаточно безобидным; площади кругов, прямоугольников, параллелограммов и т. д. являются стандартными темами изучения для студентов сегодня, как и тогда. Однако площади 90 320 произвольных 90 321 фигур не могут быть вычислены, даже если границы формы можно точно описать.
• Темпы изменений также были важны. Когда объект движется с постоянной скоростью изменения, тогда «расстояние = скорость \(\×\) время». Но что, если скорость непостоянна — можно ли по-прежнему вычислять расстояние? мы обнаруживаем скорость изменения?

Оказывается, эти два понятия были связаны. Двум математикам, сэру Исааку Ньютону и Готфриду Лейбницу, приписывают независимую формулировку системы вычислений, которая решила вышеуказанные проблемы и показала, как они связаны. Их система рассуждений была «а-исчислением». Однако по мере того, как сила и важность их открытия приобретали все большее значение, оно стало известно многим как «а-исчисление». Сегодня мы обычно сокращаем это до обсуждения «исчисления». Основой «исчисления» является предел . Это инструмент для описания конкретного поведения функции. В этой главе мы начинаем изучение предела с аппроксимации его значения графически и численно. После формального определения предела устанавливаются свойства, делающие возможным «нахождение пределов». Как только предел понят, можно подойти к проблемам площади и скорости изменения.

• 1.1: Введение в пределы

  Основой «исчисления» является предел. Это инструмент для описания конкретного поведения функции. В этой главе наше изучение предела начинается с графической аппроксимации его значения. и численно После формального определения предела устанавливаются свойства, делающие «нахождение пределов» податливым. Когда предел понятен, можно приступать к проблемам площади и скорости изменения.

• 1.2: Эпсилон-Дельта Определение предела

  В этом разделе вводится формальное определение предела. Многие называют это определение «эпсилон-дельта», имея в виду буквы ϵ и δ греческого алфавита. В этом разделе приводится ряд теорем, которые позволяют нам находить пределы намного быстрее и интуитивно. Один из основных результатов этого раздела гласит, что многие функции, которые мы регулярно используем, ведут себя очень хорошим и предсказуемым образом. В следующем разделе мы даем название для этого приятного поведения; мы называем такие функции непрерывными. Определение этого термина потребует от нас еще раз взглянуть на то, что такое предел и что является причиной того, что пределов не существует.0296

• 1.4: Односторонние пределы

  В предыдущем разделе мы получили инструменты (которые мы называем теоремами), которые позволяют нам вычислять пределы с большей легкостью. Главными среди результатов были факты, что полиномы и рациональные, тригонометрические, экспоненциальные и логарифмические функции (и их суммы, произведения и т. д.) ведут себя «хорошо». В этом разделе мы строго определяем, что мы подразумеваем под «хорошо».

• 1.5: Непрерывность

  По мере того, как мы изучали пределы, мы получили интуицию, которая ограничивает меру, «куда движется функция». Мы видели, однако, что это не обязательно хороший индикатор того, чем на самом деле является функция.

  No related posts.