Сложение чисел с разными основаниями со степенями: Свойства степеней, действия со степенями

Умножение и деление степеней с одинаковыми основаниями

Учитель математики

МБОУ СОШ№ 18.

Гаджиева Сивда Бесировна

Проверка домашнего задания

№ 388 .

Решение:

а) –1 3 + (–2) 3 = –1 + (–8) = –9;

б) –6 2 – (–1) 4 = –36 – 1 = –37;

в) –8 3 + (–3) 3 = –512 + (–27) = –539;

г) 10 – 5 · 2 4 = 10 – 5 · 16 = 10 – 80 = –70;

Устная работа №1

Ответьте на вопросы:

• Что такое степень?
• Что такое степень?

Степенью числа а с натуральным показателем n , большим 1, называется выражение а п ,

равное произведению n множителей, каждый из которых равен а .

Степенью числа а с показателем 1 называется само число

а .

a 1 = a

Устная работа №1

2 . Чему равна степень отрицательного числа с четным показателем?

Степень отрицательного числа с четным показателем – положительное число .

5 4 = 5 · 5 · 5 · 5 = 625

3. Чему равна степень отрицательного числа с нечетным показателем?

Степень отрицательного числа с нечетным показателем – отрицательное число.

(−5) 4 = (−5) · (−5) · (−5) · (−5) = 625

Однако, −5 4 = −625

4

Устная работа №1

4.Что получится при возведении нуля в степень с натуральным показателем?

При возведении в степень с натуральным показателем нуля получается нуль.

0 n = 0 ,

где n -натуральное число

5

Устная работа №2

9

— 49

1) 3² = 5) – ( — 7)²=

2) = 6) – (- 2)³ =

3) (–0,1) 4 = 7) 0 16 =

4) = 8) (–1) 18 =

6,25

8

0,0001

0

— 1,8

1

Работа в парах

Вычислите:

1000000

8

256

81

— 1

4

19683

32

?

?

Тема урока:

Умножение и деление степеней с одинаковыми основаниями.

Цели урока:

• вывести правила умножения и деления степеней с одинаковыми основаниями;
• научиться применять правила деления степеней с одинаковыми основаниями;
• научиться возводить число в степень с нулевым показателем.

Шаблон для создания презентаций к урокам математики. Савченко Е.М.

8

Новые сведения

Свойство 1. При умножении степеней с одинаковыми основаниями основание оставляют прежним, а показатели степеней складывают.

Свойство 2. При делении степеней с одинаковыми основаниями, основание оставляют прежним, а из показателя степени делимого вычитают показатель степени делителя.

Шаблон для создания презентаций к урокам математики. Савченко Е.М.

Новые сведения

Определение . Степень числа а , не равного нулю, с нулевым показателем равна единице.

где а≠0

a 0 = 1,

Шаблон для создания презентаций к урокам математики. Савченко Е.М.

Повторение

Задача

Определить во сколько раз масса земного шара больше массы всего окружающего его воздуха.

Повторение

Решение. На каждый 1 см² земной поверхности воздух давит, с силой около килограмма.

Величина поверхности земного шара равна:

510 000 000 км²=51· 10 7  км²; 1 км²= (100 000см)²;

51 · 10 7 · 10 10 см²= 51·10 17 см².

Масса атмосферы Земли:

51·10 17 кг=51·10 17 : 1000 т =51·10 17 : 10³ т = 51·10 14 т

Масса земного шара выражается числом:

6· 10 21 т

Узнаем во сколько раз масса нашей планеты тяжелее ее воздушной оболочки:

6·10 21 : 51 · 10 14 ≈ 10 6

Ответ: ≈ 1 000 000

Домашнее задание

П.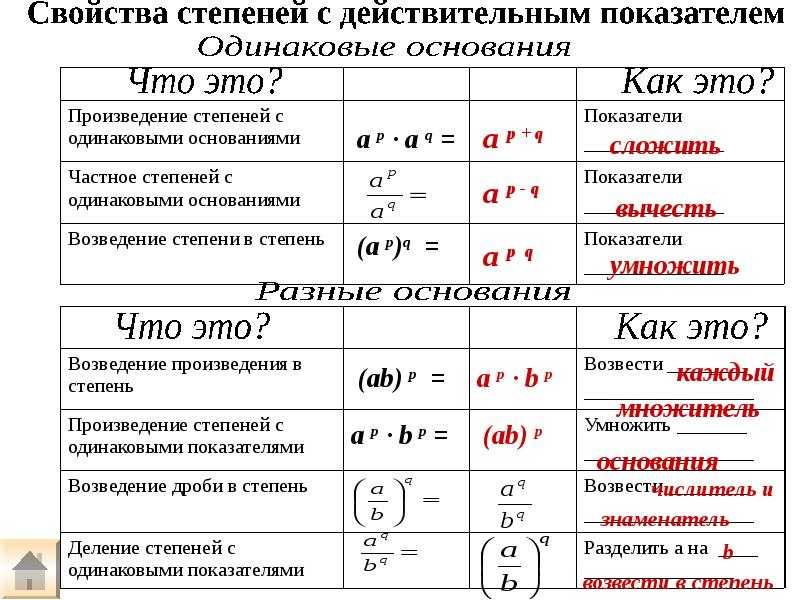 16 выучить правила.

Решить задания:

I уровень: №404, 408, 415, 418;

II уровень: №406, 412, 419 (б,г,е), 533.

Дополнительное задание:

Выразить массу Земли и Луны в различных единицах массы (в граммах, килограммах, в центнерах и тоннах)

13

Источники информации

• Алгебра. 7 класс: учеб. для общеобразоват. организаций / Ю.Н.Макарычев, Н.Г.Миндюк, К.И.Нешкова, С.Б.Суворова; под ред. С.А.Теляковского.- М.: Просвещение, 2014
• Алгебра. 7 класс: поурочные планы по учебнику Ю.Н.Макарычева, Н.Г.Миндюк, К.И.Нешкова, С.Б.Суворовой/авт.-сост. Т.Ю.Дюмина, А.А.Махонина. – Волгоград: Учитель, 2011
• Статья «Сколько вести воздух?» http://mathemlib.ru/books/item/f00/s00/z0000003/st004.shtml
• Шаблон для презентации Савенко Е.М.: http://pedsovet.su/load/412-1-0-13709
• Изображение земного шара : http://t-z-n.ru/preokean/photo/intok2. jpg
• Изображение восклицательного знака: http://svg12.edu.27.ru/files/uploads/images/_kniga_dlya_roditelya_2yq14j77a5v3hgenubrgne.jpg

2.6: Сложение и вычитание с другими основаниями

1. Последнее обновление

2. Сохранить как PDF

Идентификатор страницы

59936

• Дарлин Диаз
• Колледж Сантьяго-Каньон через Инициативу открытых образовательных ресурсов ASCCC

Сложение в других системах счисления

Как мы видели в предыдущем разделе о системе счисления майя, мы можем складывать или вычитать в других системах счисления. Ниже приведен ряд шагов, но в целом мы складываем как обычно, находя его эквивалентное число от основания 10 до нового основания.

Добавление в базу

b

1. Перепишите добавление по вертикали, если это еще не сделано.
2. Начните с разряда единиц (как обычно), но найдите число, которое представляет сумма по основанию 9.0036 б .
3. Если сумма больше, чем основание b, то b ¹ разрядное значение.
4. Повторите шаги 2 и 3 для b ² , b ³ , … разрядных значений.

Пример \(\PageIndex{1}\)

Добавьте к основанию два: 111 _два + 11 _два

Решение

Записав это вертикально, мы получим

\( t wo) 111_

\(\\ + \underline{11_{два}} \) 9{+1}11_{два} \)

\( + \underline{\;\;\;11_{два}} \)

\( 0 \;\;\; 10_{два} \)

Прибавив к 2 ² место, мы получим 1+1=2 по основанию 10, но 2 по основанию 10 равно 0 по основанию 2, и мы перенесем 1 на место 2 ³ :

\( +1\;1\;11_{два} \)

\( + \underline{\;\;\;\;\;11_{два}} \)

\( 1 \;\;\ ;010_{два} \)

Следовательно, 111 _два + 11 _два = 1010 _два . Обратите внимание, что еще один способ сделать это — преобразовать каждое число в основание 10 и добавить, как обычно, а затем преобразовать результат обратно в основание 2.

Пример \(\PageIndex{2}\)

Добавьте по основанию пять: 44 _пять + 42 _пять

Решение

Давайте попробуем это, преобразовав каждое число в основание 10, сложив их, а затем преобразовав суммируем по основанию 5:

44 _пять = 4(5) + 4(1) = 24 _десять

42 _пять = 4(5) + 2(1) = 22 _десять

4 Затем мы складываем числа с основанием 10:

24 + 22 = 46 _десять

Преобразуя 46 по основанию 10 в число по основанию 5, мы используем технику предыдущих разделов и получаем 141 _пять . Таким образом, 46 по основанию 10 эквивалентно 141 по основанию 5.

Вычитание по другим основаниям

Вычитание по основанию

b

Перепишите вычитание по вертикали, если это еще не сделано.

Начните с разряда единиц (как обычно), но найдите число, которое представляет разность в базе b .

Если разряд единиц уменьшаемого меньше разряда единиц вычитаемого, то заимствовать из разряда слева в этом основании б . Затем вычтите, как обычно.

Повторите шаги 2 и 3 для b ² , b ³ разрядных значений.

Пример \(\PageIndex{3}\)

Вычесть по основанию 5: 240 _пять — 40 _пять

Решение

\( 240_{пять} \)

{пять}} \)

Если взять разряд единиц, 0-0 = 0, что равно 0 по основанию 5, то разряд единиц останется равным 0.

\( 240_{пять} \)

\(- \underline{40_{пять}} \)

\( 0\)

Теперь займем место 5: 4-4=0. Так как 0 находится в базе 5, то пятерка занимает 0 место. Давайте посмотрим на место 5 ² . Обратите внимание, мы можем просто опустить два и получить

\( 240_{пять} \)

\(- \underline{40_{пять}} \)

\( 200_{5}\;\;\)

Итак, 240 _пять — 40 _пять = 200 _пять .

Что, если нам придется занять? Мы можем легко вычитать с заимствованием по основанию 10, но что, если мы хотим вычесть два числа, включающие заимствование? Давайте посмотрим.

Пример \(\PageIndex{4}\)

Вычесть по основанию 5: 404 _пять — 323 _пять

Решение

Переписав это по вертикали, мы получим

\0 4 \(пять)

\(- \underline{323_{пять}} \)

Вычитая единицы, получаем 4-3=1. Поскольку 1 находится в базе 5, то разряд единиц равен 1. 95 4_{пять} \)

\(- \underline{3\;2\;3_{пять}} \)

\( 0\;3\;1_{пять}\)

Теперь вычитаем как обычно: 5-2 = 3. Так как 3 находится в базе 5, то 5-й разряд равен 3. Вычитая 5 ² разряда, мы получаем 3-3=0; следовательно, место 5 ² равно 0.

Таким образом, 404 _пять — 323 _пять = 31 _пять .

Заключение

В этой главе мы кратко обрисовали развитие чисел и нашей системы счета, уделив особое внимание «краткой» части. Существует множество источников информации и исследований, которые заполняют многие тома книг по этой теме. К сожалению, мы не можем приблизиться к тому, чтобы охватить всю имеющуюся информацию.

Мы коснулись лишь поверхностной части огромного количества исследований и информации о развитии чисел и счета на протяжении всей истории человечества. Важно отметить, что система, которую мы используем каждый день, является продуктом тысячелетнего прогресса и развития. Он представляет собой вклад многих цивилизаций и культур. Оно не с неба спускается к нам, подарок богов. Это не создание издателя учебников. Она действительно такая же человеческая, как и мы, как и вся остальная математика. За каждым символом, формулой и правилом стоит искать или, по крайней мере, искать человеческое лицо.

Кроме того, мы надеемся, что теперь вы понимаете, насколько интересными и разнообразными могут быть системы счисления. Кроме того, мы почти уверены, что вы также начали осознавать, что мы воспринимаем нашу собственную систему счисления как нечто само собой разумеющееся настолько, что, когда мы пытаемся приспособиться к другим системам или системам счисления, нам действительно приходится концентрироваться и думать о том, что происходит. на.

Попробуйте сейчас Ответы

1. 1+6×3+3×6+2×12 = 61 кошка.

2. Слева направо:

Cord 1 = 2,162

Cord 2 = 301

Cord 3 = 0

Cord 4 = 2,070

3. 41065 ₇ = 9994 ₁₀

4. 143 ₁₀ = 1033 ₅

5. 21021 ₃ = 196 ₁₀

6. 657 ₁₀ = 22101 ₄

7. 8377 ₁₀ = 20271 ₈

8. 9352

10 = 244402 ₅

9. 1500 ₁₀ = 2001120 ₃

10. 1562

11. 10553 ₁₀ = 1,6,7,13 ₂₀

12. 5617 ₁₀ = 14,0,0,0,17 _{66667. Обратите внимание, что на месте 20 стоит ноль, поэтому вам нужно будет использовать соответствующий символ нуля между разрядами единиц и 400.}

13. Показан образец раствора.

---

Эта страница под названием 2. 6: Сложение и вычитание с другими базами распространяется в соответствии с лицензией CC BY-NC-SA 4.0 и была создана, изменена и/или курирована Дарлин Диаз (Инициатива открытых образовательных ресурсов ASCCC) с использованием исходного контента, который был отредактировано в соответствии со стилем и стандартами платформы LibreTexts; подробная история редактирования доступна по запросу.

1. Наверх
• Была ли эта статья полезной?

1. Тип изделия

   Раздел или Страница

   Автор

   Дарлин Диаз

   Лицензия

   CC BY-NC-SA

   Версия лицензии

   4,0

   Показать страницу TOC

   нет

2. Теги

   1. source@https://www.
      sccollege.edu/OER/Documents/MATH 105/Математика для студентов, изучающих гуманитарные науки (2017).pdf
   2. вычитание по основанию b

Различные базы

Мы склонны думать, что совершенно естественно использовать 10 символы для записи чисел: 0 , 1 , 2 , 3 , 4 , 5 , 6 , 7 , 8 , 9 . Но единственная причина, по которой мы это делаем, заключается в том, что мы растем, считая на пальцах, которых у нас, оказывается, десять. Нет никакой реальной причины, почему десять лучше для математики, чем другое число, скажем 2 , 5 , 12 или 16 .

С одной цифрой мы можем считать до 9 . Затем мы используем

место значение писать большие числа. » 10 » означает один десяток и ноль единиц. Число 5723 действительно сокращение для:

5723 «=» ( 5 × 1000 ) + ( 7 × 100 ) + ( 2 × 10 ) + ( 3 × 1 )

Места обозначают тысячи, сотни, десятки и единицы. Обратите внимание, что это все полномочия 10 :

5723 «=» ( 5 × 10 3 ) + ( 7 × 10 2 ) + ( 2 × 10 1 ) + ( 3 × 10 0 )

Что, если бы мы ограничились только тремя цифрами, 0 , 1 , и 2 , и использовали мощности 3 вместо полномочий 10 как значения места? Ниже мы считаем до 27 в базе 3 .

БАЗА 3	БАЗА 10
1	1
2	2
10	3
11	4
12	5
20	6
21	7
22	8
100	9
101	10
102	11
110	12
111	13
112	14
120	15
121	16
122	17
200	18
201	19
202	20
210	21
211	22
212	23
220	24
221	25
222	26
1000	27

Обратите внимание, что вместо разрядов «десятки», «сотни» и «тысячи» в левой колонке стоят разряды «тройки», «девятки» и «двадцать семь».

Это может показаться немного странным, но в base можно так же хорошо заниматься математикой. 3 как в базе 10 или любая другая база. Для иллюстрации решим задачу на сложение (в базе 3 слева, база 10 справа). Обратите внимание, что мы должны переносить, когда добавляем 1 + 2 !

1 1 0 1 + 1 2 _ 1 2 0 1 0 + 5 _ 1 5

Исторически так сложилось, что в большинстве, но не во всех культурах использовалась базовая 10 . Индейцы Юки в Калифорнии использовали базу 8 , потому что они считали промежутки между пальцами, а не сами пальцы. Вавилоняне использовали базу 60 , а майя использовали смесь базовых 20 и 18 . Какая-то старая база 20 терминология проникла даже во французский и английский языки. Французы говорят «soixante et onze» для 71 , что буквально означает «три двадцатки и одиннадцать». Геттисбергская речь президента США Авраама Линкольна начиналась словами «Четыре десятка и семь», что означает 87 .

Наконец, в наше время база 2 ( бинарный ) и основание 16 ( шестнадцатеричный ) часто используются в информатике. (Если вы когда-либо играли с созданием веб-страницы, вы, возможно, знаете, что HTML использует 16 -цифровой шестнадцатеричный код для указания цвета. 16 цифры 0 , 1 , 2 , 3 , 4 , 5 , 6 , 7 , 8 , 9, А , Б , С , Д , Е , Ф .

No related posts.