Сложение и умножение графиков функций с объяснением: Сложение графиков функций

Сложение графиков функций

СЛОЖЕНИЕ ГРАФИКОВ

Иногда функция, график которой должен быть построен, представляется как сумма двух или нескольких простейших функций. Графики простейших функций уже известны и без труда могут быть построены. В этом случае, рассмотрим способ сложения графиков.

Алгоритм. 1) Строим графики функций каждого слагаемого

2) Ординаты второго графика откладывают от соответствующих

ординат первого графика (можно пользоваться измерительным

циркулем).

Пример 1. Построить график функции

Представим эту функцию в виде суммы двух функций: , где

. На одной системе координат строим графики этих функций.

Затем, каждую точку графика функции смещаем параллельно оси Оу на расстояние, равное ординате графика функции в соответствующей абсциссе. То есть, при ордината графика функции равна 2, а ордината графика функции равна 0, поэтому ставим точку . Далее, при ордината графика функции равна 0, а ордината графика функции равна 1, поэтому ставим точку . При ордината графика функции равна -2, а ордината графика функции равна 8, поэтому ставим точку . При ордината графика функции равна 4, а ордината графика функции равна -1, поэтому ставим точку . И так далее. Получаем график функции

Для того, чтобы график был как можно точнее, необходимо брать значимые точки, т.е. те, в которых происходит значимое событие для графика (пересечение с осями, точки перегиба, или точки, в которых график меняет своё направление).

Определим свойства функции

1. Область определения:

2. Область значений:

3. Чётность функции:

Значит, функция не является ни чётной, ни нечётной и её график не обладает симметрией ни относительно оси Оу, ни относительно начала координат.

1. Точка пересечения с осью Оу:

2. Найдём точки экстремума:

.

.

1. Найдём экстремумы функции:

.

.

1. Функция возрастает при .

Функция убывает при .

Пример 2. Построить график функции

Представим эту функцию в виде суммы двух функций: , где

. На одной системе координат строим графики этих функций.

Производим аналогичные действия:

И так далее…

Получаем график функции .

Определим свойства функции

1. Область определения:

2. Область значений:

3. Чётность функции:

Значит, функция не является ни чётной, ни нечётной и её график не обладает симметрией ни относительно оси Оу, ни относительно начала координат.

1. Точка пересечения с осью Оу:

Точки пересечения с осью Ох:

Значит, точки пересечения с осью Ох —

1. Найдём точки экстремума:

. .

1. Найдём экстремумы функции:

.

1. Функция убывает при .Функция возрастает при .

Пример 3. Построить график функции

Представим эту функцию в виде суммы двух функций: , где

. На одной системе координат строим графики этих функций. Затем производим сложение.

Определим свойства функции

1. Область определения:

2. Область значений:

3. Чётность функции: Значит, функция является чётной, и её график симметричен относительно оси Оу.

4. Точка пересечения с осью Оу:

Точки пересечения с осью Ох:

Значит, точки пересечения с осью Ох —

1. Найдём точки экстремума:

. .

1. Найдём экстремумы функции:

.

1. Функция возрастает при .

Функция убывает при .

Пример 4. Построить график функции

Представим эту функцию в виде суммы двух функций: , где

. На одной системе координат строим графики этих функций. Затем производим сложение.

Аналогичные вычисления для отрицательного аргумента. Получаем график функции

Определим свойства функции

1. Область определения:

2. Область значений:

3. Чётность функции: Значит, функция не является ни чётной, ни нечётной, и её график не обладает симметрией ни относительно оси Оу, ни относительно начала координат.

4. Точка пересечения с осью Оу:

Точки пересечения с осью Ох:

. Значит, точки пересечения с осью Ох —

1. Найдём точки экстремума:

. .

1. Найдём экстремумы функции:

.

1. Функция возрастает при .

Функция убывает при .

Особый случай представляется при сочетании обратной пропорциональности с каким-нибудь другим графиком. Приведём такой пример.

Пример 5. Построить график функции

Представим эту функцию в виде суммы двух функций: , где

. На одной системе координат строим графики этих функций.

Что происходит? Так как график обратной пропорциональности не пересекает оси координат, то он и будет исходным. К его ординатам будем прибавлять ординаты графика функции .

График функции-суммы при значениях х, бесконечно близких к 0, практически сливается с графиком функции , располагаясь чуть выше его. А при очень больших значениях график функции-суммы почти сливается с графиком , располагаясь чуть выше его при положительных х, и чуть ниже при отрицательных х.

Определим свойства функции

1. Область определения:

2. Область значений:

3. Чётность функции:

Значит, функция не является ни чётной, ни нечётной, и её график не обладает симметрией ни относительно оси Оу, ни относительно начала координат.

1. Точек пересечения с осью Оу нет.

Точки пересечения с осью Ох:

Значит, точка пересечения с осью Ох

1. Найдём точки экстремума:

;

Найдём экстремумы функции:

.

1. Функция возрастает при .

Функция убывает при .

4

Как складывать графики

Сложение графиков функций

В разработке представлен способ сложения графиков функций и примеры с подробным объяснением.

Просмотр содержимого документа
«Сложение графиков функций»

СЛОЖЕНИЕ ГРАФИКОВ

Иногда функция, график которой должен быть построен, представляется как сумма двух или нескольких простейших функций. Графики простейших функций уже известны и без труда могут быть построены. В этом случае, рассмотрим способ сложения графиков.

Алгоритм. 1) Строим графики функций каждого слагаемого

2) Ординаты второго графика откладывают от соответствующих

ординат первого графика (можно пользоваться измерительным

Пример 1. Построить график функции

Представим эту функцию в виде суммы двух функций: , где

. На одной системе координат строим графики этих функций.

Затем, каждую точку графика функции смещаем параллельно оси Оу на расстояние, равное ординате графика функции в соответствующей абсциссе. То есть, при ордината графика функции равна 2, а ордината графика функции равна 0, поэтому ставим точку . Далее, при ордината графика функции равна 0, а ордината графика функции равна 1, поэтому ставим точку . При ордината графика функции равна -2, а ордината графика функции равна 8, поэтому ставим точку . При ордината графика функции равна 4, а ордината графика функции равна -1, поэтому ставим точку . И так далее. Получаем график функции

Для того, чтобы график был как можно точнее, необходимо брать значимые точки, т.е. те, в которых происходит значимое событие для графика (пересечение с осями, точки перегиба, или точки, в которых график меняет своё направление).

Определим свойства функции

Область определения:

Область значений:

Чётность функции:

Значит, функция не является ни чётной, ни нечётной и её график не обладает симметрией ни относительно оси Оу, ни относительно начала координат.

Точка пересечения с осью Оу:

Найдём точки экстремума:

Найдём экстремумы функции:

Функция возрастает при .

Функция убывает при .

Пример 2. Построить график функции

Представим эту функцию в виде суммы двух функций: , где

. На одной системе координат строим графики этих функций.

Производим аналогичные действия:

И так далее…

Получаем график функции .

Определим свойства функции

Область определения:

Область значений:

Чётность функции:

Значит, функция не является ни чётной, ни нечётной и её график не обладает симметрией ни относительно оси Оу, ни относительно начала координат.

Точка пересечения с осью Оу:

Точки пересечения с осью Ох:

Значит, точки пересечения с осью Ох —

Найдём точки экстремума:

Найдём экстремумы функции:

Функция убывает при .Функция возрастает при .

Пример 3. Построить график функции

Представим эту функцию в виде суммы двух функций: , где

. На одной системе координат строим графики этих функций. Затем производим сложение.

Определим свойства функции

Область определения:

Область значений:

Чётность функции: Значит, функция является чётной, и её график симметричен относительно оси Оу.

Точка пересечения с осью Оу:

Точки пересечения с осью Ох:

Значит, точки пересечения с осью Ох —

Найдём точки экстремума:

Найдём экстремумы функции:

Функция возрастает при .

Функция убывает при .

Пример 4. Построить график функции

Представим эту функцию в виде суммы двух функций: , где

. На одной системе координат строим графики этих функций. Затем производим сложение.

Аналогичные вычисления для отрицательного аргумента. Получаем график функции

Определим свойства функции

Область определения:

Область значений:

Чётность функции: Значит, функция не является ни чётной, ни нечётной, и её график не обладает симметрией ни относительно оси Оу, ни относительно начала координат.

Точка пересечения с осью Оу:

Точки пересечения с осью Ох:

. Значит, точки пересечения с осью Ох —

Найдём точки экстремума:

Найдём экстремумы функции:

Функция возрастает при .

Функция убывает при .

Особый случай представляется при сочетании обратной пропорциональности с каким-нибудь другим графиком. Приведём такой пример.

Пример 5. Построить график функции

Представим эту функцию в виде суммы двух функций: , где

. На одной системе координат строим графики этих функций.

Что происходит? Так как график обратной пропорциональности не пересекает оси координат, то он и будет исходным. К его ординатам будем прибавлять ординаты графика функции .

График функции-суммы при значениях х, бесконечно близких к 0, практически сливается с графиком функции , располагаясь чуть выше его. А при очень больших значениях график функции-суммы почти сливается с графиком , располагаясь чуть выше его при положительных х, и чуть ниже при отрицательных х.

Определим свойства функции

Область определения:

Область значений:

Чётность функции:

Значит, функция не является ни чётной, ни нечётной, и её график не обладает симметрией ни относительно оси Оу, ни относительно начала координат.

Способ сложения графиков функций

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

СЛОЖЕНИЕ ГРАФИКОВ

Иногда функция, график которой должен быть построен, представляется как сумма двух или нескольких простейших функций. Графики простейших функций уже известны и без труда могут быть построены. В этом случае, рассмотрим способ сложения графиков.

Алгоритм. 1) Строим графики функций каждого слагаемого

2) Ординаты второго графика откладывают от соответствующих

ординат первого графика (можно пользоваться измерительным

Пример 1. Построить график функции

Представим эту функцию в виде суммы двух функций: , где

. На одной системе координат строим графики этих функций.

Затем, каждую точку графика функции смещаем параллельно оси Оу на расстояние, равное ординате графика функции в соответствующей абсциссе. То есть, при ордината графика функции равна 2, а ордината графика функции равна 0, поэтому ставим точку . Далее, при ордината графика функции равна 0, а ордината графика функции равна 1, поэтому ставим точку . При ордината графика функции равна -2, а ордината графика функции равна 8, поэтому ставим точку . При ордината графика функции равна 4, а ордината графика функции равна -1, поэтому ставим точку . И так далее. Получаем график функции

Для того, чтобы график был как можно точнее, необходимо брать значимые точки, т.е. те, в которых происходит значимое событие для графика (пересечение с осями, точки перегиба, или точки, в которых график меняет своё направление).

Определим свойства функции

Область определения:

Область значений:

Чётность функции:

Значит, функция не является ни чётной, ни нечётной и её график не обладает симметрией ни относительно оси Оу, ни относительно начала координат.

Точка пересечения с осью Оу:

Найдём точки экстремума:

Найдём экстремумы функции:

Функция возрастает при .

Функция убывает при .

Пример 2. Построить график функции

Представим эту функцию в виде суммы двух функций: , где

. На одной системе координат строим графики этих функций.

Производим аналогичные действия:

И так далее…

Получаем график функции .

Определим свойства функции

Область определения:

Область значений:

Чётность функции:

Значит, функция не является ни чётной, ни нечётной и её график не обладает симметрией ни относительно оси Оу, ни относительно начала координат.

Точка пересечения с осью Оу:

Точки пересечения с осью Ох:

Значит, точки пересечения с осью Ох —

Найдём точки экстремума:

Найдём экстремумы функции:

Функция убывает при . Функция возрастает при .

Пример 3. Построить график функции

Представим эту функцию в виде суммы двух функций: , где

. На одной системе координат строим графики этих функций. Затем производим сложение.

Определим свойства функции

Область определения:

Область значений:

Чётность функции: Значит, функция является чётной, и её график симметричен относительно оси Оу.

Точка пересечения с осью Оу:

Точки пересечения с осью Ох:

Значит, точки пересечения с осью Ох —

Найдём точки экстремума:

Найдём экстремумы функции:

Функция возрастает при .

Функция убывает при .

Пример 4. Построить график функции

Представим эту функцию в виде суммы двух функций: , где

. На одной системе координат строим графики этих функций.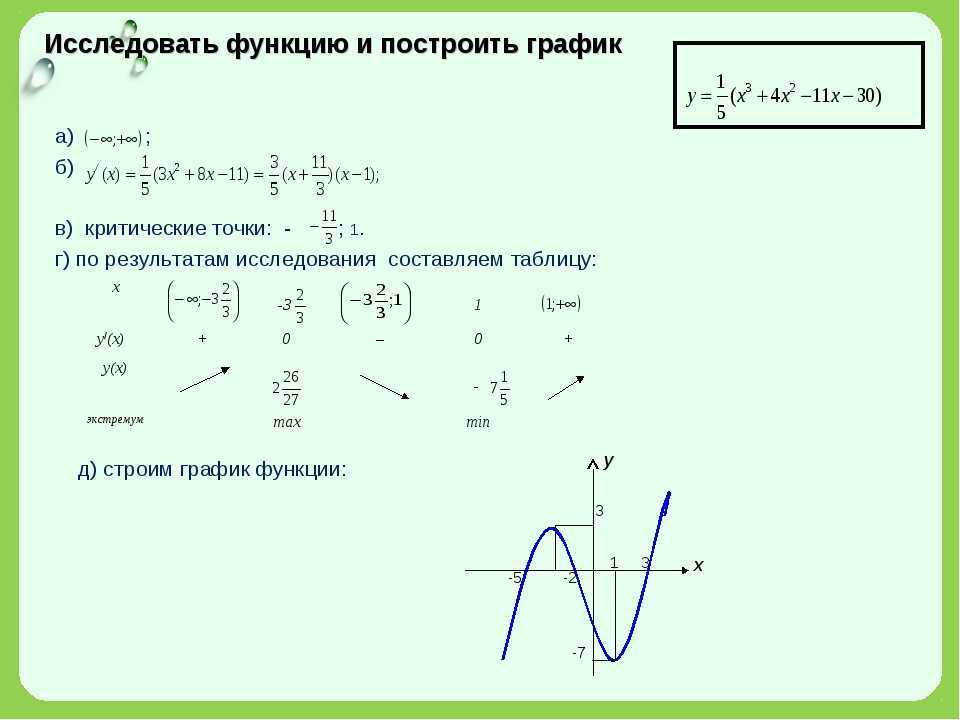 Затем производим сложение.

Аналогичные вычисления для отрицательного аргумента. Получаем график функции

Определим свойства функции

Область определения:

Область значений:

Чётность функции: Значит, функция не является ни чётной, ни нечётной, и её график не обладает симметрией ни относительно оси Оу, ни относительно начала координат.

Точка пересечения с осью Оу:

Точки пересечения с осью Ох:

. Значит, точки пересечения с осью Ох —

Найдём точки экстремума:

Найдём экстремумы функции:

Функция возрастает при .

Функция убывает при .

Особый случай представляется при сочетании обратной пропорциональности с каким-нибудь другим графиком. Приведём такой пример.

Пример 5. Построить график функции

Представим эту функцию в виде суммы двух функций: , где

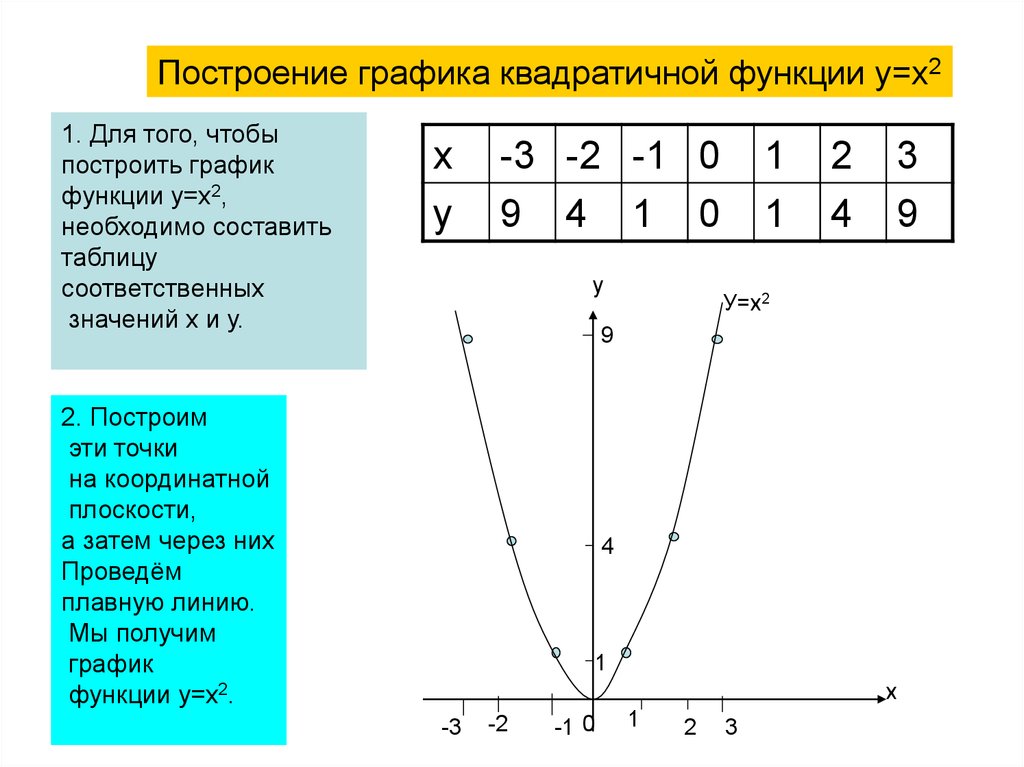. На одной системе координат строим графики этих функций.

Что происходит? Так как график обратной пропорциональности не пересекает оси координат, то он и будет исходным. К его ординатам будем прибавлять ординаты графика функции .

График функции-суммы при значениях х, бесконечно близких к 0, практически сливается с графиком функции , располагаясь чуть выше его. А при очень больших значениях график функции-суммы почти сливается с графиком , располагаясь чуть выше его при положительных х, и чуть ниже при отрицательных х.

Определим свойства функции

Область определения:

Область значений:

Чётность функции:

Значит, функция не является ни чётной, ни нечётной, и её график не обладает симметрией ни относительно оси Оу, ни относительно начала координат.

7.5 Рыночная кривая спроса. Сложение индивидуальных кривых спроса

Мы определили, что количество потребителей положительно влияет на рыночный спрос. При увеличении количества потребителей на рынке спрос при каждом уровне цены растет. В соответствии с этим утверждением и производится сложение отдельных индивидуальных кривых спроса для получения общей рыночной кривой спроса: при каждом возможном уровне цены необходимо сложить величины индивидуальных спросов отдельных потребителей. Этот принцип называется «правило сложения по горизонтали». Данное правило существует для того, чтобы подчеркнуть, что сложению подвергаются именно величины индивидуальных спросов. Данное правило гласит, что складывать индивидуальные кривые спроса следует вправо, то есть по оси Q. Именно поэтому суммарная кривая рыночного спроса по сравнению с индивидуальными кривыми имеет более пологий вид: она как бы «растягивается» по оси Q. Сложение кривых спроса следует выполнять, начиная с максимально возможного значения цены блага, постепенно переходя к минимальной, то есть нулевой. Это обусловлено тем, что цена спроса – это максимальная цена, которую потребитель готов заплатить за товар.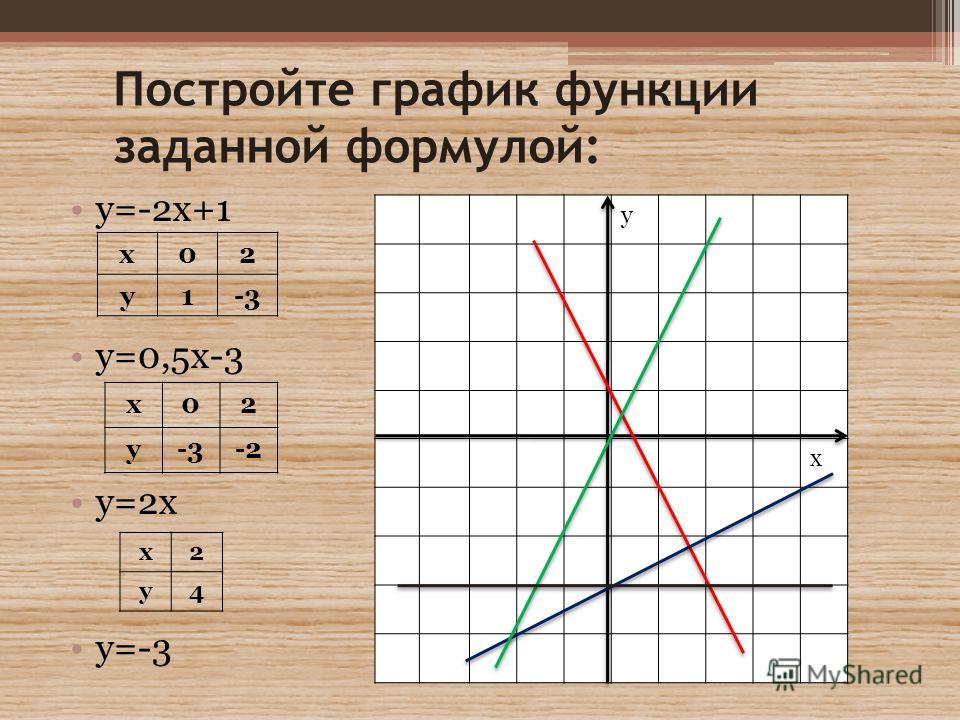

Пример горизонтального сложения спроса

Для того, чтобы найти уравнение общего спроса, необходимо воспользоваться алгоритмом «сложения индивидуальных спросов на интервалах». Поясним на примере, что это такое.
В примере выше нам даны две прямых индивидуального спроса

Требуется определить уравнение общего спроса.

Вначале найдем интервалы цены для каждого спроса

Данные значения цен разбивают ось цены на следующие интервалы:

Рассмотрим отдельно каждый интервал цены

P ∈ [0;25] в этом интервале существуют оба спроса, поэтому Q_общий = Q₁ + Q₂

P ∈ [25;50] в этом интервале существует только Q₁, поэтому Q_общий = Q₁

P > 50 в этом интервале не существует ни одного спроса, поэтому Q_общий = 0

Рассмотрим частные случаи сложения функций спроса:

Один из спросов является горизонтальной линией

Если один из спросов является горизонтальной линией, это означает, что данный покупатель готов купить любой объем товара при данной цене.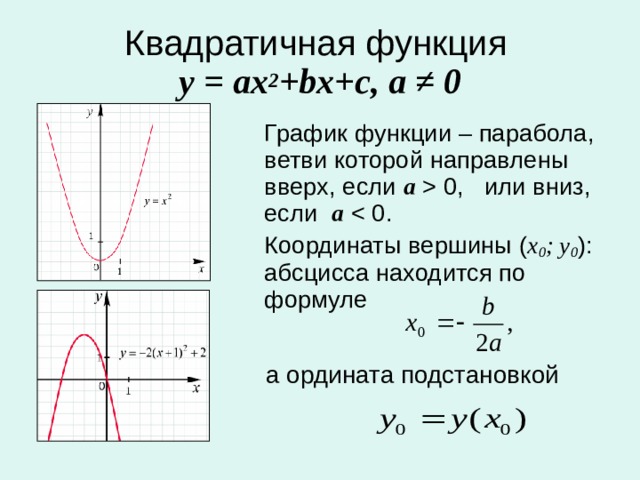 Другой покупатель имеет обычную убывающую линию спроса. Что будет суммарным спросом в этом случае?

Другими словами, что увидит продавец, который придет на данный рынок? При построении общего спроса не будем забывать, что линия спроса показывает максимальные цены, которые готов заплатить покупатель за разные объемы блага. Таким образом, при построении общего спроса мы должны выбрать максимальные уровни цены. Еще можно запомнить такое правило: горизонтальная линия спроса «стирает» все спросы, которые находятся под ней пи построении общего спроса.

Если один из спросов является вертикальной линией, то график суммарного спроса будет выглядеть так:

В этом случае один из потребителей готов купить определенный объем товара по какой-угодно цене (может быть, данный товар ему очень необходим). При сложении мы получаем, что график другого покупателя (с обычным убывающим спросом) двигается параллельно вправо.

ИНФОРМАЦИЯ О СВОБОДНЫХ МЕСТАХ

В настоящий момент активно набираю учеников на предстоящий учебный сезон. Есть около 10 мест

ТЕОРИЯ И ЗАДАНИЯ

• alt=»bg» />Лекция «За что были получены Нобелевские премии по экономике»
  (Уровень сложности: Всероссийская олимпиада)
• alt=»bg» />Пример видео-разбора тура олимпиады
  (Уровень сложности: Всероссийская олимпиада)

ИНТЕРВЬЮ С УЧЕНИКАМИ

Интервью с Дмитрием Сорокиным, абсолютным победителем Всероссийской олимпиады по экономике 2009 года

Первое интервью я взял, пожалуй, у своего самого неординарного ученика — Дмитрия Сорокина. Дмитрий являлся абсолютным победителем (1-е место) Всероссийской олимпиады школьников по экономике 2009 года. Я помню, что мне было приятно заниматься с Дмитрием, который с первого же занятия поставил максимальную планку уровня наших занятий, заявив, что его цель — победа во Всероссийской олимпиаде. С первых занятий мне показалось, что Дмитрий — будущий ученый-экономист. Траектория Дмитрия интересна: после года обучения на экономическом факультете ВШЭ, он перевелся на первый курс совместного бакалавриата ВШЭ-РЭШ, а сейчас уезжает на семестр в Нью-Йоркский университет. В данном интервью Дмитрий рассказывает об этом выборе, а также о том, почему он решил стать академическим ученым, какие задачи сейчас стоят перед молодым экономистом. подробнее…

Доступно о кватернионах и их преимуществах / Хабр

От переводчика: ровно 175 лет и 3 дня назад были изобретены кватернионы. В честь этой круглой даты я решил подобрать материал, объясняющий эту концепцию понятным языком.

Концепция кватернионов была придумана ирландским математиком сэром Уильямом Роуэном Гамильтоном в понедельник 16 октября 1843 года в Дублине, Ирландия. Гамильтон со своей женой шёл в Ирландскую королевскую академию, и переходя через Королевский канал по мосту Брум Бридж, он сделал потрясающее открытие, которое сразу же нацарапал на камне моста.

Памятная табличка на мосту Брум Бридж через Королевский канал в честь открытия фундаментальной формулы умножения кватернионов.

В этой статье я постараюсь объяснить концепцию кватернионов простым для понимания образом. Я объясню, как можно визуализировать кватернион, а также расскажу о разных операциях, которые можно выполнять с кватернионами. Кроме того, я сравню использование матриц, углов Эйлера и кватернионов, а затем попытаюсь объяснить, когда стоит использовать кватернионы вместо углов Эйлера или матриц, а когда этого делать не нужно.

Содержание

• 1. Введение
• 2. Комплексные числа
  • 2.1. Сложение и вычитание комплексных чисел
  • 2.2. Умножение комплексного числа на скалярное значение
  • 2.3. Произведение комплексных чисел
  • 2.4. Квадрат комплексных чисел
  • 2.5. Сопряжённые комплексные числа
  • 2.6. Абсолютное значение комплексного числа
  • 2.7. Частное двух комплексных чисел
• 3. Степени
• 4. Комплексная плоскость
  
  • 4.1. Роторы
• 5. Кватернионы
  • 5.1. Кватернионы как упорядоченная пара
  • 5. 2. Сложение и вычитание кватернионов
  • 5.3. Произведение кватернионов
  • 5.4. Вещественный кватернион
  • 5.5. Умножение кватерниона на скалярную величину
  • 5.6. Чистые кватернионы
  • 5.7. Аддитивная форма кватерниона
  • 5.8. Единичный кватернион
  • 5.9. Бинарная форма кватерниона
  • 5.10. Сопряжённые кватернионы
  • 5.11. Норма кватерниона
  • 5.12. Нормализация кватерниона
  • 5.13. Обратный кватернион
  • 5.14. Скалярное произведение кватернионов
• 6. Повороты
• 7. Интерполяция кватернионов
  
  • 7.1. SLERP
    
    • 7.1.1. Разность кватернионов
    • 7.1.2. Возведение кватерниона в степень
    • 7.1.3. Дробная разность кватернионов
    • 7.1.4. Факторы, которые нужно учитывать
  • 7.2. SQUAD
• 8. Заключение
• 9. Загрузка демо
• 10. Справочные материалы

Невозможно полностью понять кватернионы за 45 минут.

В этой статье чрезвычайно много математики, так что она не для слабаков.

В компьютерной графике для описания позиции в пространстве (перемещения), а также ориентации в пространстве (поворота) используются матрицы. Также можно также использовать одну матрицу преобразований для описания масштаба объекта. Эту матрицу можно считать «пространством базиса». Если умножить вектор или точку (или даже другую матрицу) на матрицу преобразований, то мы «преобразуем» этот вектор, точку или матрицу в пространство, представленное этой матрицей.

В этой статье я не буду в подробностях рассказывать о матрицах преобразований. Подробно о матрицах преобразований можно прочитать в моей статье Matrices.

В данной статье я хочу рассказать об альтернативном способе описания ориентации объекта (поворота) в пространстве при помощи кватернионов.

Для того, чтобы полностью понять кватернионы, нам сначала нужно понять, откуда они взялись. Принцип кватернионов основан на концепции системы комплексных чисел.

Наряду с хорошо известными множествами чисел (натуральным, целым, вещественным и рациональным), система комплексных чисел добавляет новое множество чисел, называемых мнимыми числами. Мнимые числа были придуманы для решения определённых уравнений, не имевших решений, например:

Чтобы решить это выражение, нам нужно заявить, что , а это, как известно, невозможно, потому что квадрат любого числа (положительного или отрицательного) всегда положителен.

Математики не могли смириться с тем, что выражение не имеет решения, поэтому было изобретено новое понятие — мнимое число, которое можно использовать для решения таких уравнений.

Мнимое число имеет следующий вид:

Не пытайтесь понять это допущение, потому что логичных причин его существования нет. Нам просто нужно принять, что — это просто некая величина, квадрат которой равен .

Множество мнимых чисел можно обозначить как .

Множество комплексных чисел (обозначаемое символом — это сумма вещественного и мнимого числа в следующей форме:

Можно также заявить, что все вещественные числа являются комплексными с , а все мнимые числа являются комплексными с .

Сложение и вычитание комплексных чисел

Комплексные числа можно складывать и вычитать сложением и вычитанием вещественной и мнимой частей.

Сложение:

Вычитание:

Умножение комплексного числа на скалярное значение

Комплексное число умножается на скаляр умножением каждого члена комплексного числа на скаляр:

Произведение комплексных чисел

Кроме того, комплексные числа можно также перемножать, используя обычные алгебраические правила.

Квадрат комплексных чисел

Также комплексное число можно возвести в квадрат, умножив на само себя:

Сопряжённые комплексные числа

Сопряжённой величиной комплексного числа является комплексное число с изменённым знаком мнимой части, обозначаемой как или как .

Перемножение комплексного числа с его сопряжённой величиной даёт интересный результат.

Абсолютное значение комплексного числа

Мы можем использовать сопряжённое число комплексного числа, чтобы вычислить абсолютное значение (или норму, или

величину) комплексного числа. Абсолютное значение комплексного числа — это квадратный корень из комплексного числа, умноженного на его сопряжённое число. Оно обозначается как :

Частное двух комплексных чисел

Чтобы вычислить частное двух комплексных чисел, мы умножаем числитель и знаменатель на сопряжённое число знаменателя.

Если мы утверждаем, что , то должна существовать возможность возводить и в другие степени.

Если мы продолжим записывать этот ряд, то заметим закономерность .

Похожая закономерность возникает при увеличении отрицательных степеней.

Возможно, вы уже видели такую закономерность в математике, но в виде , который получается поворотом точки на 90° против часовой стрелки на двухмерной декартовой плоскости; ряд создаётся поворотом точки на 90° градусов на двухмерной декартовой плоскости.

Декартова плоскость

Мы можем аналогичным образом нанести комплексные числа на двухмерную сетку, называемую комплексной плоскостью, привязав вещественную часть к горизонтальной оси, а мнимую — к вертикальной.

Комплексная плоскость

Как видно из предыдущего ряда, мы можем сказать, что если умножим комплексное число на , то сможем поворачивать комплексное число на комплексной плоскости с шагом в 90°.

Давайте проверим, верно ли это. Мы возьмём на комплексной плоскости произвольную точку :

и умножим её на , получив :

Умножив на , получим :

А умножив на , получим :

А умножив на , получим :

И мы получили ровно то, с чего начинали (). Если нанести эти комплексные числа на комплексную плоскость, то получим следующий результат.

Комплексные числа на комплексной плоскости

Теперь мы можем выполнять поворот на комплексной плоскости и по часовой стрелке, умножая комплексное число на .

Роторы

Также мы можем выполнять на комплексной плоскости произвольные повороты, задав комплексное число в следующем виде:

При умножении любого комплексного числа на ротор получаем общую формулу:

Что также можно записать в матричном виде:

Что является способом поворота против часовой стрелки произвольной точки на комплексной плоскости относительно точки начала координат.

Узнав о системе комплексных чисел и комплексной плоскости, мы можем вывести их в трёхмерное пространство, добавив к системе чисел наряду с ещё два мнимых числа.

Кватернионы имеют следующий обобщённый вид

Где в соответствии со знаменитым выражением Гамильтона:

Можно заметить, что отношения между , и очень похожи на правила векторного умножения единичных декартовых векторов:

Гамильтон также заметил, что мнимые числа , и можно использовать для представления трёх декартовых единичных векторов , и с теми же свойствами мнимых чисел, так что .

Графическое представление свойств , ,

На представленном выше изображении графически представлены взаимосвязи между декартовыми единичными векторами в виде , и .

Кватернионы как упорядоченная пара

Также мы можем представить кватернионы в виде упорядоченной пары:

Где можно также представить как его отдельные компоненты:

С помощью этой записи мы можем проще представить общие черты кватернионов и комплексных чисел.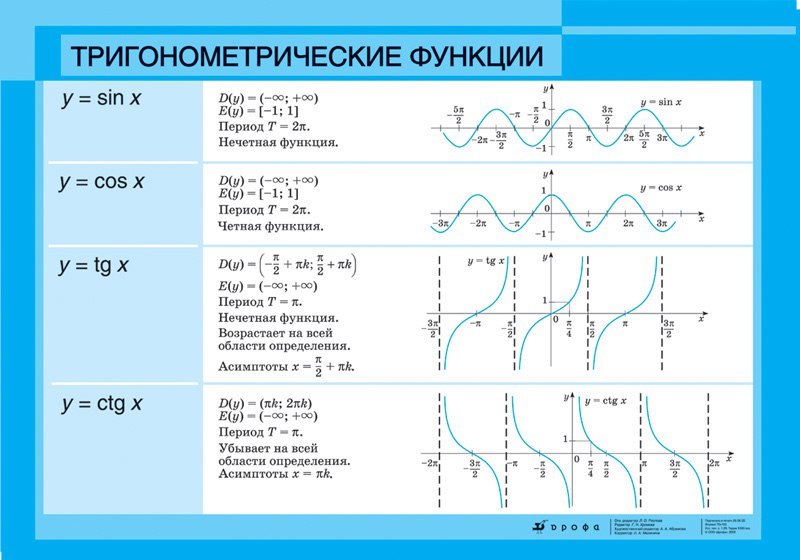

Сложение и вычитание кватернионов

Кватернионы можно складывать и вычитать аналогично комплексным числам:

Произведения кватернионов

Также мы можем выразить произведение двух кватернионов:

Что даёт нам ещё один кватернион. Если мы заменим в предыдущем выражении мнимые числа , и упорядоченными парами (также известными как кватернионные единицы), то получим

А подставив обратно в исходное выражение с , получим:

Развернув это выражение в сумму упорядоченных пар, получим:

Если умножить на кватернионную единицу и извлечь общие векторые компоненты, то можно переписать это уравнение следующим образом:

Это уравнение даёт нам сумму двух упорядоченных пар.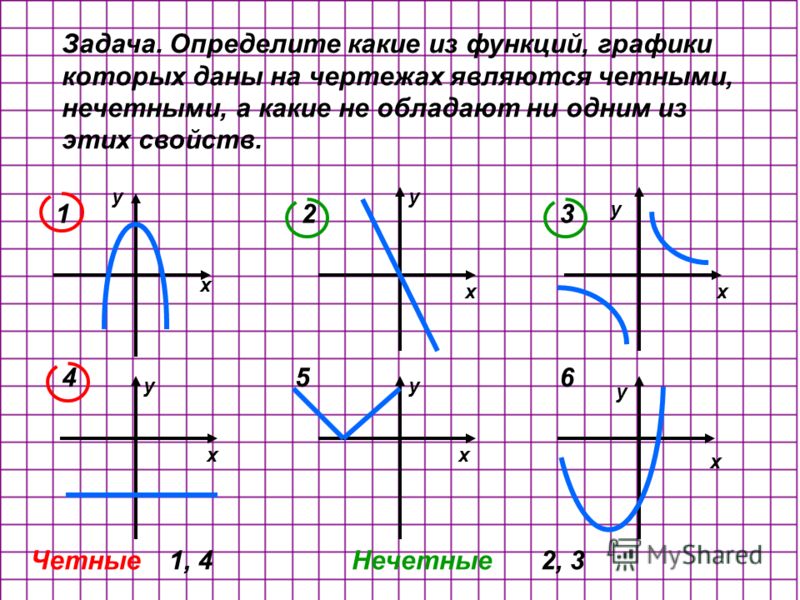 Первая упорядоченная пара — это вещественный кватернион, а вторая — чистый кватернион. Две этих упорядоченных пары можно соединить в одну упорядоченную пару:

Если подставить, то мы получим

Получаем:

Это и есть общее уравнение произведения кватернионов.

Вещественный кватернион

Вещественный кватернион — это кватернион, в который входит вектор :

А произведением двух вещественных кватернионов является ещё один вещественный кватернион:

Что аналогично произведению двух комплексных чисел, содержащих нулевой мнимый член.

Умножение кватерниона на скалярную величину

Также мы можем умножать кватернион на скаляр, при этом придерживаясь следующего правила:

Мы можем убедиться в этом с помощью показанного выше произведения вещественных кватернионов, умножив кватернион на скаляр как вещественный кватернион:

Чистые кватернионы

Кроме вещественных кватернионов, Гамильтон также определил чистый кватернион как кватернион с нулевым скалярным членом:

Или если записать по компонентам:

И мы снова можем взять произведение двух чистых кватернионов:

в соответствии с представленным выше правилом произведения кватернионов.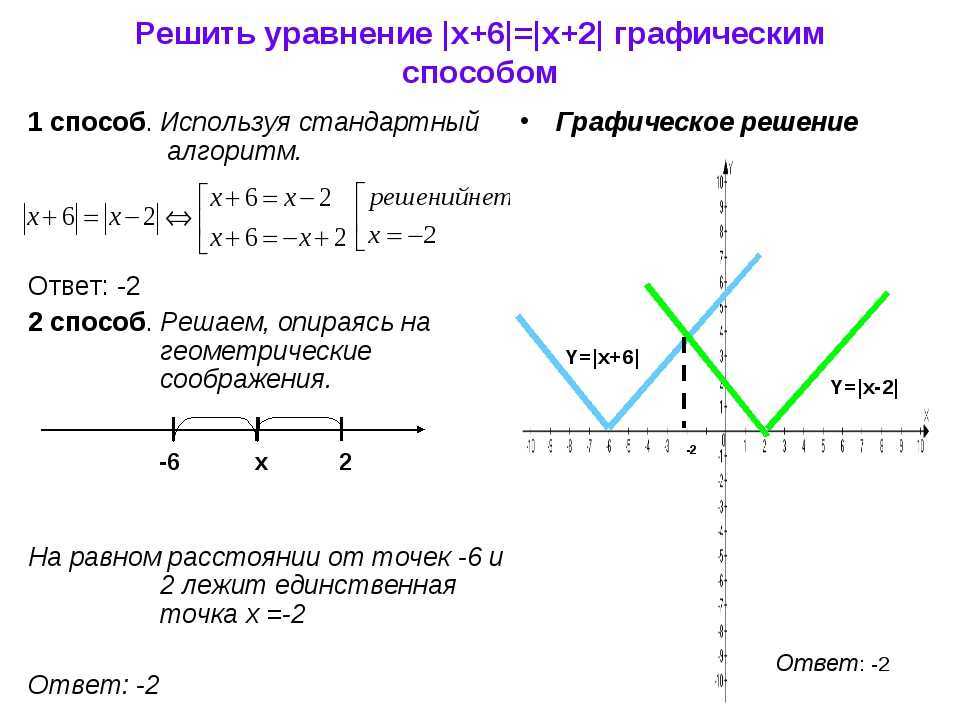

Аддитивная форма кватерниона

Кроме того, мы можем выразить кватернионы как сумму вещественной и чистой частей кватерниона:

Единичный кватернион

Взяв произвольный вектор , можно выразить этот вектор и через его скалярную величину, и через его направление следующим образом:

Объединив это определение с определением чистого кватерниона, получим:

Также мы можем описать единичный кватернион, имеющий нулевой скаляр и единичный вектор:

Бинарная форма кватерниона

Теперь мы можем объединить определения единичного кватерниона и аддитивную форму кватерниона, получив форму кватернионов, схожую с записью, используемой при описании комплексных чисел:

Что даёт нам способ представить кватернион в форме, очень похожей на комплексные числа:

Сопряжённое число кватерниона

Сопряжённое число кватерниона можно вычислить, взяв противоположную по знаку векторную часть кватерниона:

Произведение кватерниона и его сопряжённого числа даёт нам следующее:

Норма кватерниона

Вспомним определение нормы комплексного числа:

Аналогично, норма (или величина) кватерниона определяется как:

Что позволяет нам выразить норму кватерниона следующим образом:

Нормализация кватерниона

Имея определение нормы кватерниона, мы можем использовать её для нормализации кватерниона. Кватернион нормализуется делением на :

Например, давайте нормализуем кватернион:

Сначала нам нужно вычислить норму кватерниона:

Затем мы должны разделить кватернион на норму кватерниона, чтобы вычислить нормализованный кватернион:

Обратный кватернион

Обратный кватернион обозначается как . Для вычисления обратного кватерниона мы берём сопряжённое число кватерниона и делим его на квадрат нормы:

Чтобы показать это, мы можем воспользоваться определением обратной величины:

И умножить обе стороны на сопряжённое число кватерниона, что даст нам:

Подстановкой мы получаем:

Для единичных кватернионов-норм, норма которых равна 1, мы можем записать:

Скалярное произведение кватернионов

Аналогично скалярному произведению векторов мы можем вычислить скалярное произведение двух кватернионов, перемножив соответствующие скалярные части и просуммировав результаты:

Также мы можем использовать скалярное произведение кватернионов для вычисления угловой разности между кватернионами:

Для единичных кватернионов-норм мы можем упростить уравнение:

Напомню, что мы определили особую форму комплексного числа под названием ротор, которую можно использовать для поворота точки на двухмерной плоскости следующим образом:

Благодаря схожести комплексных чисел с кватернионами должна существовать возможность выразить кватернион, который можно использовать для поворота точки в трёхмерном пространстве:

Давайте проверим, верна ли эта теория, вычислив произведение кватерниона и вектора . Во-первых, мы можем выразить как чистый кватернион в следующем виде:

А — это единичный кватернион-норма в виде:

Тогда

Мы видим, что результатом является общий кватернион со скалярной и векторной частями.

Давайте сначала рассмотрим «особый» случай, при котором перпендикулярен . В таком случае член скалярного произведения и результат становится чистым кватернионом:

В таком случае для поворота относительно мы просто подставляем и .

Например, давайте повернём вектор на 45° относительно оси Z; тогда наш кватернион будет равен:

И давайте возьмём вектор , который относится к особому случаю, где перпендикулярен :

Теперь давайте найдём произведение

:

Что даёт нам чистый кватернион, повёрнутый на 45° относительно оси .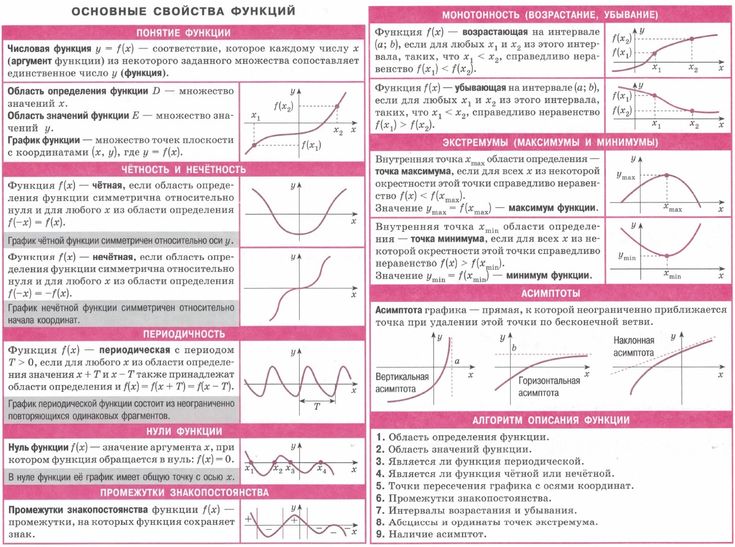 Мы можем также убедиться, что величина конечного вектора сохранилась:

В точности то, чего мы и ожидали!

Мы можем показать это графически следующим изображением:

Поворот кватерниона (1)

Теперь давайте рассмотрим кватернион, не ортогональный к . Если мы примем для векторной части кватерниона смещение в 45° от , то получим:

А умножив наш вектор на , получим:

После подстановки , и получаем:

То есть это больше не чистый кватернион, он не повёрнут на 45° а норма вектора больше не равна 2 (она уменьшилась до ).

Этот результат можно показать графически.

Поворот кватерниона (2)

Строго говоря, некорректно представлять кватернион в трёхмерном пространстве, потому что на самом деле это четырёхмерный вектор! Ради упрощения я покажу только векторный компонент кватернионов.

Однако не всё потеряно. Гамильтон выяснил (но не опубликовал этого), что если мы затем умножим результат на значение, обратное , то результатом будет чистый кватернион, а норма векторного компонента сохранится. Давайте посмотрим, можно ли применить это в нашем примере.

Для начала давайте вычислим :

При получаем:

Объединив предыдущее значение и , получим:

Что является чистым кватернионом, а норма результата равна:

что равно , то есть норма вектора сохранилась.

На изображении ниже показан результат поворота.

Поворот кватерниона (3)

Мы видим, что результат является чистым кватернионом, а норма исходного вектора сохранилась, но вектор повернулся на 90°, а не на 45°, что вдвое больше необходимого! Поэтому для корректного поворота вектора на угол относительно произвольной оси нам нужно взять половинный угол и создать следующий кватернион:

Что является общим видом кватерниона поворота!

Одна из самых важных причин использования кватернионов в компьютерной графике заключается в том, что кватернионы очень хорошо описывают повороты в пространстве.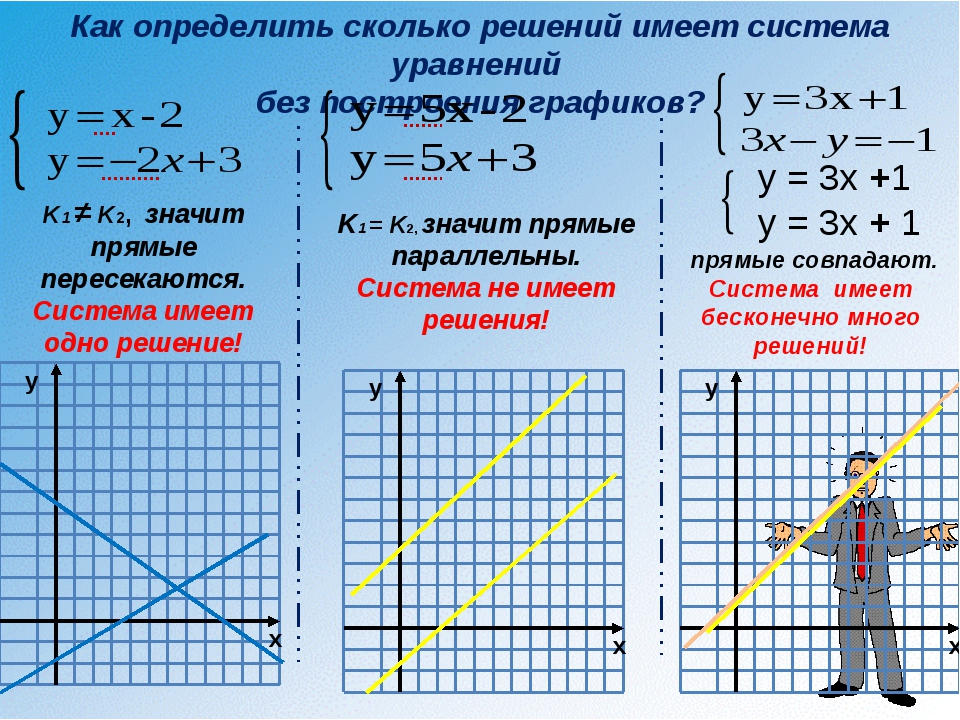 Кватернионы избавляют от проблем, отягощающих другие способы поворота точек в 3D-пространстве, такие как складывание рамок, в котором проблема заключается в представлении поворота в углах Эйлера.

С помощью кватернионов мы можем определить несколько методов, представляющих интерполяцию поворота в 3D-пространстве. Первый рассматриваемый мной метод называется SLERP. Он используется для плавной интерполяции точки между двумя ориентациями. Второй метод является развитием SLERP и называется SQUAD. Он используется для интерполяции по ряду ориентаций, задающих путь.

SLERP

SLERP расшифровывается как Spherical Linear Interpolation (сферическая линейная интерполяция). SLERP предоставляет возможность плавной интерполяции точки между двумя ориентациями.

Я обозначу первую ориентацию как , а вторую как . Интерполируемую точку обозначим как , интерполированную точку обозначим как . Параметр интерполяции будет интерполировать от при до при .

Стандартная формула линейной интерполяции имеет вид:

Вот основные шаги для применения этого уравнения:

• Вычисляем разность между и .
• Берём дробную часть этой разности.
• Корректируем исходное значение на дробную разность между двумя точками.

Мы можем использовать тот же основной принцип, чтобы выполнить интерполяцию между двумя ориентациями кватернионов.

Разность кватернионов

Первый шаг означает, что нам нужно вычислить разность между и . В контексте кватернионов это аналогично вычислению угловой разности между двумя кватернионами.

Возведение кватерниона в степень

На следующем шаге нужно взять дробную часть этой разности. Мы можем вычислить дробную часть кватерниона, возведя его в степень, значение которой находится в интервале .

Общая формула возведения кватерниона в степень имеет следующий вид:

Где экпоненциальная функция для кватернионов выглядит так:

А логарифм кватерниона имеет вид:

При мы имеем следующее:

А при мы имеем

Дробная разность кватернионов

Чтобы вычислить интерполированный угловой поворот, мы изменяем исходную ориентацию на дробную часть разности между и .

Что является общим видом сферической линейной интерполяции для кватернионов. Однако это не тот вид уравнения SLERP, который обычно используется на практике.

Мы можем применить похожую формулу для выполнения сферической интерполяции векторов в кватернионы. Общий вид сферической интерполяции для векторов задаётся так:

Графически это можно показать следующим изображением.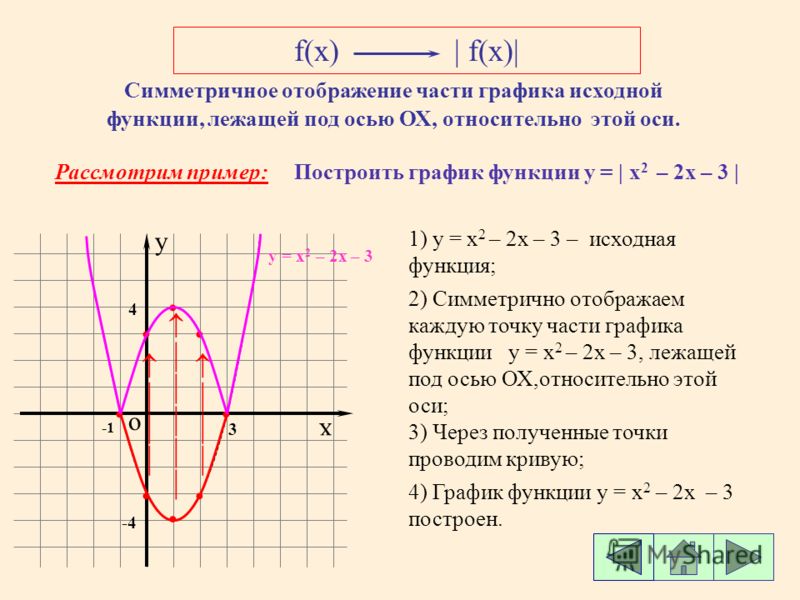

Интерполяция кватернионов

Эту формулу можно без изменений применить к кватернионам:

И мы можем получить угол , вычислив скалярное произведение и .

Факторы, которые нужно учитывать

У этой реализации есть две проблемы, которые нужно учитывать при использовании.

Во-первых, если скалярное произведение кватернионов оказывается отрицательным значением, то интерполяция пойдёт по «долгому пути» на четырёхмерной сфере, а это не всегда желательно. Чтобы решить эту проблему, мы можем проверить результат скалярного произведения и если он отрицательный, то можно взять значение, противоположное одной из ориентаций. Инвертирование скалярной и векторной части кватерниона не меняет представляемую им ориентацию, но сделав это, мы гарантируем, что поворот будет происходить по «кратчайшему» пути.

Ещё одна проблема возникает, если угловая разность между и очень мала, при этом становится 0. Если это происходит, то при делении на мы можем получить неопределённый результат. В таком случае можно вернуться к использованию линейной интерполяции между и .

SQUAD

Так же, как SLERP можно использовать для интерполяции между двумя кватернионами, SQUAD (Spherical and Quadrangle — сферическая и четырёхугольная) можно использовать для плавной интерполяции по пути поворотов.

Если у нас есть ряд кватернионов:

И мы определили «вспомогательный» кватернион (), который мы можем считать промежуточной контрольной точкой:

Ориентация вдоль части кривой определяется как:

при времени t это даёт нам:

Несмотря на сложность для понимания, при работе с поворотами кватернионы обеспечивают несколько очевидных преимуществ по сравнению с матрицами и углами Эйлера.

• Интерполяция кватернионов с помощью SLERP и SQUAD предоставляет способ плавной интерполяции между ориентациями в пространстве.
• Конкатенация поворотов с помощью кватернионов выполняется быстрее, чем объединение поворотов, выраженных в матричном виде.
• Для единичных кватернионов-норм обратная величина поворота берётся вычитанием векторной части кватерниона. Вычисление обратной величины матрицы поворота значительно медленнее, если матрица не ортонормирована (если она ортонормирована, то это всего лишь транспонирование матрицы).
• Преобразование кватернионов в матрицы немного быстрее, чем для углов Эйлера.
• Для описания поворота кватернионам требуется всего 4 числа (3, если они нормализованы. Вещественную часть можно вычислять во время выполнения программы), в то время как матрицам необходимо не менее 9 значений.

Однако наряду со всеми преимуществами использования кватернионов существует также несколько недостатков.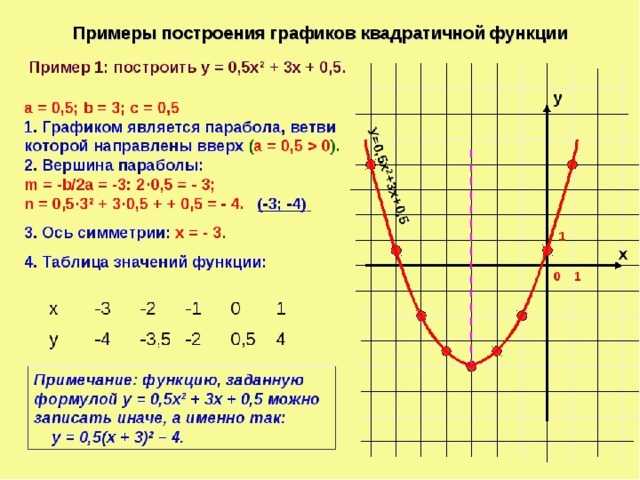

• Кватернионы могут становиться недействительными из-за ошибки округления чисел с плавающей запятой; однако эту «вкравшуюся ошибку» можно устранить ренормализацией кватерниона.
• Вероятно, самое значительное препятствие для применения кватернионов — высокая сложность их понимания. Надеюсь, эту проблему вы решите, прочитав мою статью.

Есть множество математических библиотек, реализующих кватернионы, и только некоторые из них реализуют кватернионы правильно. По моему собственному опыту хорошей математической библиотекой с качественной реализацией кватернионов является GLM (OpenGL Math Library). Если вы хотите использовать кватернионы в собственных приложениях, то рекомендую эту библиотеку.

Я создал небольшое демо, демонстрирующее использование кватерниона для поворота объекта в пространстве. Демо было создано в Unity 3.5.2, можете скачать бесплатно скачать этот движок и просмотреть исходный код демо. В файле zip также содержится двоичный исполняемый файл Windows, но в Unity вы можете собрать приложение и для Mac.

Understanding Quaternions.zip

Vince, J (2011). Quaternions for Computer Graphics. 1st. ed. London: Springer.

Dunn, F. and Parberry, I. (2002). 3D Math Primer for Graphics and Game Development. 1st. ed. Plano, Texas: Wordware Publishing, Inc.

Композиций функций | Колледж Алгебра

Результаты обучения

• Комбинирование функций с использованием алгебраических операций.
• Создать новую функцию по композиции функций.

Композиция функций — это только один из способов объединения существующих функций. Другой способ — выполнять обычные алгебраические операции над функциями, такие как сложение, вычитание, умножение и деление. Мы делаем это, выполняя операции с выходами функции, определяя результат как результат нашей новой функции.

Предположим, нам нужно сложить два столбца чисел, представляющих отдельные годовые доходы мужа и жены за определенный период, и в результате получить их общий доход домохозяйства. Мы хотим сделать это для каждого года, добавив только доходы за этот год, а затем собрав все данные в новый столбец. Если [latex]w\left(y\right)[/latex] — доход жены, а [latex]h\left(y\right)[/latex] — доход мужа в [latex]y[/latex] году , и мы хотим, чтобы [latex]T[/latex] представлял общий доход, тогда мы можем определить новую функцию.

[latex]T\left(y\right)=h\left(y\right)+w\left(y\right)[/latex]

Если это верно для каждого года, то мы можем сосредоточиться на отношение между функциями без привязки к году и записать

[латекс]Т=ч+в[/латекс]

Так же, как для этой суммы двух функций, мы можем определить функции разности, произведения и отношения для любой пары функций, которые имеют одни и те же входные данные (не обязательно числа) и одни и те же выходные данные (которые должны быть числами, чтобы к ним можно было применить обычные алгебраические операции, и которые также должны иметь одни и те же единицы измерения или не иметь их). единицы при сложении и вычитании). Таким образом, мы можем думать о сложении, вычитании, умножении и делении функций.

Для двух функций [latex]f\left(x\right)[/latex] и [latex]g\left(x\right)[/latex] с действительными числами на выходе мы определяем новые функции [latex]f+ g,f-g,fg[/latex] и [latex]\dfrac{f}{g}[/latex] соотношениями

[latex]\begin{align}{c}\left(f+g\right )\left(x\right)&=f\left(x\right)+g\left(x\right) \\[2mm] \left(f-g\right)\left(x\right)&=f\ влево(х\вправо)-г\влево(х\вправо) \\[2мм] \текст{ }\влево(фг\вправо)\влево(х\вправо)&=f\влево(х\вправо)г\ влево (х \ вправо) \\ [2 мм] \ текст { } \ влево (\ dfrac {f} {g} \ вправо) \ влево (х \ вправо) & = \ dfrac {е \ влево (х \ вправо)} {g\left(x\right)}\\& \end{align}[/latex] 92+3x-4[/латекс]

[латекс]g(x) = \dfrac{1}{x-1}[/латекс]

Теперь введите [латекс]h(x) = f(x)+g(x)[/latex] в следующей строке.

Оцените [latex]h(1)[/latex], почему вы думаете, что получили такой результат?

Создание новой функции с помощью композиции

Выполнение алгебраических операций над функциями объединяет их в новую функцию, но мы также можем создавать функции, составляя функции. Когда мы хотели рассчитать стоимость отопления по дням в году, мы создали новую функцию, которая принимает день в качестве входных данных и дает стоимость в качестве выходных данных. Процесс объединения функций, при котором результат одной функции становится вводом другой, называется композицией функций. Полученная функция называется составной функцией. Обозначим эту комбинацию следующими обозначениями:

[латекс]\влево(f\circ g\вправо)\влево(х\вправо)=f\влево(г\влево(х\вправо)\вправо)[/латекс]

Читаем слева сторона как [latex]«f[/latex] состоит из [latex]g[/latex] на [latex]x,»[/latex], а правая часть как [latex]«f[/latex ] of [latex]g[/latex] of [latex]x.»[/latex] Две части уравнения имеют одинаковый математический смысл и равны. Символ открытого круга [латекс]\цирк [/латекс] называется оператором композиции. Мы используем этот оператор главным образом, когда хотим подчеркнуть отношения между самими функциями, не обращаясь к какому-либо конкретному входному значению. Композиция — это бинарная операция, которая берет две функции и формирует новую функцию, подобно тому, как сложение или умножение берет два числа и дает новое число. Однако важно не путать композицию функций с умножением, потому что, как мы узнали выше, в большинстве случаев [латекс]f\left(g\left(x\right)\right)\ne f\left(x\right) г\влево(х\вправо)[/латекс].

Также важно понимать порядок операций при вычислении составной функции. Мы следуем обычному соглашению со скобками, начиная с самых внутренних скобок, а затем переходя к внешним. В приведенном выше уравнении функция [latex]g[/latex] сначала принимает входные данные [latex]x[/latex] и возвращает результат [latex]g\left(x\right)[/latex]. Затем функция [latex]f[/latex] принимает [latex]g\left(x\right)[/latex] в качестве входных данных и возвращает результат [latex]f\left(g\left(x\right)\ справа)[/латекс]. 9{2}+2\hfill \end{align}[/latex]

Эти выражения не равны для всех значений [latex]x[/latex], поэтому две функции не равны. Неважно, что выражения совпадают для единственного входного значения [latex]x=-\frac{1}{2}[/latex].

Обратите внимание, что диапазон внутренней функции (первой оцениваемой функции) должен находиться в пределах домена внешней функции. Менее формально, композиция должна иметь смысл с точки зрения входов и выходов. Кроме того, в прикладных настройках композиция функций обычно имеет смысл только в одном конкретном порядке.

A Общее примечание: композиция функций

Когда выход одной функции используется как вход другой, вся операция называется композицией функций. Для любых входных данных [latex]x[/latex] и функций [latex]f[/latex] и [latex]g[/latex] это действие определяет составную функцию, которую мы записываем как [latex]f\circ g[ /латекс] такой, что

[латекс]\влево(е\круг г\вправо)\влево(х\вправо)=f\влево(г\влево(х\вправо)\вправо)[/латекс]

домен составной функции [latex]f\circ g[/latex] — это все [latex]x[/latex] такие, что [latex]x[/latex] находится в домене [latex]g[/latex] и [latex]g\left(x\right)[/latex] находится в домене [latex]f[/latex].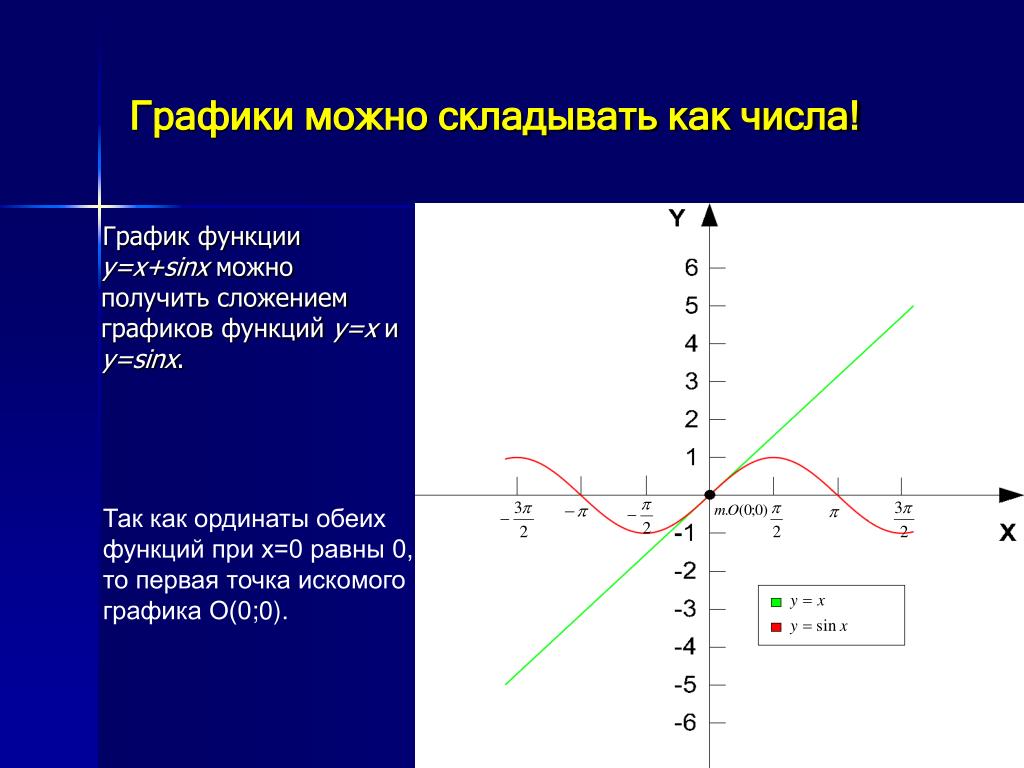

Важно понимать, что произведение функций [latex]fg[/latex] не совпадает с композицией функций [latex]f\left(g\left(x\right)\right)[/latex] , потому что в общем случае [латекс]f\влево(х\вправо)г\влево(х\вправо)\ne f\влево(г\влево(х\вправо)\вправо)[/латекс].

Пример: определение композиции функций

Используя предоставленные функции, найдите [latex]f\left(g\left(x\right)\right)[/latex] и [latex]g\left(f\left (х\право)\право)[/латекс].
[латекс]f\влево(x\вправо)=2x+1\\g\влево(x\вправо)=3-x[/латекс] 92+3x-4[/латекс]

[латекс]g(x) = \dfrac{1}{x-1}[/латекс]

Теперь определите новую функцию:

[латекс]h(x) = f(f(x))[/латекс]

Теперь увеличьте масштаб (используйте знак плюс в верхнем правом углу графика) в точке [латекс](0.23607,-3.236)[/латекс], обратите внимание, что оба графика проходят через эту точку. Продолжайте этот шаблон еще для нескольких итераций: определите новую функцию, которая содержит другую композицию [latex]f(x)[/latex] с самой собой. Например: [латекс]p(x) = f(f(f(x)))[/латекс] и так далее. Продолжайте использовать масштабирование по мере повторения. 92+3x-4[/латекс]. Фиксированные точки используются в математических приложениях, таких как алгоритм рейтинга страниц, который Google использует для создания результатов поиска в Интернете. Подробнее о фиксированных точках читайте здесь, а рейтинг страницы — здесь. Пример: интерпретация составных функций ]s\left(t\right)[/latex] дает количество приседаний, которое человек может выполнить за [latex]t[/latex] минут. Интерпретировать [латекс]с\влево(с\влево(3\вправо)\вправо)[/латекс].

Показать Показать решение

 

Пример: исследование порядка функциональной композиции

Предположим, что [latex]f\left(x\right)[/latex] дает мили, которые можно проехать за [latex]x[/latex] часов и [latex] g\left(y\right)[/latex] дает галлоны бензина, израсходованные на прохождение [latex]y[/latex] миль. Какое из этих выражений имеет смысл: [латекс]f\left(g\left(y\right)\right)[/latex] или [latex]g\left(f\left(x\right)\right)?[ /латекс]

Показать Показать решение

Попробуйте

 

Вопросы и ответы

Существуют ли ситуации, когда [латекс]f\left(g\left(y\right)\right)[/latex] и [латекс]g\left(f\ left(x\right)\right)[/latex] были бы осмысленными или полезными выражениями?

Да. Для многих чисто математических функций обе композиции имеют смысл, хотя обычно они производят разные новые функции. В реальных задачах функции, входы и выходы которых имеют одни и те же единицы измерения, также могут давать композиции, значимые в любом порядке.

Попробуйте

Гравитационная сила на планете на расстоянии [latex]r[/latex] от Солнца определяется функцией [latex]G\left(r\right)[/latex]. Ускорение планеты под действием любой силы [latex]F[/latex] определяется функцией [latex]a\left(F\right)[/latex]. Составьте осмысленную композицию из этих двух функций и объясните, что она означает.

Показать Показать решение

У вас есть идеи по улучшению этого контента? Мы будем признательны за ваш вклад.

Улучшить эту страницуПодробнее

Операции с функциями

Мы можем складывать, вычитать, умножать и делить функции! Результатом является новая функция.

Давайте попробуем выполнить эти операции над f(x) и g(x):

Дополнение

Мы можем добавить две функции:

(f+g)(x) = f(x) + g(x)

Примечание: мы поместили f+g внутрь () , чтобы показать, что они оба работают на разрешении x .

Пример: f(x) = 2x+3 и g(x) = x

²

(f+g)(x) = (2x+3) + (x ² ) = x ² + 2x+3

Иногда нам может понадобиться объединить похожие термины:

Пример: v(x) = 5x+1, w(x) = 3x-2

(v+w)(x) = (5x+1) + (3x-2) = 8x-1

Единственная другая вещь, о которой нужно беспокоиться, это Домен (набор чисел, которые входят в функцию), но мы поговорим об этом позже!

 

Вычитание

Мы также можем вычесть две функции:

(fg)(x) = f(x) − g(x)

Пример: f(x) = 2x+3 и g(x) = x

²

(f-g)(x) = (2x+3) − (x ² )

 

Умножение

Мы можем умножить две функции:

(f·g)(x) = f(x) · g(x)

Пример: f(x) = 2x+3 и g(x) = x

²

(f·g)(x) = (2x+3)(x ² ) = 2x ³ + 3x ²

 

Отдел

И мы можем разделить две функции:

(f/g)(x) = f(x) / g(x)

Пример: f(x) = 2x+3 и g(x) = x

²

(f/g)(x) = (2x+3)/x ²

Функциональная композиция

Существует еще одна специальная операция, называемая Композицией функций, прочитайте эту страницу, чтобы узнать больше!

(г º ж)(х)

Домены

До сих пор это было легко, но теперь мы должны рассмотреть домены функций.

Домен — это набор всех значений , которые входят в функцию.

Функция должна работать для всех значений, которые мы ей задаем, поэтому зависит от нас , чтобы убедиться, что мы правильно получаем домен!

Пример: домен для √x (квадратный корень из x)

Мы не можем получить квадратный корень из отрицательного числа (если только мы не используем мнимые числа, но здесь мы этого не делаем), поэтому мы должны исключить отрицательных чисел:

Домен √x состоит из всех неотрицательных действительных чисел

На числовой строке это выглядит так:

Используя нотацию конструктора наборов, записывается:

{ x | x ≥ 0}

«набор всех x, которые являются членами действительных чисел,
таких, что x больше или равен нулю »

Или, используя интервальную нотацию, это:

[0,+ ∞)

Важно правильно указать домен, иначе мы получим плохие результаты!

Итак, как нам создать новый домен после выполнения операции?

Как разработать новый домен

Когда мы выполняем операции над функциями, мы получаем ограничения как .

Это как готовить для друзей:

• нельзя есть арахис,
• другой не может есть молочные продукты.

То, что мы готовим, не может содержать арахис , а также не может содержать молочные продукты.

Пример: f(x)=√x и g(x)=√(3−x)

Домен для f(x)=√x начинается с 0 и далее:

Домен для g(x)=√(3−x) до 3 включительно:

Таким образом, новый домен (после добавления или чего-то еще) будет от 0 до 3:

Если мы выберем любое другое значение, то не будет работать та или иная часть новой функции.

Другими словами, мы хотим найти, где два домена пересекаются с .

Примечание: мы можем поместить всю эту идею в одну строку, используя нотацию Set Builder:

Dom(f+g) = { x | xDom(f) и xDom(g) }

В котором говорится, что «домен f плюс g — это набор всех действительных чисел, которые находятся в домене f И в домене g» (означает «член»)

То же правило применяется, когда мы складываем, вычитаем , умножать или делить, за исключением того, что у деления есть одно дополнительное правило.

Дополнительное правило для подразделения

Существует дополнительное правило для деления:

Так же как и ограничивающий домен как указано выше, когда мы делим :

(f/g)(x) = f(x) / g(x)

мы также должны убедиться, что g(x) не равно нулю (чтобы мы не делили на ноль).

Вот пример:

Пример: f(x)=√x и g(x)=√(3−x)

(f/g)(x) = √x / √(3−x)

1. Домен для f(x)=√x от 0 и далее:

2. Домен для g(x)=√(3−x) до 3 включительно:

3. И √(3−x) не может быть нулем , поэтому x не может быть 3:

(Обратите внимание на незакрашенный кружок на 3, что означает , не включая 3)

Итак, все вместе мы получаем:

 

Резюме

• Чтобы складывать, вычитать, умножать или делить функции, просто делайте то, что говорит операция.
• Домен новой функции будет иметь ограничения обеих функций, которые ее создали.
• Разделение имеет дополнительное правило, согласно которому функция, на которую мы делим, не может быть равна нулю.

 

1193, 1194, 2459, 2460, 8461, 559, 560, 2461, 2462, 8462

Графики общих функций: список, типы и рабочий лист

Графики общих функций представляют собой графические представления функций, которые часто используются в математике.

Помните, что функция представляет собой математическую конструкцию, которая принимает значения x в качестве входных данных и выводит значения y в соответствии один к одному или многие к одному. Функции представляют отношения между независимой переменной x и зависимой переменной y.

Представление функции, Марилу Гарсия Де Тейлор — StudySmarter Originals

Типы графиков функций

Некоторые из наиболее распространенных функций , которые вы найдете в математике, перечислены ниже:

1. Константа: где c является константой. Форма графика постоянных функций представляет собой прямую линию, параллельную оси x, пересекающую ось y, где y = c.

График постоянной функции, Марилу Гарсиа Де Тейлор — StudySmarter Originals

2. Линейный (Идентификационный) . Форма линейных графиков также представляет собой прямую линию. В этом случае линия имеет наклон, который может быть пологим или крутым в зависимости от ее значения.

График функции идентичности, Марилу Гарсия Де Тейлор — StudySmarter Originals

3. Квадратичный: . Форма графика квадратичных функций – парабола.

График квадратичной функции, Марилу Гарсиа Де Тейлор — StudySmarter Originals

4. Кубический: . Кубические графики представляют собой непрерывные и гладкие линии, которые могут иметь максимальные или минимальные точки, в которых они меняют направление в средней части кривой, а на любом конце кривой они стремятся уйти в положительную или отрицательную бесконечность.

График кубической функции, Марилу Гарсия Де Тейлор — StudySmarter Originals

5. Квадратный корень: . График функции квадратного корня имеет характерную форму из-за его ограниченной области определения (). Это потому, что квадратный корень из отрицательного числа не имеет действительного решения. Поэтому в этом типе графика используются только положительные числа.

График функции квадратного корня, Марилу Гарсия Де Тейлор — StudySmarter Originals

6. Кубический корень: . Графы кубического корня отличаются от графов квадратного корня тем, что кубический корень из отрицательных чисел имеет действительные решения. Следовательно, функции кубического корня не имеют ограниченной области определения, x может принимать как отрицательные, так и положительные значения, что показано на форме его графика.

График функции кубического корня, Марилу Гарсия Де Тейлор — StudySmarter Originals

7. Модуль или абсолютное значение: . График модульных функций имеет характерную v-образную форму. Это то же самое, что f (x) = x, но отрицательные значения y отражаются на оси x. Это потому, что модуль числа x — это то же число, но положительное.

График функции модуля или абсолютного значения, Марилу Гарсия Де Тейлор — StudySmarter Originals

8. Обратное: . На графике обратных функций есть асимптоты — линии, к которым кривая подходит очень близко, но никогда их не касается. График имеет асимптоты при x = 0 и y = 0,

График функции обратной связи, Марилу Гарсиа Де Тейлор — StudySmarter Originals

9. Квадрат обратной функции: . Форма графика функции обратного квадрата меняется по сравнению с предыдущей, потому что наличие в знаменателе означает, что все значения y будут положительными.

График функции обратного квадрата, Марилу Гарсиа Де Тейлор — StudySmarter Originals

10. Экспоненциальная функция: . График показательной функции имеет горизонтальную асимптоту при y = 0 и пересекает ось y в точке (0, 1). После этого он быстро увеличивается.

График экспоненциальной функции, Марилу Гарсиа Де Тейлор — StudySmarter Originals

11. Логарифмический: . Логарифмическая функция является обратной экспоненциальной функции, поэтому график логарифмической функции будет отражением экспоненциального графика, к которому она относится, по линии y = x. График логарифмической функции имеет вертикальную асимптоту при x = 0 и пересекает ось x в точке (1, 0).

График логарифмической функции, Марилу Гарсия Де Тейлор — StudySmarter Originals

12. Тригонометрические функции : Графики тригонометрических функций (синуса, косинуса и тангенса) имеют характерную форму, потому что они периодические, что означает, что они повторяются через определенный интервал.

а) Синус: . График для синуса имеет максимальное значение 1 и минимальное значение -1, и он повторяется каждые 2π. График синуса пересекает ось Y в начале координат (0, 0).

2π радиан = 360 °

График тригонометрической функции — sin (x), Марилу Гарсия Де Тейлор — StudySmarter Originals

б) Косинус: . График косинуса также имеет максимальное значение 1 и минимальное значение -1 и повторяется каждые 2π. Вы можете отличить его от графика синуса, потому что график косинуса пересекает ось Y в точке (0, 1).

График тригонометрической функции — cos (x), Марилу Гарсия Де Тейлор — StudySmarter Originals

c) Касательная: . Касательный граф не имеет точек максимума или минимума и повторяется через каждые π. Следовательно, он имеет вертикальные асимптоты при , , и т. д.

График тригонометрической функции — tan (x), Марилу Гарсия Де Тейлор — StudySmarter Originals

Как найти общую функцию графика?

Чтобы определить общую функцию графика, очень полезно изучить формы их графиков. Сосредоточьтесь на их характеристиках и формулах (например, на форме кривой), чтобы вы могли быстро определить, какой тип функции представляет график. Запоминание предыдущего списка графиков общих функций поможет вам приобрести этот важный навык на тот случай, если они понадобятся вам для решения конкретных задач.

Определение того, является ли график функцией

Если вам дали график и вас попросили проверить, представляет ли график функцию или нет, вы можете действовать следующим образом:

• Проверка вертикальной линии: Этот тест покажет вам, представляет ли график функцию. Вам нужно провести вертикальные линии, пересекающие график. Если в какой-либо точке вертикальная линия пересекает график более одного раза, то график не является функцией (x имеет более одного выхода). Например:

Пример теста вертикальной линии, Марилу Гарсия Де Тейлор — StudySmarter Originals

Этот график не является функцией, поскольку вертикальная линия пересекает две точки на графике.

• Тест горизонтальной линии: Этот тест показывает, является ли функция взаимно однозначной или нет. Если вы рисуете горизонтальную линию, и она пересекает график более одного раза, то это , а не однозначная функция . Например:

Пример теста горизонтальной линии, Марилу Гарсиа Де Тейлор — StudySmarter Originals

Этот график является функцией, поскольку он проходит тест вертикальной линии, но не является взаимно однозначной функцией, поскольку горизонтальная линия дважды пересекает график.

Графики общих функций. Ключевые выводы

• Функция представляет собой математическую конструкцию, которая принимает значения x в качестве входных данных и выводит значения y в соответствии один к одному или многие к одному.

• Графики общих функций — это графическое представление функций, которые часто используются в математике.

• Изучение форм различных типов графиков функций, их особенностей и формул помогает быстро определить, какой тип функции представляет график, глядя на форму кривой.

  No related posts.