Сложение и вычитание и умножение векторов: 1. Сложение и вычитание векторов. Умножение вектора на число

Понятие вектора. Действия с векторами, их свойства — сложение и вычитание векторов, умножение на число, коллинеарность. Скалярное умножение (произведение) векторов. Проекции, разложение векторов, координаты, действия в координатах, взаимное расположение

Адрес этой страницы (вложенность) в справочнике dpva.ru: главная страница / / Техническая информация / / Математический справочник / / Математика для самых маленьких. Шпаргалки. Детский сад, Школа. / / Понятие вектора. Действия с векторами, их свойства — сложение и вычитание векторов, умножение на число, коллинеарность. Скалярное умножение (произведение) векторов. Проекции, разложение векторов, координаты, действия в координатах, взаимное расположение

Содержание

Понятие вектора. Коллинеарные векторы. Действия с векторами и их свойства — сложение и
вычитание векторов, умножение вектора на число, критерий коллинеарности. Скалярное умножение
(произведение) векторов. Проекция вектора на вектор. Разложение векторов по неколлинеарным
векторам. Координаты вектора на плоскости. Действия с векторами в координатах на плоскости.
Взаимное расположение векторов. Разложение вектора по координатным векторам.

Сложение и вычитание векторов. Умножение вектора на число

1.	Выражение, содержащее векторы	1 вид — рецептивный	лёгкое	2 Б.	Упрощение выражения, содержащего векторы.
2.	Сумма векторов	1 вид — рецептивный	среднее	3 Б.	Вычисление суммы векторов, которые отложены на сторонах параллелепипеда.
3.	Сумма и разность векторов	1 вид — рецептивный	лёгкое	2 Б.	Сложение и вычитание векторов.
4.	Сложение и вычитание векторов	1 вид — рецептивный	лёгкое	2 Б.	Отработка простых операций с векторами.
5.	Арифметические операции с векторами	1 вид — рецептивный	лёгкое	2 Б.	Простейшие операции с векторами.
6.	Выражение вектора суммы	1 вид — рецептивный	среднее	3 Б.	Выражение вектора суммы через данный вектор.
7.	Выражение вектора разности	1 вид — рецептивный	среднее	3 Б.	Выражение вектора разности через данный вектор.
8.	Выражение с векторами	2 вид — интерпретация	среднее	5 Б.	Выполнение арифметических действий с векторами.
9.	Сложение и вычитание векторов	2 вид — интерпретация	среднее	4 Б.	Сложение и вычитание нескольких векторов.
10.	Сумма нескольких векторов	1 вид — рецептивный	среднее	3 Б.	Вычисление суммы нескольких векторов.
11.	Умножение вектора на число	2 вид — интерпретация	среднее	4 Б.	Нахождение числового коэффициента, выражающего отношение векторов.
12.	Сложение и умножение на число	3 вид — анализ	сложное	10 Б.	Вычисление результата нескольких операций с векторами.
13.	Арифметические действия с векторами, длина вектора	3 вид — анализ	сложное	8 Б.	Вычисление результата нескольких операций с векторами.
14.	Уравнение с векторами	3 вид — анализ	сложное	8 Б.	Нахождение неизвестного слагаемого.

Сложение и вычитание векторов. Умножение вектора на число. Геометрия, 10 класс: уроки, тесты, задания.

1.	Выражение, содержащее векторы Сложность: лёгкое	2
2.	Сумма векторов Сложность: среднее	3
3.	Сумма и разность векторов Сложность: лёгкое	2
4.	Сложение и вычитание векторов Сложность: лёгкое	2
5.	Арифметические операции с векторами Сложность: лёгкое	2
6.	Выражение вектора суммы Сложность: среднее	3
7.	Выражение вектора разности Сложность: среднее	3
8.	Выражение с векторами Сложность: среднее	5
9.	Сложение и вычитание векторов Сложность: среднее	4
10.	Сумма нескольких векторов Сложность: среднее	3
11.	Умножение вектора на число Сложность: среднее	4
12.	Сложение и умножение на число Сложность: сложное	10
13.	Арифметические действия с векторами, длина вектора Сложность: сложное	8
14.	Уравнение с векторами Сложность: сложное	8

определение, сложение, умножение, скалярное и векторное произведение

В статье узнаете что такое вектор, векторные компоненты, единичный вектор, как складывать вектора, умножать вектора на скаляр, скалярное, векторное и смешанное произведение двух векторов.

Сохранение физической величины с вектором обычно означает совершенно иную ситуацию, чем просто сохранение ее скалярной длины. Постоянное значение импульса p (скаляр) может означать совершенно иную ситуацию, чем постоянный вектор p.

Вектор должен иметь три необходимые характеристики: значение (длина), направление, начало и конец.

Любое изменение любого из этих признаков — длины, направления или начало с концом — означает, что создан другой вектор. Два вектора равны тогда и только тогда, когда они имеют равную длину, направление и начало с концом.

Векторные компоненты

Компонентами вектора являются его проекции на оси системы координат.

Также в трехмерном пространстве векторы A называются векторами, которые являются проекциями этого вектора A на оси системы координат.

Имея вектор A, мы погружаем его в систему координат x, y, z. Векторы, являющиеся проекциями вектора A на оси системы, называются векторными компонентами вектора A. Вектор A является векторной суммой составляющих векторов A_x, A_y и A_z .

Единичный вектор

Единичный вектор, имеющий то же направление, что и вектор, на который он ссылается, важен, но его длина всегда равна 1.

Единичные векторы осей координат. Мы также присваиваем единичные векторы оси системы отсчета. а) относится к правовращающей системе и б) к левосторонней системе.

Сложение векторов

Сумма вектора обычно не совпадает с суммой скалярных величин:

Добавление двух или более векторов друг к другу сводится к добавлению их компонентов, то есть проекций на опорные оси. Результирующий вектор называется случайным вектором. Для двух векторов результирующий вектор является диагональю параллелограмма, построенного на этих векторах. Метод параллелограмма.

В случае большего числа векторов результирующий вектор получается путем рисования одного из этих векторов, затем в конце первого вектора мы начинаем второй, в конце второго мы даем начало третьего и так далее. Полученный вектор является вектором, начало которого находится в начале первого из добавленных векторов. и его конец в конце последнего. При изменении порядка сложения результирующий вектор (красный) не меняет длину, направление:

Получение вектора используя соединения векторов

Это правило добавления векторов также действует в трехмерном пространстве:

Добавление векторов в трехмерном пространстве

Умножение вектора на скаляр

Самым простым умножением, выполняемым на векторах, является умножение вектора на скаляр (число). Такое умножение не меняет направление вектора, но, как правило, меняет его длину и может изменить его конец (когда скаляр является отрицательным числом). Когда вектор A умножается на α-скаляр, мы получаем новый вектор B:

Скалярное произведение и векторное произведение двух векторов являются очень важными направления в физике и геометрии. Существует также смешанное произведение трех векторов.

Скалярное произведение двух векторов

Формально скалярное произведение векторов представляет собой точку, и ее значение определяется зависимостью

Скалярное произведение описывает способ, которым оба вектора видят друг друга, то есть как долго тень (проекция) отбрасывает каждый из векторов в своего партнера, когда угол между ними равен φ

скалярное произведение векторов АБ с проекциями

B cos φ — длина тени, которую вектор B выбрасывает в вектор A. Аналогично, A cos φ — длина тени, которую вектор A выбрасывает в вектор B.

Когда длина проекции (тени) одного из векторов равна нулю, тогда длина проекции второго вектора равна нулю, то есть A • B = 0. Это означает, что эти векторы не работают в одном и том же направлении вообще. Работа, которую мы выполняем при движении автомобиля, зависит не только от приложенной силы F, но и от угла, который создает направление силы и направление пути.

Так как единичные векторы оси системы отсчета х, у и z, которые обозначают векторы е_х, е_Y и е_z, перпендикулярны друг к другу, то в виду того, что А • В = АВcosφ и что cos 0 = 1 и cos 90^o = 0, мы получаем произведение значений этих единичных векторов:

Выполнение аналогичного умножения на векторы A и B

мы получили новое выражение для скалярного произведения двух векторов A и B

Значение скалярного произведения двух векторов A и B можно записать в виде двух эквивалентных выражений:

Сравнивая оба выражения, мы находим выражение для угла между векторами A и B:

Векторное произведение двух векторов

Многие важные величины в науке и технике определяются вектором, который является произведением двух других векторов. В таких случаях произведение этих векторов, называемое векторным произведением , приводит к третьему вектору.

В этом случае задача состоит в том, чтобы определить все три особенности вектора C, являющегося произведением векторного произведения векторов A и B:

длина
направление
начало и конец

Произведение векторов A и B , приводящее к третьему вектору C, отмечено диагональным крестом

Направление

Вектор С такой, что вектор перпендикулярен к плоскости, образованной векторами A и B, которая перпендикулярна как к вектору A и B.

Длина

вектор С равен значению параллелограмма, построенного на векторах А и В. Числовой C = ABsin φ.

Начало и конец

Вектор С определяет правое направление движения шнека во время нанесения первого вектора, а именно А или B.

Изменение порядка применения векторов означает изменение знака векторного произведения.

Таким образом, действительное свойство векторного произведения выглядит следующим образом A*B= -B*A

В отличие от скалярного произведения, векторное произведение некоммутативно.

Мы встретимся с векторным произведением на протяжении всего курса физики. Это также часто встречается в механике, а также в науке об электричестве и магнетизме.

В повседневной жизни векторное произведение находится в виде момента силы во вращательном движении. Мы воздействуем на вращательное движение тем эффективнее, чем больше применяем момент силы.

При откручивании гайки гаечным ключом речь идет не только о силе F, но и о способе ее применения (длина рычага R и угол, который создает рычаг с направлением силы).

Практическое использования момента силы на примере

Все эти зависимости элегантно включены в одно выражение в виде векторного произведения:

Хотя составляющие вектора C, который является произведением векторного произведения векторов A и B, уже включены в его длину и направление, но имея данные составляющих векторов A и B, мы можем использовать их для определения компонентов вектора C в форме матрицы:

Векторное произведение двух векторов А и Б

Удобнее всего рассчитать этот определитель, расширив относительно первой строки.

Смешанное произведение трех векторов

Смешанное произведение трех векторов является скалярным значением, равным значению детерминанта

Геометрическая интерпретация: смешанное произведение численно равно объему V параллелепипеда, растянутому по векторам A, B и C:

Циклическая корректировка векторов в смешанном произведении не меняет значение этого произведения, то есть:

сложение и вычитание векторов, умножение вектора на число, свойства этих операций. — Студопедия

I) Сложение векторов

а) правило треугольника

б) правило параллелограмма

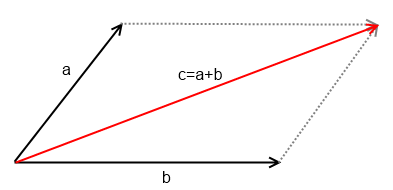
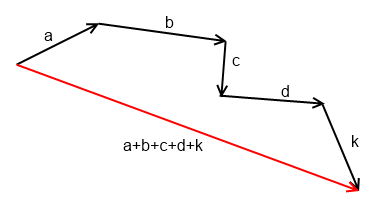
в) правило ломаной

Пусть даны несколько векторов. Тогда, чтобы построить сумму этих векторов, нужно расположить эти векторы так, чтобы начало последующего совпадало с концом предыдущего, получив таким образом ломаную. Тогда вектор, замыкающий эту ломаную, начало которого совпадает с началом первого вектора, а конец с концом последнего, будет суммой векторов.

Свойства операции сложения:

1) коммуникативность a+b=b+a

2) ассоциативность a+(b+c)=(a+b)+с

3) a+0=a

II) Разностью векторов 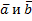называется вектор 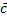такой, что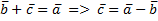

III) Умножение вектора на число

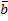Произведением вектора на число , называется вектор , коллинеарный вектору , длина которого равна , причем

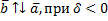
Умножение вектора на n — это растяжение этого вектора в n раз

Свойства умножения:

1) коммуникативность

2) ассоциативность

3) дистрибутивность

10 класс. Геометрия. Сложение и вычитание векторов. Умножение вектора на число. — Сложение и вычитание векторов. Умножение вектора на число.

Комментарии преподавателя

Отметим, что сложение векторов производится аналогично планиметрии, только все действия выполняются в пространстве.

Итак, пусть заданы два произвольных вектора в пространстве (рис. 1):

Рис. 1. Произвольные векторы в пространстве

Определим, что же называется суммой двух этих векторов.

Точно так же, как в планиметрии, из любой удобной точки, назовем ее точкой А, можно единственным образом отложить вектор, равный вектору . Напомним, что заданные векторы, как и любые другие, свободны, важно лишь направление и длина, сам вектор можно параллельно переносить в любое место как на плоскости, так и в пространстве. Так, мы получили вектор – в результате действия вектора точка А переместилась в точку В. Теперь из точки В откладываем единственно возможным образом вектор , получаем вектор – так, в результате действия вектора точка В переместилась в точку С. В результате точка А переместилась в точку С, получен вектор , который и называется суммой векторов и (рис. 2).

Рис. 2. Сумма двух векторов в пространстве

Так, получено правило треугольника для сложения векторов в пространстве.

Правило треугольника

Из любой точки пространства (точка А) откладываем первый вектор, из конца первого вектора (точка В) откладываем второй вектор и получаем точку С. Вектор, соединяющий начало первого вектора (точка А) и конец второго (точка С), и будет результирующим.

Отметим, что результат сложения векторов не зависит от выбора начальной точки, существует соответствующая теорема, которая это доказывает на основании того, что из точки можно отложить вектор, равный заданному, единственным образом.

Определение

Разностью двух векторов называется такой третий вектор, который, будучи сложенным со вторым вектором, даст первый вектор.

Введем разность векторов и , для этого сложим вектор с противоположным вектором :

Итак, из произвольной точки А откладываем вектор , получаем точку В. Чтобы получить вектор мы строим вектор, равный вектору по длине, но противонаправленный. Полученный вектор откладываем из точки В – получаем точку D. Вектор и будет искомым вектором разности.

Проиллюстрируем (рис. 3):

Рис. 3. Вычитание двух векторов в пространстве

Построим на заданных векторах и параллелограмм (рис. 4):

Рис. 4. Параллелограмм на двух заданных векторах

Т. к. вектор ; аналогично .

По правилу треугольника:

Так, одна из диагоналей параллелограмма, построенного на двух векторах, соответствует сумме этих векторов.

Рассмотрим разность векторов. По правилу треугольника:

Так, вторая диагональ параллелограмма, построенного на двух векторах, соответствует разности этих векторов.

Для сложения и вычитания нескольких векторов применяется правило многоугольника. Пусть заданы векторы и :

Рис. 5. Три вектора в пространстве

Необходимо построить вектор .

Видим, что перед некоторыми векторами стоят численные множители. Напомним, что при умножении вектора на число получаем сонаправленный вектор, длина которого – это длина исходного вектора, умноженная на заданное число. Получим векторы и . Вектор сонаправлен с вектором , длина его в три раза больше. Вектор противонаправлен вектору , длина его в два раза больше. Проиллюстрируем (рис. 6):

Рис. 6. Умножение вектора на число

Приступаем к сложению. Из произвольной точки А откладываем полученный вектор – получаем точку В. Из точки В откладываем вектор – получаем точку С. Из точки С откладываем вектор – получаем точку D. Согласно правилу многоугольника, вектор соответствует искомому вектору :

Рис. 7. Сложение векторов по правилу многоугольника

Задача 1:

Задан тетраэдр ABCD (рисунок 8). Доказать:

Рис. 8. Тетраэдр, задача 1

Решение:

По правилу треугольника:

Аналогично:

, ч. т. д.

По правилу треугольника:

Аналогично: , ч. т. д.

Задача 2

Упростить выражение:

Рассмотрим отдельно сумму двух векторов: , ее значение очевидно:

Проиллюстрируем (рис. 9):

Рис. 9. Сумма двух векторов

Теперь сократим противоположные векторы:

Можно было сразу заметить:

В результате упрощения получено:

Итак, мы ввели операции сложения и вычитания векторов, умножения вектора на число в стереометрии, отметили, что операции аналогичны таким же для планиметрии. Кроме того, решили несколько задач, базирующихся на описанных операциях.

ИСТОЧНИК

http://interneturok.ru/ru/school/geometry/10-klass/vektory-v-prostranstve/slozhenie-i-vychitanie-vektorov-umnozhenie-vektora-na-chislo

http://www.youtube.com/watch?v=JQzv4c5ak-0

http://www.youtube.com/watch?v=sKCfeWlmsLk

http://azdekor.ru/Spektr/SREDN_SKOOL/MATEM/026/images/Vkt3.jpg

https://www.kursoteka.ru/teacher//index.cfm/getfile/2364/7703/4155

http://azdekor.ru/Spektr/SREDN_SKOOL/MATEM/026/images/Vkt4.jpg

http://portfoliosmolgu.ucoz.ru/_ph/8/2/143950352.jpg?1445058118

http://www.mathprofi.ru/vektory_dlya_chainikov.html

Сложение и вычитание векторов [wiki.eduVdom.com]

Пусть $\overrightarrow{a}$ и $\overrightarrow{b}$ — два вектора (рис.1, а).

Сложение двух векторов
Рис.1
Возьмем произвольную точку О и построим вектор $\overrightarrow{ОА} = \overrightarrow{a}$ . Затем от точки А отложим вектор $\overrightarrow{AB} = \overrightarrow{b}$. Вектор $\overrightarrow{OB}$, соединяющий начало первого слагаемого вектора с концом второго (рис.1, б), называется суммой этих векторов и обозначается $\overrightarrow{a} + \overrightarrow{b}$$ (правило треугольника).
Ту же самую сумму векторов можно получить иным способом. Отложим от точки О векторы $\overrightarrow{ОА} = \overrightarrow{a} \,и\, \overrightarrow{ОС} = \overrightarrow{b} $ (рис.1, в). Построим на этих векторах как на сторонах параллелограмм ОABC. Вектор $\overrightarrow{ОВ}$, служащий диагональю этого параллелограмма, проведенной из вершины О, является, очевидно, суммой векторов $\overrightarrow{a} + \overrightarrow{b}$ {правило параллелограмма). Из рисунка 1, в непосредственно следует, что сумма двух векторов обладает переместительным свойством: $\overrightarrow{a} + \overrightarrow{b} = \overrightarrow{b} + \overrightarrow{a}$
Действительно, каждый из векторов $\overrightarrow{a} + \overrightarrow{b} \,и\, = \overrightarrow{b} + \overrightarrow{a}$ равен одному и тому же вектору $\overrightarrow{OB}$ .
Пример 1. В треугольнике ABC АВ = 3, ВС = 4, ∠ В = 90°. Найти: $а)\,\ \overrightarrow{|АВ|} + \overrightarrow{|ВС|};\,\,\ б)\,\ |\overrightarrow{АВ} + \overrightarrow{ВС}|$ .
Решение
а) Имеем: $|\overrightarrow{АВ}| = АВ,\,\,\ |\overrightarrow{ВС}| = ВС$ и, значит, $|\overrightarrow{АВ}| + |\overrightarrow{BC}| = 7$ .
б) Так как $\overrightarrow{AB} + \overrightarrow{ВС} = \overrightarrow{АС} \,\,,\,\, то\,\, |\overrightarrow{АВ} + \overrightarrow{ВС}| = |\overrightarrow{АС}| = АС$ .
Теперь, применяя теорему Пифагора, находим $$ AC = \sqrt{AB^2 + BC^2} = \sqrt{9 + 16} = 5 \\ т.е.\, |\overrightarrow{АВ} + \overrightarrow{ВС}| = 5. $$
Понятие суммы векторов можно обобщить на случай любого конечного числа слагаемых векторов.
Пусть, например, даны три вектора $\overrightarrow{a}, \overrightarrow{b} \,и\, \overrightarrow{c}$ (рис.2).

Сложение трех векторов
Рис.2
Построив сначала сумму векторов $\overrightarrow{a} + \overrightarrow{b}$ , а затем прибавив к этой сумме вектор $\overrightarrow{c}$, получим вектор $(\overrightarrow{a} + \overrightarrow{b}) + \overrightarrow{c}$ . На рисунке 2 $$ \overrightarrow{ОА} = \overrightarrow{a}\,; \overrightarrow{АВ} = b\,; \overrightarrow{ОВ} = \overrightarrow{a} + \overrightarrow{b}\,; \overrightarrow{BC} = \overrightarrow{c} \\ и \\ \overrightarrow{ОС} = \overrightarrow{ОВ} + \overrightarrow{ВС} = (\overrightarrow{a} + \overrightarrow{b}) + \overrightarrow{c} $$ Из рисунка 2 видно, что тот же вектор $\overrightarrow{ОС}$ мы получим, если к вектору $\overrightarrow{ОА} = \overrightarrow{a}$ прибавим вектор $\overrightarrow{АВ} = \overrightarrow{b} + \overrightarrow{c}$ . Таким образом, $(\overrightarrow{a} + \overrightarrow{b}) + \overrightarrow{c} = \overrightarrow{a} + (\overrightarrow{b} + \overrightarrow{c})$ , т. е. сумма векторов обладает сочетательным свойством. Поэтому сумму трех векторов $\overrightarrow{a}\,,\,\overrightarrow{b}\,,\,\overrightarrow{c}$ записывают просто $\overrightarrow{a} + \overrightarrow{b} + \overrightarrow{c}$ .
Разностью двух векторов $\overrightarrow{a} \,и\, \overrightarrow{b}$ называется третий вектор $\overrightarrow{c} = \overrightarrow{a} — \overrightarrow{b}$ , сумма которого с вычитаемым вектором $\overrightarrow{b}$ дает вектор $\overrightarrow{a}$. Таким образом, если $\overrightarrow{c} = \overrightarrow{a} — \overrightarrow{b}\,,\, то\, \overrightarrow{c} + \overrightarrow{b} = \overrightarrow{a}$ .
Из определения суммы двух векторов вытекает правило построения вектора-разности (рис.3).

Вычитание векторов
Рис.3
Откладываем векторы $\overrightarrow{ОА} = \overrightarrow{a} \,и\, \overrightarrow{OB} = \overrightarrow{b}$ из общей точки О. Вектор $\overrightarrow{BA}$ , соединяющий концы уменьшаемого вектора $\overrightarrow{a}$ и вычитаемого вектора $\overrightarrow{b}$ и направленный от вычитаемого к уменьшаемому, является разностью $\overrightarrow{c} = \overrightarrow{a} — \overrightarrow{b}$ . Действительно, по правилу сложения векторов $\overrightarrow{ОВ} + \overrightarrow{ВА} = \overrightarrow{ОА} \text{ , или } \overrightarrow{b} + \overrightarrow{c} = \overrightarrow{a}$ .
Пример 2. Сторона равностороннего треугольника ABC равна а. Найти: $а) |\overrightarrow{ВА} — \overrightarrow{ВС}|\,;\,\ б)\,\,\ |\overrightarrow{АВ} — \overrightarrow{АС}|$ .
Решение а) Так как $\overrightarrow{ВА} — \overrightarrow{ВС} = \overrightarrow{СА}\text{ , а }|\overrightarrow{СА}| = а\text{ , то }|\overrightarrow{ВА} — \overrightarrow{ВС}| = а$ .
б) Так как $\overrightarrow{АВ} — \overrightarrow{АС} = \overrightarrow{СВ}\text{ , а }|\overrightarrow{СВ}| = а\text{ , то }|\overrightarrow{АВ} — \overrightarrow{АС}| = а$ .
Произведением вектора $\overrightarrow{a}$(обозначается $=\lambda\overrightarrow{a}$ или $\overrightarrow{a}\lambda$) на действительное число $\lambda$ называется вектор $\overrightarrow{b}$, коллинеарный вектору $\overrightarrow{a}$, имеющий длину, равную $|\lambda||\overrightarrow{a}|$, и то же направление, что и вектор $\overrightarrow{a}$, если $\lambda > 0$ , и направление, противоположное направлению вектора $\overrightarrow{a}$, если $\lambda < 0$ . Так, например, $2\overrightarrow{a}$ есть вектор, имеющий то же направление, что и вектор $\overrightarrow{a}$ , а длину, вдвое большую, чем вектор $\overrightarrow{a}$ (рис.4).

Умножение вектора на число
Рис.4
В случае, когда $\lambda = 0$ или $\overrightarrow{a} = 0$ , произведение $\lambda\overrightarrow{a}$ представляет собой нулевой вектор. Противоположный вектор $-\overrightarrow{a}$ можно рассматривать как результат умножения вектора $\overrightarrow{a}$ на $\lambda = -1$ (см. рис.4): $$ -\overrightarrow{a} = \ (-1)\overrightarrow{a} $$ Очевидно, что $\overrightarrow{a} + (-\overrightarrow{a}) = \overrightarrow{0}$ .
Пример 3. Доказать, что если О, А, В и С — произвольные точки, то $\overrightarrow{ОА} + \overrightarrow{АВ} + \overrightarrow{ВС} + \overrightarrow{СО} = 0$ .
Решение. Сумма векторов $\overrightarrow{ОА} + \overrightarrow{АВ} + \overrightarrow{СВ} = \overrightarrow{ОС}$ , вектор $\overrightarrow{CO}$ — противоположный вектору $\overrightarrow{ОС}$ . Поэтому $\overrightarrow{ОС} + \overrightarrow{СО} = \overrightarrow{0}$ .
Пусть дан вектор $\overrightarrow{a}$. Рассмотрим единичный вектор $\overrightarrow{a_0}$ , коллинеарный вектору $\overrightarrow{a}$ и одинаково с ним направленный. Из определения умножения вектора на число следует, что $$ \overrightarrow{a} = |\overrightarrow{a}|\,\ \overrightarrow{a_0} $$ , т.е. каждый вектор равен произведению его модуля на единичный вектор того же направления. Далее из того же определения следует, что если $\overrightarrow{b} = \lambda\overrightarrow{a}$ , где $\overrightarrow{a}$ — ненулевой вектор, то векторы $\overrightarrow{a} \,и\, \overrightarrow{b}$ коллинеарны. Очевидно, что и обратно, из коллинеарности векторов $\overrightarrow{a} \,и\, \overrightarrow{b}$ следует, что $\overrightarrow{b} = \lambda\overrightarrow{a}$.
Таким образом, получаем следующую теорему.
Пример 4. Длина вектора AB равна 3, длина вектора AC равна 5. Косинус угла между этими векторами равен 1/15. Найдите длину вектора AB + AC.
Видео-решение.
добавление векторов — вычитание векторов
Классы
Класс 1 — 3
Класс 4 — 5
Класс 6 — 10
Класс 11 — 12
КОНКУРСЫ
BBS
000000000 Книги
NCERT Книги для 5 класса
NCERT Книги Класс 6
NCERT Книги для 7 класса
NCERT Книги для 8 класса
NCERT Книги для 9 класса
NCERT Книги для 10 класса
NCERT Книги для 11 класса
NCERT Книги для 12-го класса
NCERT Exemplar
NCERT Exemplar Class 8
NCERT Exemplar Class 9
NCERT Exemplar Class 10
NCERT Exemplar Class 11
NCERT Exemplar Class 12
9000al Aggar Agaris Agard Agard Agard Agard Agard 2000 12000000
Решения RS Aggarwal класса 10
Решения RS Aggarwal класса 11
Решения RS Aggarwal класса 10
90 003 Решения RS Aggarwal класса 9
Решения RS Aggarwal класса 8
Решения RS Aggarwal класса 7
Решения RS Aggarwal класса 6
Решения RD Sharma
Решения класса RD Sharma
Решения класса 9 Шарма 7 Решения RD Sharma Class 8
Решения RD Sharma Class 9
Решения RD Sharma Class 10
Решения RD Sharma Class 11
Решения RD Sharma Class 12
ФИЗИКА
Механика
000000 Электромагнетизм
ХИМИЯ
Органическая химия
Неорганическая химия
Периодическая таблица
МАТС
Теорема Пифагора
Отношения и функции
Последовательности и серии
Таблицы умножения
Детерминанты и матрицы
Прибыль и убыток
Полиномиальные уравнения
Делительные дроби
000 ФОРМУЛЫ
Математические формулы
Алгебровые формулы
Тригонометрические формулы
Геометрические формулы
КАЛЬКУЛЯТОРЫ
Математические калькуляторы
S000
S0003
Pегипс Класс 6
Образцы документов CBSE для класса 7
Образцы документов CBSE для класса 8
Образцы документов CBSE для класса 9
Образцы документов CBSE для класса 10
Образцы документов CBSE для класса 11
Образец образца CBSE pers for Class 12
CBSE Документ с вопросами о предыдущем году
CBSE Документы за предыдущий год Class 10
CBSE Вопросы за предыдущий год Class 12
HC Verma Solutions
HC Verma Solutions Класс 11 Физика
Решения HC Verma Class 12 Physics
Решения Lakhmir Singh
Решения Lakhmir Singh Class 9
Решения Lakhmir Singh Class 10
Решения Lakhmir Singh Class 8
Примечания
CBSE
Notes
CBSE Класс 7 Примечания CBSE
Класс 8 Примечания CBSE
Класс 9 Примечания CBSE
Класс 10 Примечания CBSE
Класс 11 Примечания CBSE
Класс 12 Примечания CBSE
Примечания пересмотра
CBSE Редакция
CBSE
CBSE Class 10 Примечания к пересмотру
CBSE Class 11 Примечания к пересмотру 9000 4
Замечания по пересмотру CBSE класса 12
Дополнительные вопросы CBSE
Дополнительные вопросы CBSE 8 класса
Дополнительные вопросы CBSE 8 по естественным наукам
CBSE 9 класса Дополнительные вопросы
CBSE 9 дополнительных вопросов по науке CBSE
9000 Класс 10 Дополнительные вопросы по математике
CBSE Класс 10 Дополнительные вопросы по науке
Класс CBSE
Класс 3
Класс 4
Класс 5
Класс 6
Класс 7
Класс 8
Класс 9
Класс 10
Класс 11
Класс 12
Решения для учебников
Решения NCERT
Решения NCERT для класса 11
Решения NCERT для физики класса 11
Решения NCERT для класса 11 Химия
Решения для класса 11 Биология
NCERT Решения для класса 11 Математика
9 0003 NCERT Solutions Class 11 Бухгалтерия
NCERT Solutions Class 11 Бизнес исследования
NCERT Solutions Class 11 Экономика
NCERT Solutions Class 11 Статистика
NCERT Solutions Class 11 Коммерция
NCERT Solutions для класса 12
NCERT Solutions для Класс 12 Физика
Решения NCERT для 12 класса Химия
Решения NCERT для 12 класса Биология
Решения NCERT для 12 класса Математика
Решения NCERT Класс 12 Бухгалтерский учет
Решения NCERT Класс 12 Бизнес исследования
Решения NCERT Класс 12 Экономика
NCERT Solutions Class 12 Бухгалтерский учет Часть 1
NCERT Solutions Class 12 Бухгалтерский учет Часть 2
NCERT Solutions Class 12 Микроэкономика
NCERT Solutions Class 12 Коммерция
NCERT Solutions Class 12 Макроэкономика
NCERT Solutions Для Класс 4
Решения NCERT для математики класса 4
Решения NCERT для класса 4 EVS
Решения NCERT для класса 5
Решения NCERT для математики класса 5
Решения NCERT для класса 5 EVS
Решения NCERT для класса 6
Решения NCERT для класса 6 Maths
Решения NCERT для класса 6 Science
Решения NCERT для класса 6 Общественные науки
Решения NCERT для класса 6 Английский
Решения NCERT для класса 7
Решения NCERT для класса 7 Математика
Решения NCERT для 7 класса Science
Решения NCERT для 7 класса Общественные науки
Решения NCERT для 7 класса Английский
Решения NCERT для 8 класса Математические решения
для 8 класса Математика
Решения NCERT для класса 8 Science
Решения NCERT для класса 8 Общественные науки
NCERT Solutio ns для класса 8 Английский
Решения NCERT для класса 9
Решения NCERT для класса 9 Общественные науки
Решения NCERT для класса 9 Математика
Решения NCERT для класса 9 Математика Глава 1
Решения NCERT Для класса 9 Математика 9 класса Глава 2
Решения NCERT для математики 9 класса Глава 3
Решения NCERT для математики 9 класса Глава 4
Решения NCERT для математики 9 класса Глава 5
Решения NCERT для математики 9 класса Глава 6
Решения NCERT для Математика 9 класса Глава 7
Решения NCERT для математики 9 класса Глава 8
Решения NCERT для математики 9 класса Глава 9
Решения NCERT для математики 9 класса Глава 10
Решения NCERT для математики 9 класса Глава 11
Решения NCERT для Математика 9 класса Глава 12
Решения NCERT для математики 9 класса Глава 13
Решения NCERT для математики 9 класса Глава 14
Решения NCERT для математики класса 9 Глава 15
Решения NCERT для науки 9 класса
Решения NCERT для науки 9 класса Глава 1
Решения NCERT для науки 9 класса Глава 2
Решения NCERT для класса 9 Наука Глава 3
Решения NCERT для 9 класса Наука Глава 4
Решения NCERT для 9 класса Наука Глава 5
Решения NCERT для 9 класса Наука Глава 6
Решения NCERT для 9 класса Наука Глава 7
Решения NCERT для 9 класса Научная глава 8
Решения NCERT для 9 класса Научная глава
Научные решения NCERT для 9 класса Научная глава 10
Научные решения NCERT для 9 класса Научная глава 12
Научные решения NCERT для 9 класса Научная глава 11
Решения NCERT для 9 класса Научная глава 13
Решения NCERT для 9 класса Научная глава 14
Решения NCERT для класса 9 Science Глава 15
Решения NCERT для класса 10
Решения NCERT для класса 10 Общественные науки
Решения NCERT для математики класса 10
Решения NCERT для математики класса 10 Глава 1
Решения NCERT для математики класса 10 Глава 2
решения NCERT для математики класса 10 глава 3
решения NCERT для математики класса 10 глава 4
решения NCERT для математики класса 10 глава 5
решения NCERT для математики класса 10 глава 6
решения NCERT для математики класса 10 Глава 7
решения NCERT для математики класса 10 глава 8
решения NCERT для математики класса 10 глава 9
решения NCERT для математики класса 10 глава 10
решения NCERT для математики класса 10 глава 11
решения NCERT для математики класса 10, глава 12
Решения NCERT для математики класса 10, глава 13
соль NCERT Решения для математики класса 10 Глава 14
Решения NCERT для математики класса 10 Глава 15
Решения NCERT для науки 10 класса
Решения NCERT для науки 10 класса Глава 1
Решения NCERT для науки 10 класса Глава 2
Решения NCERT для науки 10 класса, глава 3
Решения NCERT для науки 10 класса, глава 4
Решения NCERT для науки 10 класса, глава 5
Решения NCERT для науки 10 класса, глава 6
Решения NCERT для науки 10 класса, глава 7
Решения NCERT для науки 10 класса, глава 8
Решения NCERT для науки 10 класса, глава 9
Решения NCERT для науки 10 класса, глава 10
Решения NCERT для науки 10 класса, глава 11
Решения NCERT для науки 10 класса, глава 12
Решения NCERT для 10 класса Science Глава 9
Решения NCERT для 10 класса Science Глава 14
Решения NCERT для науки 10 класса Глава 15
Решения NCERT для науки 10 класса Глава 16
Программа NCERT
NCERT
Коммерция
Класс 11 Коммерческая программа Syllabus
Учебный курс по бизнес-классу 11000
Учебная программа по экономическому классу
Учебная программа по коммерческому классу
Учебная программа по 12 классу
Учебная программа по 12 классу
Учебная программа по экономическому классу
000000000000000000
Образцы коммерческих документов класса 11
Образцы коммерческих документов класса 12
Решения TS Grewal
Решения TS Grewal Класс 12 Бухгалтерский учет
Решения TS Grewal Класс 11 Бухгалтерский учет
Отчет о движении денежных средств
eurship
Защита потребителей
Что такое фиксированный актив
Что такое баланс
Формат баланса
Что такое акции
Разница между продажами и маркетингом
P000S Документы ICSE
ML Решения Aggarwal
ML Решения Aggarwal Class 10 Maths
ML Решения Aggarwal Class 9 Математика
ML Решения Aggarwal Class 8 Maths
ML Решения Aggarwal Class 7 Математические решения
ML 6 0004
ML 6
Selina Solutions
Selina Solution для 8 класса
Selina Solutions для 10 класса
Selina Solution для 9 класса 9
Frank Solutions
Frank Solutions для класса 10 Maths
Frank Solutions для класса 9 Maths
ICSE Class 9000 2
ICSE Class 6
ICSE Class 7
ICSE Class 8
ICSE Class 9
ICSE Class 10
ISC Class 11
ISC Class 12
IAS
Сервисный экзамен
UPSC Syllabus
Бесплатно IAS Prep
Текущая информация
Список статей IAS
IAS 2019 Mock Test
IAS 2019 Mock Test 1
IAS 2019 Mock Test 2
KPSC KAS экзамен
UPPSC PCS экзамен
MPSC экзамен
RPSC RAS экзамен
TNPSC группа 1
APPSC группа 1
BPSC экзамен
экзамен
JPS
экзамен
экзамен
WPSS
экзамен
JPS
экзамен
экзамен
экзамен
экзамен
экзамен
экзамен
экзамен
экзамен
экзамен
Вопросник UPSC 2019
Ключ ответа UPSC 2019
Коучинг IAS
IA S Коучинг Бангалор
IAS Коучинг Дели
IAS Коучинг Ченнаи
IAS Коучинг Хайдарабад
IAS Коучинг Мумбаи
JEE
Бумага
JEE JEE 9000
JEE
JEE-код
JEE
J0003 S0004000
JEE Вопрос
Биноминальная теорема
JEE Статьи
Квадратичное уравнение
NEET
Программа Бьюя NEET
NEET 2020
NEET Подготовка к экзамену NEET
S0003
образца
Поддержка
Жалоба Разрешение
Customer Care
Поддержка центр
Государственные платы
GSEB
GSEB Силабус
GSEB Вопрос бумаги
GSEB образец бумаги
GSEB Книги
90 004
MSBSHSE
MSBSHSE Syllabus
MSBSHSE Учебники
MSBSHSE Образцы документов
MSBSHSE Вопросные записки
AP Board
-й год APSERT
-й год SBSUS
-й год
SUBSUS
SUBSUS
SUBSUS
SUBSUS
SUBSUS
SUBSUS
SUBSUS
SUBSUS
SUBSUS
SUBSUS
SUBSUS
SUBSUS SUBSUS SUBSUS SUBSUS SUBSUS
SUBSUS
SUBSUS
SUBSUS
SUBSUS SUBSUS
SUBSUS
Всеобщая справка
MP Board
MP Board Syllabus
MP Board Образцы документов
MP Board Учебники
Assam Board
Assam Board Syllabus
Assam Board Учебники
Sample Board Paperss Sample3 P0003 BSEB
Бихарская доска Syllabus
Бихарская доска Учебники
Бихарская доска Вопросные бумаги
Бихарская модель Бумажные макеты
БСЭ Одиша
доска
Sislabus
Совет 9408 S0008
Sisplus
S0008
Sample P000S
Sample
S000S PSEB Syllabus
Учебники PSEB
Документы PSEB
RBSE
Учебное пособие Раджастхана Syllabus
Учебники RBSE
Документы RBSE
PCB
HPE HPSBE
JKBOSE
JKBOSE Syllabus
JKBOSE Образцы документов
JKBOSE Образец экзамена
TN Board
TN Board Syllabus
Board 931 JAC
JAC Силабус
JAC учебники
JAC Вопрос Papers
Telangana Совет
Telangana Совет Силабус
Telangana совет учебники
Telangana Совет Вопрос Papers
KSEEB KSEEB Силабус
KSEEB Модель Вопрос Papers
KBPE
KBPE Силабус
KBPE Учебники
KBPE Вопрос Papers
UPMSP
UP Совет Силабус
UP Совет Книги
UP Совет Вопрос Papers
Западная Бенгалия Совет
Западная Бенгалия Совет Силабус
Западная Бенгалия Совет учебниками
West Bengal совет Вопрос документы
UBSE
TBSE
Goa Board
NbSe
CGBSE
MBSE
Meghalaya Совет
Manipur Совет
Харьяны Совет
Государственные экзамены
Банк экзаменов
SBI Exams
PIL, Exams
RBI Exams
PIL, РРБ экзамен
SSC Exams
SSC JE
SSC GD
SSC CPO 900 04
SSC CHSL
SSC CGL
RRB экзаменов
RRB JE
RRB NTPC
RRB ALP
L0003000000 L0003000000000000 UPSC CAPF
Список государственных экзаменов Статьи
Обучающие дети
Класс 1
Класс 2
Класс 3
Академические вопросы
Вопросы физики
Вопросы химии
Химические вопросы
Химические вопросы
Вопросы химии
Биология
Вопросы
Вопросы по науке
Вопросы ГК
Обучение онлайн
Обучение на дому
Полные формы
CAT
Программа CAT BYJU’S
CAT
CAT
CAT
CAT
CAT
CAT
CAT
CAT
FreeBS
40004 CAT 2020 Exam Pattern
Обзор приложения Byju на CAT
КУПИТЬ КУРС
+91924350046
.
сложение и вычитание векторов — учебный материал для IIT JEE
Кинематика и вращательное движение
Предлагаемая цена: рупий636
Подробнее

Скалярные величины могут быть добавлены алгебраически.например, 4 кг сахара и 3 кг сахара при любом сочетании всегда дают 7 кг сахара. Это не всегда так в случае векторов, так как они имеют направления, в дополнение к величинам.
Ниже приведены некоторые моменты, касающиеся сложения векторов:
(а) Добавление или составление векторов означает нахождение результирующего числа векторов, действующих на тело.
(b) Векторы могут быть добавлены геометрически, а не алгебраически.
(c) Векторы, результат которых должен быть рассчитан, ведут себя независимо друг от друга.Другими словами, каждый вектор ведет себя так, как если бы другие векторы отсутствовали.
(d) Добавление вектора является коммутативным.
Итак, $\vec{a}+\vec{b} =\vec{b}+\vec{a}$
Это означает, что закон сложения векторов не зависит от порядка векторов.
Графическое представление сложения векторов

Чтобы найти $\vec{a}+\vec{b}$ , сдвиньте вектор $\vec{b}$ так, чтобы его начальная точка совпадала с конечной точкой вектора $\vec{a}$ .Теперь вектор, начальная точка которого совпадает с начальной точкой вектора $\vec{a}$ , а конечная точка совпадает с конечной точкой вектора $\vec{b}$ , представляет $\vec{a}+\vec{b}$ , как показано на приведенном выше рисунке.
Чтобы найти $\vec{b}+\vec{a}$ , сдвиньте $\vec{a}$ так, чтобы его начальная точка совпадала с конечной точкой $\vec{b}$ . Вектор, начальная точка которого совпадает с начальной точкой $\vec{b}$ , а конечная точка совпадает с конечной точкой $\vec{a}$ , представляет $\vec{b}+\vec{a}$ .

Закон векторного сложения треугольника
Это закон для сложения двух векторов.Это можно сформулировать следующим образом:
«Если два вектора представлены (по величине и направлению) двумя сторонами треугольника, взятыми в одном и том же порядке, то их результирующая величина будет представлена (по величине и направлению) третьей стороной треугольника, взятой в противоположном порядке. »
Рассмотрим два вектора $\vec{A}$ и $\vec{B}$ [ниже], действующих одновременно на тело. Представьте вектор $\vec{B}$ линией $\vec{OB}$ . На A нарисуйте еще одну линию $\vec{OA}$ , представляющую $\vec{B}$ . Присоединяйтесь к OC.Затем $\vec{OC}$ (= $\vec{R}$ ) дает результат $\vec{A}$ и $\vec{B}$ . Можно отметить, что $\vec{OB}$ и $\vec{BC}$ находятся в одном и том же порядке, а $\vec{R}$ — в противоположном. Это соответствует закону треугольника.
$\vec{R}$
Итак, $\vec{R}$ = $\vec{OC}$
= $\vec{A}$ + $\vec{B}$
= $\vec{B}$ + $\vec{A}$
Кроме того, ясно, что порядок векторов в сложении векторов не имеет значения. Итак, сложение векторов коммутативно.
Если θ — угол между $\vec{A}$ и $\vec{B}$ , то величина результирующего вектора $\vec{R}$ будет равна
R = √ (A ² + B ²) + 2AB cos θ
и
если? угол между $\vec{B}$ и $\vec{R}$ , то
? = tan ^-1 [A sinθ / (B + A cosθ)]
Если три вектора, действующих одновременно на частицу, могут быть представлены тремя сторонами треугольника, взятыми в одном и том же порядке, то частица останется в равновесии.
Математически это можно выразить следующим образом:
$\vec{A}+\vec{B}+\vec{C}=0$
Закон параллелограмма векторов
Сложение двух векторов также может быть понято по закону параллелограмма. В нем говорится, что «если два вектора, действующих одновременно в точке, представлены по величине и направлению двумя сторонами параллелограмма, нарисованного из точки, их результирующее значение будет дано по величине и направлению диагональю параллелограмма, проходящего через эту точку.”
Согласно этому закону, если два вектора $\vec{P}$ и $\vec{Q}$ представлены двумя смежными сторонами параллелограмма, оба из которых направлены наружу, как показано на рисунке ниже, то диагональ, проведенная через пересечение двух векторов, представляет результирующий результат (т.е. векторную сумму $\vec{P}$ и $\vec{Q}$ ). Если Q — это смещение от положения AD к BC, смещая его параллельно себе, этот метод становится эквивалентным методу треугольника.

В случае сложения двух векторов методом параллелограмма, как показано на рисунке, полученная величина будет иметь вид,
(AC) ² = (AE) ² + (EC) ²
или R ² = (P + Q cos θ) ² (Q sin θ) ²
или R = √ (P ² + Q ²) + 2PQcos θ
И направление результирующего от вектора P будет дано

загар? = CE / AE = Qsinθ / (P + Qcosθ)
? = tan ^-1 [Qsinθ / (P + Qcosθ)]
Особые случаи
(a) Когда θ = 0 °, cos θ = 1, sin θ = 0 °
Подставляя для cos θ в уравнение R = √ (P ² + Q ²) + 2PQcos θ, получаем
R = √ (P ² + Q ²) + 2PQcos θ
= √ (P + Q) ²
или R = P + Q (максимум)
Подставляя для sin θ и cos θ в уравнение? = tan-1 [Qsinθ / (P + Qcosθ)], получаем
? = tan ^-1 [Qsinθ / (P + Qcosθ)]
= загар ^-1 [(Q × 0) / (P + (Q × 1))]
= загар ^-1 (0)
= 0 °
Результат двух векторов, действующих в одинаковых направлениях, равен сумме двух.Направление результирующего совпадает с направлением двух векторов.
(b) Когда θ = 180 °, cos θ = -1, sin θ = 0 °
Подставляя для cos θ в уравнение R = √ (P ² + Q ²) + 2PQcos θ, получаем
R = √ (P ² + Q ²) + 2PQ (-1)
= √P ² + Q ² — 2PQ
= √ (P — Q) ² (минимум)
R = P — Q (минимум)
Подставляя для sin θ и cos θ в уравнение? = tan-1 [Qsinθ / (P + Qcosθ)], получаем
? = tan ^-1 [Qsinθ / (P + Qcosθ)]
= загар ^-1 [(Q × 0) / (P + (Q × (-1)))]
= загар ^-1 (0)
= 0 °
Эта величина результирующего двух векторов, действующих в противоположном направлении, равна разности величин двух и представляет минимальное значение.Направление результирующего в направлении большего.
(c) Когда θ = 90 °, cos θ = 0, sin θ = 1
Подставляя для cos θ в уравнение R = √ (P ² + Q ²) + 2PQcos θ, получаем
R = √ (P ² + Q ²) + (2PQ × 0)
= √P ² + Q ²
Подставляя для sin θ и cos θ в уравнение? = tan-1 [Qsinθ / (P + Qcosθ)], получаем
? = tan ^-1 [Qsinθ / (P + Qcosθ)]
= загар ^-1 [(Q × 1) / (P + (Q × (0)))]
= загар ^-1 (Q / P)
Результирующее значение двух векторов, действующих под прямым углом друг к другу, равно квадратному корню из суммы квадратов величин двух векторов.Направление результирующего зависит от их относительных величин.
вектор вычитание
Процесс вычитания одного вектора из другого эквивалентен добавлению вектора отрицательного вектора, который необходимо вычесть. Предположим, есть два вектора $\vec{A}$ и $\vec{B}$ , показанные на рисунке (А), и мы должны вычесть $\vec{B}$ и $\vec{A}$ . Это то же самое, что добавить векторы — от $\vec{B}$ до $\vec{A}$ . Результат показан на рисунке (B).

Рисунок (A)

Рисунок (B)

Свойства векторного добавления: — Добавление вектора соответствует следующим свойствам.
1. Сложение векторов является коммутативным: — Это означает, что порядок векторов, добавляемых вместе, не влияет на результат сложения. Если два вектора $\vec{a}$ и $\vec{b}$ должны быть сложены вместе, то

2. Добавление вектора является ассоциативным: — При суммировании трех трех или более векторов взаимная группировка векторов не влияет на результат.
Математически,

3. Сложение векторов является дистрибутивным: — Это означает, что скалярное время равно сумме двух векторов и равно сумме скалярного времени двух векторов в отдельности.
Математически,
$m\vec{a}+m\vec{b} = m(\vec{a}+\vec{b})$
Геометрическое представление сложения векторов

Величина и направление $\vec{a}+\vec{b}$ : —
Пусть угол между вектором $\vec{a}$ и $\vec{b}$ будет θ.
На рисунке вектор ( $\vec{OA}$ ) = вектор $\vec{a}$ , вектор ( $\vec{AB}$ ) = вектор $\vec{b}$
От ADB,
AD = b cos θ
BD = b sin θ

В прямом угле ΔODB,
OD = a + b cosθ
BD = b sin θ
Следовательно, OB = √ (OD ² + BD ²)
=> | A + b | = √ (a ² + b ² + 2ab cos θ)
| a + b | _макс. = a + b, когда θ = 2nπ
| a + b | _мин = | a — b | когда θ = (2n + 1) π
(где n = 0, 1, 2,…..)
Если a + b наклонен под углом α с вектором a, то
tan α = ((b sin θ) / (a + b cosθ))
Связанные ресурсы
Чтобы узнать больше, купите учебные материалы Units & Dimensions, включающие в себя учебные заметки, заметки о пересмотре, видео-лекции, решенные вопросы за предыдущий год и т. Д. Также ищите больше учебных материалов по физике здесь.

Особенности курса
731 Видео Лекции
Редакция Примечания
Документы за предыдущий год
Mind Map
Планировщик исследования
NCERT Solutions
Дискуссионный форум
Тестовая бумага с Video Solution

,
python — перегрузка операторов сложения, вычитания и умножения Переполнение стека
Товары
Клиенты
Случаи использования
Переполнение стека Публичные вопросы и ответы
Команды Частные вопросы и ответы для вашей команды
предприятие Частные вопросы и ответы для вашего предприятия
работы Программирование и связанные с ним технические возможности карьерного роста
Талант Нанимать технический талант
реклама Связаться с разработчиками по всему миру
Загрузка…
Авторизоваться зарегистрироваться
.
сложение и вычитание векторов
РАЗДЕЛ 7-4 Алгебраические векторы
7-4 алгебраических векторов 531 SECTIN 7-4 алгебраических векторов От геометрических векторов до алгебраических векторов Векторное сложение и единица скалярного умножения Векторы алгебраических свойств Статическое равновесие Геометрические векторы
Дополнительная информация Фигура 1.1 вектор A и вектор F
ГЛАВА I ВЕКТОРНЫЕ КОЛИЧЕСТВА Количества — это все, что можно измерить и указать числом. Количества в физике делятся на два типа; скалярные и векторные величины. Скалярные величины имеют
Дополнительная информация Аффинные преобразования
A P P E N D I X C Аффинные преобразования СОДЕРЖАНИЕ C Потребность в геометрических преобразованиях 335 C2 Аффинные преобразования 336 C3 Матри представление линейных преобразований 338 C4 Однородные координаты
Дополнительная информация Вектор или перекрестный продукт
Вектор или произведение Росса 1 Приложение Вектор или произведение Росса Мы увидели в приложении, что скалярное произведение двух векторов является скалярной величиной, которая является максимумом, когда два вектора параллельны и равна нулю
Дополнительная информация Перекрестные продукты и моменты силы
4 Перекрестные произведения и моменты силы Ссылка: Хиббелер 4.2-4.3, edford & Fowler: Statics 2.6, 4.3 В геометрических терминах перекрестное произведение двух векторов A и создает новый вектор C с перпендикулярным направлением
Дополнительная информация КОМПОНЕНТЫ ВЕКТОРОВ
КОМПОНЕНТЫ ВЕКТОРОВ Для описания движения в двух измерениях нам понадобится система координат с двумя перпендикулярными ae, и. В такой системе координат вектор A может быть уникально разложен на сумму двух
Дополнительная информация Обзор А: векторный анализ
МАССАЧУСЕТСКИЙ ИНСТИТУТ ТЕХНОЛОГИЙ Физический факультет 8.02 Обзор A: Анализ векторов A … A-0 A.1 Векторы A-2 A.1.1 Введение A-2 A.1.2 Свойства вектора A-2 A.1.3 Применение векторов
Дополнительная информация Унифицированная лекция № 4 Векторы
Объединенная лекция № 4 «Векторы» осени 2005 г. Эти заметки были написаны Дж. Перайром в качестве обзора векторов для динамики 16.07. Они были адаптированы для унифицированного проектирования Р. Радовицким. Список литературы [1] Фейнманн,
Дополнительная информация Механика 1: Векторы
Механика 1: Векторы, если говорить грубо, механические системы будут описываться комбинацией скалярных и векторных величин.скаляр — это просто (реальное) число. Например, масса или вес характеризуется
Дополнительная информация 13.4 КРЕСТОВЫЙ ПРОДУКТ
710 Глава 13 ОСНОВНОЙ ИНСТРУМЕНТ: ВЕКТОРЫ 62. Используйте следующие шаги и результаты Задач 59 60, чтобы показать (без тригонометрии), что геометрические и алгебраические определения точечного произведения
Дополнительная информация Лабораторная работа 2: векторный анализ
Лабораторная работа 2: векторный анализ. Цели: попрактиковаться в использовании графических и аналитических методов для добавления векторов в двух измерениях. Оборудование: Измерительная палка Линейка транспортира Таблица сил Кольцевые шкивы с насадками
Дополнительная информация Секция 1.1. Введение в R n
Сечение исчисления функций нескольких переменных. Введение в исчисление R n — это изучение функциональных связей и того, как связанные величины меняются друг с другом. В вашем первом воздействии на
Дополнительная информация Раздел V.3: Точечный продукт
Раздел V.3: Введение в многоточечный продукт До сих пор мы рассматривали операции с одним вектором.Есть несколько способов объединить два вектора. Вектор сложения и вычитания здесь не рассматривается,
Дополнительная информация Векторное исчисление: краткий обзор
Приложение A Векторное исчисление: краткий обзор Избранные материалы Ч.М. Ще ,. Div, Grad, Curl и все такое: неофициальный документ по исчислению векторов, W.W. Norton and Co., (1973). (Хорошее физическое введение в тему)
Дополнительная информация Геометрическая трансформация CS 211A
Геометрическое преобразование CS 211A Что такое преобразование? Перемещение точек (x, y) перемещается в (x + t, y + t). Может быть в любом измерении. Дополнительная информация
МАТ 1341: ОБЗОР II Сангхун Баек
МАТ 1341: ОБЗОР II Сангхун Баек 1.Прогнозы и перекрестный продукт 1.1. Прогнозы. Определение 1.1. Для данного вектора u прямоугольные (или перпендикулярные или ортогональные) компоненты представляют собой два вектора u 1 и
Дополнительная информация Линейная алгебра: векторы
Линейная алгебра: векторы A Приложение A: линейная алгебра: векторы СОДЕРЖАНИЕ Страница A Мотивация A 3 A2 Векторы A 3 A2 Условные обозначения A 4 A22 Визуализация A 5 A23 Специальные векторы A 5 A3 Вектор
Дополнительная информация Плоскостные преобразования напряжения
6 Преобразования напряжения в плоскости ASEN 311 — Структуры ASEN 311 Лекция 6 Слайд 1 Состояние напряжения плоскости ASEN 311 — Структуры Напомним, что в теле в плоском напряжении общее трехмерное напряженное состояние с 9 компонентами
Дополнительная информация Тригонометрия Обзор Мастерская 1
Определения семинара по обзору тригонометров: Пусть P (,) будет точкой (не началом координат) на терминальной стороне угла с мерой θ, и пусть r будет расстоянием от начала координат до P.Тогда функции Си Триг
Дополнительная информация Введение в поляризацию света
Глава 2 Введение в поляризацию света В этой главе рассматривается поляризация электромагнитных волн. В разделе 2.1 обсуждается понятие поляризации света и представлен его формализм Джонса.
Дополнительная информация 5.3. Кросс-продукт в R 3
53 Перекрестное произведение в R 3 Определение 531 Пусть u = [u 1, u 2, u 3] и v = [v 1, v 2, v 3] Тогда вектор, заданный как [u 2 v 3 u 3 v 2, u 3 v 1 u 1 v 3, u 1 v 2 u 2 v 1] называется перекрестным произведением (или
Дополнительная информация Концепции в исчислении III
Концепции в исчислении III Бета-версия УНИВЕРСИТЕТСКИЙ ПРЕССА ФЛОРИДЫ Флоридский университет A & M, Таллахасси Флоридский Атлантический университет, Бока-Ратон Флоридский университет побережья Мексиканского залива, Ft.Майерс Флорида Интернэшнл
Дополнительная информация Обзор линейной алгебры. векторы
Обзор линейной алгебры Тим К. Маркс UCSD Заимствует в значительной степени от: Яна Косецка [email protected] http://cs.gmu.edu/~kosecka/cs682.html Вирджиния де Са Когши 8F Обзор линейной алгебры UCSD Векторы Длина
Дополнительная информация
α α λ α = = λ λ α ψ = = α α α λ λ ψ α = + β => θθ β> ββθθθθβθβ γθβ = γθ> β> γθβ γ = θ β = θ β = θ β = β θ = β β θ = = = β β θ = + α α α α α = = λ λ λ λ λ λ λ = λ λ α α α α λ ψ + α =
Дополнительная информация Точка и Крест Продукты
Точечные и перекрестные произведения Две общие операции с векторами — это точечное произведение и перекрестное произведение.Пусть даны два вектора = ,, и = ,,. Точечный продукт Точечный продукт и написано и
Дополнительная информация Треугольник Тригонометрия и Круги
Математические задачи Учащиеся поймут, что тригонометрические функции угла зависят не от размера треугольника, в котором содержится угол, а от соотношения сторон
Дополнительная информация ЛИНЕЙНЫЕ ФУНКЦИИ 2 ПЕРЕМЕННЫХ
ГЛАВА 4: ЛИНЕЙНЫЕ ФУНКЦИИ 2 ПЕРЕМЕННЫХ 4.1 СКОРОСТИ ИЗМЕНЕНИЙ В РАЗЛИЧНЫХ НАПРАВЛЕНИЯХ Из Precalculus мы знаем, что это линейная функция, если скорость изменения функции постоянна. Т.е. за
Дополнительная информация Основная математика C3. Редакция Примечания
Базовые математические заметки о пересмотре C Октябрь 0 Основные математические дисциплины C Алгебраические дроби … Отмена общих множителей … Умножение и деление дробей … Сложение и вычитание дробей … Уравнения …4 функции …
Дополнительная информация Векторы и Скаляры. AP Physics B
Векторы и скаляры P Физика Скалярная SCLR — это количество Нью-Йорка в физике, которое имеет MGNITUDE, но НЕ является направлением, связанным с ним. Числовое значение величины в единицах. Скалярный пример Скорость Расстояние ge Величина
Дополнительная информация ТРЕХМЕРНАЯ ГЕОМЕТРИЯ
Глава 8 ТРЕХМЕРНАЯ ГЕОМЕТРИЯ 8.1 Введение В этой главе мы представляем подход векторной алгебры к трехмерной геометрии. Цель состоит в том, чтобы представить стандартные свойства линий и плоскостей,
Дополнительная информация МАТ188х2С Lec0101 Бурбулла
Зима 206 Линейные преобразования Линейное преобразование T: R m R n — это функция, которая переводит векторы в R m в векторы в R n такие, что и T (u + v) T (u) + T (v) T (kv) k T (v), для всех векторов u
Дополнительная информация Векторные пространства; Пространство Р н
Векторные пространства; Пространство R n. Векторные пространства. Векторное пространство (над действительными числами) — это набор V математических объектов, называемых векторами, U, V, W и т. д., в которых определена операция сложения + и в которых
Дополнительная информация ГРАММ.Графические функции
G. Графические функции Чтобы быстро понять, как выглядит график функции, очень полезно знать, как определенные простые операции на графике связаны с тем, как выражается функция
. Дополнительная информация C3: функции. Цели обучения
ГЛАВА C3: Функции Цели обучения После изучения этой главы вы должны: быть знакомыми с терминами «сопоставления один-один» и «человек-один», понимать термины «область и область действия», понимать «
». Дополнительная информация Основная математика C2.Редакция Примечания
Базовая математика C Примечания к редакции Ноябрь 0 Основная математика C Алгебра … Многочлены: + ,,, …. Факторизация … Длинное деление … Теорема о остатке … Теорема о факторе … 4 Выбор подходящего фактора .. .5 кубических уравнений …
Дополнительная информация Глава 15 Теория столкновений
Глава 15 Теория столкновений 151 Введение 1 15 Относительные системы отсчета и скорости 1 151 Система отсчета центра масс 15 Относительные скорости 3 153 Характеризация столкновений 5 154 Одномерная
Дополнительная информация ДВУМЕРНОЕ ПРЕОБРАЗОВАНИЕ
ГЛАВА 2 ДВУМЕРНАЯ ТРАНСФОРМАЦИЯ 2.1 Введение Как указывалось ранее, автоматизированное проектирование состоит из трех компонентов: проектирования (геометрическое моделирование), анализа (ВЭД и т. Д.) И визуализации
. Дополнительная информация ,
No related posts.