Арифметика
Арифметика — элементарный раздел математики, изучающий простейшие виды чисел (натуральные, целые, рациональные) и простейшие арифметические операции над ними (сложение, вычитание, умножение, деление).
С глубокой древности работа с числами подразделялась на две различные области: одна касалась непосредственно свойств чисел, другая была связана с техникой счета. Под «арифметикой» во многих странах обычно имеется ввиду именно эта последняя область, которая несомненно является старейшей отраслью математики.
На сегодняшний день главными арифметическими операциями есть сложение, вычитание, умножение, деление, возведение в степень, извлечение корня. Рассмотрим их немножко подробнее.
Сложение – это операция нахождения суммы двух или нескольких чисел, где под суммой понимается общее количество единиц, содержащихся в рассматриваемых числах вместе.
Вычитание является действием, обратным к сложению, так как это операция нахождения одного из слагаемых по сумме и другому слагаемому. Вычесть из одного числа ( уменьшаемого ) другое ( вычитаемое ) — значит найти такое третье число ( разность ), которое при сложении с вычитаемым дает уменьшаемое: 24 – 8 = 16. Здесь 24 – уменьшаемое, 8 – вычитаемое, 16 – разность.
Умножение. Умножить одно число n ( множимое ) на другое целое число m ( множитель ) — значит повторить множимое n в качестве слагаемого m раз. Результат умножения называется произведением .
Запись операции умножения: n ? m или n • m . Например, 12 ? 4 = 12 + 12 + 12 + 12 = 48. Таким образом, 12 ? 4 = 48 или 12 • 4 = 48. Здесь 12 – множимое, 4 – множитель, 48 – произведение. Если множимое n и множитель m поменять местами, то произведение не изменится. Например, 12 · 4 = 12 + 12 + 12 + 12 = 48 и соответственно, 4 · 12 = 4 + 4 + 4 + 4 + 4 + 4 + 4 + 4 + 4 + 4 + 4 + 4 = 48. Поэтому множимое и множитель часто называются сомножителями .
Деление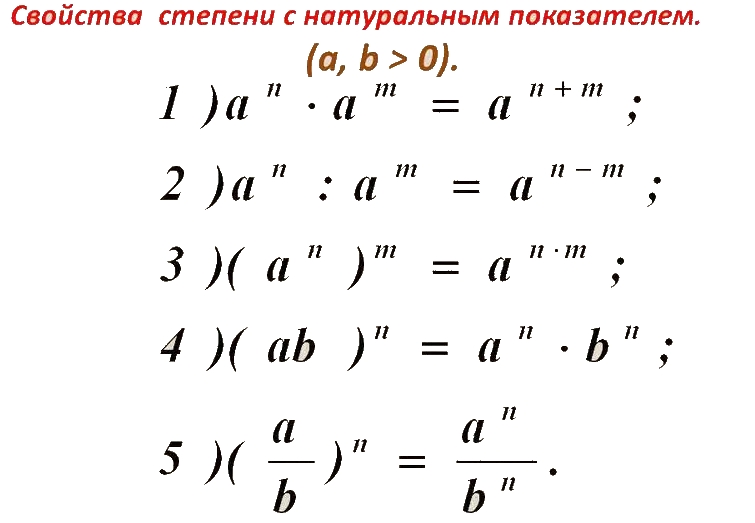 
Здесь 48 – делимое, 4 – делитель, 12 – частное. Частное от деления одного целого числа на другое целое число может и не быть целым числом. Тогда это частное представляется в виде дроби . Если частное – целое число, то говорят, что эти числа делятся нацело . В противном случае мы выполняем деление с остатком . Пример: 23 не делится на 4, в этом случае мы можем записать: 23 = 5 · 4 + 3. Здесь 3 – остаток .
Возведение в степень. Возвести число ( основание степени ) в целую степень ( показатель степени ) – значит повторить его сомножителем столько раз, каков показатель степени. Результат называется степенью . Запись возведения в степень:
3 5 = 3 · 3 · 3 · 3 · 3 = 243 .
Здесь 3 – основание степени, 5 – показатель степени, 243 – степень.
Вторая степень любого числа называется квадратом , третья – кубом .
Первой степенью любого числа является само это число.
Извлечение корня является действием, обратным к возведению в степень, так как это операция нахождения основания степени по степени и её показателю. Извлечь корень n- ой степени ( n – показатель корня ) из числа
Здесь 243 – подкоренное число, 5 – показатель корня, 3 – корень.
Корень второй степени называется квадратным , корень третьей степени – кубическим . Показатель квадратного корня не записывается:
Сложение и вычитание, умножение и деление, возведение в степень и извлечение корня являются попарно взаимно-обратными операциями в арифметике.
Основные арифметические действия
Сложение
Сложение – одна из основных операций, позволяющая объединить два слагаемых.
Запись сложения: 8 + 3 = 11
8 и 3 – слагаемые
11 – сумма
Вычитание
Вычитание – действие, обратное сложению.
Запись: 15–7 = 8
15 – уменьшаемое
7 – вычитаемое
8 – разность
Если разность 8, сложить с вычитаемым 7, это даст уменьшаемое 15. Операция сложения 8 + 7 = 15 является контрольной проверкой вычитания 15 – 7 = 8.
Умножение
Умножение – арифметическое действие в виде краткой записи суммы одинаковых слагаемых.
Запись: 12 × 5 = 60
12 • 5 = 6012 – множимое
5 – множитель
60 – произведение
12 × 5 = 12 + 12 + 12 + 12 + 12
В случае если множимое и множитель поменять ролями, произведение остается одним и тем же.
Например:
2 × 5 = 2 + 2 + 2 + 2 + 2 = 10
5 × 2 = 5 + 5 = 10
Поэтому и множитель, и множимое называются «сомножителями».
Деление
Деление – арифметическое действие обратное умножению.
Запись: 48 : 6 = 8 или 6 = 8
48 – делимое
6 – делитель
8 – частное
В данном случае произведение делителя 6 и частного 8, в качестве проверки, дает делимое 48
Если в результате операции деления, частное является не целым числом, то его можно представить дробью 3 / 5. Если частное является целым числом, в таком случае говорят, что первое из озвученных чисел нацело делится или, проще говоря, делится на второе.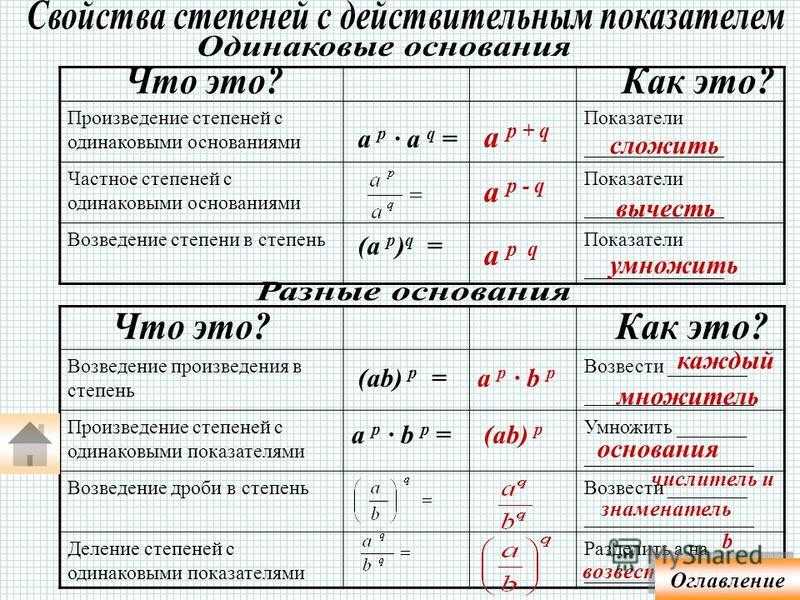
Например, число 35 полностью делится на 5, ибо частное это целое число 7.
Второе число в данном случае называется делителем первого, первое же – кратным второго.
Пример 1
Число 5 является делителем чисел 25, 60
80 и не действует в качестве делителя для чисел 4, 13, 42, 61.Пример 2
Число 60 кратное чисел 15, 20, 30 и не является кратным для чисел 17, 40, 90.
В случае, когда делимое не делится полностью, иногда применяют так называемое деление с остатком. Деление с остатком, это отыскание наибольшего подходящего целого числа, которое в произведении с делителем дает нужное число, не превышающее делимое.
Такое искомое число называется неполным частным. Разность между делимым и произведением делителя на неполное частное называется остатком, которое всегда меньше делителя.
Возведение в степень
Возведение степень – операция умножения числа на самого себя несколько (n) раз.
Основание степени называется число, которое повторяется сомножителем определённое количество раз.
Показателем степени называется число, которое указывает, сколько раз берется одинаковый множитель.
Степенью называется число, получаемое в результате взаимодействия основания и показателя степени.
Запись: 34 = 81
3 – основание степени
4 – показатель степени
81 – степень
34 = 3 × 3 × 3 × 3
Вторая степень называется иначе квадратом, третья степень – кубом. Первой степенью числа называют само это число.
Извлечение корня
Извлечение корня – арифметическое действие, обратное возведению в степень.
Запись:4√81 = 3
81 – подкоренное число
4 – показатель корня
3 – корень
З4 = 81 – возведение числа 3 в четвертую степень дает 81 (проверка извлечения корня)
2√16 = 4 – корень второй степени называется – квадратным.
При знаке квадратного корня показатель корня принято опускать: √16 = 4
3√8 = 2 – корень третьей степени называется – кубичным.
Сложение и вычитание, умножение и деление, а так же возведение в степень и извлечение корня попарно представляют собой обратными действиями.
Правила первых четырех действий регулирующие взаимодействия с целыми числами предполагаются известными. Возведение в степень выполняется повторным умножением.
Правила экспоненты— Криста Кинг Математика
Арифметические правила для показателей степени
Когда дело доходит до работы с показателями степени, мы должны следовать определенным правилам.
Сложение и вычитание
Когда мы хотим найти сумму или разность двух экспоненциальных выражений, они должны быть «подобны терминам», что означает, что они должны иметь одно и то же основание и один и тот же показатель степени; в противном случае мы не можем добавить или вычесть их.
9{а-б}???
Как применять правила экспоненты для упрощения выражений
Пройти курс
Хотите узнать больше о Pre-Algebra? У меня есть пошаговый курс для этого. 🙂
Учить больше
Получите доступ к полному курсу Pre-Algebra
Начать
Изучайте математикуКриста Кинг математика, учитесь онлайн, онлайн-курс, онлайн-математика, преалгебра, преалгебра, алгебра, показатели, правила экспонент, правила экспонент, сложение показателей, вычитание показателей, умножение показателей, деление показателей, как термины, как базы
0 лайковПорядок операций с экспонентами
Форма поиска
Поиск
Задача: вычислить это арифметическое выражение: 18 + 36 ÷ 3 2
На прошлом уроке мы научились вычислять арифметическое выражение с помощью более чем одной операции в соответствии со следующими правилами:
Правило 1:
Упрощайте все операции внутри круглых скобок.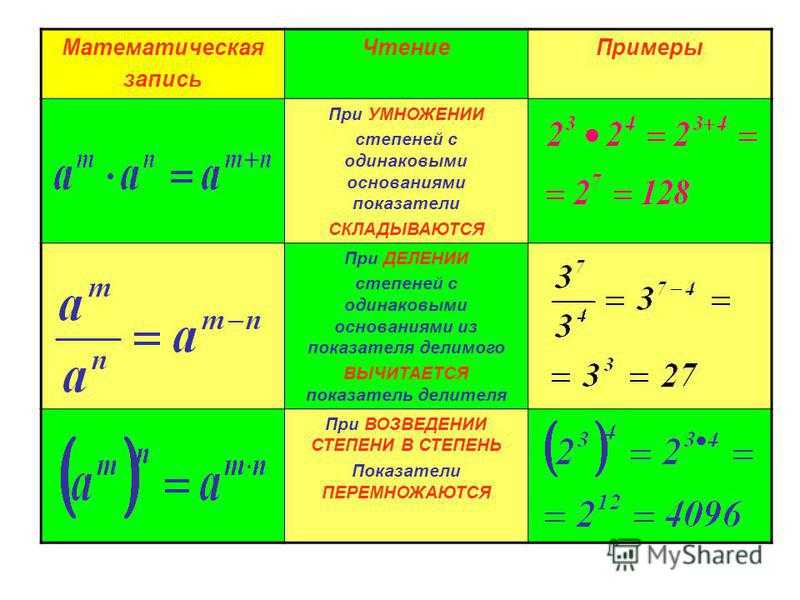
Правило 2: Выполняйте все операции умножения и деления слева направо.
Правило 3: Выполняйте все операции сложения и вычитания слева направо.
Однако в приведенной выше задаче есть экспонента, поэтому мы не можем решить ее без пересмотра наших правил.
Правило 1: Упростите все операции внутри круглых скобок.
Правило 2: Упростите все показатели, работая слева направо.
Правило 3: Выполняйте все операции умножения и деления слева направо.
Правило 4: Выполняйте все сложения и вычитания слева направо.
Мы можем решить указанную выше задачу, используя измененный порядок операций.
Задача: вычислить это арифметическое выражение: 18 + 36
Решение:
18 + 36 ÷ 3 2 8| = 18 + 36 ÷ 9 | Упростить все показатели (Правило 2) | |
| 18 + 36 ÷ 9 | = 18 + 4 | Раздел (Правило 3) |
| 18 + 4 | = 22 | Дополнение (Правило 4) |
Давайте посмотрим на некоторые другие примеры, в которых используются наши новые правила порядка операций.
Пример 1: Оценка 5 2 x 2 4
Решение:
| 5 2 x 2 4 | = 25 х 2 4 | Упростить все показатели, работая слева направо (Правило 2) |
| 25 x 2 4 | = 25 х 16 | |
| 25 х 16 | = 400 | Умножение (правило 3) |
Пример 2: вычислить 289 — (3 x 5) 2
Решение:
|
Пример 3.
Вычисление 8 + (2 x 5) x 3 4 ÷ 9
Решение:
5
|
Пример 4.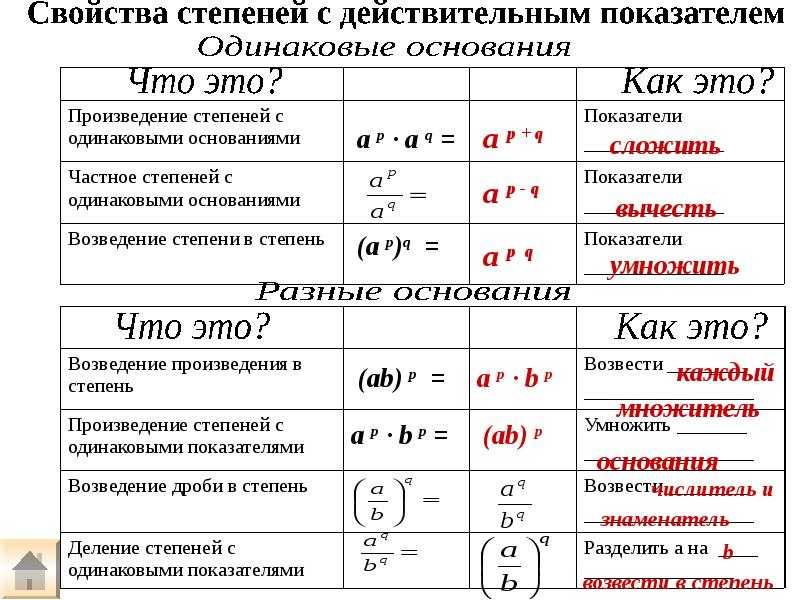
Декоратор интерьеров берет 15 долларов США за квадратный фут за укладку ковра и плату за установку в размере 150 долларов США. Если комната квадратная и каждая сторона имеет длину 12 футов, сколько будет стоить покрыть ее ковром?
Решение: если одна сторона квадратной комнаты равна 12 футам, то площадь комнаты равна (12 футам) 2 .
| 15 x 12 2 + 150 | = 15 х 144 + 150 | Упростить все показатели (Правило 2) |
| 15 x 144 + 150 | = 2160 + 150 | Умножение (правило 3) |
| 2160 + 150 | = 2310 | Дополнение (Правило 4) |
Ответ: Ковер в этой комнате будет стоить 2310 долларов.
Резюме:
Чтобы помочь нам запомнить порядок операций, мы можем использовать мнемонику PEMDAS , которая означает:
P аренда E xcuse M Y D Ear A UNT S Ally
P Arentheses, E Xponents, M Ultiplication и D IVision, A Ddition & Scrtration и D . Обратите внимание, что хотя слов и шесть, они соответствуют четырем правилам. Указания: Выполните каждое упражнение, применяя правила порядка действий. Щелкните один раз в ПОЛЕ ОТВЕТА и введите свой ответ; затем нажмите ВВОД. После того, как вы нажмете ENTER, в ОКНЕ РЕЗУЛЬТАТОВ появится сообщение, указывающее, является ли ваш ответ правильным или неправильным. Чтобы начать сначала, нажмите ОЧИСТИТЬ. ОКНО РЕЗУЛЬТАТОВ: ОКНО РЕЗУЛЬТАТОВ: ОКНО РЕЗУЛЬТАТОВ: ОКНО РЕЗУЛЬТАТОВ:
Упражнения 
1. 3 2 x 4 3 ОКНО ОТВЕТОВ: 2. 27 — 256 ÷ 4 3 ОКНО ОТВЕТОВ: 3. 9 х (5 + 3) 2 — 144 ОКНО ОТВЕТОВ: 4. 7 + 3 x 2 4 ÷ 6 ОКНО ОТВЕТОВ: 5. 