Сложение матрицы на матрицу: Онлайн калькулятор. Сложение и вычитание матриц

Теория матриц

Теория матриц

Гантмахер Ф.Р. Теория матриц. – М.: Наука, 1968. — 576 с. Оглавление Предисловие автора к первому изданию Предисловие автора ко второму изданию ЧАСТЬ I. ОСНОВЫ ТЕОРИИ Глава I. Матрицы и действия над ними § 1. Матрицы. Основные обозначения § 2. Сложение и умножение прямоугольных матриц § 3. Квадратные матрицы § 4. Ассоциированные матрицы. Миноры обратной матрицы § 5. Обращение прямоугольных матриц. Псевдообратная матрица Глава II. Алгоритм Гаусса и некоторые его применения § 1. Метод исключения Гаусса § 2. Механическая интерпретация алгоритма Гаусса § 3. Детерминантное тождество Сильвестра § 4. Разложение квадратной матрицы на треугольные множители § 5. Разбиение матрицы на блоки. Техника оперирования с блочными матрицами. Обобщенный алгоритм Гаусса Глава III. Лииейиые операторы в n-мерном векторном пространстве § 1. Векторное пространство § 2. Линейный оператор, отображающий n-мерное пространство в m-мерное § 3. Сложение и умножение линейных операторов § 4. Преобразование координат § 5. Эквивалентные матрицы. Ранг оператора. Неравенства Сильвестра § 6. Линейные операторы, отображающие n-мерное пространство само в себя § 7. Характеристические числа и собственные векторы линейного оператора § 8. Линейные операторы простой структуры Глава IV. Характеристический и минимальный многочлены матрицы § 1. Сложение и умножение матричных многочленов § 2. Правое и левое деление матричных многочленов. Обобщенная теорема Безу § 3. Характеристический многочлен матрицы. Присоединенная матрица § 4. Метод Д. К. Фаддеева одновременного вычисления коэффициентов характеристического многочлена и присоединенной матрицы § 5. 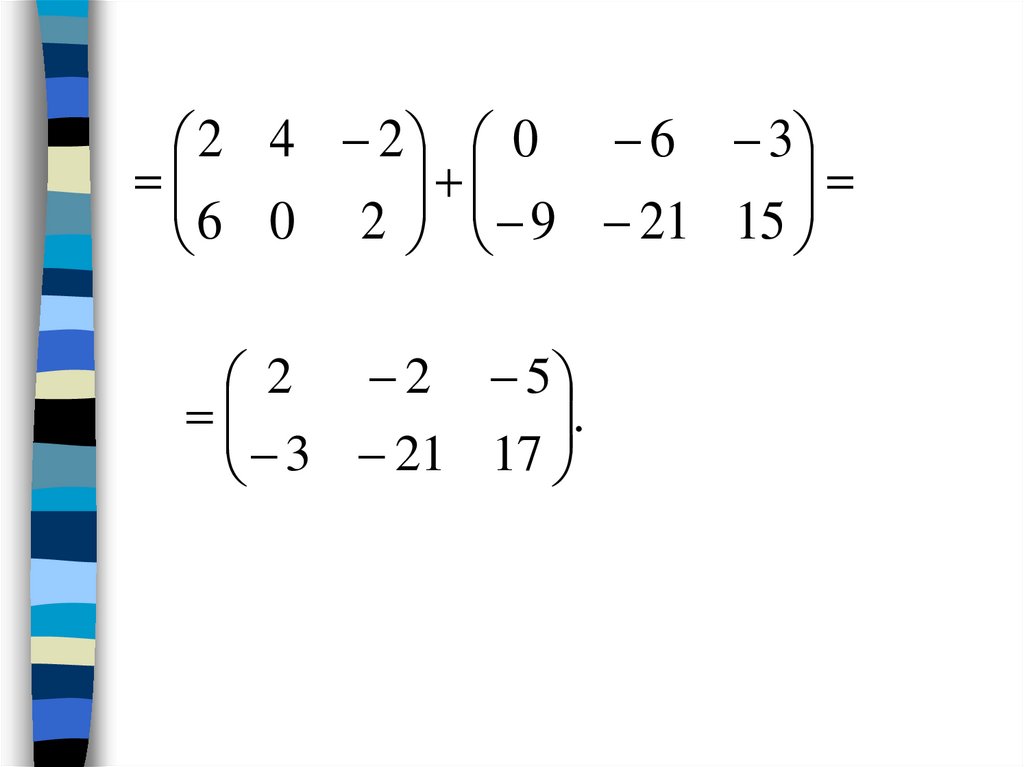Минимальный многочлен матрицы Глава V. Функции от матрицы § 1. Определение функции от матрицы § 2. Интерполяционный многочлен Лагранжа–Сильвестра § 3. Другие формы определения f(A). Компоненты матрицы A § 4. Представление функций от матриц рядами § 5. Некоторые свойства функций от матриц § 6. Применение функций от матрицы к интегрированию системы линейных дифференциальных уравнений с постоянными коэффициентами § 7. Устойчивость движения в случае линейной системы Глава VI. Эквивалентные преобразования многочленных матриц. Аналитическая теория элементарных делителей § 1. Элементарные преобразования многочленной матрицы § 2. Канонический вид матрицы § 3. Инвариантные многочлены и элементарные делители многочленной матрицы § 4. Эквивалентность линейных двучленов § 5. Критерий подобия матриц § 6. Нормальные формы матрицы § 7. Элементарные делители матрицы f(A) § 8. Общий метод построения преобразующей матрицы § 9. Второй метод построения преобразующей матрицы Глава VII. Структура линейного оператора в n-мерном пространстве (геометрическая теория элементарных делителей) § 1. Минимальный многочлен вектора, пространства (относительно заданного линейного оператора) § 2. Расщепление на инвариантные подпространства с взаимно простыми минимальными многочленами § 3. Сравнения. Надпространство § 4. Расщепление пространства на циклические инвариантные подпространства § 5. Нормальная форма матрицы § 6. Инвариантные многочлены. Элементарные делители § 7. Нормальная жорданова форма матрицы § 8. Метод акад. А. Н. Крылова преобразования векового уравнения Глава VIII. Матричные уравнения § 1. Уравнение AX=XB § 2. Частный случай: A=B. Перестановочные матрицы § 3. Уравнение AX-XB=C § 4. Скалярное уравнение f(X)=0 § 5. Матричное многочленное уравнение § 6. Извлечение корня m-й степени из неособенной матрицы § 7. Извлечение корня m-й степени из особенной матрицы § 8. Логарифм матрицы Глава IX. Линейные операторы в унитарном пространстве § 1. 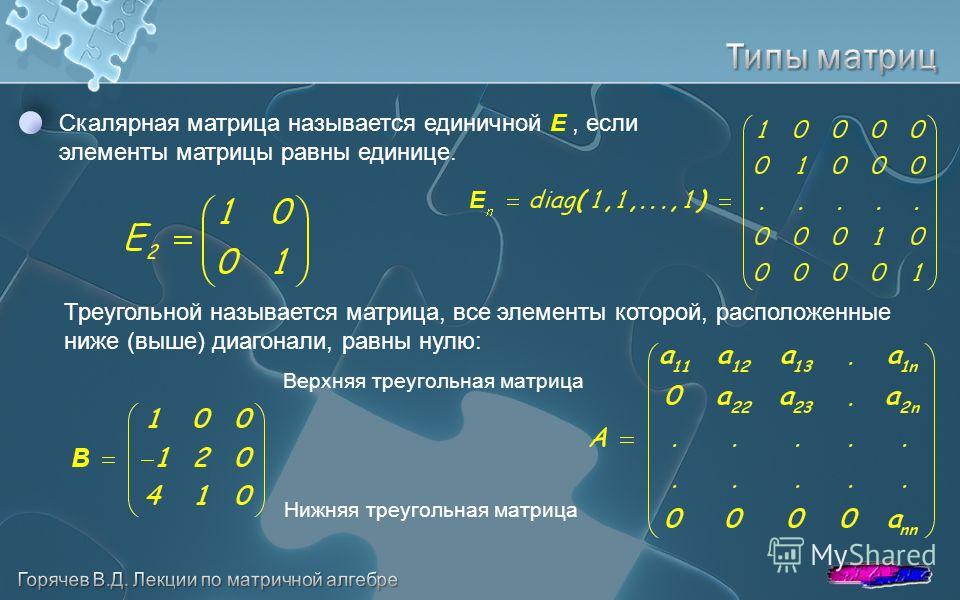Общие соображения § 2. Метризация пространства § 3. Критерий Грама линейной зависимости векторов § 4. Ортогональное проектирование § 5. Геометрический смысл определителя Грама и некоторые неравенства § 6. Ортогонализация ряда векторов § 7. Ортонормированный базис § 8. Сопряженный оператор § 9. Нормальные операторы в унитарном пространстве § 10. Спектр нормальных, эрмитовых, унитарных операторов § 11. Неотрицательные и положительно определенные эрмитовы операторы § 12. Полярное разложение линейного оператора в унитарном пространстве. Формулы Кэли § 13. Линейные операторы в евклидовом пространстве § 14. Полярное разложение оператора и формулы Кэли в евклидовом пространстве § 15. Коммутирующие нормальные операторы § 16. Псевдообратный оператор Глава X. Квадратичные и эрмитовы формы § 1. Преобразование переменных в квадратичной форме § 2. Приведение квадратичной формы к сумме квадратов. Закон инерции § 3. Метод Лагранжа приведения квадратичной формы к сумме квадратов. Формула Якоби § 4. Положительные квадратичные формы § 5. Приведение квадратичной формы к главным осям § 6. Пучок квадратичных форм § 7. Экстремальные свойства характеристических чисел регулярного пучка форм § 8. Малые колебания системы с n степенями свободы § 9. Эрмитовы формы § 10. Ганкелевы формы ЧАСТЬ II. СПЕЦИАЛЬНЫЕ ВОПРОСЫ И ПРИЛОЖЕНИЯ Глава XI. Комплексные симметричные, кососимметрические и ортогональные матрицы § 1. Некоторые формулы для комплексных ортогональных и унитарных матриц § 2. Полярное разложение комплексной матрицы § 3. Нормальная форма комплексной симметрической матрицы § 4. Нормальная форма комплексной кососимметрической матрицы § 5. Нормальная форма комплексной ортогональной матрицы ГЛАВА XII. СИНГУЛЯРНЫЕ ПУЧКИ МАТРИЦ § 1. Введение § 2. Регулярный пучок матриц § 3. Сингулярные пучки. Теорема о приведении § 4. Каноническая форма сингулярного пучка матриц § 5. Минимальные индексы пучка § 6. 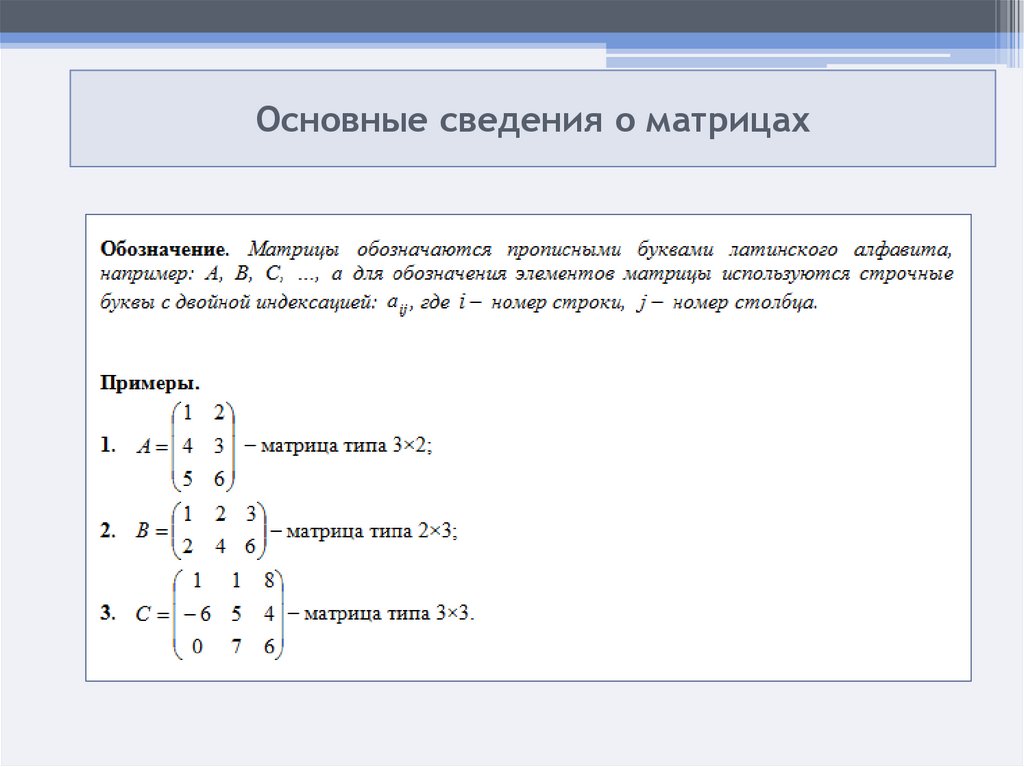Сингулярные пучки квадратичных форм § 7. Приложения к дифференциальным уравнениям ГЛАВА XIII. МАТРИЦЫ С НЕОТРИЦАТЕЛЬНЫМИ ЭЛЕМЕНТАМИ § 1. Общие свойства § 2. Спектральные свойства неразложимых неотрицательных матриц § 3. Разложимые матрицы § 4. Нормальная форма разложимой матрицы § 5. Примитивные и импримитивные матрицы § 6. Стохастические матрицы § 7. Предельные вероятности для однородной цепи Маркова с конечным числом состояний § 8. Вполне неотрицательные матрицы § 9. Осцилляционные матрицы Глава XIV. Различные критерии регулярности и локализации собственных значений § 1. Критерий регулярности Адамара и его обобщения § 2. Норма матрицы § 3. Распространение критерия Адамара на блочные матрицы § 4. Критерий регулярности Фидлера § 5. Круги Гершгорина и другие области локализации Глава XV. Приложения теории матриц к исследованию систем линейных дифференциальных уравнений § 1. Системы линейных дифференциальных уравнений с переменными коэффициентами. Общие понятия § 2. Преобразование Ляпунова § 3. Приводимые системы § 4. Каноническая форма приводимой системы. Теорема Еругина § 5. Матрицант § 6. Мультипликативный интеграл. Инфинитезимальное исчисление Вольтерра § 7. Дифференциальные системы в комплексной области. Общие свойства § 8. Мультипликативный интеграл в комплексной области § 9. Изолированная особая точка § 10. Регулярная особая точка § 11. Приводимые аналитические системы § 12. Аналитические функции от многих матриц и их применение к исследованию дифференциальных систем. Работы И. A. Лaппo-Данилевского ГЛАВА XVI. ПРОБЛЕМА РАУСА-ГУРВИЦА И СМЕЖНЫЕ ВОПРОСЫ § 1. Введение § 2. Индексы Коши § 3. Алгоритм Рауса § 4. Особые случаи. Примеры § 5. Теорема Ляпунова § 6. Теорема Рауса-Гурвица § 7. Формула Орландо § 8. Особые случаи в теореме Рауса — Гурвица § 9. Метод квадратичных форм. Определение числа различных вещественных корней многочлена § 10. Бесконечные ганкелевы матрицы конечного ранга 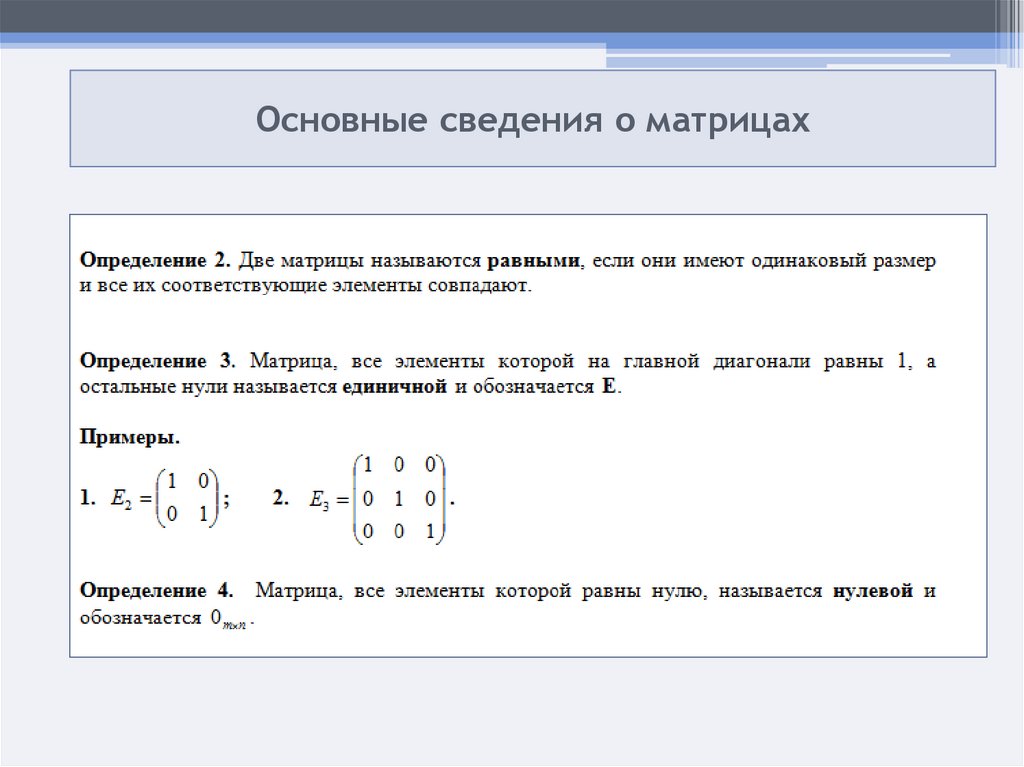§ 11. Определение индекса произвольной рациональной дроби через коэффициенты числителя и знаменателя § 12. Второе доказательство теоремы Рауса—Гурвица § 13. Некоторые дополнения к теореме Рауса—Гурвица. Критерий устойчивости Льенара и Шипара § 14. Некоторые свойства многочлена Гурвица. Теорема Стильтьеса. Представление многочленов Гурвица при помощи непрерывных дробей § 15. Область устойчивости. Параметры Маркова § 16. Связь с проблемой моментов § 17. Связь между определителями Гурвица и определителями Маркова § 18. Теоремы Маркова и Чебышева § 19. Обобщенная задача Рауса-Гурвица ДОБАВЛЕНИЕ. НЕРАВЕНСТВА ДЛЯ СОБСТВЕННЫХ И СИНГУЛЯРНЫХ ЧИСЕЛ § 1. Мажорирующие последовательности § 2. Неравенства Неймана-Хорна § 3. Неравенства Вейля § 4. Максимально-минимальные свойства сумм и произведений собственных чисел эрмитовых операторов § 5. Неравенства для собственных и сингулярных чисел сумм и произведений операторов § 6. Другая постановка задачи о спектре суммы и произведения эрмитовых операторов ЛИТЕРАТУРА

Матрицы и действия над ними.

Ступенчатая матрица. Элементарные преобразования.

Главная

» Общенаучные дисциплины

» Математика (1 семестр)

» Матрицы и действия над ними. Ступенчатая матрица. Элементарные преобразования.

 

Определения.

Матрицей называется прямоугольная  таблица чисел  или буквенных выражений, содержащая m строк и n столбцов: называют  элементами  матрицы.

Матрица, у которой число строк равно числу столбцов, т.е. m=n, называется квадратной матрицей, а число n называется порядком матрицы

 Элементы   образуют главную диагональ квадратной матрицы.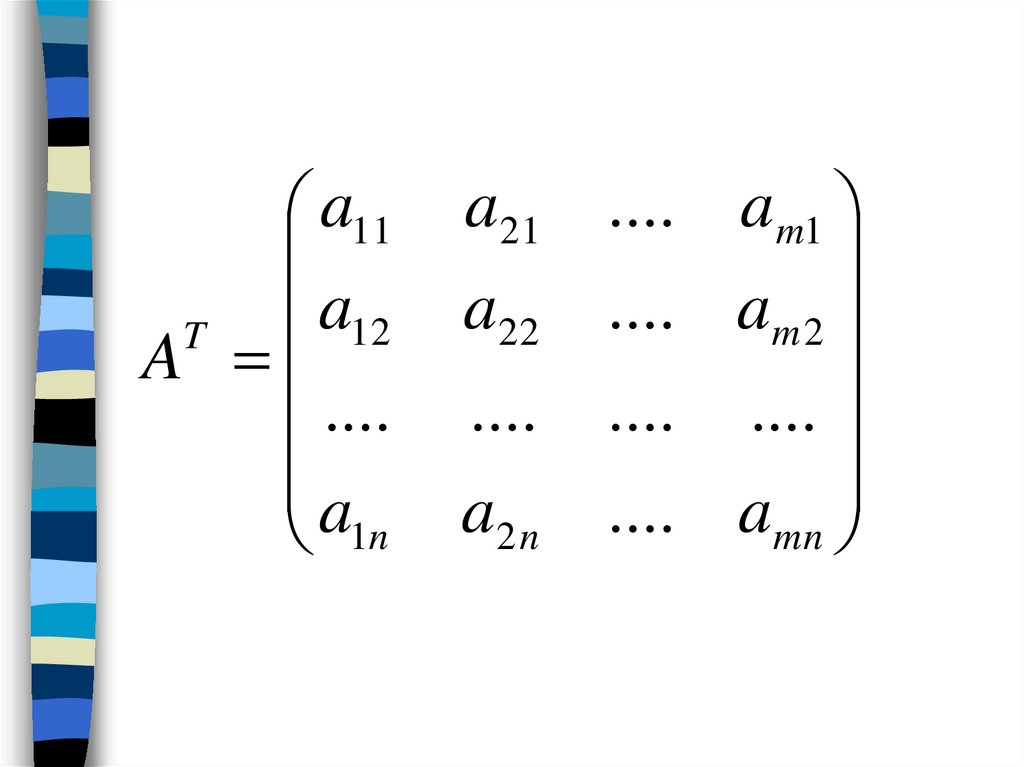 Если все элементы квадратной матрицы, расположенные вне главной диагонали, равны нулю, то матрицу называют диагональной. Если в диагональной матрице все элементы главной диагонали равны между собой, то ее называют скалярной.

Если в скалярной матрице все элементы главной диагонали равны единице, то матрицу называют единичной и обозначают буквой E .

Если все элементы матрицы  равны  0, то матрица называется нулевой и ее обозначают буквой O.

Две матрицы считаются равными, если они одинакового размера, и элементы, стоящие на пересечении строк и столбцов с одинаковыми номерами, равны

Сложение матриц.

Суммой матриц  одной и той же размерности называется матрица размерности , каждый элемент которой представляет собой сумму соответствующих элементов матриц A и B:

Матрицы разных размерностей складывать нельзя.

Пример1.

Свойства сложения матриц.
1. Коммутативность.
A+B=B+A
2. Ассоциативность.
(A+B)+C=A+(B+C)

Умножение матриц, транспонирование матриц.

Матрица C, элементы которой с_ij равны элементам матрицы A, умноженным на число α, называют произведением матрицы A на α

Пример 2.

Произведением матрицы  размерности на матрицу размерности называется матрица размерности.

Произведение матриц существует только тогда, когда число столбцов первой матрицы равно числу строк второй матрицы.

Пример 4.

Результатом транспонирования матрицы размерности является матрица размерности.

Свойства транспонированных матриц.

1).

Если E-единичная матрица, то E=E^T.

2). Двукратное транспонирование не изменяет матрицу (A^T)^T=A.

3). Транспонирование суммы матриц равносильно сложению транспонированных матриц:
(A+B)^T=A^T+B^T

4).Транспонирование произведения матриц равносильно умножению транспонированных матриц:  .

5). Транспонирование обратной матрицы равносильно вычислению обратной к транспонированной матрице:
(A^-1)^T=(A^T)^-1 .

6). Если транспонированная матрица A^T совпадает с данной матрицей A, то матрица A называется симметрической.

Преобразования, не меняющие ранг матрицы, называются элементарными. К ним относятся:
 1). Умножение строки или столбца на число, не равное нулю.
 2). Перестановка строк или столбцов местами.
 3). Прибавление к элементам одной строки или столбца элементов другой строки или столбца, умноженных на одно и то же число.
 4). Вычеркивание строки или столбца, состоящего из нулей.

 

---

Друзья! Приглашаем вас к обсуждению. Если у вас есть своё мнение, напишите нам в комментарии.

Добавление матрицы

Марко Табога, доктор философии

Эта лекция знакомит с сложением матриц, одной из основных алгебраических операций. которые могут быть выполнены на матрицах.

СОДЕРЖАНИЕ

1. Определение

2. Свойства Matrix Добавление

3. Решенные упражнения

   1. Упражнение 1

   2. Упражнение 2

   4. 11111111111119

   9. .0003

Определение

Две матрицы можно сложить тогда и только тогда, когда они имеют одинаковые измерение. Их сумма получается суммированием каждого элемента одной матрицы с соответствующий элемент другой матрицы.

Ниже приводится формальное определение.

Определение Позволять и быть двумя матрицы. Их сумма Другой матрица такая, что ее -й элемент равен сумме -й элемент и в -й элемент , для всех и удовлетворяющий и .

В следующем примере показано, как выполняется сложение матриц.

Пример Позволять и быть двумя матрицыИх сумма это

Помните, что векторы-столбцы и векторы-строки также являются матрицами. Как следовательно, они могут быть суммированы таким же образом, как показано в следующем пример.

Пример Позволять и быть двумя столбец векторыИх сумма

Свойства сложения матриц

Матричное сложение обладает свойствами, аналогичными тем, которыми обладает более привычное сложение действительных чисел.

Предложение (коммутативное свойство) Сложение матриц коммутативно, т. е. для любые матрицы и таким образом, что приведенные выше дополнения имеют осмысленное определение.

Доказательство

Это прямое следствие того факта, что что свойство коммутативности применяется к суммам скаляров и, следовательно, к поэлементные суммы, которые выполняются при выполнении сложения матриц.

Предложение (ассоциативное свойство) Сложение матриц ассоциативно, т.е. для любые матрицы , и таким образом, что приведенные выше дополнения имеют осмысленное определение.

Доказательство

Это прямое следствие того факта, что что ассоциативное свойство применяется к суммам скаляров, и, следовательно, к поэлементные суммы, которые выполняются при выполнении сложения матриц.

Решенные упражнения

Ниже вы можете найти несколько упражнений с поясненными решениями.

Упражнение 1

Позволять и быть матрицы определены поНайти их сумма.

Решение

Чтобы вычислить сумму и , нам нужно суммировать каждый элемент с соответствующим элементом :

Упражнение 2

Позволять быть следующим матрица:Определить в матрица как следует:Вычислитьгде является транспонированием .

Решение

Транспонирование матрица такая, что ее столбцы равны строкам :Сейчас, с и имеют одинаковую размерность, мы можем вычислить их сумма:

Упражнение 3

Позволять быть матрица определена byShow что сумма и его транспонированная матрица является симметричной.

Раствор

Транспонирование это сумма и это

Окончательно, симметричен, если он равен своему транспонированному. Последний Таким образом, утверждение верно.

Как цитировать

Пожалуйста, указывайте как:

Табога, Марко (2021). «Матричное сложение», Лекции по матричной алгебре. https://www.statlect.com/matrix-алгебра/matrix-дополнение.

Объяснение урока: Операции с матрицами | Nagwa

В этом эксплейнере мы научимся комбинировать операции сложения, вычитания, скалярного умножения и транспонирования. матрицы.

Начнем с того, что напомним обозначение матрицы, которое полезно для определения матричных операций. Если мы обозначим 𝑎 для целых чисел 𝑖=1,2,…,𝑚 и 𝑗=1,2,…,𝑛 быть последовательностью чисел, то (𝑎)× обозначает 𝑚×𝑛 матрица, запись которой в 𝑖-й строке и 𝑗-м столбце задается как 𝑎. Если порядок матрицы ясен из контекста, мы можем опустить 𝑚×𝑛 из обозначений, чтобы написать (𝑎).

Используя это обозначение, мы напомним несколько матричных операций, которые будут использоваться в этом объяснении. На простейшем уровне две матрицы того же порядка можно комбинировать с двумя наиболее привычными математическими средствами: сложением и вычитанием матриц.

Определение: сложение и вычитание матриц

Имея пару матриц одного порядка, мы можем складывать или вычитать эти матрицы, добавляя или вычитая каждую соответствующую вход. Другими словами, пусть 𝐴=(𝑎)× и 𝐵=𝑏×. Затем, 𝐴+𝐵=𝐶,𝐴−𝐵=𝐷, где 𝐶=(𝑐)× и 𝐷=𝑑× удовлетворительно 𝑐=𝑎+𝑏,𝑑=𝑎−𝑏.

Существует также скалярное умножение на матрицу, которое имитирует наше понимание умножения действительных чисел.

Определение: скалярное умножение матриц

Для заданных скаляра и матрицы скалярное умножение матрицы вычисляется путем умножения скаляра на каждый элемент матрицы. матрица. Другими словами, пусть 𝐴=(𝑎)× и 𝑐 — скаляр. Затем, 𝑐𝐴=𝐸, где 𝐸=(𝑒)× с 𝑒=𝑐𝑎.

Когда мы комбинируем матричное сложение, вычитание и скалярное умножение, мы должны соблюдать правильный порядок операций. Порядок операций над матрицами аналогичен порядку операций над действительными числами.

Практическое руководство. Упорядочивание операций с матрицами, включающих сложение, вычитание и скалярное умножение

Комбинация матричных операций, включающая сложение, вычитание и скалярное умножение, оценивается в в следующем порядке:

1. Вычислить операцию в круглых скобках.
2. Вычисление скалярного умножения.
3. Вычисление сложения матриц.
4. Вычислить вычитание матрицы.

Мы можем видеть, что порядок матричных операций, включающих эти операции, аналогичен порядку операций над действительными числами, который часто называют PEMDAS (круглые скобки, показатели степени, умножение, деление, сложение, вычитание). Перечисленные операции выше содержат только круглые скобки, умножение, сложение и вычитание.

В нашем первом примере мы объединим сложение матриц и скалярное умножение.

Пример 1. Нахождение суммы двух матриц с помощью скалярного умножения

Учитывая, что 𝐴=−75−4−2,𝐵=107−2, что такое 13(𝐴+𝐵)?

Ответ

Напомним, что при объединении матричных операций мы должны сначала вычислить выражение в скобках. Следовательно, чтобы вычислить 13(𝐴+𝐵), нам нужно сначала найти сложение матрицы 𝐴+𝐵. Напомним, что мы можем добавить пару матриц одного порядка, добавляя каждый соответствующий элемент в матрицах. Мы можем видеть что и 𝐴, и 𝐵 являются матрицами 2 × 2, что означает, что они того же порядка. Следовательно, сложение 𝐴+𝐵 корректно определено и задается формулой 𝐴+𝐵=−75−4−2+107−2=−7+15+0−4+7−2−2=−653−4.

Теперь, когда мы получили матрицу 𝐴+𝐵, мы можем умножить эту матрицу на скаляр 13, чтобы получить закончим наши вычисления. Напомним, что умножение скаляра на матрицу выполняется путем умножения скаляра на каждый элемент матрицы. матрица. Это дает нам 13(𝐴+𝐵)=13−653−4=⎛⎜⎜⎝13×(−6)13×513×313×(−4)⎞⎟⎟⎠=⎛⎜⎜⎝−2531−43⎞⎟ ⎟⎠.

Следовательно, 13(𝐴+𝐵)=⎛⎜⎜⎝−2531−43⎞⎟⎟⎠.

Давайте рассмотрим еще один пример сочетания матричного сложения, вычитания и скалярного умножения, следуя правильному правилу. Порядок операций.

Пример 2.

Применение операций над матрицами, включающих скалярное умножение, для нахождения неизвестной матрицы

Учитывая, что 𝑋=−3−215−8−8,𝑌=−18−9−97−2,𝑍=3−8−70−85, что такое матрица 3𝑋+𝑌−3𝑍?

Ответ

В этом примере нам нужно вычислить выражение, которое включает скалярное умножение, сложение и вычитание матриц. Напомним, что комбинация матричных операций, включающая матричное сложение, вычитание и скалярное умножение, оценивается в следующем порядке:

1. Вычислить операцию в скобках.
2. Вычисление скалярного умножения.
3. Вычисление сложения матриц.
4. Вычислить вычитание матрицы.

Поскольку данное выражение в нашем примере не содержит круглых скобок, начнем с нахождения скалярных умножений 3𝑋 и 3𝑍. Напомним, что скалярное умножение на матрицу выполняется путем умножения скаляр по каждому элементу матрицы. Это дает нам 3𝑋=3×(−3)3×(−2)3×13×53×(−8)3×(−8)=−9−6315−24−24,3𝑍=3×33×(−8)3×(−7)3×03×(−8)3×5=9−24−210−2415.

Теперь, когда мы вычислили скалярное умножение, мы можем рассмотреть сложение матриц в выражении 3𝑋+𝑌−3𝑍. Сложение в этом выражении равно 3𝑋+𝑌. Напомним, что мы можем сложить или вычесть пару одинаковых матриц. порядок путем добавления или вычитания каждого соответствующего элемента в матрицах. Мы видим, что матрицы 3𝑋 и 𝑌 являются матрицами 3 × 2, что означает, что сложение матриц корректно определено и задается формулой 3𝑋+𝑌=−9−6315−24−24+−18−9−97−2=−9+(−1)−6+83+(−9)15+(−9)−24+7−24+( −2)=−102−66−17−26.

Наконец, мы можем закончить вычисления, рассмотрев вычитание матриц. Мы видим, что 3𝑋+𝑌 и 3𝑍 — обе матрицы 3×2. Следовательно, вычитание 3𝑋+𝑌−3𝑍 хорошо определен и задается 3𝑋+𝑌−3𝑍=−102−66−17−26−9−24−210−2415=−10−92−(−24)−6−(−21)6−0−17− (−24)−26−15=−19261567−41.

Следовательно, 3𝑋+𝑌−3𝑍=−19261567−41.

В следующем примере мы будем решать матричное уравнение, чтобы найти неизвестную матрицу в уравнении.

Пример 3.

Нахождение неизвестной матрицы в уравнении

Заполните пропуск: Если −3𝑋+−30912=𝑂, то 𝑋=.

1. 10–3–4
2.  -1034
3. 30–9-12
4.  -30912

Ответ

В этом примере нам нужно найти неизвестный matrix 𝑋 От. данное уравнение. Напомним, что 𝑂, стоящая в правой части данного уравнения, является нулевой матрицей определенного порядка.

Левая часть уравнения получается путем сложения двух матриц. Мы знаем, что мы можем складывать только матрицы того же порядка, а вторая матрица в сложении представляет собой матрицу 2×2. Следовательно, матрица −3𝑋 также должна быть матрицей 2×2. Матрица −3𝑋 получается скалярным умножением на матрица 𝑋. Поскольку скалярное умножение не меняет порядок матрицы, матрица 𝑋 также имеет порядок 2×2. Мы знаем, что добавление двух матриц одного порядка сохраняет порядок матрицы. матрица. Это означает, что нулевая матрица в правой части уравнения представляет собой матрицу 2×2.

Мы можем найти неизвестную матрицу 𝑋, используя два разных метода, как мы покажем ниже.

Метод 1

Мы можем обозначить 𝑋=(𝑥) для записи −3𝑥𝑥𝑥𝑥+−30912=0000.

В левой части этого уравнения мы имеем скалярное умножение и сложение матриц. Напомним, что скалярное умножение должны быть вычислены перед сложением матриц, поэтому давайте сначала найдем скалярное умножение −3𝑋. Напомним, что умножение скаляра на матрицу выполняется путем умножения скаляра на каждый элемент матрицы. Это дает нам −3𝑥𝑥𝑥𝑥=−3𝑥−3𝑥−3𝑥−3𝑥.

Подстановка этого выражения в наше уравнение дает −3𝑥−3𝑥−3𝑥−3𝑥+−30912=0000.

Далее нам нужно вычислить сложение матриц в левой части этого уравнения. Напомним, что мы можем сложить пару матриц того же порядка путем добавления каждого соответствующего элемента в матрицы. Мы видим, что обе матрицы имеют порядок 2 × 2, поэтому сложение корректно определено и определяется выражением −3𝑥−3𝑥−3𝑥−3𝑥+−30912=−3𝑥−3−3𝑥−3𝑥+9−3𝑥+12.

Подстановка этого выражения в левую часть уравнения дает −3𝑥−3−3𝑥−3𝑥+9−3𝑥+12=0000.

Напомним, что две матрицы одного порядка равны друг другу, если соответствующие элементы в каждой матрице равны. Это дает нам четыре уравнения: −3𝑥−3=0,−3𝑥=0,−3𝑥+9=0,−3𝑥+12=0.

Мы можем изменить каждое уравнение, чтобы получить −3𝑥=3⟹𝑥=−1,𝑥=0,−3𝑥=−9⟹𝑥=3,−3𝑥=−12⟹𝑥=4.

Это дает все записи 𝑋, что означает 𝑋=−1034.

Метод 2

В качестве альтернативы, мы можем решить матричное уравнение, применяя матричные операции непосредственно к уравнению так, чтобы левая часть уравнения равно 𝑋. Начнем с уравнения −3𝑋+−30912=0000.

Мы хотим изолировать 𝑋 в левой части уравнения. Итак, вычитаем вторую матрицу из обе части уравнения написать −3𝑋+−30912−−30912=0000−−30912.

Вычитание матрицы из самой себя дает нулевую матрицу. Мы также можем рассматривать правую часть уравнения как добавление нулевая матрица и -1, умноженная на другую матрицу. Мы знаем, что нулевая матрица является аддитивной единицей в сложение матриц, что означает, что добавление матрицы к нулевой матрице не меняет матрицу. Следовательно, мы можем записать это уравнение как −3𝑋=−−30912.

Затем мы можем умножить обе части уравнения на скаляр −13, чтобы получить 𝑋=13−30912.

Наконец, нам нужно найти скалярное умножение в правой части уравнения: 𝑋=⎛⎜⎜⎝13×(−3)13×013×913×12⎞⎟⎟⎠=−1034.

Это вариант B.

В предыдущем примере мы решили матричное уравнение, включающее матричное сложение, вычитание и скалярное умножение. Эти три операции над матрицами аналогичны соответствующим операциям над действительными числами. Мы можем заметить, что второй способ Решение этого матричного уравнения очень похоже на метод решения аналогичного уравнения с действительными числами.

Транспозиция — это совершенно новая концепция для матриц, которой не существует для действительных чисел, и мы можем комбинировать эту операцию с сложение, вычитание и скалярное умножение матриц для создания задач, уникальных для матричных операций.

Определение: транспозиция матриц

Если мы транспонируем матрицу 𝑚×𝑛, мы получим матрицу 𝑛×𝑚. Мы можем получить транспонировать матрицу, записав строки матрицы как соответствующие столбцы. Используя матричные обозначения, мы можем написать (𝑎)=(𝑎).××

Где транспозиция соответствует порядку матричных операций? Мы можем заметить, что транспонирование матрицы «выглядит как” экспонента матрицы. Хотя транспозиция не аналогична взятию экспоненты, порядок транспонирования подходит аналогично порядку взятия показателя степени в операциях с действительными числами. Думая о PEMDAS, мы видим, что термин «Показатели», следовательно, перестановка, находится между круглыми скобками и умножением.

Практическое руководство. Упорядочивание матричных операций, включающих сложение, вычитание, скалярное умножение и транспонирование

Комбинация матричных операций, включающая матричное сложение, вычитание, скалярное умножение и транспонирование, оценивается в в следующем порядке:

1. Вычислить операцию в круглых скобках.
2. Вычислить транспонирование.
3. Вычисление скалярного умножения.
4. Вычисление сложения матриц.
5. Вычислить вычитание матрицы.

В следующем примере мы объединим транспонирование и вычитание матриц.

Пример 4: Комбинация матричного преобразования и вычитания

Заполните пропуск: 6−4−32−5−3−41=.

1. 1−8−61
2. 11003
3. 𝑂
4. 𝐼

Ответ

В этом примере нам нужно вычислить матрицу и вычитание. Напомним, что транспонирование матриц должно вычисляется до вычитания матрицы. Итак, начнем с нахождения транспонирования второй матрицы в левой части уравнения. Напомним, что мы можем получить транспонирование матрицы, записав строки матрицы как соответствующие столбцы. Это ведет к 5−3−41=5−4−31.

Далее рассмотрим вычитание матрицы: 6−4−32−5−4−31.

Напомним, что мы можем вычесть пару матриц одного порядка, вычитая каждый соответствующий элемент в матрицах. Мы можем видеть что обе матрицы являются матрицами 2 × 2, а это означает, что вычитание определено корректно. Вычитание соответствующие записи, мы получаем 6−5−4−(−4)−3−(−3)2−1=1001.

Это завершает указанные матричные операции. Мы можем видеть, что результирующая матрица является диагональной матрицей с 1 на каждой диагонали. вход. Напомним, что такая матрица является единичной матрицей и обозначается 𝐼.

Это вариант D.

В следующем примере мы найдем неизвестную матрицу в уравнении, которое включает сложение и транспонирование матриц.

Пример 5: Поиск неизвестной матрицы в уравнении

Решите для матрицы 𝑋 в матричном уравнении 𝑋−𝐴=2𝐼, где 𝐼 представляет собой единичную матрицу размером 2 × 2 и 𝐴=2963.

Ответ

В этом примере нам нужно найти неизвестную матрицу в заданном уравнении. Мы можем применять матричные операции непосредственно к уравнение для нахождения неизвестной матрицы 𝑋.

Начнем с нахождения транспонирования 𝐴 в левой части данного уравнения. Напомним, что мы можем получить транспонирование матрицы, записав строки матрицы как соответствующие столбцы. Это ведет к 2963=2693.

Далее найдем матрицу в правой части уравнения. Нам дано, что 𝐼 является Единичная матрица 2×2, также известная как единичная матрица. Напомним, что тождественная или единичная матрица диагональная матрица с единицами в диагональных элементах. Это означает 2𝐼=21001.

Мы можем вычислить скалярное умножение, умножив скаляр 2 на каждый элемент матрицы. Это дает нам 2𝐼=2002.

Тогда мы можем записать данное уравнение как 𝑋−2693=2002.

Далее мы добавляем матрицу 2693 к обеим частям уравнения 𝑋−2693+2693=2002+2693.

Вычитание матрицы из самой себя дает нулевую матрицу, которая является аддитивной единицей. Это означает, что левая часть приведенное выше уравнение равно 𝑋.

Правая часть этого уравнения содержит сложение матриц. Напомним, что мы можем складывать матрицы одного порядка, добавляя соответствующие им записи. Мы видим, что обе матрицы в правой части уравнения имеют размер 2×2. матрицы, поэтому мы можем вычислить сложение матриц, чтобы получить 2002+2693=2+20+60+92+3=4695.

Это дает нам 𝑋=4695.

В предыдущих примерах мы видели, как комбинировать транспонирование матриц с другими матричными операциями, такими как сложение, вычитание, и скалярное умножение. Мы можем напомнить несколько свойств транспонирования матриц, которые полезны при комбинировании этих операций.

Свойство: Распределительное свойство преобразования матриц

Пусть 𝐴 и 𝐵 — матрицы одного порядка. Затем, (𝐴+𝐵)=𝐴+𝐵,(𝐴−𝐵)=𝐴−𝐵.

Мы знаем, что умножение действительных чисел является дистрибутивным, т. е. 𝑎×(𝑏+𝑐)=𝑎×𝑏+𝑎×𝑐,𝑎,𝑏,𝑐∈ℝ.forany

Следовательно, транспонирование матрицы ведет себя как умножение в том смысле, что оно удовлетворяет дистрибутивному свойству.

Мы также можем комбинировать транспонирование матрицы с самой собой. Это означает, что мы можем дважды применить транспонирование матрицы к матрице. Напомним следующий результат о последовательных применениях транспонирования матриц.

Свойство: Последовательные применения транспонирования матриц

Пусть 𝐴 — матрица. Затем, 𝐴=𝐴.

Это утверждение говорит нам, что последовательные применения транспонирования матриц возвращают исходную матрицу.

В следующем примере мы применим свойства транспонирования матриц для вычисления заданного выражения.

Пример 6. Операции над матрицами, включающие транспонирование матрицы

Учитывая, что 𝐵=1−37−3,𝐵−𝐵=𝐴, определить значение 𝑎+𝑎.

Ответ

В этом примере нам нужно вычислить выражение 𝑎+𝑎. Напомним, что обозначения 𝑎 указывает на запись в 𝑖-й строке и 𝑗-м столбце матрицы 𝐴. Следовательно, нам нужно найти записи 𝑎 и 𝑎 и суммировать их. Для этого нам нужно сначала вычислить матрицу 𝐴.

Матрица 𝐴 задается выражением 𝐵−𝐵. Мы можем упростить это выражение, применяя свойства транспонирования матриц. Во-первых, напомним дистрибутивное свойство перестановки матриц. Для матриц 𝐶 и 𝐷 одного порядка имеем (𝐶−𝐷)=𝐶−𝐷.

Применяя это свойство с 𝐶=𝐵 и 𝐷=𝐵, получаем 𝐵−𝐵=𝐵−𝐵.

Теперь вспомним еще одно свойство транспонирования матриц. Для любой матрицы 𝐶, 𝐶=𝐶.

Это означает, что 𝐵=𝐵, что приводит к 𝐵−𝐵=𝐵−𝐵=𝐵−𝐵.

Следовательно, это приводит к 𝐴=𝐵−𝐵.

Чтобы найти матрицу 𝐴, нам нужно сначала найти транспонированную 𝐵, а затем вычесть 𝐵 из этой матрицы. Напомним, что мы можем найти транспонирование матрицы, поменяв местами ее строки и столбцы. Это дает нам 𝐵=1−37−3=17−3−3.

Тогда, 𝐵−𝐵=17−3−3−1−37−3.

Наконец, нам нужно найти вычитание матрицы. Напомним, что мы можем вычитать матрицы одного порядка, вычитая соответствующие записи. Мы видим, что обе матрицы в правой части уравнения имеют размер 2×2. матрицы, поэтому вычитание матриц корректно определено. Следовательно, мы получаем 17−3−3−1−37−3=1−17−(−3)−3−7−3−(−3)=010−100.

Следовательно, имеем 𝐴=010−100.

𝑎 — элемент этой матрицы в первой строке и втором столбце, а 𝑎 — запись во второй строке и первом столбце. Из приведенной выше матрицы получаем 𝑎=10,𝑎=−10.

Следовательно, 𝑎+𝑎=10+(−10)=0.

В нашем последнем примере мы будем комбинировать сложение матриц и транспонирование.

Пример 7: Комбинация сложения матриц и транспонирования

Выполните следующее: Если 𝐴 и 𝐵 две матрицы одинакового размера, то 𝐴+𝐵=.

Ответ

Мы решим этот пример двумя разными способами. В первом методе мы найдем ответ, разработав данная матрица операций запись за записью, чтобы определить, чему равен результат. Во втором способе применим свойства транспонирования матриц для упрощения данного выражения.

Метод 1

Мы знаем, что добавление верхнего индекса 𝑇 означает транспонирование матрицы, поэтому данное выражение объединяет матрицу сложение и перестановка. Напомним, что комбинация матричных операций, включающая матричное сложение, вычитание, скалярное умножение и транспонирование оцениваются в следующем порядке:

1. Вычислить операцию в круглых скобках.
2. Вычислить транспонирование.
3. Вычисление скалярного умножения.
4. Вычислить сложение матриц.
5. Вычислить вычитание матрицы.

В этом примере выражение 𝐴+𝐵 заключено в круглые скобки, поэтому нам нужно сначала найти это выражение. Это выражение также является комбинацией транспонирования и сложения. Следовательно, нам нужно

1. переставить матрицы 𝐴 и 𝐵, чтобы найти 𝐴 и 𝐵,
2. сложить транспонированные матрицы, чтобы найти 𝐴+𝐵,
3. переставить полученную сумму, чтобы найти 𝐳+𝐵 .

Начнем с того, что напомним обозначение матрицы, полезное для определения матричных операций. Если мы обозначим 𝑎 для целых чисел 𝑖=1,2,…,𝑚 и 𝑗=1,2,…,𝑛 последовательность чисел, тогда (𝑎)× обозначает матрицу 𝑚×𝑛 чья запись в 𝑖-й строке и 𝑗-м столбце дается как 𝑎.

Поскольку матрицы 𝐴 и 𝐵 имеют одинаковый размер, мы будем говорить, что они обе 𝑚×𝑛 матрицы. Следовательно, мы обозначаем 𝐴=(𝑎),𝐵=𝑏.××

Найдем транспонирование этих матриц. Мы знаем, что транспонирование матрицы 𝑚×𝑛 представляет собой 𝑛×𝑚 матрица, полученная перестановкой ее строк и столбцов. Это означает 𝐴=(𝑎),𝐵=𝑏.××

Далее нам нужно найти сумму 𝐴+𝐵. Напомним, что мы можем сложить пару матриц одного порядка с помощью добавление каждой соответствующей записи в матрицы. Мы видим, что и 𝐴, и 𝐵 матрицы 𝑛×𝑚, поэтому сложение 𝐴+𝐵 корректно определено и задается формулой где

Наконец, мы можем транспонировать эту матрицу, поменяв местами ее строки и столбцы: 𝐴+𝐵=(𝑐).×

Поскольку мы знаем 𝑐=𝑎+𝑏, мы можем найти 𝑐 путем замены 𝑗 и 𝑖, что приводит к 𝑐=𝑎+𝑏.

Это означает 𝐴+𝐵=𝑎+𝑏.×

Но мы также знаем, что матрица в правой части этого уравнения может быть получена сложением 𝐴 и 𝐵. Другими словами, 𝐴+𝐵=𝑎+𝑏.×

Это означает 𝐴+𝐵=𝐴+𝐵.

Метод 2

Напомним дистрибутивное свойство перестановки матриц. Для любых двух матриц 𝐶 и 𝐷 того же порядка, (𝐶+𝐷)=𝐶+𝐷.

В этом примере 𝐶=𝐴 и 𝐷=𝐵. Мы знаем, что матрицы 𝐴 и 𝐵 одного порядка, скажем 𝑚×𝑛. Как отмечалось в предыдущем методе, транспонированный матрицы 𝐴 и 𝐵 имеют порядок 𝑛×𝑚, что означает, что у них такой же порядок. Следовательно, 𝐴+𝐵=𝐴+𝐵.

Далее напомним, что последовательное применение транспонирования матриц приводит к исходной матрице. Это означает 𝐴=𝐴,𝐵=𝐵.

Подставив эти выражения в приведенное выше уравнение, мы можем написать 𝐴+𝐵=𝐴+𝐵.

Давайте закончим повторением нескольких важных понятий из объяснения.

Ключевые точки

• Даны матрицы 𝐴=(𝑎)× и 𝐵=𝑏× и скаляр 𝑐 мы определяем матричное сложение, вычитание, скалярное умножение и транспонирование следующим образом: (𝑎)+𝑏=𝑎+𝑏,(𝑎)−𝑏=𝑎−𝑏,𝑐(𝑎)=(𝑐𝑎),(𝑎)=(𝑎).

  No related posts.