Правило сложения комплексных чисел. Модуль и аргумент комплексного числа
Тема Комплексные числа и многочлены
Лекция 22
Символ
вводят соотношением
и называют мнимой единицей. Другими
словами,
.
Определение. Выражение вида
,
где
,
называется комплексным числом, при этом
числоназывают вещественной частью комплексного
числаи обозначают
,
число– мнимой частьюи обозначают
.
Из такого определения следует, что действительные числа – это те комплексные числа, мнимая часть которых равна нулю.
Комплексные числа
удобно изображать точками плоскости,
на которой задана декартова прямоугольная
система координат, а именно: комплексному
числу
соответствует точка
и наоборот. На оси
изображаются вещественные числа и её
называют вещественной осью. Комплексные
числа вида
называют чисто мнимыми. Они изображаются
точками на оси
,
которую называют мнимой осью. Эту
плоскость, служащую для изображения
комплексных чисел, называют комплексной
плоскостью.
, иногда называют мнимым.
Два комплексных числа называют равными тогда и только тогда, когда у них совпадают как вещественные, так и мнимые части.
Сложение, вычитание
и умножение комплексных чисел производится
по обычным правилам алгебры многочленов
с учётом того, что
. Операцию деления можно определить как
обратную к операции умножения и доказать
единственность результата (если делитель
отличен от нуля). Однако на практике
используется другой подход.
Комплексные числа
и
называют сопряжёнными, на комплексной
плоскости они изображаются точками,
симметричными относительно вещественной
оси. Очевидно, что:
1)
;
2)
;
3)
.
Теперь разделить наможно следующим образом:
.
Не трудно показать, что
,
где символ обозначает любую арифметическую операцию.
Пусть
некоторое мнимое
число, а
– вещественная переменная. Произведение
двух биномов
есть квадратный
трёхчлен с действительными коэффициентами.
Теперь, имея в
распоряжении комплексные числа, мы
сможем решить любое квадратное уравнение
.Если
,
то
и уравнение имеет два комплексных сопряжённых корня
.
Если
,
то уравнение имеет два различных
вещественных корня. Если
,
то уравнение имеет два одинаковых корня.
Как говорилось
выше, комплексное число
удобно изображать точкой
.
Можно также такое число отождествлять
с радиус-вектором этой точки
.
При такой интерпретации сложение и
вычитание комплексных чисел производится
по правилам сложения и вычитания
векторов. Для умножения и деления
комплексных чисел более удобной
оказывается другая форма.
Введём на комплексной
плоскости
полярную систему координат. Тогда,
где
,
и комплексное число
можно записать в виде:
Эту форму записи
называют тригонометрической (в отличие
от алгебраической формы
).
В этой форме числоназывают модулем, а– аргументом комплексного числа.
Они обозначаются:
,
.
Для модуля имеем формулу
Аргумент числа
определён неоднозначно, а с точностью
до слагаемого
,
.
Значение
аргумента, удовлетворяющего неравенствам
,
называется главным и обозначается
.
Тогда,
.
Для главного значения аргумента можно
получить такие выражения:
,
аргумент числа
считается неопределённым.
Условие равенства
двух комплексных чисел в тригонометрической
форме имеет вид: модули чисел равны, а
аргументы отличаются на число кратное
.
Найдём произведение двух комплексных чисел в тригонометрической форме:
Итак, при умножении чисел их модули умножаются, а аргументы складываются.
Аналогичным образом можно установить, что при делении модули чисел делятся, а аргументы вычитаются.
Понимая возведение в степень как многократное умножение, можно получить формулу возведения комплексного числа в степень:
Выведем формулу
для
– корня-ой
степени из комплексного числа(не путать с арифметическим корнем из
действительного числа!).
Операция
извлечения корня является обратной по
отношению к операции возведения в
степень. Поэтому
– это комплексное числотакое, что
.
Пусть
известно, а
требуется найти. Тогда
Из равенства двух комплексных чисел в тригонометрической форме следует, что
,
,
.
Отсюда
(это арифметический корень!),
,
.
Нетрудно убедиться,
что
может принимать лишьразличных по существу значений, например,
при
.
Окончательно имеем формулу:
,
.
Итак, корень
-ой
степени из комплексного числа имеетразличных значений. На комплексной
плоскости эти значения располагаются
в вершинах правильно-угольника,
вписанного в окружность радиуса
, аргументы двух “соседних” корней отличаются на
.
Пример. Извлечём корень кубический из мнимой
единицы:
,
,
.
Тогда:
,
Комплексные числа
Мнимые и комплексные числа.
Абсцисса и ордината
комплексного числа. Сопряжённые комплексные числа.
Операции с комплексными числами. Геометрическое
представление комплексных чисел. Комплексная плоскость.
форма комплексного числа. Операции с комплексными
числами в тригонометрической форме. Формула Муавра.
Начальные сведения о мнимых и комплексных числах приведены в разделе «Мнимые и комплексные числа». Необходимость в этих числах нового типа появилась при решении квадратных уравнений для случая D D – дискриминант квадратного уравнения). Долгое время эти числа не находили физического применения, поэтому их и назвали «мнимыми» числами. Однако сейчас они очень широко применяются в различных областях физики
и техники: электротехнике, гидро- и аэродинамике, теории упругости и др.
Комплексные числа записываются в виде: a
+
bi .
Здесь a и b – действительные числа ,
а i – мнимая единица, т.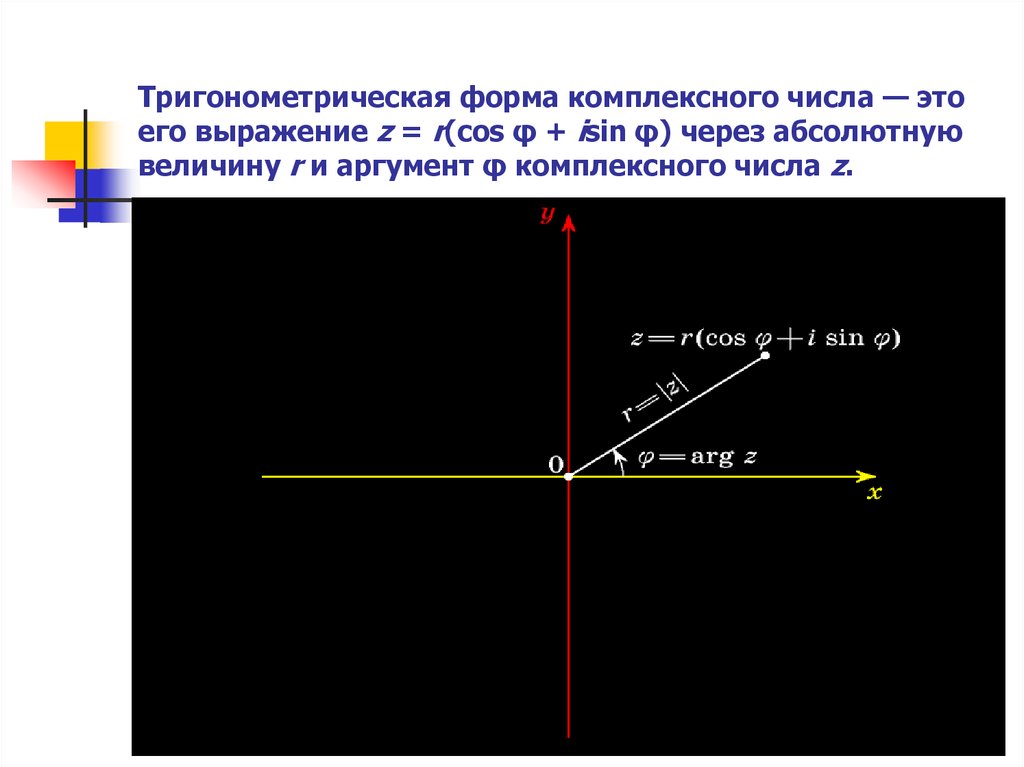
e
.
i 2 = –1. Число a называется абсциссой ,
a b
–
ординатой комплексного числа a
+
bi
. Два комплексных числа a
+
bi и a
–
bi называются
Основные договорённости:
1. Действительное число а может быть также записано в форме комплексного числа: a + 0 i или a – 0 i . Например, записи 5 + 0 i и 5 – 0 i означают одно и то же число 5 .
2. Комплексное число 0+ bi называется чисто мнимым числом . Запись bi означает то же самое, что и 0+ bi .
3. Два комплексных числа a + bi и c + di считаются равными, если a = c и b = d . В противном случае комплексные числа не равны.
Сложение. Суммой комплексных
чисел a
+
bi и c
+
di называется
комплексное число (a
+
c ) + (b
+
d ) i
.
Таким образом, при сложении комплексных чисел отдельно
складываются их абсциссы и ординаты.
Это определение соответствует правилам действий с обычными многочленами.
Вычитание. Разностью двух комплексных чисел a + bi (уменьшаемое) и c + di (вычитаемое) называется комплексное число ( a – c ) + (b – d ) i .
Таким образом, при вычитании двух комплексных чисел отдельно вычитаются их абсциссы и ординаты.
Умножение. Произведением комплексных чисел a + bi и c + di называется комплексное число:
( ac – bd ) + (ad + bc ) i . Это определение вытекает из двух требований:
1) числа a + bi и c + di должны перемножаться, как алгебраические двучлены,
2) число i обладает основным свойством: i 2 = – 1.
П р и м е р
. (a+ bi )( a –
bi ) =
a 2 + b 2 .
двух сопряжённых комплексных чисел равно действительному
положительному числу.
Деление. Разделить комплексное число a + bi (делимое) на другое c + di (делитель) — значит найти третье число e + f i (чатное), которое будучи умноженным на делитель c + di , даёт в результате делимое a + bi .
Если делитель не равен нулю, деление всегда возможно.
П р и м е р. Найти (8 + i ) : (2 – 3 i ) .
Р е ш е н и е. Перепишем это отношение в виде дроби:
Умножив её числитель и знаменатель на 2 + 3 i
И выполнив все преобразования, получим:
Геометрическое представление комплексных чисел. Действительные числа изображаются точками на числовой прямой:
Здесь точка A означает число –3, точка B
– число 2, и O – ноль. В отличие от этого комплексные числа изображаются точками на координатной плоскости.
Выберем для этого прямоугольные (декартовы)
координаты с одинаковыми масштабами на обеих осях. Тогда комплексное
число a
+
bi будет представлено точкой Р с абсциссой а
и ординатой
b (см. рис.). Эта система координат называется комплексной
плоскостью .Модулем комплексного числа называется длина вектора OP , изображающего комплексное число на координатной (комплексной ) плоскости. Модуль комплексного числа a + bi обозначается | a + bi | или буквой r
Комплексные числа. Комплексным числом называется число вида z=a+biabRi2=−1
Замечание.
Действительное число a — это действительная часть числа z и обозначается a=Rez
Действительные числа представляют собой полноценный набор чисел и действий над ними, которого, кажется, должно хватить для решения любых заданий курса математики.
Но как решить такое уравнение в действительных числах x2+1=0? Существует ещё одно расширение чисел — комплексные числа. В комплексных числах можно брать корни из отрицательных чисел. Алгебраическая форма комплексного числа. Алгебраическая форма комплексного числа имеет видz=a+bi(aRbRi2=−1)
Замечание. Если a=ReZ=0b=Imz=0, то число z называется мнимым. Если a=ReZ=0b=Imz=0, то число z называется чисто мнимым
Геометрической интерпретацией действительных чисел является действительная прямая. Кроме того, на действительной прямой «нет места для новых точек», то есть любой точке на действительной оси отвечает действительное число. Следовательно, комплексные числа на этой прямой расположить уже нельзя, однако можно попытаться рассмотреть наряду с действительной осью, на которой мы будем откладывать действительную часть комплексного числа, ещё одну ось, ей перпендикулярную; будем называть её мнимой осью. Тогда любому комплексному числу z = a + ib можно поставить в соответствие точку координатной плоскости.
На оси абсцисс будем откладывать действительную часть комплексного числа, а на оси ординат — мнимую часть. Таким образом устанавливается взаимнооднозначное соответствие между всеми комплексными числами и всеми точками плоскости. Если такое соответствие построено, то координатная плоскость называется комплексной плоскостью. Интерпритацией комплексного числа z = a + b i является вектор OA с координатами(a,b) с началом в точке O(0,0) и концом в точке A(a,b)
Сопряженные числа. Числа z=a+bi и z=a−bi называются сопряженными комплексными числами
Свойство. Сумма и произведение двух сопряженных комплексных чисел являются действительными числами:z+z=2azz=a2+b2
Противоположные числа. Числа z=a+bi и −z=−a−bi называются противоположными комплексными числами.
Свойство. Сумма двух противоположных комплексных чисел равна нулю:
z+(−z)=0
Равные числа. Два комплексных числа называются равными, если равны их действительные и мнимые части.
Действия с комплексными числами, заданными в алгебраической форме:
Свойство сложения: Сумма двух комплексных чисел z1=a+bi и z2=c+di будет комплексное число вида z=z1+z2=a+bi+c+di=a+c+(b+d)i
Пример: 5+3i+3−i=8+2i
Свойство вычитания: Разность двух комплексных чисел z1=a+bi и z2=c+di будет комплексное число вида z=z1−z2=a+bi−c+di=a−c+(b−d)i
Пример: .
5+3i−3−i=2+4i
Свойство умножения: Произведение двух комплексных чисел z1=a+bi и z2=c+di будет комплексное число вида z=z1z2=a+bic+di=ac−bd+(ad+bc)i
Пример: 3+2i4−i=12−3i+8i−2i2=14+5i
Свойство деления: Частное двух комплексных чисел z1=a+bi и z2=c+di будет комплексное число видаz=z2z1=c+dia+bi=c2+d2ac+bd+c2+d2bc−adi
Пример: . 1+i2+i=1+i1−i2+i1−i=1−i22−2i+i−i2=23−21i
Действия с комплексными числами, заданных в тригонометрической форме
Запись комплексного числа z = a + bi в виде z=rcos+isin называется тригонометрической формой комплексного числа.
Модуль комплексного числа: r=a2+b2
Аргумент комплексного числа:cos=rasin=rb
Мнимые и комплексные числа
Рассмотрим неполное квадратное уравнение:
x 2 = a ,
где а – известная величина. Решение этого уравнения можно записать как:
Здесь возможны три случая:
1). Если a = 0 , то x = 0.
2). Если а – положительное число, то его квадратный корень имеет два значения: одно положительное, другое отрицательное; например, уравнение x 2 = 25 имеет два корня: 5 и – 5.
Это часто записывается как корень с двойным знаком:
3).Если а – отрицательное число, то это уравнение не имеет решений среди известных нам положительных и отрицательных чисел, потому что вторая степень любого числа есть число неотрицательное (продумайте это!). Но если мы хотим получить решения уравнения x 2 = a также и для отрицательных значений а, мы вынуждены ввести числа нового типа – мнимые числа. Таким образом, мнимым называется число,вторая степень которого является числом отрицательным. Согласно этому определению мнимых чисел мы можем определить и мнимую единицу:
Тогда для уравнения x 2 = – 25 мы получаем два мнимых корня:
Подставляя оба эти корня в наше уравнение, получаем тождество. (Проверьте!). В отличие от мнимых чисел все остальные числа (положительные и отрицательные, целые и дробные, рациональные и иррациональные) называются действительными или вещественными числами. Сумма действительного и мнимого числа называется комплексным числом и обозначается:
Где a, b – действительные числа, i – мнимая единица.
П р и м е р ы комплексных чисел: 3 + 4 i , 7 – 13.6 i , 0 + 25 i = 25 i , 2 + i.
Комплексные числа — это минимальное расширение множества привычных нам действительных чисел. Их принципиальное отличие в том, что появляется элемент, который в квадрате дает -1, т.е. i, или .
Любое комплексное число состоит из двух частей: вещественной и мнимой :
Таким образом видно, что множество действительных чисел совпадает с множеством комплексных чисел с нулевой мнимой частью.
Самая популярная модель множества комплексных чисел — это обычная плоскость. Первая координата каждой точки будет её вещественной частью, а вторая -мнимой. Тогда в роли самих комплексных чисел бдут выступать вектора с началом в точке (0,0).
Операции над комплексными числами.
На самом деле, если брать в расчет модель множества комплексных чисел, интуитивно понятно, что сложение (вычитание) и умножение двух комплексных числе производятся так же как соответственные операции над векторами.
Причем имеется в виду векторное произведение векторов, потому что результатом этой операции является опять же вектор.
1.1 Сложение.
(Как видно, данная операции в точности соответствует )
1.2 Вычитание , аналогично, производится по следующему правилу:
2. Умножение.
3. Деление.
Определяется просто как обратная операция к умножению.
Тригонометрическая форма.
Модулем комплексного числа z называется следующая величина:
,
очевидно, что это, опять же, просто модуль (длина) вектора {a,b}.
Чаще всего модуль комплексного числа обозначается как ρ.
Оказывается, что
z = ρ(cosφ+isinφ) .Непосредственно из тригонометрической формы записи комплексного числа вытекают следующие формулы :
Последнюю формулу называют Формулой Муавра . Непосредственно из нее выводится формула корня n-ной степени из комплексного числа :
таким образом, существует n корней n-ной степени из комплексного числа z.
Умножение комплексных чисел в тригонометрической форме записи » Аналитическая геометрия f(x)dx.Ru
п.5. Умножение комплексных чисел в тригонометрической форме записи. Свойства модуля комплексных чисел.
Теорема. (Об умножении комплексных чисел в тригонометрической форме записи.)
Пусть , где и , где – два произвольных комплексных числа записанных в тригонометрической форме. Тогда
. (13)
Доказательство.
, ч.т.д.
Теорема доказана.
Отсюда вытекает правило умножения комплексных чисел в тригонометрической форме записи.
Для того, чтобы перемножить два комплексных числа в тригонометрической форме записи нужно перемножить их модули, а аргументы сложить.
Следствие 1. Пусть k натуральное число и . Пусть далее , где – произвольные n комплексных чисел записанных в тригонометрической форме записи. Тогда
.
Доказательство проводится индукцией по числу сомножителей и предоставляется читателю.
Следствие 2. Пусть n натуральное число и – произвольное комплексное число в тригонометрической форме записи. Тогда
.
Доказательство сразу же следует из Следствия 1.
Теорема. (Свойства модуля комплексного числа.)
Пусть – произвольные комплексные числа и соответствующие точки на комплексной плоскости. Тогда:
1) и . Т.е. модуль произведения комплексных чисел равен произведению их модулей и модули противоположных чисел равны;
2) расстояние между точками и комплексной плоскости равно модулю разности соответствующих комплексных чисел: ;
3) ;
4) ;
Доказательство. 1) По предыдущей теореме имеем:
, где и ,
т.е. .
Таким образом, равенства и есть тригонометрическая форма записи числа , следовательно, по теореме о равенстве комплексных чисел в тригонометрической форме записи, имеем , ч.т.д.
Далее, т.к. , то по только что доказанному свойству , ч.т.д.
Заметим, что последнее равенство можно получить и из других соображений.
Противоположные числа на комплексной плоскости изображаются точками симметричными относительно начала координат. Действительно, пусть . Тогда и точки , имеют противоположные декартовые координаты. Значит, в силу симметрии, расстояния от этих точек до начала координат равны, т.е. , ч.т.д. Заметим, также, что такой же результат можно получить с помощью формулы (12) вычисления модуля комплексного числа.
2). Пусть , . Тогда и по формуле (12) имеем:
. (14)
С другой стороны, рассмотрим числа и как точки на комплексной плоскости. Тогда точка имеет декартовые координаты , а и искомое расстояние между ними вычисляется по формуле (14), ч.т.д.
3) Рассмотрим на комплексной плоскости точки , и начало координат О. В общем случае эти три точки являются вершинами треугольника :
рис.6.
Воспользуемся известным свойством треугольника: длина стороны треугольника не превосходит суммы длин двух его других сторон.
Мы только что доказали, что длина стороны этого треугольника равна , а длины сторон и равны по определению модулям чисел и : , . Отсюда и получаем, что .
Заменим в последнем неравенстве число на противоположное число , тогда получаем:
, ч.т.д.
Заметим, что равенство в этих неравенствах достигается тогда и только тогда, когда треугольник вырождается в отрезок прямой, т.е. когда все три точки О, и лежат на одной прямой.
4) , откуда следует
. Поменяв местами и , получаем
, откуда и следует доказываемое неравенство.
Теорема доказана.
Теория комплексных чисел имеет много приложений в различных областях математики. Не могу удержаться от искушения привести хотя бы один такой пример, относящийся к области теории чисел.
Определение. Говорят, что натуральное число n представимо в виде суммы двух квадратов, если существуют такие целые числа х и у, что выполняется равенство:
.
Теорема. Если два числа представимы в виде суммы двух квадратов, то их произведение также представимо в виде суммы двух квадратов.
Доказательство. Пусть и , где .
Нам нужно доказать, что найдутся два целых числа а и b такие, что .
С этой целью рассмотрим два комплексных числа и .
Тогда и по формуле (12) имеем: .
С другой стороны, , . Так как , то или , то отсюда получаем равенство: , где , ч.т.д.
Теорема доказана.
Мнимые числа и тригонометрия
Мнимые числа и тригонометрия
Мы используем MathJax
В нашем предыдущем обсуждении мнимые числа, мы узнали, как можно нарисовать комплексное число $2+3i$.
Если мы нарисуем на картинке прямоугольный треугольник, то получим:
Части комплексного числа $2+3i$
показаны горизонтальной и вертикальной сторонами треугольника.
Гипотенуза прямоугольного треугольника имеет длину $\sqrt{13}$,
найти с помощью теоремы Пифагора или формулы расстояния.
В треугольнике, если мы используем $P$ для имени угол в начале координат, то может переписать число $2+3i$, используя его тригонометрические компоненты. Горизонтальная составляющая равна $\sqrt{13}\cos P$, вертикальная составляющая равна $\sqrt{13}(\sin P)i$, поэтому число $2+3i$ совпадает с $\sqrt{13}(\cos P + i \sin P)$. В принципе, каждое комплексное число можно записать в виде
. \begin{уравнение*} a+bi= r (\cos P + i \sin P) \end{уравнение*}Умножение и деление
В тригонометрии много тождеств, и они ключ к умножению и делению комплексных чисел. Предположим, у нас есть два комплексных числа $r (\cos P + i \sin P)$ и $s (\cos Q + i \sin Q)$. Когда мы умножаем их с помощью дистрибутивного свойства, мы получаем $rs (\cos P \cos Q + i \cos P \sin Q + i \sin P \cos Q — \sin P \sin Q)$. Но формулы синуса и косинуса суммы позволяют переписать этот результат как
\begin{уравнение*} [r (\cos P + i \sin P)][s (\cos Q + i \sin Q)] = rs[\cos(P+Q)+i\sin(P+Q)] \end{уравнение*} Другими словами, умножение комплексных чисел включает в себя умножение их
расстояния от начала координат и сложение их углов.
Мы можем вывести аналогичную формулу для деления сложных числа. Эта формула
\begin{уравнение*} \frac{r (\cos P + i \sin P)}{s (\cos Q + i \sin Q)} = \frac{r}{s}[\cos(PQ)+i\sin(PQ) ] \end{уравнение*}Силы и корни
Поскольку показатели степени представляют многократное умножение, мы может вывести формула степеней комплексных чисел. Эта формула известна как 9\frac{1}{n} \left( \cos \frac{P+2k\pi}{n}+i\sin \frac{P+2k\pi}{n} \right) \end{уравнение*}
Обратите внимание, что эта формула вычисляет не только квадратные корни, но и все виды корнеплоды.
Чему равен квадратный корень из $2+3i$? В тригонометрической форме исходное число равно $\sqrt{13}(\cos P + i\sin P)$, где угол $P = \arctan \frac32$. Следовательно, квадратные корни равны $\sqrt{\sqrt{13}}\left(\cos\frac12\arctan\frac32+i\sin\frac12\arctan\frac32\right)$ а также $\sqrt{\sqrt{13}}\left(\cos(\pi+\frac12\arctan\frac32)+i\sin(\pi+\frac12\arctan\frac32)\right)$.
Эпилог
Конечно, теперь мы можем просто попросить кого-нибудь из ручных
калькуляторы, чтобы сделать нашу комплексную арифметику чисел.
К сожалению,
калькулятор не говорит нам, почему ответы такие, какие они есть.
находятся. Это обсуждение было предназначено, чтобы помочь нашему пониманию.
Теперь, если вы усвоили квадратный корень из мнимой числа, являются вы готовы к мнимым числам в качестве показателей? Если да, прочтите Использование i в качестве экспоненты.
Назад к введению.
Комплексные числа: углы и полярные координаты
Комплексные числа: углы и полярные координаты Этот раздел предполагает знание тригонометрии. Для получения информации о тригонометрии см. Краткий курс Дейва по триггерам наhttp://www.clarku.edu/~djoyce/trig/
Полярные координаты помогут нам понять комплексные числа геометрически. С одной стороны, обычные прямоугольные координаты x и y задают комплексный номер z = x + yi , задав расстояние x вправо и расстояние y вверх. С другой стороны, полярные координаты определяют ту же точку z , говоря, как
far r от начала координат 0 и угол для линии от начала координат до точки.
Мы уже назвали расстояние r абсолютной величиной | с | z, , и мы увидели, как
Теорема Пифагора установила связь между ним и х и и :
Далее нам нужно разобраться с углом . Мы будем следовать стандартному соглашению для указания угла
. Согласно этому соглашению, положительная ось x (наша реальная ось) проходит под углом 0°, т.е.
положительная ось y (наша воображаемая ось) под углом 90°, отрицательная ось x под углом 180° и отрицательная y — ось под углом 270°. Кроме того, 360° можно добавить или вычесть из любого угла, и направление не изменится. Так,
0°, 360°, 720° и 360° относятся к положительному x — ось. Аналогично, 270° и 90°
оба относятся к отрицательной оси y . Угол 45° проходит вдоль линии y = x вверх вправо.
И так далее.
Точка z может быть задана любой парой, парой прямоугольных координат x и y или парой полярных координат.
координаты, r, что | z | и , который является arg ( z ). Поскольку любая пара
определяет точку, каждая пара должна определять другую пару. Должно быть четыре уравнения, связывающих их, и так есть. Пифагорейский
тождество было упомянуто выше, но остальные требуют тригонометрии. Из того же треугольника мы
используемые для теоремы Пифагора, мы находим следующие три соотношения:
Теперь, если мы применим эти отношения к нашему комплексному числу z = x + yi, , то мы получим альтернативное описание для z
| я | = | x + iy |
| = | r cos + i r sin | |
| = | r (cos + i sin ) | |
| = | | с | (cos + i sin ) |
Обратите внимание, что комплексное число cos + i sin имеет абсолютное значение 1, поскольку cos 2 + sin 2 равно 1 для любого угла .
Таким образом, каждое комплексное число z является
произведение действительного числа | г | и комплексное число cos + i sin .
Мы почти подошли к тому моменту, когда можем доказать последнее недоказанное утверждение предыдущего раздела об умножении, а именно, что arg( zw ) = arg( z ) + arg( w ). Как и выше, мы принимаем arg( z ) как , а теперь пусть arg( w ) будет . Затем,
Нам нужно показать, что arg( zw ) равно + . Другими словами
Если мы воспользуемся формулами сложения для косинуса и синуса в одном важном моменте, мы его получим. Напомним из тригонометрии эти сложения формулы:
sin ( + ) = cos sin + sin cos .