Калькулятор сокращения смешанных дробей. Калькулятор онлайн.Сокращение дробей (неправильных, смешанных)
Калькулятора онлайн выполняет сокращение алгебраических дробей в соответствии с правилом сокращения дробей: замена исходной дроби равной дробью, но с меньшими числителем и знаменателем, т.е. одновременное деление числителя и знаменателя дроби на их общий наибольший общий делитель (НОД). Также калькулятор выводит подробное решение, которое поможет понять последовательность выполнения сокращения.
Дано:
Решение:
Выполнение сокращения дробей
проверка возможности выполнения сокращения алгебраической дроби
1) Определение наибольшего общего делителя (НОД) числителя и знаменателя дроби
определение наибольшего общего делителя (НОД) числителя и знаменателя алгебраической дроби
2) Сокращение числителя и знаменателя дроби
сокращение числителя и знаменателя алгебраической дроби
3) Выделение целой части дроби
выделение целой части алгебраической дроби
4) Перевод алгебраической дроби в десятичную дробь
перевод алгебраической дроби в десятичную дробь
Помощь на развитие проекта сайт
Уважаемый Посетитель сайта.
Если Вам не удалось найти, то что Вы искали — обязательно напишите об этом в комментариях, чего не хватает сейчас сайту. Это поможет нам понять в каком направлении необходимо дальше двигаться, а другие посетители смогут в скором времени получить необходимый материал.
Если же сайт оказался Ваме полезен — подари проекту сайт всего 2 ₽ и мы будем знать, что движемся в правильном направлении.
Спасибо, что не прошели мимо!
I. Порядок действий при сокращении алгебраической дроби калькулятором онлайн:
- Чтобы выполнить сокращение алгебраической дроби введите в соответствующие поля значения числителя, знаменателя дроби. Если дробь смешанная, то также заполните поле, соответствующее целой части дроби. Если дробь простая, то оставьте поле целой части пустым.
- Чтобы задать отрицательную дробь, поставьте знак минус в целой части дроби.
- В зависимости от задаваемой алгебраической дроби автоматически выполняется следующая последовательность действий:
- определение наибольшего общего делителя (НОД) числителя и знаменателя дроби ;
- сокращение числителя и знаменателя дроби на НОД ;
- выделение целой части дроби , если числитель итоговой дроби больше знаменателя.
- перевод итоговой алгебраической дроби в десятичную дробь с округлением до сотых.
II. Для справки:
Дробь — число, состоящее из одной или нескольких частей (долей) единицы. Обыкновенная дробь (простая дробь) записывается в виде двух чисел (числитель дроби и знаменатель дроби), разделенных горизонтальной чертой (дробной чертой), обозначающей знак деления.
числитель дроби — число, стоящее над дробной чертой. Числитель показывает, сколько долей взяли у целого.
знаменатель дроби — число, стоящее под дробной чертой. Знаменатель показывает, на сколько равных долей разделено целое.
простая дробь — дробь, не имеющая целой части. Простая дробь может быть правильной или неправильной.
правильная дробь — дробь, у которой числитель меньше знаменателя, поэтому правильная дробь всегда меньше единицы.
III. Примечание:
- Блок исходных данных выделен желтым цветом , блок промежуточных вычислений выделен голубым цветом , блок решения выделен зеленым цветом .
- Для сложения, вычитания, умножения и деления обыкновенных или смешанных дробей воспользуйтесь онлайн калькулятором дробей с подробным решением.
Если нам нужно разделить 497 на 4, то при делении мы увидим, что 497 не делится на 4 нацело, т.е. остаётся остаток от деления.
В таких случаях говорят, что выполнено деление с остатком , и решение записывают в таком виде:
497: 4 = 124 (1 остаток).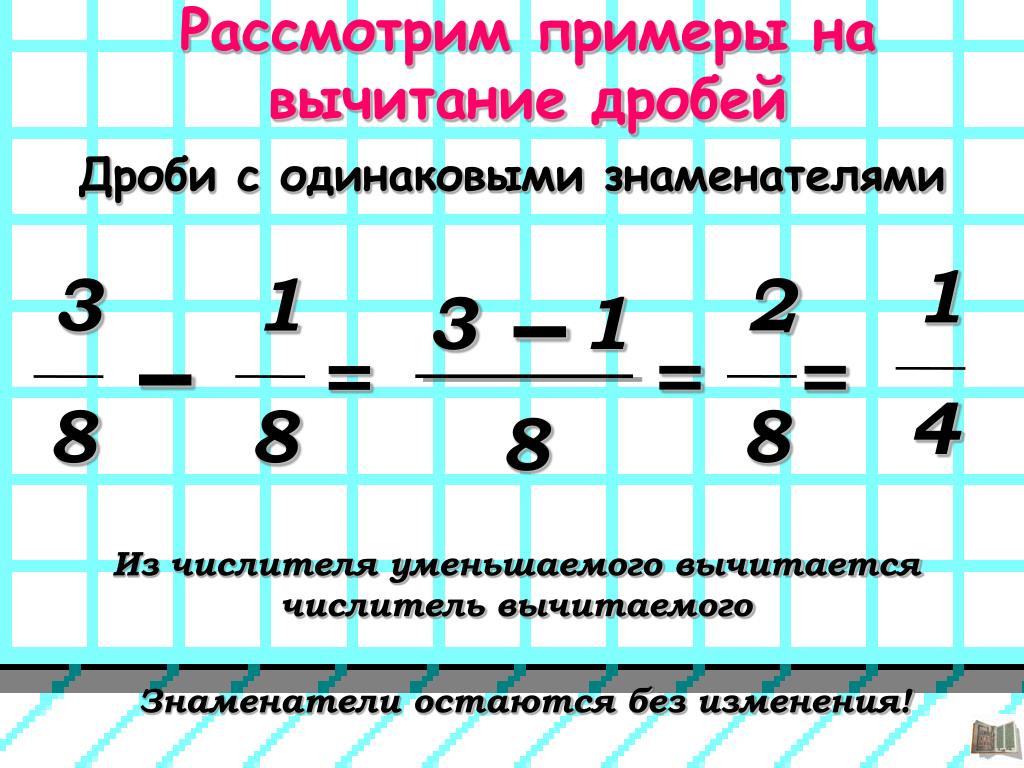
Компоненты деления в левой части равенства называют так же, как при делении без остатка: 497 —
Остаток всегда меньше делителя.
Проверку при делении можно сделать умножением. Если, например, имеется равенство 64: 32 = 2, то проверку можно сделать так: 64 = 32 * 2.
Часто в случаях, когда выполняется деление с остатком, удобно использовать равенство
а = b * n + r ,
где а — делимое, b — делитель, n — неполное частное, r — остаток.
Частное от деления натуральных чисел можно записать в виде дроби.
Числитель дроби — это делимое, а знаменатель — делитель.
Поскольку числитель дроби — это делимое, а знаменатель — делитель, считают, что черта дроби означает действие деление . Иногда бывает удобно записывать деление в виде дроби, не используя знак «:».
Частное от деления натуральных чисел m и n можно записать в виде дроби \(\frac{m}{n} \), где числитель m — делимое, а
знаменатель п — делитель:
\(m:n = \frac{m}{n} \)
Верны следующие правила:
Чтобы получить дробь \(\frac{m}{n} \), надо единицу разделить на n равных частей (долей) и взять m таких частей.
Чтобы получить дробь \(\frac{m}{n} \), надо число m разделить на число n.
Чтобы найти часть от целого, надо число, соответствующее целому, разделить на знаменатель и результат умножить на числитель дроби, которая выражает эту часть.
Чтобы найти целое по его части, надо число, соответствующее этой части, разделить на числитель и результат умножить на знаменатель дроби, которая выражает эту часть.
Если и числитель, и знаменатель дроби умножить на одно и то же число (кроме нуля), величина дроби не изменится:
\(\large \frac{a}{b} = \frac{a \cdot n}{b \cdot n} \)
Если и числитель, и знаменатель дроби разделить на одно и то же число (кроме нуля), величина дроби не изменится:
\(\large \frac{a}{b} = \frac{a: m}{b: m} \)
Это свойство называют основным свойством дроби .
Два последних преобразования называют сокращением дроби .
Если дроби нужно представить в виде дробей с одним и тем же знаменателем, то такое действие называют приведением дробей к общему знаменателю .
Правильные и неправильные дроби. Смешанные числа
Вы уже знаете, что дробь можно получить, если разделить целое на равные части и взять несколько таких частей. Например,
дробь \(\frac{3}{4} \) означает три четвёртых доли единицы. Во многих задачах предыдущего параграфа обыкновенные дроби использовались
для обозначения части целого. Здравый смысл подсказывает, что часть всегда должна быть меньше целого, но как тогда быть с такими
дробями, как, например, \(\frac{5}{5} \) или \(\frac{8}{5} \)? Ясно, что это уже не часть единицы. Наверное, поэтому такие дроби,
у которых числитель больше знаменателя или равен ему, называют неправильными дробями . Остальные дроби, т. е. дроби, у которых
числитель меньше знаменателя, называют правильными дробями .
Как вы знаете, любую обыкновенную дробь, и правильную, и неправильную, можно рассматривать как результат деления числителя на знаменатель. Поэтому в математике, в отличие от обычного языка, термин «неправильная дробь» означает не то, что мы что-то сделали неправильно, а только то, что у этой дроби числитель больше знаменателя или равен ему.
Если число состоит из целой части и дроби, то такие
Например:
\(5:3 = 1\frac{2}{3} \) : 1 — целая часть, а \(\frac{2}{3} \) — дробная часть.
Если числитель дроби \(\frac{a}{b} \) делится на натуральное число n, то, чтобы разделить эту дробь на n, надо её числитель
разделить на это число:
\(\large \frac{a}{b} : n = \frac{a:n}{b} \)
Если числитель дроби \(\frac{a}{b} \) не делится на натуральное число n, то, чтобы разделить эту дробь на n, надо её
знаменатель умножить на это число:
\(\large \frac{a}{b} : n = \frac{a}{bn} \)
Заметим, что второе правило справедливо и в том случае, когда числитель делится на n.
Поэтому мы можем его применять тогда,
когда трудно с первого взгляда определить, делится числитель дроби на n или нет.
Действия с дробями. Сложение дробей.
С дробными числами, как и с натуральными числами, можно выполнять арифметические действия. Рассмотрим сначала сложение дробей. Легко сложить дроби с одинаковыми знаменателями. Найдем, например, сумму \(\frac{2}{7} \) и \(\frac{3}{7} \). Легко понять, что \(\frac{2}{7} + \frac{2}{7} = \frac{5}{7} \)
Чтобы сложить дроби с одинаковыми знаменателями, нужно сложить их числители, а знаменатель оставить прежним.
Используя буквы, правило сложения дробей с одинаковыми знаменателями можно записать так:
\(\large \frac{a}{c} + \frac{b}{c} = \frac{a+b}{c} \)
Если требуется сложить дроби с разными знаменателями, то их предварительно следует привести к общему знаменателю. Например:
\(\large \frac{2}{3}+\frac{4}{5} = \frac{2\cdot 5}{3\cdot 5}+\frac{4\cdot 3}{5\cdot 3} = \frac{10}{15}+\frac{12}{15} = \frac{10+12}{15} = \frac{22}{15} \)
Для дробей, как и для натуральных чисел, справедливы переместительное и сочетательное свойства сложения.
Сложение смешанных дробей
Такие записи, как \(2\frac{2}{3} \), называют смешанными дробями . При этом число 2 называют целой частью смешанной дроби, а число \(\frac{2}{3} \) — ее дробной частью . Запись \(2\frac{2}{3} \) читают так: «две и две трети».
При делении числа 8 на число 3 можно получить два ответа: \(\frac{8}{3} \) и \(2\frac{2}{3} \). Они выражают одно и то же дробное число, т.е \(\frac{8}{3} = 2 \frac{2}{3} \)
Таким образом, неправильная дробь \(\frac{8}{3} \) представлена в виде смешанной дроби \(2\frac{2}{3} \). В таких случаях говорят, что из неправильной дроби выделили целую часть .
Вычитание дробей (дробных чисел)
Вычитание дробных чисел, как и натуральных, определяется на основе действия сложения: вычесть из одного числа другое — это значит
найти такое число, которое при сложении со вторым дает первое. Например:
\(\frac{8}{9}-\frac{1}{9} = \frac{7}{9} \) так как \(\frac{7}{9}+\frac{1}{9} = \frac{8}{9} \)
Правило вычитания дробей с одинаковыми знаменателями похоже на правило сложения таких дробей:
чтобы найти разность дробей с одинаковыми знаменателями, надо из числителя первой дроби вычесть числитель второй, а знаменатель
оставить прежним.
С помощью букв это правило записывается так:
\(\large \frac{a}{c}-\frac{b}{c} = \frac{a-b}{c} \)
Умножение дробей
Чтобы умножить дробь на дробь, нужно перемножить их числители и знаменатели и первое произведение записать числителем, а второе — знаменателем.
С помощью букв правило умножения дробей можно записать так:
\(\large \frac{a}{b} \cdot \frac{c}{d} = \frac{a \cdot c}{b \cdot d} \)
Пользуясь сформулированным правилом, молено умножать дробь на натуральное число, на смешанную дробь, а также перемножать смешанные дроби. Для этого нужно натуральное число записать в виде дроби со знаменателем 1, смешанную дробь — в виде неправильной дроби.
Результат умножения надо упрощать (если это возможно), сокращая дробь и выделяя целую часть неправильной дроби.
Для дробей, как и для натуральных чисел, справедливы переместительное и сочетательное свойства умножения, а также распределительное свойство умножения относительно сложения.
Деление дробей
Возьмем дробь \(\frac{2}{3} \) и «перевернем» ее, поменяв местами числитель и знаменатель.
Получим дробь \(\frac{3}{2} \).
Эту дробь называют обратной дроби \(\frac{2}{3} \).
Если мы теперь «перевернем» дробь \(\frac{3}{2} \), то получим исходную дробь \(\frac{2}{3} \). Поэтому такие дроби, как \(\frac{2}{3} \) и \(\frac{3}{2} \) называют взаимно обратными .
Взаимно обратными являются, например, дроби \(\frac{6}{5} \) и \(\frac{5}{6} \), \(\frac{7}{18} \) и \(\frac{18}{7} \).
С помощью букв взаимно обратные дроби можно записать так: \(\frac{a}{b} \) и \(\frac{b}{a} \)
Понятно, что произведение взаимно обратных дробей равно 1 . Например: \(\frac{2}{3} \cdot \frac{3}{2} =1 \)
Используя взаимно обратные дроби, можно деление дробей свести к умножению.
Правило деления дроби на дробь:
чтобы разделить одну дробь на другую, нужно делимое умножить на дробь, обратную делителю.
Используя буквы, правило деления дробей можно записать так:
\(\large \frac{a}{b} : \frac{c}{d} = \frac{a}{b} \cdot \frac{d}{c} \)
Если делимое или делитель является натуральным числом или смешанной дробью, то, для того чтобы воспользоваться правилом деления
дробей, его надо предварительно представить в виде неправильной дроби.
В этой статье мы рассмотрим основные действия с алгебраическими дробями :
- сокращение дробей
- умножение дробей
- деление дробей
Начнем с сокращения алгебраических дробей .
Казалось бы, алгоритм очевиден.
Чтобы сократить алгебраические дроби , нужно
1. Разложить числитель и знаменатель дроби на множители.
2. Сократить одинаковые множители.
Однако, школьники часто делают ошибку, «сокращая» не множители, а слагаемые. Например, есть любители, которые в дроби «сокращают» на и получают в результате , что, разумеется, неверно.
Рассмотрим примеры:
1. Сократить дробь:
1. Разложим на множители числитель по формуле квадрата суммы, а знаменатель по формуле разности квадратов
2. Разделим числитель и знаменатель на
2. Сократить дробь:
1. Разложим на множители числитель. Так как числитель содержит четыре слагаемых, применим группировку.
2. Разложим на множители знаменатель. Так же применим группировку.
3. Запишем дробь, которая у нас получилась и сократим одинаковые множители:
Умножение алгебраических дробей.
При умножении алгебраических дробей мы числитель умножаем на числитель, а знаменатель умножаем на знаменатель.
Важно! Не нужно торопиться выполнять умножение в числителе и знаменателе дроби. После того, как мы записали в числителе произведение числителей дробей, а в знаменателе — произведение знаменателей, нужно разложить на множители каждый множитель и сократить дробь.
Рассмотрим примеры:
3. Упростите выражение:
1. Запишем произведение дробей: в числителе произведение числителей, а в знаменателе произведение знаменателей:
2. Разложим каждую скобку на множители:
Теперь нам нужно сократить одинаковые множители. Заметим, что выражения и отличаются только знаком: и в результате деления первого выражения на второе получим -1.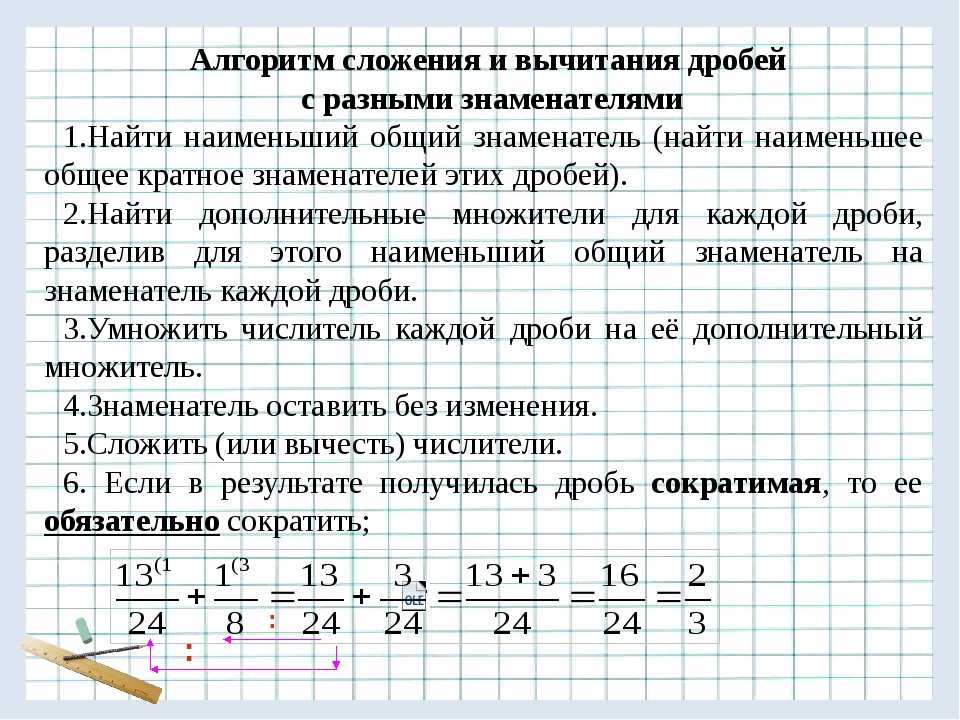
Итак,
Деление алгебраических дробей мы выполняем по такому правилу:
То есть чтобы разделить на дробь, нужно умножить на «перевернутую».
Мы видим, что деление дробей сводится к умножению, а умножение, в конечном итоге, сводится к сокращению дробей.
Рассмотрим пример:
4. Упростите выражение:
Основано на их основном свойстве: если числитель и знаменатель дроби разделить на один и тот же ненулевой многочлен, то получится равная ей дробь.
Сокращать можно только множители!
Члены многочленов сокращать нельзя!
Чтобы сократить алгебраическую дробь, многочлены, стоящие в числителе и знаменателе, нужно предварительно разложить на множители.
Рассмотрим примеры сокращения дробей.
В числителе и знаменателе дроби стоят одночлены. Они представляют собой произведение (чисел, переменных и их степеней), множители сокращать можем.
Числа сокращаем на их наибольший общий делитель, то есть на наибольшее число, на которое делится каждое из данных чисел.
Для 24 и 36 это — 12. После сокращения от 24 остается 2, от 36 — 3.
Степени сокращаем на степень с наименьшим показателем. Сократить дробь — значит, разделить числитель и знаменатель на один и тот же делитель, а показатели вычитаем.
a² и a⁷ сокращаем на a². При этом в числителе от a² остается единица (1 пишем только в том случае, когда кроме нее после сокращения других множителей не осталось. От 24 осталась 2, поэтому 1, оставшуюся от a², не пишем). От a⁷ после сокращения остается a⁵.
b и b сокращаем на b, полученные в результате единицы не пишем.
c³º и с⁵ сокращаем на с⁵. От c³º остается c²⁵, от с⁵ — единица (ее не пишем). Таким образом,
Числитель и знаменатель данной алгебраической дроби — многочлены. Сокращать члены многочленов нельзя! (нельзя сократить, к примеру, 8x² и 2x!). Чтобы сократить эту дробь, надо . В числителе есть общий множитель 4x. Выносим его за скобки:
И в числителе, и в знаменателе есть одинаковый множитель (2x-3). Сокращаем дробь на этот множитель.
В числителе получили 4x, в знаменателе — 1. По 1 свойству алгебраических дробей, дробь равна 4x.
Сокращать можно только множители (сократить данную дробь на 25x² нельзя!). Поэтому многочлены, стоящие в числителе и знаменателе дроби, нужно разложить на множители.
В числителе — полный квадрат суммы, в знаменателе — разность квадратов. После разложения по формулам сокращенного умножения получаем:
Сокращаем дробь на (5x+1) (для этого в числителе зачеркнем двойку в показатель степени, от (5x+1)² при этом останется (5x+1)):
В числителе есть общий множитель 2, вынесем его за скобки. В знаменателе — формула разности кубов:
В результате разложения в числителе и знаменателе получили одинаковый множитель (9+3a+a²). Сокращаем дробь на него:
Многочлен в числителе состоит из 4 слагаемых. первое слагаемое со вторым, третье — с четвертым и выносим из первых скобок общий множитель x². Знаменатель раскладываем по формуле суммы кубов:
В числителе вынесем за скобки общий множитель (x+2):
Сокращаем дробь на (x+2):
Калькулятор сложения дробей | Как добавить похожие и отличные дроби?
Воспользуйтесь нашим удобным калькулятором сложения дробей, чтобы найти сложение любых 2
дроби легко.
Вам просто нужно ввести дроби в качестве входных данных и нажать на кнопку расчета, чтобы
получить сумму фракций как результат в кратчайшие сроки.
Калькулятор сложения дробей: Теперь с помощью этого инструмента стало очень легко складывать 2 дроби с одинаковыми или разными знаменателями. Здесь вы можете проверить пошаговый процесс сложения одинаковых и разных дробей с решенными примерами.
- Вычитание дроби
- Умножение дроби
- Дробный отдел
- Упроститель дроби
- Эквивалент дроби
- Десятичная дробь
- Проценты в доли
- Дробь до десятичной дроби
- От дроби до процента
В следующих разделах мы предлагаем простые и легкие шаги для расчета
сложение двух фракций. Следуйте этим рекомендациям, чтобы получить быстрые результаты.
Как складывать похожие дроби?
- Возьмите любые 2 дроби с одинаковым значением знаменателя.
- Если дроби похожи на дроби, сложите значения их числителей.
- Общая дробь будет суммой в числителе, а в знаменателе останется без изменений.
Процесс сложения разных дробей
- Рассмотрим две дроби с разными значениями знаменателя.
- Найдите НОК знаменателей.
- Превратите разные дроби в одинаковые, умножив верхнюю и нижнюю части, чтобы получить НОК. значение во всех знаменателях.
- Теперь сложите значения числителя, чтобы получить добавленную дробь.
Решенные примеры сложения дробей
Вопрос 1:
Найдите сумму дробей 159/34 и 548/34?
Решение:
Даны дроби 159/34 и 548/34
Так как обе дроби имеют одинаковый знаменатель, они называются однородными дробями.
Добавьте числители к сумме.
159/34 + 548/34 = (159 + 548)/34
= 707/34
Следовательно, сложение дробей 159/34 и 548/34 равно 707/34.
Вопрос 2:
Найдите сложение дробей 1908/157 и 3689/123?
Решение:
Даны дроби 1908/157 и 3689/123
Поскольку обе дроби имеют разные знаменатели, они не похожи на дроби.
Найдите LCM знаменателей 157 и 123, т. Е. 19311
Сделайте знаменатели фракций, как 19311
SO, 1908/157 = (1908 x 123)/(157 x 123) = 2,34,684/19311
и 3689/123) = 2,34,684/19311
и 3689/123) = 2,34,684/19311
и 3689. = (3689 x 157)/(123 x 157) = 5,79,173/19311
1908/157 + 3689/123 = 2,34,684/19311 + 5,79,173/19311
= (2,34,6794,73 + 5 )/19311
= 8,13,857/19311
Следовательно, сумма дробей 1908/157 и 3689/123 равна 8,13,857/19311.
Fraction Addition Examples
0002
/90. знаменатели?
Для сложения дробей с разными знаменателями необходимо вычислить НОК знаменатели. Затем умножьте верхние и нижние части каждой дроби на количество раз в каждой. знаменатель дроби входит в LCM. Далее добавляем числители.
2.
Каковы 3 правила сложения дробей?
Вот 3 правила сложения дробей с одинаковыми знаменателями:
- Во-первых, замените смешанное число на неправильную дробь
- Добавьте числители.
- Запишите полученный числитель над знаменателем.
3. Почему мы не добавляем знаменатели при сложении дробей?
Знаменатель показывает, сколько одинаковых частей составляют одну единицу. Если добавить знаменатель при добавлении дробей новый знаменатель не будет описывать, сколько равных частей в одной Ед. изм.
4. Напишите шаги сложения дробей на калькуляторе?
Чтобы использовать калькулятор сложения дробей, мы должны указать входные дроби и нажать кнопку рассчитать.
Добавление фракций — Fractioncalculation.com
а / б +с / д | б / с + де / ф | |||
| + ̶×÷ | ||||
| Отвечать: | ||
| Результат= | ||
По нашему опыту, у многих учащихся возникает множество задач, когда им нужно решить задачи на сложение дробей.
Правда в том, что складывать дроби несложно, но нужно понимать этот процесс.
Однако, если вы просто хотите подтвердить свои результаты или вам нужно быстро сложить дроби, лучше всего воспользоваться нашим калькулятором дробей.
Использование нашего калькулятора дробей
Если вы посмотрите на наш калькулятор дробей, вы легко увидите, что он очень универсален. В конце концов, вы сможете выбрать тип фракций, которые хотите добавить. Как только вы это сделаете, вам просто нужно будет добавить числители и знаменатели в определенные поля и нажать кнопку расчета.
Но чтобы убедиться, что вы знаете, как использовать его без каких-либо проблем, давайте проверим пару примеров, используя оба типа сложения дробей.
Хотите вычитать дроби?
#1: Сложение дробей, таких как (a/b) + (c/d)
Пример #1: Давайте представим, что вы пытаетесь сложить дроби 2/3 и 1/8.
Как мы уже упоминали выше, чтобы использовать наш калькулятор с дробями, вам нужно будет добавить соответствующие числители и знаменатели дробей в соответствующие поля.
Итак, как только вы добавите числа и нажмете на кнопку «Рассчитать», вы получите результат. В этом случае результат: 19/24. Важно отметить, что прямо под результатом дроби вы также сможете увидеть результат в десятичных дробях. Итак, в этом случае:
(2/3) + (1/8) = (19/34) = 0,79
Узнайте, как делить дроби.
Пример №2: Предположим теперь, что вы пытаетесь сложить дроби 3/4 и 3/8.
Как мы уже упоминали выше, чтобы использовать наш калькулятор с дробями, вам нужно будет добавить соответствующие числители и знаменатели дробей в соответствующие поля. Итак, как только вы добавите числа и нажмете на кнопку «Рассчитать», вы получите результат. В этом случае результат: 1 (1/8). Важно отметить, что прямо под результатом дроби вы также сможете увидеть результат в десятичных дробях. Итак, в данном случае:
(3/4) + (3/8) = 1 (1/8) = 1,13
Одна из вещей, которую вы, возможно, не заметили в нашем калькуляторе с дробью, это то, что у вас есть стрелка в середине дроби.
Что ж, если вы нажмете на эту стрелку, вы сможете выбрать математическую операцию, которую хотите использовать с этими дробями. Итак, как видите, наш калькулятор сложения дробей гораздо более универсален, чем вы могли подумать на первый взгляд. Ведь можно не только складывать дроби, но и вычитать дроби, умножать дроби и даже делить дроби.
Узнайте больше о дробях здесь.
#2: Сложение дробей, таких как a (b/c) + d (e/f)
Пример #1: Давайте представим, что вы пытаетесь сложить дроби 4 (1/3) и 5 (6 /7).
Как мы уже упоминали выше, чтобы использовать наш калькулятор с дробями, вам нужно будет добавить соответствующие числители и знаменатели дробей в соответствующие поля. Итак, как только вы добавите числа и нажмете на кнопку «Рассчитать», вы получите результат. В этом случае результат: 10 (4/21). Важно отметить, что прямо под результатом дроби вы также сможете увидеть результат в десятичных дробях. Итак, в данном случае:
4 (1/3) + 5 (6/7) = 10 (4/21) = 10,19
Проблемы с умножением дробей?
Пример №2: Предположим теперь, что вы пытаетесь сложить дроби 2 (3/4) и 3 (3/8).
Как мы уже упоминали выше, чтобы использовать наш калькулятор с дробями, вам нужно будет добавить соответствующие числители и знаменатели дробей в соответствующие поля. Итак, как только вы добавите числа и нажмете на кнопку «Рассчитать», вы получите результат. В этом случае результат: 6 (1/8). Важно отметить, что прямо под результатом дроби вы также сможете увидеть результат в десятичных дробях. Итак, в данном случае:
2 (3/4) + 3 (3/8) = 6 (1/8) = 6,13
Опять же, а также в этом типе дробей вы можете видеть, что у вас также есть возможность не только складывать дроби но и вычитать, умножать и делить их.
Хотя использование нашего калькулятора сложения дробей делает все расчеты чрезвычайно простыми, важно, чтобы вы знали, как складывать дроби вручную. Итак, это то, что мы собираемся показать вам.
Узнайте, как пользоваться нашим калькулятором смешанных дробей.
Добавление дробей вручную
youtube.com/embed/tDQipFjAoT8?feature=oembed» frameborder=»0″ allow=»accelerometer; autoplay; encrypted-media; gyroscope; picture-in-picture» allowfullscreen=»»> Когда вы пытаетесь понять, как научиться складывать дроби вручную, первое, что вам нужно сделать, это посмотреть на дроби, которые вы хотите сложить. Здесь у вас будет два разных случая или ситуации:
#1: Вы хотите сложить дроби с одинаковым знаменателем:
Если вы хотите сложить две дроби с одинаковым знаменателем, все, что вам нужно сделать, это сложить числители и сохранить общий знаменатель. Как только вы это сделаете, вы должны попытаться упростить дробь до наименьших членов.
Давайте проверим пару примеров, чтобы убедиться, что вы поняли.
Пример №1: Представьте, что вы хотите сложить 5/7 и 6/7.
Как видите, у этих дробей разный числитель (5 и 6), но знаменатель тот же – 7. Как мы уже говорили, в этом случае вам нужно будет сложить числители и просто оставить знаменатель без изменений.
Это означает, что:
5/7 + 6/7 = (5 + 6)/7 = 11/7
Пример №2: Представьте, что вы хотите сложить 3/8 и 1/8.
Как видите, у этих дробей разный числитель (3 и 1), но знаменатель тот же — 8. Как мы уже говорили, в этом случае вам нужно будет сложить числители и просто оставить знаменатель без изменений. Это означает, что:
3/8 + 1/8 = (3 + 1)/8 = 4/8
Как видите, эту дробь можно упростить. В конце концов, если вы разделите дробь на 4 (и числитель, и знаменатель), вы получите:
4/8 = 1/4
#2: Вы хотите сложить дроби с другим знаменателем:
До сих пор мы показывали вам, как складывать самые простые дроби — те, у которых один и тот же знаменатель. Тем не менее, пришло время сделать все немного интереснее. Итак, вы собираетесь научиться складывать дроби с разными знаменателями.
Если вы хотите сложить дроби с разными знаменателями, прежде чем складывать дроби вместе, вам нужно иметь одинаковые знаменатели.
Один из самых простых способов сделать это — просто умножить первый знаменатель на второй и наоборот. Обратите внимание, что когда вы делаете это, вам также нужно будет умножать числители. Если вы этого не сделаете, вы получите другое значение.
Хотя это может показаться немного запутанным, на самом деле это не так. Давайте рассмотрим несколько примеров, чтобы вы могли понять весь процесс.
Пример №1: Допустим, вы хотите сложить 2/3 и 2/4.
Как видите, в данном случае знаменатели разные — 3 и 4. Итак, первое, что вам нужно будет сделать, это преобразовать дроби, чтобы получить общие знаменатели.
Просто взгляните на знаменатели и умножьте каждый на другой знаменатель. Кроме того, не забывайте, что вам также нужно умножить числитель на то же число, что и его знаменатель, чтобы значение осталось прежним.
В этом конкретном случае вам нужно будет умножить первую дробь (2/3) на 4, а вторую дробь (2/4) на 3:
[(2 х 4) / (3 х 4)] + [(2 х 3) / (4 х 3)] = (8/12) + (6/12)
Теперь у вас уже есть общий знаменатель.
Итак, вам просто нужно следовать правилу, которое мы вам уже объяснили, которое гласит, что вам просто нужно добавить числители, сохранив знаменатель. Итак:
(8/12) + (6/12) = (8 + 6)/12 = 14/12
Окончательное решение представляет собой неправильную дробь, поэтому вам нужно преобразовать его в смешанное число и упростить решение:
1 (2/12)
Разделив числитель и знаменатель на 2, можно упростить решение до:
1 (1/6)
Пример №2: /6 и 7/10.
Как видите, в данном случае знаменатели разные — 6 и 10. Итак, первое, что вам нужно будет сделать, это преобразовать дроби, чтобы получить общие знаменатели.
Просто взгляните на знаменатели и умножьте каждый на другой знаменатель. Кроме того, не забывайте, что вам также нужно умножить числитель на то же число, что и его знаменатель, чтобы значение осталось прежним.
В этом конкретном случае вам нужно будет умножить первую дробь (5/6) на 10, а вторую дробь (7/10) на 6:
[(5 х 10) / (6 х 10)] + [(7 х 6) / (10 х 6)] = (50/60) + (42/60)
Теперь у вас уже есть общий знаменатель.
Итак, вам просто нужно следовать правилу, которое мы вам уже объяснили, которое гласит, что вам просто нужно добавить числители, сохранив знаменатель. Итак:
(50/60) + (42/60) = (50+ 42) / 60 = 92/60
Окончательное решение представляет собой неправильную дробь, поэтому вам нужно преобразовать его в смешанное число и упростить решение:
1 (32/60)
Разделив числитель и знаменатель на 2, можно упростить решение до:
1 (8/15)
Как преобразовать дробь в десятичную?
#3: Вы хотите сложить дроби со смешанными числами и неправильными дробями:
Если вы не знаете, смешанное число — это число, которое содержит дробь, а также целое число, например:
5 (3/4), 3 (7/10), 6 (7/8)
Сложение этих чисел может быть немного сложнее.
Итак, чтобы максимально упростить процесс, вы должны начать с преобразования числа в неправильную дробь.
Если вы не знаете, у неправильной дроби числитель больше знаменателя. Из-за этого важно упростить дробь после нахождения решения, так как вы, вероятно, получите еще одно смешанное число.
Давайте рассмотрим пример.
Узнайте, как преобразовать десятичную дробь в дробь.
Пример: Представьте, что вы хотите сложить дроби 2 (3/4) и 1/4.
В этом уравнении вы знаете, что:
1 = 4/4
Следовательно:
2 = 8/4.
Итак, добавляем дробь к преобразованному целому числу:
[(8 + 3) / 4] + (1/4) = 11/4 + 1/4
Поскольку теперь у нас уже есть один и тот же знаменатель в обеих дробях, вам просто нужно сложить числители и сохранить знаменатель:
11/4 + 1/4 = 12/4 = 3
Узнайте все правила дробей.
Заключение
Как видите, складывать дроби не очень сложно.