Сложить матрицы онлайн: Онлайн калькулятор. Сложение и вычитание матриц

Онлайн калькулятор сложения и вычитания матриц

0
AC		+/-	÷
7	8	9	×
4	5	6	—
1	2	3	+
0	00	,	=

Данный калькулятор дает детальное решение с объяснением сложение и вычитание двух матриц. Сложить или вычесть две матрицы возможно только в том случае, если матрицы одинакового размера

Матрица размерности m × n – это таблица чисел у которой m строк и n столбцов.

Элементы матрицы обозначаются как a_ij, где i – номер строки, j – номер столбца.
Суммой матриц А и В, размеры которых одинаковы, называется матрица С такой же размерности как матрицы А и В, элементы которой равны суммам элементов матриц А и В.

Как складывать и вычитать матрицы

Складывать и вычитать можно только матрицы одинакового размера.

При сложении (вычитании) матриц A и B, размерности (m × n), получаем матрицу C такой же размерности (m × n).

Чтобы сложить две матрицы, необходимо попарно сложить их элементы.

Например, сложим две матрицы A и B размерности 3 × 3.

A =	1 3 6 4 8 0 -2 9 1

B =	0 -3 0 2 4 9 5 0 8

C =

a11 a12 a13 a21 a22 a23 a31 a32 a33

+

b11 b12 b13 b21 b22 b23 b31 b32 b33

=

a11 + b11 a 12 + b12 a13 + b13 a21 + b21 a22 + b22 a23 + b23 a31 + b31 a32 + b32 a33 + b33

=

1 + 0 3 + (-3) 6 + 0 4 + 2 8 + 4 0 + 9 -2 + 5 9 + 0 1 + 8

=

1 0 6 6 12 9 3 9 9

Вам могут также быть полезны следующие сервисы

Калькуляторы линейная алгебра и аналитическая геометрия

Калькулятор сложения и вычитания матриц

Калькулятор умножения матриц

Калькулятор транспонирование матрицы

Калькулятор нахождения определителя (детерминанта) матрицы

Калькулятор нахождения обратной матрицы

Длина отрезка. Онлайн калькулятор расстояния между точками

Онлайн калькулятор нахождения координат вектора по двум точкам

Калькулятор нахождения модуля (длины) вектора

Калькулятор сложения и вычитания векторов

Калькулятор скалярного произведения векторов через длину и косинус угла между векторами

Калькулятор скалярного произведения векторов через координаты

Калькулятор векторного произведения векторов через координаты

Калькулятор смешанного произведения векторов

Калькулятор умножения вектора на число

Калькулятор нахождения угла между векторами

Калькулятор проверки коллинеарности векторов

Калькулятор проверки компланарности векторов

Калькуляторы (Комбинаторика)

Калькулятор нахождения числа перестановок из n элементов

Калькулятор нахождения числа сочетаний из n элементов

Калькулятор нахождения числа размещений из n элементов

Калькуляторы систем счисления

Калькулятор перевода чисел из арабских в римские и из римских в арабские

Калькулятор перевода чисел в различные системы счисления

Калькулятор сложения, вычитания, умножения и деления двоичных чисел

Системы счисления теория

N2 | Двоичная система счисления

N3 | Троичная система счисления

N4 | Четырехичная система счисления

N5 | Пятеричная система счисления

N6 | Шестеричная система счисления

N7 | Семеричная система счисления

N8 | Восьмеричная система счисления

N9 | Девятеричная система счисления

N11 | Одиннадцатиричная система счисления

N12 | Двенадцатеричная система счисления

N13 | Тринадцатеричная система счисления

N14 | Четырнадцатеричная система счисления

N15 | Пятнадцатеричная система счисления

N16 | Шестнадцатеричная система счисления

N17 | Семнадцатеричная система счисления

N18 | Восемнадцатеричная система счисления

N19 | Девятнадцатеричная система счисления

N20 | Двадцатеричная система счисления

N21 | Двадцатиодноричная система счисления

N22 | Двадцатидвухричная система счисления

N23 | Двадцатитрехричная система счисления

N24 | Двадцатичетырехричная система счисления

N25 | Двадцатипятеричная система счисления

N26 | Двадцатишестеричная система счисления

N27 | Двадцатисемеричная система счисления

N28 | Двадцативосьмеричная система счисления

N29 | Двадцатидевятиричная система счисления

N30 | Тридцатиричная система счисления

N31 | Тридцатиодноричная система счисления

N32 | Тридцатидвухричная система счисления

N33 | Тридцатитрехричная система счисления

N34 | Тридцатичетырехричная система счисления

N35 | Тридцатипятиричная система счисления

N36 | Тридцатишестиричная система счисления

Дроби

Калькулятор интервальных повторений

Учим дроби наглядно

Калькулятор сокращения дробей

Калькулятор преобразования неправильной дроби в смешанную

Калькулятор преобразования смешанной дроби в неправильную

Калькулятор сложения, вычитания, умножения и деления дробей

Калькулятор возведения дроби в степень

Калькулятор перевода десятичной дроби в обыкновенную

Калькулятор перевода обыкновенной дроби в десятичную

Калькулятор сравнения дробей

Калькулятор приведения дробей к общему знаменателю

Калькуляторы (тригонометрия)

Калькулятор синуса угла

Калькулятор косинуса угла

Калькулятор тангенса угла

Калькулятор котангенса угла

Калькулятор секанса угла

Калькулятор косеканса угла

Калькулятор арксинуса угла

Калькулятор арккосинуса угла

Калькулятор арктангенса угла

Калькулятор арккотангенса угла

Калькулятор арксеканса угла

Калькулятор арккосеканса угла

Калькулятор нахождения наименьшего угла

Калькулятор определения вида угла

Калькулятор смежных углов

Калькуляторы (Теория чисел)

Калькулятор выражений

Калькулятор упрощения выражений

Калькулятор со скобками

Калькулятор уравнений

Калькулятор суммы

Калькулятор пределов функций

Калькулятор разложения числа на простые множители

Калькулятор НОД и НОК

Калькулятор НОД и НОК по алгоритму Евклида

Калькулятор НОД и НОК для любого количества чисел

Калькулятор делителей числа

Представление многозначных чисел в виде суммы разрядных слагаемых

Калькулятор деления числа в данном отношении

Калькулятор процентов

Калькулятор перевода числа с Е в десятичное

Калькулятор экспоненциальной записи чисел

Калькулятор нахождения факториала числа

Калькулятор нахождения логарифма числа

Калькулятор квадратных уравнений

Калькулятор остатка от деления

Калькулятор корней с решением

Калькулятор нахождения периода десятичной дроби

Калькулятор больших чисел

Калькулятор округления числа

Калькулятор свойств корней и степеней

Калькулятор комплексных чисел

Калькулятор среднего арифметического

Калькулятор арифметической прогрессии

Калькулятор геометрической прогрессии

Калькулятор модуля числа

Калькулятор абсолютной погрешности приближения

Калькулятор абсолютной погрешности

Калькулятор относительной погрешности

Калькуляторы площади геометрических фигур

Площадь квадрата

Площадь прямоугольника

КАЛЬКУЛЯТОРЫ ЗАДАЧ ПО ГЕОМЕТРИИ

Генератор Pdf с примерами

Тренажёры решения примеров

Тренажёр таблицы умножения

Тренажер счета для дошкольников

Тренажер счета на внимательность для дошкольников

Тренажер решения примеров на сложение, вычитание, умножение, деление. Найди правильный ответ.

Тренажер решения примеров с разными действиями

Тренажёры решения столбиком

Тренажёр сложения столбиком

Тренажёр вычитания столбиком

Тренажёр умножения столбиком

Тренажёр деления столбиком с остатком

Калькуляторы решения столбиком

Калькулятор сложения, вычитания, умножения и деления столбиком

Калькулятор деления столбиком с остатком

Конвертеры величин

Конвертер единиц длины

Конвертер единиц скорости

Конвертер единиц ускорения

Цифры в текст

Калькуляторы (физика)

Механика

Калькулятор вычисления скорости, времени и расстояния

Калькулятор вычисления ускорения, скорости и перемещения

Калькулятор вычисления времени движения

Калькулятор времени

Второй закон Ньютона. Калькулятор вычисления силы, массы и ускорения.

Закон всемирного тяготения. Калькулятор вычисления силы притяжения, массы и расстояния.

Импульс тела. Калькулятор вычисления импульса, массы и скорости

Импульс силы. Калькулятор вычисления импульса, силы и времени действия силы.

Вес тела. Калькулятор вычисления веса тела, массы и ускорения свободного падения

Оптика

Калькулятор отражения и преломления света

Электричество и магнетизм

Калькулятор Закона Ома

Калькулятор Закона Кулона

Калькулятор напряженности E электрического поля

Калькулятор нахождения точечного электрического заряда Q

Калькулятор нахождения силы F действующей на заряд q

Калькулятор вычисления расстояния r от заряда q

Калькулятор вычисления потенциальной энергии W заряда q

Калькулятор вычисления потенциала φ электростатического поля

Калькулятор вычисления электроемкости C проводника и сферы

Конденсаторы

Калькулятор вычисления электроемкости C плоского, цилиндрического и сферического конденсаторов

Калькулятор вычисления напряженности E электрического поля плоского, цилиндрического и сферического конденсаторов

Калькулятор вычисления напряжения U (разности потенциалов) плоского, цилиндрического и сферического конденсаторов

Калькулятор вычисления расстояния d между пластинами в плоском конденсаторе

Калькулятор вычисления площади пластины (обкладки) S в плоском конденсаторе

Калькулятор вычисления энергии W заряженного конденсатора

Калькулятор вычисления энергии W заряженного конденсатора. Для плоского, цилиндрического и сферического конденсаторов

Калькулятор вычисления объемной плотности энергии w электрического поля для плоского, цилиндрического и сферического конденсаторов

Калькуляторы по астрономии

Вес тела на других планетах

Ускорение свободного падения на планетах Солнечной системы и их спутниках

Генераторы

Генератор примеров по математике

Генератор случайных чисел

Генератор паролей

Матричный онлайн калькулятор

Матричный онлайн калькулятор

Инструкция матричного онлайн калькулятора

С помощью матричного онлайн калькулятора вы можете сложить, вычитать, умножить, транспонировать матрицы, вычислить обратную матрицу, псевдообратную матрицу, ранг матрицы, определитель матрицы, сделать скелетное разложение матрицы, удалить из матрицы линейно зависимые строки или линейно зависимые столбцы, проводить исключение Гаусса, решить матричное уравнение AX=B, сделать LU разложение матрицы,вычислить ядро (нуль пространство) матрицы, сделать ортогонализацию Грамма-Шмидта и ортонормализацию Грамма-Шмидта.

Вычисление суммы, разности, произведения матриц онлайн

Матричным онлайн калькулятором можно вычислить сумму, разность или произведение матриц. Для вычисления суммы или разности матриц, необходимо, чтобы они были одинаковой разменрости, а для вычисления произведения матриц, количество столбцов первой матрицы должен быть равным количеству строк второй матрицы.

Для вычисления суммы, разности или произведения матриц:

1. Введите размерности матриц.
2. Введите элементы матриц.
3. Нажмите на кнопку «A+B «,»A-B» или «A×B».

Вычисление обратной матрицы онлайн

Матричным онлайн калькулятором можно вычислить обратную матрицу. Для того, чтобы существовала обратная матрица, исходная матрица должна быть невырожденной квадратной матрицей.

Для вычисления обратной матрицы:

1. Выберите матрицу с помощью радиокнопки .
2. Введите размерность матрицы.
3. Введите элементы матрицы.
4. Нажмите на кнопку «обратное «.

Вычисление псевдообратной матрицы онлайн

Матричным онлайн калькулятором можно вычислить псевдообратную матрицу. Псевдообратная к данной матрице всегда существует.

Для вычисления псевдобратной матрицы:

1. Выберите матрицу с помощью радиокнопки .
2. Введите размерность матрицы.
3. Введите элементы матрицы.
4. Нажмите на кнопку «псевдообратное «.

Удаление линейно зависимых строк или столбцов матрицы онлайн

Матричным онлайн калькулятор позволяет удалить из матрицы линейно зависимые строки или столбцы, т.е. создать матрицу полного ранга.

Для удаления линейно зависимых строк или столбцов матрицы:

1. Выберите матрицу с помощью радиокнопки .
2. Введите размерность матрицы.
3. Введите элементы матрицы.
4. Нажмите на кнопку «полный ранг строк » или «полный ранг столбцов».

Скелетное разложение матрицы онлайн

Для проведения скелетного разложения матрицы онлайн

1. Выберите матрицу с помощью радиокнопки .
2. Введите размерность матрицы.
3. Введите элементы матрицы.
4. Нажмите на кнопку «скелетное разложение «.

Решение матричного уравнения или системы линейных уравнений AX=B онлайн

Матричным онлайн калькулятором можно решить матричное уравнение AX=B по отношению матрицы X. В частном случае, если матрица B является вектор-столбцом, то X , будет решением системы линейных уравнений AX=B.

Для решения матричного уравнения:

1. Введите размерности матриц A и B.
2. Введите элементы матриц A и B.
3. Нажмите на кнопку «решение AX=B».

Учтите, что матрицы A и B должны иметь равное количество строк .

Исключение Гаусса или приведение матрицы к треугольному (ступенчатому) виду онлайн

Матричный онлайн калькулятор проводит исключение Гаусса как для квадратных матриц, так и прямоугольных матриц любого ранга. Сначала проводится обычный метод Гаусса. Если на каком то этапе ведущий элемент равен нулю, то выбирается другой вариант исключения Гаусса с выбором наибольшего ведущего элемента в столбце.

Для исключения Гаусса или приведения матрицы к треугольному виду

1. Выберите матрицу с помощью радиокнопки .
2. Задайте размерность матрицы.
3. Введите элементы матрицы.
4. Нажмите на кнопку «Треугольный вид».

LU-разложение или LUP-разложение матрицы онлайн

Данный матричный калькулятор позволяет проводить LU-разложение матрицы (A=LU) или LUP-разложение матрицы (PA=LU), где L нижняя треугольная матрица, U-верхняя треугольная (трапециевидная) матрица, P- матрица перестановок. Сначала программа проводит LU разложение, т.е. такое разложение , при котором P=E, где E-единичная матрица (т.е. PA=EA=A). Если это невозможно, то проводится LUP-разложение. Матрица A может быть как квадратной, так и прямоугольной матрицей любого ранга.

Для LU(LUP)-разложения:

1. Выберите матрицу с помощью радиокнопки .
2. Задайте размерность матрицы.
3. Введите элементы матрицы.
4. Нажмите на кнопку «LU-разложение».

Построение ядра (нуль-пространства) матрицы онлайн

С помощю матричного калькулятора можно построить нуль-пространство (ядро) матрицы.

Для построения нуль-пространства (ядра) матрицы:

1. Выберите матрицу с помощью радиокнопки .
2. Задайте размерность матрицы.
3. Введите элементы матрицы.
4. Нажмите на кнопку «ядро (·)».

Ортогонализация Грамма-Шмидта и Ортонормализация Грамма-Шмидта онлайн

С помощю матричного калькулятора можно сделать ортогонализацию и ортонормализацию Грамма-Шмидта матрицы онлайн.

Для ортогонализации или ортонормализации матрицы:

1. Выберите матрицу с помощью радиокнопки .
2. Задайте размерность матрицы.
3. Введите элементы матрицы.
4. Нажмите на кнопку «Ортогонализация Г.-Ш. (·)» или «Ортонормализация Г.-Ш. (·)».

Если у вас на компьютере установлено Java, то можете использовать матричный онлайн калькулятор (на Java) с помощью которого вы можете выполнить более сложные вычисления.

Сложение, вычитание, умножение и деление матриц

Используйте этот онлайн-калькулятор для выполнения операций с матрицами (суммирование, вычитание, умножение и деление).

Как сложить две матрицы?

Обе матрицы должны иметь одинаковую размерность, то есть одинаковое количество строк и одинаковое количество столбцов.
Сложить две матрицы просто: просто добавьте соответствующие элементы и поместите сумму в ту же соответствующую позицию.

Пример:

A и B — две матрицы размерности 2 x 2

`A = [[1,5], [6, -4]]`

`B = [[0, -12], [3,7] ]`

Тогда мы можем просуммировать,

`A + B = [[1+0,5-12], [6+3, -4+7]] = [[1, -7], [9, 3]]`

Как вычесть две матрицы?

Точно так же две матрицы должны иметь одинаковую размерность, то есть одинаковое количество строк и одинаковое количество столбцов.
Чтобы их вычесть, просто вычтите элементы, находящиеся в одной и той же позиции, и поместите результат в ту же соответствующую позицию.

Пример:

A и B две матрицы размерности 3 x 2

`A = [[2,6], [7, -2], [5,11]]`

`B = [[ 1, -10], [4,7], [-9,13]]`

затем,

`А — В = [[2-1,6-(-10)], [7-4, -2-7], [5- (-9) ,11-13]] = [[1,16], [3, -9], [14, -2]]`

Как перемножить две матрицы?

Для заданных двух матриц A и B умножение двух матриц A.B возможно только в том случае, если число столбцов матрицы A равно числу строк матрицы B. Таким образом, можно умножить матрицу 2 x 3 на матрицу 3 x 4. но не матрицей 2 x 2. Мы можем обобщить следующим образом

Произведение матриц A.B определено только для матриц со следующими размерами:
Размер A m x n
Размер B n x p

Произведение двух матриц P = A.B является матрицей размера m x p.

Обратите внимание: порядок A и B в произведении имеет значение, это A. B, а не B.A, который не определен, если p отличается от m (умножение матриц не является коммутативным).

Как рассчитать произведение матриц?

Предположим, что A — матрица 2 x 3, а B — матрица 3 x 2. В соответствии с приведенными выше определениями (m=2, n=3 и p=2) умножение возможно, и произведение матриц P = A.B имеет размерность 2 x 2

`A = [[1,5,2], [ 3,4,7]]`

`B = [[0, -1], [8,6], [-2,10]]`

`P = A*B = [[\color {red } {1},\цвет {красный} {5},\цвет {красный} {2}], [3,4,7]] * [[\цвет {красный} {0}, -1], [\ цвет {красный} {8}, 6], [\цвет {красный} {-2}, 10]] = [[\цвет {красный} {c_11}, c_12], [c_21, c_22]]`

— Для расчета коэффициента `c_11` мы «умножаем» 1-ю строку на 1-й столбец. Итак, мы имеем

`c_11 = [1,5,2] * [[0], [8], [-2]] = 1*0 +5*8 +2* (-2) = 36`

— Для расчета коэффициента `c_12` мы «умножаем» 1-ю строку на 2-й столбец. Итак, мы имеем

`c_12 = [1,5,2] * [[-1], [6], [10]] = 1* (-1) +5*6 +2* (10) = 49 `

— Для расчета коэффициента `c_21` мы «умножаем» 2-ю строку на 1-й столбец. Итак, мы имеем

`c_21 = [3,4,7] * [[0], [8], [-2]] = 3*0 +4*8 +7* (-2) = 18`

— Для расчета коэффициента `c_22` мы «умножаем» 2-ю строку на 2-й столбец. Итак, мы имеем

`c_22 = [3,4,7] * [[-1], [6], [10]] = 3* (-1) +4*6 +7* (10) = 91 `

Запишем окончательный результат,

`P = A*B = [[36,49], [18,91]]`

Мы обобщаем этот метод следующим образом,
Предположим, что A и B две матрицы соответствующих размерностей m x n и n x p, то произведение P = A.B является матрицей размерности m x p. Обозначим через `c_ (ij)` элемент матрицы P, находящийся в первой строке и j-м столбце. 9(-1)`

Это приводит к умножению двух матриц, как описано выше. Возьмем пример.

Пример: Как разделить А на В?

`A = [[1,2], [5,7]]`

`B = [[-1,2], [10,7]]`

Проверим условия делимости, описанные выше:

— Является ли B квадратной матрицей? да, потому что количество столбцов совпадает с количеством строк (= 2).
— Является ли B обратимым? да, потому что его определитель отличен от 0 (det[B] = -1*7-2*10 = -27).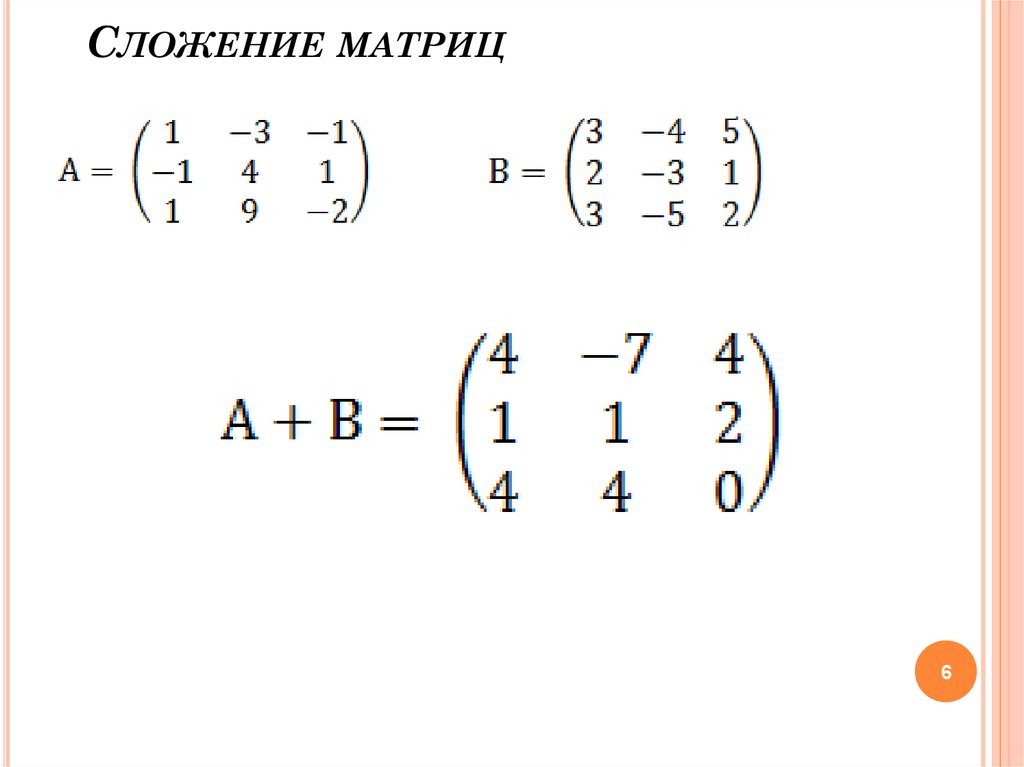 9(-1) = [[1,2], [5,7]] * [[-7/27,2/27], [10/27,1/27]]`

Получаем окончательный результат,

`D = [[13,4], [35,17]]`

См. также

Калькуляторы линейной алгебры

---

Умножение, сложение и вычитание матриц онлайн

Список помощи по математике — — Быстрый переход по математике — Научный онлайн-калькулятор — Общая математика — Калькулятор дробейКалькулятор процентовКалькулятор квадратного корняКалькулятор факторингаУпрощение выраженийКалькулятор делителейКалькулятор множителейКалькулятор наибольшего общего множителя (НОК)Калькулятор наименьшего общего кратного (НОК)Калькулятор и проверка простых чиселВалидатор идеальных чиселВалидатор идеальных квадратных чисел-Интерполяция-Интерполяционный калькулятор — Алгебра и комбинаторика -Решатель уравненийРешатель квадратных уравненийРешатель систем уравненийКомбинаторикаПерестановкиПолиномыПолиномы -Сложение и вычитаниеПолиномы -Умножение и делениеПолиномы -Дифференцирование и интегрированиеПолиномы -Калькулятор четности (нечетные, четные, нет)Полиномы -Поиск корняПолиномы -Сгенерировать из корнейМатрицаМатрицаМатрица-детерминантКалькулятор Сложение, вычитание, умножение-Исчисление-Интегральный калькуляторКалькулятор определенных интеграловКалькулятор производныхЧисловой производный калькуляторПредельный калькуляторКалькулятор расширения ряда Тейлора-Графики и геометрия-Двумерный графический калькулятор3D-графический калькулятор-Комплексные числа и тригонометрия-Калькулятор комплексных чиселТригонометрический калькулятор-Теория чисел-Калькулятор дзета-функции Римана Генератор чиселГенератор полиномов Бернулли-Статистика и вероятность-Калькулятор PDFКалькулятор CDFКвантильный калькуляторКалькулятор среднегоКалькулятор стандартного отклоненияКалькулятор дисперсииКалькулятор эксцессаКалькулятор асимметрии-Калькуляторы описательной статистики-Матрица Калькулятор центрального моментаМатрица корреляцииКалькулятор матрицыКовариацияМатрица калькуляторМатрица Калькулятор геометрического среднегоМатрица Калькулятор гармонического среднегоКалькулятор матрицы центральный калькулятор моментаМатрица среднего калькуляторМатрица максимума калькуляторМатрица Калькулятор минимумаКалькулятор медианы матрицыКалькулятор среднего отклонения матрицыКалькулятор среднего отклонения матрицыКалькулятор квантиля матрицыКалькулятор асимметрии матрицы квартиляКалькулятор асимметрии матрицыКалькулятор стандартного отклонения матрицыКалькулятор дисперсии матрицыКалькулятор коэффициента вариации матрицы-Калькуляторы непрерывных распределений -Калькуляторы бета-распределенияКалькуляторы распределения хи-квадратовЭкспоненциальное распределение Калькуляторы распределенияРаспределение Ла-Гамма КалькуляторыКалькуляторы логарифмически нормального распределенияНормальный (гауссовский) Калькуляторы распределенияКалькуляторы распределения ПаретоКалькуляторы распределения РэлеяКалькуляторы студенческого t-распределенияКалькуляторы равномерного распределенияКалькуляторы распределения Вейбулла-Калькуляторы дискретных распределений-Калькуляторы биномиального распределенияКалькуляторы геометрического распределенияКалькуляторы распределения ПуассонаКалькуляторы равномерного (дискретного) распределения

Электронная почта     Печать

Добро пожаловать в SolveMyMath.

No related posts.