Смешанное произведение векторов, онлайн калькулятор
Наш онлайн калькулятор позволяет найти смешанное произведение двух векторов всего за пару минут. Для вычисления смешанного произведения векторов выберите форму их представления (по точкам или через координаты), заполните все координаты векторов и нажмите кнопку «Вычислить», калькулятор выдаст пошаговое решение и ответ! Каждый шаг будет детально расписан, это поможет вам понять, как был получен ответ и, при необходимости, проверить свое решение.
Введите данные, чтобы найти смешанное произведение векторовкоординатами точками
Формула : |
| Понравился сайт? Расскажи друзьям! | |||
ru.solverbook.com
Смешанное произведение векторов онлайн калькулятор
Скалярное произведение вектора а на векторное произведение вектора b и вектора считается смешанным произведением векторов и равняется определителю матрицы, составленной из этих векторов.
Для нахождения смешанного произведения векторов, заданных координатами a = {ax; ay; az}, b = {bx; by; bz} и c = {cx; cy; cz}, воспользуемся формулой:
| a · [b × c] = | ax | ay | az |
| bx | by | bz | |
| cx | cy | cz |
Если смешанное произведение трех не нулевых векторов будет равняться нулю, вектора — компланарные.
Модуль смешанного произведения трех векторов (а,b,с) равняется объему образованного ими параллелепипеда
Vпарал = |a · [b х c]|
Объем пирамиды, образованной векторами а,b,с равняется одной шестой от модуля смешанного произведения этих векторов.
Vпир = 1/6 |a · [b х c]|
Воспользовавшись онлайн-калькулятором, вы сможете быстро и правильно рассчитать смешанное произведение векторов.
Введите значения векторов Первый вектор a = {,,} Начальная точка Второй вектор b = {,,} Начальная точка Третий вектор c = {,,} Начальная точка |
infofaq.ru
Смешанное произведение векторов онлайн
Вычисление смешанного произведения векторов онлайн.
Форма представления первого вектора: КоординатамиТочками
Форма представления второго вектора: КоординатамиТочками
Форма представления третьего вектора: КоординатамиТочками
Введите значения векторов.
Первый вектор
Второй вектор
Третий вектор
Вводить можно числа или дроби. Например: 1.5 или 1/7 или -1/4 и т.д.
Получить ответВоспользуйтесь также:
Скалярное произведение векторов
Векторное произведение векторов
Проверка образуют ли вектора базис
Разложение вектора по заданному базису
Смешанное произведение векторов онлайн
Смешанное произведение
Смешанное произведение векторов — скалярное произведение вектора
a
на векторное произведение векторовb
иc
.Смешанное произведение векторов равно определителю матрицы, составленной из этих векторов.
Свойства смешанного произведения векторов
- Геометрический смысл смешанного произведения. Модуль смешанного произведения трех векторов равен объёму параллелепипеда, образованного этими векторами.
a
· [b
×c
] =b
· [c
×a
] =c
· [a
×b
] = —a
· [c
×b
] = —b
· [a
×c
] = —c
· [b
×a
]- Если смешанное произведение трех не нулевых векторов равно нулю, то эти векторами компланарные.
matematikam.ru
Как найти смешанное произведение векторов онлайн · Как пользоваться Контрольная Работа РУ
Если вам необходимо найти смешанное произведение трёх векторов, то данная статья вам поможет.
Здесь будет приведён пример, как воспользоваться калькулятором он-лайн по нахождению смешанного произведения.
Этот калькулятор выдаёт не только ответ, но ещё подробное решение с определениями и объяснениями.
Давайте рассмотрим пример:
Пусть вам надо найти смешанное произведение векторов:
a = (1, 3, 5)
b = (5, 7 ,12)
c = (8, 3, 1)
Воспользуйтесь следующими шагами:
1. Перейти на сервис
2. Ввести первый вектор a, входящий в смешанное произведение, как показано ниже:
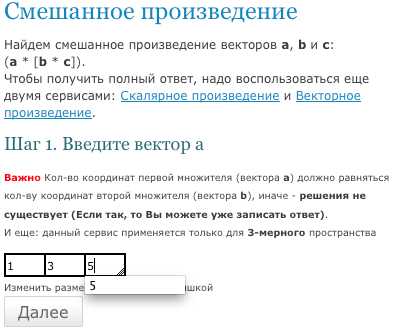
3. После того, как нажмёте кнопку «Далее», введите второй вектор b:

4. Ещё раз нажимаем кнопку «Далее» и остаётся ввести третий последний вектор c:
5. Всё, после того, как нажмете кнопку, то получите подобный ответ с подробным решением. У вас будут свои вектора и своё решение:
Вектора a,b и c введены!
Даны вектора:
| a = |
[1 3 5] |
| b = |
[ 5 7 12] |
| c = |
[8 3 1] |
Найдем смешанное произведение векторов (a * [b * c])
Находим:
-
Сначала найдём векторное произведение x = [b * c] = | i j k | | a1 a2 a3 | | b1 b2 b3 |
| i j k | | 5 7 12 | | 8 3 1 |
= [-29 91 -41]
- Потом скалярное произведение
(a * x) = (1) * (-29) + (3) * (91) + (5) * (-41) = 39
Т.к. (a * [b * c]) = (a * x) = 39 — это ответ 🙂
www.kontrolnaya-rabota.ru
Смешанное произведение векторов.
Навигация по странице:
Определение. Смешанное произведение векторов — скалярное произведение вектора a на векторное произведение векторов b и c.
Формулы вычисления смешанного произведения векторов
Смешанное произведение векторов равно определителю матрицы, составленной из этих векторов.
Смешанное произведение векторов a = {ax; ay; az}, b = {bx; b y; bz} и c = {cx; cy; cz} в декартовой системе координат можно вычислить, используя следующую формулу:
| a · [b × c] = | ax | ay | az |
| bx | by | bz | |
| cx | cy | cz |
Свойства смешанного произведения векторов
Геометрический смысл смешанного произведения.
Модуль смешанного произведения трех векторов a, b и с равен объёму параллелепипеда, образованного этими векторами:Vпарал = |a · [b × c]|
Геометрический смысл смешанного произведения.
Объем пирамиды образованной тремя векторами a, b и с равен одной шестой части от модуля смешанного произведения этих векторов:Vпир = 1 |a · [b × c]| 6 a · [b × c] = b · (a · c) — c · (a · b)
a · [b × c] = b · [c × a] = c · [a × b] = -a · [c × b] = -b · [a × c] = -c · [b × a]
a · [b × c] + b · [c × a] + c · [a × b] = 0 — тождество Якоби.
Примеры задач на вычисления смешанного произведения векторов
Пример 1. Найти смешанное произведение векторов a = {1; 2; 3}, b = {1; 1; 1}, c = {1; 2; 1}.Решение:
| a · [b × с] = | 1 | 2 | 3 | = |
| 1 | 1 | 1 | ||
| 1 | 2 | 1 |
= 1·1·1 + 1·1·2 + 1·2·3 — 1·1·3 — 1·1·2 — 1·1·2 = 1 + 2 + 6 — 3 — 2 — 2 = 2
Пример 2.
Найти объем пирамиды построенной на векторах a = {1; 2; 3}, b = {1; -1; 1}, c = {2; 0; -1}.Решение: Найдем смешанное произведение этих векторов:
| a · [b × с] = | 1 | 2 | 3 | = |
| 1 | -1 | 1 | ||
| 2 | 0 | -1 |
= 1·(-1)·(-1) + 2·1·2 + 3·1·0 — 3·(-1)·2 — 2·1·(-1) — 1·1·0 =
= 1 + 4 + 0 + 6 + 2 — 0 = 13
Найдем объем пирамиды воспользовавшись свойствами:
| Vпир = | 1 | |a · [b × c]| = | 13 | = 2 | 1 |
| 6 | 6 | 6 |
Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!
0oq.ru
Вычисляем онлайн смешанное произведение векторов
Я уже рассказывал о скалярном и о векторном произведении векторов. Ну и как следствие, сегодня я просто должен говорить о смешанном произведении векторов. Потому что последнее строится на понятии двоих первых, и оно также имеет немалый вес в математики, и часто используется при решении задач. Так что если вам надо будет найти смешанное произведение векторов, то вы можете сделать это онлайн с помощью моей новой программки.
Ну, а теперь немножко, в общем, о смешанном произведении векторов и более подробно о самой программке.
Смешанное произведение трёх векторов – это число, что равно скалярному произведению векторного произведения первых двух векторов на третий. То есть, если вам надо найти смешанное произведение трёх векторов a, b, c, то вам сначала надо найти векторное произведение двух первых a на b, а потом результат скалярно помножить на вектор c. В зависимости от того, какой репер будут создавать эти векторы: правый или левый, то соответственно число смешанного произведения может быть положительным или отрицательным. Если эти векторы компланарные (лежат в одной плоскости), то их смешанное произведение будет равно нулю – это свойство часто используется для проверки компланатности векторов.
Также очень интересным есть то, что модуль величины смешанного произведения трёх векторов равный объёму параллелепипеда построенного на этих векторах. То есть таким образом можно вычислять объёмы многих геометрических фигур. А если векторы заданны в ортонормированном базисе, то это вообще будет определитель, который будет состоять из координат этих векторов, только взят по модулю.
Так что теперь эта программка поможет вам проверять векторы на компланарность и вычислять объёмы фигур. При этом она выдаёт пошаговое решение со всеми формулами и подробными подсчетами.
Материалы по теме:
Поделиться с друзьями:
Загрузка…matemonline.com
Смешанное произведение векторов
ОпределениеСмешанным произведением трех векторов $\overline{a}$, $\overline{b}$, $\overline{c}$ называется число, равное скалярному произведению вектора $\overline{a} \times \overline{b}$ на вектор $\overline{c}$: $(\overline{a}, \overline{b}, \overline{c})=([\overline{a}, \overline{b}], \overline{c})$
Геометрический смысл смешанного произведения
Геометрический смысл смешанного произведения: если тройка векторов $\{\overline{a}, \overline{b}, \overline{c}\}$ правая, то их смешанное произведение равно объему параллелепипеда построенного на этих векторах: $(\overline{a}, \overline{b}, \overline{c})=V$. В случае левой тройки $\{\overline{a}, \overline{b}, \overline{c}\}$ смешанное произведение указанных векторов равно объему параллелепипеда со знаком минус: $(\overline{a}, \overline{b}, \overline{c})=-V$. Если $\overline{a}$, $\overline{b}$ и $\overline{c}$ компланарны, то их смешанное произведение равно нулю.
Итак, из выше сказанного можно сделать вывод, что объем параллелепипеда, построенного на векторах $\overline{a}$, $\overline{b}$ и $\overline{c}$ равен модулю смешанного произведения этих векторов:
Объем пирамиды, построенной на этой тройке векторов равен
Свойства смешанного произведения:
1° $(\overline{a}, \overline{b}, \overline{c})=(\overline{a},[\overline{b}, \overline{c}])$
2° $(\overline{a}, \overline{b}, \overline{c})=(\overline{b}, \overline{c}, \overline{a})=(\overline{c}, \overline{a}, \overline{b})=-(\overline{b}, \overline{a}, \overline{c})=-(\overline{c}, \overline{b}, \overline{a})=-(\overline{a}, \overline{c}, \overline{b})$
3° Три вектора компланарны тогда и только тогда, когда $(\overline{a}, \overline{b}, \overline{c})=0$
4° Тройка векторов является правой тогда и только тогда, когда $(\overline{a}, \overline{b}, \overline{c})>0$. Если же $(\overline{a}, \overline{b}, \overline{c})
5° $(\lambda \overline{a}, \
www.webmath.ru
