Делитель и делимое числа. Делимость суммы и разности числа.
Операции сложения и умножения всегда возможно, но операции вычитания и деления без остатка возможны только при определенных условиях. В вычитании мы можем легко увидеть, возможно это или нет: достаточно, чтобы уменьшаемое было больше или равно вычитаемому. В делении не всегда просто увидеть, делится ли число без остатка. Есть определенные случаи деления, в которых, используя некоторые признаки числа, мы можем увидеть заранее, можно ли деление сделать без остатка или нет.
Делитель и делимое
Если число может быть разделено на другое без остатка, мы говорим, что первое число делимое или что оно делится на второе, а второе — это делитель первого числа.
Например: число 8 делится на 4 , и 4 это делитель 8. Но 8 не делится на 3 и 3 не является делителем 8.
15 делится на 1, 3, 5, 15, и каждое из этих чисел — делитель 15
Каждый число делится на себя. 1 есть делителем для всех чисел. Например: 4/4 = 1; 7/7 = 1; 9/1 = 1; 12/1 = 12
Делимость суммы числа
Числа 6 и 14 делятся на 2; их сумма 20 также делится на 2.
Числа 12, 18, 30 делятся на 6; их сумма 60 делится на 6
Если каждое слагаемое отдельно делится на число, их сумма также делится на это число.
Мы можем использовать это свойство, чтобы определить, делится ли одно число на другое, не проводя операции деления
Например: Делится ли число 742 на 7?
Для ответа на вопрос, запишем 742 в виде суммы слагаемых: 742 = 700 + 42. Поскольку оба числа 700 и 42 делится на 7, то их сумма 742 также делится на 7.
15 делится на 3, а 10 не делится на 3. Их сумма 25 не делится на 3
10 и 30 делятся на 5, но 8 не делится на 5 и их сумма 48 также не делится на 5
Если только одно слагаемое не делится на число, сумма также не делится на это число.
Делимость разности числа
40 и 12 делится на 4. Их разница 28 делится на 4.
Если уменьшаемое и вычитаемое отдельно делятся на число, то их разность делится тоже на это число.
www.math10.com
Урок математики на тему: «Делимое. Делитель. Проверка деления.»
Конспект урока математики в 3-м классе по теме » Делимое, делитель. Проверка деления «
Учебник: «Математика» 3 класс часть 2; авторы М.И. Моро, М.А. Бантова, Г.В. Бельтюкова и др.
Образовательная система: «Школа России»
Цели:
Научить выполнять проверку деления умножением; закреплять навыки решения задач, уравнений и примеров.
Развитие умений наблюдать, выделять главное, анализировать, обобщать, сравнивать; развивать внимание, логическое мышление; развивать математическую речь, память; развивать познавательную активность.
Воспитывать доброжелательность, взаимопомощь.
Задачи:
познакомить детей с проверкой деления умножением, дать представление об использовании её на практике;
учить выделять главное и второстепенное, развивать мыслительную деятельность, внимание, речь;
формировать интерес к математике, расширять математический кругозор.
Тип урока:
— урок открытия нового знания.
Методы обучения: проблемно-диалогическое и личностно ориентированная технология обучения.
Формы организации познавательной деятельности учащихся:
— фронтальная;
— индивидуальная;
— самостоятельная.
Область применения: проводится в 3 классе, обучающемся по образовательной программе «Школа России».
Эффективность: достигается за счет применения на уроке активизирующих методов, различных форм работы, разнообразных заданий, организации оперативной обратной связи. На протяжении всего урока поддерживается интерес учащихся, создается благоприятный психологический климат.
Результативность: учащиеся познакомятся проверкой деления, научатся её выполнять, усвоят практическое значение проверки деления умножением и её применение на практике. Высокие результаты достигаются за счет совместного «открытия» новой темы.
Оборудование урока: мультимедийный проектор; интерактивная доска; мультимедийная презентация; карточки для индивидуальной работы и работы в парах.
Планируемые результаты:
Предметные:
Овладение основами логического мышления, основами счёта.
Умение проверять результат деления умножением.
Умение самостоятельно решать задачи изученных видов.
Умение построения логической цепи рассуждения.
Личностные:
Развитие мотивации учебной деятельности и личностного смысла учения.
Умение анализировать свои действия и управлять ими.
Метапредметные:
Умение планировать, контролировать и оценивать учебные действия в соответствии с поставленной задачей и условиями её выполнения, определять наиболее эффективные способы достижения результата.
— Умение участвовать в диалоге при выполнении заданий в парах.
.
1.Самоопределение к деятельности.
Пусть сегодня для нас всех,
На урок придёт успех!
Поприветствуем гостей,
С ними нам вдвойне теплей,
Пожелайте нам удачи,
И успешности в придачу!
-Подумайте, какие качества нужны для успешной работы, чтобы для всех урок стал полезным? (внимание, активность, старание, сообразительность …)
Возьмите карточку личных достижений и отметьте знаком «+», чего бы ты хотел достичь на уроке.
2. Мотивация и актуализация опорных знаний.-Начинаем успешно трудиться. Работаем на карточках белого цвета, которые находятся у вас в конверте. Вычислите значения выражений.
63:9= 64:8=
42:7= 72:9=81:9= 54:6=
27:3= 96:8=
Обменялись карточками с соседом. Проверяем ответы на экране. Поставьте соседу оценку.
-Кто поставил своему соседу пятёрку, чей сосед допустил ошибку? Какой совет дадите?
Ответы на слайде: 7 6 9 9 (Слайд №3)
8 8 9 12
-Чем похожи выражения? Как называются компоненты действия деления?
-Какое выражение отличается от других? А в чём отличие? (внетабличное деление)
-Поднимите руки, кто допустил ошибку в последнем выражении? Помогите исправить ошибку. (Объяснение у доски) Запись на доске 96:8= (80+16):8=
-Что помогло нам исправить ошибку?
3. Постановка учебной проблемы
— Перед вами выражение: 15:5=3. Прочитайте его, используя названия компонентов действия деления и его результата.
— Объясни, как из первого выражения (15:5=3) получилось 5х3=15?
— Дополните предложение: «Если делитель умножить на частное, то получится….» (Слайд №4)
-Как получили второе выражение?
— Дополни предложение «Если делимое разделить на частное, то получится…» (Слайд №4)
(Запись на доске)
15:5=3
5*3=15
15:3=5
-Где можно найти эти правила? (В учебнике на с. 16) Прочитайте эти правила. Расскажите соседу. Знакомы мы с этими правилами?
Работа в парах.
Поработайте в паре со своим соседом. Возьмите сиреневую карточку и выполните задание вместе.
40:8=5 27:9= 56:7=
8*5= 9* = * =
40:5= 27: = : =
Проверка на доске. Ученики выходят к доске и вставляют пропущенные числа.
— Что помогло вам выполнить задание. Как вы думаете, когда они могут нам пригодиться?
4. «Открытие» нового знания
-Вернёмся к нашему выражению, в котором мы исправляли ошибку.
96:8= (80+16):8=10+2=12
— А как ещё мы можем проверить деление? (нужно частное умножить на делитель).
Проверка:
12*8=96
96=96
— Что мы сейчас делали?
— А теперь ребята попробуйте ответить, какая тема нашего урока? (Слайд № 5)
-Да, сегодня мы научимся проверять деление умножением.
Физкультминутка.
Игра «Зеркало».
Зарядка для глаз (слайды 6,7,8,9)
Первичное закрепление.
Работа с комментированием по учебнику (стр.17 №1)
Запись на доске и в тетради.
81:3=27
Проверка:
27*3=81
81=81
Последнее выражение самостоятельно.
-Чему учились, выполняя это задание?
6. Работа над пройденным материалом.
Решение задачи.
-Отгадай загадку: «Волосата, зелена, в листьях прячется она. Хоть и много ножек, бегать все равно не может». (Слайд №11)
Что вы знаете о гусеницах? Ученик рассказывает. (Гусеницы – это личинки бабочек. Гусеницы имеют мягкое вытянутое тело. Крыльев у них нет. Многие имеют яркую окраску и красивое опушение или выросты. Питаются в основном растительной пищей. Поэтому гусеница — это злостный вредитель. Гусеницы являются особым лакомством для птиц, но с помощью различных уловок им удается спасаться от гибели. Есть гусеницы похожие ветки и сучки, а другие маскируются под цвет листьев или цветов. А некоторые, наоборот, своей резкой окраской хотят отпугнуть своих врагов.)
(Слайд №12) Задача
Гусеница проползла по ветке до ствола яблони 3 дм, что составило четвёртую часть всего её пути до земли.
-Что известно в условии задачи?
Выберите для себя одно задание на экране.
1.Поставь вопрос к данному условию.
2.Поставь вопрос так, чтобы задача решалась в два действия.
-Какой вопрос вы поставили в первом задании? (Сколько всего дециметров проползёт гусеница до земли?) Повторите вопрос.
-А какой ещё можно вопрос задать? ( Сколько дециметров осталось проползти гусенице до земли?) Повторите вопрос.
-Сделайте чертёж и выполните решение задачи. Кому нужна карточка-помощница, найдите её в конверте, она жёлтого цвета.
Проверка решения по эталону на экране. (Слайд №13)
1 решение
3*4=12(дм)
Ответ: 12 дм проползёт гусеница до земли.
2 решение
3*4=12(дм) весь путь гусеницы
12-3=9 (дм)
Ответ: гусенице осталось проползти до земли 9 дм.
(Слайд №14)
-Посмотрите фрагменты из мультфильма. Как он называется? (Лунтик и его друзья).
-О чем этот мультфильм? (О дружбе) Назовите имена отрицательных героев в этом мультфильме. (Гусеницы Вупсень и Пупсень)
(Слайд №15)
-Прочитайте задачу про этих гусениц.
На завтрак Тутси съел 19 листочков, а Пупси – в 4 раза больше.
Объясните, что обозначают эти выражения:
19*4
19*4-19.
(Устное объяснение данных выражений учащимися).
-Ребята, мы с вами знаем, что гусеницы очень вредят растениям. А что произойдёт, если уничтожить всех гусениц на земле?
-Нарушатся экологические цепочки, связи. Ведь в природе всё взаимосвязано.
— И в такой науке, как математика, тоже существуют взаимосвязи, которые помогают нам выполнить…. Продолжите предложение.
7.Самостоятельная работа.
Работа по печатной тетради с. 26 № 62
Проверка по эталону на доске.
8.Рефлексия деятельности
-Как вы думаете, успешным был для вас сегодняшний урок?
-Что мы вспомнили и повторили? (Слайд №16)
-А что новое открыли? А где нам пригодятся эти знания?
Возьмите карточку личных достижений и отметьте знаком «+», что у вас получилось на уроке.
-Поднимите руки, у кого совпали «+» в той и другой графе.
infourok.ru
Урок матаматики во 2 классе «Делимое, делитель, частное»
Урок математики во 2 классе
по программе «Перспектива».
Тема урока: «Делимое, делитель, частное»
Цели урока:
- Познакомить с названием компонентов действия деления;
- Установить взаимосвязь между компонентами и результатом действия деления;
- Сформировать умение читать выражения, используя названия компонент деления;
- Совершенствовать навыки счета, повторить таблицу умножения и деления на 2;
- Включать учащихся в оценочную деятельность;
- Развивать мышление, внимание, математически грамотную речь, творческие способности;
- Воспитывать познавательный интерес у учащихся;
Ход урока.
- Организационный момент (проверка готовности к уроку, настрой на работу)
Пусть сегодня для нас всех,
На урок придёт успех!
Поприветствуем гостей,
С ними нам вдвойне теплей,
Пожелайте нам удачи,
И успешности в придачу!
Подумайте, какие качества нужны для успешной работы, чтобы для всех урок стал полезным? (внимание, активность, старание, сообразительность …)
Возьмите карточку личных достижений и отметьте знаком «+» , чего бы ты хотел достичь на уроке.
|
|
Я хотел У меня получилось бы достичь
|
|
Работать старательно и активно |
|
|
Выполнить записи в тетради аккуратно и без ошибок |
|
|
Узнать что – то новое самостоятельно |
|
|
Порадоваться за товарища |
|
|
Получить «5» |
|
2. Устные вычисления. Игра «Молчанка». Запишите только ответы в тетради.
Дан ряд чисел: 7 12 9 16 10 2 20
Все однозначные числа умножь на 2, а двузначные раздели на 2.
Что повторили выполняя это задание? (таблицу умножения и деления на 2).
Посмотрите на ряд чисел, который у вас получился. Оцените свою работу. Нарисуй на полях тетради соответствующий смайлик. (Самооценка).
Поднимите руку, кто поставил улыбающийся смайлик.
Объясни, за что ты себе поставил улыбающийся смайлик. (Я выполнила задание правильно без ошибок и аккуратно).
Кто поставил простой смайлик? Почему ты себе поставил такой смайлик?
( У меня есть исправления).
Кто поставил грустный смайлик? Почему?
Те, кто поставил улыбающийся смайлик, вы уверены, что у вас все правильно.
Как проверить? Где посмотреть?
Я даю образец, эталон, как должно быть: 14 6 18 8 5 4 10
Сравните. У кого, так как у меня? Поднимите руку те, кто свою работу оценил правильно.
У кого есть ошибки? Где ошибся?
3. Постановка целей и формулирование темы урока.
На экране даны числовые выражения: 6 * 3 8 : 2 4 * 5 7 * 2
Найдите лишнее выражение. Объясни, почему ты так считаешь.
Прочитай математические записи со знаком умножения, используя названия компонентов.
Произведение чисел 6 и 3; Первый множитель 4, второй множитель 5.
Произведение чисел 7 и 2.
Проблемная ситуация: Прочитай выражение со знаком «деление».
Где возникла трудность? Почему не можем прочитать это выражение?
Какая же задача будет стоять перед вами сегодня на уроке?
(узнать, как называются числа при делении).
Зачем нужно знать название чисел при делении?
Эти цели, которые вы поставили, запомните.
Что за тема урока? Как ты думаешь?
Попробуйте сформулировать тему урока. (Компоненты действия деления)
4. «Открытие» нового знания.
8 : 2
Назовите первое число в выражении. Что делают с этим числом? Подумайте, какое бы название вы дали этому числу (варианты ответов учащихся)
Прочитайте, как называется число, которое делят (делимое)
Назовите число в выражении, на которое делят. Прочитайте, как оно называется … делитель
Чему равно значение этого выражения?
4 – это часть от деления чисел 8 и 2. Попробуйте предположить, как называется результат действия деления (частное)
Как бы вы назвали одним словом выражение 8 : 2 ? частное
Какие же главные слова будут звучать на уроке математики сегодня?
делимое делитель частное
Это тема нашего урока.
Справились мы с задачей, которую определили в начале урока?
( Да. Узнали, как называются числа при делении).
А какие еще задачи нам предстоит решить в ходе урока? Как вы думаете?
Научиться читать выражения разными способами, называя компоненты деления.
А теперь, когда вы узнали, как называются числа при делении, кто попробует прочитать это выражение? 8 : 2 = 4
5. Первичное закрепление (коллективная работа с экраном)
а) Составь к рисунку выражение на деление, назови, как называется каждое число в этом выражении. Прочитай выражение, используя названия компонентов.
12 : 3 = 4
б) работа по учебнику стр. 79 № 1
6. Физминутка:
Поработали, ребятки, а теперь все на зарядку!
Мы ногами топ – топ, мы руками хлоп – хлоп,
Мы глазами миг – миг, мы плечами чик – чик.
Раз — присели, два — привстали, руки к верху мы подняли,
Сели – встали, сели – встали и на месте зашагали.
Но закончилась игра – заниматься нам пора.
7.Тренировочные упражнения по теме урока.
а) Самостоятельная работа по учебнику стр. 80 № 3.
Решай только те примеры, в которых делимое больше 10.
Сколько примеров ты решил? Сверь с экраном:
18 : 2 = 9 14 : 2 = 7 16 : 2 = 8
Оцени себя. Поставь «+», если ты справился верно.
б) Составь и запиши в тетрадь 2 примера на деление, в которых частное равно:
для учащихся 1 колонки – 5; 2 колонки – 4; 3 колонки – 6;
Кому нужна помощь?
Взаимопроверка с соседом. Поменяйтесь тетрадками, проверь работу соседа.
Поднимите руку те, кто может похвалить своего соседа.
За что ты можешь похвалить своего соседа? (Я могу похвалить Лизу за то, что
она с этим заданием справилась сама без помощи, правильно
составила примеры, работа у нее без исправлений и аккуратная).
Поставьте плюс, если ваш сосед справился с заданием верно.
в) Работа в парах. Сейчас вы займетесь исследовательской деятельностью и
все потом расскажите: какой компонент неизвестен и как его нашли.
Карточка: примеры с окошками:
12 : 3 =
6 : = 2
: 2 = 7
Найди неизвестное число, вставь в окошко, подпиши компоненты деления.
Перед тем, как будете работать в паре, вспомним правила дружной работы:
- Выскажи мнение;
- Выслушай мнение соседа;
- Придите к единому мнению;
- Действуйте!
Пара, которая справится с заданием, поднимает руки вверх.
Учащиеся объясняют, какой компонент был неизвестен, как его нашли. Сверяют правильность выполнения задания с экраном.
Пара, которая справилась с заданием верно, поставьте «плюс»
Поднимите руку, кто думает, что сам сможет найти неизвестный компонент, воспользовавшись полученными знаниями. Тогда я предлагаю следующее задание.
г) Работа с таблицей.
|
Делимое |
Делитель |
Частное |
|
8 |
4 |
2 |
|
6 |
|
3 |
|
|
3 |
6 |
|
15 |
5 |
|
Работаем самостоятельно. Кому нужна помощь?
Включение учащихся в контрольно — оценочную деятельность.
Оцени свою работу. Поставь соответствующий смайлик и дай
свои комментарии.
8. Закрепление новых знаний.
Тест
а) Подчеркни выражения, в которых надо найти частное.
4 + 3 5 * 2 6 : 3 8 – 4 4 > 3 12 : 2
б) В данных равенствах подчеркни делитель.
16 : 2 = 8 3 * 5 = 15 2 * 7 = 14 8 : 4 = 2
в) В данных равенствах обведи кружочком делимое.
15 : 3 = 5 3 * 2 = 6 14 : 2 = 7 9 – 4 = 5
г) В данных равенствах подчеркни частное чисел.
2 * 9 = 18 18 : 3 = 6 12 : 4 = 3 10 : 2 = 5
д) Подчеркни правильный ответ на вопрос: «Какое самое большое число при делении?»
частное делимое делитель
Проверка с экраном. Кто справился верно, поставьте «5».
9. Итог урока.
Подведем итог урока. Хотела бы побеседовать с вами.
Вспомните цели, которые ставили в начале урока. Достигли мы этих целей?
Какое задание было самым трудным?
Кто набрал за урок 4 плюса, вы молодцы!
10. Рефлексия.
Возьмите карточку личных достижений и отметьте знаком «+» (в графе у меня получилось). Расскажи, ч его тебе удалось достичь за урок. Что не получилось?
ext.spb.ru
Урок матаматики во 2 классе «Делимое, делитель, частное»
Урок математики во 2 классе
по программе «Перспектива».
Тема урока: «Делимое, делитель, частное»
Цели урока:
- Познакомить с названием компонентов действия деления;
- Установить взаимосвязь между компонентами и результатом действия деления;
- Сформировать умение читать выражения, используя названия компонент деления;
- Совершенствовать навыки счета, повторить таблицу умножения и деления на 2;
- Включать учащихся в оценочную деятельность;
- Развивать мышление, внимание, математически грамотную речь, творческие способности;
- Воспитывать познавательный интерес у учащихся;
Ход урока.
- Организационный момент (проверка готовности к уроку, настрой на работу)
Пусть сегодня для нас всех,
На урок придёт успех!
Поприветствуем гостей,
С ними нам вдвойне теплей,
Пожелайте нам удачи,
И успешности в придачу!
Подумайте, какие качества нужны для успешной работы, чтобы для всех урок стал полезным? (внимание, активность, старание, сообразительность …)
Возьмите карточку личных достижений и отметьте знаком «+» , чего бы ты хотел достичь на уроке.
|
|
Я хотел У меня получилось бы достичь
|
|
Работать старательно и активно |
|
|
Выполнить записи в тетради аккуратно и без ошибок |
|
|
Узнать что – то новое самостоятельно |
|
|
Порадоваться за товарища |
|
|
Получить «5» |
|
2. Устные вычисления. Игра «Молчанка». Запишите только ответы в тетради.
Дан ряд чисел: 7 12 9 16 10 2 20
Все однозначные числа умножь на 2, а двузначные раздели на 2.
Что повторили выполняя это задание? (таблицу умножения и деления на 2).
Посмотрите на ряд чисел, который у вас получился. Оцените свою работу. Нарисуй на полях тетради соответствующий смайлик. (Самооценка).
Поднимите руку, кто поставил улыбающийся смайлик.
Объясни, за что ты себе поставил улыбающийся смайлик. (Я выполнила задание правильно без ошибок и аккуратно).
Кто поставил простой смайлик? Почему ты себе поставил такой смайлик?
( У меня есть исправления).
Кто поставил грустный смайлик? Почему?
Те, кто поставил улыбающийся смайлик, вы уверены, что у вас все правильно.
Как проверить? Где посмотреть?
Я даю образец, эталон, как должно быть: 14 6 18 8 5 4 10
Сравните. У кого, так как у меня? Поднимите руку те, кто свою работу оценил правильно.
У кого есть ошибки? Где ошибся?
3. Постановка целей и формулирование темы урока.
На экране даны числовые выражения: 6 * 3 8 : 2 4 * 5 7 * 2
Найдите лишнее выражение. Объясни, почему ты так считаешь.
Прочитай математические записи со знаком умножения, используя названия компонентов.
Произведение чисел 6 и 3; Первый множитель 4, второй множитель 5.
Произведение чисел 7 и 2.
Проблемная ситуация: Прочитай выражение со знаком «деление».
Где возникла трудность? Почему не можем прочитать это выражение?
Какая же задача будет стоять перед вами сегодня на уроке?
(узнать, как называются числа при делении).
Зачем нужно знать название чисел при делении?
Эти цели, которые вы поставили, запомните.
Что за тема урока? Как ты думаешь?
Попробуйте сформулировать тему урока. (Компоненты действия деления)
4. «Открытие» нового знания.
8 : 2
Назовите первое число в выражении. Что делают с этим числом? Подумайте, какое бы название вы дали этому числу (варианты ответов учащихся)
Прочитайте, как называется число, которое делят (делимое)
Назовите число в выражении, на которое делят. Прочитайте, как оно называется … делитель
Чему равно значение этого выражения?
4 – это часть от деления чисел 8 и 2. Попробуйте предположить, как называется результат действия деления (частное)
Как бы вы назвали одним словом выражение 8 : 2 ? частное
Какие же главные слова будут звучать на уроке математики сегодня?
делимое делитель частное
Это тема нашего урока.
Справились мы с задачей, которую определили в начале урока?
( Да. Узнали, как называются числа при делении).
А какие еще задачи нам предстоит решить в ходе урока? Как вы думаете?
Научиться читать выражения разными способами, называя компоненты деления.
А теперь, когда вы узнали, как называются числа при делении, кто попробует прочитать это выражение? 8 : 2 = 4
5. Первичное закрепление (коллективная работа с экраном)
а) Составь к рисунку выражение на деление, назови, как называется каждое число в этом выражении. Прочитай выражение, используя названия компонентов.
12 : 3 = 4
б) работа по учебнику стр. 79 № 1
6. Физминутка:
Поработали, ребятки, а теперь все на зарядку!
Мы ногами топ – топ, мы руками хлоп – хлоп,
Мы глазами миг – миг, мы плечами чик – чик.
Раз — присели, два — привстали, руки к верху мы подняли,
Сели – встали, сели – встали и на месте зашагали.
Но закончилась игра – заниматься нам пора.
7.Тренировочные упражнения по теме урока.
а) Самостоятельная работа по учебнику стр. 80 № 3.
Решай только те примеры, в которых делимое больше 10.
Сколько примеров ты решил? Сверь с экраном:
18 : 2 = 9 14 : 2 = 7 16 : 2 = 8
Оцени себя. Поставь «+», если ты справился верно.
б) Составь и запиши в тетрадь 2 примера на деление, в которых частное равно:
для учащихся 1 колонки – 5; 2 колонки – 4; 3 колонки – 6;
Кому нужна помощь?
Взаимопроверка с соседом. Поменяйтесь тетрадками, проверь работу соседа.
Поднимите руку те, кто может похвалить своего соседа.
За что ты можешь похвалить своего соседа? (Я могу похвалить Лизу за то, что
она с этим заданием справилась сама без помощи, правильно
составила примеры, работа у нее без исправлений и аккуратная).
Поставьте плюс, если ваш сосед справился с заданием верно.
в) Работа в парах. Сейчас вы займетесь исследовательской деятельностью и
все потом расскажите: какой компонент неизвестен и как его нашли.
Карточка: примеры с окошками:
12 : 3 =
6 : = 2
: 2 = 7
Найди неизвестное число, вставь в окошко, подпиши компоненты деления.
Перед тем, как будете работать в паре, вспомним правила дружной работы:
- Выскажи мнение;
- Выслушай мнение соседа;
- Придите к единому мнению;
- Действуйте!
Пара, которая справится с заданием, поднимает руки вверх.
Учащиеся объясняют, какой компонент был неизвестен, как его нашли. Сверяют правильность выполнения задания с экраном.
Пара, которая справилась с заданием верно, поставьте «плюс»
Поднимите руку, кто думает, что сам сможет найти неизвестный компонент, воспользовавшись полученными знаниями. Тогда я предлагаю следующее задание.
г) Работа с таблицей.
|
Делимое |
Делитель |
Частное |
|
8 |
4 |
2 |
|
6 |
|
3 |
|
|
3 |
6 |
|
15 |
5 |
|
Работаем самостоятельно. Кому нужна помощь?
Включение учащихся в контрольно — оценочную деятельность.
Оцени свою работу. Поставь соответствующий смайлик и дай
свои комментарии.
8. Закрепление новых знаний.
Тест
а) Подчеркни выражения, в которых надо найти частное.
4 + 3 5 * 2 6 : 3 8 – 4 4 > 3 12 : 2
б) В данных равенствах подчеркни делитель.
16 : 2 = 8 3 * 5 = 15 2 * 7 = 14 8 : 4 = 2
в) В данных равенствах обведи кружочком делимое.
15 : 3 = 5 3 * 2 = 6 14 : 2 = 7 9 – 4 = 5
г) В данных равенствах подчеркни частное чисел.
2 * 9 = 18 18 : 3 = 6 12 : 4 = 3 10 : 2 = 5
д) Подчеркни правильный ответ на вопрос: «Какое самое большое число при делении?»
частное делимое делитель
Проверка с экраном. Кто справился верно, поставьте «5».
9. Итог урока.
Подведем итог урока. Хотела бы побеседовать с вами.
Вспомните цели, которые ставили в начале урока. Достигли мы этих целей?
Какое задание было самым трудным?
Кто набрал за урок 4 плюса, вы молодцы!
10. Рефлексия.
Возьмите карточку личных достижений и отметьте знаком «+» (в графе у меня получилось). Расскажи, ч его тебе удалось достичь за урок. Что не получилось?
ext.spb.ru
Деление в столбик | интернет проект BeginnerSchool.ru
Деление многозначных или многоразрядных чисел удобно производить письменно в столбик. Давайте разберем, как это делать. Начнем с деления многоразрядного числа на одноразрядное, и постепенно увеличим разрядность делимого.
Итак, поделим 354 на 2. Для начала разместим эти числа как показано на рисунке:
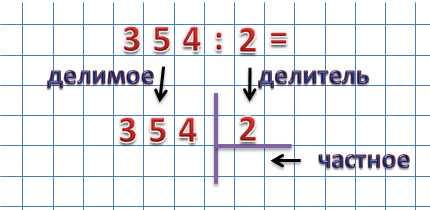
Делимое размещаем слева, делитель справа, а частное будем записывать под делителем.
Теперь начинаем делить делимое на делитель поразрядно слева на право. Находим первое неполное делимое, для этого берем первый слева разряд, в нашем случае 3 и сравниваем с делителем.
3 больше 2, значит 3 и есть неполное делимое. Ставим точку в частном и определяем, сколько ещё разрядов будет в частном – столько же, сколько осталось в делимом после выделения неполного делимого. В нашем случае в частном столько же разрядов, сколько в делимом, то есть старшим разрядом будут сотни:
Для того чтобы 3 разделить на 2 вспоминаем таблицу умножения на 2 и находим число при умножении которого на 2 получим наибольшее произведение, которое меньше 3.
2 × 1 = 2 (2 < 3)
2 × 2 = 4 (4 > 3)
2 меньше 3, а 4 больше, значит, берем первый пример и множитель 1.
Записываем 1 в частное на место первой точки (в разряд сотен), а найденное произведение записываем под делимым:
Теперь находим разность, между первым неполным делимым и произведением найденного разряда частного и делителем:
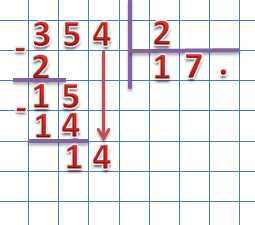
Далее находим второе неполное делимое, для этого значение следующего разряда делимого опускаем к разности:
Полученное значение сравниваем с делителем. 15 больше 2, значит, мы нашли второе неполное делимое. Для того чтобы найти результат деления 15 на 2 вновь вспоминаем таблицу умножения на 2 и находим наибольшее произведение, которое меньше 15:
2 × 7 = 14 (14 < 15)
2 × 8 = 16 (16 > 15)
Искомый множитель 7, записываем его в частное на место второй точки (в десятки). Находим разность между вторым неполным делимым и произведением найденного разряда частного и делителя:
Продолжаем деление, для чего находим третье неполное делимое. Спускаем следующий разряд делимого:
Делим неполное делимое на 2, полученное значение ставим в разряд единиц частного. Проверим правильность деления:
2 × 7 = 14
Результат деления третьего неполного делимого на делитель пишем в частное, находим разность:
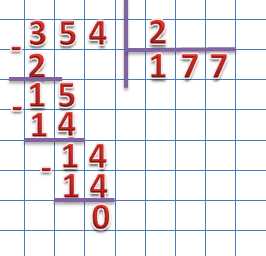
Разность мы получили равную нулю, значит деление произведено правильно.
Усложним задачу и приведем другой пример:
1020 ÷ 5
Запишем наш пример в столбик и определим первое неполное частное:
Разряд тысяч делимого составляет 1, сравниваем с делителем:
1 < 5
Добавляем в неполное делимое разряд сотен и сравниваем:
10 > 5 – мы нашли неполное делимое.
Делим 10 на 5, получаем 2, записываем результат в частное. Разность между неполным делимым и результатом умножения делителя и найденного разряда частного.
10 – 10 = 0
0 мы не пишем, опускаем следующий разряд делимого – разряд десятков:
Сравниваем второе неполное делимое с делителем.
2 < 5
Нам следует добавить в неполное делимое ещё один разряд, для этого в частное, на разряд десятков ставим 0:
20 ÷ 5 = 4
Записываем ответ в разряд единиц частного и проверяем: записываем произведение под второе неполное делимое и вычисляем разность. Получаем 0, значит пример решён правильно.
И ещё 2 правила деления в столбик:
1. Если в делимом и делителе в младших разрядах стоят нули, то перед делением их можно сократить, например:
Сколько нулей в младшем разряде делимого мы убираем, столько же нулей убираем в младших разрядах делителя.
2. Если в делимом после деления остались нули, то их следует перенести в частное:
Итак, сформулируем последовательность действий при делении в столбик.
- Размещаем делимое слева, делитель справа. Помним, что делимое мы делим, поразрядно выделяя неполные делимые и деля их последовательно на делитель. Разряды в неполное делимое выделяются слева направо от старших к младшим.
- Если в делимом и делителе в младших разрядах стоят нули, то перед делением их можно сократить.
- Определяем первый неполный делитель:
а) выделяем в неполный делитель старший разряд делимого;
б) сравниваем неполное делимое с делителем, если делитель больше, то переходим к пункту (в), если меньше, значит, мы нашли неполное делимое и можем переходить к пункту 4;
в) добавляем в неполное делимое следующий разряд и переходим к пункту (б).
- Определяем сколько разрядов будет в частном, и ставим столько точек на месте частного (под делителем) сколько будет в нем разрядов. Одна точка (один разряд) за все первое неполное делимое и остальных точек (разрядов) столько же, сколько осталось разрядов в делимом после выделения неполного делимого.
- Делим неполное делимое на делитель, для этого находим число, при умножении которого на делитель получилось бы число либо равное неполному делимому, либо меньше его.
- Найденное число записываем на место очередного разряда частного (точки), а результат умножения его на делитель записываем под неполным делимым и находим их разность.
- Если найденная разность меньше или равна неполному делимому значит, мы правильно поделили неполное делимое на делитель.
- Если в делимом остались еще разряды, то продолжаем деление, иначе переходим к пункту 10.
- Опускаем к разности следующий разряд делимого и получаем очередное неполное делимое:
а) сравниваем неполное делимое с делителем, если делитель больше, то переходим к пункту (б), если меньше, значит, мы нашли неполное делимое и можем переходить к пункту 4;
б) добавляем к неполному делимому следующий разряд делимого, при этом в частное на место следующего разряда (точки) пишем 0;
в) переходим к пункту (а).
10. Если мы выполняли деление без остатка и последняя найденная разность равна 0, то мы правильно выполнили деление.
Мы говорили о делении многоразрядного числа на одноразрядное. В случае, когда разрядность делителя больше, деление выполняется аналогично:
Спасибо, что вы с нами.
Понравилась статья — поделитесь с друзьями:
Подпишитесь на новости сайта:
Оставляйте пожалуйста комментарии в форме ниже
beginnerschool.ru
Ответы@Mail.Ru: как найти делимое?
частное умножить на делитель
делитель * частное
Разложить числа на простые множители, затем взять все множители из первого числа, добавить последовательно недостающие множители из других чисел и все выписанные множителия перемножить.
Деление – действие обратное умножению. И если умножение тождественно многократному сложению, то деление – многократному вычитанию. Например: 120: 60 = 2 2 В делении присутствую три компонента: делимое (120) – число, которое делят (уменьшают) , делитель (60) – число, на которое делят, частное (2) – число, полученное в результате деления. Основные правила деления натуральных чисел: — делить на нуль нельзя; — если разделить любое число на единицу, получим это же число; — если разделить любое число на него же, получим единицу; — если разделить любое число на нуль, получим нуль; — чтобы найти делитель, нужно делимое разделить на частное; — чтобы найти делимое, нужно делитель умножить на частное; — частное показывает во сколько раз делимое больше делителя. 3 Однако не всякое натуральное число делится на другое без остатка. В таких случаях применимо деление с остатком. Вот основное правило такого деления: — делимое (а) равно произведению делителя (p) и неполного частного (q), сложенного с остатком (r): a = p*q + r, причем остаток дожжен попадать в интервал от 0 до p, взятого по модулю. 4 Так же существует несколько правил, позволяющих определить, делится ли данное число на заданный делитель. 5 Деление целых чисел осуществляется по тем же правилам, что и натуральных, но в делении участвуют модули чисел, знак делимого определяется по правилу. Однако при делении с остатком, в некоторых случаях остаток оказывается того же знака, что и делимое или делитель (например, -11: (-7) = 1 с остатком (-4)).
Разложить числа на простые множители, затем взять все множители из первого числа, добавить последовательно недостающие множители из других чисел и все выписанные множитель перемножить. пример: 120:60=2(ост. 0)
делитель умножить на частное
Делитель умножить на частное\
Чтобы найти Делимое-надо Дилитель умножить На Частное. Например: У: 2=4 Надо: 8:2=4
делитель умножить на частное
Чтобы найти неизвестное делимое, надо делитель умножить на частное.
делитель умножить на частное. например 18 / 3 = 6 18 делимое 3 делитель 6 частное. 6*3 = 18.
делитель умножить на частное
touch.otvet.mail.ru
Урок 34 «Когда делимое меньше делителя» (1 урок) — МегаЛекции
Предметные задачи:
— знакомство со случаем действия деления с остатком меньшего числа на большее;
— выполнение заданий, в которых применяется правило: если при делении с остатком делимое меньше делителя, то неполное частное равно 0, а остаток равен делимому;
Формирование УУД: Познавательные УУД: применение правила для проверки правильности выполнения задания. Регулятивные: умение определять задачи урока, анализировать достигнутые результаты Коммуникативные: умение излагать своё мнение и аргументировать свою точку зрения, управлять действиями партнёраЛичностные: ориентация на самоанализ и самоконтроль результата, на анализ соответствия результатов требованиям конкретной задачи, на понимание предложений и оценок учителей, товарищей
Пропедевтика: деление с остатком столбиком, если неполное частное в середине записи содержит 0.
Повторение: табличные случаи деления
Методы и приемы организации учебной деятельности учащихся: изучение нового материала по тексту и заданиям учебника. Учебно-методическое обеспечение: У-1, Т-1.
Вводная часть урока
Просим учащихся прочитать тему урока «Когда делимое меньше делителя» и привести примеры частных, в которых делимое меньше делителя.
Выслушиваем ответы учеников, записывая на доске приведённые ими примеры: 2 : 6 5 : 12 и др.
Спрашиваем, возможно ли найти значение частного, если делимое меньше делителя?
Ожидаемый ответ: в этом случае значение частного найти невозможно. Сообщаем ученикам, что на уроке мы всё же научимся делить меньшее число на большее.
Продолжение урока
Задание № 180 (У – 1, с. 60)
Учащиеся читают задание и вспоминают правило: если делитель умножить на неполное частное и к полученному результату прибавить остаток,то в итоге получитсяделимое.
Выясняем, что для равенства 58 = 8 7 + 2 приведён соответствующий ему случай деления с остатком: 58 : 8 = 7 (ост. 2)
Предлагаем ученикам, используя это правило записать соответствующий случай деления с остатком для равенства 12 = 15 0 + 12 (пауза) Ожидаемый ответ: 12 : 15 = 0 (ост. 12).
Подводим итог, если делитель меньше делителя, то неполное частное равно0, а остаток – делимому!
Следовательно, деление меньшего числа на большее возможно!
Задание № 181 (У – 1, с. 60)
Учащиеся читают первую часть задания: раздели с остатком на 10 последовательно следующие числа: 48, 38, 28, 18. Даём время на выполнение задания, проверяем на доске:
48 : 10 = 4 (ост. 8) 38 : 10 = 3 (ост. 8) 28 : 10 = 2 (ост. 8) 18 : 10 = 1 (ост. 8) Спрашиваем, что общего во всех этих случаях и чем они отличаются? Ожидаемый ответ: похожи тем, что во всех случаях остаток равен 8, а отличаются – неполными частными.
Сравниваем остаток в каждом случае с числом в разряде единиц делимого, а неполное частное — с числом в разряде десятков делимого.
Делаем вывод, что при делении на 10 остаток равен числу, стоящему вразряде единиц делимого (48 : 10 = 4 (ост. 8)) а неполное частное равночислу, стоящему в разряде десятков делимого (48 : 10 = 4 (ост. 8))
Спрашиваем, какой должен быть остаток при делении числа 8 на число 10, и какое неполное частное должно получиться в этом случае деления с остатком?
Ожидаемый ответ: остаток равен числу, стоящему в разряде единиц делимого, неполное частное равно числу, стоящему в разряде десятков делимого 8 : 10 = 0 (ост. 8) Проверяем, правильно ли выполнено деление с остатком 8 : 10 = 0 (ост. 8). Записывая на доске равенство 10 0 + 8 = 8, делаем вывод, что деление состатком 8 : 10 = 0 (ост. 8) выполнено правильно.
Задание № 182 (У – 1, с. 60)
Один из учеников вслух читает первую часть задания: какому условию должны удовлетворять делимое и делитель для того, чтобы в результате деления с остатком неполное частное равнялось 0?
Ожидаемый ответ: чтобы в результате деления с остатком неполное частное равнялось 0, делимое должно быть меньше делителя.
Предлагаем ученикам привести три примера случаев деления с остатком, чтобы в результате деления неполное частное равнялось 0?
Записываем на доске под диктовку учеников приведённые примеры:
3 : 6 = 0 (ост. 3), 56 : 100 = 0 (ост. 56), 14 : 60 = 0 (ост. 14) и др.
Спрашиваем, как в рассмотренных случаях остаток связан с делимым? Ожидаемый ответ: остаток равен делимому.
Задание № 183 (У – 1, с. 60)
Учащиеся читают задание и самостоятельно записывают три случая деления с остатком, в каждом из которых делимое равно остатку.
Организуем проверку в условиях парной работы.
Задание № 176 (У – 1, с. 59)
Учащиеся читают задание: запиши по порядку первые шесть натуральных чисел, которые при делении на 7 дают в остатке 1.
Вспоминаем, если делитель умножить на неполное частное и кполученному результату прибавить остаток, то получится делимое. Следовательно, искомые делимые можно найти, если к делимым (7, 14, 21, 28, 35), которые делятся на 7 без остатка прибавить остаток 1. Записываем на доске под диктовку учеников равенства и проверяем правильность выполнения деления с остатком:
7 + 1 = 8 8 : 7 = 1 (ост. 1)
14 + 1 = 15 15 : 7 = 2 (ост. 1)
21 + 1 = 22 22 : 7 = 3 (ост. 1)
28 + 1 = 29 29 : 7 = 4 (ост. 1)
35 + 1 = 36 36 : 7 = 5 (ост. 1)
Дополняем данный ряд чисел числом 1, так как 1 : 7 = 0 (ост. 1) Итак, записанные числа 1, 8, 15, 22, 29, 36 делятся на число 7 и дают в остатке 1.
Задание № 184 (У – 1, с. 61)
Учащиеся читают задание и самостоятельно выполняют деление с остатком.
Даём время на выполнение задания, проверяем на доске:
9 : 10 = 0 (ост. 9) 12 : 24 = 0 (ост. 12) 1 : 100 = 0 (ост. 1)
364 : 387 = 0 (ост. 364) 1000 : 10000 = 0 (ост. 1000)
Обращаем внимание учеников на то, что в каждом из выполненных случаев деления делимое меньше делителя, неполное частное равно 0, а остаток равен делимому.
Ученики читают правило на голубой плашке: если при делении с остаткомделимое меньше делителя, то неполное частное равно 0, а остаток равенделимому и с помощью него проверяют правильность выполнения деления с остатком.
Задание № 185* (У – 1, с. 61)
Учащиеся читают задание: приведи пример двух чисел, которые при делении на 56897 дают в остатке число 1.
Ожидаемый ответ: 1) 56898 : 56897 = 1 (ост. 1) 2) 1 : 56897 = 0 (ост. 1)
Задание № 186 (У – 1, с. 61)
Вспоминаем, что при делении с остатком в случаях, где делимое меньшеделителя, остаток равен делимому.
Записываем на доске пример деления на число 5 с остатком 4 (4 : 5 = 0 (ост. 4))
Оставшиеся случаи деления ученики самостоятельно записывают в тетрадях.
Проверяем устно или на доске: 4 : 6 = 0 (ост. 4) 4 : 7 = 0 (ост. 4) 4 : 8 = 0 (ост. 4) 4 : 9 = 0 (ост. 4) 4 : 10 = 0 (ост. 4)
Задание № 187 (У – 1, с. 61)
Учащиеся самостоятельно читают задание.
Выясняем, что согласно правилу: если при делении с остатком делимое меньше делителя, то неполное частное равно 0, а остаток равен делимому, значит, если остаток равен 9, то делимое в этом случае тоже равно 9. Делаем вывод, что число, которое при делении на любое двузначное число даёт в остатке 9 – это число 9.
Просим учеников привести несколько примеров, доказывающих, что при делении числа 9 на любое двузначное число в остатке получается.
Задание № 188* (У – 1, с. 61)
Учащиеся самостоятельно читают задание и вспоминают, если при делении с остатком делимое меньше делителя, то неполное частное равно 0, а остаток равен делимому, значит, если остаток равен 1, то делимое в этом случаетоже равно 1.
Делаем вывод, что число, которое при делении на все натуральные числа даёт в остатке 1 – это число 1.
Просим учеников самостоятельно записать в тетрадях несколько примеров, некоторые из них записываем на доске под диктовку учеников:
1 : 23 = 0 (ост. 1) 1 : 258 = 0 (ост. 1) 1 : 4300 = 0 (ост. 1)
Задание № 189 (У – 1, с. 61)
Учащиеся читают задание: какими могут быть делимое и делитель, если неполное частное равно 0, а остаток равен 5?
Ожидаемый ответ: если неполное частное равно 0, то делимое должно бытьменьше делителя, а остаток (5) равен делимому. Следовательно, искомое делимое должно быть равно 5, а в качестве делителя можно брать любое натуральное число, которое больше 5.
Просим учеников самостоятельно записать в тетрадях несколько примеров, некоторые из них записываем на доске под диктовку учеников:
5 : 34 = 0 (ост. 5) 5 : 28 = 0 (ост. 5) 5 : 763 = 0 (ост. 5)
Задание № 190 (У – 1, с. 61)
Вспоминаем условие, при котором в неполном частном получается 0:
делимое должно быть меньше делителя.
Делаем вывод, что учащиеся должны выписать все натуральные однозначные числа, которые меньше 10: 1, 2, 3, 4, 5, 6, 7, 8, 9. Подводим итог, что при делении каждого из этих чисел на число 10 в неполном частном получится 0. (Например, 5 : 10 = 0 (ост.5))
Спрашиваем, чему равен остаток в каждом таком случае? (остаток равен делимому)
Задание № 94 (Т – 1, с. 50)
Учащиеся читают задачу и выясняют, что задача с известным результатом разностного сравнения.
Просим учеников самостоятельно начертить схему и записать решение задачи (пауза)
Проверяем на доске:
3 м 50 см
? ? 1 м 30 см
1) 3 м 50 см – 1 м 30 см = 2 м 20 см – удвоенное количество ткани второго вида
2) 2м 20 см : 2 = 1 м 10 см – купили ткани второго вида
3) 1 м 10 см + 1 м 30 см = 2 м 40 см – купили ткани первого вида Просим учеников прочитать требование задачи: можно ли сшить костюм из этой ткани, если на брюки нужно 2 м ткани первого вида, а на пиджак – 1 м 20 см ткани второго вида?
Ожидаемый ответ: нельзя, так как на пиджак нужно 1 м 20 см ткани второго вида, а купили 1 м 10 см.
Ученики самостоятельно записывают ответ задачи в тетрадях.
Задание на дом: № 90 — 93 (Т – 1, с. 49)
Рекомендуемые страницы:
Воспользуйтесь поиском по сайту:
megalektsii.ru
