Смежные углы это какие углы: Свойства смежных углов — ответ на Uchi.ru

Смежные углы треугольника. Угол

Геометрия — это весьма многогранная наука. Она развивает логику, воображение и интеллект. Конечно, из-за своей сложности и огромного количества теорем и аксиом, она не всегда нравится школьникам. Кроме этого, существует необходимость постоянно доказывать свои выводы, используя общепринятые стандарты и правила.

Смежные и вертикальные углы — это неотъемлемая составляющая геометрии. Наверняка многие школьники просто обожают их по той причине, что их свойства понятны и просты в доказательстве.

Образование углов

Любой угол образуется путем пересечения двух прямых или проведения двух лучей из одной точки. Они могут называться либо одной буквой, либо тремя, которые последовательно обозначают точки построения угла.

Углы измеряются в градусах и могут (в зависимости от их значения) по-разному называться. Так, существует прямой угол, острый, тупой и развернутый. Каждому из названий соответствует определенная градусная мера или ее промежуток.

Острым называется угол, мера которого не превышает 90 градусов.

Тупым является угол, превышающий 90 градусов.

Угол называется прямым в том случае, когда его градусная мера равна 90.

В том случае, когда он образован одной сплошной прямой, и его градусная мера равна 180, его называют развернутым.

Углы, имеющие общую сторону, вторая сторона которых продолжает друг друга, называются смежными. Они могут быть как острыми, так и тупыми. Пересечение линией образует смежные углы. Свойства их следующие:

1. Сумма таких углов будет равна 180 градусам (существует теорема, доказывающая это). Поэтому можно легко вычислить один из них, если известен другой.
2. Из первого пункта следует, что смежные углы не могут быть образованы двумя тупыми или двумя острыми углами.

Благодаря этим свойствам, можно всегда вычислить градусную меру угла, имея значение другого угла или, по крайней мере, отношение между ними.

Вертикальные углы

Углы, стороны которых являются продолжением друг друга, называются вертикальными. В качестве такой пары могут выступать любые их разновидности. Вертикальные углы всегда равны между собой.

Они образуются при пересечении прямых. Совместно с ними всегда присутствуют и смежные углы. Угол может быть одновременно смежным для одного и вертикальным для другого.

При пересечении произвольной линией также рассматривают еще несколько видов углов. Такая линия называется секущей, она и образует соответственные, односторонние и накрест лежащие углы. Они равны между собой. Их можно рассматривать в свете свойств, которые имеют вертикальные и смежные углы.

Таким образом, тема углов представляется довольно простой и понятной. Все их свойства легко запомнить и доказать. Решение задач не представляется сложным до тех пор, пока углам соответствует числовое значение. Уже дальше, когда начнется изучение sin и cos, придется запоминать множество сложных формул, их выводов и следствий. А до того времени можно просто наслаждаться легкими задачками, в которых необходимо найти смежные углы.

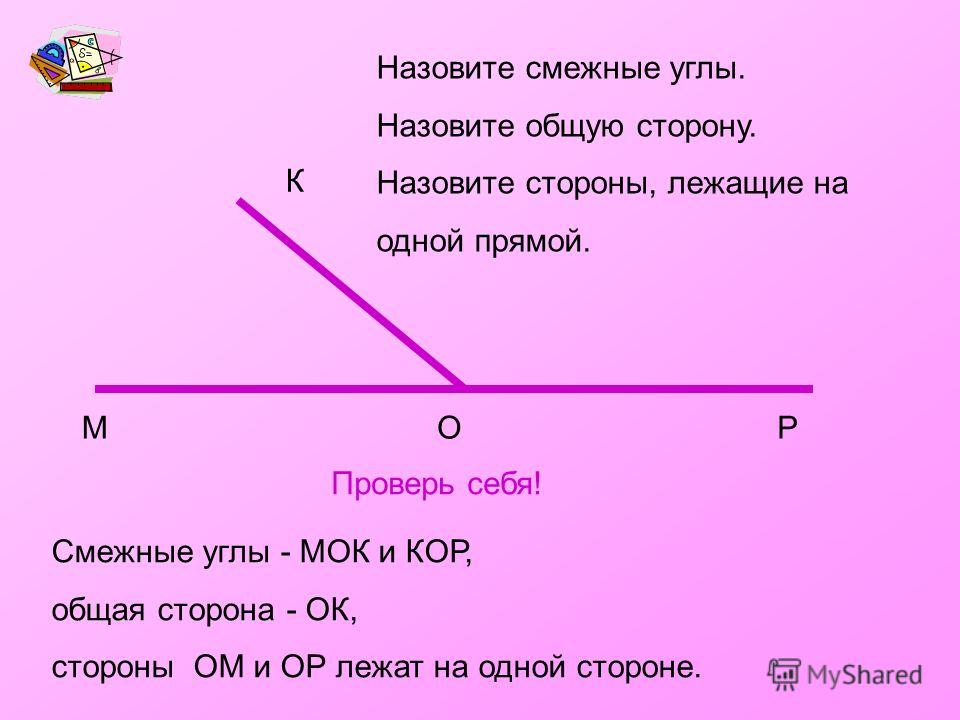
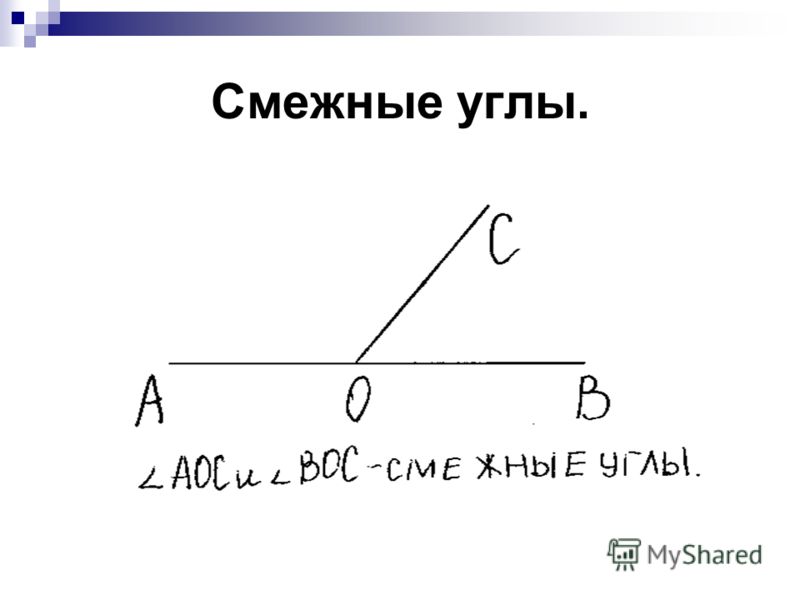
Два угла называются смежными, если у них одна сторона общая, а другие стороны этих углов являются дополнительными лучами. На рисунке 20 углы АОВ и ВОС смежные.

Сумма смежных углов равна 180°

Теорема 1. Сумма смежных углов равна 180°.

Доказательство. Луч ОВ (см. рис.1) проходит между сторонами развернутого угла. Поэтому ∠ АОВ + ∠ ВОС = 180° .

Из теоремы 1 следует, что если два угла равны, то смежные с ними углы равны.

Вертикальные углы равны

Два угла называются вертикальными, если стороны одного угла являются дополнительными лучами сторон другого. Углы АОВ и COD, BOD и АОС, образованные при пересечении двух прямых, являются вертикальными (рис. 2).

Теорема 2. Вертикальные углы равны.

Доказательство. Рассмотрим вертикальные углы АОВ и COD (см. рис. 2). Угол BOD является смежным для каждого из углов АОВ и COD. По теореме 1 ∠ АОВ + ∠ BOD = 180°, ∠ COD + ∠ BOD = 180°.

Отсюда заключаем, что ∠ АОВ = ∠ COD.

Следствие 1.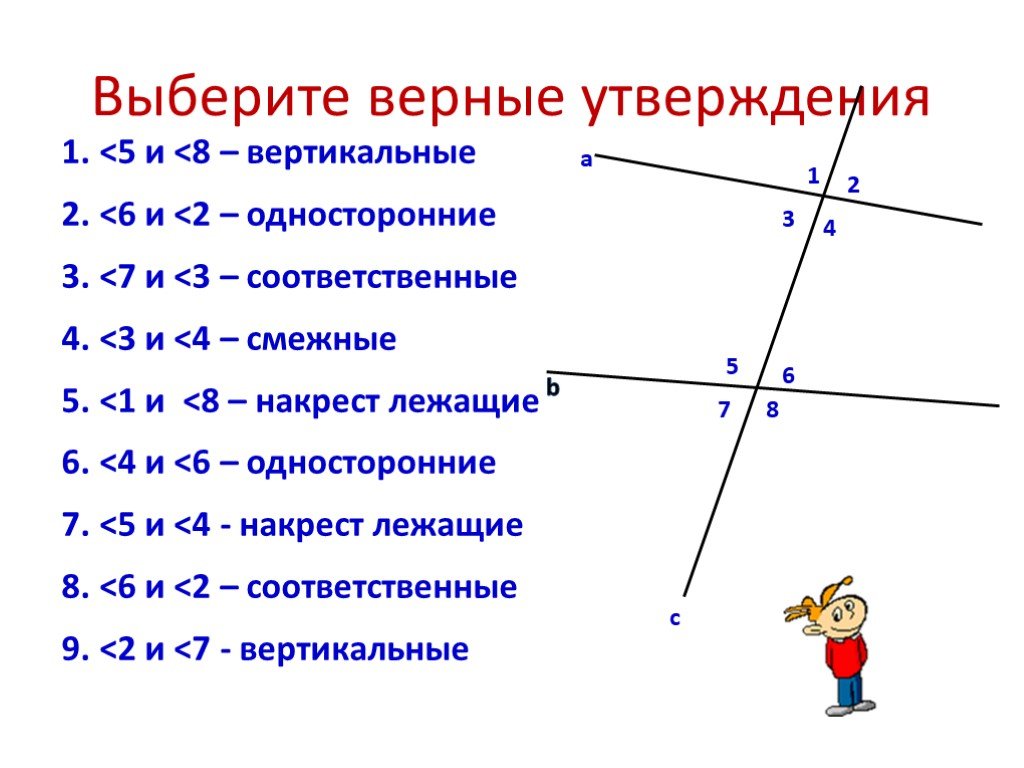 Угол, смежный с прямым углом, есть прямой угол.

Рассмотрим две пересекающиеся прямые АС и BD (рис.3). Они образуют четыре угла. Если один из них прямой (угол 1 на рис.3), то остальные углы также прямые (углы 1 и 2, 1 и 4 — смежные, углы 1 и 3 — вертикальные). В этом случае говорят, что эти прямые пересекаются под прямым углом и называются перпендикулярными (или взаимно перпендикулярными). Перпендикулярность прямых АС и BD обозначается так: AC ⊥ BD.

Серединным перпендикуляром к отрезку называется прямая, перпендикулярная к этому отрезку и проходящая через его середину.

АН — перпендикуляр к прямой

Рассмотрим прямую а и точку А, не лежащую на ней (рис.4). Соединим точку А отрезком с точкой Н прямой а. Отрезок АН называется перпендикуляром, проведенным из точки А к прямой а, если прямые АН и а перпендикулярны. Точка Н называется основанием перпендикуляра.

Чертежный угольник

Справедлива следующая теорема.

Теорема 3. Из всякой точки, не лежащей на прямой, можно провести перпендикуляр к этой прямой, и притом только один.

Для проведения на чертеже перпендикуляра из точки к прямой используют чертежный угольник (рис.5).

Замечание. Формулировка теоремы обычно состоит из двух частей. В одной части говорится о том, что дано. Эта часть называется условием теоремы. В другой части говорится о том, что должно быть доказано. Эта часть называется заключением теоремы. Например, условие теоремы 2 — углы вертикальные; заключение — эти углы равны.

Всякую теорему можно подробно выразить словами так, что ее условие будет начинаться словом «если», а заключение — словом «то». Например, теорему 2 можно подробно высказать так: «Если два угла вертикальные, то они равны».

Пример 1. Один из смежных углов равен 44°. Чему равен другой?

Решение. Обозначим градусную меру другого угла через x , тогда согласно теореме 1.
44° + х = 180°.
Решая полученное уравнение, находим, что х = 136°. Следовательно, другой угол равен 136°.

Пример 2. Пусть на рисунке 21 угол COD равен 45°. Чему равны углы АОВ и АОС?

Решение. Углы COD и АОВ вертикальные, следовательно, по теореме 1.2 они равны, т. е. ∠ АОВ = 45°. Угол АОС смежный с углом COD, значит, по теореме 1.
∠ АОС = 180° — ∠ COD = 180° — 45° = 135°.

Пример 3. Найти смежные углы, если один из них в 3 раза больше другого.

Решение. Обозначим градусную меру меньшего угла через х. Тогда градусная мера большего угла будет Зх. Так как сумма смежных углов равна 180° (теорема 1), то х + Зх = 180°, откуда х = 45°.
Значит, смежные углы равны 45° и 135°.

Пример 4. Сумма двух вертикальных углов равна 100°. Найти величину каждого из четырех углов.

Решение. Пусть условию задачи отвечает рисунок 2. Вертикальные углы COD к АОВ равны (теорема 2), значит, равны и их градусные меры. Поэтому ∠ COD = ∠ АОВ = 50° (их сумма по условию 100°). Угол BOD (также и угол АОС) смежный с углом COD, и, значит, по теореме 1
∠ BOD = ∠ АОС = 180° — 50° = 130°.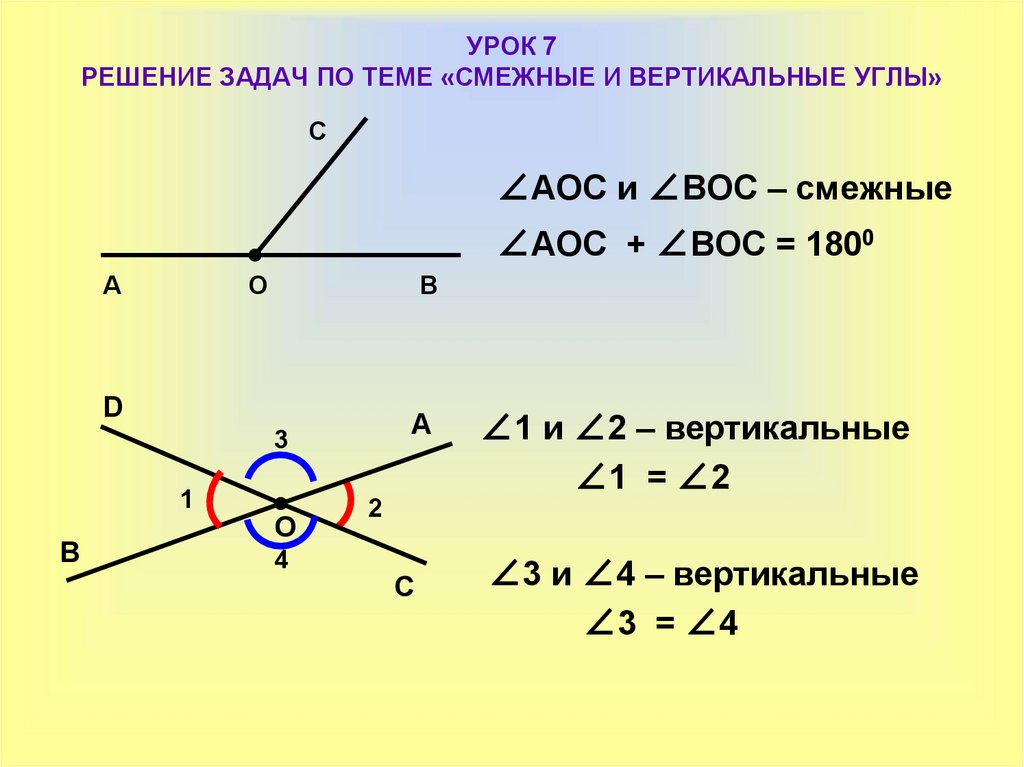

Смежные углы – два угла, у которых одна сторона общая, а две другие являются продолжениями одна другой.

Сумма смежных углов равна 180°

Вертикальные углы — это два угла, у которых стороны одного угла являются продолжение сторон другого.

Вертикальные углы равны.

2. Признаки равенства треугольников:

I признак : Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны.

II признак : Если стороны и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны.

III признак : Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то такие треугольники равны

3. Признаки параллельности двух прямых: односторонние углы, накрест лежащие и соответственные:

Две прямые на плоскости называются параллельными , если они не пересекаются.

Накрест лежащие углы: 3 и 5, 4 и 6;

Односторонние углы: 4 и 5, 3 и 6; рис. Стр55

Соответственные углы: 1 и 5, 4 и 8, 2 и 6, 3 и 7;

Теорема : Если при пересечении двух прямых секущей накрест лежащие углы равны, то прямые параллельны.

Теорема : Если при пересечении двух прямых секущей соответственные углы равны, то прямые параллельны.

Теорема : Если при пересечении двух прямых секущей сумма односторонних углов равна 180°, то прямые параллельны.

Теорема : если две параллельные прямые пересечены секущей, то накрест лежащие углы равны

Теорема : если две параллельные прямые пересечены секущей, то соответственные углы равны

Теорема : если две параллельные прямые пересечены секущей, то сумма односторонних углов равна 180°

4. Сумма углов треугольника:

Сумма углов треугольника равна 180°

5. Свойства равнобедренного треугольника:

Теорема: В равнобедренном треугольнике углы при основании равны.

Теорема: В равнобедренном треугольнике биссектриса, проведенная к основанию, являетсямедианой и высотой (медиана наоборот), (биссектриса делит угол пополам, медиана делит сторону пополам, высота образует угол 90°)

Признак: Если два угла треугольника равны, то треугольник равнобедренный.

6. Прямоугольный треугольник:

Прямоугольный треугольник — это треугольник, в котором один угол прямой (то есть составляет 90 градусов)

В прямоугольном треугольнике гипотенуза больше катета

1. Сумма двух острых углов прямоугольного треугольника равна 90°

2. Катет прямоугольного треугольника, лежащий против угла в 30°, равен половине гипотенузы

3. Если катет прямоугольного треугольника равен половине гипотенузы, то угол, лежащий против этого катета, равен 30°

7. Равносторонний треугольник:

РАВНОСТОРОННИЙ ТРЕУГОЛЬНИК, плоская фигура, имеющая три стороны равной длины; три внутренних угла, образуемых сторонами, также равны и составляют 60 °С.

Сумма углов четырёхугольника равна 2 π = 360°.

Четырёхугольник можно вписать в окружность тогда и только тогда, сумма противоположных углов равна 180°

10. Признаки подобия треугольников:

I признак : если два угла одного треугольника соответственно равны двум углам другого, то такие треугольники подобны

II признак : если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы, заключенные между этими сторонами, равны, то такие треугольники подобны.

III признак : если три стороны одного треугольника порциональны трем сторонам другого, то такие треугольники подобны

11. Формулы:

· Теорема Пифагора: a 2 +b 2 =c 2

· Теорема sin:

· Теорема cos:

· 3 формулы площади треугольника:

· Площадь прямоугольного треугольника: S= S=

· Площадь равностороннего треугольника:

· Площадь параллелограмма: S = ah

· Площадь квадрата: S = a2

· Площадь трапеции:

· Площадь ромба:

· Площадь прямоугольника: S=ab

· Равносторонний треугольник.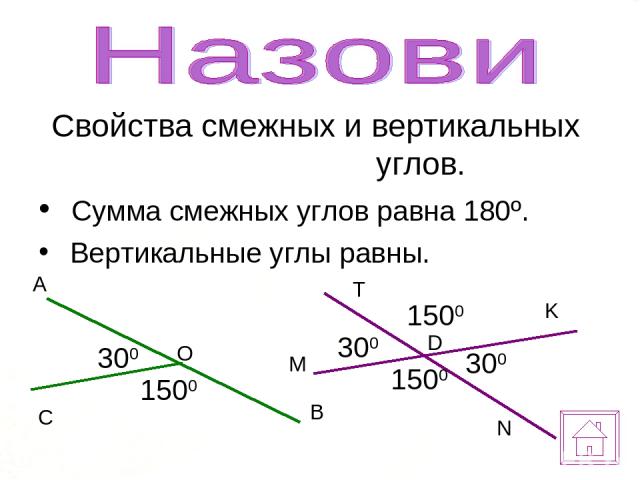 Высота: h=

· Тригонометрическая единица: sin 2 a+cos 2 a=1

· Средняя линия треугольника: S=

· Средняя линия трапеции : МК=

©2015-2019 сайт
Все права принадлежать их авторам. Данный сайт не претендует на авторства, а предоставляет бесплатное использование.
Дата создания страницы: 2017-12-12

по теме: Смежные и вертикальные углы, их свойства.

(3 занятия)

В результате изучения темы нужно:

УМЕТЬ:

Понятия: смежных и вертикальных углов, перпендикулярных прямых

Различать понятия смежные и вертикальные углы

Теоремы смежных и вертикальных углов

Решать задачи с использованием свойств смежных и вертикальных углов

Свойства смежных и вертикальных углов

Строить смежные и вертикальные углы, перпендикулярные прямые

ЛИТЕРАТУРА:

1. Геометрия. 7 класс. Ж. Кайдасов, Г. Досмагамбетова, В. Абдиев.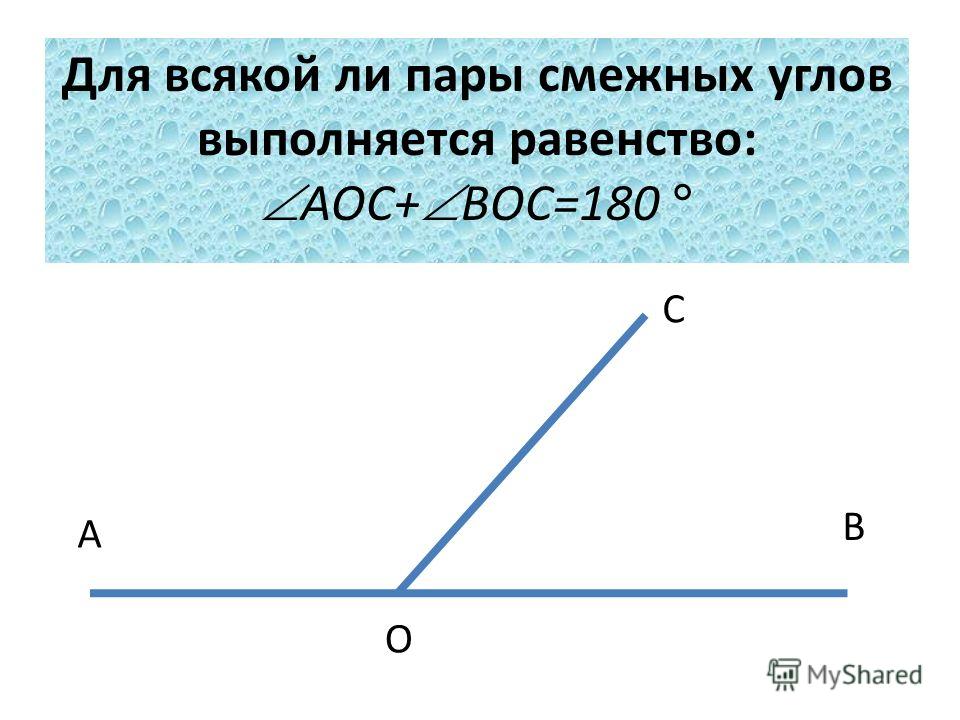 Алматы «Мектеп». 2012

2. Геометрия. 7 класс. К.О.Букубаева, А.Т. Миразова. Алматы « Атамұра ». 2012

3. Геометрия. 7 класс. Методическое руководство. К.О.Букубаева. Алматы « Атамұра ». 2012

4. Геометрия. 7 класс. Дидактический материал. А.Н.Шыныбеков. Алматы « Атамұра ». 2012

5. Геометрия. 7 класс. Сборник задач и упражнений. К.О.Букубаева, А.Т.Миразова. Алматы « Атамұра ». 2012

Помни, что работать нужно по алгоритму!

Не забывай проходить проверку, делать пометки на полях,

Пожалуйста, не оставляй без ответа, возникшие у тебя вопросы.

Будь объективен во время взаимопроверки, это поможет и тебе, и тому,

кого ты проверяешь.

ЖЕЛАЮ УСПЕХА!

ЗАДАНИЕ №1.

Прочитай определение и выучи (2б):

Определение. Углы, у которых одна сторона общая, а две другие стороны являются дополнительными лучами, называются смежными.

2) Выучи и запиши в тетрадь теорему: (2б)

Сумма смежных углов равна 180.

Дано:

∠ АОД и ∠ ДОВ –данные смежные углы

ОД — общая сторона

Доказать:

∠ АОД + ∠ ДОВ = 180

Доказательство:

На основе аксиомы III 4:

∠ АОД + ∠ ДОВ = ∠ АОВ.

∠ АОВ — развернутый. Следовательно,

∠ АОД + ∠ ДОВ = 180

Теорема доказана.

3) Из теоремы следует: (2б)

1) Если два угла равны, то смежные с ними углы равны;

2) если смежные углы равны, то градусная мера каждого из них равна 90°.

Запомни!

Угол, равный 90°, называется прямым углом.

Угол, меньше 90°, называется острым углом.

Угол, больше 90° и меньше 180°, называется тупым углом.

Прямой угол Острый угол Тупой угол

Так как сумма смежных углов равна 180°, то

1) угол, смежный с прямым углом, прямой;

2) угол, смежный с острым углом, тупой;

3) угол, смежный с тупым углом, острый.

4) Рассмотри образец решения з адачи:

а) Дано: ∠ h k и ∠ kl — смежные; ∠ h k больше ∠ kl на 50° .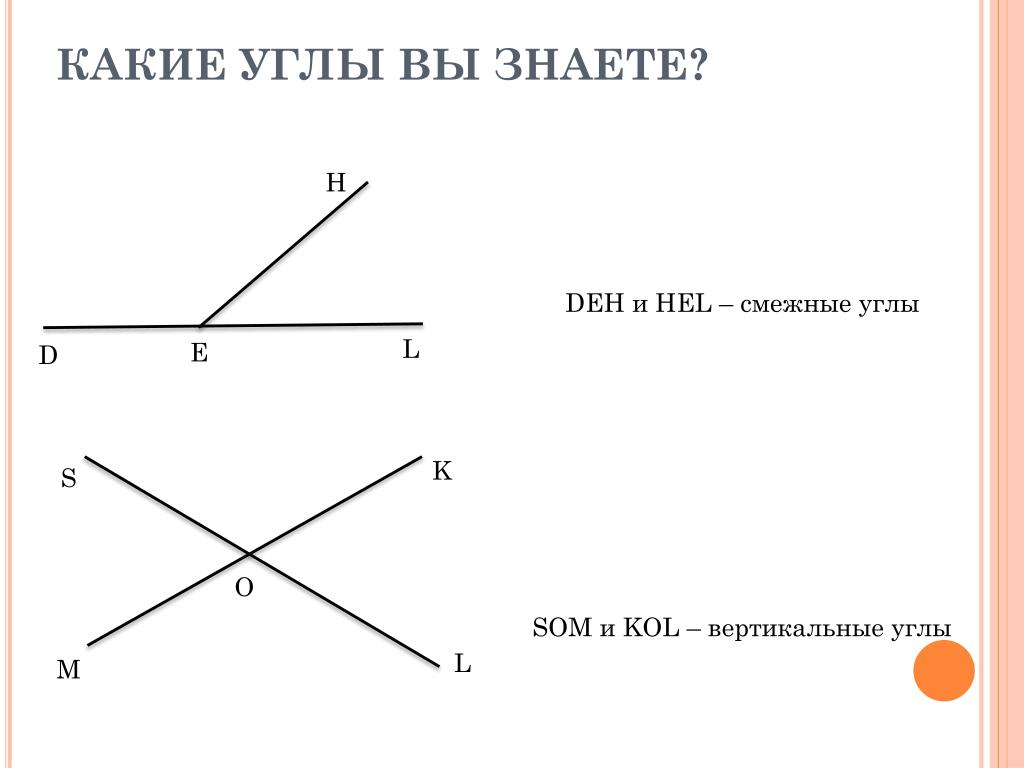

Найти: ∠ h k и ∠ kl .

Решение: Пусть ∠ kl = х, тогда ∠ h k = х + 50°. По свойству о сумме смежных углов ∠ kl + ∠ h k = 180°.

х + х + 50° = 180°;

2х = 180° — 50°;

2х = 130°;

х = 65°.

∠ kl = 65°; ∠ h k = 65°+ 50° = 115°.

Ответ: 115° и 65°.

б) Пусть ∠ kl = х, тогда ∠ h k = 3х

х + 3х = 180°; 4х = 180°; х = 45°; ∠ kl = 45°; ∠ hk = 135°.

Ответ: 135° и 45°.

5) Работа с определением смежных углов: (2 б)

6) Найди ошибки в определениях: (2б)

Пройди проверку №1

Задание №2

1)Построй 2 смежных угла так, чтобы их общая сторона проходила через точку C и сторона одного из углов совпадала с лучом AB.(2б)

2). Практическая работа на открытие свойства смежных углов: (5б)

Ход работы

1. Построй угол смежный углу а , если а : острый, прямой, тупой.

2. Измерь величины углов.

3. Данные измерений занеси в таблицу.

4. Найди соотношение между величинами углов а и .

5. Сделай вывод о свойстве смежных углов.

Пройди проверку №2

Задание №3

Начертите неразвернутый ∠ АОВ и назовите лучи, являющиеся сторонами этого угла.

Проведите луч О, являющийся продолжение луча ОА, и луч ОД, являющийся продолжение луча ОВ.

Запишите в тетради: углы ∠ АОВ и ∠ СОД называются вертикальными. (3б)

Выучи и запиши в тетрадь: (4б)

Определение: Углы, у которых стороны одного из них являются дополнительными лучами другого, называются вертикальными углами.

1 и

Лучи OF и OA , OC и OE являются попарно дополнительными лучами.

Теорема: Вертикальные углы равны.

Доказательство.

Вертикальные углы образуются при пересечении двух прямых. Пусть прямые а и b пересекаются в точке О. ∠ 1 и ∠ 2 –вертикальные углы.

∠ АОС-развернутый, значит ∠ АОС= 180°. Однако ∠ 1+ ∠ 2= ∠ АОС, т.е.

∠ 3+ ∠ 1= 180°, отсюда имеем:

∠ 1= 180 — ∠ 3. (1)

Также имеем, что ∠ ДОВ= 180°, отсюда ∠ 2+ ∠ 3= 180°, или ∠ 2= 180°- ∠ 3. (2)

Так как в равенствах (1) и (2) прямые части равны, то ∠ 1= ∠ 2.

Теорема доказана.

5). Работа с определением вертикальных углов:(2б)

6) Найди ошибку в определении:(2б).

Пройди проверку №3

Задание №4

1)Практическая работа на открытие свойства вертикальных углов:(5б)

Ход работы:

1.Построй угол β вертикальный углу α , если α :

острый, прямой, тупой.

2.Измерь величины углов.

3.Данные измерений занеси в таблицу

4.Найди соотношение между величинами углов α и β.

5.Сделай вывод о свойстве вертикальных углов.

2)Доказательство свойств смежных и вертикальных углов. (3б)

2) Рассмотри образец решения з адачи.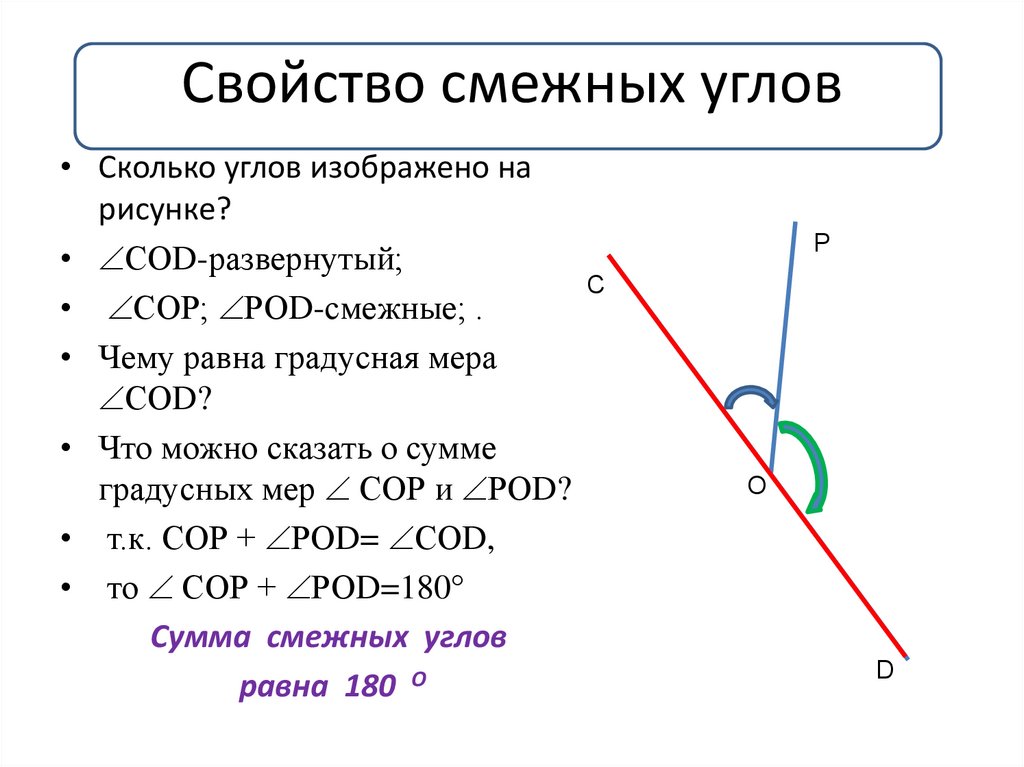

Задача. Прямые АВ и СД пересекаются в точке О так, что ∠ AOД = 35°. Найдите углы АОС и ВОС.

Решение:

1) Углы АОД и АОС смежные, поэтому ∠ BOC = 180° — 35° = 145°.

2) Углы АОС и ВОС также смежные, поэтому ∠ BOC = 180° — 145° = 35°.

Значит, ∠ BOC = ∠ АОД = 35°, причем эти углы являются вертикальными. Вопрос: верно ли утверждение, что любые вертикальные углы равны?

3) Решение задач на готовых чертежах: (3б)

1. Найти углы АОВ, АОD, COD.

3) Найти углы BOC, FOA.: (3б)

3. Найди на рисунке смежные и вертикальные углы. Пусть известны величины двух углов, отмеченных на чертеже, 28? и 90?. Можно ли найти величины остальных углов, не выполняя измерений (2б)

Пройди проверку №4

Задание №5

Проверь свои знания, выполнив проверочную работу №1

Задание №6

1) Самостоятельно докажи свойства вертикальных углов и запиши эти доказательства в тетрадь. (3б)

Учащиеся самостоятельно, используя свойства вертикальных и смежных углов, должны обосновать тот факт, что если при пересечении двух прямых один из образовавшихся углов прямой, то остальные углы также прямые.

2) Реши на выбор две задачи:

1.Градусные меры смежных углов относятся как 7:2. Найдите эти углы.(2б)

2.Один из углов, образовавшихся при пересечении двух прямых, в 11 раз меньше другого.Найдите каждый из углов.(3б)

3.Найдите смежные углы,если их разность и их сумма относятся как 2:9.(3б)

Задание №7

Молодец! Можешь приступать к проверочной работе №2.

Проверочная работа №1.

Реши на выбор любой из вариантов (10б)

Вариант 1

г)

Смежные

д) Начертите (на глаз) угол в 30° и

е) Какие углы называются вертикальными?

Два угла называются вертикальными, если орни равны.

ж) Из точки А провести две прямые, перпендикулярные прямой а

Можно провести только одну прямую.

Вариант 2

1.Ученик, отвечая на вопросы учителя, дал соответствующие ответы. Проверьте, верны ли они, пометив в третьем столбике словом «ДА», «НЕТ», «НЕ ЗНАЮ». В случает «НЕТ» запишите там же верный ответ или добавьте недостающее.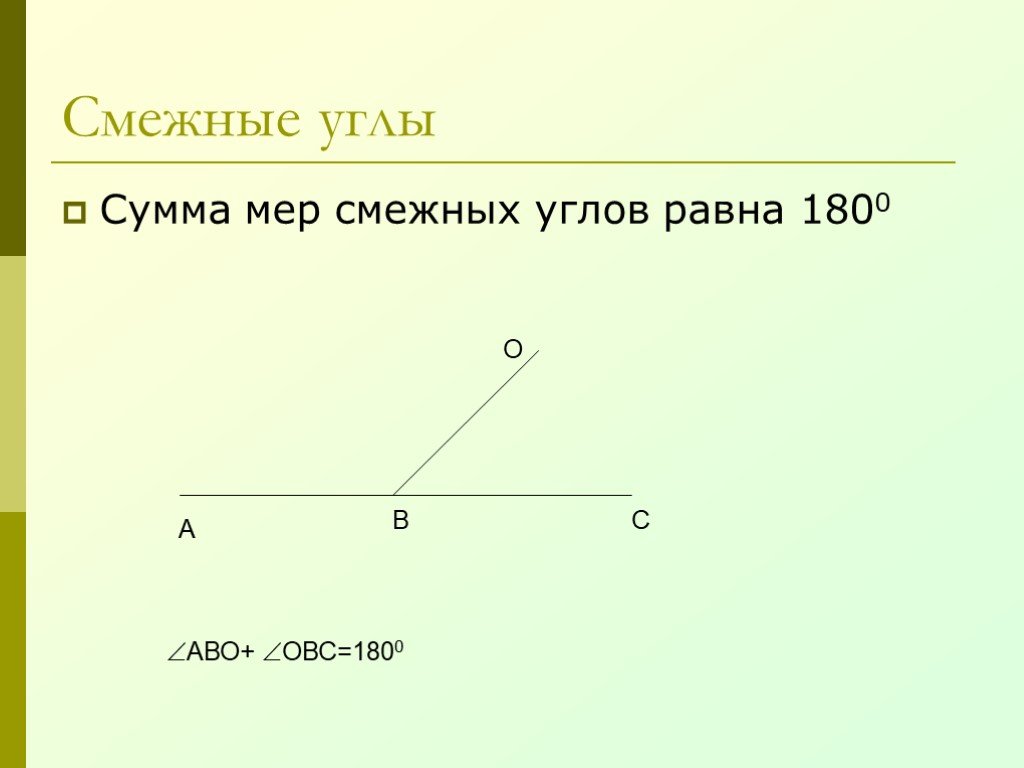

Д)

Нет. Они вертикальные

Е) Какие прямые называются перпендикулярными?

Две прямые называются перпендикулярными, если они пересекаются под прямым углом

Ж) Начертите вертикальные углы так, чтобы их стороны были перпендикулярными прямыми.

2. Назовите вертикальные углы на данном рисунке.

Итого:10 баллов

«5»-10баллов;

«4»-8-9 баллов;

«3»-5-7 баллов.

Проверочная работа №2.

Реши на выбор любой вариант

Вариант I

Найдите смежные углы, если их разность и их сумма относятся как 2:9. (4б)

Найдите все неразвернутые углы, образованные при пересечении двух прямых, если один из них на 240°, меньше суммы двух других.(6б)

Вариант II

1) Найдите смежные углы, если их разность и их сумма относятся как 5:8(4б)

2) Найдите все неразвернутые углы, образованные при пересечении двух прямых, если один из них на 60°, больше суммы двух других. (6б)

Итого:10 баллов

«5»-10баллов;

«4»-8-9 баллов;

«3»-5-7 баллов.

Что значит смежные углы находятся в отношении. Смежные углы

Что значит смежные углы находятся в отношении. Смежные углы

В процессе изучения курса геометрии понятия “угол”, “вертикальные углы”, “смежные углы” встречаются достаточно часто. Понимание каждого из терминов поможет разобраться в поставленной задаче и правильно ее решить. Что такое смежные углы и как их определять?

Смежные углы – определение понятия

Термин “смежные углы” характеризует два угла, образованных общим лучом и двумя дополнительными полупрямыми, лежащими на одной прямой. Все три луча выходят из одной точки. Общая полупрямая является одновременно стороной как одного, так и второго угла.

Смежные углы – основные свойства

1. Исходя из формулировки смежных углов, нетрудно заметить, что сумма таких углов всегда образует развернутый угол, градусная мера которого равна 180°:

• Если μ и η являются смежными углами, то μ + η = 180°.
• Зная величину одного из смежных углов (например, μ), можно легко вычислить градусную меру второго угла (η), используя выражение η = 180° – μ.

2. Данное свойство углов позволяет сделать следующий вывод: угол, являющийся смежным прямому углу, также будет прямым.

3. Рассматривая тригонометрический функции (sin, cos, tg, ctg), основываясь на формулах приведения для смежных углов μ и η справедливо следующее:

• sinη = sin(180° – μ) = sinμ,
• cosη = cos(180° – μ) = -cosμ,
• tgη = tg(180° – μ) = -tgμ,
• ctgη = ctg(180° – μ) = -ctgμ.

Смежные углы – примеры

Пример 1

Задан треугольник с вершинами M, P, Q – ΔMPQ. Найти углы, смежные углам ∠QMP, ∠MPQ, ∠PQM.

• Продлим каждую из сторон треугольника прямой.
• Зная о том, что смежные углы дополняют друг друга до развернутого угла, выясняем, что:

смежным для угла ∠QMP будет ∠LMP,

смежным для угла ∠MPQ будет ∠SPQ,

смежным для угла ∠PQM будет ∠HQP.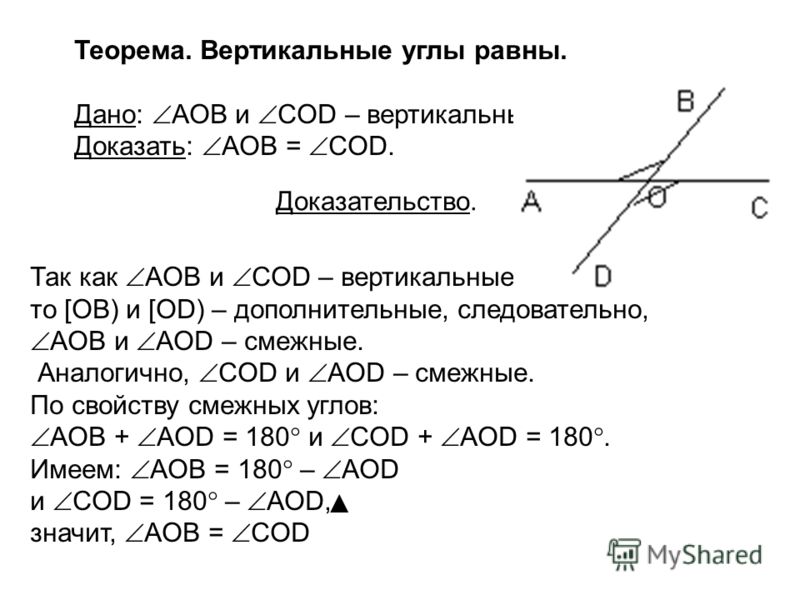

Пример 2

Величина одного смежного угла составляет 35°. Чему равна градусная мера второго смежного угла?

• Два смежных угла в сумме образуют 180°.
• Если ∠μ = 35°, то смежный ему ∠η = 180° – 35° = 145°.

Пример 3

Определить величины смежных углов, если известно, что градусная мера одного из низ втрое больше градусной меры другого угла.

• Обозначим величину одного (меньшего) угла через – ∠μ = λ.
• Тогда, согласно условию задачи, величина второго угла будет равна ∠η = 3λ.
• Исходя из основного свойства смежных углов, μ + η = 180° следует

λ + 3λ = μ + η = 180°,

λ = 180°/4 = 45°.

Значит первый один угол ∠μ = λ = 45°, а второй угол ∠η = 3λ = 135°.

Умение апеллировать терминологией, а также знание основных свойств смежных углов поможет справиться с решением многих геометрических задач.

угол до развернутого, то есть равного 180°, поэтому для их нахождения вычтите из этого известную величину основного угла α₁ = α₂ = 180°-α.

Из этого имеются . Если два угла одновременно являются и смежными, и равными, то они прямые. Если один из смежных углов является прямым, то есть составляет 90 градусов, то другой угол тоже прямой. Если один из смежных углов острый, то другой будет тупым. Аналогично, если один из углов тупой, то второй, соответственно, будет острым.

Острый угол – это такой, градусная мера которого меньше 90 градусов, но больше 0. Тупой угол имеет градусную меру больше 90 градусов, но меньше 180.

Другое свойство смежных углов формулируется так: если два угла равны, то углы, смежные с ними, также равны. Это , что если есть два угла, градусная мера для которых совпадает (например, она составляет 50 градусов) и при этом из них имеет смежный угол, то значения этих смежных углов тоже совпадают (в примере их градусная мера будет равна 130 градусам).

Источники:

• Большой Энциклопедический Словарь — Смежные углы
• угол 180 градусов

Слово « » имеет различные толкования. В геометрии угол – это часть плоскости, ограниченная двумя лучами, выходящими из одной точки – вершины. Когда речь идет о прямых, острых, развернутых углах, то подразумеваются именно геометрические углы.

Как и любые фигуры в геометрии, углы можно сравнивать. Равенство углов определяется с помощью движения. Угол нетрудно разделить на две равные части. Разделить на три части немного сложнее, но все же это можно сделать с помощью линейки и циркуля. Кстати, эта задача казалась довольно трудной. Описать, что один угол больше или меньше другого, геометрически несложно.

В качестве единицы измерения углов принят – 1/180

Углы, у которых одна сторона общая, а другие стороны лежат на одной прямой (на рис. углы 1 и 2 смежные). Рис. к ст. Смежные углы … Большая советская энциклопедия

СМЕЖНЫЕ УГЛЫ — углы, имеющие общую вершину и одну общую сторону, а две др. их стороны лежат на одной прямой … Большая политехническая энциклопедия

См. Угол … Большой Энциклопедический словарь

СМЕЖНЫЕ УГЛЫ, два угла, сумма которых равна 180°. Каждый из этих углов дополняет другой до развернутого угла … Научно-технический энциклопедический словарь

См. Угол. * * * СМЕЖНЫЕ УГЛЫ СМЕЖНЫЕ УГЛЫ, см. Угол (см. УГОЛ) … Энциклопедический словарь

— (Angles adjacents) такие, которые имеют общую вершину и общую сторону. Преимущественно под этим именем подразумеваются такие С. углы, которых остальные две стороны лежат по противоположным направлениям одной прямой, проведенной через вершину … Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона

См. Угол … Естествознание. Энциклопедический словарь

Две прямые пересекаются, создавая пару вертикальных углов. Одна пара состоит из углов A и B, другая из C и D. В геометрии, два угла называются вертикальными, если они созданы пересечением двух … Википедия

Пара комплементарных углов, дополняющих друг друга до 90 градусов Комплементарные углы это пара углов, которые дополняют друг друга до 90 градусов. Если два комплементарных угла являются соседними (т.е. имеют общую вершину и разделяются только… … Википедия

Пара дополнительных углов, дополняющих друг друга до 90 градусов Дополнительные углы это пара углов, которые дополняют друг друга до 90 градусов. Если два дополнительных угла являются с … Википедия

Книги

• О доказательстве в геометрии , Фетисов А.И.. Эта книга будет изготовлена в соответствии с Вашим заказом по технологии Print-on-Demand. Однажды, в самом начале учебного года, мне пришлось услышать разговор двух девочек. Старшая из них…
• Комплексная тетрадь для контроля знаний. Геометрия. 7 класс. ФГОС , Бабенко Светлана Павловна, Маркова Ирина Сергеевна. В пособии представлены контрольно-измерительные материалы (КИМы) по геометрии для проведения текущего, тематического и итогового контроля качества знаний учащихся 7 класса. Содержание пособия…

Как найти смежный угол?

Математика — древнейшая точная наука, которую в обязательном порядке изучают в школах, колледжах, институтах и университетах. Однако, базовые знания всегда закладываются еще в школе. Порой, ребенку задают достаточно сложные задания, а родители не в силах помочь, потому что просто забыли некоторые вещи из математики. Например, как найти смежный угол по величине основного угла и т. п. Задача проста, но может вызвать затруднения при решении из-за незнания того, какие углы называются смежными и как их найти.

Рассмотрим подробнее определение и свойства смежных углов, а также как их вычислить по данным в задаче.

Определение и свойства смежных углов

Два луча, исходящие из одной точки образуют фигуру под названием «плоский угол». При этом эта точка именуется вершиной угла, а лучи являются его сторонами. Если продолжить один из лучей дальше начальной точки по прямой, то образуется еще один угол, который и называется смежным. У каждого угла в этом случае есть два смежных угла, так как стороны угла равнозначны. То есть всегда присутствует еще смежный угол в 180 градусов.

К основным свойствам смежных углов относят

• Смежные углы имеют общую вершину и одну сторону;
• Сумма смежных углов равна всегда 180 градусам или числу Пи, если вычисление ведется в радианах;
• Синусы смежных углов всегда равны;
• Косинусы и тангенсы смежных углов равны, но имеют противоположные знаки.

Как найти смежные углы

Обычно даются три вариации задач на нахождение величины смежных углов

• Дана величина основного угла;
• Дано соотношение основного и смежного угла;
• Дана величина вертикального угла.

Каждый вариант задачи имеет свое решение. Рассмотрим их.

Дана величина основного угла

Если в задаче указана величина основного угла, то найти смежный угол очень просто. Для этого достаточно из 180 градусов вычесть величину основного угла, и вы получите величину смежного угла. Данное решение исходит из свойства смежного угла — сумма смежных углов равна всегда 180 градусам.

Если же величина основного угла дана в радианах и в задаче требуется найти смежный угол в радианах, то необходимо вычесть из числа Пи величину основного угла, так как величина полного развернутого угла в 180 градусов равна числу Пи.

Дано соотношение основного и смежного угла

В задаче может быть дано соотношение основного и смежного угла вместо градусов и радиан величины основного угла. В этом случае решение будет выглядеть, как уравнение пропорции:

1. Обозначаем долю пропорции основного угла, как переменную «Y».
2. Долю относящуюся к смежному углу обозначаем, как переменную «Х».
3. Количество градусов, которые приходятся на каждую пропорцию, обозначим, например, «a».
4. Общая формула будет выглядеть так — a*X+a*Y=180 или a*(X+Y)=180.
5. Находим общий множитель уравнения «a» по формуле a=180/(X+Y).
6. Затем полученное значение общего множителя «а» умножаем на долю угла, который необходимо определить.

Таким образом мы можем найти величину смежного угла в градусах. Однако, если необходимо найти величину в радианах, то нужно просто перевести градусы в радианы. Для этого умножаем угол в градусах на число Пи и делим все на 180 градусов. Полученное значение будет в радианах.

Дана величина вертикального угла

Если в задаче не дана величина основного угла, но дана величина вертикального угла, то вычислить смежный угол можно по такой же формуле, что и в первом пункте, где дана величина основного угла.

Вертикальный угол — это угол, который исходит из той же точки, что и основной, но при этом он направлен в строго противоположном направлении. Тем самым получается зеркальное отражение. Это значит, что вертикальный угол по величине равен основному. В свою очередь, смежный угол вертикального угла равен смежному углу основного угла. Благодаря этому можно вычислить смежный угол основного угла. Для этого просто вычитаем из 180 градусов величину вертикального и получаем значение смежного угла основного угла в градусах.

Если же величина дана в радианах, то необходимо вычесть из числа Пи величину вертикального угла, так как величина полного развернутого угла в 180 градусов равна числу Пи.

Также вы можете прочесть наши полезные статьи и .

Геометрия — это весьма многогранная наука. Она развивает логику, воображение и интеллект. Конечно, из-за своей сложности и огромного количества теорем и аксиом, она не всегда нравится школьникам. Кроме этого, существует необходимость постоянно доказывать свои выводы, используя общепринятые стандарты и правила.

Смежные и вертикальные углы — это неотъемлемая составляющая геометрии. Наверняка многие школьники просто обожают их по той причине, что их свойства понятны и просты в доказательстве.

Образование углов

Любой угол образуется путем пересечения двух прямых или проведения двух лучей из одной точки. Они могут называться либо одной буквой, либо тремя, которые последовательно обозначают точки построения угла.

Углы измеряются в градусах и могут (в зависимости от их значения) по-разному называться. Так, существует прямой угол, острый, тупой и развернутый. Каждому из названий соответствует определенная градусная мера или ее промежуток.

Острым называется угол, мера которого не превышает 90 градусов.

Тупым является угол, превышающий 90 градусов.

Угол называется прямым в том случае, когда его градусная мера равна 90.

В том случае, когда он образован одной сплошной прямой, и его градусная мера равна 180, его называют развернутым.

Углы, имеющие общую сторону, вторая сторона которых продолжает друг друга, называются смежными.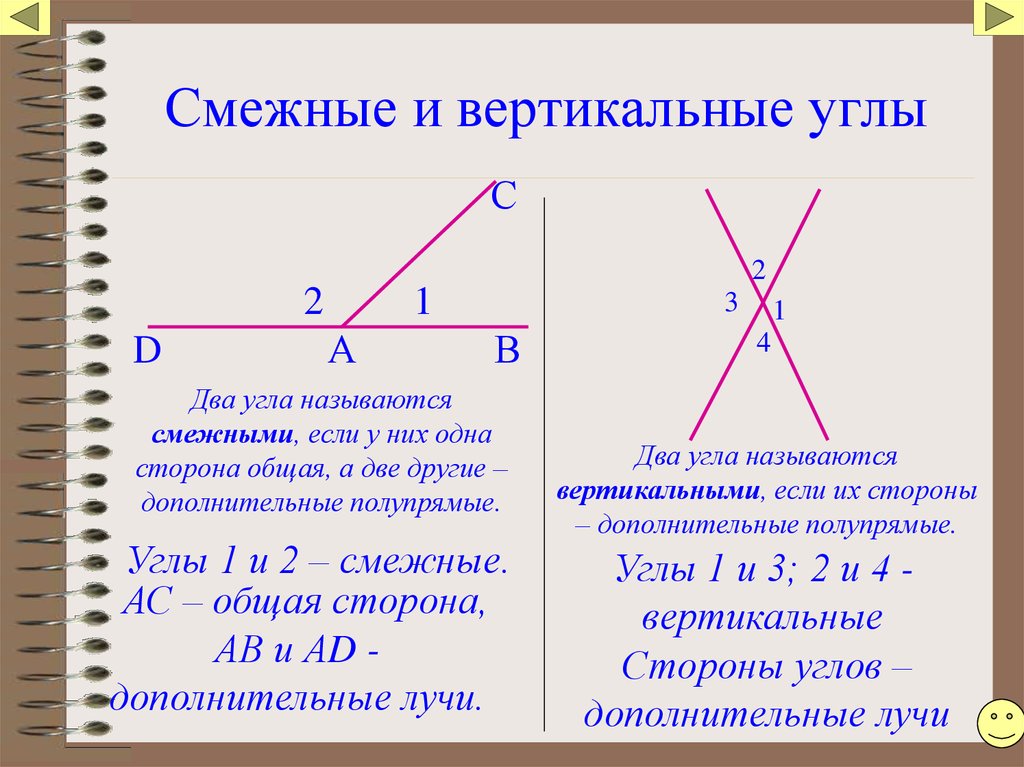 Они могут быть как острыми, так и тупыми. Пересечение линией образует смежные углы. Свойства их следующие:

1. Сумма таких углов будет равна 180 градусам (существует теорема, доказывающая это). Поэтому можно легко вычислить один из них, если известен другой.
2. Из первого пункта следует, что смежные углы не могут быть образованы двумя тупыми или двумя острыми углами.

Благодаря этим свойствам, можно всегда вычислить градусную меру угла, имея значение другого угла или, по крайней мере, отношение между ними.

Вертикальные углы

Углы, стороны которых являются продолжением друг друга, называются вертикальными. В качестве такой пары могут выступать любые их разновидности. Вертикальные углы всегда равны между собой.

Они образуются при пересечении прямых. Совместно с ними всегда присутствуют и смежные углы. Угол может быть одновременно смежным для одного и вертикальным для другого.

При пересечении произвольной линией также рассматривают еще несколько видов углов.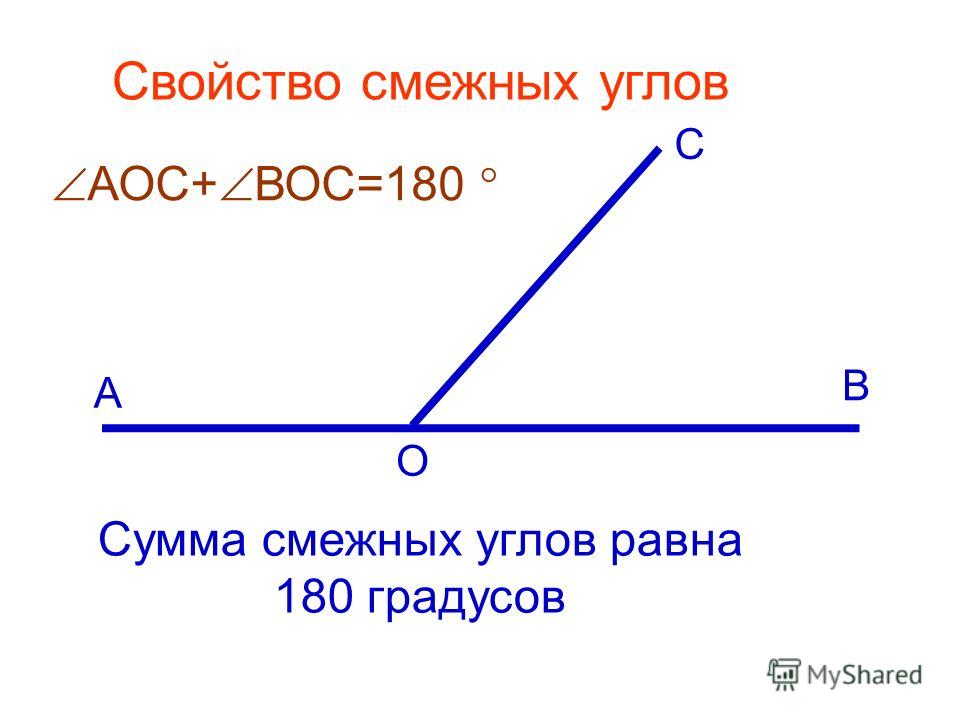 Такая линия называется секущей, она и образует соответственные, односторонние и накрест лежащие углы. Они равны между собой. Их можно рассматривать в свете свойств, которые имеют вертикальные и смежные углы.

Таким образом, тема углов представляется довольно простой и понятной. Все их свойства легко запомнить и доказать. Решение задач не представляется сложным до тех пор, пока углам соответствует числовое значение. Уже дальше, когда начнется изучение sin и cos, придется запоминать множество сложных формул, их выводов и следствий. А до того времени можно просто наслаждаться легкими задачками, в которых необходимо найти смежные углы.

Смежные углы – определение с примерами

Что такое смежные углы

Два угла называются смежными, если они имеют общее плечо и общую вершину. Простыми словами, углы, которые образованы рядом, называются смежными углами. Одной из основных особенностей смежных углов является то, что они не пересекаются. Углы, которые не являются смежными, называются несмежными углами.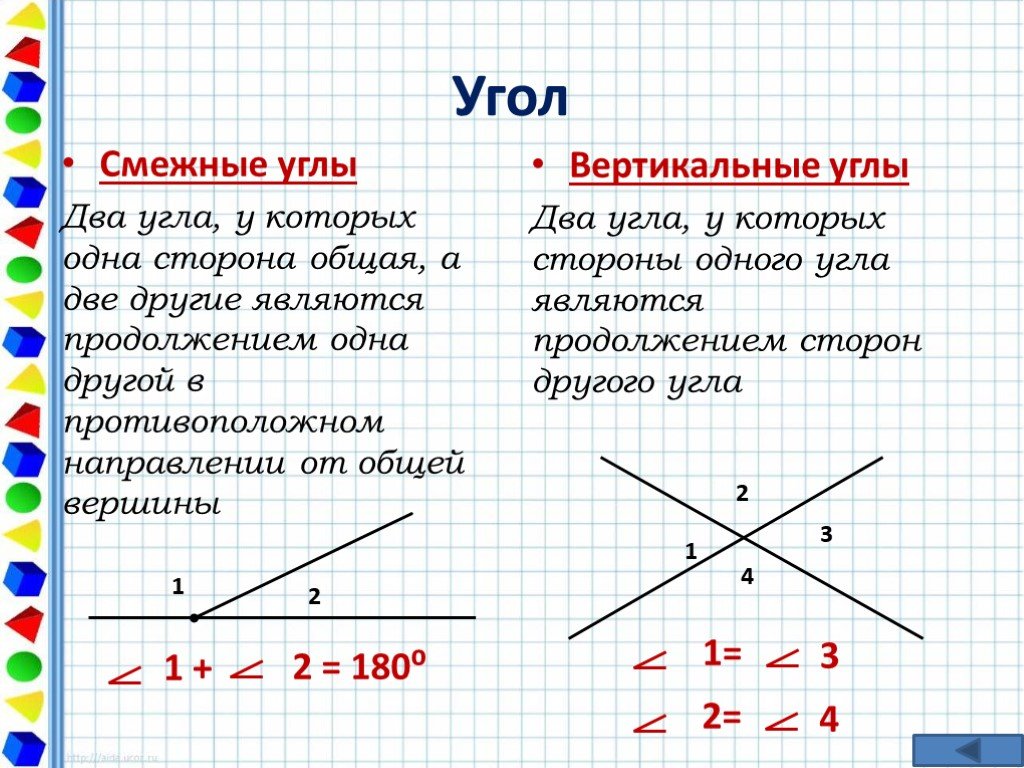

Смежные углы

На рисунке выше показаны два смежных угла, имеющих общую сторону и общую вершину.

Смежные углы являются дополнительными или дополнительными

Смежные углы могут быть как дополнительными, так и дополнительными. Когда два угла в сумме составляют 90°, это называется смежными дополнительными углами, а когда два угла в сумме составляют 180°, это называется смежными дополнительными углами. Два смежных дополнительных угла образуют линейную пару.

Подробнее см. в нашей статье «Дополнительные и дополнительные углы».

Как найти смежные углы

Чтобы определить, являются ли углы смежными или нет, мы должны помнить его основные свойства, которые приведены ниже:

• Они должны иметь общее плечо между собой
• Они должны иметь общую вершину между собой
• Они не должны пересекаться
• Они должны иметь не общее плечо по обеим сторонам общего плеча

Смежные углы Congruent

Смежные углы конгруэнтны только тогда, когда их общая сторона делит их сумму пополам.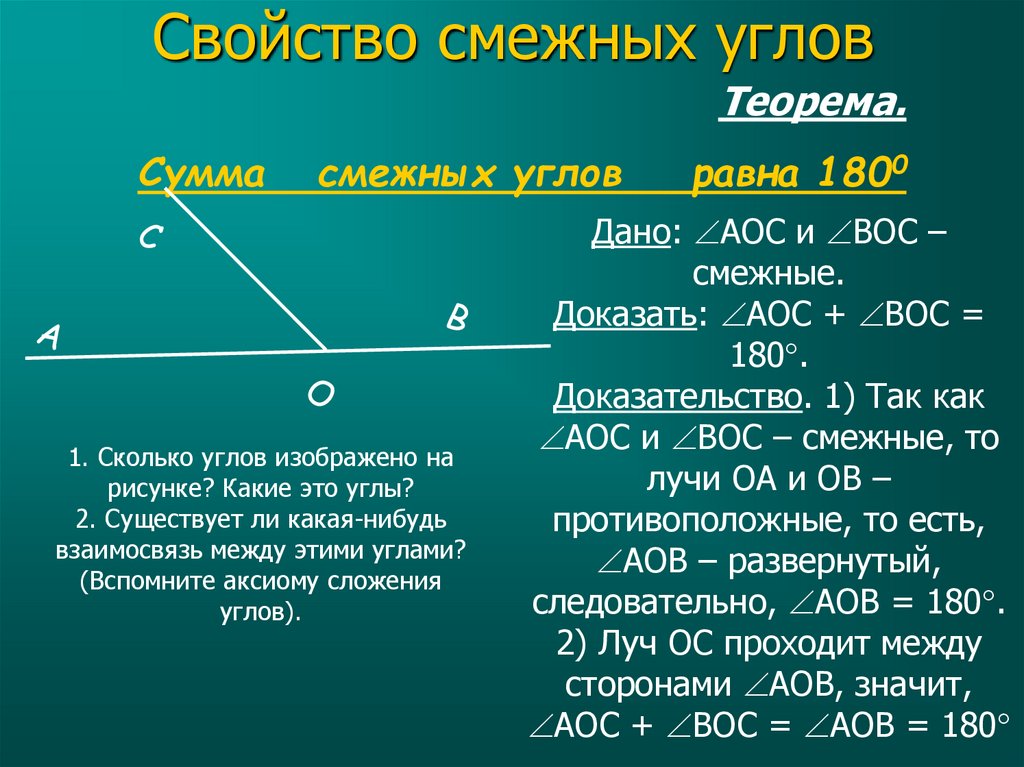 Это происходит, когда:

• Прямой угол делится пополам из двух смежных углов, каждый по 45°
• Прямой угол делится пополам из двух смежных углов, каждый из которых является прямым углом, равным 90°

Найдите смежный угол, отмеченный x. Учитывая, что ∠AOB = 120° и ∠AOC = 80°

Решение:

Учитывая ∠AOB = 120° и ∠AOC = 80°
Так как ∠AOC и ∠COB являются смежными углами
Таким образом, ∠AOC и ∠COB являются смежными углами
∠COB = ∠AOB, здесь ∠COB = x
80° + x = 120°
x = 120° – 80°
x = 40°

Какой из приведенных ниже пар углов является смежным в заданная фигура.

Решение:

∠AOP и ∠POQ, ∠POQ и ∠QOR, ∠QOR и ∠ROB — три смежные пары углов на данном рисунке.

Какие из приведенных ниже пар углов являются смежными? Обоснуйте свой ответ.

Решение:

а) ∠1 и ∠2 — смежные углы, так как они имеют общую сторону и общую вершину
б) ∠1 и ∠2 — несмежные углы, так как не имеют общей стороны
в ) ∠1 и ∠2 — несмежные углы, так как у них нет общей вершины
г) ∠1 и ∠2 — несмежные углы, так как они накладываются друг на друга
д) ∠1 и ∠2 — несмежные углы, так как не имеют общей вершины

Примеры из жизни

• Открытая книга с страница между ними
• Стрелки часов, показывающие 3 часа дня, и секундная стрелка, указывающая на цифру 2
• Углы, образованные в центре колеса тележки
• Нарезанная пицца или торт

Смежные и несмежные углы — Криста Кинг Математика

Что такое смежные углы?

В этом уроке мы рассмотрим, как идентифицировать смежные углы на диаграмме и как формировать названия углов.

Привет! Я Криста.

Я создаю онлайн-курсы, чтобы помочь вам в учебе по математике. Читать далее.

Смежные углы

Смежные углы имеют общую вершину и один общий луч (или сторону).

На этой диаграмме углы ???1??? и ???2??? смежны, так как имеют общую вершину ???G??? и луч ???\vec{GB}???.

Несмежные углы

Несмежные углы могут иметь или не иметь общую вершину, но у них нет общих лучей.

На этой диаграмме углы ???1??? и ???2??? не смежны, даже если они имеют общую вершину ???W???, потому что они не имеют общего луча.

Нахождение смежных и несмежных углов

Пройти курс

Хотите узнать больше о геометрии? У меня есть пошаговый курс для этого.

🙂

Учить больше

Нахождение пар смежных углов с диаграммой и без нее

Пример

Перечислите пары смежных углов на диаграмме.

Смежные углы имеют общую вершину и общий луч.

• ???\угол DWA??? примыкает к ???\угол AWB???; они имеют общую вершину ???W??? и луч ???\vec{WA}???.

• ???\угол DWA??? примыкает к ???\угол DWC???: они имеют общую вершину ???W??? и луч ???\vec{WD}???.

• ???\угол DWC??? примыкает к ???\угол CWB???; они имеют общую вершину ???W??? и луч ???\vec{WC}???.

• ???\угол CWB??? примыкает к ???\угол AWB???; они имеют общую вершину ???W??? и луч ???\vec{WB}???.

Обратите внимание, что по написанию углов можно сказать, какой луч они разделяют. Например,

???\угол CWB??? примыкает к ???\угол AWB???; они имеют общую вершину ???W??? и луч ???\vec{WB}???. Так как ???\угол AWB??? и ???\угол CWB??? оба имеют буквы ???W??? и ???Б??? от луча ???\vec{WB}???.

Давайте посмотрим, как определить возможные смежные углы без диаграммы.

Несмежные углы могут иметь или не иметь общую вершину, но у них нет общих лучей.

Пример

Все пары углов взяты из одной схемы. Классифицируйте каждую пару как смежные или несмежные.

А. ???\угол ABC??? и ???\угол CBD???

B. ???\угол XYZ??? и ???\угол ZYX???

C. ???\угол LMN??? и ???\угол MNP???

D. ???\угол CED??? и ???\угол КЭП???

Помните, что смежные углы имеют одну вершину и имеют один общий луч. Имя угла всегда имеет вершину посередине. Затем вы можете использовать имя угла, чтобы найти лучи, образующие угол.

Давайте посмотрим на каждую пару углов.

А. ???\угол ABC??? и ???\угол CBD???. Оба этих угла имеют общую вершину ???B???. Теперь нам нужно найти один общий луч.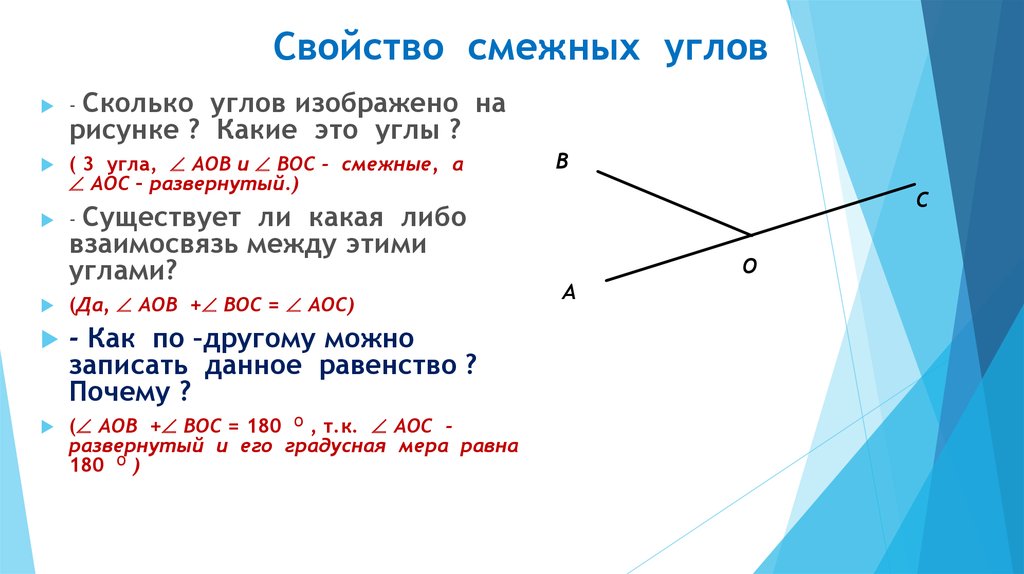 ???\угол АВС??? имеет лучи ???\vec{BA}??? и ???\vec{BC}??? и ???\угол CBD??? имеет лучи ???\vec{BC}??? и ???\vec{BD}???, что означает, что оба угла имеют общий луч ???\vec{BC}???. Следовательно, ???\угол ABC??? и ???\угол CBD??? являются смежными углами.

B. ???\угол XYZ??? и ???\угол ZYX???. Оба этих угла имеют общую вершину ???Y???. Теперь нам нужно найти один общий луч. ???\угол XYZ??? имеет лучи ???\vec{YX}??? и ???\vec{YZ}??? и ???\угол ZYX??? имеет лучи ???\vec{YZ}??? и ???\vec{YX}???, что означает, что оба угла имеют общие лучи ???\vec{YX}??? и ???\vec{YZ}???. Следовательно, ???\угол XYZ??? и ???\угол ZYX??? разные способы назвать один и тот же угол.

C. ???\угол LMN??? и ???\угол MNP???. ???\угол LMN??? имеет вершину ???M??? и ???\угол MNP??? имеет вершину ???N???, значит, эти углы не имеют общей вершины и несмежны.

D. ???\угол CED??? и ???\угол КЭП???. Оба этих угла имеют общую вершину ???E???. Теперь нам нужно найти один общий луч. ???\угол CED??? имеет лучи ???\vec{EC}??? и ???\vec{ED}??? и ???\угол КЭП??? имеет лучи ???\vec{EC}??? и ???\vec{EP}???, что означает, что оба угла имеют общий луч ???\vec{EC}???.